Measuring synchrony in the mammalian central circadian circuit

Abstract

Circadian clocks control daily rhythms in physiology and behavior across all phyla. These rhythms are intrinsic to individual cells that must synchronize to their environment and to each other to anticipate daily events. Recent advances in recording from large numbers of cells for many circadian cycles have enabled researchers to begin to evaluate the mechanisms and consequences of intercellular circadian synchrony. Consequently, methods have been adapted to estimate the period, phase and amplitude of individual circadian cells and calculate synchrony between cells. Stable synchronization requires that the cells share a common period. As a result, synchronized cells maintain constant phase relationships to each (e.g. with cell 1 peaking an hour before cell 2 each cycle). This chapter reviews how circadian rhythms are recorded from single mammalian cells and details methods for measuring their period and phase synchrony. These methods have been useful, for example, in showing that specific neuropeptides are essential to maintain synchrony among circadian cells.

Introduction

What is synchrony?

When a good marching band enters the field, the players step at exactly the same moment. The drummers keep time so that each band member synchronizes their paces to their neighbors’. The musicians perform with the same period. As they march across the field, the line of trumpeters might arrive at midfield first followed by, perhaps, the trombonists. The trombonists share the same period as the trumpeters, but are phase delayed in their time of arrival. In this way, they synchronize their periodicity while assuming unique phase relationships. Period synchrony (also called frequency entrainment) does not require oscillators to peak together. Instead, synchronized oscillators can establish unique, and stable, phase relationships with other oscillators in the population (phase synchrony or phase locking). In nature, noise (internal and external to the oscillators) introduces a small, bounded variation in the phase differences. Many studies of mechanical, electrical, chemical and biological oscillators have focused on mechanisms that can produce period synchrony and conditions that can alter phase synchrony (Kurths, 2003; Strogatz, 2003).

What is circadian synchrony?

Daily changes at both cellular and systemic levels arise from biological oscillators that keep near 24-hour rhythms and entrain to the 24-h cues associated with day and night. These self-sustained circadian rhythms are intrinsic to individual cells. The period of the individual cells depends predominantly on their genetics and light-dark history, and less so on the ambient temperature (i.e. their period is temperature compensated) or other environmental inputs. These cells must synchronize to each other and the environment to coordinate daily rhythms including feeding-fasting, waking-sleeping, hormone levels, metabolism and gene expression. Circadian synchrony describes when cells (or organisms) express the same, near 24-h period (Bloch, Herzog, Levine, & Schwartz, 2013). Much like the synchronized marching of a band of musicians, circadian clocks are often comprised of populations of cells that share the same daily period, but with some cells leading (by up to 12 hours) other cells. Critically, oscillators may share the same period and a constant phase relationship for one of three reasons: 1) they communicate with each other, 2) they both receive the same synchronizing signal from other cells or the environment or 3) coincidence. By measuring circadian synchrony following a perturbation, we can distinguish whether cells are entraining each other, to their environment, or simply express the same near 24-h period by chance.

Synchrony among circadian cells has been described in single celled organisms like cyanobacteria and dinoflagellates and metazoans including plants, fungi, flies and rodents. In a few cases, there is evidence that the synchrony arises primarily due to environmental inputs (e.g. cyanobacteria, dinoflagellates and plants) while cells in other systems appear to have evolved the ability to synchronize to each other (e.g. fungi, flies and rodents).

To illustrate how to measure and use synchrony in a circadian system, this chapter will focus on the mammalian suprachiasmatic nucleus (SCN). The SCN of mice and humans contains approximately 20,000 cells with many of them functioning as individual self-sustained circadian oscillators. SCN cells receive information about local day-night changes indirectly from other cell types. For example, the cells of the SCN normally entrain to input from the retina and other brain areas so that their peak metabolism and electrical activity occur during the day. For the SCN to function as a circadian pacemaker, individual SCN cells must synchronize to each other to coordinately drive rhythms in neural activity and transmitter release. Strikingly, the degree of phase synchrony among SCN cells can change with conditions. During short winter days, for example, SCN cells tend to peak together whereas, they spread out their times of peak activity during the long days of summer.

Goals of this review

This chapter aims to review how to measure synchrony between circadian cells with a focus on analyzing single-cell SCN slice bioluminescence recordings. Briefly, we summarize methods for discriminating circadian rhythms from single cells. We then discuss the strengths and weaknesses of independent methods that quantify period and phase synchrony among a population of oscillating cells. Finally we provide examples of how perturbations affect cell-cell synchrony in the SCN.

Monitoring SCN rhythms with cellular resolution

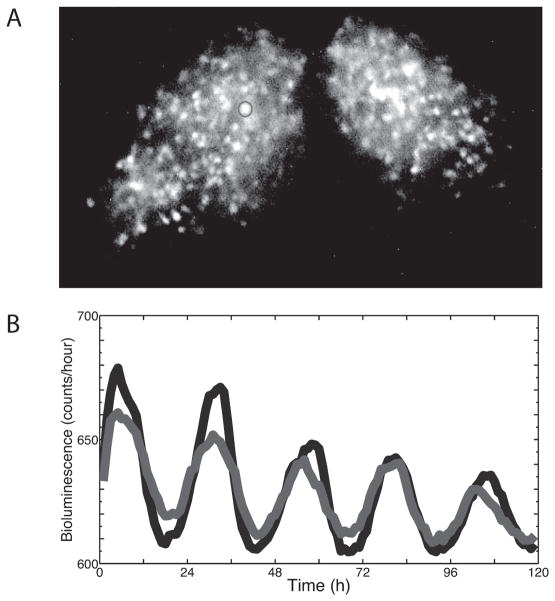
To study synchrony among SCN cells, researchers have used a variety of direct and indirect indicators of circadian physiology. The best methods share the following features: 1) relatively non-invasive monitoring of single-cell physiology, 2) high frequency sampling for more than four days, 3) sensitive enough to detect circadian rhythms above background, 4) a dynamic range that allows recording of daily, biological changes without saturating and 5) can be combined with genetic or pharmacological perturbations. To date, circadian synchrony has been assessed based on daily rhythms in cytosolic calcium, gene expression, firing rate and cAMP activity (Table 1). Figure 1 illustrates a representative, long-term recording of PERIOD2 (PER2) protein levels from SCN neurons using the PER2-luciferase (PER2::LUC) knockin reporter.

Table 1.

Methods that have been used to monitor circadian rhythms with cellular resolution.

Daily rhythms in:	Method	Examples	Sampling period	References
Intracellular calcium	Fluorescent calcium-sensitive reporter	Yellow Cameleon 2.1 or 3.6 or 6.0, or GCaMP3-WPRE	0.5 sec every 60 minutes	(Brancaccio, Maywood, Chesham, Loudon, & Hastings, 2013; Ikeda & Ikeda, 2014; Ikeda et al., 2003; Enoki, Kuroda, et al., 2012; Enoki, Ono, Hasan, Honma, & Honma, 2012; Irwin & Allen, 2013)
Gene expression	Bioluminescent (luciferase) or fluorescent (e.g. destabilized GFP) reporter of transcription or translation	Per1::Luc, Per1:GFP, Per1-Venus, PER2::LUC, Per2-DsRED or Bmal1::Luc	Integrated over 15–60 minutes	(Day & Schaufele, 2008; Hastings, Reddy, McMahon, & Maywood, 2005; Herzog et al., 2004; Welsh et al., 2005; Welsh & Kay, 2005; Welsh & Noguchi, 2012; Yoo et al., 2004; Cheng et al., 2009; Kuhlman, Quintero, & McMahon, 2000; Yamaguchi et al., 2003; Yamazaki et al., 2000)
Firing rate	Multielectrode array	MEA 60 or MED 64	Sampled every 50 μsec to report spikes per second	(Herzog, 2007; Honma et al., 2012)
cAMP activity	Bioluminescent (luciferase) reporter of CREB activity or fluorescent (e.g. destabilized GFP) reporter cAMP levels	CRE::Luc, ELISA kit or ICUE2	Integrated over 60 minutes	(Brancaccio, Maywood, Chesham, Loudon, & Hastings, 2013; An, Irwin, Allen, Tsai, & Herzog, 2011; O’Neill, Maywood, Chesham, Takahashi, & Hastings, 2008)

Figure 1.

Recording circadian rhythms in gene expression from a SCN slice culture. (A) An image of a SCN carrying the PER2::Luc reporter construct with two representative cells encircled with Regions Of Interest (ROI). With single-cell resolution, at least 100 ROIs can be identified from each half of the bilateral SCN. (B) The bioluminescence over time of the two cells from Figure 1A. Note that one cell (blue line) consistently peaked a few hours before the other cell (red line).

Isolating data from single cells

Once data have been collected from a population of cells, we discriminate rhythms expressed by single cells. For example, extracellular spikes originating from individual neurons can be separated from the activities of other neurons based on their shape (e.g. spike height, polarity and duration) and confirmation that they occur at intervals greater than 1 ms (i.e. do not violate the absolute refractory period of neuronal firing). Once separated, these spikes can be counted to produce firing rate (in spikes/second) as a function of recording time.

In imaging experiments (e.g. calcium or gene expression), the experimenter should be able to track light intensity from each cell by defining a region of interest over each cell. We use ImageJ software (Rasband, 1997–2014) to track circadian rhythms from cells in movies of bioluminescence reporters. To date, no one has reported an algorithm that allows for automated tracking of circadian rhythms from single cells that can dim below detection, move and overlap in space. Therefore, we provide step-by-step instructions for setting up and analyzing cellular bioluminescence from SCN slices at the end of this chapter.

Resolving the contributions of single cells allows us to resolve the contributions of each cell to the amplitude and phase of the population rhythm. The approach, however, requires a user’s time and subjective decision about which cells can be tracked over many frames in a movie. Conversely, analyses can be performed on every pixel in the image (Evans, Leise, Castanon-Cervantes, & Davidson, 2011, 2013; Foley et al., 2011; Myung et al., 2012; Pauls et al., 2014). This has the advantage of being relatively quick and automated and possible when the recorded light is too dim to visualize individual cells. It has the disadvantage that it does not track the activity of individual cells so that measures of circadian similarity (e.g. phase or period synchrony) reflect regions that contain unknown numbers of cells.

Defining a rhythm

Once we have a physiological measure from a cell over multiple days, we can assess its rhythmicity. Rhythmicity cannot be determined with methods that evaluate simply whether the data vary over time (e.g. One-way ANOVA). Instead, rhythmic data typically fulfill the requirement of being fit with a periodic (e.g. cosine) function for the duration of the recording. For each cell, we estimate its amplitude and period and its phase relative to other cells. Waveform (e.g. a cosine versus a square wave or saw-tooth function) and stability of amplitude (e.g. damping) and period (e.g. cycle-to-cycle phase variation) can dramatically influence the estimates of period, amplitude and phase. We therefore prefer to present the data in formats that allow easy visual inspection for rhythmicity and results from multiple, independent algorithms for estimating rhythmicity.

Plotting rhythmic data for visual inspection

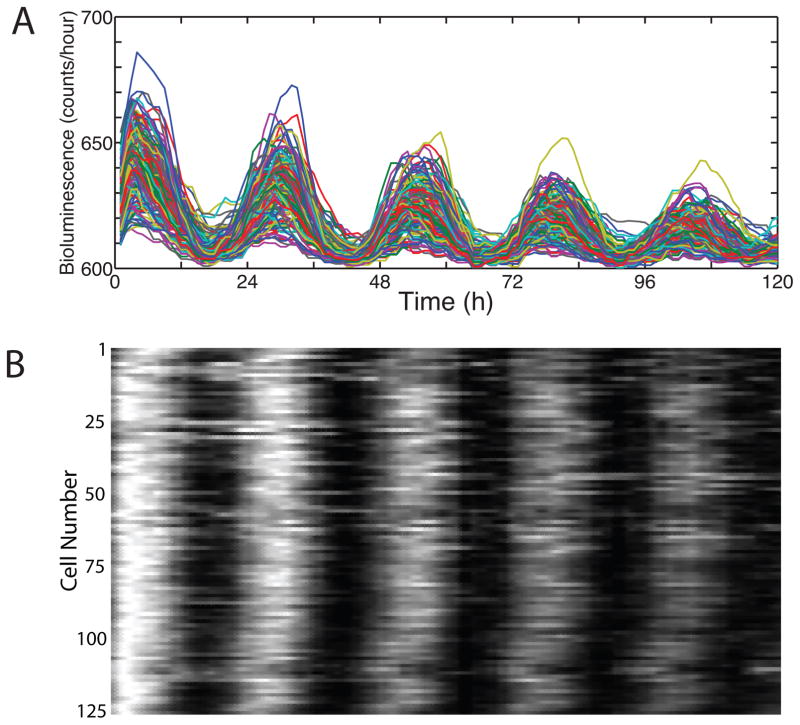
To illustrate how firing rate, gene expression or other physiological measures vary on a daily basis, experimenters will superimpose the traces of many cells using multiple colors (Fig. 2). This format allows us to inspect rapidly the amplitude and phase of the cells within the population without paying too much attention to data from each cell. To easily visualize the phase relationships between cells, we present the data from each cell as a row in a raster plot. Raster plots can be generated in ImageJ by importing the inverted normalized values for each cell as a text image.

Figure 2.

Methods to visual phase and period synchrony in circadian cells. A) Superimposed traces from 125 cells, normalized to intensity values between 0.7 and 0.9. B). A raster plot of the same data. This sort of synchrony can arise from cell-cell communication within the culture, an external drive on the culture, or, although unlikely, coincidence.

We inspect the data for trends and outliers. Some methods of period estimation are particularly sensitive to gradual increases or decreases in the baseline, amplitude or period. Removing trends or outliers that are not of interest can then be applied during the analysis of the data. For example, when recording bioluminescence from dim cells, single cosmic radiation events can cause the apparent gene expression to increase more than 1000-fold for a single time point. We replace such values with the average of the two adjacent time points. Methods for detrending and removing outliers in circadian data have been nicely reviewed elsewhere (Welsh & Kay, 2005; Welsh & Noguchi, 2012; Zielinski, Moore, Troup, Halliday, & Millar, 2014).

Period Synchrony: Methods to extract and compare periods between cells

Once we have inspected the data in the time series and raster plots, we estimate the period of each cell. Most methods assume that the period and amplitude are stationary. If there were perturbations that could cause a phase shift or period change (e.g. addition of a drug) during the recording, we estimate separately the period from the data before and after the perturbation. Then, we seek to confirm any period estimates using independent methods. It is important to realize that each method has its limitations. Any report of biological periodicity approximates period and amplitude and should, ideally, include an estimate of confidence or variability. We use the period and phase estimation from rhythmic cells to characterize the synchrony in the network. Here we briefly review how three independent methods can be implemented (Table 2). Other excellent reviews compare these methods and detail others (Zielinski et al., 2014; Refinetti, Lissen, & Halberg, 2007; Refinetti, 2004; Welsh, Imaizumi, & Kay, 2005; Parati, 2004; Sokolove & Bushell, 1978; Moore, Zielinski, & Millar, 2014; Shono et al., 2000; Levine, Funes, Dowse, & Hall, 2002; Diez-Noguera, 2013; Dowse, 2009).

Table 2.

Comparison of available methods for period and phase estimation. Each method provides an independent assessment of rhythmicity with different algorithms and assumptions. Reporting similar periods and phases obtained with multiple methods gives strength to the assessment of rhythmicity and synchrony.

	Characteristics extracted
	Period	Amplitude	Phase	P value	Notes
Chi-squared Periodogram	Yes	Circadian amp	No	95% CI	Weakened by cycle-to-cycle period or amplitude variations. Typically requires at least 5 days of data for reasonable period estimates.
FFT-NLLS	Yes	Power or Rel-amp	Yes	95% CI	Weakened by cycle-to-cycle period or amplitude variations. Typically requires at least 5 days of data for reasonable period estimates. Can be computationally slow.
Cross-over	Yes	Peak-to-trough	Yes	Not yet implemented	Does not assume period and amplitude stationarity. Provides cycle-to-cycle estimates of period and phase. Fails if noisy data produce excessive daily crossings.
MESA	Yes	Spectral density	No	Signal-to-Noise ratio	Weakened by cycle-to-cycle period or amplitude variations. Typically requires at least 5 days of data for reasonable period estimates.
Autocorrelation	Yes	Power	No	95% CI	Weakened by cycle-to-cycle period or amplitude variations. Typically requires at least 5 days of data for reasonable period estimates.
Wavelet	Yes	Power	Yes	Not yet implemented	Provides continuous estimates of period and phase.

Chi-squared Periodogram

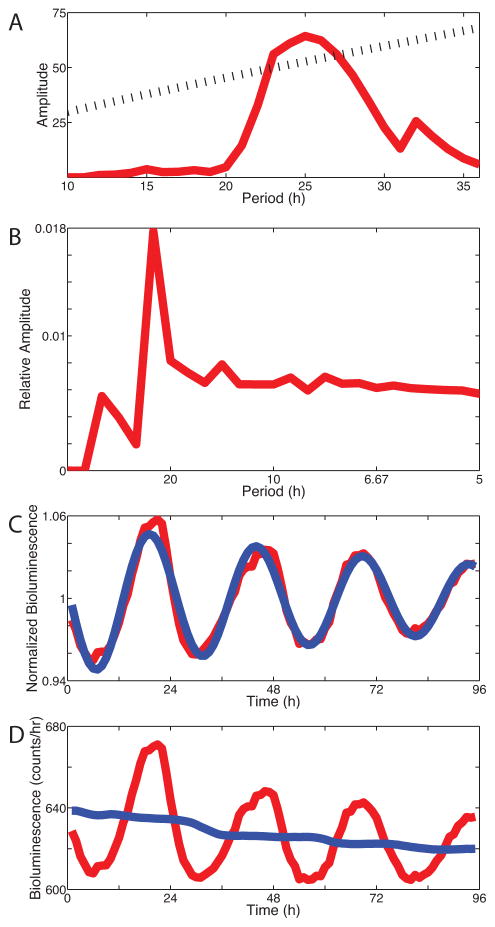
Perhaps the most popular method for estimating circadian period is the Chi-squared Periodogram as developed by Sokolove and Bushell (Sokolove & Bushell, 1978). The method estimates the power at all periods in the data based on a simple, fast algorithm. At its core, the method cuts the data at different period lengths (e.g. between 18 and 32 hours) and quantifies the variance in the data explained by each period. It has no assumptions about waveform and does not fit the data with a function. The resulting plot of power as a function of test periods indicates which periods exceed a user-defined confidence interval (e.g. 99%). Typically, researchers report the period with the maximal power, termed the dominant circadian period. The magnitude of this peak above the confidence interval is termed circadian amplitude and provides an estimate of the strength of rhythmicity at the dominant period. Circadian amplitude increases with the amplitude of the recorded rhythm (e.g. the difference from peak to trough gene expression). Circadian amplitude, however, diminishes if the period or amplitude varies from cycle-to-cycle (e.g. with reduced period precision or amplitude damping). Many software packages support Chi-squared Periodogram analysis (Fig. 3a) including Clocklab and Lumicycle Analysis (Actimetrics Inc., Evanston, IL), BioDare (www.biodare.ed.ac.uk)(Zielinski et al., 2014), El Temps (www.el-temps.com), Circadian Rhythm Lab (www.circadian.org/periodogram.html), or Hutlab (hutlab.nl/).

Figure 3.

Four independent methods to compare period, phase and amplitude of circadian cells. (A) The Chi-squared periodogram estimated the dominant period at 25.0 h, B) FFT-NLLS estimated the period at 23.8 h, (C) Cosinor analysis estimates the period at 24.8 h and (C) Cross-over analysis found the average period was 24.5 h based on cycle-by-cycle period measurement.

Fast Fourier Transform (FFT)

FFT is an independent method based on fitting the data with several cosine functions that differ in their periods, amplitudes and phase relationships (Johnson & Frasier, 1985; Moore et al., 2014). The dominant periodicity in the data is fit by the cosine function with the highest amplitude. We use FFT-NLLS(Straume, Frasier-Cadoret, Johnson, & Lakowicz, 1991) to estimate the dominant circadian period, its amplitude and phase, with estimates of their significance based on Monte Carlo resampling of the randomized raw data (Fig. 3b). FFT-NLLS, a variation of cosinor analysis(Halberg, 1969) (Fig 3c), is reported to be less sensitive to missing or noisy data and computationally faster than Chi-squared periodogram. We implement FFT-NLLS in Matlab; it is also available through BioDare (Zielinski et al., 2014)(www.biodare.ed.ac.uk).

Cross-over analysis

We also use “cross-over analysis” to estimate the period, peak-to-trough amplitude and phase from cycle-to-cycle because, unlike Chi-squared periodogram and FFT-NLLS, it does not assume these parameters are constant in the biological data. This approach calculates two running averages from the raw data, with a 3-h and a 24-h window, respectively. The 24-h smooth removes non-circadian trends and provides a baseline, while the 3-h smooth reveals the circadian oscillations around this baseline. We calculate the period from the daily intersections of these two lines (Fig. 3d). The method is based on a simplified Poincaré-section based recurrence time analysis(Kurths, 2003). To date, no statistical tests have been integrated into this method and it can be sensitive to missing or noisy data, but it is fast, intuitive, and provides details about how the rhythm changes from day to day.

Other methods of period estimation

The above list emphasizes some of the most common methods used to estimate circadian periodicity. Other methods including Maximum Entropy Spectral Analysis (MESA) and autocorrelation (Levine et al., 2002) have been used, especially by researchers studying fly circadian biology. In addition, wavelet-based methods are gaining popularity in the field (Leise, 2013; Leise, Indic, Paul, & Schwartz, 2013; Bours, Muthuraman, Bouwmeester, & van der Krol, 2012; Harang, Bonnet, & Petzold, 2012; Leise & Harrington, 2011; Meeker et al., 2011; Price, Baggs, Curtis, Fitzgerald, & Hogenesch, 2008; Chan, Wu, Lam, Poon, & Poon, 2000) and are reviewed elsewhere in this volume (Leise et al. Chapter). The field will benefit from a comprehensive toolbox that allows easy comparisons of periodicity estimated by multiple, independent methods. Furthermore, we lack careful validation of all of these methods using realistic, synthetic data (e.g. with known period and noise characteristics that resemble data we collect (Deckard, Anafi, Hogenesch, Haase, & Harer, 2013; Refinetti, 1993). Although we must always balance sampling rate and sampling duration against experimental realities of time, resources and money consumed, we have arrived at a point where we have multiple, independent methods that, when they converge on a period estimate, allow us to assess whether circadian cells are synchronized.

Do cells share the same period?

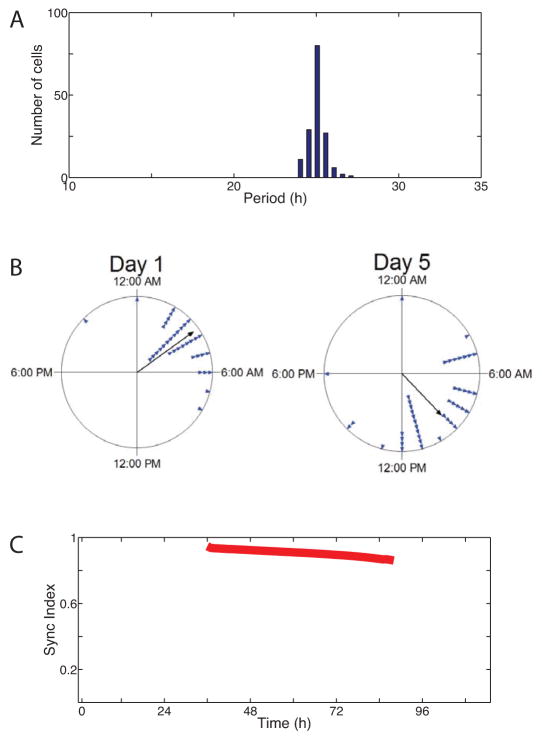
To test whether cells are likely to have synchronized their circadian periods, we next examine the distribution of dominant periods in the population (Fig. 4a). We use the standard deviation of the distribution as an indicator of the degree of period synchrony. Statistical tests comparing the variation between populations (e.g. Levene’s or Brown-Forsythe’s) can provide additional evidence for changes in the degree of period synchrony.

Figure 4.

Period and phase synchrony estimation in a population of cells. (A) The period distribution of the population of cells within the cultured SCN from Fig 1A. Note that the narrow distribution indicates the cells were period synchronized. (B) The times of peak Per2 expression for each cell (triangles) on days 1 and 5 of a recording presented as Rayleigh plots. Note that phases remained significantly clustered during the recording. (C) The phase synchrony (termed Sync Index, Kuramoto Order Parameter or Raleigh Statistic, R) of all cells (n=125) indicates that synchrony decreased modestly over the recording.

Phase Synchrony: Methods to extract and compare phase relationships between cells

Just as a raster plot (Fig. 2b) provides a convenient method to visualize whether the phase relationships between cells remain stable during a recording, Rayleigh plots provide a statistical test of phase clustering among cells (Fig. 4b). The first step is to identify a marker that reliably indicates the phase of the oscillating cell. For example, the time of daily peak of PER2 expression is often used as a reliable phase marker of SCN cells. For the most accurate estimation of clock phase within each cell, conventional wisdom holds that you should use the phase marker with the least variability from cycle to cycle (Herzog, Aton, Numano, Sakaki, & Tei, 2004; Liu & Reppert, 2000).

Next, we apply the Rayleigh test (Batschelet & Batschelet, 1981), from circular statistics to quantify the degree of synchrony among cells. This test is appropriate because phase (e.g. the time of day when a cell fires maximally) cannot be outside a specific range (e.g. 0–24 hours or 0–360 degrees). For this reason, it is not possible to test whether cells are synchronized using linear statistics like a One-Way ANOVA. The resulting Rayleigh Statistic, R (also termed the “Sync Index”), quantifies the degree of clustering among cells, ranging from 0 (uniformly distributed phases across the day) to 1.0 (all cells peak at the same time of day). The resulting p-value indicates the likelihood that the observed clustering occurred by chance. We implement the Rayleigh Test with Oriana Software (Kovach Computing Services, Pentraeth, UK).

It is important to understand that Sync Index is an imperfect measure of synchrony. A population of synchronized oscillators can have a low or high R value. For example, cells that communicate to have identical periods and phases will have an R equal to 1 while cells that coordinate to have identical periods, but that peak in anti-phase, will have an R equal to 0. In addition, phase definition inconsistencies can induce a biased (often increased) R(Kralemann, Cimponeriu, Rosenblum, Pikovsky, & Mrowka, 2008). Therefore, it can be helpful to monitor how cellular periods and their sync index change over time or as a result of a perturbation.

Perturbations reveal synchronization mechanisms

To test whether synchrony changes during a recording, we can apply the Rayleigh Test for each cycle of data. Alternatively, we can use methods like wavelet to extract the phase of each cell at all times in the recording and calculate the Sync Index over time (Fig. 4c). The Sync Index provides a convenient metric to monitor when treatments perturb phase synchrony among cells.

This approach has been applied to test, for example, whether the neuropeptide, vasoactive intestinal polypeptide (VIP), is required for circadian synchrony. Normally, the Sync Index of dispersed SCN cells cultured on multi-electrode arrays approaches 0.4 based on firing rate recordings. When the gene for Vip or its receptor, Vipr2, were deleted, the sync index dropped to 0.05 (Aton, Colwell, Harmar, Waschek, & Herzog, 2005). Similarly, pharmacological disruption of cell-cell communication with drugs like tetrodotoxin or pertussis toxin can reduce the sync index of PER2::Luc rhythms in a SCN slice from nearly 0.7 to 0.1(Aton, Huettner, Straume, & Herzog, 2006; Webb, Taylor, Thoroughman, Doyle III, & Herzog, 2012). Importantly, the reduction in phase synchrony was accompanied by a broadened distribution of periods expressed by the cells, demonstrating that these genetic and pharmacological interventions disrupted the mechanisms underlying synchronization.

Methods awaiting application in circadian biology

Over the past 20 years, fields such as non-linear physics have been inspired by biological systems to develop methods for measuring synchrony. Here, we highlight a few that could be applied in circadian biology. The Perturbation-free Method evaluates statistically significant levels of synchrony based on a twin-surrogate analysis of recurrence plots(Thiel, Romano, Kurths, Rolfs, & Kliegl, 2006). Synchrony induced by direct connections (versus indirect connections) between oscillators can be distinguished using Granger Causality(Nawrath et al., 2010). Synchrony measures have been developed for systems like the bilateral SCN where groups of oscillators interact(Kiss, Quigg, Chun, Kori, & Hudson, 2008). When the network topology is known, cell-specific measures of Sync Index have been proposed to characterize spatially-organized, partially synchronized states(Kuramoto & Battogtokh, 2002). The application of these methods awaits circadian data with more samples per day and for more days.

Step-by-step instructions for measuring synchrony in SCN slice

Bioluminescence recordings using a charge-coupled device (CCD) camera

1. To record from a cultured SCN slice containing a bioluminescence reporter (e.g. PER2::LUC), we use spatial (2 x 2 pixels) and temporal binning (e.g. 1-h integration) to reliably collect enough light to track over 100 cells distributed throughout the unilateral SCN.

2. We record for at least 4 days.

   Note: Culturing the SCN slice for at least 2 days before recording allows the slice to flatten and minimizes SCN cell movement during the recording.

Image processing

1. Using an image processing program (e.g. ImageJ), we maximize the signal to noise ratio from glowing cells in three standard steps:

2. Adjacent Frame Minimization: We compare each pixel’s intensity in adjacent frames and assign the lower value to that pixel. This effectively removes noise due to dark current in the CCD camera and absorbed cosmic radiation.

3. Thresholding: If cosmic radiation persists after adjacent frame minimization, we can set the max threshold of the movie at the value of the cosmic radiation. This takes advantage of the brightness of cosmic spots in comparison to the rest of the movie.

4. Post-collection temporal binning: We can bin frames in segments up to 4 hours, this makes individual cells brighter and also cuts down on the length of the movie – facilitating tracking.

Single cell tracking

1. We identify single cells that persist for the duration of the movie by eye.

2. We encircle each cell with a region of interest (ROIs).

3. We quantify the integrated intensity within each ROI for the duration of the movie.

   Note: Some cells cannot be tracked by this method. If a cell disappears for more than a two hours, we do not include it in the final analysis. This can be particularly problematic, for example, when measuring dim reporters where cells have expression near the detection limits of available cameras (e.g. PER2::Luc in the ventral SCN or Bmal1:Luc in astrocytes).

Data presentation

1. Raster Plot: Raster plots use inverted normalized data. First, we normalize the data from each individual ROI, with the highest and lowest bioluminescence values in the recording becoming 1 and 0, respectively. These data are inverted and saved as a text file.

2. We import the normalized bioluminescence over time into ImageJ,

3. We generate a raster plot using the text image function as a raster plot.

   Note: When normalizing data, it becomes critical that cosmic radiation has been removed. Looking at the individual raw data traces can help identify any spurious peaks.

4. Rayleigh Plot: For any 24 hours of data, we measure and plot the times of peak of bioluminescence from each cell in degrees (0–360).