Harmonisation of Osmolal Gap – Can We Use a Common Formula?

Abstract

Osmolal gap is the difference between the measured osmolality and a calculated osmolality based on the major commonly measured osmotically active particles. The perceived gap indicates the presence of unmeasured osmotically active particles. The major use of osmolal gap today is to screen for the possible presence of exogenous toxic substances in patients in an emergency department or intensive care unit. There is a long history of osmolal gap calculations and it needs to be appreciated that the uncertainty of the osmolal gap will be determined by the sum of errors in the calculated osmolality, error in measured osmolality and variability in unmeasured analytes. Since 1958 there has been a constant trickle of papers proposing both simple and sophisticated formulae to calculate the ‘ultimate’ osmolal gap. A gap as close to zero as possible and with a low coefficient of variation across multiple clinical conditions and analytical platforms are also determinants of ‘fitness for purpose’ of any osmolal gap calculations. The Smithline-Gardner formula for calculated osmolality [2(Na) + Glu + Urea] is fit for purpose in both normal people and general hospital patients. It also performs well across different analytical platforms. This simple formula can be used for rapid mental calculation at the bedside and automated laboratory information system reporting whenever a measured osmolality is requested. In this era of harmonisation, we propose that this formula be adopted by all clinicians and laboratories.

Introduction

Osmolality is a colligative property of a solution and is a measure of solute concentration, defined as the number of osmoles of solute per kilogram of solvent. It may be thought of as a count of the number of dissolved particles in a fluid. Osmolal gap (OG) is the difference between the measured osmolality, usually determined by freezing point depression (or less commonly vapour pressure), and a calculated osmolality (CO) based on the major commonly measured osmotically active particles. The perceived gap indicates the presence of unmeasured osmotically active particles.¹ A wide range of substances may contribute to a raised OG, particularly ethanol, methanol, ethylene glycol, mannitol, other drugs and abnormally high levels of naturally occurring analytes.^2–8 The major use today, however, is to screen for the possible presence of exogenous toxic substances in patients in an emergency department or intensive care unit.^9–12 For example, the OG may be used to screen for alcohol intoxication where ethanol testing is not immediately available.² On the other hand, where ethanol testing is available, the OG allows screening for other toxic alcohols such as ethylene glycol by the use of an additional factor to allow for any ethanol that is also present.^9,10 A factor of 1.20 or 1.25 has been proposed for ethanol (mmol/L) as ethanol contributes more to the OG than would be expected from its molecular weight.^13,14 Following ingestion of ethylene glycol or methanol, a raised OG is an early finding compared to the late onset of raised anion gap which appears after the toxic alcohol is converted to its metabolites.¹⁵ Some clinical conditions such as chronic kidney disease and diabetic ketoacidosis can also raise the OG due to an increase in endogenous particles and these confounding factors must be taken into account when using the OG to screen for exogenous substances.^16–18

Finding the Balance Between an Endless Quest for the Ultimate Osmolal Gap Formula and Fitness for Purpose

There is a long history of OG calculations and it needs to be appreciated that the uncertainty of the OG will be determined by the sum of errors in the CO, error in measured osmolality and variability in unmeasured analytes.^19,20 This uncertainty has undoubtedly varied across the analytical platforms in the past more significantly than in this current era of better technical harmonisation.²¹ It is perhaps not surprising that since at least 1958 there has been a constant trickle of papers proposing both simple and sophisticated formulae to calculate the ‘ultimate’ OG.^{1,10,14,22–28} It is hard to decide, however, whether this represents genuine improvements in measurements using various analytical platforms including osmometers or if it is an ongoing debate by biochemists with an interest in this topic?

In reviewing the literature it is important to remind ourselves of the purpose of the calculation. Our view is that it is primarily used in practice for a quick, convenient estimate of a significant quantity of a selected range of unmeasured, osmotically active analytes. ‘Quick’ is ideally a mental calculation and ‘significant’ has been thought to be at least 5 mOsm/kg H₂O.¹⁰ Of course many toxins such as paracetamol and digoxin can reach toxic and even fatal concentrations without significantly affecting the OG. Having said that we also believe that a gap as close to zero as possible and with a low coefficient of variation (CV) across multiple clinical conditions^13,26 and analytical platforms are also determinants of ‘fitness for purpose’ of any OG calculations.

In 1975 Dorwart and Chalmers reviewed 13 formulae applied to 750 random serum specimens from a major teaching hospital.¹ The authors ascertained that four formulae, all of which utilised only sodium, glucose and urea, provided the highest correlation and, importantly, the lowest standard deviation (SD) of difference with the measured osmolality.¹ However, based on linear regression analysis they proposed a further formula: CO = 1.86(Sodium) + Glucose + Urea + 9.¹ The following year, Smithline and Gardner pointed out that using a factor of 2 rather than 1.86, being the osmotic coefficient of sodium chloride, does not overestimate plasma osmolality since other cations namely potassium, calcium and magnesium as well as the constant of +9 are excluded from the calculation, giving a very simple formula: CO = 2(Sodium) + Glucose + Urea.²³

Nine years later, in 1984, Bhagat et al²⁴ revisited the Dorwart-Chalmers formula. Using 100 plasma specimens from hospitalised patients they proposed a further more complex formula with the inclusion of potassium, CO = 1.89(Sodium) + 1.38(Potassium) + 1.08(Glucose) + 1.03(Urea) + 7.45, with an expected gap in normal subjects also of 0 mOsm/kg (SD, 3.2).²⁴ They also derived a simpler alternative formula, CO = 1.86(Sodium + Potassium) + Glucose + Urea + 10.²⁴ Not long after, in 1987, Worthley et al²⁶ applied five commonly used CO formulae to mixed serum pools taken from three separate cohorts consisting of 100 normal people, 100 general hospital patients and 100 intensive care patients and concluded that the simple Smithline-Gardner formula, CO = 2(Sodium) + Glucose + Urea, best fulfilled the criterion of giving an OG close to zero in different patient cohorts.²⁶ It produced a mean OG of −2 mOsm/kg (SD, 4.3 in normal subjects).²⁶

Analytical methods continued to improve over the subsequent decades. In 2013, Fazekas et al. reviewed 36 formulae by applying them to 236 patient specimens (from a mix of outpatients and acute care inpatients) analysed on point-of-care analysers. They found that only four formulae gave mean OG of less than 1 mOsm/kg and only one gave an SD of less than four.¹⁰ However, while having the best performance in the specific clinical settings, this formula was complex as it required multiple inputs: CO = 0.985(Sodium + Potassium + Chloride + Bicarbonate + Lactate + Glucose + Urea + 6.5) (Formula number 36 in Table 1).¹⁰ Clearly, this would not be appropriate for a quick mental calculation. It is also of interest that this formula requires the input of the major anions such as chloride, bicarbonate and lactate while most other formulae simply allow for these by a factor of 1.86 or 2 assuming the necessity of electrical balance.

Table 1.

Formulae available for calculated osmolality (units for all analytes are mmol/L).^*

Number	Formula
1	1.75(Na) + Glu + 0.5(Urea) + 10.1
2	2.63(Na) − 65.4
3	1.86(Na) + Glu + 0.5(Urea)
4	2(Na + K) + Glu + 0.5(Urea)
5	1.85(Na) + 1.84(K) + 1.15(iCa) + 1.17(Mg) + Glu + 0.5(Urea)
6	2(Na)
7	2(Na) + Glu + 0.5(Urea)
8	2(Na) + 7
9	2(Na) + 10
10	2(Na) + Glu
11	2.1(Na)
12	2(Na) + Glu + 0.93 × 0.5(Urea)
13	0.985[2(Na + K) + Glu + 0.5(Urea)]
14	1.86(Na) + Glu + 0.5(Urea) + 5
15	2(Na) + 0.9(Glu) + 0.93(Urea) × 0.5
16	2(Na) + 0.5(Urea)
17	[1.86(Na) + Glu + 0.5(Urea)] / 0.93
18	1.9(Na + K) + Glu + 0.5(Urea)
19	1.8(Na + K + iCa) + Glu + 0.47 × 0.5(Urea)
20	1.85(Na) + Glu + 0.5(Urea) + 8.55
21	1.86(Na) + Glu + 0.5(Urea) + 9
22	1.86(Na) + Glu + Urea + 9
23	2(Na + K) + Glu + 0.93 × 0.5(Urea)
24	1.89(Na) + 1.38(K) + 1.08(Glu) + 1.03(Urea) + 7.47
25	1.86(Na + K) + Glu + Urea + 10
26	2(Na) + 0.9(Glu) + 0.93 × 0.5(Urea) + 8
27	0.985[1.86(Na) + 1.03(Glu) + 1.28 × 0.5(Urea)]
28	1.36(Na) + 1.6(Glu) + 0.45(Urea) + 91.75
29	0.985[2(Na) + Glu + Urea + 35.2)]
30	1.897(Na) + Glu + 0.5(Urea) + 13.5
31	1.9(Na + K) + Glu + 0.5(Urea) + 5
32	1.86(Na + K) + Glu + Urea
33	2(Na) + 1.15(Glu) + Urea
34	1.86(Na + K) + 1.15(Glu) + Urea + 14
35	1.09 × 1.86(Na) + Glu + Urea
36	0.985(Na + K + Cl + HCO3+ Lactate + Glu + Urea + 6.5)
37	2(Na) + Glu + Urea

^*Formulae 1–36 adapted from Fazekas et al¹⁰; formula 37 from Smithline and Gardner²³

Abbreviations: Na, sodium; Glu, glucose; K, potassium; Mg, magnesium; iCa, ionised calcium; Cl, chloride

Performance of formulae across analytical platforms

A recent study applied 34 usable formulae (listed in Table 1) to data from the Royal College of Pathologists of Australasia Quality Assurance Program (RCPAQAP) Liquid Serum Chemistry (LSC) Survey 2013.²⁹ A total of 118 laboratories reported common chemistry results on serum pools from two healthy individuals, allowing calculation of CO. Thirty-five of these laboratories also submitted measured osmolality, allowing calculation of OG. This study demonstrated that only six of the 34 CO formulae gave mean OG within +/−2 mOsm/kg of zero (Table 2). The smallest OG was seen with the Smithline-Gardner formula (Formula number 37 in Table 1).

Table 2.

Calculated osmolality (CO) and osmolal gap (OG).^*

Formula	CO		OG
	Mean	SD	Mean	SD
2(Na) + Glu + 0.5(Urea)	291	3.2	1.8	4.7
2(Na) + 10	293	3.1	−0.9	4.5
0.985[2 (Na + K) + Glu + 0.5(Urea)]	294	3.2	−1.4	4.8
1.89(Na) +1.38(K) + 1.08(Glu) + 1.03(Urea) + 7.45	291	3.1	1.8	4.7
2(Na) + 1.15(Glu) + Urea	294	3.2	−1.3	4.7
2(Na) + Glu + Urea	293	3.2	−0.6	4.8

^*Calculated osmolality (CO) formulae that gave mean osmolal gap (OG) values within +/−2 mOsm/kg of zero when applied to common chemistry results on serum pools from two healthy individuals reported by 35 laboratories in the RCPAQAP Liquid Serum Chemistry Program 2013. Unit for osmolality is mOsm/kg.

Performance of the two most widely used formulae on individual analytical platforms

The RCPAQAP Chemical Pathology Calculated Results Program Survey 2014 revealed that 26 laboratories (63%) used the simplified Bhagat formula [CO = 1.86(Sodium + Potassium) + Glucose + Urea + 10] while 12 laboratories (32%) used the very simple Smithline-Gardner formula [CO = 2(Sodium) + Glucose + Urea]. Using data from the RCPAQAP LSC Survey 2014 involving serum pools from two healthy individuals, a study evaluated CO in different instrument groups, and also for all instruments combined, using the two most widely used formulae.³⁰ The mean measured osmolality was taken as the gold standard to determine the OG for each formula (Table 3). Applying the Smithline-Gardner formula, the mean CO for different instrument groups for the two healthy serum pools ranged from 283 – 289 mOsm/kg for Serum 1 and 285 – 290 mOsm/kg for Serum 2. Using the Bhagat formula, the mean CO for different instruments ranged from 281 – 287 mOsm/kg for Serum 1 and 283 – 288 mOsm/kg for Serum 2. When the mean CO was compared to the mean measured osmolality the Smithline-Gardner formula gives an OG close to zero. The Bhagat formula gives an OG of 1 – 3 mOsm/kg.

Table 3.

Calculated osmolality (CO) across different instrument groups using data from RCPAQAP Liquid Serum Chemistry Program 2014 (serum pools from two healthy individuals).^*

	Instrument	Number of laboratories	Smithline-Gardner formula23		Simplified Bhagat formula24
			Mean CO	SD	Mean CO	SD
Serum 1 (Mean Measured Osmolality 286)	Beckman Coulter UniCel DxC	2	283	1.1	281	1.0
	Roche Integra	24	284	2.0	282	2.6
	Abbott Architect	37	285	2.4	283	2.3
	Ortho Clinical Vitros	27	287	2.9	285	2.8
	Siemens Advia & Dimension	30	289	2.4	287	2.1
	Roche Hitachi Cobas & Modular	25	289	2.4	287	2.4
	All	145	286	3.2	285	3.1
Serum 2 (Mean Measured Osmolality 289)	Beckman Coulter UniCel DxC	2	287	4.0	285	3.9
	Roche Integra	24	285	2.0	283	1.9
	Abbott Architect	37	286	2.1	284	2.1
	Ortho Clinical Vitros	27	290	2.5	288	2.4
	Siemens Advia & Dimension	30	290	2.4	288	2.3
	Roche Hitachi Cobas & Modular	25	289	2.4	287	2.2
	All	145	288	3.1	286	3.0

^*Smithline-Gardner formula for calculated osmolality is 2(Na) + Glu + Urea. Simplified Bhagat formula for calculated osmolality is 1.86(Na + K) + Glu + Urea. Unit for osmolality is mOsm/kg.

Performance of the two most widely used formulae applied to patients in which an osmolality was clinically indicated

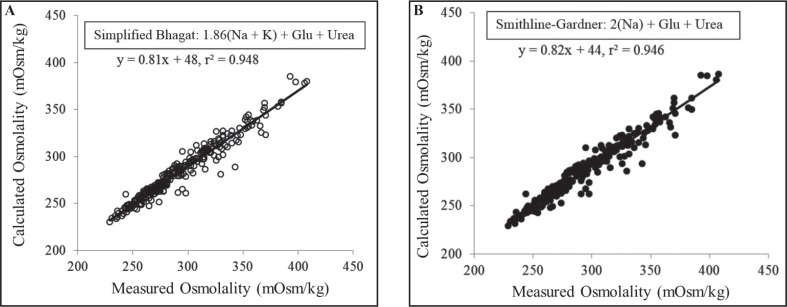
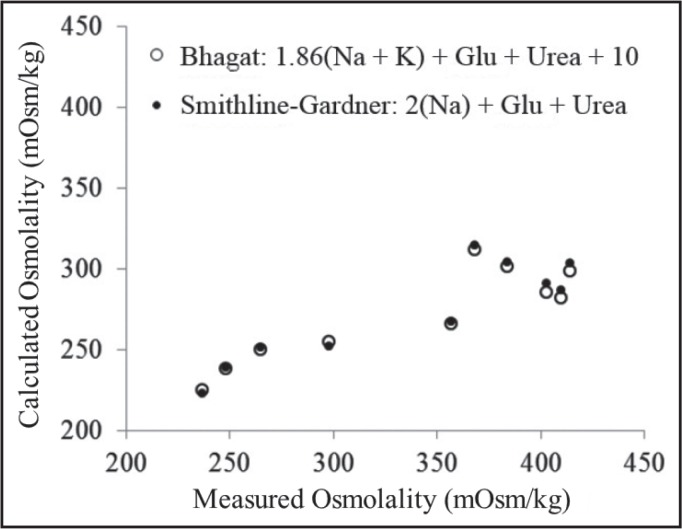
The use of formulae was further reviewed at the AACB Harmonisation Workshop in May 2015 (Doery JCG, Harmonisation of calculated osmolality. Presented at the Australasian Association of Clinical Biochemists 4th Harmonisation Workshop, 18 May, 2015, Sydney). Evidence was presented on the performance of the two most widely used formulae (Smithline-Gardner and simplified Bhagat) applied to results from actual hospital patients in whom an osmolality measurement had been requested, i.e. where osmolality measurement was clinically important. Both formulae gave very similar results in patients in whom a serum or plasma ethanol level was not requested (intoxication was not under serious consideration) (Figures 1a & 1b). In the intoxicated patients in whom a serum or plasma ethanol was requested in addition to serum osmolality, OG’s were clearly present with similar performance of both formulae (Figure 2).

Figure 1.

Smithline-Gardner (Fig. 1a) and simplified Bhagat formulae (Fig. 1b) applied to non-intoxicated patients requiring osmolality measurements.

Figure 2.

Smithline-Gardner and simplified Bhagat formulae applied to intoxicated patients requiring osmolality measurements.

At the conclusion of the presentation the assembled experts were asked to vote for the preferred formula for harmonisation with a clear majority vote for the simple Smithline-Gardner formula; CO = 2(Sodium) + Glucose + Urea. A significant advantage of the Smithline-Gardner formula is that it can also easily be automated even into the most unsophisticated laboratory information system (LIS) as well as being applied readily at the bedside. Given the between-method differences for ethanol assays, the inclusion of a common factor for ethanol (whether 1.20¹⁴ or 1.25¹³) may require further work and is beyond the scope of this paper.

In view of the similarity of results across analytical platforms, it should be possible to suggest an appropriate reference limit for the calculated OG using the proposed Smithline-Gardner formula. It must be noted that as the output values from such calculations as serum osmolality are often used to provide only rough clinical information, the uncertainty of measurement which concerns uncorrelated variables in the formula for the CO will also provide only a rough estimate of values.³¹ The variability in the OG result due to the uncertainty in measurements of serum/plasma sodium, glucose, urea and osmolality is approximately +/− 7 mmol/L. CO formulae have been derived or proposed for use based on their ability to give an OG close to zero; for the Smithline-Gardner formula, an OG close to zero and an SD of 4 mmol/L were found when applied to healthy subjects²⁶ and across analytical platforms^29,30. Given the uncertainty of measurement (2SD of 8 mmol/L), we propose that 10 mmol/L be considered the reference limit for the OG. This proposed limit should be validated in healthy volunteers similar to that performed by Worthley et al²⁶ but using data obtained from more current analysers such as the ‘Aussie normals’.³²

Units

While the use of SI units for reporting measured osmolality, CO and OG results appears to be most desirable option, the Standardisation of Pathology Units and Terminology (PUTS) project of the RCPA has recommended ‘mOsm/kg’ be used for both measured osmolality and CO. Fazekas et al. astutely highlighted that some previous studies had negligently used osmolarity (mOsm/L) and osmolality (mOsm/kg) interchangeably. If a formula was originally derived to calculated osmolarity instead of osmolality, then a correction coefficient of 0.985 was added to obtain osmolality. Provided that the formula for CO has accounted for the difference between osmolarity and osmolality, we propose that the unit for OG be reported in mOsm/kg, in line with the PUTS recommendations.³³

Specimen types

Both serum and heparin plasma specimen types are suitable for measured osmolality by freezing-point depression. They are stable at room temperature for up to 36 hours before separation from cells and osmolality measurement although cooling the specimens to 4–8°C is suggested if delays beyond 12 hours are expected.³⁴ Using the Smithline-Gardner formula, serum and heparin plasma specimens give similar results for CO and OG.³⁵

Conclusion

Extensive effort has been expended over more than 50 years in the pursuit of the ultimate formula for CO. However, it remains true that the simple and most popular Smithline-Gardner formula is indeed fit for purpose²⁶ on the basis of:

• An OG close to zero with an SD of less than 4 in normal subjects and general hospital patients;

• Applicability across all major analysers;

• A simplicity amenable to both bedside use and automated LIS reporting whenever a measured osmolality is requested.³⁶

Once complete harmonisation has been achieved in terms of the units of reporting, the formula used to determine the OG and the reference limit to be applied using such a formula, then this would have the additional benefit that results provided by different laboratory services could be more readily compared and integrated into an electronic health record.