Integration of parallel mechanosensory and visual pathways resolved through sensory conflict

Significance

Animals rely on information drawn from a host of sensory systems to control their movement as they navigate in and interact with their environment. How the nervous system consolidates and processes these channels of information to govern locomotion is a challenging reverse engineering problem. To address this issue, we asked how a hawkmoth feeding from a moving flower combines visual and mechanical (force) cues to follow the flower motion. Using experimental and theoretical approaches, we discover that the brain performs a remarkably simple summation of information from visual and mechanosensory pathways. Moreover, we reveal that the moth could perform the behavior with either visual or mechanical information alone, and this redundancy provides a robust strategy for movement control.

Abstract

The acquisition of information from parallel sensory pathways is a hallmark of coordinated movement in animals. Insect flight, for example, relies on both mechanosensory and visual pathways. Our challenge is to disentangle the relative contribution of each modality to the control of behavior. Toward this end, we show an experimental and analytical framework leveraging sensory conflict, a means for independently exciting and modeling separate sensory pathways within a multisensory behavior. As a model, we examine the hovering flower-feeding behavior in the hawkmoth Manduca sexta. In the laboratory, moths feed from a robotically actuated two-part artificial flower that allows independent presentation of visual and mechanosensory cues. Freely flying moths track lateral flower motion stimuli in an assay spanning both coupled motion, in which visual and mechanosensory cues follow the same motion trajectory, and sensory conflict, in which the two sensory modalities encode different motion stimuli. Applying a frequency-domain system identification analysis, we find that the tracking behavior is, in fact, multisensory and arises from a linear summation of visual and mechanosensory pathways. The response dynamics are highly preserved across individuals, providing a model for predicting the response to novel multimodal stimuli. Surprisingly, we find that each pathway in and of itself is sufficient for driving tracking behavior. When multiple sensory pathways elicit strong behavioral responses, this parallel architecture furnishes robustness via redundancy.

Animals rely on a convergence of information across parallel sensory pathways to control locomotion. In these neural control strategies, one sensory modality may contribute concurrently to several behaviors (a one-to-many mapping), and conversely, several sensory modalities may collectively govern a single behavior (a many-to-one mapping). A continuing aim in studies of animal behavior is to extricate the contribution of an individual sensory modality from the ensemble of pathways (that is, the one-to-one mapping from a sensory percept to the locomotor action; e.g., the optomotor response, chemotaxis, vestibular postural reflex, etc.). The dynamics of locomotor behaviors, however, are shaped by the combination of and interactions between sensorimotor pathways. Therein remains a fundamental challenge in understanding multisensory integration: how does the nervous system combine these streams of information to control behavior, and how do we separate the relative contributions of sensory pathways in the context of a parallel topology?

There is no single answer. Across taxa and behaviors, nervous systems instantiate varied policies for integrating sensory information across modalities. In many instances, parallel sensory pathways serve complementary roles. For example, when humans perform reaching tasks, the planning of motion trajectories relies heavily on visual information, whereas the control of arm movements favors proprioceptive cues (1). In flies, the visual and haltere mechanosensory systems are sensitive to slower and faster rotational motions, respectively, extending the behavioral response to a broader range of motion by this separation of sensory sensitivities (2). In contrast, this work explores a behavior in which parallel sensory pathways contribute to the same task concurrently and over the same frequency spectrum.

The nectivorous hawkmoth, Manduca sexta, feeds via a long proboscis while hovering in front of a flower, continually modulating flight to maintain a frontal position as the flower sways. This flower-tracking behavior has become an experimental paradigm for the study of visuomotor responses (3, 4). However, the proboscis is covered with mechanosensory sensilla, and specifically, the basal sensilla of pilifer are thought to encode the deflection of the proboscis with respect to the head (5).

The relative contributions of sensory pathways are commonly tested by means of sensory isolation (e.g., isolating mechanosensory pathways by ablating or painting the eyes, inhibiting the visual pathway, or eliminating visual cues). However, this approach would fail to reveal particular neural control strategies. In redundant neural control systems, inhibiting a single pathway manifests little change in performance. Moreover, animals may adapt to such manipulations; recent studies of this flower-tracking behavior have illuminated mechanisms that compensate for reduced light (4). Thus, sensory isolation may not be informative of the sensory dynamics under natural conditions, when a suite of senses participate. Instead, we present conflicting visual and mechanosensory stimuli to dissociate the two modalities while maintaining the sensory pathways intact—similar to human psychophysical experiments in reaching (1) and posture control (6) and experiments in joint visual-electrosensory tracking behaviors in knifefish (7).

Flying insects rely on a concert of sensory inputs to control flight, but the sufficiency and necessity of the visual system often overshadow the contribution of other sensory pathways. Indeed, mechanosensory organs serve key roles in insect flight control: antennae (8–11), halteres (2, 12), or wings (13). Prior studies have suggested that visual and mechanosensory responses sum linearly (9, 10). We apply a control theoretic analysis (6, 14, 15) to show that, without assumption of model structure, the data themselves evince linearity and the summation of parallel pathways. This approach furnishes a generative multiple-input model capable of predicting the response to novel stimuli. Contrary to prevailing belief (16), we found that the behavior is dominantly mediated by this mechanosensory pathway. We further show that visual and mechanosensory pathways are each, in and of themselves, sufficient for mediating flower following, providing redundancy. This parallel architecture furnishes robustness in the control theoretic sense that behavioral performance is relatively insensitive to uncertainty in or variation of the parameters of the underlying mechanisms. Also, this parallel summation may confer other benefits, such as improved state estimation in the context of sensor noise or unreliable sensory cues (17, 18). The sensory conflict paradigm provides inroads into revealing these redundant control architectures and overcoming the experimental and analytical challenges that they entail.

Results

Lateral Flower Tracking Is a Multisensory Behavior.

We first explore if moths attend to both visual and mechanosensory cues during flower tracking and whether incongruence between these stimuli affect behavior. In the laboratory, a robotically actuated two-part artificial flower allows independent presentation of visual and mechanosensory cues (Fig. 1A and SI Materials and Methods) along prescribed and repeatable trajectories. We present freely flying moths with flower motion stimuli in an assay spanning both coupled motion, for which the facade and nectary motions are the same as would be expected in naturalistic conditions, and sensory conflict, in which the two sensory modalities encode different motion stimuli (either the facade or nectary moves, while the other remains stationary) (Movie S1). In both sensory conflict categories, one sensory modality indicates that the flower is moving, whereas the other encodes that the flower is stationary. Soon after the moth initiates feeding, one or both flower components are commanded to oscillate along a prescribed trajectory, a linear combination of sinusoids with frequencies spanning 0.2–20 Hz (as in ref. 4) (so as to include and extend beyond the motion spectrum moths experience when feeding in nature, 0–1.7 Hz).

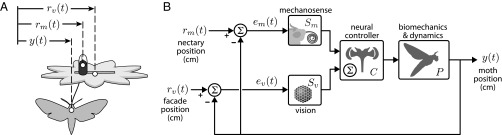
Fig. 1.

(A) A two-part robotically actuated artificial flower provides independent control of visual and mechanical stimuli. The flower facade furnishes a moving visual stimulus, $r_v\left(t\right)$. Accessible through a narrow slit in the facade, the proboscis dips into an independently actuated nectar spur (painted black to minimize its visual salience). As the nectar spur moves, $r_m\left(t\right)$, it deflects the proboscis. In sensory conflict experiments, the position of the moth, $y\left(t\right)$, is directed by both visual and mechanosensory cues imposed by the flower facade, $r_v\left(t\right)$, and nectary, $r_m\left(t\right)$. (B) A simplified block diagram illustrates the parallel pathways that underlie the tracking behavior. Each block represents a transformation from of a neural or mechanical signal. Because moths are freely flying in experiments, the block diagram is closed loop; the moth perceives its relative motion (the difference between the motion stimulus and its own trajectory) with respect to the facade and nectary: the signals $e_v\left(t\right)$ and $e_m\left(t\right)$, respectively. The forward cascade of transformations from the error signals, $e_v\left(t\right)$ and $e_m\left(t\right)$, to the motion output $y\left(t\right)$ is referred to as the sensorimotor transforms (open loop). The closed-loop transformation from exogenous motion, $r_v\left(t\right)$ and $r_m\left(t\right)$, to motion output is referred to as the behavioral transform.

When flower facade and nectary move in unison (the coupled condition) (Fig. 2A), moth trajectories (Fig. 2A, green) follow the reference trajectory (Fig. 2A, black) with high fidelity. In the frequency domain (Fig. 2 A, ii), each peak corresponds to a constituent frequency of the sum of sines stimulus; the fact that the peaks of the moth trajectory are coincident with the peaks of the input stimulus is an indication that the observed behavior is, in fact, a response to the presented motion stimulus.

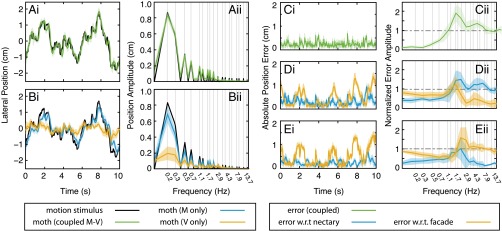
Fig. 2.

Tracking performance of moths following fictive flowers under three motion stimulus conditions: (A) the flower face and nectary move through identical trajectories, $r_m\left(t\right)=r_v\left(t\right)$ (green; the coupled condition; mean and 95% confidence; n = 8), (B) the nectary oscillates while the flower face is stationary, $r_v\left(t\right)=0$ (blue; the M-only condition; n = 8), and the nectary is stationary, $r_m=0$ (gold; the V-only condition; n = 8), while the flower face oscillates. (A, i and B, i) Time traces of tracking trials show slightly deprecated tracking in response to only nectary motion and severely impaired tracking when the flower face provides the motion stimulus. (A, ii and B, ii) The magnitude of the Fourier transform of the moth’s trajectory compared with the motion stimulus reveals that, for all conditions, the moth attends to the moving target; the spectra of moth positions show spikes in power at those frequencies that compose the input motion stimulus. (C, i) For the coupled condition, the visual and mechanosensory slips (green) are equivalent and therefore, can be simultaneously minimized. (D and E) For the M- and V-only conditions, respectively, the errors $e_v\left(t\right)$ (gold) and $e_m\left(t\right)$ (blue) reflect a balance of competing sensory pathways. The similarity in error signals between the two conflict conditions is notable considering the categorical differences in stimulus presentation and moth response. w.r.t., with respect to.

Moth trajectories are noticeably altered in both sensory conflict conditions (Fig. 2B). When only the nectary is actuated (the M-only condition in blue in Fig. 2B), moths maintain good tracking with only slight reduction in amplitude compared with the coupled condition. In response to only facade motion (the V-only condition in gold in Fig. 2B), tracking performance is dramatically diminished, but the peaks of the frequency spectrum of moth motion are still coincident to the motion stimulus. Moths respond coherently to both visual and mechanosensory cues to actively control flight while feeding; the behavior is multisensory. However, the unexpectedly anemic response to the visual stimulus challenges the prior suggestion that this is an exclusively visual behavior (16).

Open-Loop Sensorimotor Gains of Visual and Mechanosensory Pathways Are Consistent Across Sensory Conflict Conditions.

Sensory systems measure exogenous motion with respect to the animal’s body frame coordinates, $e\left(t\right)=r\left(t\right)-y\left(t\right)$ (Fig. 1), referred to as the sensory slip or sensory error. An animal that is tracking a moving reference does so by minimizing this sensory error. During flower feeding, the different sensory modalities typically encode the same motion stimulus, and as such, the same locomotor response simultaneously minimizes both error signals ($e_m$ and $e_v$ in Fig. 1B).

In a sensory conflict experiment paradigm, we present the animal with uncorrelated visual and mechanosensory stimuli such that there does not exist a motor output, which simultaneously minimizes both error signals. In the M-only paradigm, the mechanosensory error signal encodes the positional difference of the moth with respect to the moving nectary, $e_m\left(t\right)=r_m\left(t\right)-y\left(t\right)$, whereas the visual slip represents the position of the moth with respect to the motionless flower facade, $e_v\left(t\right)=-y\left(t\right)$. Conversely, in the V-only condition, $e_v\left(t\right)=r_v\left(t\right)-y\left(t\right)$, whereas $e_m\left(t\right)=-y\left(t\right)$. As such, we consider not only the tracking error to the motion stimulus but also the error with respect to the motionless stimulus. By putting the sensory pathways into conflict (a sensory tug of war), we reveal the relative gain assigned to each pathway (the open-loop transforms $G_m$ and $G_v$ in Eq. 3) and show that these weights are unchanged as a function of the stimulus motion content. It is important to note that, unlike assays that test sensory weighting as a function of reliability, the agreement (or lack thereof) between the motion stimuli does not affect the signal-to-noise ratio of either sensory pathway.

Remarkably, the time courses of the error signals are quite similar in the M- and V-only conditions (Fig. 2 D and E), despite the dramatic differences in moth flight trajectories in these experiments. For the coupled condition, nectary and flower face move coherently, giving a single error signal $e_m\left(t\right)=e_v\left(t\right)$ (Fig. 2C). For the M- and V-only conditions (Fig. 2 D and E, respectively), we compare the mechanosensory (blue in Fig. 2 D and E) and visual errors (gold in Fig. 2 D and E). In the M-only condition, the moths’ trajectories closely follow the mechanical stimulus (the moving nectary), resulting in a greater visual slip. In the V-only case, the trajectory of the moths’ lateral motion is substantially attenuated, again yielding close tracking of the now stationary nectary. The resulting error is nearly identical to that from the M-only condition, favoring lower mechanosensory error at the expense of increased visual slip. Comparing M- and V-only conditions in the frequency-domain representation of error (Fig. 2 D, ii and E, ii), the behavior favors lower mechanosensory error at the expense of increased visual slip at the lower behaviorally relevant frequencies; at high frequencies, tracking performance attenuates (for all conditions), and as a result, the errors converge to a baseline, in which slip with respect to the moving stimulus nears unity and error with respect to the motionless stimulus approaches zero (Fig. S1).

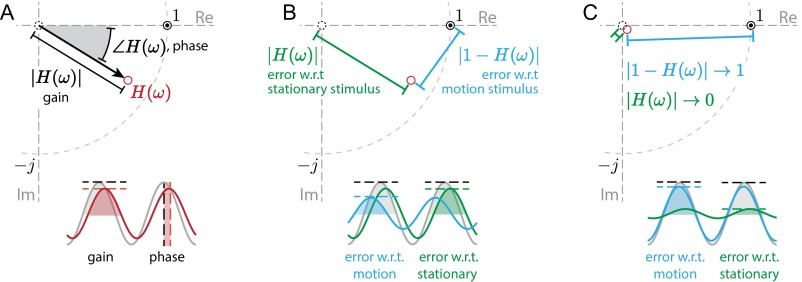
Fig. S1.

(A) The behavior transfer function $H\left(\omega \right)$ is a complex-valued function of frequency. At each frequency, the transfer function prescribes a gain, the ratio of output and input amplitudes, and a phase, the relative timing of the output sinusoid with respect to the input as an angular difference (measured in degrees or radians). On the complex plane, gain and phase are represented as the magnitude and angle (with respect to the positive real axis) of this vector. Perfect tracking occurs at the point $1+j\cdot 0$, the point where gain is unity and phase is zero, which is denoted by the bullseye. (B) The normalized tracking error with respect to the motion stimulus is the magnitude of the difference between perfect tracking and the behavioral response (that is, the gain of the error signal; shown in cyan). The tracking error with respect to the motionless stimulus is simply the magnitude of the behavioral response (green). (C) As the behavioral response decays (as H, $H_v$, and $H_m$ all do at high frequency), the tracking errors with respect to the moving and stationary stimuli approach one and zero, respectively. This condition serves as a baseline case, and deviations from this condition evidence a control policy favoring one sensory modality over another (Fig. 2 D, ii and E, ii). w.r.t., with respect to.

In sensory conflict, it is not the case that moths are worse at tracking the motion stimulus for lack of sensory information. Rather, the observed attenuation is the response to the motion stimulus mitigated by a response to the stationary stimulus. Surprisingly, the mechanosensory pathway is more heavily weighted than the visual.

Mechanosensory and Visual Contributions Sum Linearly.

The control strategy that underlies this behavior balances (with some unequal weighting) the perceived visual and mechanosensory slips, and this strategy is consistent across the conflict paradigms tested. How are these signals consolidated in the coupled condition? A simple hypothesis—and one that has been proposed for the interaction of visual and antennal pathways (9, 10)—is linear summation, and the sensory conflict paradigm is ideally suited for testing this hypothesis.

The frequency-domain approach leverages a convenient property of linear dynamical systems: when excited by a sinusoidal input, the output of a linear dynamical system is a sinusoid at the same frequency, consistently scaled in amplitude and shifted in time by frequency-dependent gain and phase, respectively (Fig. 3). This frequency-preserving property is evinced by the alignment of peaks between the input and output frequency spectra (Fig. 2 A and B). A linear dynamical system is described by its transfer function, represented graphically as a Bode plot of the frequency-dependent gains and phases. Behavioral transfer functions are estimated empirically as the ratio of the Fourier transforms of the sampled output (moth motion) and input signal (flower motion), $H\left(\omega \right)=Y\left(\omega \right)/R\left(\omega \right)$, where ω is the frequency variable (Fig. 3 and Fig. S1).

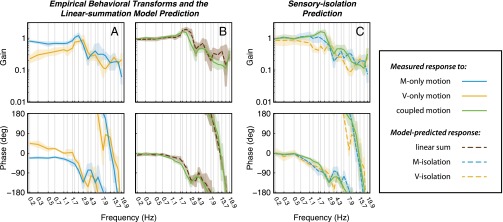
Fig. 3.

Bode plots represent graphically the transfer function in terms of two quantities, gain and phase, both as a function of frequency. (Upper) Gain is defined as the relative amplitude of the output with respect to the input for the specified frequency component, $\left|H\left(\omega \right)\right|$; (Lower) phase is the relative timing of the output and input signals, $\angle H\left(\omega \right)$. Hence, perfect tracking would correspond to unity gain and zero phase (i.e., moth and flower motions are at the same amplitude and synchronized). For a multiinput, single-output system, the transfer function relating the output to an input describes the system response assuming that all other inputs are zero just as we have done experimentally. (A) Over the behaviorally relevant frequency band, 0–1.7 Hz (4), the response in the M-only condition (blue; mean and 95% confidence) is characterized by slight attenuation in gain and increased phase lag. In the V-only condition (gold), gain is severely attenuated, even at the lowest frequencies, but phase is leading. (B) In response to flower motion with coherent visual and mechanosensory cues, moths track with high fidelity at low frequencies characterized by near-unity gain and small phase lags. The sum of the complex-valued transfer functions is superimposed on the coherent response (brown dashed line). The linear sum of M- and V-only responses qualitatively predicts the measured response to coherent stimuli over the entire frequency range tested. (C) Assuming linear summation between sensory pathways, we may predict the behavioral response to hypothetical isolation experiments in which one or the other sensory pathway is inhibited or ablated. These data are presented in Tables S1 and S2.

Moths exhibit slight attenuation and phase lag in the M-only stimulus condition (Fig. 3A, blue). In the V-only condition (Fig. 3A, gold), the mean gain is severely attenuated, even at the lowest frequencies (between 0.23 and 0.43 in the range 0.2–1 Hz), and phase is leading in this band. When presented coherent visual and mechanosensory cues (Fig. 3B, green), moths track with high fidelity at low frequencies characterized by near-unity gain and small phase lags.

The block diagram depicted in Fig. 1B suggests a deconstruction of these transfer functions into constituent dynamical blocks. Coupled motion yields the following behavioral transform (we omit the frequency argument ω for clarity):

$$H=\frac{\left(S_m+S_v\right)CP}{1+\left(S_m+S_v\right)CP}\hspace{0.17em}\text{and}\hspace{0.17em}Y=HR.$$ [1]

Also, for the sensory conflict paradigms, the transfer function for the M- and V-only responses is

$$Y=\underset{H_m}{\underbrace{\frac{S_{m}CP}{1+\left(S_m+S_v\right)CP}}}{R}_m+\underset{H_v}{\underbrace{\frac{S_{v}CP}{1+\left(S_m+S_v\right)CP}}}{R}_v.$$ [2]

Note that, in conflict conditions, both sensory transforms, $S_v$ and $S_m$, appear in the denominator; the denominator reflects the reafferent pathway, the negative feedback that represents ego motion with respect to both the moving and stationary features. These behavioral transforms reveal an interaction between sensory pathways in closed loop, and therefore, the M- and V-only responses do not transparently represent the open-loop dynamics of the underlying sensory processes.

Still, linear summation implies that the sum of M- and V-only responses predicts the coupled response, $H=H_m+H_v$ (Eqs. 1 and 2). The close agreement between the sum of the M- and V-only responses (Fig. 3B, brown dashed line) and the response to coupled stimuli is consistent with a model in which mechanosensory and visual processing occurs on parallel and independent pathways that sum linearly. Moreover, the sensory weights are constant across our stimulus conditions.

Linear Summation Furnishes a Predictive Model.

If the linear summation hypothesis truly reflects the underlying computation, then these transfer functions should provide a predictive model, allowing us to forecast the response to novel combinations of visual and mechanosensory stimuli.

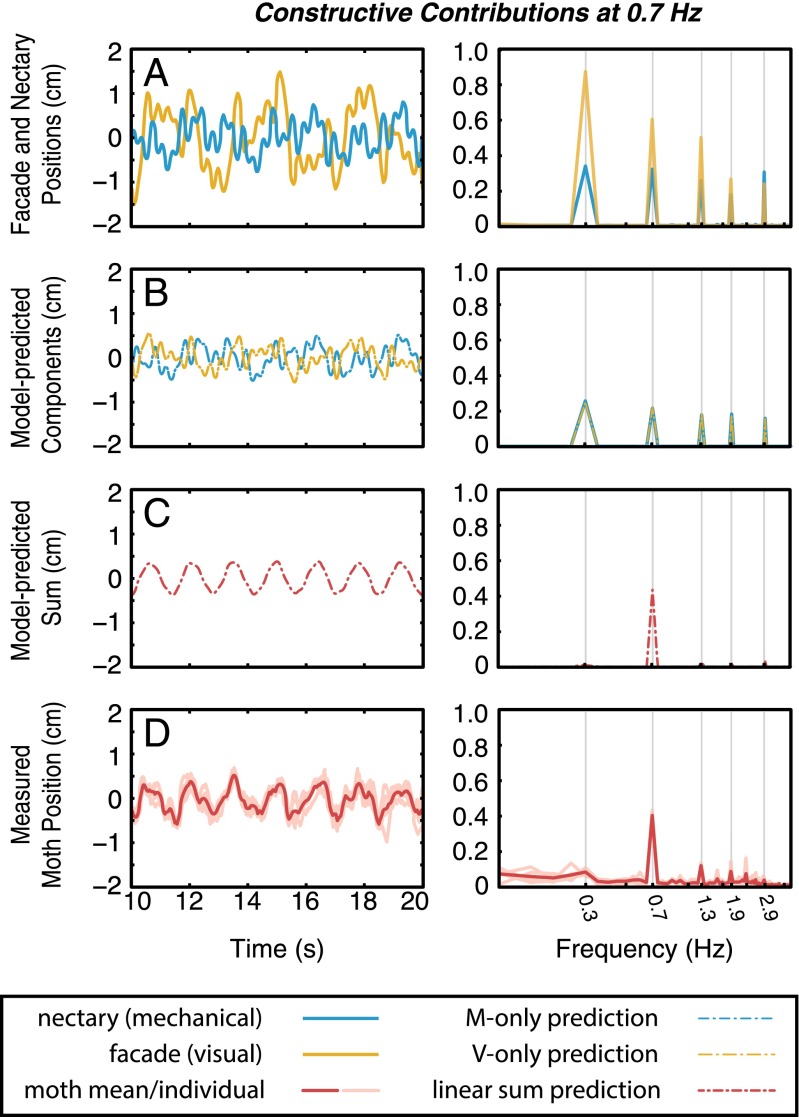
In a final set of experiments, we simultaneously actuate both the nectary and flower face with dramatically different and particularly crafted trajectories. We design two new sum of sines stimuli, $r_m\left(t\right)$ and $r_v\left(t\right)$, composed of five frequency components at 0.2, 0.7, 1.3, 1.9, and 2.9 Hz (Fig. 4A). Using the empirical transfer functions $H_v$ and $H_m$, we design the inputs (selecting appropriate amplitude and phase at each frequency from Tables S1 and S2), such that the predicted visual and mechanosensory contributions are identical in amplitude and perfectly antiphase (Fig. 4B). The linear summation model predicts that the combined effect of these trajectories should elicit a zero motion response. However, it would then be impossible to differentiate between this cancellation of responses and no response at all (which might be reasonable to expect from an animal presented such a confounding set of sensory stimuli). Therefore, we select a single frequency (0.7 Hz) at which the outputs sum constructively. Hence, the moth receives largely antagonistic sum of sines stimuli and is predicted to respond with a pure sinusoidal trajectory at the prescribed frequency (Fig. 4C).

Fig. 4.

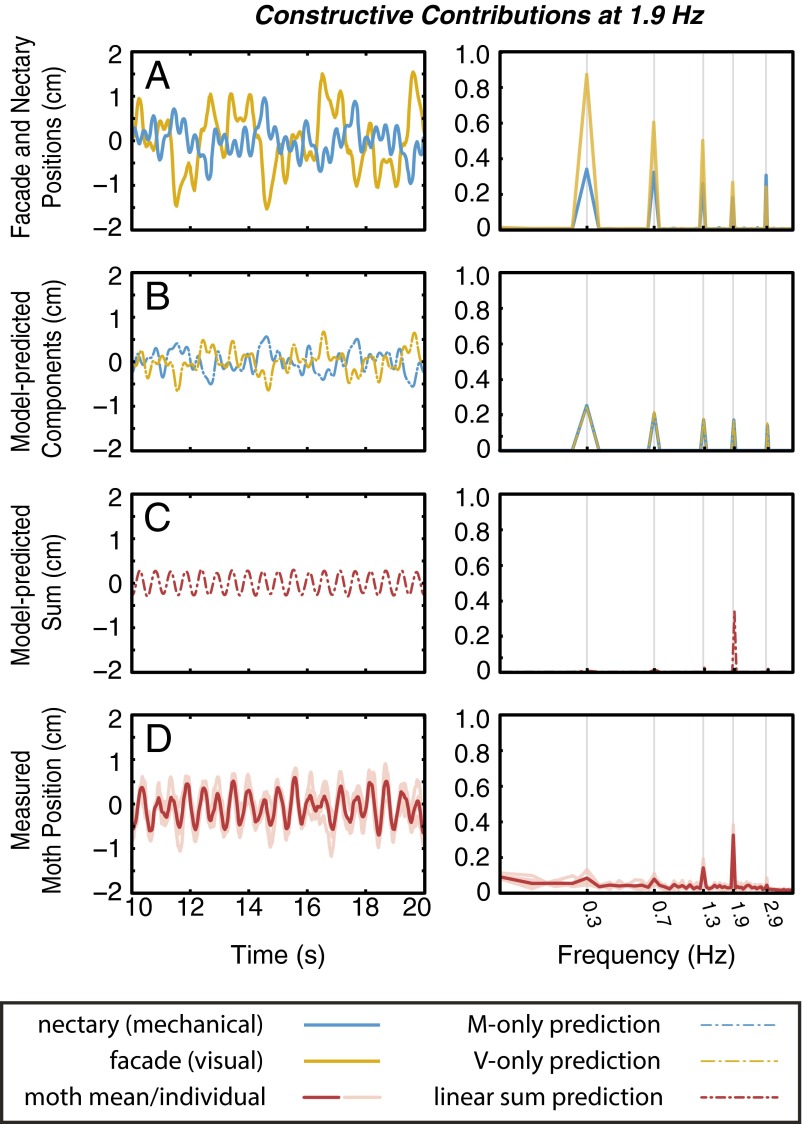
(A) Specially designed nectary (blue) and flower facade (gold) trajectories should elicit largely destructive motor contributions, in which all frequency components are annihilated except a selected frequency: 0.7 Hz for this case. Note that the amplitude of the visual stimulus is significantly higher to account for the lower gain of the visual pathway in this frequency band. The model predicts (B) the contribution from each sensorimotor pathway (blue and gold dashed lines) as well as (C) their linear summation (red dashed lines). Although we design inputs that would yield a purely sinusoidal moth response, small errors in generating input trajectories result in a slightly imperfect sinusoid prediction. The predicted response represents the empirically measured inputs filtered through the associated behavioral transform functions. (D) Empirical results (n = 5) recreate the model prediction. This experiment is repeated with the constructive frequency at 1.9 Hz (Fig. S2).

Table S1.

The empirical behavioral transfer functions, H, $H_m$, and $H_v$, are detailed as frequency-dependent gains and phases (0.2–2.9 Hz)

Behavioral transforms	Frequency (Hz)
	0.2	0.3	0.5	0.7	1.1	1.3	1.7	1.9	2.3	2.9
Empirical behavioral transforms
H
Gain	0.96	1.03	0.96	1.06	1.15	1.17	1.46	1.60	1.49	0.66
Phase	$-1.0°$	$-5.3°$	$-1.4°$	$-11.8°$	$-24.5°$	$-35.5°$	$-46.0°$	$-59.3°$	$-98.3°$	$-134.8°$
$H_m$
Gain	0.80	0.74	0.65	0.69	0.68	0.69	0.84	1.05	1.20	0.62
Phase	$-21.8°$	$-20.6°$	$-22.3°$	$-18.0°$	$-26.1°$	$-31.6°$	$-43.1°$	$-49.4°$	$-79.4°$	$-132.6°$
$H_v$
Gain	0.23	0.30	0.34	0.38	0.43	0.39	0.49	0.75	0.79	0.88
Phase	$44.6°$	$40.2°$	$19.7°$	$21.3°$	$0.2°$	$1.4°$	$3.3°$	$-26.4°$	$-47.3°$	$-113.9°$
Behavioral transform predicted by linear summation model
$H_m+H_v$
Gain	0.92	0.92	0.94	1.01	1.08	1.04	1.23	1.77	1.92	1.49
Phase	$-8.7°$	$-4.2°$	$-8.1°$	$-4.3°$	$-15.9°$	$-19.8°$	$-26.4°$	$-39.8°$	$-66.8°$	$-121.7°$
Predicted behavioral transforms in sensory isolation
$H_m^{\prime }$
Gain	0.96	1.08	0.95	1.11	1.15	0.98	1.10	1.01	0.82	0.60
Phase	$-2.1°$	$-6.7°$	$-3.1°$	$-18.3°$	$-43.9°$	$-58.3°$	$-81.3°$	$-82.8°$	$-91.0°$	$-133.0°$
$H_v^{\prime }$
Gain	0.85	0.85	0.88	0.80	0.70	0.48	0.41	0.56	0.40	0.76
Phase	$3.1°$	$-15.1°$	$-1.1°$	$-26.6°$	$-51.3°$	$-56.4°$	$-62.9°$	$-76.9°$	$-74.5°$	$-96.8°$

From these empirical transforms, we derive the linear summation prediction, $H_m+H_v$, and predict the isolated visual and mechanosensory behavioral transforms, $H_v^{\prime }$ and $H_m^{\prime }$, respectively. These data are represented graphically as Bode plots (Fig. 3).

Table S2.

The empirical behavioral transfer functions, H, $H_m$, and $H_v$, are detailed as frequency-dependent gains and phases (3.7–19.9 Hz)

Behavioral transforms	Frequency (Hz)
	3.7	4.3	5.3	6.1	7.9	8.9	11.3	13.7	16.7	19.9
Empirical behavioral transforms
H
Gain	0.32	0.46	0.47	0.43	0.26	0.18	0.15	0.14	0.11	0.32
Phase	$-108.7°$	$-108.4°$	$-132.3°$	$-159.6°$	$161.0°$	$150.0°$	$83.5°$	$-40.7°$	$-155.9°$	$-36.8°$
$H_m$
Gain	0.22	0.30	0.40	0.31	0.31	0.28	0.17	0.18	0.18	0.06
Phase	$-77.0°$	$-77.3°$	$-133.9°$	$-109.5°$	$-174.8°$	$156.0°$	$17.4°$	$-73.5°$	$153.1°$	$54.9°$
$H_v$
Gain	0.35	0.27	0.30	0.21	0.12	0.11	0.17	0.25	0.16	0.21
Phase	$-154.0°$	$-101.6°$	$-119.7°$	$175.2°$	$12.6°$	$85.5°$	$72.5°$	$-26.2°$	$-73.8°$	$75.3°$
Behavioral transform predicted by linear summation model
$H_m+H_v$
Gain	0.46	0.56	0.69	0.42	0.20	0.33	0.30	0.40	0.14	0.27
Phase	$-126.0°$	$-88.9°$	$-127.7°$	$-138.7°$	$-179.2°$	$138.0°$	$45.2°$	$-45.8°$	$-148.5°$	$70.8°$
Predicted behavioral transforms in sensory isolation
$H{\prime }_m$
Gain	0.19	0.25	0.38	0.24	0.33	0.31	0.15	0.19	0.19	0.08
Phase	$-81.5°$	$-84.1°$	$-137.1°$	$-103.3°$	$-168.0°$	$154.6°$	$22.4°$	$-68.7°$	$145.4°$	$37.8°$
$H{\prime }_v$
Gain	0.44	0.25	0.26	0.17	0.09	0.09	0.16	0.22	0.14	0.24
Phase	$-164.6°$	$-110.5°$	$-123.8°$	$167.2°$	$15.0°$	$84.6°$	$71.8°$	$-25.3°$	$-68.4°$	$48.9°$

From these empirical transforms, we derive the linear summation prediction, $H_m+H_v$, and predict the isolated visual and mechanosensory behavioral transforms, $H_v^{\prime }$ and $H_m^{\prime }$, respectively. These data are represented graphically as Bode plots (Fig. 3).

The spectrum of the moth trajectory clearly shows a peak at the selected frequency and attenuation of all other responses (Fig. 4D, Right). We repeat this experiment, designing the stimuli such that responses at 1.9 Hz sum constructively (Fig. S2), and as predicted, we observe a significant peak at the desired frequency and attenuation at all others. Importantly, the stimuli used in these two iterations have identical power spectra; only the relative phases between visual and mechanosensory stimuli are changed. The annihilation of antagonistic stimuli further corroborates the hypothesis that sensory integration attenuates noise; if we presume that noise signals on different sensory pathways are independent, these components would not combine constructively, yielding reduced noise in the summed output.

Fig. S2.

(A) As in Fig. 4, nectary (blue) and flower facade (gold) trajectories are designed to yield mostly antagonistic visual and mechanosensory contributions. For this repetition, (B) we select the visual and mechanosensory contributions to sum constructively at 1.9 Hz. Again, (D) the empirical results (n = 5) are in agreement with (C) the model prediction.

The summation model allows us to predictably direct the moths’ trajectories. Perhaps most telling, the predictive models that we used to design these trajectories (the M- and V-only Bode plots depicted in Fig. 3A) were each derived from different sets of animals. A third independent group was used to test the predictive model. The population responses predict the individual response, suggesting that the relative gains and phases of responses are highly preserved across individuals.

Mechanosensory and Visual Pathways Provide Redundancy for Control.

“Sensory pathway” refers to the aggregate transformation from error signal to motion output, the cascade of sensory, neural, and physical transforms $S_{v}CP$ and $S_{m}CP$. From these input–output data, it is not possible to further parse the contributions of the constituent blocks. However, we may exploit the commonality between the transfer functions $H_m$ and $H_v$ to calculate the relative gain of the visual and mechanosensory systems, specifically $\left|S_m\right|/\left|S_v\right|=\left|H_m\right|/\left|H_v\right|$.

In the decade from 0.2 to 2 Hz, the gain of the mechanosensory pathway ranges from 3.9 to 1.6 times greater than that of the visual system (Tables S1 and S2). It seems logical that the mechanosensory pathway would carry such weight; the sensory cue is provided by the nectar spur, the actual location of the food source. However, under most natural conditions, the visual cues would be highly correlated to the flower motion as well. In fact, the visual response is not impoverished; rather, it only seems meager when pitted against the more sensitive mechanosensory response.

A statistically optimal sensory summation weights modalities commensurate to their reliability (19). In our experiments, the reliability of each sensory modality is unaffected across presentations, and accordingly, we observe consistent weighting in response to the coupled and conflicting motion stimuli. However, the seemingly feeble visual response raises an important question: for our experiment conditions (lighting, flower geometry, visual background, etc.), are visual percepts deemed unreliable and as a result, attenuated as noise? If so, we should not expect the visual pathway to be sufficient to mediate the behavior on its own in the absence of mechanosensory cues. To the contrary, the visual pathway is independently sufficient. Although this isolation experiment is infeasible, we can estimate the responses of each modality given our existing empirical model.

From the formulations in Eqs. 1 and 2, we could estimate the individual sensorimotor (open-loop) transforms for mechanosensory and visual pathways $G_m$ and $G_v$:

$$\begin{array}{l}{G}_m=S_{m}CP=\frac{H_m}{1-H}\hspace{0.17em}\text{and}\hspace{0.17em}{G}_v=S_{v}CP=\frac{H_v}{1-H}\hspace{0.17em},\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{where}\hspace{0.17em}Y=\underset{G_m}{\underbrace{S_{m}CP}}{E}_m+\underset{G_v}{\underbrace{S_{v}CP}}{E}_v\hspace{0.17em}.\end{array}$$ [3]

Using the estimated sensorimotor transforms, we further construct hypothetical responses for a pair of sensory isolation experiments (Fig. 3C), experiments that we could not perform. Let $H_m^{\prime }$ be the transfer function describing the feeding response using only mechanosensory cues (e.g., were the moth to feed in complete darkness) (Fig. 3C, blue dashed line). These transfer functions can be represented in terms of empirically measured responses as

$$H_m\prime =\frac{S_{m}CP}{1+S_{m}CP}=\frac{G_m}{1+G_m}=\frac{H_m}{1-H+H_m}\hspace{0.17em}.$$ [4]

Also, similarly, $H_v^{\prime }$ would be the isolated visual response (e.g., were we to ablate or inhibit the sensilla on the proboscis) (Fig. 3C, gold dashed line).

For comparison, we replot the mean empirical response from our coupled motion condition (Fig. 3C, green). At low frequencies, the predicted responses are qualitatively similar to the coupled motion condition. Each sensory pathway in isolation seems sufficient to achieve good tracking performance; the pathways are redundant in the context of control.

Discussion

Behavioral Context Shapes Sensory Weighting.

In this behavior, the proboscis plays a significant sensory role. However, for a similar task in which moths regulate distance from a looming flower, Farina et al. (16) concluded the opposite: that proboscis-mediated mechanosensory pathways contribute negligibly to the behavioral response. Moths tracking a fictive corolla moving longitudinally along a stationary nectary tube (analogous to our V-only condition) showed only slight attenuation in tracking performance compared with that for an intact flower (analogous to our naturalistic motion condition). It is likely that the lateral motions that we presented provide a more salient mechanical stimulus than the axial motions associated with looming movements, whereas looming visual motion elicits a strong optomotor response (20). Additionally, Farina et al. (16) conducted experiments on the diurnal moth, Macroglossum stellatarum, which may further impact the relative weighting of visual pathways compared with the crepuscular M. sexta. Analogously, in the interaction of vision and olfaction, nocturnal moths rely more heavily on olfactory cues, whereas diurnal moths favor visual cues (21). Hence, the weighting between modalities may well depend on the direction of stimulus motion as well as the ecological context to which the moth is adapted.

Sensory Conflict Reveals Redundancy.

Although we observe dramatically unequal weighting between visual and mechanosensory transforms, each pathway is in itself sufficient for mediating accurate tracking. Accurate tracking—a behavioral transform $H\left(\omega \right)$ near one (Fig. S1)—can be achieved by any sufficiently large sensorimotor transform, $\left|G\left(\omega \right)\right|\gg 1$ (again, we omit the argument ω):

$$H=\frac{G}{1+G}.$$ [5]

Moreover, as the gain of the sensorimotor transform increases, there are diminishing returns in terms of tracking performance, and this insensitivity endows robustness. A behavior arising from parallel sensorimotor transforms, $G_1\left(\omega \right)$ and $G_2\left(\omega \right)$, and a pair of tunable weighting variables, ${\alpha }_1$ and ${\alpha }_2$, is described by the following:

$$Y=\underset{H}{\underbrace{\frac{{\alpha }_1{G}_1+{\alpha }_2{G}_2}{1+{\alpha }_1{G}_1+{\alpha }_2{G}_2}}}R\hspace{0.17em}.$$ [6]

The above equation represents the behavioral response when both sensory pathways encode the same motion stimulus—the coupled condition. In a sensory isolation paradigm, a single sensory modality is isolated by inhibiting other modalities by either manipulating the animal (e.g., surgical, genetic, or pharmacological) or altering the sensory milieu. In the mathematical representation in Eq. 6, the isolation effectively modulates the weighting variables, ${\alpha }_1$ and ${\alpha }_2$. However, if both $G_1\left(\omega \right)$ and $G_2\left(\omega \right)$ are sufficiently large, the behavioral response is relatively insensitive to modulation of those weights. In nature, this redundancy can confer robustness to damage of a sensory organ or impoverished sensory information that the pathways mutually insure each other. In the laboratory, this robustness presents an experimental challenge in isolating the individual contributions of parallel pathways.

In contrast to isolation, sensory conflict effectively splits the behavioral transform into independently stimulated pathways:

$$Y=\underset{H_1}{\underbrace{\frac{{\alpha }_1{G}_1}{1+{\alpha }_1{G}_1+{\alpha }_2{G}_2}}}{R}_1+\underset{H_2}{\underbrace{\frac{{\alpha }_2{G}_2}{1+{\alpha }_1{G}_1+{\alpha }_2{G}_2}}}{R}_2.$$ [7]

Assuming $H\left(\omega \right)$ near one, $H_1\left(\omega \right)$ and $H_2\left(\omega \right)$ are complementary; in conflict, either one or both must exhibit depreciation. For this investigation, we resort to sensory conflict out of necessity (to circumvent the requisite role of vision in insect flight), but the conflict paradigm furnishes a uniquely powerful tool for studying sensory integration.

Conclusion

Through sensory conflict, we show that the flower tracking behavior is mediated by a linear summation of parallel visual and mechanosensory pathways. We do not preclude adaptive sensory reweighting in response to changes in sensory salience or reliability (signal-to-noise ratio). This model provides a general description of the visual–mechanosensory combination that is consistent with previous observations (2, 9, 10) and as such, may represent a more general topology for this sensory integration. More importantly, a single model explains the behavioral responses to both coupled and conflicting motion cues, even when the sensory inputs suggest antagonistic motor outputs. Visual and mechanosensory pathways are, as such, independent, and their summation gives rise to robustness via redundancy.

SI Materials and Methods

We performed animal husbandry and prepared experimental lighting, temperature, flower scent, and food source following the protocols enumerated in ref. 4.

Experimental Apparatus.

For coherent motion trials (Fig. 2A), we used the same flower as in ref. 4. For the sensory conflict experiments, we designed (Solidworks; Dassault Systèmes S.A.) and fabricated (UPrint SE; Stratasys) a two-part fictive flower. The nectary consisted of an elbow-shaped tube 7.5 mm in diameter, to which we attached a centrifuge tube containing ∼0.75 mL 20% (wt/vol) sucrose solution. The nectary was painted black to minimize visual salience. The nectary is accessible through a 2-mm-wide arced slot in the flower facade. In the M- and V-only conflict conditions (Fig. 2B), we actuated one flower component using a servo motor harvested from a chart recorder (Model 15–6327-57; Gould Inc.), the same as was used in ref. 4; the unactuated flower component was rigidly attached to the support scaffold. For the destructive–constructive conflict experiments (Fig. 4), facade and nectary were each actuated by a stepper motor and stepper controller (1067_0 PhidgetStepper Bipolar HC; Phidgets Inc.).

Dissociating Visual and Mechanosensory Cues.

The two-part flower design aims at separating visual and mechanosensory cues. Here, we consider possible confounds of this design.

If the moth can see its proboscis at the point of insertion, the proboscis would provide a visual cue correlated to the nectary motion. The interommatidial angle for the Manduca eye is ∼0.94° (22). However, the crepuscular Manduca have superposition eyes, a spatial integration over several adjacent ommatidia trading off improved brightness for reduced resolution. At the insertion point into the flower, the proboscis would subtend an angle of less than 2.8° (assuming a proboscis diameter of 1 mm and insertion distance of 2 cm), which is on the order of a single pixel in moth vision. We do not believe that this would provide a strong visual cue compared with the contrasting silhouette of the flower facade.

Conversely, at the point of insertion, the proboscis might detect the motion of the facade, providing a mechanosensory cue correlated to what we consider to be solely a visual input. There are mechanosensory sensilla along the entire length of the proboscis: sensilla trichodea throughout and most densely at the proboscis elbow, sensilla styloconica at the proboscis tip, and sensilla of pilifer at the base (5). The sensilla of pilifer are thought to detect the flexion of the proboscis with respect to the head (similar to the Johnston organ at the base of the antenna and the campaniform sensilla at the base of fly halteres, each sensitive to strain caused by the deflection of its respective structure). Although we suspect that the mechanosensory control signal arises largely from these basal sensilla of pilifer, it is unclear what role the other sensilla types might play in the behavior; we are not aware of any neurophysiological support for input from proboscis mechanosensory cells. That said, only a small fraction of the mechanosensory sensilla could be in contact with flower facade. Furthermore, the width of the facade slot is twice the width of the proboscis diameter, and therefore, it is unlikely that the slit deflects the proboscis. The rubbing of the facade against the proboscis would suggest a phase-leading derivative (velocity) response, where as we observe, low phase lags consistent with a proportional (positional) response.

If the moth draws visual cues from the sight of its proboscis, it would suggest that some of the mechanosensory response should be attributed to the visual pathway and vice versa if the proboscis is perturbed by facade motion. We have made design choices—painting the nectary black and allowing ample clearance for the proboscis in the facade slot—to mitigate these confounds as much as possible.

Experiment Design.

A common trajectory was used for the coherent motion and M- and V-only trials: a sum of sinusoids comprising 20 frequency components selected as prime multiples of 0.1 Hz (to avoid harmonic coincidence) logarithmically spaced and spanning a band from 0.2 to 19.9 Hz (Figs. 2 and 3). At each frequency, the constituent signals were designed to have equal velocity amplitudes. Trials were 20 s in length, from which we extract 10 s from the middle.

For constructive–destructive trials, we design independent trajectories for the flower facade and the nectary, such that the predicted locomotor contributions at each frequency are equal in magnitude and antiphase; at one frequency, the predicted locomotor contributions from each pathway sum constructively, with equal magnitude and in phase:

$$\begin{array}{l}{r}_m\left(t\right)=-{\displaystyle \sum _{i=1}^5\frac{A_i}{\left|H_m\left({\omega }_i\right)\right|}\cos \left(2\pi \cdot {\omega }_i\cdot t+{\theta }_i-\angle H_m\left({\omega }_i\right)\right)}\end{array}$$

$$\begin{array}{l}{r}_v\left(t\right)={\displaystyle \sum _{i=1}^5{\delta }_{ij}\frac{A_i}{\left|H_v\left({\omega }_i\right)\right|}\cos \left(2\pi \cdot {\omega }_i\cdot t+{\theta }_i-\angle H_v\left({\omega }_i\right)\right)}\end{array}$$

where

$$\begin{array}{l}{\delta }_{ij}=\{\begin{array}{l}-1\hspace{1em}\text{for}\hspace{1em}i\ne j\\ 1\hspace{1em}\text{for}\hspace{1em}i=j\end{array},\end{array}$$

where ${\omega }_i\in \mathrm{\Omega }$, $\mathrm{\Omega }=2\pi \cdot \left\{0.2,0.7,1.3,1.9,2.9\right\}{s}^{-1}$, and ${\delta }_{ij}$ determines the constructively summing frequency (the frequency ${\omega }_j$ selected from the set $\mathrm{\Omega }$). A and θ are free parameters. The linear summation model thus predicts the moth positional output as

$$y\left(t\right)=-2A_j\cos \left(2\pi \cdot {\omega }_j\cdot t+{\theta }_j\right)\hspace{0.17em}.$$

These experiments were conducted for ${\omega }_j$, the constructive frequency, at 0.7 (Fig. 4) and 1.9 Hz (Fig. S2). Trials were 30 s in duration, and we analyzed the tracking bout from 5 to 25 s, video recorded at 100 frames ${\text{s}}^{-1}$, and digitized using DLTdataviewer (23). To compensate for the different heights of nectary and facade markers, the measured lateral displacement of the facade is scaled (by similar triangles) to provide the equivalent displacement at the z height of the nectary.

Frequency-Domain Analysis.

At each frequency, a transfer function, H, assumes a complex value:

$$H=a+j\cdot b,$$ [S1]

where $j=\sqrt{-1}$. Equivalently, in polar coordinates, the transfer function can be represented as

$$H=g\exp \left(j\cdot \theta \right),$$

where $g=\sqrt{a^2+b^2}$ is the gain, and $\theta =\arctan \left(b/a\right)$ is the phase. Taking the logarithm of the above, we get

$$\ln H=\ln g+j\cdot \theta \hspace{0.17em}.$$ [S2]

In this log-space representation, the real and imaginary arguments are the log gain and phase, respectively, and these quantities are depicted in Bode plots. For the Bode plots in Fig. 3, we have demarcated the y axis with the values for gain (as opposed to log gain in decibels, which is typical) but maintained logarithmic spacing.

Statistics for gain in the behavioral transform are calculated on the log gain and exponentiated back to gain:

$$\begin{array}{c}{\left|H\left(\omega \right)\right|}_{\text{log}\hspace{0.17em}\text{mean}}=\frac{1}{N}{\displaystyle \sum _{k=1}^N\ln \left|H_k\left(\omega \right)\right|}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\left|H\left(\omega \right)\right|}_{\text{log}\hspace{0.17em}\text{std}}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=\sqrt{\frac{1}{N-1}{\displaystyle \sum _{k=1}^N{\left(\ln \frac{\left|H_k\left(\omega \right)\right|}{\left|H\left(\omega \right)\right|}\right)}^2}}.\end{array}$$

Subsequently,

$$\begin{array}{c}{\left|H\left(\omega \right)\right|}_{\text{mean}}=\exp \left({\left|H\left(\omega \right)\right|}_{\text{log}\hspace{0.17em}\text{mean}}\right)\\ {\left|H\left(\omega \right)\right|}_{\pm \text{std}}\hspace{0.17em}=\exp \left({\left|H\left(\omega \right)\right|}_{\text{log}\hspace{0.17em}\text{mean}}\pm {\left|H\left(\omega \right)\right|}_{\text{log}\hspace{0.17em}\text{std}}\right)\hspace{0.17em}.\end{array}$$

Statistics for phase are calculated as the circular mean and SD:

$$\begin{array}{l}\angle H{\left(\omega \right)}_{\text{mean}}=\angle \frac{1}{N}{\displaystyle \sum _{k=1}^N\exp \angle H_k\left(\omega \right)\cdot j}\\ \angle H{\left(\omega \right)}_{\text{std}}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=\sqrt{-2\ln R},\end{array}$$

where R is the vector strength

$$R=\left|\frac{1}{N}{\displaystyle \sum _{k=1}^N\exp \left(\angle H_k\left(\omega \right)\cdot j\right)}\right|.$$

For predicted values (the summation prediction and the isolation predictions in Figs. 3 B and C, respectively), confidence intervals are estimated using a propagation of uncertainty analysis. As an example, we consider the summation prediction, mapping empirical measurements of $H_m$ and $H_v$ to their predicted sum. We define a vector of log-gain and phase parameters for the M- and V-only responses:

$$\mathbf{x}=\left[g_m,{\theta }_m,g_v,{\theta }_v\right]\hspace{0.17em}.$$

Accordingly, the sample means and SDs are denoted by

$$\begin{array}{l}\overline{x}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=\left[{\overline{g}}_m,{\overline{\theta }}_m,{\overline{g}}_v,{\overline{\theta }}_v\right]\\ \mathrm{\Sigma }\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=\left(\begin{array}{cccc}{\sigma }_{g,m}& & & \\ & {\sigma }_{\theta ,m}& & \\ & & {\sigma }_{g,v}& \\ & & & {\sigma }_{\theta ,v}\end{array}\right)\hspace{0.17em}.\end{array}$$

A prediction is described by two mapping functions: $F_g$, which maps measurements of log gain and phase to the predicted log gain; and $F_{\theta }$, which maps those same empirical quantities to the predicted phase. These mappings require first an exponentiation from the log space (Eq. S2) to the Cartesian representation (Eq. S1), then the prescribed arithmetic manipulation (in this case, a summation), and finally, a transformation back into the log space. The predicted mean response is calculated at each frequency as

$$\begin{array}{l}\widehat{g}=F_g\left(\overline{x}\right)\\ \widehat{\theta }=F_{\theta }\left(\overline{x}\right)\hspace{0.17em}.\end{array}$$

Also, for each frequency, the SDs are predicted by

$$\begin{array}{l}{\widehat{\sigma }}_g=\sqrt{J_g{\mathrm{\Sigma }}^2{J}_g^T}\\ {\widehat{\sigma }}_{\theta }=\sqrt{J_{\theta }{\mathrm{\Sigma }}^2{J}_{\theta }^T},\end{array}$$

where $J_{g,\theta }$ is the Jacobian for each mapping:

$${\mathbf{J}}_{g,\theta }={\frac{d{F}_{g,\theta }}{d\mathbf{x}}|}_{\overline{x}}\hspace{0.17em}.$$