Significance
Although many studies have shown that chromosomes are folded into cells in a nonrandom fashion, the functional significance of this spatial organization remains poorly understood. Combining theory and fluorescence microscopy, we demonstrate that the folded state of yeast chromosome III changes in response to a DNA double-strand break at the MAT locus, in agreement with previous studies. Importantly, we show that the change in the folded state of the chromosome after the break quantitatively accounts for the dynamics of homology search during DNA repair. Our study provides an example of a cell changing the folded state of one of its chromosomes in response to an internal chemical cue (DNA break), thereby affecting its function (DNA repair).
Keywords: chromosome organization, homologous recombination, random-walk polymers, quantitative fluorescent microscopy, statistical physics
Abstract
Chromosomes are folded into cells in a nonrandom fashion, with particular genetic loci occupying distinct spatial regions. This observation raises the question of whether the spatial organization of a chromosome governs its functions, such as recombination or transcription. We consider this general question in the specific context of mating-type switching in budding yeast, which is a model system for homologous recombination. Mating-type switching is induced by a DNA double-strand break (DSB) at the MAT locus on chromosome III, followed by homologous recombination between the cut MAT locus and one of two donor loci (HMLα and HMRa), located on the same chromosome. Previous studies have suggested that in MATa cells after the DSB is induced chromosome III undergoes refolding, which directs the MAT locus to recombine with HMLα. Here, we propose a quantitative model of mating-type switching predicated on the assumption of DSB-induced chromosome refolding, which also takes into account the previously measured stochastic dynamics and polymer nature of yeast chromosomes. Using quantitative fluorescence microscopy, we measure changes in the distance between the donor (HMLα) and MAT loci after the DSB and find agreement with the theory. Predictions of the theory also agree with measurements of changes in the use of HMLα as the donor, when we perturb the refolding of chromosome III. These results establish refolding of yeast chromosome III as a key driving force in MAT switching and provide an example of a cell regulating the spatial organization of its chromosome so as to direct homology search during recombination.
Chromosomes in bacteria and eukaryotic nuclei are folded in a nonrandom fashion, which leads to specific DNA sequences assuming narrowly distributed positions within the cell or the nucleus (1–4). An interesting question is, then, to what extent does this spatial organization of chromosomes determine their function? For example, differential gene expression during development and the maintenance of genomic integrity in response to damaging agents have both been linked to chromosome organization. In both cases the folded state of chromosomes determines which functionally related DNA sequences are spatially close to each other, which in turn enables their function (5–11). Furthermore, earlier theoretical studies addressing aspects of long-distance regulatory interactions between DNA sequences have suggested that formation of chromosomal loops can be used to modulate the frequency of these interactions (12, 13).
Double-strand breaks (DSBs) are deleterious DNA lesions that can be repaired by homologous recombination. The repair process requires spatial proximity, of about 10 nm or so, of the region around the DSB and a homologous DNA sequence, which is located either on the same or on a different chromosome (14–17). Recent studies have revealed a role for the spatial organization of chromosomes in homologous recombination whereby sequences that are closer to each other within the volume of the nucleus recombine more readily (10, 11, 18–21). This is to be expected in a model where the search for the homologous sequence is driven by random motion of the chromosomes within the nucleus. Here we present a quantitative model and quantitative data that show that a regulated change in the folded state of a yeast chromosome after a DSB is directly responsible for steering recombination toward one of the two available homologous DNA sequences.
In the budding yeast Saccharomyces cerevisiae the spatial organization of chromosomes in interphase is determined by their polymer nature. Namely, the chromosomes’ spatial organization is described in quantitative detail by a simple model of chromosomes as random-walk polymers confined to a spherical volume, which represents the nucleus (20–29). Another element of organization is the tethering of chromosomes to the nuclear envelope at their telomeres and to the spindle pole body at their centromeres (2, 22).
Spatial organization of chromosomes in yeast plays an important role in DNA recombination. For example, telomeres in yeast are spatially clustered, and rates of telomere–telomere recombination are higher than those between telomeres and interstitial regions of the genome (30–32). Two recent studies examined recombination between pairs of homologous loci placed at different locations in the yeast genome, showing that recombination is more likely to occur between loci that occupy overlapping spatial regions in the nucleus (10, 11). As remarked earlier this relation between the spatial organization of chromosomes and recombination is consistent with the idea that random, diffusive motion of the chromosomes drives homology search. Here we show that yeast cells take advantage of this relation between spatial proximity of genetic loci and the rates of their recombination by refolding their chromosome after a site-specific DSB to direct recombination to a specific donor locus and thus achieve a specific gene conversion event. Moreover, we show that the loss of polymer entropy due to chromosome refolding quantitatively accounts for the measured differences in efficiency with which competing donor sequences are used in repairing a double-stranded DNA break during mating-type switching.
Mating-type switching in yeast is a well-studied example of DNA DSB repair using homologous recombination that occurs during interphase (33). In haploid yeast, the mating type is determined by two alleles, MATa or MATα, which reside on chromosome III (Chr III). A programmed, site-specific DSB at the MAT locus is repaired by gene conversion with one of the homologous donor loci, HMLα or HMRa, located at the opposite ends of the same chromosome. The break at MAT is caused by the site-specific homothallic switching endonuclease (HO) that recognizes a 24-bp degenerate sequence, cleaving either MATa or MATα (34). HMLα and HMRa are both heterochromatic and transcriptionally silent and cannot be cleaved by HO, but they serve as templates to repair the DSB at MAT (33).
When the expression of HO is under the control of a galactose-inducible promoter it is possible to monitor the kinetics of mating-type switching and identify a number of distinct slow (tens of minutes) steps during the DSB repair event (35). MAT switching is thus an excellent model system for studying different aspects of DSB repair via homologous recombination.
One important feature of yeast mating-type switching that is central to our story is the directionality in the selection of donors during this gene conversion event. MATa cells use HMLα 85–90% of the time, whereas MATα cells choose HMRa as a donor 90% of the time (36). This preference is particularly puzzling if one were simply to predict donor preference in MATa cells based on the distances (in base pairs) between MAT and its two donors. Given that the HML–MAT distance along Chr III is twice as large as the HMR–MAT distance (188 kb and 93 kb, respectively), one would predict that the more proximally located HMR would be the favored donor. Specifically, the random-walk nature of the yeast chromosome predicts that the probability of a close contact between two genetic loci falls off with their genomic separation to the power −3/2; this property of intrachromosomal contact probabilities has also been observed in chromosome conformation capture experiments (24, 37). Based on this scaling relation HMR should be favored about threefold over HML. This simple estimate therefore leads to a puzzle: How is it that HML is used 90% of the time (i.e., nine times more frequently than HMR) in MATa cells?
The donor-preference puzzle is resolved, at least in part, by the action of the recombination enhancer (RE) sequence, a ∼275-bp cis-acting locus located 17 kb centromere-proximal to HML on the left arm of Chr III (34, 38). RE binds several proteins, including multiple copies of forkhead family transcription factor homologue 1 (Fkh1), which contains a phosphothreonine binding domain that seems to have affinity for one or more damage-dependent phosphorylated proteins bound near the DSB (39). This attraction can thus bring HML within about 20 kb of MAT, but only after MAT is cut by HO. In MATα cells, RE is inactivated and HMR is the preferred donor. Similarly, when RE is deleted in MATa cells, HMR is strongly preferred over HML (34, 40). RE is “portable” in that it can facilitate the preferential use of non-MAT sequences as donors even in interchromosomal recombination (11, 39).
Recent experiments have found that the conformation of Chr III differs between MATa and MATα cells before the break is induced at MAT (41). These differences, though, do not account for the strong donor preferences in the two mating types, because contacts between MAT and HMR predominate in the absence of a DSB in both cases. Moreover, when RE is deleted (again in the absence of DNA damage) there is no significant difference in initial chromosome conformation. However, there is a second Matα2–Mcm1 repressor binding site located next to the region that we have defined as RE (42); deletion of this region, interestingly, does alter the conformation of the left arm, leading to a conformation different from that seen in either mating type. Still, the question of the conformation of Chr III after the break at MAT remains.
Here we propose a quantitative model of mating-type switching that takes into account RE-mediated refolding of Chr III after the DSB at MAT (Fig. 1A). This refolding model makes specific predictions about the probability distributions of the distances between MAT and the donor loci after the break, until homologous recombination is completed. We quantitatively test these predictions by direct visualization of the MAT and HML loci, which are labeled with fluorescent proteins bound to DNA sequences inserted nearby. The measured distances between these two loci in the wild type and two mutant yeast strains (one in which RE is deleted and another in which HML is synthetically tethered to the nuclear periphery) are consistent with the predictions of our chromosome-refolding model. The model quantitatively connects chromosome organization to donor preference, and we successfully test predictions of the model against our measurements and previously published donor preference data (43). Unexpectedly, this comparison also reveals a possible role for the folding of the right arm of Chr III in determining donor preference. Taken together, our theory and experiments help establish DSB-induced refolding of yeast Chr III as the mechanism for donor preference in mating-type switching. These results provide an example of a cell regulating communication between distant genetic loci by manipulating the spatial organization of its chromosome within the nucleus in response to an internal (DNA-damage-dependent) cue.
Fig. 1.
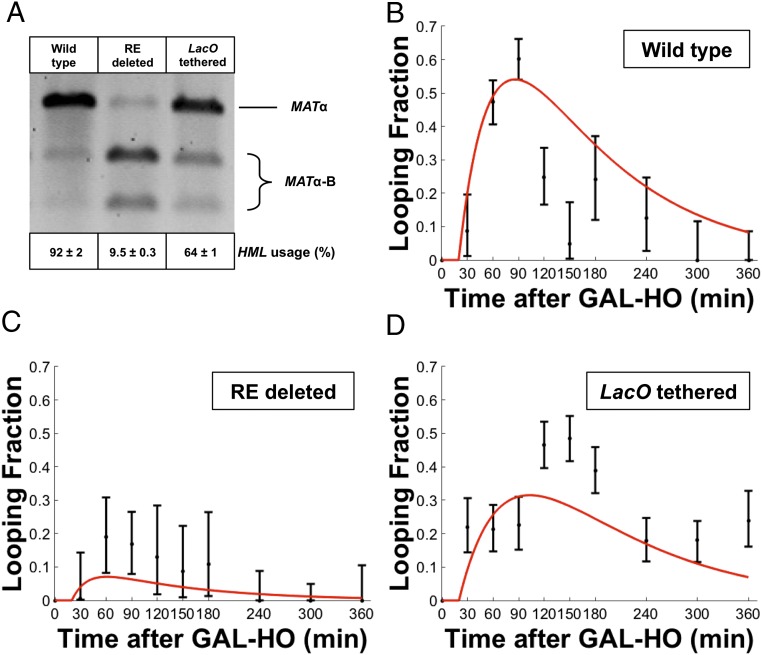
Chromosome-refolding model of donor preference in mating-type switching. (A) Kinetics of mating-type switching. The black line represents yeast Chr III. Circles show the genetic loci MAT (white), HML (gray), and HMR (black). The two steps leading to repair are the formation of a synapsed state between one of the donor loci (HML or HMR) and MAT and the repair of the DNA break, which leads to the breakup of the paired state. Both steps are assumed to be irreversible. The rates of synapse formation ( and are different for the two loci, leading to a difference in the use of one donor over the other. The synapse formation rates depend on the folded state of the chromosome after the DSB, which is described in B by a thermodynamic model. The rate of DNA break repair is independent of the selected donor (10, 11). Time-dependent probabilities of the MAT–HML synapsed and MAT–HMR synapsed states of the chromosome are and , respectively, and they can be calculated in terms of the rate parameters (Eq. 1). (B) Folded states of yeast Chr III after the DSB and their thermodynamic weights. Each state is defined by the specific contacts shown as the schematic in the leftmost column. The ’s represent the reduction in the number of chromosome configurations compared with the unfolded (first) state. is the energy of interaction between RE (yellow) and MAT (white), mediated by the Fkh1 protein (39, 53); and are absolute temperature and the Boltzmann constant, respectively. The folded states that have an HML and MAT (gray and white) or HMR and MAT (black and white) in close contact all lead to a formation of a synapsed state with the same rate The centromere (C) is shown in purple. (C) Conformations of yeast chromosomes are modeled using a random-walk polymer model. The polymer is confined to a sphere of radius , representing the nucleus; the polymer is tethered to the nuclear periphery at its ends, which represent telomere sequences (gray circles), and at the centromere, which is attached to the spindle pole body (SPB tether). The left (light-yellow cylinders) and right (pink cylinders) arms of the chromosome are composed of rigid segments of equal length (Kuhn length) connected by flexible linkers. The spindle pole body (SPB) tether is positioned at the north pole whereas the telomere tethers are allowed to take any position on the surface of the sphere. In addition to the spherical confinement, an impenetrable volume (red spherical cap), representing the nucleolar region, limits the space available for the chromosome, and it is located at the south pole. Loci of interest are represented as colored circles RE (yellow), MAT (white), HML (gray), and HMR (black). (D) Predicted distribution of distances between HML and MAT. Distributions are computed for two separate cases depending on the folded state of Chr III: (i) before the DNA break at MAT (solid line), when the chromosome is not folded, and (ii) after the DNA break (dashed line), when RE and the HML locus are synapsed with MAT, leading to a two-loop folded state of the chromosome. Polymer model parameters are given in Table S1. Distributions were computed using distances between the polymer segments that represent the two fluorescent arrays placed proximal to HML and MAT in the experiments (Fig. 2A).
Results
Chromosome-Refolding Model of Mating-Type Switching.
In order for the repair of the DSB at MAT to commence, one of the two donor loci has to come in close proximity (tens of nanometers) to the location of the DSB. We model the repair process as consisting of two irreversible kinetic steps. The first step is the formation of a synapsed state between MAT and one of the two donor loci. This is followed by DSB repair and subsequent dissociation of MAT and the donor locus. The first step is assumed to occur at rate or , depending on whether MAT associates with HML or HMR, whereas the second repair step is assumed to occur at the same rate regardless of which donor is used (Fig. 1A), which is consistent with recently published data (10, 11).
This simple model asserts that the donor ratio , where we define the donor ratio as the fraction of cells that use HML divided by the fraction of cells that use HMR to repair the DNA break at MAT. Furthermore, the model predicts the probability that HML is synapsed with MAT at time after the break:
| [1] |
An equivalent formula holds for the probability of HMR being synapsed with MAT, with and swapped.
The rates of synapse formation are related to chromosome conformations. If the conformation is such that HML is more likely to be in close proximity to MAT than HMR is, MAT will synapse proportionally more often with the left donor. Simple estimates based on measured chromosome dynamics in yeast with or without a DSB (44–50) suggest that collisions between HML (or HMR) and MAT, which are driven by chromosome diffusion, happen on the minute time scale. This is much faster than the time for synapse formation and the repair time , which ChIP/Southern blot and PCR experiments, respectively, suggest happen on the tens of minutes to hour time scale (35, 39, 51). This separation of time scales implies that multiple collisions between MAT and the donor loci occur before a synapsed state between MAT and one of the donors occurs. Therefore, the formation of the synapsed state can be modeled as a slow conversion to the synapsed state (with rate ) from a state of close contact between MAT and one of the donor sequences, as illustrated in Fig. 1B. The probability of close contact between two DNA sequences on Chr III can in turn be computed using equilibrium statistical mechanics (52).
In Fig. 1B we list all of the folded states of Chr III that play a role in mating-type switching. Folded states are defined by the close contact between MAT and the two donor loci, and the binding of RE to MAT, which occurs after the DSB in MATa cells (39, 43, 53, 54). Using the equilibrium probabilities of the folded states we can compute the rates of synapse formation, and . As described above, is the rate of synapse formation assuming that the left or the right donor is in close contact with the DSB at MAT. Using these expressions for the rates of synapse formation we compute the donor ratio as
| [2] |
where the numerator is simply the contact probability between HML and MAT and the denominator corresponds to the probability of an HMR–MAT contact.
The probabilities of the different folded states follow directly from the thermodynamics weights listed in Fig. 1B: For each state, the probability ( etc.) of the state equals the state’s thermodynamic weight divided by the sum of all of the thermodynamic weights. The multiplicities ( etc.) in Fig. 1B account for the loss of entropy due to chromosome folding, and they are readily computed using the polymer model of Chr III illustrated in Fig. 1C (23). The thermodynamic weights are nothing but the relative probabilities of a contact occurring between the different genetic loci involved in mating-type switching, as illustrated in the first column of Fig. 1B (the weights are relative to the probability of no contact occurring, which is the first state in Fig. 1B). Note that even though the thermodynamic weights, and the corresponding contact probabilities, depend on the distance cutoff used to define what is meant by a close contact (in our calculations we take the cutoff to be 10 nm), the donor ratio is independent of the choice of cutoff, because it drops out when taking the ratio of contact probabilities (Eq. 2).
A key prediction of the chromosome-refolding model is that the probability of a contact occurring between HML and MAT increases due to (Fkh1-mediated) RE–MAT binding after the break. Therefore, in MATa cells in which RE is deleted we expect no increase in the probability of the folded state in which HML and MAT are in contact, compared with what is measured before the break. These two scenarios are illustrated in Fig. 1D, where we show predictions from the polymer model of Chr III for the distance distribution between the HML and MAT loci for the folded and unfolded state of Chr III in yeast. A quantitative increase in the probability distribution at small distances observed due to folding is responsible for the change in the rate of synapse formation of MAT and HML (), which in turn is predicted to increase the donor ratio (). Similarly, any perturbation to the folded state of the chromosome after the DSB that alters contact probabilities between MAT and donor loci will have a quantifiable effect on the donor ratio. We exploit this by constructing mutant cells to test the refolding model. We also test the model by comparing its predictions (Eq. 2) to previously published experiments that measured changes in donor preference when the MAT locus, the donor loci, and RE were moved to different positions on Chr III (43).
In Vivo Imaging of Genetic Loci Involved in Mating-Type Switching Is in Quantitative Agreement with the Chromosome-Refolding Model.
To quantitatively test predictions based on the chromosome-refolding model we made use of the wild-type yeast strain with a 256-copy tandem array of LacO sequences, which bind LacI-GFP, inserted 1.5 kb proximal to the HML locus, and a 112-copy tandem array of TetO sequences, which bind TetR-RFP, inserted 5 kb distal to the MAT locus (Fig. 2A) (23, 55–57).
Fig. 2.
In vivo imaging of genetic loci during mating-type switching is in quantitative agreement with the chromosome-refolding model. (A) Schematic views of budding yeast Chr III, with distances of each locus from the left telomere end indicated in kilobase pairs; 256 tandem repeats of Lac operators are inserted at a site 1.5 kb proximal to HML, and 112 tandem repeats of Tet operators are inserted at a site 5 kb distal to MAT. LacI-GFP and TetR-RFP fusion proteins mark the spatial location of the genetic loci in the proximity of HML and MAT, respectively. The top view shows the linear (truncated) representation of Chr III with inserted fluorescent reporters, and a 3D representation of the chromosome is shown in the bottom view with green for HML + LacO and red for MAT +TetO; insets show the relative position between the donor loci and their respective fluorescent arrays. (B) Representative wide-field microscopy images of yeast strain YBA009. Images from formaldehyde-fixed cells were collected before and after inducing a double-strand DNA break at MAT (Materials and Methods). (Scale bar, 1 μm.) (C) Comparison of chromosome-refolding model predictions (Eq. 3), shown in red, with measurements (black bars) of the probability density function (in units of 1 per micrometer) for the distances (in units of micrometers) between the LacO and TetO arrays, proximal to HML and MAT loci, respectively. Distances were measured at different time points during mating-type switching in wild-type cells. For each time point, the area under the red curve is equal to 1; also, the sum of histogram bar areas is equal to 1. Ten time points were collected over a 6-h-long time-course measurement. is the fraction of cells with HML–MAT paired, which was obtained by fitting the data to Eq. 3 for every time point . Experimental error bars represent the 95% confidence interval of the counting error. (Time point/number of cells analyzed: 0 min/431, 30 min/190, 60 min/541, 90 min/556, 120 min/334, 150 min/149, 180 min/139, 240 min/154, 300 min/178, and 360 min/104.)
We imaged cells (Fig. 2B) before and after generating the DSB at the MAT locus. The DSB was generated using a galactose-inducible HO endonuclease (GAL-HO) (35). We then collected cells at different time points (t) after inducing the DSB, fixed them with paraformaldehyde, and imaged the fixed yeast cells using confocal microscopy. The images were analyzed using the ImageJ plugin SpotDistance to measure the 3D distances (d) between fluorescent markers at MAT and HML (23, 58). Details of quantitative fluorescence microscopy are explained in Materials and Methods.
In Fig. 2C (also see Figs. S2 and S3) we show the experimental distribution of distances that we obtained in this manner. The raw distance data are shown in Fig. S1, and in Table S2 we make a statistical comparison of measured distances for every pair of time points to test the likelihood that they are drawn from the same distribution.
Fig. S2.
Comparison of model predictions (red curves) with in vivo measurements of the distributions of distances between LacO and TetO arrays (black bars) during MAT switching in RE-deleted cells (strain YBA010). Ten time points were collected over a 6-h-long time-course measurement. The distance distribution at every time point is fitted to Eq. 3 to obtain the probability of HML–MAT synapse , which is shown for every individual time point. Experimental error bars represent the 95% confidence interval of the counting error. (Time point/number of cells analyzed; 0 min/102, 30 min/132, 60 min/168, 90 min/264, 120 min/106, 150 min/125, 180 min/108, 240 min/163, 300 min/137, and 360 min/126.)
Fig. S3.
Comparison of model predictions (red curves) with in vivo measurements of the distributions of distances between LacO and TetO arrays (black bars) during mating-type switching in mutant cells (strain YBA013) in which HML-proximal LacO is tethered to the nuclear envelope. Ten time points were collected over a 6-h-long time-course measurement. The distance distribution at every time point is fitted to Eq. 3 to obtain the probability of HML–MAT synapse , which is shown for every individual time point. Here experimental error bars represent the 95% confidence interval of the counting error. (Time point/number of cells analyzed; 0 min/184, 30 min/259, 60 min/349, 90 min/253, 120 min/357, 150 min/422, 180 min/393, 240 min/390, 300 min/359, and 360 min/231.)
Fig. S1.
Raw data representation of in vivo chromosome-refolding time-course measurements. LacO–TetO distance measurements during mating-type switching in fixed budding yeast cells. Individual distance measurements of each time point are shown as black dots. For each time point the bottom and top black lines of the colored boxes highlight the first and third quartiles, and the bands inside the boxes show the median distance values. (A) Wild-type cells, light-red boxes (strain YBA009); (B) RE-deleted mutant cells, light-purple boxes (strainYBA010); (C) mutant cells in which HML proximal LacO is tethered at the nuclear envelope, light-green boxes (strain YBA013). For the number of cells at each time point analyzed in A–C see the legends of Fig. 2 and Figs. S2 and S3, respectively.
Table S2.
Statistical P values computed with two-sample Kolmogorov–Smirnov test indicating which measured distance distributions are significantly different
| WT 0 | WT 30 | WT 60 | WT 90 | WT 120 | WT 150 | WT 180 | WT 240 | WT 300 | WT 360 | |
| WT 0 | 1 | |||||||||
| WT 30 | 4.27E-01 | 1 | ||||||||
| WT 60 | 4.55E-14 | 1.92E-07 | 1 | |||||||
| WT 90 | 6.05E-24 | 2.83E-12 | 3.92E-03 | 1 | ||||||
| WT 120 | 3.20E-04 | 2.80E-02 | 2.27E-04 | 2.60E-08 | 1 | |||||
| WT 150 | 6.41E-02 | 8.70E-02 | 1.06E-08 | 5.95E-13 | 7.78E-03 | 1 | ||||
| WT 180 | 8.73E-03 | 2.83E-01 | 2.40E-03 | 7.75E-06 | 8.90E-01 | 2.25E-02 | 1 | |||
| WT 240 | 2.21E-01 | 1.91E-01 | 1.77E-06 | 1.06E-09 | 6.45E-02 | 7.62E-01 | 1.70E-01 | 1 | ||
| WT 300 | 1.37E-01 | 7.28E-01 | 3.96E-11 | 1.17E-16 | 2.26E-04 | 4.35E-01 | 3.41E-02 | 2.05E-01 | 1 | |
| WT 360 | 6.95E-06 | 4.57E-04 | 1.78E-14 | 3.85E-18 | 4.31E-07 | 2.19E-02 | 5.30E-06 | 2.96E-03 | 1.86E-03 | 1 |
| re 0 | 5.42E-01 | 4.41E-01 | 1.66E-08 | 5.24E-12 | 7.47E-03 | 6.57E-01 | 2.27E-02 | 3.22E-01 | 6.72E-01 | 2.24E-03 |
| re 30 | 4.30E-03 | 1.07E-01 | 2.31E-09 | 6.98E-15 | 6.05E-04 | 5.25E-01 | 2.68E-03 | 1.20E-01 | 2.64E-01 | 1.29E-01 |
| re 60 | 3.18E-02 | 2.52E-01 | 3.99E-05 | 3.47E-08 | 6.67E-01 | 2.58E-01 | 5.64E-01 | 3.22E-01 | 7.54E-03 | 2.08E-04 |
| re 90 | 9.48E-02 | 1.71E-01 | 5.20E-07 | 3.47E-11 | 4.85E-01 | 2.24E-02 | 7.43E-01 | 7.91E-02 | 3.90E-03 | 9.46E-07 |
| re 120 | 2.34E-01 | 6.17E-01 | 1.71E-05 | 1.53E-08 | 1.75E-01 | 1.93E-01 | 3.07E-01 | 3.49E-01 | 1.23E-01 | 1.42E-03 |
| re 150 | 1.25E-01 | 7.82E-02 | 1.19E-05 | 8.39E-09 | 7.20E-02 | 7.46E-01 | 2.37E-01 | 6.74E-01 | 4.47E-01 | 7.89E-03 |
| re 180 | 5.45E-01 | 7.65E-01 | 5.61E-05 | 1.60E-07 | 9.28E-02 | 1.33E-01 | 2.87E-01 | 2.10E-01 | 1.72E-01 | 6.23E-04 |
| re 240 | 3.25E-01 | 1.59E-01 | 7.56E-12 | 3.15E-17 | 4.85E-04 | 4.09E-01 | 7.77E-03 | 1.00E-01 | 9.24E-01 | 3.85E-03 |
| re 300 | 7.68E-08 | 3.65E-05 | 1.04E-19 | 5.04E-26 | 1.70E-10 | 1.56E-03 | 1.57E-07 | 8.73E-05 | 5.30E-04 | 9.55E-01 |
| re 360 | 2.66E-03 | 1.41E-02 | 2.30E-11 | 4.37E-16 | 4.11E-05 | 1.86E-01 | 5.70E-04 | 2.94E-02 | 1.33E-01 | 3.42E-01 |
| FFAT 0 | 2.16E-08 | 1.63E-05 | 2.63E-26 | 1.57E-35 | 1.82E-14 | 2.14E-04 | 3.36E-08 | 4.44E-07 | 8.81E-04 | 6.13E-01 |
| FFAT 30 | 4.18E-04 | 1.86E-03 | 2.40E-14 | 9.89E-23 | 1.34E-05 | 5.31E-01 | 3.39E-04 | 7.37E-02 | 8.11E-02 | 1.46E-01 |
| FFAT 60 | 3.15E-03 | 2.76E-02 | 4.25E-18 | 1.40E-28 | 8.76E-07 | 3.23E-01 | 1.62E-03 | 2.19E-02 | 3.72E-01 | 2.38E-02 |
| FFAT 90 | 3.56E-04 | 4.40E-02 | 5.60E-15 | 7.76E-24 | 6.60E-06 | 4.55E-01 | 3.16E-04 | 2.57E-02 | 1.53E-01 | 1.17E-01 |
| FFAT 120 | 6.61E-03 | 5.26E-02 | 2.53E-07 | 6.48E-13 | 6.16E-01 | 8.05E-03 | 2.85E-01 | 7.30E-02 | 8.85E-04 | 2.57E-07 |
| FFAT 150 | 9.00E-04 | 4.81E-02 | 1.10E-05 | 4.92E-11 | 8.43E-01 | 8.78E-03 | 6.00E-01 | 7.37E-02 | 3.81E-04 | 7.15E-08 |
| FFAT 180 | 7.12E-02 | 4.75E-01 | 1.04E-08 | 3.06E-16 | 8.89E-02 | 2.17E-01 | 1.84E-01 | 8.00E-01 | 2.45E-02 | 2.68E-05 |
| FFAT 240 | 1.20E-05 | 3.16E-04 | 2.07E-22 | 2.66E-33 | 1.16E-08 | 9.77E-02 | 5.53E-05 | 4.28E-03 | 1.67E-02 | 1.63E-01 |
| FFAT 300 | 1.30E-08 | 1.85E-05 | 2.48E-24 | 1.63E-36 | 6.29E-10 | 4.99E-02 | 3.12E-07 | 5.04E-04 | 7.93E-04 | 6.19E-01 |
| FFAT 360 | 5.78E-04 | 4.31E-03 | 5.19E-14 | 8.54E-21 | 2.98E-05 | 4.75E-01 | 1.05E-03 | 5.86E-02 | 9.68E-02 | 8.38E-02 |
| re 0 | re 30 | re 60 | re 90 | re 120 | re 150 | re 180 | re 240 | re 300 | re 360 | |
| re 0 | 1 | |||||||||
| re 30 | 2.76E-01 | 1 | ||||||||
| re 60 | 1.24E-01 | 3.90E-02 | 1 | |||||||
| re 90 | 9.41E-02 | 1.03E-03 | 7.12E-01 | 1 | ||||||
| re 120 | 3.57E-01 | 1.15E-01 | 7.33E-01 | 7.56E-01 | 1 | |||||
| re 150 | 5.23E-01 | 3.97E-01 | 2.68E-01 | 1.23E-01 | 2.59E-01 | 1 | ||||
| re 180 | 4.50E-01 | 4.61E-02 | 6.60E-01 | 8.02E-01 | 7.77E-01 | 1.78E-01 | 1 | |||
| re 240 | 7.66E-01 | 2.98E-01 | 2.73E-02 | 1.25E-02 | 1.62E-01 | 3.56E-01 | 1.74E-01 | 1 | ||
| re 300 | 1.62E-03 | 1.96E-02 | 5.96E-07 | 1.74E-08 | 7.76E-05 | 1.01E-03 | 5.13E-05 | 1.42E-03 | 1 | |
| re 360 | 5.36E-02 | 7.49E-01 | 2.47E-03 | 4.81E-04 | 9.46E-03 | 1.55E-01 | 2.11E-02 | 1.45E-01 | 2.12E-01 | 1 |
| FFAT 0 | 2.85E-04 | 1.83E-03 | 1.40E-09 | 2.85E-10 | 2.60E-06 | 9.32E-05 | 3.19E-06 | 1.92E-03 | 4.55E-01 | 1.04E-01 |
| FFAT 30 | 1.62E-01 | 7.87E-01 | 4.52E-03 | 7.63E-05 | 1.54E-02 | 2.20E-01 | 3.21E-03 | 3.79E-02 | 2.00E-02 | 8.66E-01 |
| FFAT 60 | 2.73E-01 | 6.86E-01 | 9.81E-04 | 3.47E-04 | 2.63E-02 | 2.14E-01 | 4.80E-02 | 4.46E-01 | 1.03E-02 | 2.27E-01 |
| FFAT 90 | 1.35E-01 | 8.60E-01 | 1.54E-03 | 4.81E-05 | 1.54E-02 | 2.82E-01 | 2.04E-02 | 1.80E-01 | 1.70E-02 | 4.59E-01 |
| FFAT 120 | 5.84E-02 | 3.23E-04 | 6.08E-01 | 8.62E-01 | 6.16E-01 | 4.91E-02 | 5.04E-01 | 2.19E-03 | 8.92E-10 | 6.44E-05 |
| FFAT 150 | 1.20E-02 | 1.35E-04 | 5.09E-01 | 4.45E-01 | 3.38E-01 | 6.26E-02 | 1.52E-01 | 5.80E-04 | 1.88E-10 | 2.80E-05 |
| FFAT 180 | 1.44E-01 | 1.16E-02 | 5.21E-01 | 3.68E-01 | 6.85E-01 | 3.48E-01 | 5.75E-01 | 5.58E-02 | 7.71E-07 | 6.85E-03 |
| FFAT 240 | 4.46E-02 | 6.76E-01 | 1.06E-04 | 7.64E-06 | 3.58E-03 | 1.34E-01 | 1.45E-03 | 3.62E-02 | 5.41E-02 | 5.69E-01 |
| FFAT 300 | 9.22E-03 | 2.01E-01 | 2.53E-05 | 5.27E-09 | 5.74E-04 | 8.18E-03 | 3.23E-04 | 2.93E-03 | 1.97E-01 | 5.41E-01 |
| FFAT 360 | 9.73E-02 | 8.01E-01 | 1.23E-02 | 1.01E-04 | 9.43E-03 | 3.93E-01 | 5.38E-03 | 5.11E-02 | 1.91E-02 | 5.66E-01 |
| FFAT 0 | FFAT 30 | FFAT 60 | FFAT 90 | FFAT 120 | FFAT 150 | FFAT 180 | FFAT 240 | FFAT 300 | FFAT 360 | |
| FFAT 0 | 1 | |||||||||
| FFAT 30 | 1.36E-03 | 1 | ||||||||
| FFAT 60 | 2.76E-03 | 4.05E-02 | 1 | |||||||
| FFAT 90 | 6.91E-03 | 1.69E-01 | 5.21E-01 | 1 | ||||||
| FFAT 120 | 4.33E-13 | 9.88E-06 | 6.01E-06 | 5.22E-06 | 1 | |||||
| FFAT 150 | 2.87E-14 | 2.78E-06 | 1.35E-06 | 1.52E-06 | 6.68E-01 | 1 | ||||
| FFAT 180 | 4.66E-10 | 2.16E-03 | 1.87E-03 | 1.40E-03 | 1.14E-01 | 9.38E-02 | 1 | |||
| FFAT 240 | 1.27E-02 | 8.47E-01 | 4.13E-02 | 1.60E-01 | 4.77E-09 | 1.99E-08 | 1.38E-04 | 1 | ||
| FFAT 300 | 4.09E-02 | 3.31E-01 | 6.34E-03 | 3.01E-02 | 6.04E-11 | 3.20E-12 | 2.31E-07 | 2.88E-01 | 1 | |
| FFAT 360 | 1.74E-03 | 9.45E-01 | 6.38E-02 | 1.72E-01 | 7.69E-06 | 6.83E-06 | 7.23E-03 | 8.08E-01 | 1.28E-01 | 1 |
Next, we compared our experimental distance measurements with theoretical predictions based on the chromosome-refolding model described above. The probability distribution of distances between HML and MAT at time is
| [3] |
which accounts for the fact that a fraction of cells has HML and MAT in a synapsed state. The distance distribution is computed from the polymer model assuming that HML and MAT are in contact, whereas corresponds to the situation when there is no contact between HML and MAT (Fig. 1D).
As shown in Fig. 2C we find excellent agreement between the theoretical and experimentally measured distance distribution . To make the comparison we used a maximum likelihood procedure that takes into account all of the data obtained at different time points; this approach produces the most likely values of at different time points (Materials and Methods), which are given in the insets of individual graphs in Fig. 2C. These values of are plotted as a function of time in Fig. 3B and compared with the prediction of the chromosome-refolding model, Eq. 1. (This experimental test of the model is discussed in detail in Results, Chromosome Refolding Quantitatively Accounts for Donor Preference in Mating-Type Switching.)
Fig. 3.
Change in chromosome folding quantitatively accounts for donor preference in mating-type switching. (A) Quantitative analysis of donor use in yeast mating-type switching is done by a PCR and restriction digest-based assay (39). Each lane is the digested product of the switch experiment for the corresponding strain. The top bands show MATα and the lower two bands show the digested MATα-BamHI. Average use of the HML donor is given with its SD (a minimum of three replicate experiments). The numbers are computed by taking the ratio of the intensities of the top band to the sum of all three bands for each lane. In the absence of RE (middle lane), HML is the preferred donor only 9.5% ± 0.3 of the time, whereas the wild-type (left lane) donor use is 92% ± 2, which is consistent with the previous results from our laboratory (38, 39, 43). The rightmost lane corresponds to a strain where HML mobility is constrained by tethering the proximal LacO array to the nuclear envelope, and it shows use of HML during mating-type switching reduced to 64% ± 1. (B–D) Change over time of the fraction of cells with HML and MAT paired, for wild-type, RE-deleted, and LacO-tethered strains, respectively. Red curves represent the theoretical predictions (Eq. 1) with the rate parameters (Table 1) obtained using a maximum likelihood procedure. Error bars represent 95% confidence intervals obtained through maximum likelihood estimation when fitting theoretical LacO–TetO distance distributions to experimental distance distributions (Fig. 2C).
Deletion of RE disrupts chromosome refolding during mating-type switching.
To test the idea that RE is responsible for chromosome refolding after the DSB at MAT we constructed a yeast strain with RE deleted and repeated the quantitative microscopy time-course analysis described above to obtain for this mutant. The model predictions from Eq. 3 agree with the measured distance distributions at each time point (Fig. S2). Notably, we find that the probability of an HML–MAT synapsed state is dramatically reduced compared with that observed for wild-type cells; compare Fig. 3 B and C. These data confirm that in MATa cells RE increases the probability of contacts between the HML and MAT locus after the DNA break (39).
Chromosome tethering to the nuclear envelope disrupts its refolding during mating-type switching.
To further explore the role of the spatial organization of Chr III in determining donor preference during mating-type switching, we constructed a mutant strain in which the region near HML would be more strongly tethered to the nuclear envelope. LacI-GFP was fused to a nuclear membrane-targeting FFAT peptide motif (two phenylalanines in an acidic tract) (23, 59, 60) so that Chr III was tethered to the nuclear periphery at the LacO operator array, the center of which is 7 kb proximal to HML. This tethering should limit the mobility of HML and act in opposition to RE by reducing the probability of HML–MAT contacts, and should therefore lead to a decrease in the use of HML as a donor when the DSB at MAT is repaired. (The measurements of donor preference, consistent with this prediction, are described below.)
Measurements of distances between HML and MAT in this strain, after the DNA break is induced, are again in agreement with the polymer model prediction, Eq. 3 (Fig. S3). Now, in addition to the tethering of the telomeres to the nuclear periphery shown in Fig. 1C, we add to the model a tethering interaction between the LacO operator array and nuclear envelope. Our model assumes that the probability of tethering interaction between FFAT and membrane receptors occurring is 0.8, which was measured experimentally in a previous study (59) (and discussed further in Materials and Methods).
As in the previous two cases, comparison of the measured distance distribution and the theoretical prediction given by Eq. 3 yields a maximum likelihood value of the looping probability , which is plotted in Fig. 3D. Comparison between Fig. 3 B and D leads to the conclusion that the extra tethering interaction reduces the probability of HML–MAT synapse formation compared with wild-type cells.
Chromosome Refolding Quantitatively Accounts for Donor Preference in Mating-Type Switching.
So far, our in vivo experiments give support to the idea that RE-mediated refolding of Chr III accompanies mating-type switching in MATa cells. Next we demonstrate that changes in the folded state of the chromosome after the DSB quantitatively account for donor preference in mating-type switching.
We measured the relative use of the HML and HMR donors during MAT switching in wild-type and mutant MATa cells with a PCR-based assay as described previously (38–40, 43). Fig. 3A shows the average experimental donor uses for the wild-type and mutant cells ( for each), which we use to compute the donor ratio by taking the ratio of HML to HMR use. In agreement with previous studies (38–40, 61), we find that in the absence of RE HML is used only 9.5 ± 0.3% of the time (, as opposed to the 92 ± 2% ( wild-type case where RE is present. Similarly, when we artificially tethered the HML proximal LacO array to the nuclear envelope and repeated the same measurement the average of three independent experiments showed that HML donor use drops significantly, to 64 ± 1% () (Fig. 3A).
Next we asked to what extent the chromosome-refolding model is in quantitative agreement with our measurements of donor ratios. To make this comparison, we use a maximum likelihood procedure to fit Eq. 1 to the values extracted from distance data (Fig. 2 and Figs. S2 and S3), while taking into account the relation between donor ratio and the rates of synapse formation, . To take into account the time delay () between the time at which the cells are exposed to galactose and the time at which HO cuts the DNA at the MAT locus, we replace with in Eq. 1.
The maximum likelihood procedure yields the rates and time delay shown in Table 1, which are all consistent with the conclusions of ChIP and PCR measurements regarding the timing of different events in the course of MAT switching (35, 39, 51). In Fig. 3 B–D we show the comparison between our measurements and Eq. 1, which was computed using the rates shown in Table 1.
Table 1.
Rate parameters of the chromosome-refolding model of mating-type switching
| Strain name (genotype) | Rate of HML–MAT synapse kL, h−1 | Rate of HMR–MAT synapse kR, h−1 | Rate of repair r, h−1 | Time delay , min |
| YBA009 (wild-type) | 1.4 (1.0, 2.0) | 0.093 (0.066, 0.13) | 0.50 (0.45, 0.56) | 20 (7, 20) |
| YBA013 (LacO-tethered) | 0.63 (0.50, 0.89) | 0.37 (0.29, 0.52) | 0.50 (0.45, 0.56) | 20 (7, 20) |
| YBA010 (RE-deleted) | 0.32 (0.11, 0.63) | 2.9 (1.0, 5.7) | 0.50 (0.45, 0.56) | 20 (7, 20) |
The parameters were determined using a maximum likelihood procedure for comparing the theoretical prediction of the model (Eq. 1) with data obtained from the three different strains of yeast, shown in Fig. 3 B–D. The numbers in parentheses correspond to the 95% confidence interval for each parameter.
Another prediction of the chromosome-refolding model of mating-type switching is that the donor ratio () is given by the relative probabilities of contact of the MAT locus with the left and the right donor, after the DNA break at MAT (Eq. 2). These contact probabilities can be computed based on the random-walk polymer model of interphase chromosomes while taking into account the binding affinity of RE to MATa after the DSB (23, 62). To test this we examined previously published data on donor preference for yeast strains in which RE and the HML donor were moved to different locations on Chr III, or RE was removed and the location of HML was varied (43).
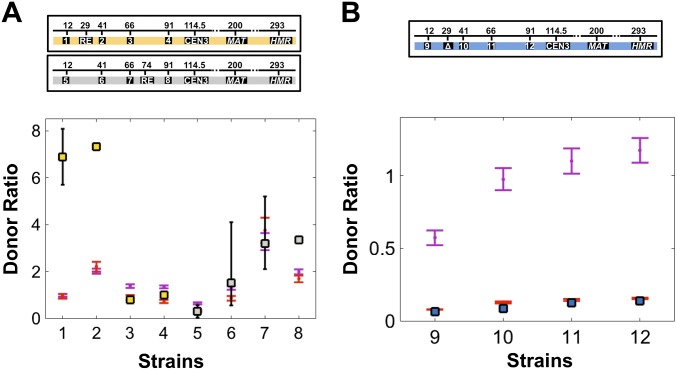
In Fig. 4A we compare the computed probability for HML being in contact with MAT ) and the measured donor ratio for eight different strains from ref. 43. In the case of strains in which RE is removed (Fig. 4B), there is only one state with HML in contact with MAT (Fig. S4), so the corresponding contact probability is . The refolding model predicts a linear relationship between the donor ratio and the probability of an HML–MAT contact (Eq. 2), which is consistent with the data from ref. 43, except for a few significant outliers.
Fig. 4.
Chromosome-refolding model of yeast mating-type switching quantitatively explains changes in donor preference. Comparison of the computed contact probability between HML and MAT (red points) with experimentally determined donor ratios taken from ref. 43 (squares). For each strain, we plot a point whose y coordinate indicates the strain’s experimentally measured donor ratio and whose x coordinate is the probability of an HML–MAT contact calculated from the polymer model. The model assumes all strains containing RE (strains 1–8) have the same probability of an HMR–MAT contact and therefore the donor ratio (Eq. 2) is predicted to be the probability of an HML–MAT contact multiplied by a constant (i.e., the reciprocal of the contact probability between HMR and MAT), as indicated by the red line. Likewise, the model assumes all strains lacking RE (strains 1–4) have the same probability of an HMR–MAT contact. (A) To compute the contact probability between HML and MAT , we assumed that contact occurs when the distance between these two loci is less than 10 nm. We also determined the probability of RE bound to MAT to be 0.58 for strains 1–4 and 0.63 for strains 5–8; this difference is due to the entropic contribution to the probability, which stems from different positions of RE (Supporting Information). Experiments had either RE at its wild-type position (yellow data points) or positioned 74 kb from the left telomere (gray data points), whereas HML was moved to different locations (indicated by labels 1–8). (B) In the absence of RE the contact probability between HML and MAT is simply ; this contact probability was computed assuming a cutoff distance of 10 nm for a contact to occur. Data (blue data points) from ref. 40 correspond to different location of HML (labels 9–12). Error bars on both the experimental data (where available) and our polymer simulations (red squares) represent 95% confidence intervals. The errors on the simulated data are due to the finite number of chromosome configurations generated in our simulations.
Fig. S4.
Thermodynamic model of the folded state of Chr III in the absence of RE. In the absence of RE there are only three possible states as opposed to the six shown in Fig. 1B: the unlooped state and two looped states, with either HML (gray) or HMR (black) in contact with MAT (white). The thermodynamic weights of the looped states correspond to the fraction of polymer conformations that have a contact between two loci, either HML–MAT or HMR–MAT.
An important assumption we make in Fig. 4 is that moving HML and RE along the left arm of Chr III does not affect the probability for an HMR–MAT contact, which is the denominator in the equation for the donor ratio (Eq. 2). In the case of strains with RE present, the probability of an HMR–MAT contact is , whereas in the absence of RE it is just (Fig. S4). Also, in strains in which RE is present, to compute the contact probabilities we need the binding energy () between RE and MAT (Fig. 1B). We account for this parameter of the model by extracting the probability that RE is bound to MAT, , from the experimental data (see Supporting Information for details). We find good agreement between the theory and experiments for when RE is at its wild-type position (29 kb from left telomere) and when it is placed 74 kb away from the left telomere. This difference in is completely accounted for by the entropic factor (i.e., the thermodynamic weight ), which is different for different positions of RE on Chr III.
Discussion
Recent advances in imaging and chromosome conformation capture techniques combined with polymer models of chromosomes have greatly improved our understanding of the spatial organization and dynamics of chromosomes within the nucleus. However, the quantitative relationship between polymer physics and in vivo chromosome biology remains elusive. In this study, we provide a theoretical framework and direct biological evidence for nuclear organization being modified so as to regulate the repair of a DNA double-stranded break via homologous recombination. Our model makes quantitative predictions about the dynamics of the selection of competing donor loci for homologous recombination during mating-type gene switching in yeast, which is a well-established eukaryotic model system for this ubiquitous DNA break-repair process.
The key idea of the chromosome-refolding model is that the chromosome conformation changes after the DNA break so as to direct mating-type switching in yeast by favoring one donor over the other (Fig. 1 A and B). The model makes specific quantitative predictions, which we test experimentally. We measured the distribution of distances between the left donor and the MAT sequence before and at different times after the DNA break at MAT. We also measured the preference of using the left donor over the donor on the right arm of Chr III. We repeated these experiments for wild-type and mutant cells and found agreement between our data and predictions of the chromosome-refolding model. Notably, by tethering the left arm of Chr III to the nuclear periphery so as to change the folded state of the chromosome after the break, and therefore reduce the contact probability between HML and MAT, we were able to reduce the preference for the left donor (Fig. 3). Similarly, by deleting the RE sequence, which in previous experiments has been shown to associate with chromatin close to the break at MAT, we were able to show a significant reduction in contact probability between HML and MAT, and this too led to a reduction in the use of the left donor, consistent with conclusions from previous studies (38, 39).
The refolding model quantitatively relates the frequencies of recombination between HML and MAT for different mutant strains (Fig. 4), which strongly suggests that the rate of formation of a synapse between HML and MAT ( is dictated by the polymer nature of yeast chromatin. Notably, for the wild-type strain (1 in Fig. 4A) the theory and experiment seem to be in disagreement. One possible explanation might be heterogeneities in the degree of compaction of DNA into yeast chromatin throughout Chr III (63, 64). If the chromatin in the wild-type strain is more compact in the region between HML and RE, the physical length of the chromosome between HML and RE would be shorter than the length used in our calculations, making HML be even closer to MAT when RE and MAT are bound. When included in our polymer model of Chr III this local chromatin compaction can account for the discrepancy noted above (Supporting Information).
Although our polymer model accurately accounts for the variations in the donor ratio for different strains in which sequences on the left arm of Chr III are mutated (Fig. 4), Eq. 2 does not successfully reproduce the absolute value of the donor ratio for most strains. For example, in strains deleted for RE the predicted donor ratio values are an order of magnitude greater than those measured in experiments (43): For strains 9–12 in Fig. 4B our polymer calculations yield absolute donor ratio values of , and , respectively, whereas the experimental values are about 10 times smaller (, and , respectively. Given our finding that the refolding model accounts quantitatively for the rate of synapse formation between HML and MAT, we are left with the surprising conclusion that the probability of HMR contacting MAT is higher than expected. This conclusion is bolstered by our finding that the value of the rate of synapse formation between HMR and MAT () is significantly larger in RE-deleted strains than in wild-type cells (Table 1). Moreover, an estimate of the increase in upon RE deletion can be obtained from the ratio of the slopes of the best-fit lines in Fig. 4 A and B (Supporting Information). In this way we compute an increase in by a factor of 3.3 (2.4–8.5 is the 95% confidence interval), which is also consistent with measured HML–MAT distances after the DSB in wild-type and mutant yeast cells (Fig. S5 and Table S3).
Fig. S5.
Comparison of theoretical and measured probability of synapse between HML and MAT after the DSB. (A–C) The fraction of cells with HML–MAT pairing over time for wild-type, RE-deleted, and LacO-tethered strains, respectively. Red curves correspond to (Eq. 1) in which rate parameters from Table S3 were used. Error bars represent 95% confidence intervals obtained through maximum likelihood estimation when fitting simulated LacO–TetO distance distributions to experimental distance distributions.
Table S3.
Rate parameters of the chromosome-refolding model of mating-type switching, assuming fixed kR ratios
| Strain name (genotype) | Rate of HML–MAT synapse kL, h−1 | Rate of HMR–MAT synapse kR, h−1 | Rate of repair r, h−1 | Time delay , min |
| YBA009 (wild-type) | 3.4 (2.9, 3.2) | 0.23 (0.19, 0.23) | 0.53 (0.48, 0.60) | 20 (18, 20) |
| YBA013 (LacO-tethered) | 0.39 (0.33, 0.37) | 0.23 (0.19, 0.23) | 0.53 (0.48, 0.60) | 20 (18, 20) |
| YBA010 (RE-deleted) | 0.21 (0.18, 0.22) | 1.9 (1.6, 2.0) | 0.53 (0.48, 0.60) | 20 (18, 20) |
The parameters were determined using a maximum likelihood procedure for comparing the theoretical prediction of the model (Eq. 1) with data obtained from three different strains of yeast. When fitting the rate values, we impose the constraint that kR be the same in the wild-type and LacO-tethered strain, and the ratio of kR in the RE-deleted strain to kR in the wild type is constrained to be 8.5. The constraint on the ratio of RE-deleted kR to wild-type kR is discussed in Supporting Information; 8.5 was chosen because it gives the best fit to of any value within the 95% confidence interval of possible kR ratios. The numbers in parentheses define the 95% confidence interval for each parameter.
An increase of contact probability between HMR and MAT in RE-deleted cells could be explained by the presence of a heretofore unidentified mating-type-independent RE-like element located in the vicinity of HMR. In cells in which RE is active we speculate this RE-like element will be ineffective, being outcompeted by RE for binding to MAT. This possibility is supported by the observations of Ostrow et al. (65), who found several Fkh1 binding sites within a few tens of kilobases proximal to HMR; such sites, in the absence of RE binding to MAT, might draw HMR closer to the DSB in a fashion similar to the way RE does for HML. We tested this possibility by performing polymer simulations that include an Fkh1 binding site located 5 kb proximal to HMR, which could bind to MAT after the break. The computed donor ratio is consistent with the experimentally measured donor ratio in MATa cells deleted for RE (Fig. S6), whereas it does not significantly affect the computed donor ratio in the presence of RE.
Fig. S6.
Predicted donor ratios for models with or without an Fkh1 binding site near HMR. (A) Strains that contain RE and (B) strains in which RE is deleted. The experimental donor ratios are shown in black squares filled either with yellow (1–4 in A), gray (5–8 in A), or blue (9–12 in B). Magenta data points show the predicted donor ratios for the model used throughout the paper in which RE can bind to MAT after the DNA break at MAT ( is determined from maximum likelihood). Data points shown in red are the predicted donor ratios for the model in which, in addition to MAT binding to RE, MAT can bind to an Fkh1 binding site 5 kb proximal to HMR, but MAT cannot bind both loci simultaneously. As seen in B, the model with the Fkh1 binding site predicts the donor ratio much more accurately than the model described in the main text. For the model with the Fkh1 binding site, the parameter values used to model the strains containing RE are the following: MAT binds to RE in 77% of the cells, MAT binds to the HMR-proximal Fkh1 site in 19% of the cells, and MAT binds neither locus in 4% of the cells. For the interaction of MAT and the HMR-proximal Fkh1 site we use the same binding energy regardless of whether the strain contains RE or not. Thus, in strains in which RE is deleted MAT binds the HMR-proximal Fkh1 site in 82% of cells because RE does not compete to bind MAT. Because there are only 1.6 Kuhn segments between HMR and the HMR-proximal Fkh1 site, the worm-like chain model is used to calculate the probability of HMR–MAT contact in the case when MAT is bound to the HMR-proximal Fkh1 site. We use the formula for the worm-like chain end-to-end distance distribution from ref. 69. Error bars represent 95% confidence intervals.
A larger-than-expected synapsing of HMR with MAT is also consistent with results of experiments by Renkawitz et al. (51), who investigated the genome-wide Rad51 binding to chromatin after inducing a DSB at MAT. They showed that both in MATa cells deleted for RE and in MATα cells Rad51 binding within a region 50 kb proximal to HMR was almost fourfold higher than for the rest of the Chr III. This suggests that the collisions between these sites on the right arm and Rad51 bound to ssDNA near MAT are more frequent than collisions with the rest of the chromosome.
The possibility of RE being in competition with an RE-like HMR proximal sequence for binding to MAT is consistent with findings of Li et al. (39), who created strains in which RE was replaced by LexA operators. In one strain they expressed a fusion protein of LexA and the FHA domain of Fkh1, which bound to LexA operators independent of the presence of the DSB but only bound near MAT after DSB induction. The donor preference of this strain is similar to that measured in wild-type cells, whereas in the strain without the fusion protein the donor preference is close to what is observed in RE-deleted cells. Because the polymer nature of the chromosome cannot account for the roughly 100-fold change in donor ratio, we are again led to the conclusion that FHA-induced binding of the LexA operators to MAT must have an additional effect on donor preference besides bringing HML and MAT into close proximity. One possibility is that this binding blocks the purported binding of MAT to Fkh1 binding sites near HMR.
The thrust of this paper is a quantitative comparison between measurements of chromosome conformations during DNA break repair by homologous recombination, and a model that connects the spatial organization of the chromosome to this function. This type of comparison between theory and experiments is particularly powerful in yeast, which has the distinction that the spatial organization of its chromosomes is well described by the simplest of polymer models, the random-walk chain (23, 27–29). In all other cells studied to date, polymer properties of interphase chromosomes are such that mechanisms other than polymer entropy have been invoked to explain the observed spatial organization of their chromosomes (66). We believe that this makes yeast an excellent model system in which to study the quantitative relationship between chromosome organization and chromosome function. In particular, novel molecular mechanisms could be identified upon finding significant deviations between predictions based on the random-walk model of the yeast chromosomes and measurements in which chromosome function is perturbed by changing chromosome conformation. This is exemplified nicely by this study, where our inability to correctly account for the measured value of donor preference (while correctly accounting for changes in donor preference and the observed chromosome conformations) in wild-type and mutant yeast strains strongly suggests that RE-like sequences might be present on the right arm of Chr III. The presence of Fkh1 binding sites on the right arm also gives us a reasonable hypothesis for the nature of these RE-like sequences, and a specific target for future experiments. We believe that similar quantitative comparisons between polymer models of chromosomes and experiments that perturb chromosome organization and measure concomitant changes in chromosome function will help further establish causal links between the spatial organization of chromosomes and their cellular functions.
Materials and Methods
Yeast Strains and Plasmids.
The yeast strains used in this study can be found in Table S4. All strains used were variants of YDB076 (56). YDB101 was constructed by transforming YDB076 with NheI digest of pDB030 (56). YBA008 and YBA011, the strains carrying the TetO array 5 kb distal to MAT, were constructed by transforming YDB101 and YDB076, respectively, with the BamHI + XbaI restriction fragment of pJH2145 (J.E.H. laboratory plasmid collection). YBA009 and YBA012, the strains with fluorescent labeling of the TetO array distal to MAT, were constructed by transforming YBA008 and YBA011, respectively, with HpaI digest of pBA002 to integrate the URA3pro-TetR-mRFP-ADHter-C.glabrataTRP1 in yGL119w intergene. pBA002, the plasmid carrying the TetR-mRFP fusion construct, was derived by subcloning the Candida glabrata TRP1 gene (BamHI and NotI digest of pJH2778; J.E.H. laboratory plasmid collection) gene fragment into plasmid containing CgLEU2-TetR-mRFP-iYGL119W (a gift from Yuko Nakajima, Brandeis University, Waltham, MA) cut with the same to replace the CgLEU2. YBA010, the strain that is deleted for RE, was constructed by transforming YBA009 with the PCR product carrying hygromycin resistance gene (hphMX6) amplified from pAG32 (67) with primers (sense: AAACTCTTCTCAAAACCAAATTGCGCAAGGATTGATTCAGTACAATTATGcggatccccgggttaattaa) and (antisense: CCTAGAATTTGGAATTGGATAATTTAACTCTTTAGAATATAACATCTACCgaattcgagctcgttt) (a gift from Anuja Mehta, Brandeis University, Waltham, MA). Here uppercase and lowercase letters show homologous sequences to RE and pAG32, respectively. Transformations were confirmed with PCR using sense (TGGCTGGGTTATAGTGAGCCCA) and antisense (GGGCACAGTCAATGAGTAGTAGA) primer pairs that show a 1,248-bp-long product band in wild-type cells and a 2,227-bp band in cells deleted for RE. YBA013 was constructed by transforming YBA012 with pBA001 cut with NheI. pBA001 was derived by subcloning a KAN-MX cassette, NotI restriction digest fragment from pJH1512 (J.E.H. laboratory plasmid collection) into the plasmid pGFP-FFAT-LacI (a gift from Jason Brickner, Northwestern University, Evanston, IL) (59) cut with the same (NotI).
Table S4.
List of yeast strains used in this study
| Strain | Genotype |
| YDB076 | ho HMLα HMLprox::LacO(256)-LEU2 MATa HMRα-BamHI ade1 ade3::GAL-HO leu2 trp1:hisG ura3-52 |
| YDB101 | YDB076 with HIS3::URA3pro-LacI-GFP-(KAN) |
| YBA008 | YDB101 with MATdist::TetO(112)-NAT |
| YBA009 | YBA008 with iYGL119W::URA3pro-TetR-mRFP-ADHter-C.glabrata TRP1 |
| YBA010 | YBA009 with re::HPH |
| YBA011 | YDB076 with MATdist::TetO(112)-NAT |
| YBA012 | YBA011 with iYGL119W::URA3pro-TetR-mRFP-ADHter-C.glabrata TRP1 |
| YBA013 | YBA012 with HIS3::HIS3pro-LacI-FFAT-GFP-(KAN-MX) |
Acquisition and Processing of Fixed Cell Images.
Images of fixed cells were acquired on Marianas spinning disk confocal microscopes (3i Intelligent Imaging Innovations) equipped either with a Cascade II:512 electron-multiplying CCD (EMCCD) camera (Photometrics) or with a QuantEM: 512SC EMCCD camera (Photometrics). The pixel size of the images taken with the Cascade II:512 camera (at 150× magnification) is 107:107:230 nm (X:Y:Z) and for the images taken with the QuantEM: 512SC camera (at 120× magnification) is 129:129:270 nm (X:Y:Z); 16–20 Z-sections were acquired using a Plan-Apochromat 100×/1.4 oil M27 with a differential interference contrast prism with 1 × 1 binning along with a 1.5× or 1.2× optovar. Cells with multiple fluorescent spots of the same color and with deformed cell membrane were excluded from imaging to protect sample uniformity. Cells were imaged using a Semrock FITC cube Marianas excitation/emission filter cube set with exposure times of 100 ms with a 488-nm (50-mW) laser and exposure times of 300 ms with a 561-nm (50-mW) laser. Images were recorded with Slidebook software (3i Intelligent Imaging Innovations), converted into TIFF format, and analyzed with the ImageJ plugin SpotDistance (EPFL Biomedical Imaging Group) (58), with pixel sizes described above for x, y, and z axes to calculate the 3D distances between the fluorescent spots. Corresponding distance measurements are given in Supporting Information.
Galactose Induction of MAT Switching.
Single colonies were grown overnight in 5 mL yeast extract/peptone/dextrose (YEPD) media at 30 °C. The following day these cultures were washed with 5 mL of fresh media in which YEPD was replaced with YEP-lactate and grown for at least 6 h. Then a small portion of the saturated cultures were inoculated into fresh YEP-lactate media such that they would reach a density of 5 to per mL within 10 h (average time at which cells begin to grow logarithmically starting from the G0 phase) at 30 °C. Once the cultures reached the appropriate density, a t = 0 sample was taken to be fixed for imaging or to check the mating type at the beginning of the experiment. HO was induced by adding galactose to a final concentration of 2% (wt/vol). At time points separated by 30-min intervals, samples were collected for 6 h. Each time point sample was fixed with paraformaldehyde to a final concentration of 2% (wt/vol). Dextrose was added [2% (wt/vol)] to the cultures 1 h after galactose addition to prevent further HO expression and to allow the cells to complete the mating-type switch.
Measurement of Donor Preference via a PCR-Based Assay.
Strains that were used for fluorescent measurements (YBA009, YBA010, and YBA013) were also assayed for donor preference, as described by Li et al. (39). Six hours after sample collection for the time-course experiments, genomic DNA from the remaining cultures was extracted using the MasterPure yeast DNA purification kit (Epicentre). The switched products were amplified using a Yα-specific PCR primer and another primer specific for sequences just distal to MAT. The PCR product was digested with BamHI restriction enzyme, and the digested samples were visualized on an agarose gel stained with ethidium bromide. Repair events using HMR show a 1,470-bp band, whereas when the HMR-BamHI cassette is used as a donor the PCR product is digested into two smaller bands with sizes 920 and 550 bp. HML donor preference was measured by taking the ratio of the intensities of the top band to the sum of all three bands for each lane. Following DNA extraction, PCR and restriction digest steps are followed. Agarose gel band signals were quantified using ImageJ (68).
Computational and Theoretical Methods.
Freely jointed chain simulation.
Yeast Chr III was simulated in MATLAB as a freely jointed chain. The number of segments in the chain is determined by the number of base pairs in the chromosome, the chromosome extension parameter γ, and the Kuhn length, as described previously (23). Each genetic locus is a point along the freely jointed chain whose location is determined based on the number of base pairs between the centromere and the center of the locus. The nuclear membrane is represented by a sphere of radius , and each chromosome conformation must remain entirely within this sphere. To mimic the natural variability in nuclear volume, for each trial of the simulation the sphere’s radius is randomly selected from a Gaussian distribution. We also model the nucleolus as a spherical cap at the south pole of the sphere, which chromosome conformations cannot penetrate (23).
Chromosome attachments are also included in the simulation. To represent the centromere’s attachment to the spindle pole body via a microtubule (2) the simulated chromosome’s centromere is positioned 50 nm from the north pole of the sphere. The simulated chromosome’s telomeres can be located anywhere on the surface of the sphere. When simulating strains with the FFAT fusion protein, in 80% of the conformations the point on the polymer chain representing the LacO array is located anywhere on the surface of the sphere, and in 20% of the conformations the LacO point is located anywhere within the sphere. The nuclear membrane association probability of is consistent with a previous experimental study (59) (Table S1). When simulating cases in which two loci are bound (e.g., RE bound to MAT), a certain fraction (determined by maximum likelihood or least squares) of the conformations have the two loci positioned at exactly the same point in space. To compute theoretical distance distributions, chromosome conformations are generated as random walks with all of the constraints described above, and the distance between the points representing genetic loci of interest is measured for each conformation. For consistency with the experimentally measured distributions, an additional procedure is implemented to take into account the random error due to the resolution of the microscope. Because of this random error, a particle’s measured position will be displaced from the particle’s true position, and this displacement is equally likely to be in any direction. We mimic this distance shift by including the microscope’s error in the simulation. Specifically, after each polymer simulation trial we randomly displace the simulated TetO position by adding a different random number to each of its Cartesian coordinates. The random numbers are chosen from a Gaussian distribution with a zero mean and a variance given by our estimate of the microscope’s random error, which we estimate to be 110 nm.
Table S1.
Parameter values used in the freely jointed chain simulations of Chr III
| Parameter | Value used in the model (range tested in MLE) |
| Mean nuclear radius (a) | 1.1 μm (0.8–1.2 μm) |
| SD of nuclear radius | 0.12 μm (0.04–0.14 μm) |
| Nucleolar volume fraction (VN) | 35% of the volume of a sphere of radius 1.1 μm (0–35%) |
| Chromosome extension parameter (γ) | 13 μm2/Mbp (3–13 μm2/Mbp) |
| FFAT association with nuclear envelope (pLacO-Teth) | 80% (50–86%) |
| SPB to centromere distance | 0.050 μm (0–0.200 μm) |
| Kuhn length | 0.200 μm (see ref. 21) |
| HML association with MAT [pL(t)] | 0 (before the DNA break), [0,1] (after the DNA break) |
The ranges of values tested during maximum likelihood estimation are shown in parentheses.
Maximum likelihood methods.
The values of the polymer model parameters, displayed in Table S1, are obtained by performing maximum likelihood estimation to fit the simulated LacO–TetO distance distributions to the experimental distributions. The values of the first four model parameters in Table S1 were determined by using the experimental distance distributions of the t = 0 min time points for the wild-type, the LacO-tethered, and the RE-deleted strains. The maximum likelihood procedure tested the parameter values spanning the range of values reported by previous experimental studies (Table S1). The parameter was fit using the LacO-tethered strain’s t = 0 min distance data. The supplementary information of ref. 23 describes how we determined what range of possible values to test in the maximum likelihood estimation. After the determination of the five polymer parameters, the looping fraction parameter was fit for each time point of each strain. values are displayed in Fig. 2 and Figs. S2 and S3. Note that is assumed to be 0 for the t = 0 min time points of all strains. The model contains two additional parameters that have little effect on the distance distributions (23). These parameters are the distance from the centromere to the spindle pole body and the Kuhn length.
As discussed above, simulated LacO–TetO distance distributions incorporate the microscope’s random error. We use these simulated distributions for maximum likelihood estimation. For all LacO–TetO distance distribution plots displayed we use 110 nm as the SD of the Gaussian from which we choose a distance for shifting each Cartesian coordinate. However, we estimate that the SDs could be as high as 220 nm for the x and y coordinates and 460 nm for the z coordinate. These estimates are based on the microscope’s resolution as well as a comparison of position measurements of single fluorescent beads in the red channel versus position measurements of the same beads in the green channel. Therefore, we repeated the maximum likelihood estimation using these larger SDs, and we still found agreement between the simulated and experimental distributions, as we did for the 110-nm error. Using the large SDs results in the maximum likelihood estimation’s finding slightly different values of three of the model parameters: The mean nuclear radius a is found to be 0.8 μm, and the nucleolar volume fraction VN is found to be 25% of the volume of a sphere of radius 0.8 μm (Table S1), and values are also somewhat higher than those in Fig. 2 and Figs. S2 and S3. Still, all of the main conclusions in Results remain unchanged.
Determination of rates of synapse formation.
For the three yeast strains the rates of synapse formation were obtained by using maximum likelihood estimation to fit Eq. 1 to , as shown in Fig. 3. The rates of synapse formation are displayed in Table 1. The start of the homology search begins a time after the addition of galactose because it takes time, up to 20 min (34), before HO finds and cleaves the MAT locus. Therefore, when fitting Eq. 1 to , we also included a lag time parameter , which simply shifts the plot of the function in Eq. 1 to the right by minutes. When performing maximum likelihood estimation we imposed the constraint that the parameters and be the same for all three strains because we assume that and do not vary from one strain to another. We also constrain the and values by requiring that the ratio of to be equal to the experimentally measured donor ratio for each strain. The values in Table 1 are determined by fitting to a obtained by assuming the microscope’s random error has an SD of 110 nm. We also found the rates of synapse formation by fitting to a obtained by assuming the microscope’s error has an SD of 220 nm for the x and y coordinates and 460 nm for the z coordinate. These values are displayed in Table S5 and are similar to those in Table 1. The ranges of rate values tested during maximum likelihood estimation are consistent with previous experiments (33).
Table S5.
Rate parameters of the chromosome-refolding model of mating-type switching, assuming the microscope’s random error is large
| Strain name (genotype) | Rate of HML-MAT synapse kL, h−1 | Rate of HMR–MAT synapse kR, h−1 | Rate of repair r, h−1 | Time delay , min |
| YBA009 (wild-type) | 4.0 (2.2, 6.3) | 0.26 (0.15, 0.42) | 0.32 (0.25, 0.40) | 20 (13, 20) |
| YBA013 (LacO-tethered) | 0.89 (0.56, 1.58) | 0.52 (0.33, 0.92) | 0.32 (0.25, 0.40) | 20 (13, 20) |
| YBA010 (RE-deleted) | 0.28 (0.11, 0.63) | 2.6 (1.0, 5.7) | 0.32 (0.25, 0.40) | 20 (13, 20) |
The parameters were determined using a maximum likelihood procedure for comparing the theoretical prediction of the model (Eq. 1) with data obtained from three different strains of yeast. When fitting the rate values, the microscope’s random error is assumed to have an SD of 220 nm for the x and y coordinates and 460 nm for the z coordinate. These rates are similar to those displayed in Table 1, in which the microscope’s error is assumed to have an SD of 110 nm for all Cartesian coordinates. The numbers in parentheses define the 95% confidence interval for each parameter.
Theoretical donor ratio calculation.
We use the chromosome-refolding model to compute the donor ratio, Eq. 2, for a variety of yeast strains described in ref. 43. In these experiments, donor ratio was measured for mutant strains in which HML and RE are located at different positions along Chr III, and in some strains RE is deleted. We use our polymer model to compute the entropic contributions to the thermodynamic weights in Fig. 1B. For example, is the fraction of chromosome conformations in which HML and MAT are within a small distance of each other. Based on the thickness of chromatin, a reasonable estimate of is between 0 and 50 nm. The effect that the chosen value of has on the computed donor ratio is negligible relative to the error bars on the computed donor ratios (red points in Fig. 4). The Boltzmann weights associated with states in which RE in bound to MAT also contain the Boltzmann factor , where is the binding energy between RE and MAT, which we treat as a fitting parameter of the model.
Experimental Donor Ratio Data for Wild-Type Cells
To calculate the mean and 95% confidence interval for the experimental value of strain 1 in Fig. 4A we used data from a number of studies all using an identical wild-type strain. The donor ratios from these studies (and their reference numbers) are the following: 9 (ref. 36); 9 (ref. 38); 9 (ref. 40); 5.7 (ref. 67); 5.7, 6.1, 6.1, and 8.1 (ref. 37); and 5.4 ± 1.2 (SD) (ref. 50).
Polymer Model Simulation Details
When performing random walks to generate chromosome conformations it is exceedingly rare to generate a conformation that fulfills all of the constraints described in Materials and Methods, Computational and Theoretical Methods, Freely Jointed Chain Simulation. To decrease the otherwise prohibitive simulation time, we developed an algorithm in which we alter conformations to fit the constraints. Each arm of Chr III is simulated as a random walk, starting from the centromere (located 50 nm below the north pole of the nuclear sphere). During each step of the random walk, the Kuhn segment is reoriented if it exits the nucleus or enters the nucleolus and is also reoriented so that chromosomal loci (telomeres, LacO, MAT, RE, HML, and HMR) are positioned according to the constraints. This reorientation, however, would result in the generation of some allowed conformations more frequently than others, in violation of the requirement that all freely jointed chain conformations that satisfy the constraints be equally likely. We therefore calculate the resulting increase in the probability of each conformation and assign to each conformation a weight to counteract the increase in the probability.
When performing simulations for Fig. 4A, a fraction of chromosome conformations have RE located at the same point in space as MAT. is 0.58 for strains 1–4 and 0.63 for strains 5–8 in Fig. 4A (the difference is accounted for by the different locations of RE on chromosome III in the two sets of strains; for more details see the next section). When simulating strains deleted for RE (Fig. 4B) the chromosome arms are independent random walks (i.e., MAT is not bound to RE or any other locus). When performing simulations for Fig. 2 and Figs. S2 and S3, a fraction of chromosome conformations have HML located at the same point in space as MAT.
When performing simulations for Fig. 4 and Fig. S6, the chromosome length used is that of wild-type yeast: 316 kb. When simulating yeast strains containing LacO and TetO we simulated an additional 10 kb of chromatin starting 1.5 kb proximal to HML, and we simulated an additional 5 kb of chromatin starting 5 kb distal to MAT (10 kb and 5 kb are the approximate lengths of LacO and TetO, respectively).
Donor Ratio Calculation Details
We use our freely jointed chain simulations to compute the donor ratio values measured experimentally in ref. 43. To do so, we rewrite the expression for the donor ratio D (Eq. 2) using quantitates whose values can be readily obtained using the freely jointed chain simulations.
First, note that in Fig. 1B each ω represents the multiplicity of a state divided by the total number of all possible microstates. For example, is the number of chromosome conformations in which HML is in close proximity to MAT divided by the total number of all possible chromosome conformations. We refer to each ω as the entropic probability of the state. We use the term “entropic probability” to differentiate it from a probability that depends on energy in addition to entropy.
In Eq. 2, we replace with , where is the entropic probability of HML and RE both coming in close proximity to MAT. We then replace with , where is the entropic probability that RE is in close proximity to MAT, and is the entropic probability that HML is in close proximity to MAT given that RE is already bound to MAT. Thus, we have
| [S1] |
The partition function Z is the sum of all of the thermodynamic weights in Fig. 1B:
| [S2] |
The third and fourth terms ( and ) are small compared to the first term, and the fifth and sixth terms ( and ) are small compared to the second term (), so neglecting the small terms we can rewrite the partition function simply as
| [S3] |
This simplification is justified for the following reasons: Although we do not know the precise values of and due to our ignorance of the cutoff distance that we use to decide when two genetic loci are in contact (discussed in Materials and Methods, Computational and Theoretical Methods, Theoretical Donor Ratio Calculation), these entropic probabilities are predicted by the polymer model to be between 10−6 and 10−3. Furthermore, we know that and are also much smaller than 1 because the experimentally measured donor ratios are all between about 0.1 and 10, so and must always be within an order of magnitude of the and values.
Plugging in Eq. S3 into Eq. S1, we obtain
| [S4] |
where
| [S5] |
is the fraction of cells in which RE is bound to MAT. is the binding energy of RE to MAT. It is a free parameter in our model, and it is assumed to be the same in all yeast strains in which RE is present. The value used for strains 1–4 in Fig. 4A is different from that of strains 5–8 because differs between strains in which RE is at different positions along the chromosome.
Derivations similar to the one above reveal that , , and . Plugging these results into Eq. 2, we obtain
| [S6] |
, , and are calculated using the freely jointed chain simulations, as discussed in Materials and Methods, Computational and Theoretical Methods. For many yeast strains (especially those deleted for RE), the simulated donor ratio values do not agree with the experimental donor ratio values when we use our freely jointed chain model to calculate and (Fig. S6), indicating that the model is incomplete. Therefore, to make the comparison between the refolding model and experimental results shown in Fig. 4A we do not use the freely jointed chain model to compute and , but rather we replace the denominator of Eq. S6 with a fitting parameter CA, which is assumed to be the same for all strains in Fig. 4A. This is tantamount to assuming that the folding of the right arm of Chr III in unperturbed when HML and RE are moved to different locations on the chromosome. Thus, the formula for the donor ratio that we use is
| [S7] |
This allows us to test our predictions of the frequency of HML recombination with MAT and how it depends on the position of HML and RE along the left arm of Chr III, without having to know the frequency of HMR recombination with MAT.
is assumed to be the same for all strains in Fig. 4A for the following reasons: (i) We assume that the frequency of HMR–MAT recombination is unaffected by the position of HML and (ii) strains 1–4 differ from strains 5–8 by the position of RE on Chr III, but the values for strains 1–4 and 5–8 are within 10% of each other, which results in no more than a 10% difference in (we assume that the difference in RE location affects only the value of and has no other effect on HMR–MAT recombination). Thus, it is a reasonable approximation to have the value of in strains 1–4 be the same as in strains 5–8.
Because the same value of is used for all strains 1–8, the predicted donor ratio (Eq. S7) is a linear function of the HML–MAT contact probability, with slope and a y intercept of 0. This predicted line is plotted in red in Fig. 4A using values of and that were determined through a maximum likelihood fit to only the experimental data points that have error bars (i.e., strains 1, 5, 6, and 7).
Because the data points in Fig. 4 generally lie on the red line, we see that there is agreement between the theory and experiment. However, it should be noted that there is little certainty in the values of the fitting parameters. Although the most likely value of is 0.58 for strains 1–4 and 0.63 for strains 5–8, there is a large uncertainty in this value: The 95% confidence interval is 0.11–1.00. The most likely value of is −13 or −8 kBT (depending on whether we choose a of 10 nm or 50 nm, discussed in Materials and Methods, Computational and Theoretical Methods, Theoretical Donor Ratio Calculation), which is the value used in the calculations for Fig. 4A, but because of the uncertainty in the uncertainty in is infinite.
For the strains in which RE is deleted there are no states in which RE is bound to MAT (Fig. S4), so the donor ratio is simply
| [S8] |
As before, we replace the denominator by a fitting parameter, which we call in this case:
| [S9] |
is assumed to be the same for all strains in Fig. 4B; is the slope of the line in Fig. 4B, and the value of is determined by a least-squares fit to all of the experimental data displayed in Fig. 4B.
Difference in HMR–MAT Synapse Formation Rates in the Absence and Presence of RE
The fitted value of tells us the ratio of the rates of HMR–MAT synapse formation in the absence and presence of RE. The derivation of this result is the following: As described in Results, Chromosome-Refolding Model of Mating-Type Switching, the rate of HMR–MAT synapse formation in the presence of RE is . As discussed in Donor Ratio Calculation Details above, the contact probabilities can be rewritten, which yields
| [S10] |
and the expression in parentheses is simply what we had named , so we have
| [S11] |
where we now write as to emphasize that this is the rate of HMR–MAT synapse formation in strains containing RE.
For strains in which RE is deleted, a similar derivation reveals that
| [S12] |
Therefore, the ratio of the rates of HMR–MAT synapse formation in the absence and presence of RE is
| [S13] |
As previously mentioned, we obtained the values of and through fits of the theory to the experimental data in Fig. 4, and we obtain = 3.3 (95% confidence interval is 2.4–8.5). Thus, from the experimental data we have extracted that the rate of HMR–MAT synapse formation is higher in strains lacking RE than in strains containing RE.
Effect of Local Chromatin Compaction
As mentioned in Discussion, the experimentally measured donor ratio in the wild type is higher than that predicted by our model. As one possible explanation of this discrepancy we speculate that the DNA may have a higher degree of compaction in the chromatin region between HML and RE compared to other regions of Chr III. This would bring HML closer to MAT when RE is bound to MAT. We calculate a new value of when we change our model to have a chromosome extension parameter (γ) equal to 4 for the region between HML and RE (instead of using γ = 13, as we do in all other calculations). Also, we use a Kuhn length of 100 nm. (The Kuhn length used in all of our other simulations is 200 nm, but that choice was arbitrary—using a 100-nm Kuhn length in all of our simulations does not affect their outcome. We change to a 100-nm Kuhn length in this calculation because it does affect the outcome for such short polymer chains.) For γ = 4 and a Kuhn length of 100 nm, we find that is multiplied by 6.9 compared with when we use γ = 13. To obtain the highest donor ratio, in addition to increasing, there would need to be a high value of (close to 1). The maximum likelihood estimation (discussed in Donor Ratio Calculation Details above) tells us that a sufficiently high value of is within the 95% confidence interval. For = 0.92, we obtain a donor ratio of D = 6.9, which is the same as the experimental donor ratio.
Acknowledgments
We thank the members of the J.E.H. and J.K. laboratories for fruitful discussions and Jason Brickner for generously providing reagents. This work was supported by National Science Foundation Grants DMR1206146 (to J.K.) and NSF-MRSEC-1420382 (to J.K. and J.E.H.) and NIH Grant GM20056 (to J.E.H.).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1607103113/-/DCSupplemental.
References
- 1.Cremer T, Cremer C. Chromosome territories, nuclear architecture and gene regulation in mammalian cells. Nat Rev Genet. 2001;2(4):292–301. doi: 10.1038/35066075. [DOI] [PubMed] [Google Scholar]
- 2.Taddei A, Gasser SM. Structure and function in the budding yeast nucleus. Genetics. 2012;192(1):107–129. doi: 10.1534/genetics.112.140608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Takizawa T, Meaburn KJ, Misteli T. The meaning of gene positioning. Cell. 2008;135(1):9–13. doi: 10.1016/j.cell.2008.09.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Marshall WF. Order and disorder in the nucleus. Curr Biol. 2002;12(5):R185–R192. doi: 10.1016/s0960-9822(02)00724-8. [DOI] [PubMed] [Google Scholar]
- 5.Akhtar A, Gasser SM. The nuclear envelope and transcriptional control. Nat Rev Genet. 2007;8(7):507–517. doi: 10.1038/nrg2122. [DOI] [PubMed] [Google Scholar]
- 6.Lanctôt C, Cheutin T, Cremer M, Cavalli G, Cremer T. Dynamic genome architecture in the nuclear space: Regulation of gene expression in three dimensions. Nat Rev Genet. 2007;8(2):104–115. doi: 10.1038/nrg2041. [DOI] [PubMed] [Google Scholar]
- 7.Misteli T, Soutoglou E. The emerging role of nuclear architecture in DNA repair and genome maintenance. Nat Rev Mol Cell Biol. 2009;10(4):243–254. doi: 10.1038/nrm2651. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Mekhail K, Moazed D. The nuclear envelope in genome organization, expression and stability. Nat Rev Mol Cell Biol. 2010;11(5):317–328. doi: 10.1038/nrm2894. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Sexton T, Cavalli G. The role of chromosome domains in shaping the functional genome. Cell. 2015;160(6):1049–1059. doi: 10.1016/j.cell.2015.02.040. [DOI] [PubMed] [Google Scholar]
- 10.Agmon N, Liefshitz B, Zimmer C, Fabre E, Kupiec M. Effect of nuclear architecture on the efficiency of double-strand break repair. Nat Cell Biol. 2013;15(6):694–699. doi: 10.1038/ncb2745. [DOI] [PubMed] [Google Scholar]
- 11.Lee CS, et al. Chromosome position determines the success of double-strand break repair. Proc Natl Acad Sci USA. 2016;113(2):E146–E154. doi: 10.1073/pnas.1523660113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Mukhopadhyay S, Schedl P, Studitsky VM, Sengupta AM. Theoretical analysis of the role of chromatin interactions in long-range action of enhancers and insulators. Proc Natl Acad Sci USA. 2011;108(50):19919–19924. doi: 10.1073/pnas.1103845108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Doyle B, Fudenberg G, Imakaev M, Mirny LA. Chromatin loops as allosteric modulators of enhancer-promoter interactions. PLOS Comput Biol. 2014;10(10):e1003867. doi: 10.1371/journal.pcbi.1003867. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Pâques F, Haber JE. Multiple pathways of recombination induced by double-strand breaks in Saccharomyces cerevisiae. Microbiol Mol Biol Rev. 1999;63(2):349–404. doi: 10.1128/mmbr.63.2.349-404.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Krogh BO, Symington LS. Recombination proteins in yeast. Annu Rev Genet. 2004;38(1):233–271. doi: 10.1146/annurev.genet.38.072902.091500. [DOI] [PubMed] [Google Scholar]
- 16.Symington LS, Rothstein R, Lisby M. Mechanisms and regulation of mitotic recombination in Saccharomyces cerevisiae. Genetics. 2014;198(3):795–835. doi: 10.1534/genetics.114.166140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Mehta A, Haber JE. Sources of DNA double-strand breaks and models of recombinational DNA repair. Cold Spring Harb Perspect Biol. 2014;6(9):a016428. doi: 10.1101/cshperspect.a016428. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Roukos V, et al. Spatial dynamics of chromosome translocations in living cells. Science. 2013;341(6146):660–4. doi: 10.1126/science.1237150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Cho NW, Dilley RL, Lampson MA, Greenberg RA. Interchromosomal homology searches drive directional ALT telomere movement and synapsis. Cell. 2014;159(1):108–121. doi: 10.1016/j.cell.2014.08.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Roukos V, Misteli T. The biogenesis of chromosome translocations. Nat Cell Biol. 2014;16(4):293–300. doi: 10.1038/ncb2941. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Lichten M, Haber JE. Position effects in ectopic and allelic mitotic recombination in Saccharomyces cerevisiae. Genetics. 1989;123(2):261–268. doi: 10.1093/genetics/123.2.261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Rosa A, Everaers R. Structure and dynamics of interphase chromosomes. PLOS Comput Biol. 2008;4(8):e1000153. doi: 10.1371/journal.pcbi.1000153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Avşaroğlu B, et al. Effect of chromosome tethering on nuclear organization in yeast. PLoS One. 2014;9(7):e102474. doi: 10.1371/journal.pone.0102474. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Duan Z, et al. A three-dimensional model of the yeast genome. Nature. 2010;465(7296):363–367. doi: 10.1038/nature08973. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Rodley CDM, Bertels F, Jones B, O’Sullivan JM. Global identification of yeast chromosome interactions using Genome conformation capture. Fungal Genet Biol. 2009;46(11):879–886. doi: 10.1016/j.fgb.2009.07.006. [DOI] [PubMed] [Google Scholar]
- 26.Gehlen LR, et al. Spatially confined polymer chains: Implications of chromatin fibre flexibility and peripheral anchoring on telomere–telomere interaction. J Phys Condens Matter. 2006;18(14):S245–S252. [Google Scholar]
- 27.Wong H, et al. A predictive computational model of the dynamic 3D interphase yeast nucleus. Curr Biol. 2012;22(20):1881–1890. doi: 10.1016/j.cub.2012.07.069. [DOI] [PubMed] [Google Scholar]
- 28.Tjong H, Gong K, Chen L, Alber F. Physical tethering and volume exclusion determine higher-order genome organization in budding yeast. Genome Res. 2012;22(7):1295–1305. doi: 10.1101/gr.129437.111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Gehlen LR, et al. Chromosome positioning and the clustering of functionally related loci in yeast is driven by chromosomal interactions. Nucleus. 2012;3(4):370–383. doi: 10.4161/nucl.20971. [DOI] [PubMed] [Google Scholar]
- 30.Louis EJ, Naumova ES, Lee A, Naumov G, Haber JE. The chromosome end in yeast: Its mosaic nature and influence on recombinational dynamics. Genetics. 1994;136(3):789–802. doi: 10.1093/genetics/136.3.789. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Marvin ME, Griffin CD, Eyre DE, Barton DBH, Louis EJ. In Saccharomyces cerevisiae, yKu and subtelomeric core X sequences repress homologous recombination near telomeres as part of the same pathway. Genetics. 2009;183(2):441–51, 1SI–12SI. doi: 10.1534/genetics.109.106674. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Marvin ME, et al. The association of yKu with subtelomeric core X sequences prevents recombination involving telomeric sequences. Genetics. 2009;183(2):453–467. doi: 10.1534/genetics.109.106682. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Lee C-S, Haber JE. Mating-type gene switching in Saccharomyces cerevisiae. Microbiol Spectr. 2015;3(2):A3–A0013, 2014. doi: 10.1128/microbiolspec.MDNA3-0013-2014. [DOI] [PubMed] [Google Scholar]
- 34.Haber JE. Mating-type genes and MAT switching in Saccharomyces cerevisiae. Genetics. 2012;191(1):33–64. doi: 10.1534/genetics.111.134577. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Hicks WM, Yamaguchi M, Haber JE. Real-time analysis of double-strand DNA break repair by homologous recombination. Proc Natl Acad Sci USA. 2011;108(8):3108–3115. doi: 10.1073/pnas.1019660108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Wu X, Moore JK, Haber JE. Mechanism of MAT alpha donor preference during mating-type switching of Saccharomyces cerevisiae. Mol Cell Biol. 1996;16(2):657–668. doi: 10.1128/mcb.16.2.657. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Hsieh T-HS, et al. Mapping nucleosome resolution chromosome folding in yeast by Micro-C. Cell. 2015;162(1):108–119. doi: 10.1016/j.cell.2015.05.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Wu X, Haber JE. A 700 bp cis-acting region controls mating-type dependent recombination along the entire left arm of yeast chromosome III. Cell. 1996;87(2):277–285. doi: 10.1016/s0092-8674(00)81345-8. [DOI] [PubMed] [Google Scholar]
- 39.Li J, et al. Regulation of budding yeast mating-type switching donor preference by the FHA domain of Fkh1. PLoS Genet. 2012;8(4):e1002630. doi: 10.1371/journal.pgen.1002630. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Wu X, Haber JE. MATa donor preference in yeast mating-type switching: Activation of a large chromosomal region for recombination. Genes Dev. 1995;9(15):1922–1932. doi: 10.1101/gad.9.15.1922. [DOI] [PubMed] [Google Scholar]
- 41.Belton JM, et al. The conformation of yeast chromosome III is mating type dependent and controlled by the recombination enhancer. Cell Reports. 2015;13(9):1855–1867. doi: 10.1016/j.celrep.2015.10.063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Wu C, et al. Mcm1 regulates donor preference controlled by the recombination enhancer in Saccharomyces mating-type switching. Genes Dev. 1998;12(11):1726–1737. doi: 10.1101/gad.12.11.1726. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Coïc E, Richard GF, Haber JE. Saccharomyces cerevisiae donor preference during mating-type switching is dependent on chromosome architecture and organization. Genetics. 2006;173(3):1197–1206. doi: 10.1534/genetics.106.055392. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Marshall WF, et al. Interphase chromosomes undergo constrained diffusional motion in living cells. Curr Biol. 1997;7(12):930–939. doi: 10.1016/s0960-9822(06)00412-x. [DOI] [PubMed] [Google Scholar]
- 45.Weber SC, Spakowitz AJ, Theriot JA. Nonthermal ATP-dependent fluctuations contribute to the in vivo motion of chromosomal loci. Proc Natl Acad Sci USA. 2012;109(19):7338–7343. doi: 10.1073/pnas.1119505109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Hajjoul H, et al. High-throughput chromatin motion tracking in living yeast reveals the flexibility of the fiber throughout the genome. Genome Res. 2013;23(11):1829–1838. doi: 10.1101/gr.157008.113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Backlund MP, Joyner R, Weis K, Moerner WE. Correlations of three-dimensional motion of chromosomal loci in yeast revealed by the double-helix point spread function microscope. Mol Biol Cell. 2014;25(22):3619–3629. doi: 10.1091/mbc.E14-06-1127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Houston PL, Broach JR. The dynamics of homologous pairing during mating type interconversion in budding yeast. PLoS Genet. 2006;2(6):e98. doi: 10.1371/journal.pgen.0020098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Dion V, Kalck V, Horigome C, Towbin BD, Gasser SM. Increased mobility of double-strand breaks requires Mec1, Rad9 and the homologous recombination machinery. Nat Cell Biol. 2012;14(5):502–509. doi: 10.1038/ncb2465. [DOI] [PubMed] [Google Scholar]
- 50.Miné-Hattab J, Rothstein R. Increased chromosome mobility facilitates homology search during recombination. Nat Cell Biol. 2012;14(5):510–517. doi: 10.1038/ncb2472. [DOI] [PubMed] [Google Scholar]
- 51.Renkawitz J, Lademann CA, Kalocsay M, Jentsch S. Monitoring homology search during DNA double-strand break repair in vivo. Mol Cell. 2013;50(2):261–272. doi: 10.1016/j.molcel.2013.02.020. [DOI] [PubMed] [Google Scholar]
- 52.Phillips R. Napoleon is in equilibrium. Annu Rev Condens Matter Phys. 2015;6(1):85–111. doi: 10.1146/annurev-conmatphys-031214-014558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Sun K, Coïc E, Zhou Z, Durrens P, Haber JE. Saccharomyces forkhead protein Fkh1 regulates donor preference during mating-type switching through the recombination enhancer. Genes Dev. 2002;16(16):2085–2096. doi: 10.1101/gad.994902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Coïc E, Sun K, Wu C, Haber JE. Cell cycle-dependent regulation of Saccharomyces cerevisiae donor preference during mating-type switching by SBF (Swi4/Swi6) and Fkh1. Mol Cell Biol. 2006;26(14):5470–5480. doi: 10.1128/MCB.02443-05. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Straight AF, Belmont AS, Robinett CC, Murray AW. GFP tagging of budding yeast chromosomes reveals that protein-protein interactions can mediate sister chromatid cohesion. Curr Biol. 1996;6(12):1599–1608. doi: 10.1016/s0960-9822(02)70783-5. [DOI] [PubMed] [Google Scholar]
- 56.Bressan DA, Vazquez J, Haber JE. Mating type-dependent constraints on the mobility of the left arm of yeast chromosome III. J Cell Biol. 2004;164(3):361–371. doi: 10.1083/jcb.200311063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Lisby M, Mortensen UH, Rothstein R. Colocalization of multiple DNA double-strand breaks at a single Rad52 repair centre. Nat Cell Biol. 2003;5(6):572–577. doi: 10.1038/ncb997. [DOI] [PubMed] [Google Scholar]
- 58.Schober H, et al. Controlled exchange of chromosomal arms reveals principles driving telomere interactions in yeast. Genome Res. 2008;18(2):261–271. doi: 10.1101/gr.6687808. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Brickner JH, Walter P. Gene recruitment of the activated INO1 locus to the nuclear membrane. PLoS Biol. 2004;2(11):e342. doi: 10.1371/journal.pbio.0020342. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Loewen CJ, Roy A, Levine TP. A conserved ER targeting motif in three families of lipid binding proteins and in Opi1p binds VAP. EMBO J. 2003;22(9):2025–2035. doi: 10.1093/emboj/cdg201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Szeto L, Fafalios MK, Zhong H, Vershon AK, Broach JR. Alpha2p controls donor preference during mating type interconversion in yeast by inactivating a recombinational enhancer of chromosome III. Genes Dev. 1997;11(15):1899–1911. doi: 10.1101/gad.11.15.1899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Zimmer C, Fabre E. Principles of chromosomal organization: Lessons from yeast. J Cell Biol. 2011;192(5):723–733. doi: 10.1083/jcb.201010058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Ercan S, Simpson RT. Global chromatin structure of 45,000 base pairs of chromosome III in a- and alpha-cell yeast and during mating-type switching. Mol Cell Biol. 2004;24(22):10026–10035. doi: 10.1128/MCB.24.22.10026-10035.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Dekker J. Mapping in vivo chromatin interactions in yeast suggests an extended chromatin fiber with regional variation in compaction. J Biol Chem. 2008;283(50):34532–34540. doi: 10.1074/jbc.M806479200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Ostrow AZ, et al. Fkh1 and Fkh2 bind multiple chromosomal elements in the S. cerevisiae genome with distinct specificities and cell cycle dynamics. PLoS One. 2014;9(2):e87647. doi: 10.1371/journal.pone.0087647. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Fudenberg G, Mirny LA. Higher-order chromatin structure: Bridging physics and biology. Curr Opin Genet Dev. 2012;22(2):115–124. doi: 10.1016/j.gde.2012.01.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Goldstein AL, McCusker JH. Three new dominant drug resistance cassettes for gene disruption in Saccharomyces cerevisiae. Yeast. 1999;15(14):1541–1553. doi: 10.1002/(SICI)1097-0061(199910)15:14<1541::AID-YEA476>3.0.CO;2-K. [DOI] [PubMed] [Google Scholar]
- 68.Schneider CA, Rasband WS, Eliceiri KW. NIH Image to ImageJ: 25 years of image analysis. Nat Methods. 2012;9(7):671–675. doi: 10.1038/nmeth.2089. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Becker NB, Rosa A, Everaers R. The radial distribution function of worm-like chains. Eur Phys J E Soft Matter. 2010;32:53–69. doi: 10.1140/epje/i2010-10596-0. [DOI] [PubMed] [Google Scholar]