Universality in human cortical folding in health and disease

Significance

Despite of the enormous diversity in size and function of the mammalian cerebral cortex, it has been shown that the cortices of different species fold according to a simple universal law. In this study, we investigate if this law also applies to variation within a single species—our own. Specifically, we examine how the law is affected by sex, age, or the presence of Alzheimer’s disease. By investigating and quantifying what remains invariant and what changes in each case, we shed some light on the underlying mechanisms through which the cortex changes in health and disease and argue that morphological complexity could emerge from a few simple rules.

Abstract

The folding of the cortex in mammalian brains across species has recently been shown to follow a universal scaling law that can be derived from a simple physics model. However, it was yet to be determined whether this law also applies to the morphological diversity of different individuals in a single species, in particular with respect to factors, such as age, sex, and disease. To this end, we derived and investigated the cortical morphology from magnetic resonance images (MRIs) of over 1,000 healthy human subjects from three independent public databases. Our results show that all three MRI datasets follow the scaling law obtained from the comparative neuroanatomical data, which strengthens the case for the existence of a common mechanism for cortical folding. Additionally, for comparable age groups, both male and female brains scale in exactly the same way, despite systematic differences in size and folding. Furthermore, age introduces a systematic shift in the offset of the scaling law. In the model, this shift can be interpreted as changes in the mechanical forces acting on the cortex. We also applied this analysis to a dataset derived from comparable cohorts of Alzheimer’s disease patients and healthy subjects of similar age. We show a systematically lower offset and a possible change in the exponent for Alzheimer’s disease subjects compared with the control cohort. Finally, we discuss implications of the changes in offset and exponent in the data and relate it to existing literature. We, thus, provide a possible mechanistic link between previously independent observations.

The expansion of the cerebral cortex is the most obvious feature of mammalian brain evolution and generally accompanied by increasing degrees of folding of the cortical surface. The mechanisms that drive gyrification have been a matter of intense research interest lately (1–4), with a number of proposals being put forward to explain it. Most such studies have focused on human cortices, using detailed MRI data to postulate folding as driven by the [possibly differential (5) or multilayered (6)] expansion of the cortical surface. In contrast, we have recently proposed a model (7), in which folding is a consequence of the dynamics of surface expansion and self-avoidance coupled with a negative tension term. This model was partly inspired by the axonal tension hypothesis by Van Essen (8) and the statistical physics of membranes (9). By assuming that healthy adult mammalian cortices have a shape that minimizes an effective free energy term that takes into account these effects, this model predicts a power law relation between cortical average thickness T, exposed area $A_e$, and total area $A_t$, namely

$$A_t{T}^{1/2}=k{A}_e^{5/4}.$$ [1]

The only free parameter is k, or offset, a dimensionless coefficient that is presumed to be related to both the axonal tension and the pressure of cerebral spinal fluid (CSF) (supplemental text in ref. 7). In geometric terms, the variables T, $A_t$, and $A_e$ associated with each cortex define a point in the $\log T\times \log A_t\times \log A_e$ space, and Eq. 1 constrains these points to a plane: $1/2\log T+\log A_t-5/4\log A_t=\log k$. In effect, this relationship eliminates the degree of freedom associated with the direction $\overrightarrow{k}=\left\{1/2,1,5/4\right\}$. In other words, this approach essentially provides a mapping to a new, more natural set of variables with which to describe cortical morphology.

Using data from different mammalian species, we had previously verified that this relation is closely followed by gyrified and lissencephalic cortices. In adaptive terms, cortical folding scales universally across clades and species, implying a single conserved mechanism throughout evolution. Indeed, comparing $A_t{T}^{1/2}$ with $A_e$ for all 51 land mammals in our data shows an excellent fit for $A_t{T}^{1/2}=k{A}_e^{1.305\pm 0.007}$. The empirical exponent for $A_e$, 1.305, is very close to but statistically distinct from the predicted 1.25. We previously discussed that the source of this may have a number of reasons (7) (indeed, we provide an alternative explanation in Discussion).

Regardless, the existence of such precise regularity as predicted by a model derived from simple assumptions is quite remarkable and revealing. This regularity does not at all imply that other omitted details are not important but rather, that they simply are not the main drivers of the coarse-grained cortical morphology. At this whole-cortex level, gyrification seems to be determined by an extremely limited set of degrees of freedom described by a simple scaling law. The exact explanation of this relation in terms of our model has also been questioned (10, 11) and defended (12). However, even if one is not convinced about its proposed explanation, the fact remains that a strong and seemingly universal empirical relation exists between the coarse-grained morphological features of cortices of different mammalian species. It is, therefore, worthwhile to investigate whether the same relation holds for individuals of a single species.

Previous studies of cortical folding in a single species mainly focused on MRI data in humans and examined the changes in gyrification, for example, with age (13), with sex (14), and in dementia (15). We now seek to test our model against such human cortical surface reconstructions from MRI data and examine its applicability over variations across different human subjects in sex, age, and health or disease. This analysis allows us to delve deeper into the factors that neither a purely comparative approach, with one or two specimens for each species, nor a descriptive detailed analysis of one or a few human cortices can examine.

Specifically, we investigate how diversity in cortical morphology between species [as reported by comparative neuroanatomy (7)] relates to diversity within a species (as reported by human MRI). We examine how the factors that drive the latter affect the model parameters, both those constrained (exponents) and unconstrained (offset) by theory. For instance, it is known that the cortex generally shrinks and slightly changes in folding with age (13, 16–18) and that males have, on average, larger brains than females, with a slightly increased degree of folding (14, 17, 19). However, it is unknown if and how these changes affect the scaling law.

Results

Human Brains Fold Like Other Mammalian Cortices.

Previously, Mota and Herculano-Houzel (7) showed that, although mammalian cortices vary greatly in size, thickness, and the degree of folding, empirically, they all closely follow a simple universal scaling law. Here, we investigate if such an invariant relation also exists within and across cohorts of human subjects. Not only is this testing the previously proposed theory in an intraspecies study (in contrast to the previous interspecies study), but the range over which the measurements of total cortical surface area, cortical thickness, and exposed surface area vary is also dramatically reduced. Finally, the method of data acquisition differs: here, we use MRI-derived measures of cortical surface area ($A_t$), cortical thickness (T), and exposed surface area ($A_e$) rather than manual tracing of scanned cortical slices. Given these major differences in data acquisition, species, and range of measurements, it is not immediately obvious that the human cohort data will conform to the interspecies scaling law.

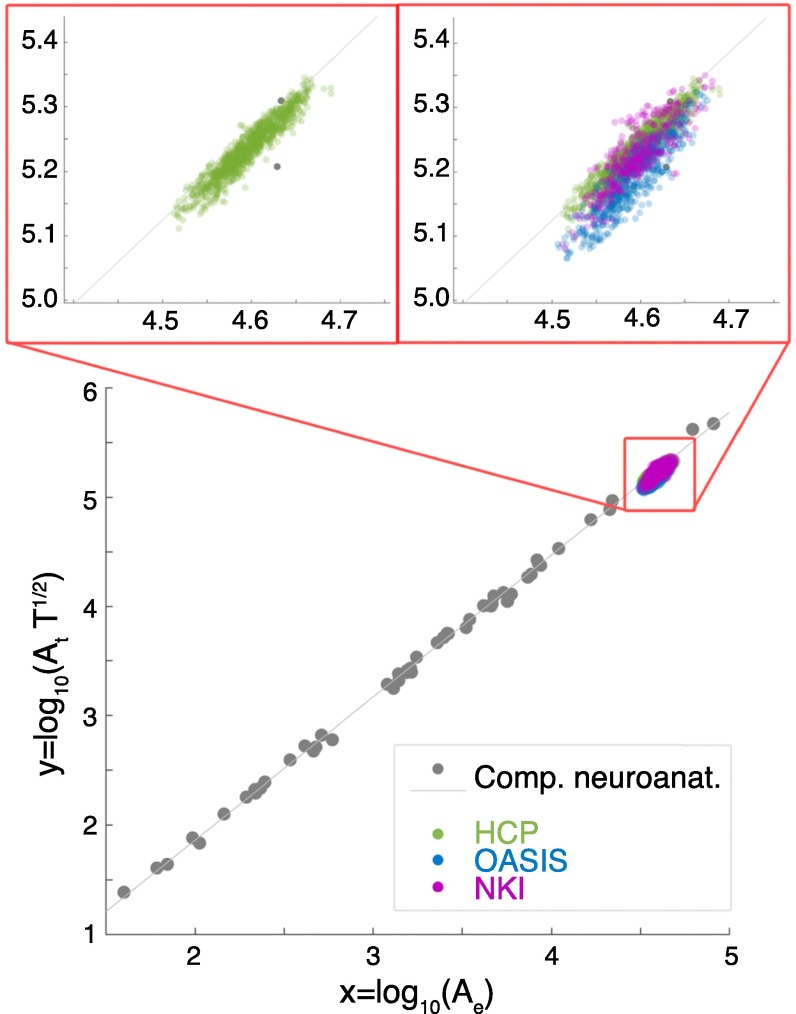
To test if both the previously published interspecies data and our human MRI-derived data are comparable, we show both in Fig. 1 in the same plot. We used three independent healthy datasets, which were acquired on separate scanners, using different acquisition protocols. These datasets are the Human Connectome Project (HCP), the Open Access Series of Imaging Studies (OASIS), and the Nathan Kline Institute (NKI) (Materials and Methods has more details). Indeed, the MRI-derived datasets align well with the previously obtained mammalian dataset, despite the fundamentally different methods of obtaining them. In particular, the adult human dataset (the HCP) (Fig. 1, Left Inset) shows a very good agreement with the regression based on the previously published mammalian dataset, apart from a slight systematic offset.

Fig. 1.

Comparing MRI-derived human datasets with the established neuroanatomy dataset for mammalian brains. The scaling law for the comparative neuroanatomy (Comp. neuroanat.) data across different species is shown in gray. The gray regression line is also obtained for these data, with a slope of 1.305. Overlaid are the human MRI-derived datasets: green for the HCP, blue for the OASIS, and magenta for the NKI. Insets (red frame) show the human MRI-derived data in more detail relative to the regression line of the interspecies data. Note that the two gray dots in Left Inset are from the previous Comp. neuroanat. dataset for humans.

This alignment can be quantified by comparing the quantity $k\prime =A_t{T}^{1/2}{A}_e^{-1.305}$ derived from the fit for the comparative neuroanatomy dataset (gray line in Fig. 1). We obtain $k_{ComparativeNeuroanatomy}^{\prime }=0.1861\pm 0.0184$, $k_{HCP}^{\prime }=0.1822\pm 0.0057$, $k_{OASIS}^{\prime }=0.1669\pm 0.0086$, and $k_{NKI}^{\prime }=0.1786\pm 0.0109$. The variance in the comparative neuroanatomy dataset is somewhat larger than that of the human MRI datasets, whereas the means in the latter all fall within 1 standard deviation of the former, indicating that the linear fit in the comparative neuroanatomy dataset is also a similarly good fit for the human MRI dataset, except for some change in the offset. Strikingly, the HCP dataset has a much smaller variance than the other human MRI datasets, and we will see later that this is caused by the narrow age range in the HCP data.

The systematic differences in offset between the human MRI datasets are probably attributable to different imaging protocols, scan resolution, processing pipelines, and field strength, which are known to produce systematically different measured values, most notably for the cortical thickness (20–24). Indeed, we show that cortical thickness differs systematically between the datasets (SI Appendix, Text S1). The three different datasets also contain different age ranges and sex distributions. Thus, they are not aggregated in the following analyses, and we will investigate the effect of gender and age on the parameters of the scaling law separately.

Male and Female Brains Fold in the Same Way, Despite Differences in Average Sizes and Folding Index.

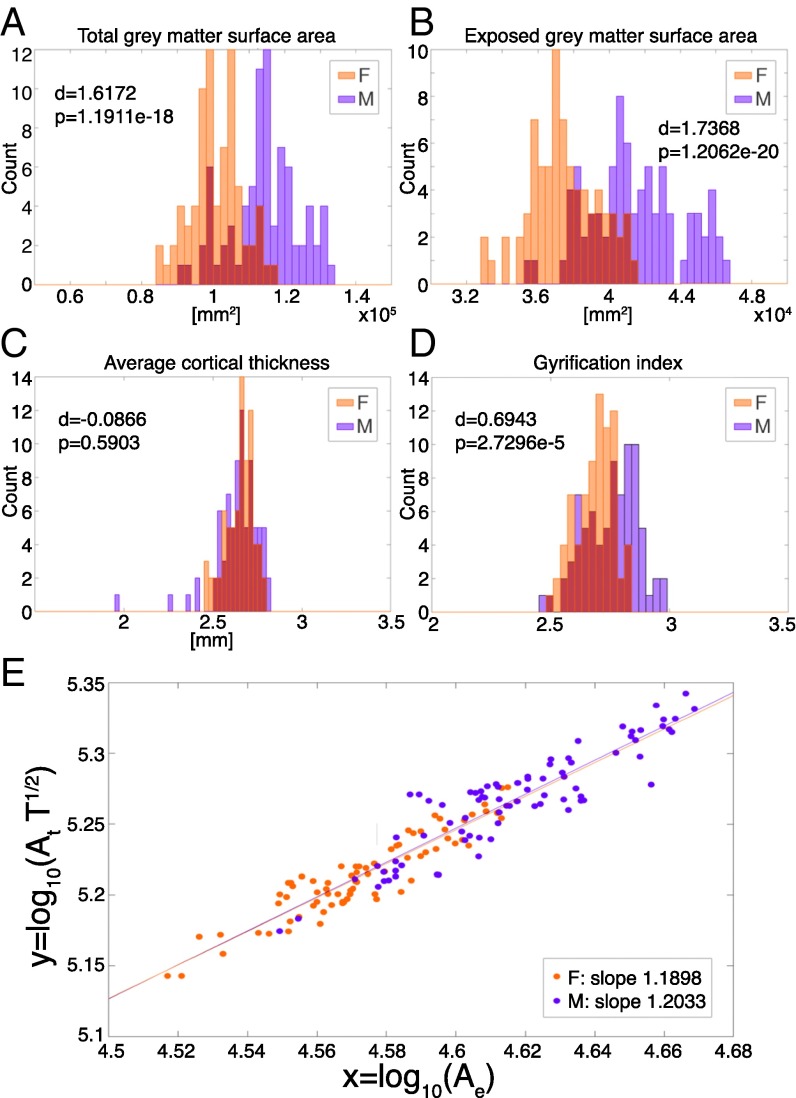
In the same age group, on average, females have smaller brains with a smaller cerebrum volume and a smaller total cortical surface area (17, 19, 25). We reproduced these findings in all of our MRI-derived datasets and also show that there are no sex differences in cortical thickness but a slight difference in the gyrification index ($A_t/A_e$). Fig. 2 shows an example from the HCP dataset in the age range of 22–25 years old. We chose a very narrow age range in adulthood to eliminate the effect of age on the results. The exposed and total surface areas are significantly smaller in females compared with males ($P\ll 0.001$), and the effect size is very large (Cohen’s $D>1.5$) (Fig. 2 A and B). However, there is no difference in average cortical thickness between male and females ($P=0.59$, Cohen’s $D=-0.09$) (Fig. 2C). To test if both surface areas changed systematically, we also tested for differences in gyrification index. We found that it varies significantly between males and females ($P\ll 0.001$), with a moderate effect size (Cohen’s $D=0.69$) (Fig. 2D). These results essentially indicate that female brains are slightly less folded than male brains of the same age.

Fig. 2.

Sex differences in (A) exposed and (B) total surface area, (C) cortical thickness, (D) gyrification index, and (E) scaling behavior. The subjects are selected from a narrow adult age range (22–25 years old in the HCP dataset) to exclude interaction effects with age. P values are from a two-tailed t test, and d represents effect size measured by Cohen’s D (Materials and Methods). SI Appendix, Text S2 also repeats this analysis for other age groups and datasets. F, female; M, male.

To test if a single invariant relationship exists for both males and females, despite the difference in the gyrification index, we performed a multiple linear regression analysis with sex as a categorical variable on the same HCP dataset in the age range of 22–25 years old. Indeed, the same scaling law is obeyed by both males and females, with no significant differences in offset or slope (Fig. 2E). In fact, the regression lines almost overlap for the range of the measurement. The previously observed differences between males and females are still visible (females tend to be found near the bottom left and males tend to be found near the top right in Fig. 2E) but in a way that is perfectly aligned along the direction of the scaling law. We repeated this analysis on all of the other age groups and cohorts and come to the same conclusion (SI Appendix, Text S2). In other words, despite differences between males and females in terms of total gray matter surface areas, exposed surface areas, and degrees of gyrification, the manner in which these quantities change is perfectly constrained by the previously proposed invariant relationship; both obey the same principles in how the cortical folding occurs.

We conclude that there is a single scaling law relating cortical average thickness, total and exposed areas, for both male and female subjects of the same age. Thus, we will not differentiate between sexes in the following analysis of the effect of age.

Throughout the Healthy Lifespan, the Scaling Changes in Offset but Does Not Change in Slope.

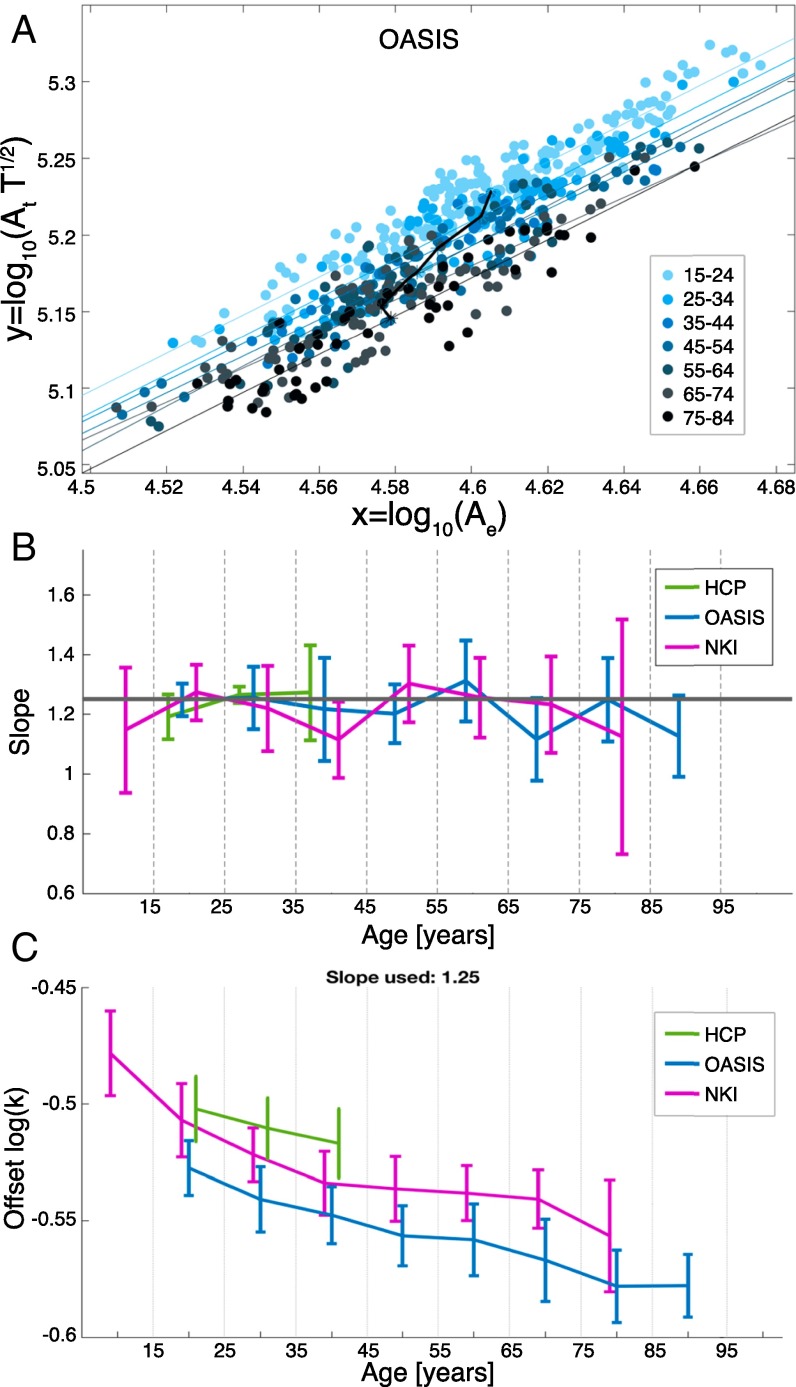
We examined the effect of age on the scaling law, because it is also well-documented that cortical thickness, total and exposed gray matter surface area, and the gyrification index change with age (13, 16, 17). In terms of the scaling law, we found no change in the slope but a systematic decrease in the offset with increasing age (Fig. 3) in all datasets. With age, average values additionally shift systematically (illustrated by the black line in Fig. 3A indicating the age group average, which moves in negative y direction and negative x direction) as the brain shrinks with increasing age.

Fig. 3.

Change in the scaling behavior with age. (A) Scaling law for different age groups in the OASIS dataset using both males and females. Regression lines are shown in the corresponding color as the age group. The age group average is shown as a black solid line. (B) The scaling law slope estimate is shown with 95% confidence intervals for each age group for all three datasets. The solid gray line indicates the 1.25 slope predicted by the theory. (C) Using the predicted slope of 1.25, the average estimated offset is shown for all three datasets over age (details are in Materials and Methods). The error bars indicate the standard deviations. The original data for the estimated offset are shown in SI Appendix, Fig. S3.

We compared the slope of all age groups in all cohorts against each other and against the theoretically predicted value of 1.25 (Fig. 3B). Essentially, there is no difference in the slope estimation, because all 95% confidence intervals of the slope overlap with each other and with the predicted value of 1.25. One exception is the NKI age group 35–45 years old, which falls just short of 1.25. We show that this is likely because of an uneven distribution of age in the group (SI Appendix, Text S4). We also repeated the multiple linear regression analysis with age as a continuous regressor and found in all datasets a significant age main effect (in all cohorts, $P\ll 0.001$) but no age interaction effect on the slope (in all cohorts, $P>0.01$) (SI Appendix, Text S2); also, the slope is not different to 1.25 within a 95% confidence interval.

Finally, we estimated the rate of decrease in offset with age (Fig. 3C) in the different cohorts. The estimate was obtained by assuming a slope of 1.25 (Materials and Methods). Despite some systematic differences between the cohorts, the evolution of the offset with age seems very consistent across cohorts. The offset seems to decrease rapidly between the ages of 4 and 30 years old (especially as seen from the NKI cohort) and more gradually afterward.

In Alzheimer’s Disease, the Scaling Behavior Is Significantly Altered.

Finally, we investigated if the scaling behavior shown in the previous sections is altered in brain diseases. Specifically, we focused on Alzheimer’s disease, because there are known changes in cortical thickness, total brain volume, and gyrification (15, 26, 27). To that end, we use the publicly available Alzheimer’s Disease Neuroimaging Initiative (ADNI) database, which contains a big cohort of patients and controls.

As a first step, we repeated our previous analysis of sex differences in different age groups on the ADNI data. In the control group, as expected, we detected no difference in scaling between males and females, but in the Alzheimer’s disease patient group, we detected significant differences in slope and/or offset in two age groups (SI Appendix, Text S5). Hence, we performed our subsequent analysis and comparison of patients vs. controls for different sexes separately.

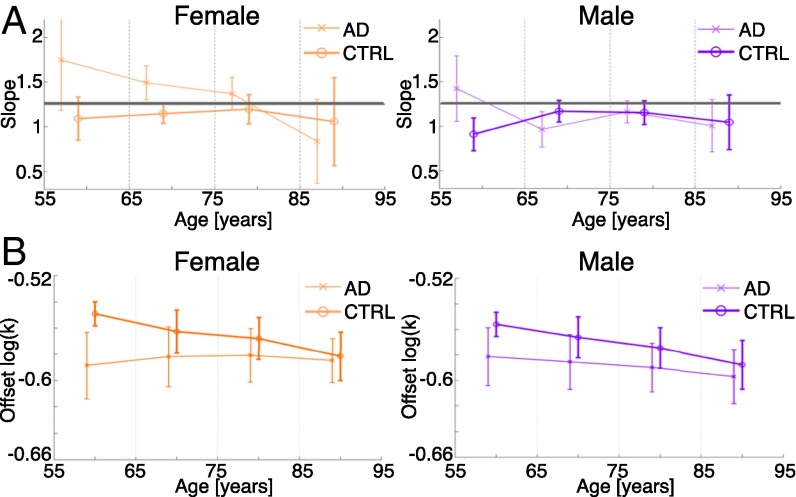
When we examined the slope of the regression, we found no significant difference from the theoretically predicted slope of 1.25 in the control male or female group (with the exception of those in the 55–64-year-old male control group, probably caused by the low sample size of four subjects). In Alzheimer’s disease patients, we found a significantly different slope from 1.25 in both male and females in the age group of 65–74 years old (Fig. 4A). In females, the slope is significantly higher than 1.25 and different from the control group. In males, the slope is significantly lower than 1.25 but not different from the control group. To test if this slope change is genuine, we further restricted the age range to 70–74 year olds and detected essentially the same effect in both males and females. We also performed a multiple linear regression with age as a continuous regressor and sex and disease as categorical regressors. We found a significant interaction effect of sex, disease, and sex:disease on the slope ($P=0.002$, P = 0.005, and P = 0.01, respectively), meaning that, depending on sex and disease, the slope of regression may change significantly. Finally, we repeated the entire analysis with a subset of the data, where the patients and controls were age and sex matched. The main findings highlighted here essentially stay the same. Together, these results hint at a possible genuine slope difference between sexes, patients, and controls.

Fig. 4.

Scaling behavior in Alzheimer’s disease. (A) Slope of scaling law for females and males for different age groups of Alzheimer’s disease patients (AD) and healthy controls (CTRL). The vertical dashed gray lines mark the boundaries used for the age groups. The horizontal solid gray lines indicate the theoretically predicted slope value of 1.25. (B) Means and standard deviations of the estimated offset are also shown. The offset was estimated assuming the theoretically predicted slope value of 1.25.

Next, we turned our attention to the offset of the scaling law, which we showed in healthy controls to be a monotonically decreasing function of age. We repeated the analysis as before by estimating the offset using the theoretically predicted slope of 1.25. In the control group, we found that the estimated offset decreases with age for both males and females as expected (Fig. 4B). However, we did not find the same trend in the Alzheimer’s disease patients. The offset in the Alzheimer’s disease group starts off lower than that in the control group but essentially stays at this level throughout age. These observations were confirmed by performing a multiple linear regression analysis with age as a continuous regressor and sex and disease as categorical regressors (significant main effects in age, disease, and age:disease with $P\ll 0.001$ and a main effect in sex:disease with $P=0.031$).

The most striking difference between the Alzheimer’s disease and control groups is their difference in offset, regardless of age and sex, most likely because of the significantly lower cortical thickness in the Alzheimer’s disease group (SI Appendix, Text S6). Furthermore, the decrease in offset with age, seen in other healthy cohorts, is also found in the control group but not in the Alzheimer’s disease group. Finally, there are indications that males and females differ in the Alzheimer’s disease group relative to each other as well as relative to the control group in terms of offset and slope.

Discussion

In conclusion, adult healthy human cortices conform to the same theoretically predicted relation that also seems to apply to the full range of mammalian species. Analyzed separately, healthy human adult MRI data from a variety of sources also fit the predicted power law well, although different datasets have small systematic differences in the offset parameter. Each dataset can be further segmented by age and sex. We show that the gyrification of male and female cortices of similar ages follows the same scaling rule, although the latter is, on average, slightly smaller and less gyrified than the former. Over different age groups, however, we show that, although the exponents do not vary significantly, the offset term decreases smoothly. These results suggest that the universal mechanisms that shape the mammalian cortex continue to operate over the development of healthy adults, and that possibly all variation across age in terms of these coarse-grained variables may be attributed to a monotonic change in the mechanical properties of the brain.

It is important to note that this relation between the three coarse-grained variables, $A_e$, $A_t$, and T, does not fully specify the shape of the cortex but rather, constrains it by eliminating one degree of freedom. Thus, these values can vary significantly between healthy individuals and may change significantly with age. However, they are constrained in their changes in such a way that the combination $A_t{T}^{1/2}{A}_e^{-5/4}=k\left(age\right)$ remains constant for each age (Fig. 3B).

Taken separately and disaggregated by age, the slopes of the scaling laws in all of the MRI datasets agree well with the theoretically predicted slope of 1.25. This result is significant in another way, because for this value and this value only, one can scale all areas as multiples of the square of the average cortical thickness and obtain a power law relation between an intrinsic ($A_t$) and an extrinsic ($A_e$) measure of the cortical surface. The exponent of the latter is then simply one-half the fractal dimension of the surface: From Eq. 1, $A_t/T^2=k{\left(A_e/T^2\right)}^{d_f/2}$, and $d_f=5/2$. Thus, empirically, we would expect the human cortical surface to scale like a fractal of dimension 2.5 for typical lengths larger than $k^{-1/2}T$ (27–30).

With age, the value of k decreases monotonically, and it appears that the rate of decrease is initially (up to the early 20s) faster. There is a range of factors that could account for this observation. As the theory postulates, k is related to the negative tension term of the cortical surface. Changes in k could, for example, correlate with changes in the elastoplastic properties of underlying white matter, or they could correspond to changes in CSF pressure. In the literature, there is evidence of slight changes of CSF pressure with age (31), but systematic studies are lacking, making conclusive answers impossible at this stage. In terms of the elastoplastic properties of the white matter, one study systematically measured the stiffness of the white matter using magnetic resonance elastography (MRE) and found no changes with age (32). However, another study, also using MRE, reported a systematic decrease in viscoelastic modulus with age (33). Interestingly, a significantly reduced stiffness was recorded in patients with Alzheimer’s disease (34), where we also find a decreased k value. Altogether, both theory and observation seem to suggest that the value of k is a function of the internal tensions and external pressure applied to the gray matter. This hypothesis is one of the key contributions that one can derive from the scaling law. It suggests the existence of a link between mechanical properties of the brain and measures of brain morphology. In other words, we can hope to mechanistically relate MRI-derived measures of the brain with MRE or other mechanical measurements of the brain via the scaling law. To fully accomplish this goal, however, will probably take a more fine-grained iteration of our model of gyrification.

It is also worth noting that the change in k with age in healthy subjects is not simply an effect of decreasing cortical thickness (SI Appendix, Text S6) but rather, is an emergent effect from correlated changes in all three primary variables of cortical thickness, total surface area, and exposed surface area. Hence, k can be understood as a new, more natural variable, which on its own, might correlate with biologically interpretable properties of the brain. Indeed, we also show that k might not be the only biologically relevant new variable (SI Appendix, Text S6). This reinterpreting of the previously proposed scaling law as a constraint is another contribution from this work. Even if one is not convinced about the simplifications and assumptions that have been made to deduce the proposed scaling law, it becomes clear that it captures a principal direction in the data, which other measures, such as the gyrification index, do not.

In Fig. 3, we showed that age-related changes introduced further variance in the data, which when not accounted for, may skew the data fit. Indeed, the direction of the age component of the variance is toward negative $x=\text{log}\left(A_e\right)$ and negative $y=\text{log}\left(\sqrt{T}{A}_t\right)$. These results might explain the previously found statistically significant difference between the theoretical exponent (1.25) and empirical exponent (1.305) in the comparative neuroanatomy data (7). Because age was not accounted for in each species, the variance along the direction of the age-related change might incorrectly lead to a regression that gives a higher slope than expected. Similarly, it would be interesting to investigate the interspecies variation for other nonhuman species and check how much of the variability is because of variations that are intraspecific as opposed to interspecific. If humans are typical, we may very well verify that there is more of the former than the latter, which would be truly remarkable. Similar to analogous studies on the source of variance in cortical area (35, 36), such a comparison might also hint at the evolutionary source of the variability.

In Alzheimer’s disease, we show a slope significantly different from 1.25 in the data for a subset of subjects. There are several potential reasons for this deviation. It could be a genuine effect in that the slope is altered compared with the healthy brains, in which case the proposed theory breaks down and cannot provide any more insight. A more fine-grained analysis might be needed in this case to determine what the alterations are in Alzheimer’s disease. However, we might also be lumping a heterogeneous cohort of subjects (e.g., different in disease severity, duration, time from onset, and recruitment center) together in one group. Independent of this point, the systematically low values of k, comparable with those of very old healthy cortices, tentatively suggest that the main morphological effect of Alzheimer’s disease is akin to a premature aging of the cortex.

More generally, in this work and previous works, we used coarse-grained measures for an entire hemisphere. Thus, strong regional variations in, for example, cortical thickness may skew the data away from theoretical predictions. Future work could extend the model to incorporate more fine-grained variables, such as the systematic differences in cortical thickness between gyri and sulci. Similarly, the segmentation of a hemisphere into, for example, lobes might yield additional regional insight. This approach may be particularly useful in the study of diseases that affect different cortical regions differently.

We would also like to note that the term “universality” refers specifically to the universality of the scaling exponent. A key contribution of this study is that we have shown that the offset in the scaling law is not universal and that it indeed changes with age. One question that arises is if other measures could also show universal properties. For example, the gyrification index ($A_t/A_e$) has been shown to be a useful measure in detecting subtle changes in cortical folding (37). However, we show in SI Appendix, Text S6 that the gyrification index does not appear to capture the trend in the data in a universal manner. Additional studies are needed to show if any other biologically interpretable measures also show universality.

There are also important caveats to the claim of universality in the scaling law. Even for similar age groups, there is, of course, still some residual variation for the value of the offset around the predicted “universal” value. This residual variation indicates that there may be other neglected processes influencing the cortical geometry. The theoretical model that we use to predict the slope is a coarse-grained approximation that relies on a number of simplifying assumptions. The fact that it manages to capture so much of its morphological outcome in such a simple framework is remarkable, but it cannot be regarded as a full or final description.

Finally, we would like to highlight that our proposed scaling law relationship, although simple in nature, is highly meaningful and not a mere linear regression analysis. Such as other studies, our model also directly addresses the underlying mechanisms through its assumptions. Where other studies choose to test assumptions through simulations to recreate a cortex that is then compared with the shape of the brain (bottom-up approach), we test our assumptions through derivations of properties that should be fulfilled given the assumptions (top-down approach). In our case, such a property is a relation between three (hitherto independent) morphological variables. The relation is derived from a theoretical model with a single free parameter (k), and it was then verified empirically, with exponents that were very close (comparative neuroanatomy) or statistically the same (human MRI) as the expected values. To our knowledge, no other proposed mechanism has either predicted this regularity or generated it numerically in simulations. Nevertheless, the fact remains that the field is split between competing gyrification models and approaches (1), each of which may explain some but not all of the features of cortical morphology. We believe that the bottom-up and the top-down approaches are, in fact, complementary and that only when they are successfully combined will a more complete and detailed model emerge.

Materials and Methods

Data Sources and Processing.

We used four publicly available datasets in this study. The HCP dataset has been obtained from the 500 subjects release from the HCP (38). The OASIS data have been obtained from the Open Access Series of Imaging Studies Project. We used the cross-sectional dataset (39) and only included the subset of healthy subjects. The NKI data (40) have been obtained from the NKI Rockland Sample. The ADNI data have been obtained from the ADNI. We included subjects from the “ADNI1,” the “ADNI GO,” and the “ADNI2” cohorts (41) and selected all 3-T sessions. More details for all of the datasets, including where our derived data are available for download, can be found in SI Appendix, Text S7.

Because we only used publicly available datasets, no informed consent procedure was required. We confirm that we complied with all of the data use policies of each of the datasets that we used.

For all datasets, we used Freesurfer for processing. We ran the Freesurfer recon-all pipeline on all subjects in the NKI and the ADNI datasets. For the HCP dataset, we used the preprocessed package provided by the HCP, which already includes the Freesurfer subjects. Details regarding the preprocessing can be found in ref. 38. For the OASIS dataset, we used the Freesurfer subjects provided.

To find the exposed surface, we ran the local gyrification pipeline in Freesurfer with the standard settings and used the surfaces *h.pial-outer-smoothed produced by that pipeline.

We then calculated the cortical thickness and total and exposed surface areas from the Freesurfer outputs; details can be found in SI Appendix, Text S7.

Statistical Analysis.

To test for differences in surface area, cortical thickness, and gyrification index, we used t tests to determine the P value. To determine effect size, Cohen’s D was used: $D=m_2-m_1/s$, $m_1,m_2$ being the means of the two groups to be compared; $s=\sqrt{\left(n_1-2\right)\times s_1^2+\left(n_2-1\right)\times s_2^2/n_1+n_2-2}$, with $n_1,n_2$ as the sample size for each group, and $s_1,s_2$ is the standard deviation for each group.

To determine differences in the scaling law between sex or age groups, we used multiple linear regression with sex or age as a categorical variable. We report P values for the main and interaction effects.

Offset Estimation.

To estimate the offset in the scaling law, we decided not to use a regression-based approach, because the estimates for offsets can vary widely with small changes in the slope. Instead, we chose an alternative approach.

Assuming a linear relationship with the slope of 1.25 as predicted by the theory, we can rewrite the relationship $y=1.25x+c$ as $c=y-1.25x$. Here, $x={\text{log}}_{10}\left(A_e\right)$, $y={\text{log}}_{10}\left(A_t\sqrt{T}\right)$, and $c=\text{log}\left(k\right)$ is the offset for each pair of values of x and y.