Significance
The design of vaccination strategies that generate potent Abs directed against diverse strains of highly mutable pathogens, like HIV and malaria, will significantly impact global health. Such Abs are called broadly neutralizing Abs (bnAbs). Abs are produced by a Darwinian evolutionary process called affinity maturation. Induction of bnAbs will likely require vaccination with diverse mutant antigens. How affinity maturation occurs in the presence of multiple diverse antigens is not well-understood, thus hindering rational design of immunization strategies. We study this issue using computer simulations and statistical mechanical theory. Our results provide guides for the rational design of optimal vaccination strategies, and they reveal mechanistic principles at a crossroad of immunology and evolutionary biology.
Keywords: HIV, broadly neutralizing antibodies, statistical mechanics, evolutionary biology, biophysics
Abstract
Strategies to elicit Abs that can neutralize diverse strains of a highly mutable pathogen are likely to result in a potent vaccine. Broadly neutralizing Abs (bnAbs) against HIV have been isolated from patients, proving that the human immune system can evolve them. Using computer simulations and theory, we study immunization with diverse mixtures of variant antigens (Ags). Our results show that particular choices for the number of variant Ags and the mutational distances separating them maximize the probability of inducing bnAbs. The variant Ags represent potentially conflicting selection forces that can frustrate the Darwinian evolutionary process of affinity maturation. An intermediate level of frustration maximizes the chance of evolving bnAbs. A simple model makes vivid the origin of this principle of optimal frustration. Our results, combined with past studies, suggest that an appropriately chosen permutation of immunization with an optimally designed mixture (using the principles that we describe) and sequential immunization with variant Ags that are separated by relatively large mutational distances may best promote the evolution of bnAbs.
Vaccination has saved more lives than any other medical intervention, but some pathogens have evolved to defy the empirical immunization paradigms pioneered by Jenner and Pasteur. These pathogens often share two characteristics: they present themselves in diverse guises (e.g., by being highly mutable), and they hide from or degrade the immune system. HIV is a prominent example of a pathogen with these traits.
More than 30 y into the HIV/AIDS epidemic, no widely effective vaccine has yet been developed. Among many obstacles, the most difficult to confront may be the ability of HIV to evolve rapidly and create an enormous diversity of mutated viral strains, thereby evading vaccine-induced immune responses directed at only a few strains. A potent vaccine will likely need to elicit broadly neutralizing Abs (bnAbs), which can neutralize and thus, protect against a large fraction of circulating viral strains (1–9).
A number of potent bnAbs have recently been isolated from patients (10–15). In most cases, these bnAbs developed only after years of chronic infection when the infecting strain had mutated into a diverse viral population. Still, these cases prove that the human immune system can evolve bnAbs against HIV, and they raise the exciting possibility that rationally designed immunogens and immunization protocols may be able to elicit bnAbs efficiently in diverse people.
After natural infection or vaccination, Abs are produced by a Darwinian evolutionary process called affinity maturation (AM) (16). Naive B cells are activated by productive interactions between their B-cell receptors (BCRs) and the immunogen- or pathogen-derived antigen (Ag). These activated B cells then seed structures called germinal centers (GCs), where they replicate and undergo AM. Mutations are introduced into the BCRs followed by an affinity-based competition for selection and survival of the B cells. Multiple rounds of mutation and selection occur, resulting in B cells with BCRs that bind to the Ag with increasingly higher affinity as AM ensues. Plasma B cells secrete Abs, which are modified forms of the BCR. There is a growing consensus that guiding this Darwinian evolutionary process toward the production of bnAbs will require immunization with an Ag that activates the correct germline B cells (17–21) followed by multiple variant Ags that share a set of conserved residues and mimic the HIV viral spike (3, 6, 8, 20, 22).
If one must immunize with multiple variant Ags, there are at least three major questions to address. (i) What form should the variant Ags take so that AM can be steered toward evolving bnAbs? (ii) In what temporal order (e.g., as a mixture, sequentially, or in other permutations) should the variant Ags be administered? (iii) What should be the concentrations of the variant Ags? Answers to these questions are drawn from a large space of possibilities. Mechanistic understanding of AM could serve as a guide, but how AM occurs when there are multiple variant Ags is poorly understood. Important advances are being made to trace bnAb evolution during natural infection (23–28) and find conditions and immunogens that can induce bnAbs (7, 19, 29). However, even if empirical sampling of conditions leads to success, this advance would not provide design rules that could be used to rationally optimize protocols to be effective in diverse people and provide information pertinent for other highly mutable pathogens. Thus, there is a role for modeling and simulation to complement fundamental and applied experimental efforts on this topic.
Building on earlier modeling and simulation of AM with a single Ag (30–32), a few relevant studies with multiple Ags have been reported. Chaudhury et al. (33) studied the generation of protective and cross-reactive Abs against diverse strains of malaria on immunization with a few strains. The malaria apical membrane has a cluster of conserved epitopes (binding targets for B cells) and a cluster of highly variable ones. Thus, the authors studied a situation where each Ag was composed of a single conserved epitope (shared by all Ags) and one variable epitope. They found that immunization with multiple Ags enhances the fraction of B cells that target the conserved epitope (compared with the use of one Ag) and importantly, also enhances the development of Abs that are more cross-reactive to the variable epitopes. Thus, the polyclonal response from all Abs together results in a protective response to multiple strains. Notice that, in the model used in ref. 33, which may be realistic for malaria, epitopes are composed of either purely conserved residues or variable residues.
Motivated by the challenge of inducing bnAbs against HIV, Wang et al. (34) developed a computational model of AM in the presence of multiple variant Ags and studied the relative efficacy of different temporal patterns of immunization. They reported that immunization with a mixture of variant Ags separated by relatively large mutational distances led to production of low Ab titers and low breadth. This result occurred, because the different variant Ags represent potentially conflicting selection forces that can severely frustrate the Darwinian evolutionary process of AM. This frustration can be alleviated by varying the Ag concentration and changing other conditions. Abs are then produced in greater quantities, but they still exhibit low breadth. Wang et al. (34) found that the probability of inducing cross-reactive Abs was improved by sequential immunization with the same variant Ags that produced Abs with low breadth when presented as a mixture. These in silico predictions were tested in model experiments in mice. A recent report (35) provides further experimental support for this strategy.
Luo and Perelson (36) subsequently reported that, during the coevolution of viral strains and Ab responses after infection, Ab breadth increased with the number of variant Ags and the mutational distances separating them. This result likely reflects the fact that, like Chaudhury et al. (33), Luo and Perelson (36) assume that there is one conserved epitope shared by all Ags, different Ags contain distinct epitopes composed of variable residues only, and B cells target either the conserved epitope or a variable epitope. The authors considered broadly cross-reactive Abs to be those with high affinity for the conserved epitope. The structure of the HIV viral spike (37–39) indicates that the conserved residues, such as those that are part of the CD4 binding site, are surrounded by highly variable residues and protective glycans, which can be part of an epitope that also contains the conserved residues [such as is the case in the study by Wang et al. (34)]. Childs et al. (40) also studied a problem pertinent to the development of cross-reactive Abs. They reported that, in the presence of multiple antigenic sites, the breadth of the Abs that evolve is reduced, which is consistent with the findings in ref. 34.
In this paper, we develop analytical and computational models of AM on immunization with a mixture of variant Ags in diverse situations. We study the evolution of Ab breadth across a wide range of conditions, including the number of Ags, their concentration, and the mutational distances separating them. Based on our results, we elaborate a principle of optimal frustration of the AM process: an intermediate level of conflict between the selection forces represented by the multiple variant Ags maximizes the probability of evolving bnAbs. We also describe the biological reasons for the existence of this optimum and how it is influenced by the variables that we study. Our simulations exhibit some of the qualitative behavior observed during the course of natural infection (23–27) and in laboratory studies of AM (41, 42). Finally, we discuss how our results may provide conceptual guidelines for the design of optimal immunization protocols to elicit bnAbs to HIV and other highly mutable pathogens.
Model
Our model for BCRs, Ags, and the interactions between them is coarse-grained and lacks atomic resolution. In the past, we have used string models of BCRs and Ags augmented by nonlocal interactions (34), and others have used string models without such couplings (36). Here, we use a model that is further coarse-grained following the seminal work of Perelson and Oster (43). BCRs and Ags are points in a Euclidean vector space or shape space. Each dimension represents one or more amino acids composing the BCRs and Ags (Fig. 1). Coordinates correspond to biochemical properties relevant for protein interactions, like hydrophobicity or polarity. Perelson and Oster (43) recommend 5–10 dimensions to reflect the size of the Ab repertoire. Additional theoretical considerations and comparisons with immunological data suggest five to eight dimensions (44, 45).
Fig. 1.
A 2D shape space is sketched for illustration. There is one variable dimension along the horizontal axis and one conserved dimension along the vertical axis: . Five Ags are shown as red diamonds. They are on the variable axis, where their identical conserved coordinate (zero) represents conserved amino acids shared by all. Five initial germline or founder BCRs are drawn as blue Y shapes distributed randomly on a hypersphere (dashed circle) centered at the origin. As AM proceeds, BCRs move within this space by mutating, and those moving closer to the Ags are preferentially selected.
This shape-space representation captures the specificity of BCR–Ag interactions. BCRs near an Ag have complementary characteristics that allow them to bind strongly, whereas those far away bind weakly. We make this precise by defining the binding free energy E as
| [1] |
where is the shape-space dimensionality, r and a are the coordinates of the BCR and Ag, and denotes the Euclidian distance between them. The free energy is expressed in units of the thermal energy, . The strongest possible binding corresponds to , when the BCR and Ag overlap exactly, whereas larger positive values of E represent weaker interactions.
It is often more natural to describe strong binding in terms of high (positive) affinity, and therefore, we define affinity as , where is a reference free energy that sets the binding threshold for activation. The equilibrium constant for BCR–Ag binding, , is given by
| [2] |
We set , so that may increase nearly 3,000-fold during AM (46) as B cells evolve from barely meeting the activation threshold () to binding as strongly as allowed by Eq. 1 ().
Ag Variability.
A few structural elements on the HIV envelope are conserved across the viral population and present immunogenic epitopes for BCRs (39). Germline B cells that can target such epitopes have a chance to evolve into bnAbs, and recent studies have shown how designed immunogens can activate such cells (17–21). We study how these germline B cells might evolve on immunization with different types of mixtures of variant Ags. The conserved residues are surrounded by highly variable residues and glycans that can be part of the epitope to which a BCR binds.
The variant Ags that we consider share a set of conserved residues but have nonoverlapping mutations in the variable residues that surround the conserved residues. In our shape space, we select the first dimensions to be variable (generated stochastically for all Ags) and the remaining dimensions to be conserved (identical for all Ags). Conserved and variable regions reside on the same epitope, and BCRs can span both regions, such as with most epitopes targeted by bnAbs for HIV (4, 6).
Variable coordinates are distributed independently with probability density
| [3] |
where is the normal density function with mean zero and variance . All conserved coordinates reside at the center of shape space:
| [4] |
The multidimensional distribution of Ag coordinates is then
| [5] |
where is the Dirac delta function. Taken with the binding free energy from Eq. 1, this coordinate distribution defines a characteristic energy scale for viral mutations:
| [6] |
BCRs that match one viral variant perfectly will bind other mutant strains with a free energy that is typically weaker on the order of . Values of correspond approximately to Ags that differ by mutations in one or two amino acids (SI Appendix, Fig. S1). Below, we study the effects of varying the number of Ags and the mutational distances between them, where we vary the mutational distance by changing the value of .
BCR Mutation.
High-affinity Abs evolve during AM through a series of mutations in the BCRs. We represent mutations as displacements from the previous receptor coordinate r:
| [7] |
where superscripts denote the B-cell generation. The displacements are drawn from an independent and identically distributed normal distribution:
| [8] |
where is the normal density function with mean zero and variance .
This formulation of BCR mutation, together with Eq. 1, reproduces two important features of protein interactions. Consider a receptor r and Ag a with binding free energy E. On mutation , the expected change in binding free energy is
| [9] |
The mean change in binding free energy is always positive (reflecting weaker binding) and independent of the initial BCR structure. Previous models of AM (30, 34) have reproduced these characteristics to match data from the protein interaction (PINT) database (47). We choose , so that , corresponding approximately to single-amino acid mutations as quantified by refs. 47 and 48 (SI Appendix, Fig. S1).
GC Simulation.
We simulate AM in a GC (16) with the steps below. The model parameters are summarized in SI Appendix, Tables S1 and S2. Our qualitative conclusions are robust with respect to the parameters chosen as shown in SI Appendix, Figs. S4–S10.
Step 1: Specify the number of variable and conserved shape-space dimensions, and . In the text, we present results for . Other choices produce qualitatively similar results (SI Appendix, Figs. S4 and S5).
Step 2: Specify the concentration of each immunizing variant Ag in the GC (equal for all Ags and constant through time).
Step 3: Specify a mutational variability, which corresponds to an average mutational distance separating the variant Ags, by setting the energy scale defined by Eq. 6.
Step 4: Generate variant Ags with shape-space coordinates drawn from Eq. 5 and present them as a mixture.
Step 5: Seed the GC with founder B cells placed randomly on a hypersphere centered at the origin of the shape space (Fig. 1). The radius is specified in terms of the binding energy of a founder cell for Ags at the origin. We choose , so that founders just meet the activation threshold. Using Eq. 1, we translate the energy into a radius: . Recent imaging studies suggest that the number of founders may be larger (49), and therefore, we studied the effect of varying and found that the qualitative conclusions remained unchanged (SI Appendix, Fig. S6).
Step 6: Replicate the founder B cells without mutation to generate a total GC population of 1,500 B cells (50).
Step 7: Simulate the Darwinian evolution of B cells through the iterative processes of selection and mutation implemented in steps 8 to 12 below.
Step 8: For each B cell, indexed by j, simulate Ag binding under two scenarios of Ag presentation by follicular dendritic cells (FDCs). In the first scenario, which we call see one, the Ag distribution on FDCs is heterogeneous, and therefore, each B cell encounters only one Ag variant chosen randomly in each round of selection. In the second scenario, named see all, Ags are distributed homogeneously on FDCs, and B cells encounter all Ag variants on every round of selection. These two limiting cases should encompass the true biological conditions.
- These scenarios can be defined by the set of Ag variants encountered by B cell j on this round of selection. Under the see one scenario, contains only a single element chosen at random. This stochastic selection is made independently for each B cell at each round of selection. Under the see all scenario, contains all Ags: . With this Ag set, the simulation of binding proceeds as follows.
-
i)Compute the total amount of Ag bound:
The index k identifies immunizing Ags, and[10]
with[11]
where and are BCR and Ag coordinates.[12] - ii)
-
i)
Step 9: Simulate competition for T follicular helper (Tfh) cells. Rank the remaining B cells by , which should be monotonically related to the amount of Ag bound in step 8. The fraction having the largest receives Tfh help and survives; the others die by apoptosis. This deterministic rule ignores a stochastic element introduced by the search for Tfh cells (32). Other values of yield qualitatively similar results (SI Appendix, Fig. S7).
Step 10: With probability , classify remaining B cells as memory cells and remove them from the GC.
Step 11: With probability , classify remaining B cells with affinity of at least for the Ag bound in step 8 as Ab-secreting plasma cells and remove them. Applying a threshold ensures that Abs have high affinity for at least one Ag (51).
Step 12: Divide remaining B cells into two daughter cells, which mutate independently with probability . Mutations are lethal, and daughter cells are removed, with probability . Mutations alter affinity, and the BCR evolves stochastically according to Eq. 8, with probability ; otherwise, mutations are silent, and the BCR is unchanged (30, 34, 52, 53).
Step 13: Repeat steps 8–12 (one round of selection and mutation) until (i) no B cells remain and the GC is extinguished, (ii) the number of surviving B cells surpasses the initial size after founder replication (simulating Ag consumption), or (iii) the number of cycles reaches 100 (simulating Ag decay to low levels).
Step 14: Generate viral challengers with coordinates drawn from Eqs. 5 and 6 with mutational variability , where the superscript (C) distinguishes the variability of the challenger Ags from the immunizing Ag variability. This energy scale corresponds to mutations in a few amino acids (47, 48) and is consistent with the typical variability in HIV-1 epitopes targeted by bnAbs (23, 25, 27). Other choices for challenger diversity yield qualitatively similar results (SI Appendix, Fig. S8).
Step 15: For each Ab, compute its affinity for each challenger and define the neutralization breadth as the fraction of challengers to which the Ab binds with affinity exceeding . Numerical values of breadth depend on the threshold chosen, but the rank ordering of immunization protocols (e.g., which is best) is independent of this choice (SI Appendix, Fig. S9).
Step 16: Run additional independent AM trajectories (steps 4–15) until or more Ab-secreting plasma cells are collected for each case studied to ensure sufficient statistical accuracy when averaging over the Ab population to determine the breadth of coverage.
Results
The breadth of an Ab increases monotonically with its average affinity for viral variants (SI Appendix, Fig. S11). Strain-specific Abs may have very strong affinity for one particular Ag, but bnAbs will have higher affinity when averaged across the spectrum of viral mutants.
The mean binding free energy for a BCR at coordinate r, averaged over an Ag distribution , is
| [14] |
Substituting the separable distribution from Eq. 5 yields
| [15] |
Receptors at the origin in shape space (minimizing ) have the highest average affinity (lowest ) (Eq. 2) and highest breadth. Receptors near the origin have optimal binding with conserved Ag residues, which allows them to have some favorable interactions with all Ags. They have also reached the center of the distribution of variable residues. Thus, they may not bind strongly with the variable region of any single variant Ag, but in a compromise of sorts, they do not have strongly unfavorable interactions that abrogate recognition.
The second term in Eq. 15 depends only on characteristics of the Ag distribution. It is independent of receptor structure and therefore, cannot be optimized by vaccination. This result implies that pathogens with greater diversity, quantified by either the fraction of the genome that is variable () or the diversity within the variable regions (), will elicit Abs with lower breadth regardless of the immunization protocol.
Optimal Number of Ags Leads to Maximal Breadth.
Fig. 2 illustrates the variation of key characteristics of Abs produced by immunization with mixtures containing different numbers of Ag variants. Ag coordinates are chosen from the probability distribution in Eqs. 5 and 6, with the same average mutational distance between variant Ags, regardless of the number of Ags. The concentration per Ag ( from Eq. 13) is fixed at 0.2, and B cells encounter only one Ag at each round of selection (the see one scenario in step 8 above). Ab characteristics are averaged over a population of or more plasma cells produced by thousands of independent AM trials.
Fig. 2.
Optimal Ag number. The immunization protocol uses an Ag mixture at a fixed concentration () and mutational variability (). In these simulations, B cells encounter only one randomly chosen Ag at each round of mutation and selection. (A) Neutralization breadth, averaged over the Ab population, is largest when the immunogens are composed of four to six Ags. (B) The number of mutations accumulated by Ab-secreting plasma cells is strongly correlated with breadth: Abs with the highest breadth have the most mutations. (C) The average affinity for challenger Ags, the wide range of viral mutants used to evaluate breadth, is also strongly correlated with breadth.
At the concentration simulated (and for other parameters in our model), breadth is maximized for four to six Ags (Fig. 2A), which also corresponds to a maximum in the number of somatic mutations (Fig. 2B) and average affinity for “challenger” Ags that represent the full population of viral variants (Fig. 2C). With a single Ag, the B cells most likely to survive the competition during AM are those with mutations that drive them closest to the single immunizing Ag that they see in the GC. The resulting Abs have very high affinity for that one target, but that specificity for one specific variable Ag structure results in low average affinity and low breadth (Fig. 2) across the full spectrum of viral variants (the challenger Ags). As the number of Ags increases, B cells sacrifice some affinity for the specific targets presented by the immunogens and instead, develop moderate affinity for a broader range of Ags through additional mutations that focus Ab binding to the conserved residues and minimize interactions with the variable residues.
As the number of Ags increases beyond six, the breadth decreases along with the number of mutations and affinity for both immunizing and challenger Ags. As noted by Wang et al. (34), when B cells encounter only one type of Ag during each interaction with FDCs, the multiple variant Ags in the GC present potentially conflicting selection forces that can frustrate AM. Because B cells are likely to encounter different Ags on successive rounds of mutation and selection, the normal course of AM is disrupted, because it is difficult to be positively selected in successive cycles.
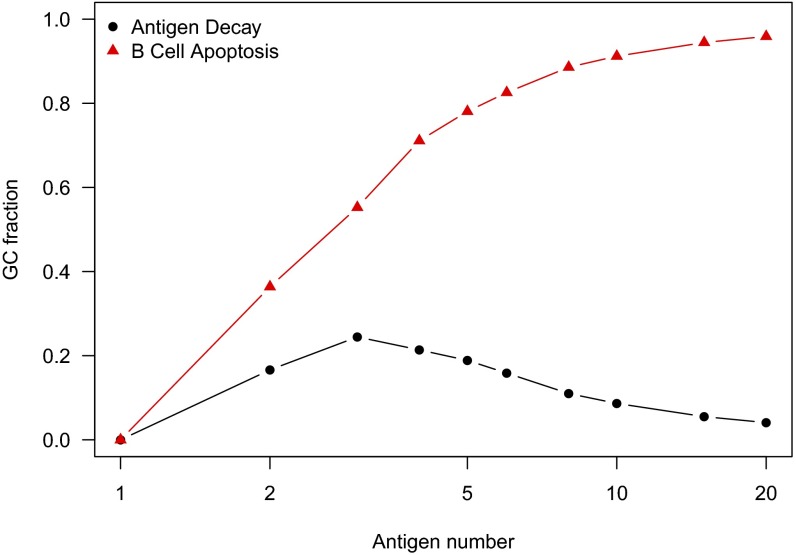
After immunization with a single Ag, frustration is absent, and B cells easily evolve high affinity for that single Ag. Strain-specific Abs of low breadth are produced, because there is no driving force for the Darwinian evolutionary process of AM to evolve cross-reactive Abs. As shown in Fig. 3, under these conditions of low frustration, very few GCs are extinguished because of apoptosis of all B cells. As the number of variant Ags increases, the frustration level increases, and there is an evolutionary driving force that favors the development of cross-reactive B cells. However, the increasing frustration also results in the extinction of a higher fraction of GCs (Fig. 3) because of the increasing likelihood that a population of B cells undergoing AM will be unable to survive owing to the potentially conflicting selection forces. In the GCs that are not extinguished, unlike when there is only one immunizing Ag, the population of B cells does not rise rapidly, fill up the GC, and consume all of the Ag. This behavior occurs because many B cells are not sufficiently cross-reactive to survive successive rounds of mutation and selection. For the B cells that do survive, AM continues for a relatively long time, thus enabling them to acquire the many mutations required for cross-reactive B cells to evolve. Thus, as the number of variant Ags increases, there is an increase in the fraction of GC reactions that reach the maximum time allowed in our simulations (a proxy for Ag decay). Correspondingly, the number of mutations evolved and breadth of the Abs increase (Fig. 2). As the number of variant Ags increases further, however, the level of frustration becomes too high, most GCs extinguish (Fig. 3), and low titers of Abs exhibiting low breadth result.
Fig. 3.
GC fate as a metric of frustration. Conditions are identical to those in Fig. 2. Among the thousands of independent AM trajectories, we show the fraction of GCs that extinguish after apoptosis of all B cells (red triangles) and the fraction that survive until all Ag has decayed (black circles). The remaining GCs (not shown) rapidly fill with proliferating B cells and terminate after consuming all Ag as described in step 13 in GC Simulation.
This last situation was previously described by Wang et al. (34). Because of differences in the model for BCR–Ag affinity, the high frustration limit emerged in the work in ref. 34 at lower Ag numbers. For the immunization protocols and conditions that lead to the results shown in Fig. 2, the level of frustration progressively increases with the number of variant Ags used in the immunogen. In this case, the probability of evolving bnAbs is maximized at an intermediate level of frustration.
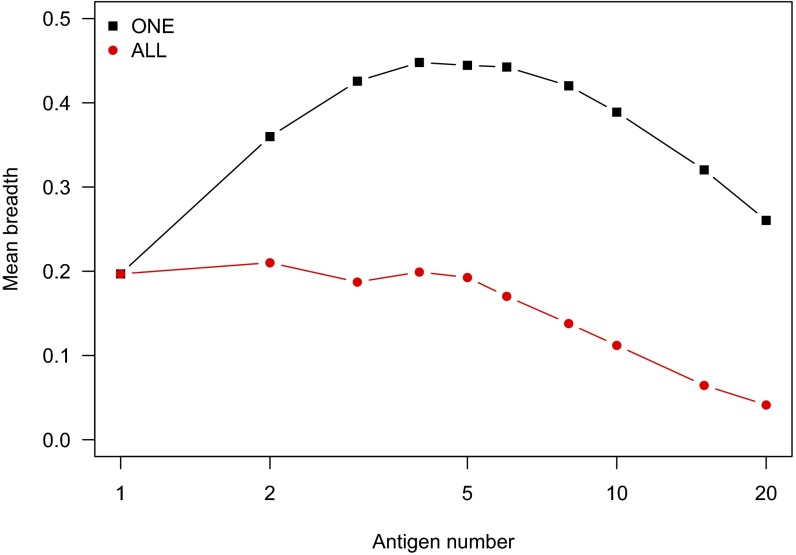
Fig. 4 shows results for the scenario in which all types of Ags are encountered simultaneously during B cell–FDC interactions (the see all scenario in step 8 above); otherwise, conditions are identical to Fig. 2. Each B cell can potentially be positively selected by binding the same variant Ag in every cycle, and therefore, the frustration is substantially alleviated compared with the case where only one type of variant Ag is encountered in every cycle. As a consequence, strain-specific Abs are likely to emerge. Thus, the breadth of Abs produced is substantially lower compared with the case where only one type of Ag is encountered at a time.
Fig. 4.
Comparison of breadth for see one vs. see all Ag presentation by FDCs. Conditions are identical to those in Fig. 2, with the exception of Ag presentation by FDCs. The legend indicates whether the B cells interact with only one Ag (selected randomly) or all Ags at each cycle of the GC reaction. Frustration during AM is reduced when B cells interact with all Ags on each round of selection, and breadth is lower as strain-specific Abs emerge in this case.
In our model, during each round of mutation and selection, a B cell has only one chance to interact with FDCs, and the total amount of Ag bound and internalized is given by Eq. 10. In reality, B cells have several chances to interact with FDCs separated by refractory periods (54). Eq. 10 is approximate and may well capture the effects of multiple opportunities to interact with FDCs. If it does not, then the case where only one type of Ag is encountered in every B cell–FDC interaction but between refractory periods, there are enough opportunities for a B cell to interact with all types of Ags in a single cycle is similar to the situation when all types of Ags are encountered during every round of selection (but with one B cell–FDC interaction per cycle). An example may be when there are very few types of variant Ags and there are multiple opportunities to be positively selected. Of course, in such a case, the frustration is alleviated, and strain-specific Abs will likely result. The frustration can be increased by lowering the Ag concentration.
Optimal Ag Concentration Leads to Maximal Breadth.
The Ag concentration in the GC, which we assume to be proportional to the immunization dosage, plays a major role in determining the survival probability of B cells. Fig. 5 shows neutralization breadth, averaged over Abs, for , 4, and 20 variant-immunizing Ags as a function of the total Ag concentration, . As before, the average mutational distance between variant Ags is independent of their number.
Fig. 5.
Optimal Ag concentration. Conditions are identical to those in Fig. 2, except that Ag concentration is varied over a wide range. The legend indicates the number of Ags, , administered as a mixture, and the mean neutralization breadth is plotted against the total Ag concentration, the product . For each Ag count, the induced Ab breadth reaches a maximum at an optimal Ag concentration.
For each Ag number, breadth reaches a maximum at a particular Ag concentration, a result also noted by Wang et al. (34). Far below the optimum, the probability of productive binding to an Ag (proportional to concentration in Eq. 10) is low, B-cell survival probability is small, most B cells quickly die by apoptosis after failing to bind sufficient Ag for survival, and the GC extinguishes before the maturing B cells accumulate sufficient mutations to acquire breadth. Well above the optimal concentration, the probability of productive Ag binding is large for all B cells, survival probabilities are high, and the GC reaction terminates quickly as the B cells proliferate and consume all Ag. Again, too few mutations accumulate to acquire breadth.
The maximum breadth increases with the number of Ags, but the concentration required to achieve that maximum also increases with . This correlation occurs because the degree of frustration increases as increases, requiring higher Ag concentration to alleviate the frustration. More detailed examination (SI Appendix, Fig. S2) shows that the optimal total Ag concentration increases quadratically with . The high doses required for large Ag numbers may be impractical, or the corresponding Ag concentration within GCs may be biologically unrealistic. It may also be difficult to achieve the relatively low concentrations required for breadth to evolve for smaller Ag numbers (4–6) near the optimum shown in Fig. 2.
Increasing the Number of Ags While Decreasing Their Mutational Distance Reduces the Dependence on Ag Concentration.
We explored whether the pragmatic difficulties associated with the strong optimal concentration dependence on the number of Ags can be overcome by decreasing the mutational distance between the immunizing variant Ags as their number increases. To this end, we specify the following inverse relationship between mutational variation and Ag number:
| [16] |
where the constant λ is the largest Ag count that we wish to consider. With this restriction, immunization with the most variant Ags, , corresponds to the smallest mutational variability between them. The parameters are such that this choice generates the smallest mutational distance that is biologically relevant, , corresponding approximately to mutations in single amino acids (SI Appendix, Fig. S1).
Fig. 6 shows that, in this case as well, there is an optimal number of Ags (and corresponding mutational distance between Ags) that results in maximal breadth. The reason underlying the optimum is different, however. When there are few Ags, the level of frustration is very low, and Abs with low breadth are produced. Frustration increases as the number of immunizing variant Ags grows, leading to increased breadth. However, as the number of variant Ags increases further, the level of frustration is also alleviated, because the variant Ags are also closer to each other in mutational distance. If the number of Ags becomes too high (and mutational distance between them becomes sufficiently small), then the frustration level is quite low. Frustration is low because in subsequent rounds of selection, a given B cell will interact with very similar Ags. Thus, above a threshold number of Ags, the breadth begins to decline. Therefore, in this case, as we increase , we traverse conditions ranging from low frustration to intermediate frustration to low frustration again. This temporal pattern is made vivid in Fig. 7, where we see that the fraction of GCs that extinguish after apoptosis of all B cells and the fraction that survive until Ag has decayed both exhibit a maximum at intermediate numbers of variant Ags. This behavior is in contrast to Fig. 2, where increasing corresponds to traversing conditions that range from low frustration to intermediate frustration to high frustration. In both types of immunization protocols, an intermediate level of frustration maximizes the probability of evolving bnAbs.
Fig. 6.
Optimal Ag number and mutational variability. Ags are administered as a mixture with fixed concentration (); the mutational distance between Ags varies inversely with their number (according to Eq. 16 with ). The outer x axis shows the number of Ags increasing from left to right; the inner x axis shows the mutational distance between them decreasing from left to right. Breadth is maximized at an intermediate number of Ags and mutational distance.
Fig. 7.
GC fate as a metric of frustration. Conditions are identical to those in Fig. 6. The outer x axis shows the number of Ags increasing from left to right; the inner x axis shows the mutational distance between them decreasing from left to right. The fraction of GCs that extinguish after apoptosis of all B cells, a proxy for the level of frustration during AM, is nonmonotonic, reaching a maximum at an intermediate number of Ags and mutational distance.
Fig. 8 shows that, when the mutational distance between immunizing variant Ags is reduced as their number increases, the sensitivity of the optimal concentration to the number of Ags is much reduced, as is the required Ag concentration (compare Fig. 8 with Fig. 5). This reduction occurs because rather than increasing concentration to alleviate frustration, we are achieving this goal by decreasing the mutational distance between Ags. The lower sensitivity to Ag concentration may be practically important, because it may be difficult to precisely control the amount of Ag expressed on FDCs. Our results suggest that an optimal number of immunizing variant Ags with an optimal mutational variability can be chosen to maximize the chance of evolving bnAbs across a relatively broad range of Ag dose.
Fig. 8.
Optimal total concentration. The legend indicates the number of Ags, , administered as a mixture. The mutational distance between Ags varies inversely with according to Eq. 16 with . The mean neutralization breadth is plotted against the total Ag concentration, the product . The optimal total concentration is much less sensitive to when mutational variability decreases as more Ags are presented (compared with Fig. 5).
Principle of Optimal Frustration.
The essential origin of optimal conditions resulting in maximal breadth is easy to understand. During each cycle of selection, division, and mutation, each B cell can undergo one of four possible fates: (i) it can fail to be selected and die by apoptosis, (ii) it can be positively selected and divide into two identical cells, (iii) it can be positively selected and divide into one mutated daughter cell and one identical cell, and (iv) it can be positively selected and divide into two mutated daughter cells. Let the probability of positive selection be and the probability (per cycle) of mutation be μ. The probability of the first possibility is , the second is , the third is , and the fourth is (SI Appendix). The probability of positive selection depends on the BCR and the other conditions that determine the degree of frustration: the number of Ags, their concentration, the mutational distance between them, and how many types of Ag are encountered at each round.
If the extent of frustration is large, apoptosis is the likely outcome ( is small), most B cells will die, and the GC will be rapidly extinguished. This situation will produce few Abs and bnAbs. If the degree of frustration is small (when Ag concentration is high, when is large and the mutational distance separating the Ags is small, or when all types of Ags are encountered in every B cell–FDC interaction), then positive selection is likely ( is large). Now, because the mutation probability (μ) is much less than one, the GC will rapidly be populated by B cells that have not acquired the number of mutations required to confer breadth by the time that all Ag has been consumed. This situation will not result in bnAbs either but rather, strain-specific Abs. Only when the conditions lead to intermediate levels of frustration (intermediate values of ) will the GC reaction continue long enough for the B cells to acquire the number of mutations required for bnAbs to develop. Numerical solutions of this model show that an optimal value of naturally emerges (SI Appendix).
In short, an optimal level of frustration leads to maximal breadth. In our calculations, this optimal frustration manifested as an optimal number of Ags, an optimal mutational distance separating Ags, and as previously described (34), an optimal Ag concentration. In the language of dynamical systems, there are two strong attractors for the dynamical processes occurring in the GC when multiple variant Ags are part of the immunogen: one that corresponds to apoptosis when the frustration level is too high, and one that corresponds to strain-specific Abs when the extent of frustration is too low. Perhaps, a narrow ridge line leads to the attractor corresponding to bnAbs. [The sharpness of the maximum does indeed suggest a strong sensitivity to the level of frustration and a narrow region of bnAb production (SI Appendix, Fig. S3).] Future research, both experimental and theoretical, aims to determine how to design immunization protocols that will stabilize B cells as they traverse this ridge line to reach the bnAb attractor with high probability.
Dead-End and Off-Track Abs.
Most bnAbs accumulate many mutations during AM (6, 55). For example, Bhiman et al. (27) observe high degrees of somatic hypermutation (SHM) in their bnAb lineage. In addition, however, they and others (13, 56–58) find two other Ab classes: “off-track” Abs with the same large number of mutations but low breadth and “dead-end” Abs with few mutations and low breadth. Similar findings have been reported for Abs to the influenza virus (59).
Our simulations also produce dead-end and off-track Abs, as shown in Fig. 9. We collect Abs from simulations that generate bnAbs (identical to those in Fig. 2 with ), count the number of mutations from the germline, and separate the sample into those with four or fewer (Fig. 9A) and seven or more mutations (Fig. 9B and SI Appendix, Fig. S14). In set A, the developing Abs could not tolerate the diversity of variant immunizing Ags, failed to evolve beyond four mutations from the germline, and have breadth below 0.3. In set B, the Abs have accumulated at least seven mutations. Nearly 60% of Abs with this high degree of SHM are broadly neutralizing, with breadth greater than 0.5. Five percent, however, have breadth below 0.2, despite significant evolution from the germline. Note that these results reflect the different ways in which the same germline B cells evolved under identical conditions, resulting in bnAbs but also, off-track and dead-end Abs. The production of off-track and dead-end Abs is a consequence of the intrinsically stochastic character of evolutionary processes and may be difficult to eliminate by tuning immunization strategies.
Fig. 9.
Dead-end and off-track Abs. The histogram shows the distribution of neutralization breadth for Abs with (A) four or fewer and (B) seven or more mutations produced in simulations with conditions identical to those in Fig. 2 and . The ordinates are probability densities. Most Abs that reach an evolutionary dead-end (A) have very low breadth. Most Abs with a high degree of SHM (B) are broadly neutralizing, with breadth greater than 0.4, but a small subset of off-track Abs has breadth below 0.2, despite having accumulated a large number of mutations. SI Appendix, Fig. S14 shows the full distribution of mutations.
Discussion
The development of vaccination strategies that can elicit bnAbs against diverse strains of highly mutable pathogens would have a significant impact on global health. Enormous advances are being made in isolating bnAbs against HIV from patients (10–15), understanding the evolutionary pathways that lead to bnAbs in individuals (23–28), and developing immunogens to activate the germline B cells that can mature into bnAbs (17–21, 35). Laboratories have synthesized structures, such as stabilized envelope trimer variants, that aim to mimic the trimeric viral spike and can contain customized mutations, thus creating variant Ags that share conserved residues (29, 60, 61).
On activation of the correct germline B cells, what should be the temporal pattern of immunization with the variant Ags, their number, concentrations, and mutational separation to optimally induce bnAbs? We and others have suggested sequential immunization with variant Ags as one solution (3, 6, 8, 20, 22, 34). Our past work leading to this conclusion considered variant Ags separated by relatively large mutational distances. In this circumstance, we found that temporal separation of the potentially conflicting selection forces represented by the variant Ags had a greater chance of inducing bnAbs compared with immunization with a mixture of the same Ags. In this paper, we studied the possibility of evolving bnAbs on immunization with a mixture of variant Ags across a wide range of conditions.
Our principal findings are as follows. If the average mutational distance between immunizing variant Ags is fixed, an optimal number of Ags maximizes the probability of eliciting bnAbs. In this case, there is also an optimal Ag concentration, and it is a very strong function of the number of immunizing Ags. If we reduce the mutational distance between Ags as their number increases, we also find that there exists an optimal number of Ags separated by an optimal mutational distance. In this case, there is only a modest dependence of the optimal Ag concentration on the number of variant Ags. The reduced concentration dependence is a practical advantage, because Ag concentration in GCs is difficult to control by manipulating the Ag dose in an injected vaccine. Our findings for a few Ags separated by many mutations (Fig. 6 with ) are qualitatively consistent with those obtained by Wang et al. (34) using a more detailed string model of BCR and Ag structure, which is expected to yield quantitatively different results (31).
The optimal conditions that we describe emerge when the level of frustration because of the conflicting selection forces is neither too high nor too low. When the frustration level is too low (e.g., many variant Ags separated by small mutational distances), strain-specific Abs are likely to develop. If the frustration level is too high (e.g., several variant Ags separated by large mutational distances), AM cannot be sustained, and few Abs are produced. Only intermediate levels of frustration inhibit strain-specific Abs while allowing B cells to survive enough rounds of selection to accumulate the mutations required for breadth. We develop a simple intuitive picture and model to describe this principle of optimal frustration. We also show that, even in circumstances where bnAbs are likely to emerge, dead-end and off-track Abs also develop (27). It would be difficult to completely prevent the evolution of such Abs by controlling vaccination protocols because of the inherently stochastic character of the evolutionary process of AM.
A single mixture of optimally designed immunogens is more appealing from a logistic and feasibility perspective than a sequence of distinct vaccines. An example of such a scheme aimed at eliciting bnAbs targeting the V2 region of the Env trimer (which is commonly targeted during infection) might be to use stabilized envelope trimers (SOSIPs) from strains previously shown to have enhanced interactions with the rare B cells that mature into V2-directed bnAbs (39, 62). Thereafter, incorporation of mutations within the V2 region would result in a mixture of variant immunogens to drive tolerance of diversity. Immunization with different numbers of SOSIP variants separated by different mutational distances may be able to test the predictions that we report in this paper.
After eliciting the correct germline B cells, the optimal strategy for inducing bnAbs efficiently may require a combination of immunization with a mixture of an optimal number of variant Ags separated by an optimal mutational distance (Fig. 6) followed by sequential immunization with variant Ags separated by a larger mutational distance (3, 6, 8, 20, 22, 34). Alternatively, the most efficient strategy may be sequential immunization followed by a mixture of variant Ags, as in ref. 35. Study of these situations to determine optimal conditions as we report here, both computationally and experimentally, is an important direction of future research. We also note that we have not considered the distracting epitopes (which are completely variable) in addition to those that contain a conserved set of residues that are present in immunogens, such as SOSIPs. It is unknown whether eliciting the right germline B cells first is sufficient to focus AM on these B cells that target epitopes that contain conserved residues. Study of this issue is also warranted.
The mutations that separate the variant Ags must be in the variable residues that are spatially adjacent to the conserved residues that are shared between them. Where possible, the immunogens should exhibit some affinity for the germline B cells associated with bnAbs. In Fig. 6, we predict optimal breadth for 8–10 Ags separated by roughly three mutations. In earlier simulations of mixtures with model Ags, supported by model experiments (34), variant Ags separated by 11 mutations did not elicit bnAbs. We, therefore, expect optimal immunogens to contain six to eight Ags with variation in 3–10 locations.
To further guide studies with trimeric variant Ags, such as SOSIP mutants (29, 61), additional computational investigations are required. Specifically, a set of SOSIP Ags must first be chosen that bears mutations in variable residues spatially adjacent to the conserved part of the target epitope and that is the most mutable in the circulating HIV population (63). Detailed atomistic molecular dynamics calculations must be performed with these mutants to assay the binding affinity of germline Abs [or Abs first induced by germline-targeting immunogens (17–19)]. The subset that displays weak to moderate affinity for at least one of the variants should then be selected. Simulations, such as those reported in this paper but now coupled to detailed atomistic calculations to compute binding energies of mutated BCRs for these Ags before every round of selection, should then be carried out to screen for the best sets of variant Ags. Such studies are planned.
Finally, although our model was inspired by the problem of inducing bnAbs against the HIV envelope, it is a coarse-grained representation that is meant to reveal general principles and may, therefore, also apply to other highly mutable viruses.
Supplementary Material
Acknowledgments
We thank Joy E. Louveau, Jinal N. Bhiman, and Shenshen Wang for helpful discussions. Financial support was provided by the Ragon Institute of Massachusetts General Hospital, Massachusetts Institute of Technology, and Harvard University. P.L.M. is supported by the South African Research Chairs Initiative of the Department of Science and Technology and National Research Foundation of South Africa and the South African Medical Research Council Strategic Health Innovation Partnerships Program.
Footnotes
The authors declare no conflict of interest.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1614940113/-/DCSupplemental.
References
- 1.Xiao X, et al. Germline-like predecessors of broadly neutralizing antibodies lack measurable binding to HIV-1 envelope glycoproteins: Implications for evasion of immune responses and design of vaccine immunogens. Biochem Biophys Res Commun. 2009;390(3):404–409. doi: 10.1016/j.bbrc.2009.09.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Dimitrov DS. Therapeutic antibodies, vaccines and antibodyomes. MAbs. 2010;2(3):347–356. doi: 10.4161/mabs.2.3.11779. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Haynes BF, Kelsoe G, Harrison SC, Kepler TB. B-cell-lineage immunogen design in vaccine development with HIV-1 as a case study. Nat Biotechnol. 2012;30(5):423–433. doi: 10.1038/nbt.2197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Burton DR, et al. A blueprint for HIV vaccine discovery. Cell Host Microbe. 2012;12(4):396–407. doi: 10.1016/j.chom.2012.09.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Klein F, et al. Antibodies in HIV-1 vaccine development and therapy. Science. 2013;341(6151):1199–1204. doi: 10.1126/science.1241144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Kwong PD, Mascola JR, Nabel GJ. Broadly neutralizing antibodies and the search for an HIV-1 vaccine: The end of the beginning. Nat Rev Immunol. 2013;13(9):693–701. doi: 10.1038/nri3516. [DOI] [PubMed] [Google Scholar]
- 7.West AP, Jr, et al. Structural insights on the role of antibodies in HIV-1 vaccine and therapy. Cell. 2014;156(4):633–648. doi: 10.1016/j.cell.2014.01.052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.de Taeye SW, Moore JP, Sanders RW. HIV-1 envelope trimer design and immunization strategies to induce broadly neutralizing antibodies. Trends Immunol. 2016;37(3):221–232. doi: 10.1016/j.it.2016.01.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Burton DR, Hangartner L. Broadly neutralizing antibodies to HIV and their role in vaccine design. Annu Rev Immunol. 2016;34:635–659. doi: 10.1146/annurev-immunol-041015-055515. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Binley JM, et al. Comprehensive cross-clade neutralization analysis of a panel of anti-human immunodeficiency virus type 1 monoclonal antibodies. J Virol. 2004;78(23):13232–13252. doi: 10.1128/JVI.78.23.13232-13252.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Li Y, et al. Broad HIV-1 neutralization mediated by CD4-binding site antibodies. Nat Med. 2007;13(9):1032–1034. doi: 10.1038/nm1624. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Doria-Rose NA, et al. Frequency and phenotype of human immunodeficiency virus envelope-specific B cells from patients with broadly cross-neutralizing antibodies. J Virol. 2009;83(1):188–199. doi: 10.1128/JVI.01583-08. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Walker LM, et al. Protocol G Principal Investigators Broad and potent neutralizing antibodies from an African donor reveal a new HIV-1 vaccine target. Science. 2009;326(5950):285–289. doi: 10.1126/science.1178746. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Bonsignori M, et al. Two distinct broadly neutralizing antibody specificities of different clonal lineages in a single HIV-1-infected donor: Implications for vaccine design. J Virol. 2012;86(8):4688–4692. doi: 10.1128/JVI.07163-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Hraber P, et al. Prevalence of broadly neutralizing antibody responses during chronic HIV-1 infection. AIDS. 2014;28(2):163–169. doi: 10.1097/QAD.0000000000000106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Victora GD, Nussenzweig MC. Germinal centers. Annu Rev Immunol. 2012;30:429–457. doi: 10.1146/annurev-immunol-020711-075032. [DOI] [PubMed] [Google Scholar]
- 17.Jardine J, et al. Rational HIV immunogen design to target specific germline B cell receptors. Science. 2013;340(6133):711–716. doi: 10.1126/science.1234150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Jardine JG, et al. HIV-1 VACCINES. Priming a broadly neutralizing antibody response to HIV-1 using a germline-targeting immunogen. Science. 2015;349(6244):156–161. doi: 10.1126/science.aac5894. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Jardine JG, et al. HIV-1 broadly neutralizing antibody precursor B cells revealed by germline-targeting immunogen. Science. 2016;351(6280):1458–1463. doi: 10.1126/science.aad9195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Dosenovic P, et al. Immunization for HIV-1 broadly neutralizing antibodies in human Ig knockin mice. Cell. 2015;161(7):1505–1515. doi: 10.1016/j.cell.2015.06.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.McGuire AT, et al. Specifically modified Env immunogens activate B-cell precursors of broadly neutralizing HIV-1 antibodies in transgenic mice. Nat Commun. 2016;7:10618. doi: 10.1038/ncomms10618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Mouquet H. Tailored immunogens for rationally designed antibody-based HIV-1 vaccines. Trends Immunol. 2015;36(8):437–439. doi: 10.1016/j.it.2015.07.001. [DOI] [PubMed] [Google Scholar]
- 23.Liao HX, et al. NISC Comparative Sequencing Program Co-evolution of a broadly neutralizing HIV-1 antibody and founder virus. Nature. 2013;496(7446):469–476. doi: 10.1038/nature12053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Wibmer CK, et al. Viral escape from HIV-1 neutralizing antibodies drives increased plasma neutralization breadth through sequential recognition of multiple epitopes and immunotypes. PLoS Pathog. 2013;9(10):e1003738. doi: 10.1371/journal.ppat.1003738. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Doria-Rose NA, et al. NISC Comparative Sequencing Program Developmental pathway for potent V1V2-directed HIV-neutralizing antibodies. Nature. 2014;509(7498):55–62. doi: 10.1038/nature13036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Wu X, et al. NISC Comparative Sequencing Program Maturation and diversity of the VRC01-antibody lineage over 15 years of chronic HIV-1 infection. Cell. 2015;161(3):470–485. doi: 10.1016/j.cell.2015.03.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Bhiman JN, et al. Viral variants that initiate and drive maturation of V1V2-directed HIV-1 broadly neutralizing antibodies. Nat Med. 2015;21(11):1332–1336. doi: 10.1038/nm.3963. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.MacLeod DT, et al. IAVI Protocol C Investigators & The IAVI African HIV Research Network Early antibody lineage diversification and independent limb maturation lead to broad HIV-1 neutralization targeting the Env high-mannose patch. Immunity. 2016;44(5):1215–1226. doi: 10.1016/j.immuni.2016.04.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Sanders RW, et al. A next-generation cleaved, soluble HIV-1 Env trimer, BG505 SOSIP.664 gp140, expresses multiple epitopes for broadly neutralizing but not non-neutralizing antibodies. PLoS Pathog. 2013;9(9):e1003618. doi: 10.1371/journal.ppat.1003618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Zhang J, Shakhnovich EI. Optimality of mutation and selection in germinal centers. PLOS Comput Biol. 2010;6(6):e1000800. doi: 10.1371/journal.pcbi.1000800. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Heo M, Zeldovich KB, Shakhnovich EI. Diversity against adversity: How adaptive immune system evolves potent antibodies. J Stat Phys. 2011;144(2):241–267. [Google Scholar]
- 32.Meyer-Hermann M, et al. A theory of germinal center B cell selection, division, and exit. Cell Reports. 2012;2(1):162–174. doi: 10.1016/j.celrep.2012.05.010. [DOI] [PubMed] [Google Scholar]
- 33.Chaudhury S, Reifman J, Wallqvist A. Simulation of B cell affinity maturation explains enhanced antibody cross-reactivity induced by the polyvalent malaria vaccine AMA1. J Immunol. 2014;193(5):2073–2086. doi: 10.4049/jimmunol.1401054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Wang S, et al. Manipulating the selection forces during affinity maturation to generate cross-reactive HIV antibodies. Cell. 2015;160(4):785–797. doi: 10.1016/j.cell.2015.01.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Escolano A, et al. Sequential immunization elicits broadly neutralizing anti-HIV-1 antibodies in Ig knockin mice. Cell. 2016;166(6):1445–1458. doi: 10.1016/j.cell.2016.07.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Luo S, Perelson AS. Competitive exclusion by autologous antibodies can prevent broad HIV-1 antibodies from arising. Proc Natl Acad Sci USA. 2015;112(37):11654–11659. doi: 10.1073/pnas.1505207112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Julien JP, et al. Crystal structure of a soluble cleaved HIV-1 envelope trimer. Science. 2013;342(6165):1477–1483. doi: 10.1126/science.1245625. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Lyumkis D, et al. Cryo-EM structure of a fully glycosylated soluble cleaved HIV-1 envelope trimer. Science. 2013;342(6165):1484–1490. doi: 10.1126/science.1245627. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Gorman J, et al. NISC Comparative Sequencing Program Structures of HIV-1 Env V1V2 with broadly neutralizing antibodies reveal commonalities that enable vaccine design. Nat Struct Mol Biol. 2016;23(1):81–90. doi: 10.1038/nsmb.3144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Childs LM, Baskerville EB, Cobey S. Trade-offs in antibody repertoires to complex antigens. Philos Trans R Soc Lond B Biol Sci. 2015;370(1676):20140245. doi: 10.1098/rstb.2014.0245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Eisen HN, Siskind GW. Variations in affinities of antibodies during the immune response. Biochemistry. 1964;3(7):996–1008. doi: 10.1021/bi00895a027. [DOI] [PubMed] [Google Scholar]
- 42.Kang M, Eisen TJ, Eisen EA, Chakraborty AK, Eisen HN. Affinity inequality among serum antibodies that originate in lymphoid germinal centers. PLoS One. 2015;10(10):e0139222. doi: 10.1371/journal.pone.0139222. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Perelson AS, Oster GF. Theoretical studies of clonal selection: Minimal antibody repertoire size and reliability of self-non-self discrimination. J Theor Biol. 1979;81(4):645–670. doi: 10.1016/0022-5193(79)90275-3. [DOI] [PubMed] [Google Scholar]
- 44.Smith DJ, Forrest S, Hightower RR, Perelson AS. Deriving shape space parameters from immunological data. J Theor Biol. 1997;189(2):141–150. doi: 10.1006/jtbi.1997.0495. [DOI] [PubMed] [Google Scholar]
- 45.Lapedes A, Farber R. The geometry of shape space: Application to influenza. J Theor Biol. 2001;212(1):57–69. doi: 10.1006/jtbi.2001.2347. [DOI] [PubMed] [Google Scholar]
- 46.Yang PL, Schultz PG. Mutational analysis of the affinity maturation of antibody 48G7. J Mol Biol. 1999;294(5):1191–1201. doi: 10.1006/jmbi.1999.3197. [DOI] [PubMed] [Google Scholar]
- 47.Kumar MDS, Gromiha MM. PINT: Protein-protein interactions thermodynamic database. Nucleic Acids Res. 2006;34(Database issue):D195–D198. doi: 10.1093/nar/gkj017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Miyazawa S, Jernigan RL. Residue-residue potentials with a favorable contact pair term and an unfavorable high packing density term, for simulation and threading. J Mol Biol. 1996;256(3):623–644. doi: 10.1006/jmbi.1996.0114. [DOI] [PubMed] [Google Scholar]
- 49.Tas JMJ, et al. Visualizing antibody affinity maturation in germinal centers. Science. 2016;351(6277):1048–1054. doi: 10.1126/science.aad3439. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Küppers R, Zhao M, Hansmann ML, Rajewsky K. Tracing B cell development in human germinal centres by molecular analysis of single cells picked from histological sections. EMBO J. 1993;12(13):4955–4967. doi: 10.1002/j.1460-2075.1993.tb06189.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Smith KGC, Light A, Nossal GJV, Tarlinton DM. The extent of affinity maturation differs between the memory and antibody-forming cell compartments in the primary immune response. EMBO J. 1997;16(11):2996–3006. doi: 10.1093/emboj/16.11.2996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Shlomchik MJ, Watts P, Weigert MG, Litwin S. Clone: A Monte-Carlo computer simulation of B cell clonal expansion, somatic mutation, and antigen-driven selection. Curr Top Microbiol Immunol. 1998;229:173–197. doi: 10.1007/978-3-642-71984-4_13. [DOI] [PubMed] [Google Scholar]
- 53.Shannon M, Mehr R. Reconciling repertoire shift with affinity maturation: The role of deleterious mutations. J Immunol. 1999;162(7):3950–3956. [PubMed] [Google Scholar]
- 54.Meyer-Hermann ME, Maini PK, Iber D. An analysis of B cell selection mechanisms in germinal centers. Math Med Biol. 2006;23(3):255–277. doi: 10.1093/imammb/dql012. [DOI] [PubMed] [Google Scholar]
- 55.Moore PL, Williamson C, Morris L. Virological features associated with the development of broadly neutralizing antibodies to HIV-1. Trends Microbiol. 2015;23(4):204–211. doi: 10.1016/j.tim.2014.12.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Mouquet H, et al. Memory B cell antibodies to HIV-1 gp140 cloned from individuals infected with clade A and B viruses. PLoS One. 2011;6(9):e24078. doi: 10.1371/journal.pone.0024078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Walker LM, et al. Protocol G Principal Investigators Broad neutralization coverage of HIV by multiple highly potent antibodies. Nature. 2011;477(7365):466–470. doi: 10.1038/nature10373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Sok D, et al. Recombinant HIV envelope trimer selects for quaternary-dependent antibodies targeting the trimer apex. Proc Natl Acad Sci USA. 2014;111(49):17624–17629. doi: 10.1073/pnas.1415789111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Pappas L, et al. Rapid development of broadly influenza neutralizing antibodies through redundant mutations. Nature. 2014;516(7531):418–422. doi: 10.1038/nature13764. [DOI] [PubMed] [Google Scholar]
- 60.Sanders RW, et al. Stabilization of the soluble, cleaved, trimeric form of the envelope glycoprotein complex of human immunodeficiency virus type 1. J Virol. 2002;76(17):8875–8889. doi: 10.1128/JVI.76.17.8875-8889.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.de Taeye SW, et al. Immunogenicity of stabilized HIV-1 envelope trimers with reduced exposure of non-neutralizing epitopes. Cell. 2015;163(7):1702–1715. doi: 10.1016/j.cell.2015.11.056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Andrabi R, et al. Identification of common features in prototype broadly neutralizing antibodies to HIV envelope V2 apex to facilitate vaccine design. Immunity. 2015;43(5):959–973. doi: 10.1016/j.immuni.2015.10.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Seaman MS, et al. Tiered categorization of a diverse panel of HIV-1 Env pseudoviruses for assessment of neutralizing antibodies. J Virol. 2010;84(3):1439–1452. doi: 10.1128/JVI.02108-09. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.