Identifying the elusive link between amino acid sequence and charge selectivity in pentameric ligand-gated ion channels

Significance

The cation-versus-anion selectivity of pentameric ligand-gated ion channels cannot always be predicted on the basis of their amino acid sequences alone. Indeed, the relationship between amino acid sequence and function contains subtle elements that have eluded prior investigation. Here, we found that ion–ion interactions between the passing ions and ionized side chains in the first turn of the M2 α-helices dominate the permeation free-energy landscape, but we also found that the mere presence of an ionized residue in the first turn of M2 does not ensure that its charge is “felt” by permeating ions. Instead, there seems to be a requirement for a proper conformation for a charged side chain to exert its effect on selectivity.

Abstract

Among neurotransmitter-gated ion channels, the superfamily of pentameric ligand-gated ion channels (pLGICs) is unique in that its members display opposite permeant-ion charge selectivities despite sharing the same structural fold. Although much effort has been devoted to the identification of the mechanism underlying the cation-versus-anion selectivity of these channels, a careful analysis of past work reveals that discrepancies exist, that different explanations for the same phenomenon have often been put forth, and that no consensus view has yet been reached. To elucidate the molecular basis of charge selectivity for the superfamily as a whole, we performed extensive mutagenesis and electrophysiological recordings on six different cation-selective and anion-selective homologs from vertebrate, invertebrate, and bacterial origin. We present compelling evidence for the critical involvement of ionized side chains—whether pore-facing or buried—rather than backbone atoms and propose a mechanism whereby not only their charge sign but also their conformation determines charge selectivity. Insertions, deletions, and residue-to-residue mutations involving nonionizable residues in the intracellular end of the pore seem to affect charge selectivity by changing the rotamer preferences of the ionized side chains in the first turn of the M2 α-helices. We also found that, upon neutralization of the charged residues in the first turn of M2, the control of charge selectivity is handed over to the many other ionized side chains that decorate the pore. This explains the long-standing puzzle as to why the neutralization of the intracellular-mouth glutamates affects charge selectivity to markedly different extents in different cation-selective pLGICs.

The physiological role of a neurotransmitter-gated ion channel (NGIC) depends, to a large extent, on whether it is permeable to cations or anions. In excitable tissues, for example, cation-selective NGICs are excitatory because their opening leads to an influx of Na⁺ that depolarizes the cell. Anion-selective NGICs, on the other hand, are mostly inhibitory, but they can also be excitatory depending on a number of factors that include the values of the Cl^– and HCO₃^– equilibrium (Nernst) potentials and the resting membrane potential. Among these ion channels, only the superfamily of pentameric ligand-gated ion channels (“pLGICs”) has evolved to give rise to members that are highly selective for either cations or anions while retaining the same overall structure; all other NGICs (that is, those gated by glutamate or ATP) are selective for cations. Thus, because all cation-selective NGICs discriminate poorly between Na⁺ and K⁺, fast inhibitory synaptic transmission is mediated, exclusively, by the anion-selective pLGICs.

Few aspects of pLGICs are as intriguing—and, at the same time, have remained as elusive and controversial—as the physicochemical basis of their opposite charge selectivities. Certainly, the relationship between primary sequence and cation-versus-anion selectivity in these channels is so difficult to encapsulate in a few rules that predicting charge selectivity from the mere inspection of sequences is not a trivial task, especially when it comes to mutant sequences or wild-type sequences from bacteria, Archaea, or invertebrate organisms. For example, the presence (in the wild-type cation-selective pLGICs) or absence (in the wild-type anion-selective pLGICs) of a “ring” of pore-lining glutamates at the intracellular end of the transmembrane portion of the pore (position –1′; Fig. 1) is often invoked to explain selectivity for cations or anions, respectively, even when α7 (1, 2) and muscle (3) nicotinic acetylcholine receptors (AChRs) remain highly cation selective upon neutralization of all of the negatively charged side chains at this position. Also, the presence of an additional residue in the M1–M2 linker of all wild-type anion-selective pLGICs from vertebrates (Fig. 1), and the effect of inserting (in the cation-selective members) or deleting (in the anion-selective ones) one residue from this region, are often taken as evidence for a tight relationship between the length of this linker and charge selectivity (1, 2, 4, 5). However, wild-type anion-selective AChRs with short M1–M2 linkers (6) and cation-selective γ-aminobutyric acid type A receptors (GABA_ARs) with long M1–M2 linkers (7) have been thoroughly characterized in invertebrates. These inconsistencies, along with the fact that many mutations in the charge-selectivity filter region of these channels nearly abolish channel expression (5, 8), have led to a confusing picture that becomes increasingly more blurred as new mutational data are added (9, 10) and new nonvertebrate genomes are sequenced (e.g., refs. 11–15). Indeed, although much effort has been devoted to the identification of the mechanism underlying the cation-versus-anion selectivity of these channels, a careful analysis of the literature reveals that a large number of discrepancies exist, that disparate explanations for the same phenomenon have often been put forth, and that no consensus view has yet been reached. For example, whereas some authors have suggested that the charge selectivity of pLGICs is governed solely by interactions between the passing ions and backbone atoms (2, 4, 16), others have favored the notion that only pore-facing charged side chains underlie this process in both the cation-selective and the anion-selective pLGICs (5). Notably, thus far, no unifying mechanism has been proposed that can account for the results of mutational studies obtained with different pLGICs and that explains the molecular basis of charge selectivity for the entire superfamily.

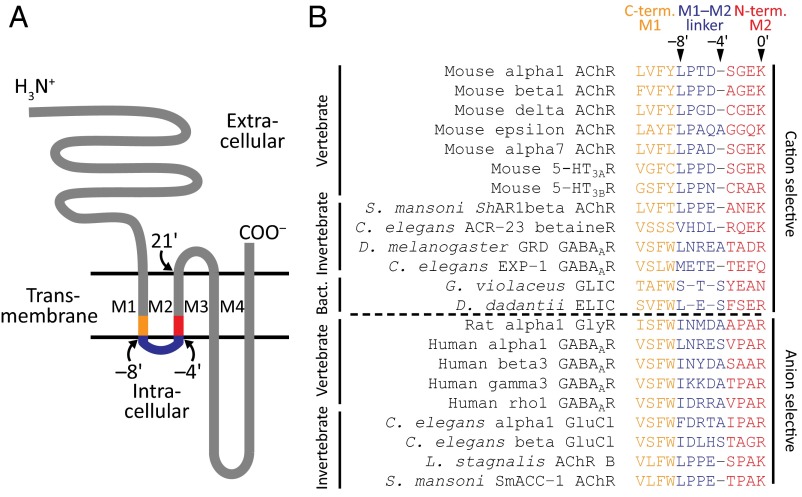
Fig. 1.

The charge-selectivity filter of wild-type pLGICs. (A) Schematic representation of the membrane-threading pattern of individual pLGIC subunits. The C terminus of M1, the M1–M2 linker, and the N terminus of M2 are highlighted. The approximate location of some residues is indicated with the prime notation used throughout this work. (B) Alignment of residues in and flanking the M1–M2 linker. The classification of these residues as belonging to the linker or to one of the flanking α-helical termini is tentative and was made on the basis of the structural models of the anion-selective β₃ GABA_AR (PDB ID code 4COF; ref. 24) and the cation-selective Gloeobacter violaceus ligand-gated ion channel, GLIC (PDB ID code 4HFI; ref. 27). The broken horizontal line separates the sequences of subunits that form cation-selective channels (Top) from those that form anion-selective ones (Bottom). The invertebrate organisms in this list are Schistosoma mansoni (a parasitic flatworm), Caenorhabditis elegans (a nematode), Drosophila melanogaster (an arthropod), and Lymnaea stagnalis (a mollusc), and the bacteria are G. violaceus and Dickeya dadantii (formerly classified as Erwinia chrysanthemi). The color code identifying the M1–M2 linker and flanking regions is the same as in A.

To elucidate the relationship between primary sequence and charge selectivity in the pLGIC superfamily—especially now that several structural models have become available—we performed extensive mutagenesis on a diverse panel of cation-selective and anion-selective homologs, and assessed the effect of mutations on function using macroscopic patch-clamp electrophysiology. We present compelling evidence for the critical involvement of ionized side chains in this process—regardless of whether they are pore-facing or buried—and propose a mechanism whereby not only their charge sign but also their conformation determines charge selectivity.

Results

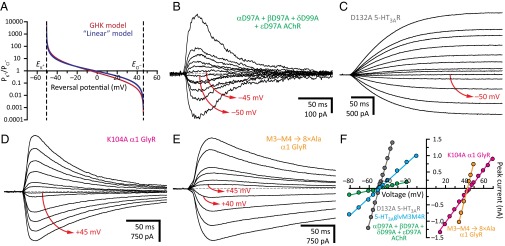
Previous mutational studies have identified the intracellular end of the transmembrane pore as the region that controls the charge selectivity of pLGICs (e.g., refs. 1, 2, 4, 5, 16, and 17). An alignment of amino acid sequences from vertebrate homologs reveals that this short stretch of amino acids is highly conserved in these animals. Indeed, most cation-selective pLGIC-forming subunits (and, certainly, all of those that can form homomeric pentamers) have either a GEK or a GER motif in the first turn of the M2 α-helix and a four-residue M1–M2 linker. Similarly, all anion-selective pLGIC subunits have either a PAR or an AAR motif in the first turn of M2 and a five-residue linker (Fig. 1). However, extending the alignment to the invertebrate and bacterial members of the superfamily reveals that the filter’s sequences vary widely (Fig. 1), and thus that the relationship between sequence and charge selectivity seems more tenuous than hinted by the inspection of vertebrate sequences alone. Therefore, in an attempt to capture this breadth of sequence space, we included vertebrate, invertebrate, and bacterial pLGICs in the mutational study presented here. Charge selectivities were inferred from zero-current (“reversal”) potentials estimated under near KCl-dilution conditions using the whole-cell configuration of the patch-clamp technique and were expressed in terms of permeability-coefficient ratios (P_K⁺/P_Cl^– or P_Cl^–/P_K⁺) calculated using the Goldman–Hodgkin–Katz (GHK) equation (Fig. 2A and SI Materials and Methods). Means and SEs of these values are indicated in Tables S1–S4 for the wild-type and mutant constructs of the muscle AChR, the homomeric serotonin type 3A receptor (5-HT_3AR), the heteromeric serotonin type 3A–3B receptor (5-HT_3A-3BR), and the α1 glycine receptor (GlyR) from mammals, respectively; in Table S5 for a chimeric chick–Caenorhabditis elegans α7-AChR–β-GluCl receptor channel (16); and in Table S6 for the bacterial Erwinia chrysanthemi ligand-gated ion channel (ELIC). To establish a “baseline,” we started by studying the wild-type constructs (including the chimera) and found all six of them to be highly selective for either cations or anions (P_K⁺/P_Cl^– = 97 for the muscle AChR; 31 for the 5-HT_3AR; 42 for the 5-HT_3A-3BR; and 44 for ELIC; P_Cl^–/P_K⁺ = 119 for the α1 GlyR; and 410 for the α7-AChR–β-GluCl chimera). The observations and conclusions from our mutational study were as follows.

Fig. 2.

Location of the charge-selectivity filter. (A) Relationship between permeability ratio and reversal potential calculated for the solutions most frequently used in this work (110 mM KCl and 40 mM KF on the intracellular side, 15 mM KCl on the extracellular side) assuming that the permeability of pLGICs to F^– is negligible, as it was shown for the wild-type α1 GlyR (38). The equilibrium (Nernst) potentials at 22 °C, calculated using ion activities, were –50.6 mV for K⁺, and +46.2 mV for Cl^–. The plotted functions were calculated using the GHK equation at 22 °C (in red) and a simpler, “linear” model (in blue) described in SI Materials and Methods. Note that, because of the asymptotic nature of the relationship, the errors associated with the calculated permeability ratios increase as the reversal potentials approach either equilibrium potential, that is, as the charge selectivity approaches ideal values. (B–E) Example whole-cell recordings from representative constructs. Current transients were elicited by the application of 10- or 20-ms pulses of agonist (100 μM ACh, 100 μM 5-HT or 1 mM Gly) at different voltages. For each panel, the holding voltage(s) closest to the reversal potential is (are) indicated in red. (F) Current–voltage relationships generated from the recordings in B–E. Only the linear portion of each curve is shown.

Table S1.

AChR reversal potentials and permeability-coefficient ratios

AChR position –1′ αεαβδ*	Other mutations αεαβδ*	Reversal potential, mean ± SE, mV†	PK+/PCl–, mean ± SE‡	PCl–/PK+, mean ± SE‡	n§
EQEEE	—	−48.7 ± 0.5	97 ± 23	0.022 ± 0.005	20
EQEEE	AAAAA (97/99 ECD)	−49.8 ± 0.3	200 ± 72	0.007 ± 0.003	3
QQQQQ	—	−44.3 ± 0.6	19 ± 2	0.055 ± 0.006	3
AAAAA	—	−44.8 ± 0.8	22 ± 3	0.051 ± 0.008	5
AQAAA	AQAAK (M2 20′)	−43.4 ± 1.1	16 ± 2	0.065 ± 0.011	3
AQAAA	AQAAA (M1–M2 –5′)	−44.8 ± 0.3	20 ± 1	0.050 ± 0.003	4
AQAAA	AQAAK (M2 20′) + AQAAA (M1–M2 –5′)	−41.5 ± 0.5	12 ± 1	0.085 ± 0.005	3
EQEAA	—	−49.4 ± 0.6	88 ± 27	0.007 ± 0.003	4
EAEAA	—	−50.2 ± 0.8	279 ± 222	0.012 ± 0.006	5
AAAEE	—	−49.2 ± 0.5	147 ± 67	0.011 ± 0.004	4
AAADD	—	−45.7 ± 0.9	28 ± 7	0.042 ± 0.009	4
DADAD	—	−47.9 ± 2.3	30	0.040	3
DADDD	—	−47.7 ± 0.5	45 ± 9	0.024 ± 0.004	3
EQEKE	—	−44.8 ± 0.9	21 ± 4	0.050 ± 0.009	3
EQEEK	—	−43.9 ± 0.7	17 ± 2	0.060 ± 0.007	4
AQAEK	—	−36.1 ± 1.4	7.1 ± 1.1	0.16 ± 0.02	6
Steeper gradient
EQEEE	—	−68.7 ± 0.6	110 ± 23	0.010 ± 0.002	4
AAAAA	—	−66.1 ± 1.1	55 ± 15	0.021 ± 0.004	3

^*The amino acids occupying the indicated positions are given for the five muscle-AChR subunits in the order α1, ε, α1, β1, and δ. Mutant residues are given in bold. Positions in and flanking the M2 α-helix are given using the prime notation. ECD, extracellular domain.

^†The equilibrium (Nernst) potentials at 22 °C, calculated using ion activities, were –50.6 mV for K⁺, and +46.2 mV for Cl^–. For the steeper KCl gradient, these values were –71.7 mV for K⁺, and +73.1 mV for Cl^–.

^‡Means and SEs were calculated as described in detail in SI Materials and Methods. Therefore, the mean values of the permeability ratios in this table (columns 4 and 5) are different from the permeability ratios that could be calculated by applying the GHK equation to the mean reversal potentials (column 3).

^§Number of independent whole-cell recordings.

Table S4.

α1 GlyR reversal potentials and permeability-coefficient ratios

α1 GlyR filter motif*	Other mutations	Reversal potential, mean ± SE, mV†	PK+/PCl–, mean ± SE‡	PCl–/PK+, mean ± SE‡	n§
INMDAAPAR	—	+44.1 ± 0.8	0.017 ± 0.003	119 ± 57	12
INMDAAPAR	K104A (ECD)¶	+44.1 ± 0.5	0.010 ± 0.003	123 ± 28	5
INMDAAPAR	M3–M4 8×Ala#	+44.5 ± 0.8	0.009 ± 0.004	271 ± 187	3
INMDAAPAR	R271A (M2 19′)	+45.0 ± 0.5	0.006 ± 0.002	285 ± 161	3
INMDAAPAK	—	+45.6 ± 1.2	0.008	312	3
INMDAAAAR	—	+44.8 ± 1.2	0.018 ± 0.005	89 ± 34	8
INMDAAGAR	—	+48.4 ± 0.5	0	∞	3
INMDAAPER	—	−29.2 ± 1.2	3.8 ± 0.3	0.27 ± 0.02	3
INMDAAAER	—	−28.4 ± 0.8	3.6 ± 0.2	0.28 ± 0.02	5
INMDAAGER	—	−10.5 ± 2.4	1.3 ± 0.2	0.85 ± 0.11	6
INMD–APAR	—	+40.4 ± 0.6	0.032 ± 0.003	36 ± 6	10
INMD–AAAR	—	+25.5 ± 1.0	0.16 ± 0.01	6.5 ± 0.5	3
INMD–AGAR	—	−1.3 ± 0.8	0.75 ± 0.03	1.3 ± 0.1	3
INMD–APER	—	−15.9 ± 1.9	1.7 ± 0.2	0.61 ± 0.06	3
INMD–AAER	—	−40.2 ± 0.9	11 ± 2	0.10 ± 0.01	6
INMD–AGER	—	−36.2 ± 1.1	6.9 ± 0.8	0.15 ± 0.02	5

^*Mutant residues are given in bold.

^†The equilibrium (Nernst) potentials at 22 °C, calculated using ion activities, were –50.6 mV for K⁺, and +46.2 mV for Cl^–.

^‡Means and SEs were calculated as described in detail in SI Materials and Methods. Therefore, the mean values of the permeability ratios in this table (columns 4 and 5) are different from the permeability ratios that could be calculated by applying the GHK equation to the mean reversal potentials (column 3).

^§Number of independent whole-cell recordings.

^¶Extracellular domain.

^#74 residues of the ∼80–90-residue-long M3–M4 linker were replaced with a string of eight alanines.

Table S5.

α7-AChR–β-GluCl chimera reversal potentials and permeability-coefficient ratios

α7-AChR–β-GluCl filter motif*	Other mutations	Reversal potential, mean ± SE, mV†	PK+/PCl–, mean ± SE‡	PCl–/PK+, mean ± SE‡	n§
IDLHSTAGR	—	+47.8 ± 1.0	0.003	410	6
IDLHSTAGG	—	+23.9 ± 0.7	0.17 ± 0.01	5.8 ± 0.3	5
IDLHSTAGN	—	−9.1 ± 1.4	1.1 ± 0.1	0.89 ± 0.07	3
IDLHSTAGN	D96N + E97Q (ECD)¶	+11.9 ± 2.1	0.37 ± 0.05	2.8 ± 0.3	3

^*Mutant residues are given in bold.

^†The equilibrium (Nernst) potentials at 22 °C, calculated using ion activities, were –50.6 mV for K⁺, and +46.2 mV for Cl^–.

^‡Means and SEs were calculated as described in detail in SI Materials and Methods. Therefore, the mean values of the permeability ratios in this table (columns 4 and 5) are different from the permeability ratios that could be calculated by applying the GHK equation to the mean reversal potentials (column 3).

^§Number of independent whole-cell recordings.

^¶Extracellular domain.

Table S6.

ELIC reversal potentials and permeability-coefficient ratios

ELIC filter motif*	Reversal potential, mean ± SE, mV†	PK+/PCl–, mean ± SE‡	PCl–/PK+, mean ± SE‡	n§
LE–S–FSER	−47.7 ± 0.4	44 ± 7	0.024 ± 0.003	3
LE–S–FSAR	−34.1 ± 0.2	5.5 ± 0.1	0.18 ± 0.003	4
LA–S–FSAR	−34.6 ± 0.5	5.8 ± 0.2	0.17 ± 0.01	3
LE–S–FGAR	−31.0 ± 1.1	4.4 ± 0.4	0.23 ± 0.02	4
LE–S–FPAR	−24.8 ± 1.0	2.8 ± 0.2	0.36 ± 0.02	4
LE–S–APAR	−25.1 ± 1.6	2.9 ± 0.3	0.35 ± 0.04	5

^*Mutant residues are given in bold.

^†The equilibrium (Nernst) potentials at 22 °C, calculated using ion activities, were –50.6 mV for K⁺, and +46.2 mV for Cl^–.

^‡Means and SEs were calculated as described in detail in SI Materials and Methods. Therefore, the mean values of the permeability ratios in this table (columns 3 and 4) are different from the permeability ratios that could be calculated by applying the GHK equation to the mean reversal potentials (column 2).

^§Number of independent whole-cell recordings.

Table S2.

5HT_3AR reversal potentials and permeability-coefficient ratios

5HT3AR filter motif*	Other mutations	Reversal potential, mean ± SE, mV†	PK+/PCl–, mean ± SE‡	PCl–/PK+, mean ± SE‡	n§
LPPD–SGER	—	−46.2 ± 0.6	31 ± 4	0.037 ± 0.005	10
LPPD–SGER	D132A (ECD)¶	−46.2 ± 1.5	52 ± 23	0.048 ± 0.015	8
LPPD–SGER	M3–M4 SQPARAA#	−48.3 ± 0.7	88 ± 33	0.019 ± 0.005	5
LPPD–SGER	K436A + R437A + R441A + R445A (M3–M4)	−46.1 ± 0.7	32 ± 8	0.039 ± 0.007	6
LPPD–SGQR	—	−23.1 ± 1.8	2.6 ± 0.3	0.40 ± 0.04	5
LPPD–SGAR	—	−22.3 ± 0.7	2.4 ± 0.1	0.42 ± 0.02	5
LPPD–SGAR	M3–M4 SQPARAA#	−36.2 ± 0.3	6.6 ± 0.2	0.15 ± 0.005	3
LPPD–SGAR	K436A + R437A + R441A + R445A (M3–M4)	−36.8 ± 0.3	7.1 ± 0.2	0.14 ± 0.005	6
LPPD–SGEK	—	−48.4 ± 1.0	119 ± 79	0.018 ± 0.008	3
LPPD–SGAK	—	−31.3 ± 0.7	4.4 ± 0.2	0.23 ± 0.01	3
LPPDSAGAR	—	−37.6 ± 0.6	7.6 ± 0.5	0.13 ± 0.01	3
LPPDSAPAR	—	>+30||	<0.11||	>9.2||	8
LPPDSAGER	—	−45.9 ± 1.0	28 ± 7	0.040 ± 0.010	3
LPPDSAAER	—	−49.2 ± 0.7	192 ± 123	0.012 ± 0.006	3
LPPDSAPER	—	−46.1 ± 0.5	27 ± 3	0.038 ± 0.005	4
LPPD–SAER	—	−45.6 ± 0.4	24 ± 2	0.043 ± 0.003	4
LPPD–SPER	—	−45.9 ± 0.4	26 ± 2	0.040 ± 0.004	3
LPPD–SRER	—	−39.0 ± 0.6	8.9 ± 0.7	0.11 ± 0.01	4
LPPD–SAAR	—	−12.3 ± 1.7	1.4 ± 0.1	0.75 ± 0.07	4
LPPD–SPAR	—	−1.8 ± 1.5	0.78 ± 0.06	1.3 ± 0.1	6
Steeper gradient
LPPD–SGER	—	−65.9 ± 1.5	107 ± 57	0.022 ± 0.006	6
LPPD–SGAR	—	−33.1 ± 2.3	3.4 ± 0.4	0.30 ± 0.04	3

^*Mutant residues are given in bold.

^†The equilibrium (Nernst) potentials at 22 °C, calculated using ion activities, were –50.6 mV for K⁺, and +46.2 mV for Cl^–. For the steeper KCl gradient, these values were –71.7 mV for K⁺, and +73.1 mV for Cl^–.

^‡Means and SEs were calculated as described in detail in SI Materials and Methods. Therefore, the mean values of the permeability ratios in this table (columns 4 and 5) are different from the permeability ratios that could be calculated by applying the GHK equation to the mean reversal potentials (column 3).

^§Number of independent whole-cell recordings.

^¶Extracellular domain.

^#115 residues of the ∼135-residue-long M3–M4 linker were replaced with the SQPARAA heptapeptide. Following ref. 18, we refer to this construct as 5-HT_3A-glvM3M4R.

^||This construct displayed marked inward rectification, and thus, clear outward currents could not be detected. Inward currents, however, could be recorded up to approximately +30 mV.

Table S3.

5HT_3A-3BR reversal potentials and permeability-coefficient ratios

5HT3A–3BR filter motif*	Reversal potential, mean ± SE, mV†	PK+/PCl–, mean ± SE‡	PCl–/PK+, mean ± SE‡	n§
LPPD–SGER (3A)	−48.4 ± 1.0	42 ± 7	0.026 ± 0.005	4
LPPN–CRAR (3B)
LPPD–SGAR (3A)	−22.3 ± 2.9	2.5 ± 0.5	0.43 ± 0.07	3
LPPN–CRAR (3B)

^*Mutant residues are given in bold.

^†The equilibrium (Nernst) potentials at 22 °C, calculated using ion activities, were –50.6 mV for K⁺, and +46.2 mV for Cl^–.

^‡Means and SEs were calculated as described in detail in SI Materials and Methods. Therefore, the mean values of the permeability ratios in this table (columns 3 and 4) are different from the permeability ratios that could be calculated by applying the GHK equation to the mean reversal potentials (column 2).

^§Number of independent whole-cell recordings.

Location of the Charge-Selectivity Filter.

The notion that charge selectivity is governed by the intracellular end of the transmembrane pore has been established. However, more recently, it has been suggested that a ring of aspartates that line the (extramembranous) extracellular portion of the ion-permeation pathway of most cation-selective pLGICs may also contribute to charge selectivity on the basis of their effect on single-channel conductance (10). Intriguingly, these residues align with well-conserved basic residues in anion-selective pLGICs, thus lending credence to this idea. To test this notion, we mutated the aligned aspartates of the muscle AChR (Asp-97 in the α1, β1, and ε subunits, and Asp-99 in the δ subunit) and the 5-HT_3AR (Asp-132), as well as the aligned lysine of the α1 GlyR (Lys-104), to alanine and estimated the charge selectivities of the resulting constructs; in all three cases, the selectivity was wild type-like (P_K⁺/P_Cl^– = 200, P_K⁺/P_Cl^– = 52, and P_Cl^–/P_K⁺ = 123, respectively; Fig. 2 B–D and F). Furthermore, we estimated the charge selectivity of a α7-AChR–β-GluCl chimeric construct consisting of the extracellular domain of the (cation-selective) α7 AChR and the transmembrane and intracellular domains of the (anion-selective) β GluCl channel (16). As such, this channel carries an aspartate at the aligned extracellular position (Asp-96)—and also a glutamate at the adjacent position 97—that could compromise the anion selectivity of its β GluCl pore. However, we found this channel to be almost ideally selective for anions (P_Cl^–/P_K⁺ = 410). Finally, providing further support to these findings, we noticed that wild-type homomeric anion-selective AChRs from molluscs, annelids, and flatworms contain an aspartate at this extracellular position (much like their cation-selective homologs), yet they form highly anion-selective channels (in the particular case of the AChR B from Lymnaea stagnalis, P_Cl^–/P_K⁺ = 93; ref. 6).

We also estimated the effect of the (also extramembranous) intracellular domain on the charge selectivities of the 5-HT_3AR and the α1 GlyR. In the case of the 5-HT_3AR, we used the 5-HT_3A-glvM3M4R construct described in ref. 18 where most of the M3–M4 linker (115 out of a total of ∼135 residues) was replaced with the SQPARAA heptapeptide (SI Materials and Methods). In the case of the α1 GlyR, we replaced most of the M3–M4 linker (more specifically, the fragment between Lys-312 and Lys-385, that is, 74 out of a total of ∼80–90 residues) with a string of eight alanines (19). We found that neither the cation selectivity of the 5-HT_3AR (see also ref. 18) nor the anion selectivity of the α1 GlyR is any lower upon removal of their intracellular domains (P_K⁺/P_Cl^– = 88 and P_Cl^–/P_K⁺ = 271, respectively; Fig. 2 E and F).

Finally, we tested the effect of neutralizing the ring of ionizable side chains that line the extracellular “mouth” of the transmembrane portion of the pore of many pLGICs. In the α1 GlyR, for example, we found that mutating the arginine at position 19′ (Arg-271) to alanine does not decrease the wild-type channel’s high selectivity for anions (P_Cl^–/P_K⁺ = 285). Collectively, these results underscore the dominant role of the intracellular end of the transmembrane pore in charge selectivity.

A Hierarchy of Side Chains.

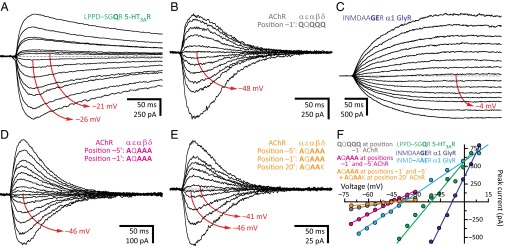
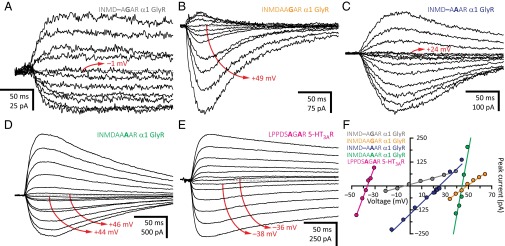
A sequence alignment reveals that all known wild-type cation-selective members of the superfamily contain a ring of three, four, or five acidic residues (depending on subunit composition) at the intracellular end of the transmembrane pore—occupying position –1′ or, much more rarely, –2′—whereas no known anion-selective pLGIC bears acidic side chains at these positions (Fig. 1). Also, mutating the ring of alanines at position –1′ of the anion-selective α1 GlyR to glutamates rendered the channel somewhat cation selective (P_K⁺/P_Cl^– = 3.8), whereas neutralizing this ring lowered the cation selectivity of the 5-HT_3AR (P_K⁺/P_Cl^– ≅ 2.5; Fig. 3), the heteromeric 5-HT_3A-3BR (P_K⁺/P_Cl^– = 2.5), and ELIC (P_K⁺/P_Cl^– = 5.5). In marked contrast, however, negatively charged side chains at the intracellular end of the pore were not necessary for cation selectivity in the muscle AChR. Indeed, whether position –1′ contained the four wild-type glutamates (the ε subunit carries a glutamine at this position) or consisted, instead, of a ring of five glutamines (P_K⁺/P_Cl^– = 19; Fig. 3 B and F) or five alanines (P_K⁺/P_Cl^– = 22) did not compromise the high selectivity for cations, even when neutralizing these four glutamates lowered the channel’s unitary conductance from ∼140 to ∼30 pS (3). Furthermore, we found that the mutant 5-HT_3AR with a LPPDSAGAR motif in the M1–M2 linker and first turn of M2 (positions –8′ through 0′, with mutated positions indicated in bold; Fig. 1) is moderately cation selective (P_K⁺/P_Cl^– = 7.6) even when lacking acidic side chains at position –1′ or –2′. Perhaps even more surprisingly, we found that acidic residues are not sufficient for cation selectivity. Certainly, the α1 GlyR with an INMDAAGER (P_K⁺/P_Cl^– = 1.3; Fig. 3 C and F) or INMD–APER (P_K⁺/P_Cl^– = 1.7) motif forms rather nonselective channels, thus indicating that the mere presence of glutamates at position –1′ does not guarantee selectivity for cations.

Fig. 3.

A hierarchy of side chains. (A–E) Example whole-cell recordings from representative constructs. Current transients were elicited by the application of 10- or 20-ms pulses of agonist (100 μM 5-HT, 100 μM ACh, or 1 mM Gly) at different voltages. For each panel, the holding voltage(s) closest to the reversal potential is (are) indicated in red. The equilibrium (Nernst) potentials at 22 °C, calculated using ion activities, were –50.6 mV for K⁺, and +46.2 mV for Cl^–. Mutant residues are indicated in bold. (F) Current–voltage relationships generated from the recordings in A–E. Only the linear portion of each curve is shown; some of these were truncated to better appreciate the curves of lower slope.

To challenge the finding that the ring of glutamates at position –1′ affects charge selectivity in the 5-HT_3AR more than it does in the muscle AChR, we measured reversal potentials under a steeper KCl-dilution condition: 150–5 mM instead of 150–15 mM K⁺. Our results amply confirmed this idea: neutralization of the glutamate ring lowered the cation-to-anion selectivity of the AChR from P_K⁺/P_Cl^– = 110 to P_K⁺/P_Cl^– = 55 and that of the 5-HT_3AR, from P_K⁺/P_Cl^– = 107 to P_K⁺/P_Cl^– = 3.4. We also found that different combinations of glutamates, aspartates, glutamines, and alanines at position –1′ of the (heteromeric) muscle AChR do not have a major effect on cation selectivity, which remained high (P_K⁺/P_Cl^– > 28) despite these perturbations. To test the possibility that other pore-lining negatively charged side chains contribute to the cation selectivity of this channel, we also mutated the acidic side chains at position –5′ of the M1–M2 linker (an aspartate in the wild-type α1, β1, and δ subunits, and a glutamine in the ε subunit; Fig. 1) and position 20′, in the last turn of M2 (a glutamate in α1, an aspartate in β1, a lysine in δ, and a glutamine in ε), to alanine in the background of an all-neutral position –1′. We chose these two other rings of acidic side chains because their effect on single-channel conductance—although much weaker than that of the glutamates at position –1′—is the next largest (3, 20). When mutated in a pairwise manner, neither combination, that is, mutant –5′ and –1′ positions (P_K⁺/P_Cl^– = 20; Fig. 3 D and F) or mutant –1′ and 20′ positions (P_K⁺/P_Cl^– = 16), affected charge selectivity much more than did the neutralization of position –1′ alone (P_K⁺/P_Cl^– ≅ 20). Neutralization of the acidic residues at all three positions (a total of 11 side chains), on the other hand, lowered the cation selectivity to P_K⁺/P_Cl^– = 12 (Fig. 3 E and F), a value that is still higher than that of the 5-HT_3AR with only position –1′ neutralized (P_K⁺/P_Cl^– ≅ 2.5). Moreover, even engineering a lysine at position –1′ of one of the five subunits had little effect (P_K⁺/P_Cl^– = 21, in the β subunit; P_K⁺/P_Cl^– = 17, in the δ subunit). It was only in the background of a pentamer carrying only one glutamate at this position that the introduction of a lysine lowered the selectivity for cations to a larger extent (P_K⁺/P_Cl^– = 7.1). We could not measure currents in the complete absence of glutamates as long as a lysine occupied one of the five positions –1′; the currents were, probably, too small.

Puzzled by the resilience of the AChR’s cation selectivity to neutralization of its pore-lining acidic side chains, we then turned to the 5-HT_3AR. We wondered whether the larger effect of glutamate-to-alanine or glutamate-to-glutamine mutations in the latter could be ascribed to the larger number of anion-attracting, basic residues in its intracellular M3–M4 linkers. These basic residues occupy positions that “frame” five intracellular openings or “portals” (one per pair of adjacent subunits; Fig. S1; ref. 21) that ions must traverse upon entering or exiting the channel, and their removal was found to increase the 5-HT_3AR’s single-channel conductance from <1 to 20–40 pS (9, 18). Whereas the 5-HT_3AR has seven basic residues per subunit framing these portals, the muscle AChR has only two (ε subunit) or three (α1, β1, and δ subunits), and although these residues exert little to no effect on the charge selectivity of wild-type pLGICs (Fig. 2 E and F), they could conceivably dominate the energetics of ion permeation once the glutamates at position –1′ are neutralized. To address this point, we first mutated the glutamates at position –1′ to alanines in the background of the 5-HT_3A-glvM3M4R construct (that is, the 5-HT_3AR with much shortened M3–M4 linkers; ref. 18) and estimated its charge selectivity. We found that, indeed, neutralizing position –1′ in the background of a channel that lacks the arginine-lined portals lowers the cation selectivity to a more moderate extent (P_K⁺/P_Cl^– = 6.6) than does neutralizing these glutamates in the wild-type 5-HT_3AR background (P_K⁺/P_Cl^– ≅ 2.5). Second, in an attempt to minimize the structural perturbations that such an extensive shortening of the M3–M4 linker could have had, we simply mutated four of the seven portal-framing basic residues (Lys-436, and Arg-437, 441, and 445; Fig. S1) to alanine (more than four substitutions were not tolerated) and obtained, essentially, the same result (P_K⁺/P_Cl^– = 7.1). Remarkably, the charge selectivity of the all-alanine mutant at position –1′ of the bacterial channel ELIC (which naturally, contains a very short M3–M4 linker that does not form basic residue-lined portals) was nearly the same (P_K⁺/P_Cl^– = 5.5) as that of the all-alanine mutant 5-HT_3AR with a shortened or partially neutralized linker.

Fig. S1.

Basic and acidic residues in the intracellular portal-framing α-helices. (A) Sequence alignment of the M3–M4-linker α-helices of the cation-selective 5-HT_3AR, the cation-selective (heteromeric) muscle AChR, and the anion-selective α1 GlyR. Basic and acidic residues are indicated in red and blue bold, respectively. The underlined basic residues are Lys-436, and Arg-437, 441, and 445, that is, the four basic residues of the mouse 5-HT_3AR whose mutation to alanine recapitulated the effect of the replacement of almost its entire M3–M4 linker with the SQPARAA heptapeptide on charge selectivity. The arginines of this sequence that align with those mutated in the so-called “QDA” mutant of the human 5-HT_3AR (9) are indicated with a yellow background. The boundaries of the aligned α-helices are only approximate and were taken from an inspection of the structural models of the Torpedo AChR (PDB ID code 2BG9; ref. 21) and the mouse 5-HT_3AR (PDB ID code 4PIR; ref. 44), as well as from ref. 45. (B) Number of basic and acidic residues.

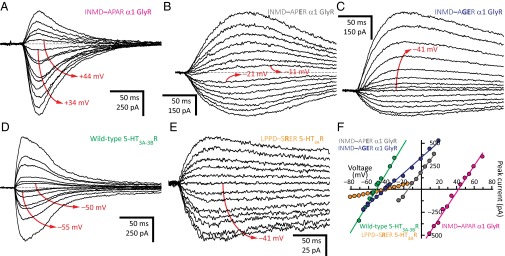
We also wondered whether the larger effect of glutamate neutralization on the charge selectivity of the 5-HT_3AR, compared with that of the AChR, could additionally be ascribed to the presence of an arginine in the former, and a (less basic) lysine in the latter, at position 0′ (Fig. 1). Strikingly, we found that in going from a LPPD–SGAR motif to LPPD–SGAK, the cation selectivity of the 5-HT_3AR increases from P_K⁺/P_Cl^– = 2.4 to P_K⁺/P_Cl^– = 4.4 (Fig. 4), a small change in terms of permeability-coefficient ratios (a factor of ∼1.8) that corresponds, however, to a robust shift of 9.0 mV in reversal potential (Fig. 2A). Although it is possible that the positively charged side chains of arginine and lysine at position 0′ adopt rotamers that affect ion permeation to different extents (as we have observed for the glutamates at position –1′ of the muscle AChR; refs. 3, 22), our results are also consistent with the possibility that the lysine side chain spends at least some fraction of the time deprotonated, thus providing a more favorable environment for the permeation of cations. Whichever the case may be, it is clear that the additional arginines in the M3–M4 linker of the 5-HT_3AR, as well as the presence of an arginine (rather than a lysine) at position 0′, contribute to the larger impact of glutamate neutralization on the charge selectivity of this channel.

Fig. 4.

The basic side chain at position 0′. (A–E) Example whole-cell recordings from representative constructs. Current transients were elicited by the application of 10- or 20-ms pulses of agonist (100 μM 5-HT or 100 μM ACh) at different voltages. For each panel, the holding voltage(s) closest to the reversal potential is (are) indicated in red. The equilibrium (Nernst) potentials at 22 °C, calculated using ion activities, were –50.6 mV for K⁺, and +46.2 mV for Cl^–. Mutant residues are indicated in bold. (F) Current–voltage relationships generated from the recordings in A–E. Only the linear portion of each curve is shown; one of these was truncated to better appreciate the other curves, which had lower slopes.

Overall, we conclude that a ring of glutamates at position –1′ dominates the permeation free-energy landscape of wild-type cation-selective pLGICs. However, upon neutralization of these side chains, the control of charge selectivity is handed over to the rest of the protein—that is, the extracellular and intracellular domains, and the rest of the transmembrane domain. In the AChR, the rest of the protein still favored the permeation of cations (P_K⁺/P_Cl^– ≅ 20; Fig. 3 B and F), but in the 5-HT_3AR, the rest of the protein formed a nonselective channel, instead (P_K⁺/P_Cl^– ≅ 2.5; Figs. 3 A and F and 4 A and F). Regarding the glutamates at position –1′, we emphasize the notion that the mere presence of such ring is not enough to confer selectivity for cations. Instead, the local conformation of the protein seems to be crucial to orient the acidic side chains favorably so as to ensure that they are both deprotonated and optimally positioned with respect to the axis of permeation. This is best exemplified by the α1 GlyR mutants having an INMDAAGER or an INMD–AAER motif. Both have glutamates at position –1′, but whereas the former is rather nonselective for cations or anions (P_K⁺/P_Cl^– = 1.3; Fig. 3 C and F), the latter selects for cations with P_K⁺/P_Cl^– = 11 (Fig. 3F).

The Basic Side Chain at Position 0′.

Although not all naturally occurring cation-selective pLGICs contain a lysine or an arginine at position 0′ (certainly, a few exceptions can be identified in bacteria and nematodes), no known anion-selective pLGIC lacks a lysine or an arginine at this position (Fig. 1). Thus far, however, it has been difficult to elucidate the contribution of this conserved basic amino acid to ion permeation because mutations to nonionizable residues in, for example, the muscle AChR (8) or the α1 GlyR (5) were found to reduce their functional expression to impractical levels. Nevertheless, as indicated above, an arginine-to-lysine mutation in the background of a rather nonselective 5-HT_3AR (LPPD–SGAR→LPPD–SGAK) was tolerated well, and it was found to increase the selectivity for cations by a factor of ∼1.8. Irrespective of the mechanism underlying this effect, this result strongly suggested that the positive charge on the side chain at position 0′ can indeed be “felt” by the passing ions—even when located as far as on the backside of M2 (23)—especially when a glutamate is not present at the (adjacent) pore-lining position –1′. Moreover, in contrast to the mutant 5-HT_3AR with an all-neutral –1′ ring, replacing most of the M3–M4 linker of the wild-type α1 GlyR (which naturally lacks glutamates at position –1′) with a stretch of eight alanines did not lower the channel’s high selectivity for anions (P_Cl^–/P_K⁺ = 271; Fig. 2 E and F), even when its putative portal-framing α-helices contain as many as eight basic residues per subunit (Fig. S1). This result suggested to us that, in anion-selective pLGICs, the arginine at position 0′ (Fig. 1) may dominate the energetics of ion permeation in such a way that their anion selectivity is oblivious to the presence or absence of intact basic-residue–rich M3–M4 linkers.

Intrigued by these findings, we kept trying to mutate the 0′ basic side chain to nonionizable residues. Mutation of the arginine of the α1 GlyR to glutamine (the amino acid tentatively occupying this position in the EXP-1 GABA_AR; Fig. 1), asparagine (the amino acid occupying this position in GLIC; Fig. 1), or glycine, nearly abolished the functional expression of the channel. In addition, mutating at the same time Glu-300 in M3, which according to the crystal structures of the anion-selective α1 GluCl channel [Protein Data Bank (PDB) ID code 3RHW; ref. 23] and the β3 GABA receptor (PDB ID code 4COF; ref. 24) forms a salt bridge with the 0′ arginine, to glutamine did not make any noticeable difference. Hence, to avoid channels having a PAR motif in the first turn of M2, we turned to β GluCl from C. elegans, an anion-selective, glutamate-gated homomeric pLGIC having an AGR motif, instead (Fig. 1). Because our attempts [and those of others (25, 26)] to express β GluCl in HEK-293 cells proved unsuccessful, we tested the α7-AChR–β-GluCl chimera (16), which is known to express well in these cells (Fig. 4 C and F). Although the arginine-to-glutamine mutation reduced the size of the chimera’s currents to the point that it was difficult to estimate a reversal potential with certainty, the currents were clearly outward at the Cl^– equilibrium potential. The loss of anion selectivity hinted by this construct was confirmed by the asparagine mutant, which displayed more robust currents; the arginine-to-asparagine mutation rendered the channel almost ideally nonselective (P_Cl^–/P_K⁺ = 0.89; Fig. 4 D and F). We also recorded robust currents from the arginine-to-glycine mutant and obtained a similar result (P_Cl^–/P_K⁺ = 5.8; Fig. 4 E and F). Although this glycine mutant remained anion selective, the selectivity for anions was much smaller than that of the “wild-type” chimera (P_Cl^–/P_K⁺ = 410; Fig. 4 C and F). Overall, the simplest explanation for the effect of arginine neutralization is that the positive charges on these non–pore-facing side chains can be oriented in such a way as to create an electrostatically favorable environment for the passing anions. Therefore, as is the case for their cation-selective counterparts, ionized side-chain–ion interactions seem to dominate the permeation free-energy landscape of anion-selective pLGICs. However, the mere presence of a ring of basic side chains at position 0′ was not enough to impart selectivity for anions. Indeed, the α1 GlyR with an INMD–AGAR motif, for example, did not discriminate cations from anions (P_Cl^–/P_K⁺ = 1.3). We conclude that, much as we observed for the glutamates at position –1′ of cation-selective pLGICs, a proper conformation of the positively charged side chain at position 0′ seems to be crucial for anion selectivity.

Finally, we wondered about the effect of the acidic residues in the chimera’s α7-AChR extracellular domain on the charge selectivity of the arginine-to-asparagine mutant at position 0′. To address this point, we neutralized Asp-96 and Glu-97 (in the background of the arginine-to-asparagine mutant) and found that the channel becomes more selective for anions (P_Cl^–/P_K⁺ = 2.8) than is the arginine-to-asparagine mutant with a wild-type α7-AChR extracellular domain (P_Cl^–/P_K⁺ = 0.89; Fig. 4 D and F). This result is fully consistent with the expected effect of neutralization of lumen-facing negatively charged residues and with the idea that, once the positive charges on the arginines at position 0′ are removed, the control of charge selectivity is handed over to the rest of the protein (here, the extracellular domain).

Having unveiled the key role that the (buried) basic residues at position 0′ play in anion selectivity, we wondered why these residues are also present in nearly all wild-type cation-selective pLGICs. Indeed, with glutamates at the pore-lining position –1′, these channels display high cation-to-anion permeability ratios, undoubtedly reflecting the relative proximities of these two positions to the axis of ion permeation. We surmise that, in the cation-selective channels, five basic side chains at position 0′ may be necessary to stabilize the deprotonated state of the adjacent glutamates at position –1′. Note that, in the few cation-selective pLGICs that lack a basic residue at position 0′ (Fig. 1), the glutamate occupies a more solvent-exposed position (position –2′) in the first turn of M2.

The Length of the M1–M2 Linker.

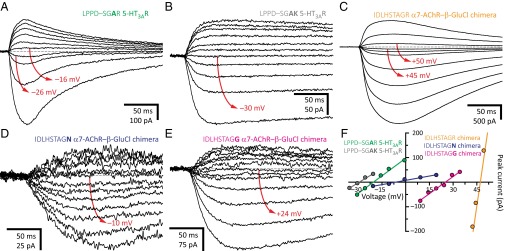
A sequence alignment reveals that the intracellular end of the transmembrane pore of nearly all wild-type cation-selective pLGICs from animals have one fewer residue than those from anion-selective pLGICs. Although this correlation is, by no means, a strict rule (certainly, a few exceptions can be identified; Fig. 1), we wondered whether, for any given channel, a generalization could be made as to the effect of inserting or deleting a residue from this region of the protein on charge selectivity. In the case of the α1 GlyR, we found that in going from an INMD–AGAR motif (P_Cl^–/P_K⁺ = 1.3) to INMDAAGAR (P_Cl^–/P_K⁺ = ∞), from INMD–AAAR (P_Cl^–/P_K⁺ = 6.5) to INMDAAAAR (P_Cl^–/P_K⁺ = 89), from INMD–AGER (P_Cl^–/P_K⁺ = 0.15) to INMDAAGER (P_Cl^–/P_K⁺ = 0.85), and from INMD–AAER (P_Cl^–/P_K⁺ = 0.10) to INMDAAAER (P_Cl^–/P_K⁺ = 0.28), the channel becomes more selective for anions (or less selective for cations), with the INMD–AGAR-to-INMDAAGAR insertion having the largest effect (Fig. 5). Indeed, this alanine insertion converts a nonselective channel into one that seems to be perfectly selective for anions. Similarly, in the 5-HT_3AR, going from a LPPD–SPAR (P_Cl^–/P_K⁺ = 1.3) motif to LPPDSAPAR (P_Cl^–/P_K⁺ > 9.2) confers anion selectivity to a nonselective channel. However, running counter to the trend hinted by these observations, we also found that going from INMD–APER (P_K⁺/P_Cl^– = 1.7) to INMDAAPER (P_K⁺/P_Cl^– = 3.8) in the α1 GlyR, and from LPPD–SGAR (P_K⁺/P_Cl^– = 2.4; Fig. 4 A and F) to LPPDSAGAR (P_K⁺/P_Cl^– = 7.6; Fig. 5 E and F) in the 5-HT_3AR, makes these two channels more selective for cations.

Fig. 5.

The length of the M1–M2 linker. (A–E) Example whole-cell recordings from representative constructs. Current transients were elicited by the application of 10- or 20-ms pulses of agonist (1 mM Gly or 100 μM 5-HT) at different voltages. For each panel, the holding voltage(s) closest to the reversal potential is (are) indicated in red. The equilibrium (Nernst) potentials at 22 °C, calculated using ion activities, were –50.6 mV for K⁺, and +46.2 mV for Cl^–. Mutant residues are indicated in bold. (F) Current–voltage relationships generated from the recordings in A–E. Only the linear portion of each curve is shown; one of these was truncated to better appreciate the other curves, which had lower slopes.

It could be argued that some of the effects of alanine insertion on charge selectivity seem small when expressed in terms of permeability-coefficient ratios. For example, the INMD–AAER-to-INMDAAAER insertion increased the selectivity for anions by a factor of only 2.8, whereas the INMD–APER-to-INMDAAPER insertion increased the selectivity for cations by a factor of only 2.2. However, it should be noted that the corresponding changes in reversal potential were robust, having shifted by ∼12–13 mV in opposite directions (in these two particular examples) upon alanine insertion. It is also worth noting that this ambivalent effect of residue insertion was observed for both an anion-selective channel (α1 GlyR) and a cation-selective channel (5-HT_3AR), and that the presence or absence of glutamates at position –1′ did not make any difference in this respect.

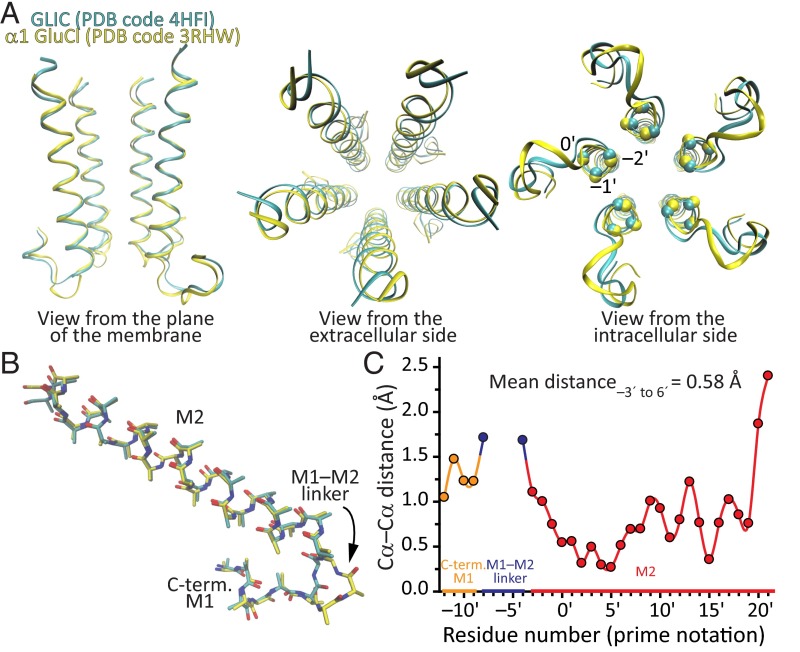
To gain further insight into the structural consequences of inserting or deleting residues from this region of the channel, we structurally aligned the models of the bacterial cation-selective channel GLIC (PDB ID code 3HFI; resolution, 2.4 Å; ref. 27) and the invertebrate anion-selective channel α1 GluCl (PDB ID code 3RHW; resolution, 3.26 Å; ref. 23), two models that (despite some reservations) have been deemed to represent the open-channel conformation (Fig. 6). The comparison between these two models seemed particularly pertinent because GLIC has two (not just one) fewer residues than α1 GluCl in this region (Fig. 1), and thus, the corresponding structural differences were expected to be magnified. Intriguingly, the length, and the rotational and tilt angles of the M2 α-helices turned out to be, essentially, the same. Indeed, the mean distance between aligned Cα atoms computed over the first 10 residues of M2 and averaged across all five subunits was 0.58 Å. The two additional residues of α1 GluCl are fully accommodated within the M1–M2 linker, which forms a longer loop. We do not know whether the same is the case for the engineered one-alanine insertions and deletions we studied here, but to the extent that these mutations recapitulate the effect of naturally occurring insertions and deletions on charge selectivity, we surmise that these maneuvers may also result in longer or shorter M1–M2 linkers without causing major changes to the backbone of M2.

Fig. 6.

Structural alignment of GLIC and α1 GluCl. (A) Alignment of GLIC (PDB ID code 4HFI; cyan) and α1 GluCl (PDB ID code 3RHW; yellow) shown in ribbon representation. To maximize the structural alignment between the regions of interest, we reduced each model to five fragments containing the last four residues of the M1 α-helix, the M1–M2 linker, and the entire M2 α-helix of each subunit. The resulting reduced files, one per original model, were aligned as pentamers with STAMP (39) as implemented within the MultiSeq plugin (40) in Visual Molecular Dynamics (VMD) molecular graphics software (41). In the leftmost panel, the front subunit was removed, for clarity. In the rightmost panel, the approximate locations of the Cα atoms of positions –2′, –1′, and 0′ are indicated with spheres for the five subunits and the two structural models. (B) Structural alignment of single-subunit fragments of GLIC and α1 GluCl shown in stick representation. To facilitate the visual comparison of the backbone atoms, all side chains were converted to alanine side chains with the exception of those of glycine (two in the α1 GluCl fragment, none in GLIC’s), which remained unaltered. The carbon atoms of GLIC are shown in cyan, and those of α1 GluCl, in yellow. Nitrogen and oxygen atoms are shown in blue and red, respectively, for both models. (C) Distances between aligned Cα atoms obtained from the structural alignment of pentameric fragments in A. The values corresponding to the five pairs of subunits were averaged; SEs were smaller than the width of the symbols. The two additional residues of α1 GluCl, which are fully accommodated within the M1–M2 linker, create a gap in this plot.

It is tempting to conclude, then, that inserting or deleting an alanine (and perhaps, other residues, too) from this region of the channel must lead to slight changes in the backbone of the first turn of M2, too subtle to be clearly characterized at the resolution of the available structural models, yet large enough to cause a reorientation of the charged side chains at positions –1′ and/or 0′. In turn, this would reshape the permeation free-energy landscape of cations and anions, eventually changing the charge selectivity. We highlight, however, the enigmatic nature of these structural rearrangements because the insertion of an alanine, for example, favored the permeation of anions in some cases and the permeation of cations in others.

The Importance of Position –2′.

With the exception of the 5-HT_3BR subunit (which does not form homomers), all wild-type cation-selective pLGIC subunits from vertebrates contain a glycine at position –2′, whereas most anion-selective pLGICs subunits contain a proline, in some cases an alanine, but never a glycine at this position (Fig. 1). Thus, we wondered whether, for any given channel, the amino acid at position –2′ matters for charge selectivity. To address this question, we compared the charge selectivities of receptors differing only in the –2′ side chain. We found that the α1 GlyR with an INMD–APAR motif is highly anion selective (P_Cl^–/P_K⁺ = 36; Fig. 7), whereas the α1 GlyR with an INMD–AGAR motif does not discriminate cations from anions (P_Cl^–/P_K⁺ = 1.3; Fig. 5 A and F). Also, we found that the 5-HT_3AR with a LPPDSAGAR motif is moderately selective for cations (P_K⁺/P_Cl^– = 7.6; Fig. 5 E and F), whereas the 5-HT_3AR with a LPPDSAPAR motif is selective for anions (P_Cl^–/P_K⁺ > 9.2). In the presence of a glutamate at position –1′, a similar (albeit less pronounced) effect could be observed. For example, whereas the α1 GlyR with an INMD–APER motif was rather nonselective (P_K⁺/P_Cl^– = 1.7; Fig. 7 B and F), the same channel with an INMD–AGER (P_K⁺/P_Cl^– = 6.9; Fig. 7 C and F) or INMD–AAER motif (P_K⁺/P_Cl^– = 11) became selective for cations. Admittedly, our dataset is limited, and some of the glycine–proline channel pairs could not easily be compared because the corresponding reversal potentials were too close to either the K⁺ or the Cl^– equilibrium potentials, where the accurate estimation of permeability ratios from reversal potentials is most prone to errors (Fig. 2A). However, it does seem as though a glycine at position –2′ tends to favor the permeation of cations, whereas a proline at this position tends to favor the permeation of anions, much as hinted by the prevalence of these residues in naturally occurring sequences. Remarkably, as was the case for the alanine insertions discussed above, these glycine or proline substitutions did not involve ionizable side chains directly. Instead, these mutations may have perturbed the torsional free-energy landscapes of the arginine and glutamate side chains at the nearby positions 0′ and –1′, and thus may well have affected the occupancies of their different rotamers.

Fig. 7.

The importance of position –2′. (A–E) Example whole-cell recordings from representative constructs. Current transients were elicited by the application of 10- or 20-ms pulses of agonist (1 mM Gly or 100 μM 5-HT) at different voltages. For each panel, the holding voltage(s) closest to the reversal potential is (are) indicated in red. The equilibrium (Nernst) potentials at 22 °C, calculated using ion activities, were –50.6 mV for K⁺, and +46.2 mV for Cl^–. Mutant residues are indicated in bold. (F) Current–voltage relationships generated from the recordings in A–E. Only the linear portion of each curve is shown; some of these were truncated to better appreciate the curves of lower slope.

The 5-HT_3BR subunit bears an arginine at position –2′, and hence, the heteromeric 5-HT_3A-3BR likely (28) contains three glycines and two arginines at this pore-lining position (and three glutamates and two alanines at the adjacent position –1′; Fig. 1). However, despite these additional positive charges, we found the 5-HT_3A-3BR to be highly selective for cations (P_K⁺/P_Cl^– = 42; Fig. 7 D and F), suggesting a minimal electrostatic effect of these arginines even when located at what is expected to be the narrowest constriction of the open-channel pore. Moreover, we found that even the mutant homomeric 5-HT_3AR containing five arginines at position –2′ (that is, with a LPPD–SRER motif) retains selectivity for cations (P_K⁺/P_Cl^– = 8.9; Fig. 7 E and F), which is remarkable because the Cα atom at position –2′ (here occupied by an arginine) is expected to be closer to the long axis of the pore than is the Cα atom at position –1′ (occupied by a glutamate; Fig. 6). It seems inescapable to conclude that the arginine side chains at position –2′ must orient themselves in such a way as to minimize their impact on ion permeation. In turn, this observation reinforces the notion that side-chain conformation is a key determinant of charge selectivity.

The Effect of Mutations Is Context Dependent.

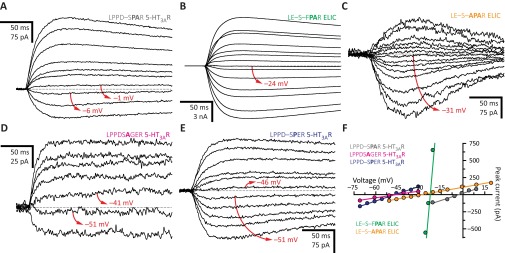
Mutations confined to the intracellular end of the pore not only affect but also can switch the sign of the charge selectivity of pLGICs. For example, we found that mutating the anion-selective α1 GlyR so that the wild-type INMDAAPAR motif (P_K⁺/P_Cl^– = 0.02) becomes INMD–AGER (P_K⁺/P_Cl^– = 6.9; Fig. 7 C and F) or INMD–AAER (P_K⁺/P_Cl^– = 11) makes the channel cation selective. Similarly, we found that mutating the cation-selective 5-HT_3AR so that the wild-type LPPD–SGER motif (P_Cl^–/P_K⁺ = 0.04) becomes LPPDSAPAR (P_Cl^–/P_K⁺ > 9.2) confers selectivity for anions. These observations indicate that, at least in these two pLGICs, the rest of the protein is able to accommodate opposite charge selectivities. Thus, to determine whether similar sequences in the first turn of M2 impart similar selectivities, we mutated the α1 GlyR and the 5-HT_3AR, and compared the results. We found that, whereas the mutant α1 GlyR with an INMD–APAR motif (P_Cl^–/P_K⁺ = 36; Fig. 7 A and F) and the wild-type AChR B from the invertebrate L. stagnalis (P_Cl^–/P_K⁺ = 93; ref. 6), which bears an LPPE–SPAK motif, are selective for anions, the 5-HT_3AR with a LPPD–SPAR motif does not discriminate cations from anions (P_Cl^–/P_K⁺ = 1.3; Fig. S2). Moreover, we noticed that the bacterial ELIC with a LE–S–FPAR motif (P_K⁺/P_Cl^– = 2.8) or a LE–S–APAR motif (P_K⁺/P_Cl^– = 2.9) is slightly selective for cations (Fig. S2 B, C, and F). Also, the α1 GlyR with an INMDAAGAR motif seemed to be perfectly anion selective (Fig. 5 B and F), whereas the 5-HT_3AR with a LPPDSAGAR motif was moderately cation selective (P_K⁺/P_Cl^– = 7.6; Fig. 5 E and F). Importantly, in the presence of a glutamate at position –1′, the results were similar: the α1 GlyR with an INMDAAGER motif formed nonselective channels (P_K⁺/P_Cl^– = 1.3; Fig. 3 C and F), whereas the 5-HT_3AR with a LPPDSAGER motif was highly selective for cations (P_K⁺/P_Cl^– = 28; Fig. S2 D and F). Also, the α1 GlyR with an INMD–APER motif selected poorly between cations and anions (P_K⁺/P_Cl^– = 1.7; Fig. 7 B and F), whereas the 5-HT_3AR with a LPPD–SPER motif was highly cation selective (P_K⁺/P_Cl^– = 26; Fig. S2 E and F).

Fig. S2.

The effect of mutations is context dependent. (A–E) Example whole-cell recordings from representative constructs. Current transients were elicited by the application of 10- or 20-ms pulses of agonist (100 μM 5-HT or 1 mM propylamine) at different voltages. For each panel, the holding voltage(s) closest to the reversal potential is (are) indicated in red. The equilibrium (Nernst) potentials at 22 °C, calculated using ion activities, were –50.6 mV for K⁺ and +46.2 mV for Cl^–. Mutant residues are indicated in bold. (F) Current–voltage relationships generated from the recordings in A–E. Only the linear portion of each curve is shown; one of these was truncated to better appreciate the other curves, which had lower slopes.

Together, these results highlight the difficulty in designing new protein functions by simply engineering short amino acid sequences. Certainly, the functional properties conferred by a given stretch of amino acids “transplanted” into different pLGIC homologs often depended on the rest of the sequence. This is a well-known concept in the framework of protein evolution (commonly referred to as “epistasis”; e.g., refs. 29 and 30) that turns out to also apply to the charge-selectivity filter of pLGICs.

SI Materials and Methods

cDNA Clones, Mutagenesis, and Heterologous Expression.

cDNA clones coding the adult mouse muscle AChR subunits (accession numbers: α1, P04756; β1, P09690; δ, P02716; ε, P20782) in pRBG4 were provided by S. M. Sine, Mayo Clinic College of Medicine, Rochester, MN. cDNA coding the isoform b of the α1 subunit of the rat GlyR (accession number: P07727-2) in pcDNA3.1 was provided by M. M. Slaughter (University at Buffalo, Buffalo, NY), and that coding its human counterpart (accession number: P23415-2) was obtained by mutating the rat ortholog as described previously (19). cDNAs coding a variant of the isoform S of the mouse 5-HT_3AR subunit (containing the F459L mutation at the C terminus of the M3–M4 linker; accession number: P23979-2) and the mouse 5-HT_3BR subunit (accession number: Q9JHJ5) in pXOON were provided by M. H. Akabas, Albert Einstein College of Medicine, Bronx, NY, and were subcloned into pcDNA3.1. cDNA coding the chimeric construct consisting of the extracellular domain of the chick α7 AChR (accession number: P22770) and the transmembrane and intracellular domains of the β subunit of the Caenorhabditis elegans glutamate-gated Cl^– channel (GluCl; accession number: Q17328) in pMT3 (16) was provided by Y. Paas, Bar-Ilan University, Ramat Gan, Israel. cDNA coding the bacterial homolog ELIC (accession number: P0C7B7) in pcDNA3.1 was prepared as described previously (42). cDNA coding the 5-HT_3A-glvM3M4R subunit in pXOON, a construct where most of the M3–M4 linker of the isoform S of the mouse 5-HT_3AR subunit (more specifically, the fragment between Gln-338 and Tyr-452) was replaced with the SQPARAA heptapeptide (18), was provided by M. H. Akabas (Albert Einstein College of Medicine, Bronx, NY) and was used without further subcloning. Mutations were engineered using either the QuikChange kit (Agilent Technologies) or the overlap-extension PCR method. The sequences of all constructs were verified by dideoxy sequencing of the entire coding region (ACGT). The different pLGICs were heterologously expressed in HEK-293 cells upon transient transfection with the appropriate cDNAs using the calcium phosphate precipitation method. For the muscle AChR, the proportion of subunit-coding cDNAs in the transfection mixture was (α1:β1:δ:ε) 2:1:1:1, and for the 5-HT_3A-3BR, the proportion (3A:3B) was 1:9. Cells were incubated with the cDNA precipitate for 16–18 h, and electrophysiological recordings were performed 28–56 h thereafter.

Electrophysiology.

We previously found that several mutations in the charge selectivity filter region of pLGICs lower the single-channel conductance and/or the level of protein expression in the plasma membrane of HEK-293 cells to the point that, for some constructs, reliable reversal potentials could not be estimated from currents recorded in the outside-out patch-clamp configuration (3, 8). Hence, to increase the size of the currents, here we used the whole-cell configuration. Currents were recorded at ∼22 °C with an effective bandwidth of DC–5 kHz using an Axopatch 200B amplifier (Molecular Devices) and were digitized at 100 kHz. Throughout the paper, the displayed current traces were decimated by a factor of 100. Data were acquired and analyzed using pCLAMP 9.2 software (Molecular Devices). Series-resistance compensation was used and set to ∼80%. The reference Ag/AgCl wire was connected to the extracellular solution through an agar bridge containing 200 mM KCl; a new, fresh agar bridge was connected every ∼2 h. Agonist concentration jumps were applied to patched whole cells using a piece of double-barreled “θ-tubing” (Siskiyou) (19). The flow of solution through the θ-tube was controlled using a gravity-fed system (ALA BPS-8; ALA Scientific Instruments), and the movement of the θ-tube was achieved using a piezoelectric arm (Burleigh-LSS-3100; discontinued) controlled by pCLAMP 9.2 software and a Digidata 1322A interface (Molecular Devices). Signals from this interface were low-pass filtered (900C; Frequency Devices) at a cutoff frequency of 5–15 Hz before their arrival at the piezoelectric arm to reduce ringing in the θ-tube motion. The relative positioning of the θ-tube and the patch pipette was adjusted so as to optimize the perfusion of the entire cell, which remained attached to a piece of glass coverslip placed at the bottom of the recording chamber during the experiments. This system achieved a solution-exchange time of ∼3 ms for the t_10–90% and ∼0.4 ms for the t_90–10%, as estimated from changes in the liquid-junction potential measured with an open-tip patch pipette; clearly, this perfusion is slower than that of outside-out patches. Moreover, these estimates do not take into account the geometry of the cell, which is expected to slow down the solution exchange even further. Charge selectivity was inferred from reversal potentials estimated under near KCl-dilution conditions. Current–voltage (I–V) curves were generated by plotting the peak values of current transients elicited by brief (10- or 20-ms) applications of agonist at holding voltages straddling the reversal potential. Peak values were calculated by subtracting the value of the current before each agonist application from the maximum current attained on application of agonist. For each construct, this procedure was repeated for a number of different cells, indicated in Tables S1–S6 as n. Reversal potentials were estimated as the x-axis intercept of linear fits to only the linear portion of the recorded I–V curves. The liquid-junction potential between the intracellular (“pipette”) and extracellular solutions was calculated with the JPCalc module in pCLAMP 9.2 software using ion activities, and the holding-voltage values were corrected, accordingly. To minimize the changes in the concentration of ions bathing the membrane that are likely to occur when large currents (a few nanoamperes in peak amplitude) flow into or out of small cells (such as HEK-293 cells; ref. 43), extracellular solution with or without agonist was continuously perfused onto the whole-cell patches, and consecutive agonist applications were kept short (10 or 20 ms) and separated by long (10 or 20 s) agonist-free intervals.

Permeability-Coefficient Ratios.

The charge selectivity of each tested construct was expressed throughout this work as the mean value of the cation-to-anion (in our case, P_K⁺/P_Cl^–), and its reciprocal, the anion-to-cation (P_Cl^–/P_K⁺) permeability-coefficient ratios. Both ratios were calculated for each independent experiment (that is, for each patched cell), and these were averaged across experiments. For each individual I–V curve, permeability ratios were calculated by substituting the appropriate ion activities (rather than concentrations) and the estimated reversal potential in the GHK equation; on the basis of previous work on the wild-type α1 GlyR (38), we assumed that the permeability of all studied pLGICs to F^– (present in the pipette solution) is negligible. For a subset of constructs, in some cells, the estimated reversal potentials lay outside of the “allowed range” bounded by the K⁺ and Cl^– equilibrium potentials. Although these values were included in the calculation of the mean and SE of reversal potentials displayed in Tables S1–S6, the permeability ratios calculated from them were not included in the calculation of the mean and SE of permeability ratios displayed in these tables. This is because, for reversal potentials that lie outside of the expected range, the calculated permeability ratios lack physical meaning (their values are negative). As a result, for those constructs having fewer than three meaningful permeability ratios, only the mean (but not the SE) was presented. For one mutant of the α1 GlyR (Table S4), for example, all three reversal potentials were more positive than the Cl^– equilibrium potential (by 1.3, 2.3, and 2.8 mV), and thus, the charge selectivity was expressed, simply, as zero (P_K⁺/P_Cl^–) or infinity (P_Cl^–/P_K⁺). When they occurred, the deviations of the reversal potentials from the allowed range were relatively small and of similar magnitude in either direction: more positive than the Cl^– equilibrium potential by 2.1 ± 1.4 mV (mean ± SD; 14 cells) and more negative than the K⁺ equilibrium potential by 0.8 ± 0.7 mV (mean ± SD; 10 cells). Although a nonzero permeability to F^– (which was only present in the pipette solution, and hence, whose equilibrium potential was +∞) could explain the finding of reversal potentials more positive than the Cl^– equilibrium potential, a finite permeability to F^– could not explain the finding of reversal potentials more negative than the K⁺ equilibrium potential. Therefore, we ascribed these deviations to random experimental errors and to some uncertainty regarding the values of the activity coefficients used to calculate the K⁺ and Cl^– equilibrium potentials. It seems prudent, then, to conclude that the charge selectivity of this subset of constructs was close to ideal and that the contribution of F^– to anion permeation can, indeed, be neglected. We included F^– in the pipette solution because the stability of the whole-cell seals seemed to increase when this anion was present on the intracellular side.

Because we calculated permeability ratios using a particular mathematical model (that is, the GHK equation), we wondered how different their values would have been if a different framework had been considered. Thus, we explored the following alternative model for a channel facing two solutions of the same binary salt at different concentrations (“dilution conditions”). We started by decomposing the total current through this channel into a cation-carried component and an anion-carried component, and assumed that each of these can be represented (at least for the voltage range spanned experimentally) by a linear I–V curve with a characteristic slope (γ_cation or γ_anion) and x intercept (E_cation or E_anion). The slope of each curve would be the conductance of the cation or the anion in the saline solutions under dilution conditions, whereas the x intercept would correspond to the cation’s or the anion’s equilibrium potential. In symbols, denoting the current as i and the membrane potential as V, we have the following:

$$i_{total}=i_{cation}+i_{anion}$$

$$i_{cation}={\mathrm{\gamma }}_{cation}\left(V-E_{cation}\right)$$

$$i_{anion}={\mathrm{\gamma }}_{anion}\left(V-E_{anion}\right)$$

and thus

$$i_{total}=\left({\mathrm{\gamma }}_{cation}+{\mathrm{\gamma }}_{anion}\right)V-\left({\mathrm{\gamma }}_{cation}{E}_{cation}+{\mathrm{\gamma }}_{anion}{E}_{anion}\right).$$

According to this “linear” model, the zero-current, reversal potential (V_rev) is given by the weighted average of the cation and anion equilibrium potentials, where the weighting factors are the fractional slopes:

$$V_{rev}=\frac{{\mathrm{\gamma }}_{cation}{E}_{cation}+{\mathrm{\gamma }}_{anion}{E}_{anion}}{\left({\mathrm{\gamma }}_{cation}+{\mathrm{\gamma }}_{anion}\right)}.$$

In turn, the expression above—which gives the expected results of V_rev = E_cation when γ_cation >> γ_anion, and V_rev = E_anion when γ_anion >> γ_cation—can be rearranged to express the relative permeabilities (γ_cation/γ_anion or γ_anion/γ_cation) in terms of V_rev, E_cation, and E_anion. In the case of the cation-to-anion ratio, we have the following:

$$\frac{{\mathrm{\gamma }}_{cation}}{{\mathrm{\gamma }}_{anion}}=\frac{E_{anion}-V_{rev}}{V_{rev}-E_{cation}}.$$

Hence, in this alternative framework, the permeability ratio has a well-defined and straightforward physical meaning: it is the ratio of conductances that would be obtained if one could estimate separately the single-channel conductances of the cation and anion under the dilution conditions used to estimate the reversal potential.

In Fig. 2A, we compared the linear-I–V and GHK models. To allow for a more convenient comparison of the corresponding mathematical expressions, the GHK equation can be written in terms of the (positive) differences between the reversal (V_rev) and equilibrium potentials (E_anion and E_cation) as follows. For a binary salt of a monovalent cation and a monovalent anion, we have the following:

$$\frac{P_{cation}}{P_{anion}}=-\frac{aAnio{n}_{extracellular}\left(1-\exp \left(\frac{F}{RT}\left(E_{anion}-V_{rev}\right)\right)\right)}{aCatio{n}_{\mathit{intracellular}}\left(1-\exp \left(-\frac{F}{RT}\left(V_{rev}-E_{cation}\right)\right)\right)},$$

where aAnion and aCation denote the ion activities of the anion and cation in the saline solutions, and F, R, and T have their usual meanings. As expected, for both models, the permeability ratio expressions give identical results (0 and ∞) at the ends of the reversal-potential range (E_cation ≤ V_rev ≤ E_anion), and for the particular salt dilution conditions used in our experiments, they stay remarkably close to each other at all other values of V_rev. Throughout this work, we presented and discussed permeability-coefficient ratios calculated using the GHK equation. Having presented the values calculated using the linear I–V model, instead, would not have made much difference and, importantly, would not have affected our conclusions.

Discussion

In proteins, side-chain and/or backbone atoms often come together to create environments that select for certain ions over others. In K⁺-selective channels (31), voltage-dependent Na⁺ (32) and Ca²⁺channels (33), cyclic-nucleotide–gated channels (34), and ClC Cl^– channels (35), for example, the identity of these chemical groups has been firmly established on the basis of electrophysiological and/or X-ray crystallographical observations. In pLGICs, in contrast, although the sequence conservation and pore location of the oppositely charged side chains at positions –1′ and 0′ may have suggested that they are the main contributors to charge selectivity, the experimental data recorded before this work had failed to provide compelling evidence for this idea. Actually, backbone carbonyl oxygens (acting as Lewis bases) and backbone amide groups (acting as hydrogen-bond donors) were previously proposed to underlie cation and anion selectivity, respectively, in these channels. Here, we showed that it is the side chains of ionized residues, instead, that matter.

Undoubtedly, some of the factors that have contributed to obscure the key role of the formal charges on the acidic and basic side chains at positions –1′ and 0′ in charge selectivity are as follows: (i) the little impact of glutamate neutralization at position –1′ on the charge selectivity of the AChR and the failure to recognize that, once this ring is neutralized, the charge selectivity is dictated by “whatever is left,” which can be very different for different pLGICs; (ii) the detrimental effect of lysine and arginine neutralization at position 0′ on the functional expression of the muscle AChR (8) and the α1 GlyR (5); (iii) the location of the basic side chains at position 0′ on the (non–pore-lining) backside of M2 and the misconception that charges need to face the pore directly to have a major effect on the energetics of ion permeation (see refs. 36 and 37 for the sizable effect of buried, ionized basic side chains on single-channel conductance); (iv) the misconception that all rotamers of an ionizable side chain contribute similarly to ion permeation and that rotamers interconvert so quickly that, even if some of them contributed much more than others, it is the average properties of their mixture—not the properties of individual rotamers—that matter (3, 22); and (v) the rather low resolution thus far achieved by direct structural methods in this particular region of the channel.

Having worked around some of these difficulties, our results paint now a clear (although not necessarily simple) picture of charge selectivity in pLGICs as follows.

First, it is the ion–ion interactions between the passing ions and ionized side chains in the first turn of the M2 α-helices that dominate the permeation free-energy landscape. We did not find any reason to invoke the involvement of backbone-atom electrostatics or the α-helix macrodipole in this process.

Second, there is a requirement for a proper orientation of the charged moieties. Indeed, we found that the mere presence of an ionized residue at position –1′ or 0′, in the first turn of M2, does not ensure that the charge is “felt” by permeating ions. Insertions, deletions, and residue-to-residue mutations in the intracellular end of the pore affect charge selectivity very likely by changing the rotamer preferences of these ionized side chains while leaving the length, and the rotational and tilt angles of the M2 α-helices largely unaffected. In support of this idea, previous electrophysiological (3) and computational (22) studies from our group on the muscle AChR provided compelling evidence for the notion that the different rotamers of the glutamate side chain at position –1′ make widely different contributions to the single-channel conductance. Hence, realizing that single-channel conductance and charge selectivity are actually two related aspects of the same (ion permeation) phenomenon, and taking together all of the experimental results on charge selectivity presented in this work, it seems natural now to extend this concept to include not only conductance but also selectivity, not only the acidic side chains at position –1′ but also the basic side chains at the adjacent position 0′, and not only the muscle AChR but also all other members of the pLGIC superfamily.

Third, the charges on ionized side chains act in a hierarchical manner. Certainly, properly oriented glutamates at position –1′ and arginines or lysines at position 0′ dominate the permeation landscape of wild-type cation-selective and anion-selective pLGICs, respectively, but in their absence (say, upon substitution with neutral residues), the remaining ionized residues that decorate the ion permeation pathway, both within and outside the membrane, take control over these energetics. This is an important concept that explains why, for example, the neutralization of the glutamates at position –1′ manifests differently in different cation-selective members of the superfamily.

In hindsight, we realize the importance of having included six different pLGICs in this study. Clearly, no single pLGIC could have provided enough insight to come up with a general mechanism that explains the molecular basis of charge selectivity for the entire superfamily. Multiscale computer simulations closely benchmarked by further electrophysiological observations and higher-resolution structures will now be needed to take the next step into a chemically rigorous understanding of the remarkably versatile charge selectivity of pLGICs.

Materials and Methods

Whole-cell currents were recorded at ∼22 °C from transiently transfected HEK-293 cells using an Axopatch 200B amplifier (Molecular Devices), and charge selectivity was inferred from reversal potentials estimated under near KCl-dilution conditions. Current–voltage (I–V) curves were generated by plotting the peak values of current transients elicited by brief (10- or 20-ms) applications of agonist at holding voltages straddling the reversal potential. Peak values were calculated by subtracting the value of the current before each agonist application from the maximum current attained on application of agonist. In all experiments, the intracellular solution was as follows (in mM): 110 KCl, 40 KF, and 5 Hepes/KOH, pH 7.4 (measured osmolarity: ∼265 mOsm; Wescor). In most experiments, the extracellular solution (flowing through the two barrels of a piece of θ tubing) was as follows (in mM): 15 KCl, 5 Hepes/KOH, pH 7.4, and enough mannitol (∼230 mM) to reach an osmolarity of ∼265 mOsm, with or without agonist. With these intracellular and extracellular solutions, the equilibrium potentials (calculated at 22 °C using ion activities) were –50.6 mV for K⁺ and +46.2 mV for Cl^–. In experiments where a steeper KCl dilution was imposed across the membrane, the concentration of KCl in the extracellular solution was lowered to 5 mM, and the concentration of mannitol was raised (to ∼250 mM) to maintain the osmolarity. Under these conditions, the equilibrium potential for K⁺ became –71.7 mV, and that for Cl^–, +73.1 mV. The concentration of the agonist was 100 μM (ACh and 5-HT) or 1 mM (Gly and propylamine). Additional details are described in SI Materials and Methods.