Ordinary–extraordinary transition in dynamics of solutions of charged macromolecules

Significance

The experimentally observed phenomenon of the “ordinary–extraordinary” transition from dynamic light-scattering measurements of solutions of charged macromolecules has remained mysterious for the past four decades and has prohibited the use of the Stokes–Einstein law in characterizing the sizes of charged polymers, using light-scattering techniques. The diffusion coefficients of polymers with molecular weight of about 1 million can be merely one-fourth of those of metallic ions such as K⁺, independent of polymer molecular weight and concentration. Similarly charged macromolecules can clump together to make aggregates when electrostatic repulsion between them is dominant and they break apart when the electrostatics are screened. A theory based on counterion dynamics and dipolar interactions is presented in resolving these mysteries.

Abstract

The occurrence of the ubiquitous and intriguing “ordinary–extraordinary” behavior of dynamics in solutions of charged macromolecules is addressed theoretically by explicitly considering counterions around the macromolecules. The collective and coupled dynamics of macromolecules and their counterion clouds in salt-free conditions are shown to lead to the “ordinary” behavior (also called the “fast” mode) where diffusion coefficients are independent of molar mass and polymer concentration and are comparable to those of isolated metallic ions in aqueous media, in agreement with experimental facts observed repeatedly over the past four decades. The dipoles arising from adsorbed counterions on polymer backbones can form many pairwise physical cross-links, leading to microgel-like aggregates. Balancing the swelling from excluded volume effects and counterion pressure with elasticity of the microgel, we show that there is a threshold value of a combination of polymer concentration and electrolyte concentration for the occurrence of the “extraordinary” phase (also called the “slow” mode) and the predicted properties of diffusion coefficient for this phase are in qualitative agreement with well-known experimental data.

The “ordinary–extraordinary” transition has been known over the past four decades from dynamic light-scattering (DLS) experiments on aqueous solutions of charged macromolecules such as DNA, polylysine, polystyrene sulfonate, polyvinyl pyridine, etc. (1–22). In the so-called “ordinary” behavior, the diffusion coefficient D determined from DLS increases, from the value $D_{SE}$ expected from the Stokes–Einstein law for dilute polyelectrolyte solutions at high enough monovalent salt concentrations $c_s$ sufficient to screen electrostatic interactions, to even higher values upon a decrease in $c_s.$ This observation is already intriguing, because the chain swells due to stronger intrachain electrostatic repulsion at lower values of $c_s$ and hence D is expected to decrease according to the Stoke–Einstein law. However, D actually increases! Even more strangely, upon further decrease in $c_s,$ an additional diffusion coefficient with very small values emerges, suggesting the presence of large aggregates. It is surprising that similarly charged, and hence electrostatically repulsive, polymers would aggregate at all and that they would break apart when electrostatic repulsion is screened by added electrolyte. In view of this mysterious nature, this behavior is called “extraordinary.” In addition to these tantalizing facts, the occurrence of the ordinary–extraordinary behavior for solutions of charged macromolecules completely undermines the utility of the Stokes–Einstein law, which is the routine methodology for characterizing uncharged macromolecules in solutions.

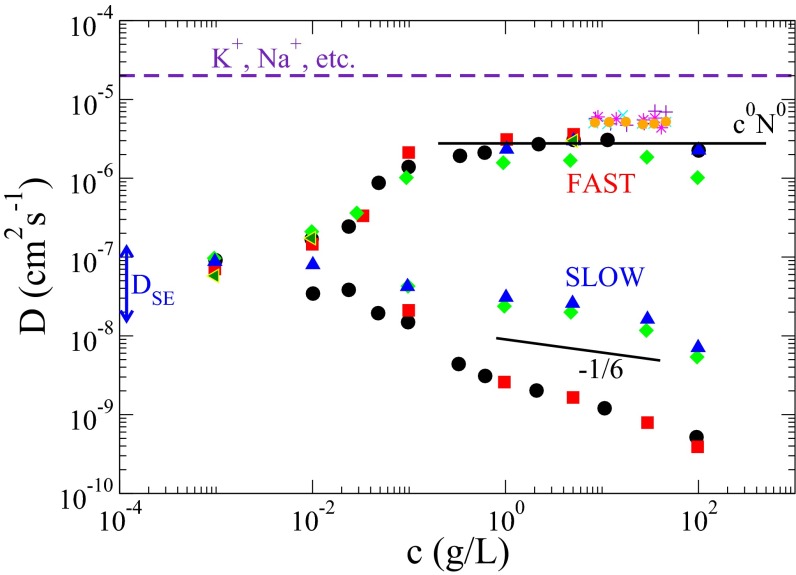
The diffusional modes corresponding to the ordinary and extraordinary behaviors are also called “fast” and “slow” modes, with their respective diffusion coefficients $D_f$ and $D_s.$ The diffusion coefficients $D_f$ and $D_s,$ collected from literature originating from many laboratories worldwide (1, 11, 15, 16), are given in Fig. 1 as functions of polymer concentration c and degree of polymerization N. In addition to the abovementioned puzzles, several features characterize the ubiquitous and intriguing simultaneous occurrence of the fast and slow modes.

Fig. 1.

Collected data on diffusion coefficient for the fast (ordinary) mode, $D_f,$ and the slow (extraordinary) mode, $D_s.$ The fast and slow modes emerge for polymer concentrations above a threshold value. For the fully developed two-mode regime, $D_f$ is independent of polymer concentration c and degree of polymerization N over several orders of magnitude and is only about a factor of 4 smaller than the diffusion coefficient of a metallic ion such as Na⁺ in water. $D_s$ is smaller than $D_f$ by three orders of magnitude and it depends on c and N, suggesting formation of aggregates by similarly charged polymers. Upon addition of electrolytes, the slow mode disappears and $D_f$ progressively becomes smaller, approaching eventually the diffusion coefficient $D_{SE}$ expected from the Stokes–Einstein law. Blue triangle, green diamond, red square, black circle, and green triangle data are from Förster et al. (11) for quarternized poly(2-vinylpyridine) with molecular weight $M=1.09\times {10}^5\hspace{0.17em}\text{g/mol},\hspace{0.5em}2\times {10}^5\hspace{0.17em}\text{g/mol},\hspace{0.5em}7.8\times {10}^5\hspace{0.17em}\text{g/mol},\hspace{0.5em}5.8\times {10}^5\hspace{0.17em}\text{g/mol,}$ and $2.26\times {10}^6$ g/mol and degree of quarternization $q=0.65,\hspace{0.5em}0.98,\hspace{0.5em}0.75,\hspace{0.5em}0.4,$ and 1.0, respectively. Purple plus, aqua cross, purple star, and gold circle data are from Sedlak and Amis (15) for sodium poly(styrene sulfonate) with $M=5\times {10}^3\hspace{0.17em}\text{g/mol},\hspace{0.5em}3.82\times {10}^4\hspace{0.17em}\text{g/mol},\hspace{0.5em}1.0\times {10}^5\hspace{0.17em}\text{g/mol,}$ and $1.2\times {10}^6$ g/mol, respectively. The solid lines represent predictions from the present theory.

The fast diffusion coefficient $D_f$ is several orders of magnitude higher than the expected value $D_{SE}$ from its size based on the Stokes–Einstein law. Remarkably, $D_f$ for c above a threshold value is independent of c and N over several orders of magnitude. Even more remarkably, $D_f$ of say ${10}^6$ Da sodium polystyrene(sulfonate) is only a factor of 4 smaller than the diffusion coefficient of a metallic ion such as K⁺, Na⁺, etc. As mentioned above, the fast mode behavior is called ordinary because, upon addition of small molecular salt such as NaCl, $D_f$ decreases continuously with salt concentration $c_s,$ eventually reaching $D_{SE}.$

The slow diffusion coefficient $D_s$ is several orders of magnitude smaller than $D_f$ and $D_{SE}$ and it decreases strongly with an increase in either c or N. Using the Stokes–Einstein law, $D_s$ has been interpreted in the literature with the conjecture of formation of large aggregates made of many chains. Such clustering is also seen in suspensions of charged colloidal particles and worm-like micelles (22). Concomitant to the onset of the slow mode, the scattering intensity at very small scattering angles appears to diverge (10), consistent with the conjecture of formation of aggregates (20). Upon addition of salt ($c_s>c$), the slow mode disappears. As already mentioned, this extraordinary behavior of aggregation among self-repelling chains is enigmatic. The junction point at which one diffusive mode (fast) splits into two modes (fast and slow), either when $c_s$ is reduced or c is increased, is identified as the ordinary–extraordinary transition point. This paper provides a theory of the ordinary–extraordinary phenomenon of charged macromolecules in solutions.

Results

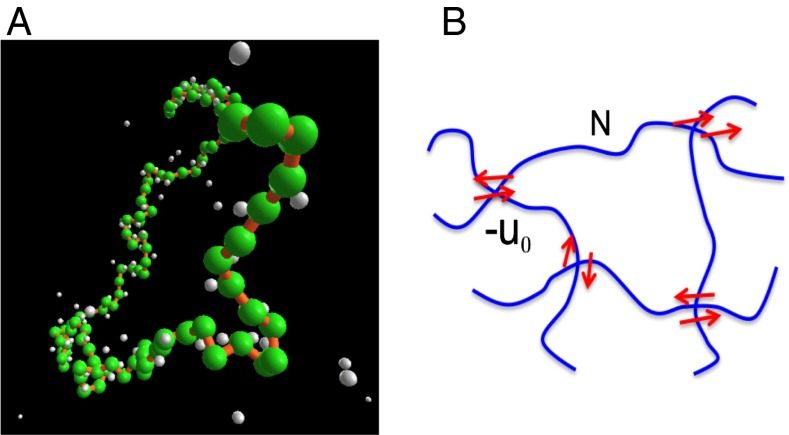
The resolution of these puzzles lies in the omnipresent cloud of counterions that surrounds the polymer chains (23, 24). Due to an optimization between translational entropy of counterions and attraction between the polymer and counterions, there is a net amount of counterions adsorbed around each chain, making a counterion worm (Fig. 2A), and indeed the effective charge of the chain is reduced from its chemical charge (23, 24). As a result, the chains do not move independently. Their dynamics are coupled to those of the counterion cloud. Therefore, direct implementation of the Stokes–Einstein law enunciated for isolated ions is not allowed in describing the dynamics of charged macromolecules. The coupled dynamics of the chains and their counterion clouds must be treated self-consistently, and proper description of the independence of electrophoretic mobility on molar mass of charged macromolecules must be taken into account (25–27). As shown below, these considerations lead to the observed fast diffusion behavior. Furthermore, when a counterion adsorbs on the polymer chain, it makes a strong dipole (23, 24). Although these dipoles are individually transients, simultaneous occurrence of several dipole–dipole pairings can result in microgel-like aggregates (Fig. 2B). As shown below, such dipole-mediated aggregates, originating from adsorbed counterions, are responsible for the extraordinary behavior associated with the slow mode.

Fig. 2.

(A) Counterion cloud (white) surrounding a polyelectrolyte chain (green). The coupled dynamics of the chains and their counterion clouds are measured in the fast mode. (B) Cartoon of several dipole–dipole pairings responsible for microgel-like aggregate formation attributed to the slow mode. Each red arrow denotes a dipole formed by an adsorbed counterion on the polymer backbone. $u_0$ is the magnitude of the average attractive energy between two adjacent dipoles in contact, averaged over different favorable orientations. N is the number of segments between two such physical cross-links.

Fast Mode.

The diffusion coefficients given in Fig. 1 are obtained from DLS by analyzing the time dependence of the monomer density correlation function $\langle {\rho }_{\mathbf{k}}\left(t\right){\rho }_{-\mathbf{k}}\left(0\right)\rangle ,$ where the Fourier transform of the local monomer density is defined as (28, 29)

$${\rho }_{\mathbf{k}}\left(t\right)=\frac{1}{V}{\displaystyle \sum _{\beta j}{e}^{i\mathbf{k}\cdot {\mathbf{R}}_{\beta j}\left(t\right)}}.$$ [1]

The whole system consists of n polyelectrolyte chains of uniform length $N\ell ,$ with N Kuhn segments of length $\ell ,$ dispersed in a polar solvent of volume V containing fully dissociated salt at concentration $c_s.$ The average polymer concentration is $c=nN/V.$ Each monomer of the chains is ionizable and the ionized groups are assumed to be uniformly distributed along the chain with α as the average degree of ionization. The concentration of the monovalent counterions arising from the dissociated monomers is $\alpha z_{p}c,$ where $z_p$ is the number of ionizable groups per Kuhn segment. ${\mathbf{R}}_{\beta j}\left(t\right)$ is the position vector at time t of the jth monomer of the βth chain ($1\le j\le N,1\le \beta \mathrm{\le }n$). $\mathbf{k}$ is the scattering wave vector. Using the standard theory of polymer dynamics (25–31), the time evolution of ${\rho }_{\mathbf{k}}\left(t\right)$ is given by

$$\frac{\partial {\rho }_{\mathbf{k}}\left(t\right)}{\partial t}=-{\mathrm{\Gamma }}_k{\rho }_{\mathbf{k}}+f_{\mathbf{k}},$$ [2]

where $f_{\mathbf{k}}$ is the white noise satisfying the fluctuation–dissipation theorem and

$${\mathrm{\Gamma }}_k=k_{B}T{\displaystyle \int \frac{d^{3}q}{{\left(2\pi \right)}^3}\frac{\mathbf{k}\cdot \left(1-\widehat{\mathbf{q}}\widehat{\mathbf{q}}\right)\cdot \mathbf{k}}{{\eta }_0\left(q^2+{\xi }_h^{-2}\right)}\frac{g\left(\mathbf{k}+\mathbf{q}\right)}{g\left(\mathbf{k}\right)}}.$$ [3]

Here, $k_{B}T$ is the Boltzmann constant times the absolute temperature, ${\xi }_h$ is the hydrodynamic screening length (27), and the scattering function per segment is (32)

$$g\left(\mathbf{k}\right)=\frac{V}{c}\langle {\rho }_{\mathbf{k}}\left(t\right){\rho }_{-\mathbf{k}}\left(t\right)\rangle .$$ [4]

For polyelectrolyte solutions, where monomer density fluctuations are strongly correlated by long-ranged electrostatic interactions, $g\left(\mathbf{k}\right)$ is a complicated function of c and $c_s,$ depending on three quantities, $v,w_c,$ and κ: excluded volume parameter $v=\left(1/2-\chi \right){\ell }^3,$ where χ is the Flory–Huggins parameter for solvent–polymer backbone interaction (33); strength of the segment–segment electrostatic interaction (34) $w_c=4\pi {\alpha }^2{z}_p^2{\ell }_B,$ where ${\ell }_B$ is the Bjerrum length $e^2/\left(4\pi {\mathit{ϵ}}_0\mathit{ϵ}{k}_{B}T\right)$ ($e=$ the electronic charge, ${\mathit{ϵ}}_0=$ permittivity of vacuum, and $\mathit{ϵ}=$ dielectric constant of the solution); and range of electrostatic interaction given by the Debye length ${\kappa }^{-1}={\left[4\pi {\ell }_B\left(\alpha z_{p}c+2c_s\right)\right]}^{-1/2},$ where the counterions and dissociated salt ions are taken as monovalent. Analytical results emerge in the asymptotic limits of low salt ($\kappa \to 0$) and high salt (${\kappa }^2{\ell }^2\gg 1$). In the high-salt limit, $g\left(\mathbf{k}\right)$ is the same as for solutions of uncharged polymers (with v replaced by $v+w_c/{\kappa }^2$), decreasing monotonically with k.

In the low-salt limit, $g\left(\mathbf{k}\right)$ is nonmonotonic in k and exhibits the “polyelectrolyte peak” at $k_m$ for all polyelectrolyte concentrations (1, 5, 10, 35–48). For c less than the overlap concentration $c\ast ,$ $g\left(\mathbf{k}\right)$ is the product of the form factor $P\left(k\right)$ and intermolecular structure factor $S_{int}\left(\mathbf{k}\right),$

$$g\left(\mathbf{k}\right)=P\left(k\right)S_{int}\left(\mathbf{k}\right),$$ [5]

where $P\left(k\right)=\left(1-k^2{R}_g^2/3+\cdots \right)$ for $k{R}_g\ll 1$ and $P\left(k\right)\sim k^{-\nu }$ for $k{R}_g\gg 1,$ with $R_g$ being the radius of gyration of a chain, and ν is the size exponent given by $R_g\sim N^{\nu }.$ For infinitely dilute solutions, so dilute that the chains are not electrostatically correlated, the intermolecular structure factor exhibits a scattering peak at $k_m\sim c^{1/3}$ as a manifestation of average interchain distance given geometrically by $c^{-1/3}.$ When c is increased, but still in dilute regime, the chains are electrostatically correlated with their average separation distance given by the Debye length ${\kappa }^{-1}$ ($\sim c^{-1/2}$ for $c_s=0$). Therefore, $k_m\sim c^{1/2}.$ For $c\ge c\ast ,$ the chains interpenetrate and are correlated both electrostatically and topologically, resulting in a coupled double screening (Edwards screening and Debye–Hückel screening) (25). Now, $g\left(\mathbf{k}\right)$ is of the form

$$g\left(\mathbf{k}\right)=\frac{1}{c{w}_c}\frac{k^2}{\left(1+k^4{\xi }^4\right)},$$ [6]

where $\xi \sim c^{-1/2}$ for semidilute solutions (where concentration fluctuations are strong) and $\xi \sim c^{-1/4}$ for concentrated solutions (where concentration fluctuations are weak). Therefore, $g\left(\mathbf{k}\right)$ exhibits a peak at $k_m\sim c^{1/2}$ for semidilute solutions and at $k_m\sim c^{1/4}$ for concentrated solutions. Thus, in the low-salt limit, four regimes of polyelectrolyte concentration may be identified and in each regime, $g\left(\mathbf{k}\right)$ exhibits a peak at $k_m:$ (i) infinitely dilute and electrostatically uncorrelated, $k_m\sim c^{1/3};$ (ii) dilute and electrostatically correlated, $k_m\sim c^{1/2};$ (iii) semidilute with strong concentration fluctuations, $k_m\sim c^{1/2};$ and (iv) concentrated with weak concentration fluctuations, $k_m\sim c^{1/4}.$ Substitution of these results in Eqs. 2 and 3 yields expressions for the diffusion coefficient.

For the high-salt limit, as $g\left(\mathbf{k}\right)$ is a monotonically decaying function of k, ${\mathrm{\Gamma }}_k$ is diffusive for small k,

$${\mathrm{\Gamma }}_k=D_c{k}^2+0\left(k^4\right),$$ [7]

where $D_c$ is the cooperative diffusion coefficient. Now $D_c$ is proportional to $R_g^{-1}$ for dilute solutions ($c<c\ast$) and to ${\xi }^{-1}$ for $c>c\ast .$ For salt-free conditions, in view of $g\left(\mathbf{k}\right)$ of Eq. 6 being $\sim k^2$ for small k, ${\mathrm{\Gamma }}_k$ is not purely diffusive,

$${\mathrm{\Gamma }}_k={\mathrm{\Gamma }}_0+D_c{k}^2+0\left(k^4\right),$$ [8]

where ${\mathrm{\Gamma }}_0\sim {\xi }^{-3}$ and $D_c\sim {\xi }^{-1}.$

In addition to the cooperative diffusion addressed in the above equations, the local motion of monomers is coupled to the dynamics of the counterions in the neighborhood of the monomers (29). The counterion cloud generates an electric field $\mathbf{E}$ on the monomer, and as a result there is an additional convective contribution to the flux, $\rho {\mu }_0\mathbf{E},$ where ${\mu }_0$ is the monomer electrophoretic mobility $\alpha /{\zeta }_0$ (${\zeta }_0$ is the monomer friction coefficient). Inclusion of this coupling, to leading order in monomer density, into the continuity equation of Eq. 2 gives

$$\frac{\partial {\rho }_{\mathbf{k}}\left(t\right)}{\partial t}=-{\mathrm{\Gamma }}_k{\rho }_{\mathbf{k}}-{\mu }_0{z}_{p}c\left(i\mathbf{k}\cdot \mathbf{E}\right).$$ [9]

Now, according to Poisson’s equation

$$i\mathbf{k}\cdot \mathbf{E}=\frac{1}{{\mathit{ϵ}}_0\mathit{ϵ}}\left(\alpha {\rho }_{\mathbf{k}}+z_c{\rho }_{c,\mathbf{k}}\right)$$ [10]

for salt-free solutions, where ${\rho }_c$ is the local concentration of counterions (of valency $z_c$). Therefore, the time evolution of ${\rho }_{\mathbf{k}}$ is coupled to ${\rho }_c.$ Analogous to Eq. 9, the time evolution of ${\rho }_{c,\mathbf{k}}$ can be written as

$$\frac{\partial {\rho }_{c,\mathbf{k}}}{\partial t}=-D\prime k^2{\rho }_{c,\mathbf{k}}-\frac{\mu \prime c_c}{{\mathit{ϵ}}_0\mathit{ϵ}}\left(\alpha {\rho }_{\mathbf{k}}+z_c{\rho }_{c,\mathbf{k}}\right),$$ [11]

where $c_c=\alpha c/z_c,$ and $D\prime$ and $\mu \prime =z_{c}D\prime /\left(k_{B}T\right)$ are the diffusion coefficient and electrophoretic mobility of the counterion, respectively. Due to the coupling of ${\rho }_{\mathbf{k}}$ and ${\rho }_{c,\mathbf{k}},$ there are two decay rates, which we label as superfast and fast modes. If there are additional charged species, there will be additional modes.

As we anticipate that the fluctuation in the counterion distribution would come to equilibrium more rapidly than the macromolecule (29), we can approximate $\partial {\rho }_{c,\mathbf{k}}/\partial t\sim 0.$ This enables an analytical expression for $\partial {\rho }_{\mathbf{k}}/\partial t$ as

$$\frac{\partial {\rho }_{\mathbf{k}}}{\partial t}=-{\mathrm{\Gamma }}_0{\rho }_{\mathbf{k}}-D_c{k}^2{\rho }_{\mathbf{k}}-\frac{c{\mu }_0\alpha z_{p}e}{{\mathit{ϵ}}_0\mathit{ϵ}\left(k^2+{\kappa }^2\right)}{k}^2{\rho }_{\mathbf{k}}.$$ [12]

For small $k<\kappa ,$ this becomes

$$\frac{\partial {\rho }_{\mathbf{k}}}{\partial t}=-{\mathrm{\Gamma }}_0{\rho }_{\mathbf{k}}-D_f{k}^2{\rho }_{\mathbf{k}},$$ [13]

where the fast diffusion coefficient is given as

$$D_f=D_c+\frac{c{\mu }_0\alpha z_{p}e}{{\mathit{ϵ}}_0\mathit{ϵ}{\kappa }^2}.$$ [14]

Noting that ${\mu }_0=e\alpha /{\zeta }_0,\hspace{0.5em}{\kappa }^2=e^2\alpha z_{p}c{z}_c^2/\left({\mathit{ϵ}}_0\mathit{ϵ}{k}_{B}T\right),$ and $z_c=1$ for monovalent counterions,

$$D_f=D_c+\alpha D_0,$$ [15]

where $D_0=k_{B}T/{\zeta }_0$ is the monomer diffusion coefficient. Because $D_c$ of a macromolecule is orders of magnitude smaller than the monomer diffusion coefficient (if the monomer were to be alone and not a part of the chain), the fast diffusion coefficient is predicted as

$$D_f\simeq \alpha D_0,\hspace{1em}\text{independent}\hspace{0.17em}\text{of}\hspace{0.17em}N\hspace{0.17em}\text{and}\hspace{0.17em}c.$$ [16]

As the effective degree of ionization is about 0.25–0.3 due to counterion adsorption, and taking $D_0$ as that of a metallic ion, the fast diffusion coefficient is about $5\times {10}^{-6}\hspace{0.17em}{\text{cm}}^2/\text{s}$ as seen in Fig. 1. The derived theory of $D_f$ as the renormalized $D_c$ is also of relevance to other systems such as critical fluids, colloidal suspensions, gels, etc.

Slow Mode.

When two dipoles ${\mathbf{p}}_1$ and ${\mathbf{p}}_2,$ each constituted by a monomer charge and its adsorbed counterion, are oriented either parallel or antiparallel, their interaction energy $U\left(r\right)$ is attractive given by $-p_1{p}_2{\ell }_B{k}_{B}Tf\left(\kappa r\right)/r^4,$ where $f\left(\kappa r\right)$ is a known function. If these dipoles are randomly oriented, the interaction energy is

$$\frac{U\left(r\right)}{k_{B}T}=-\frac{p_1^2{p}_2^2{\ell }_B^2}{r^6}{e}^{-2\kappa r}\left[1+2\kappa r+\frac{5}{3}{\left(\kappa r\right)}^2+\frac{2}{3}{\left(\kappa r\right)}^3+\frac{1}{6}{\left(\kappa r\right)}^4\right].$$ [17]

As a typical example, $U\left(r\right)\sim -10k_{B}T$ if the separation distance between the dipoles and the dipole length are 0.25 nm, comparable to the monomer separation distance along the chain for salt-free water at room temperature. If we define the Flory–Huggins parameter ${\chi }_{\text{dipole}}$ as a contact potential arising from pairwise dipolar interaction according to

$$\left(\frac{1}{2}-{\chi }_{\text{dipole}}\right)\equiv -u_0=\frac{1}{{\ell }^3}{\displaystyle \int d\mathbf{r}\left[1-e^{-U\left(r\right)/k_{B}T}\right]},$$ [18]

then $\left(1/2-{\chi }_{\text{dipole}}\right)$ is −12.6 at $c_s={10}^{-4}$ M, showing that ${\chi }_{\text{dipole}}$ is enormously positive due to such dipolar attractions.

Due to such strong attractive contact energy between two dipoles (constituted by adsorbed counterions on charged monomers), we allow aggregation of m uniformly charged chains (Fig. 2B). The standard theory (49) of micellization gives the mole fraction of m-mers as

$$X_m=m{\left[X_1{e}^{\left(1/k_{B}T\right)\left(F_1-F_m/m\right)}\right]}^m,$$ [19]

for a fixed mole fraction of the polymer, $X={\displaystyle {\sum }_{m=1}^{\infty }{X}_m}.$ Here, $X_1$ and $F_1$ are the mole fraction and free energy of unaggregated unimer, and $F_m$ is the free energy of the m-mer.

Consider a microgel with m chains, each of N segments, with polymer volume fraction ϕ inside the microgel. The free energy of this system is given by the classical theory of Flory (33) as

$$\begin{array}{c}\frac{F_m}{k_{B}T}=mN\left[\left(\frac{1}{2}-\chi \right)\varphi +\frac{1}{6}{\varphi }^2+\cdots \right]+\frac{3m}{2}\left[N^{-1/3}{\varphi }^{-2/3}+\frac{1}{3}\ln \varphi \right]\\ +\hspace{0.17em}\left[\sqrt{{\alpha }^2{m}^2{N}^2+4n_s^2}-2n_s\right]\ln \hspace{0.17em}\varphi -\frac{m}{2}{u}_0,\end{array}$$ [20]

where the first three terms on the right-hand side arise from the thermodynamic theory of free energy of mixing, rubber elasticity theory, and excess osmotic pressure inside the microgel (Donnan equilibrium of dissociated ions), respectively. The last term denotes the attractive energy arising from the dipolar junctions ($u_0$ is the strength of the contact energy, $m/2$ is the number of junctions in accordance with Flory’s mean-field theory, χ is the Flory–Huggins parameter for the solvent quality, and $2n_s$ is the number of dissociated salt ions inside the microgel. In general, N can depend on polymer concentration for physical microgels. Eq. 20 is minimized with respect to ϕ and $F_m$ is calculated for the equilibrated microgel.

For salt-free conditions, the equilibrium polyelectrolyte concentration of the microgel is

$${\varphi }^{-2/3}=N^{4/3}\left(\alpha +\frac{1}{2N}\right),$$ [21]

and $F_m$ becomes

$$\frac{F_m}{m{k}_{B}T}=-\frac{u_0}{2}+\frac{3N}{2}\left(\alpha +\frac{1}{2N}\right)\left\{1-\ln \left[N^{4/3}\left(\alpha +\frac{1}{2N}\right)\right]\right\},$$ [22]

apart from a constant term. The free energy of the unimer is given for salt-free conditions as (34)

$$\frac{F_1}{k_{B}T}=1.11{\left(\frac{{\alpha }^2{\ell }_B}{\ell }\right)}^{2/3}N.$$ [23]

Combining the above two equations gives

$$\frac{F_1}{k_{B}T}-\frac{F_m}{m{k}_{B}T}=\left(1-\frac{1}{m}\right)\theta ,$$ [24]

where θ is given by

$$\theta =1.11{\left(\frac{{\alpha }^2{\ell }_B}{\ell }\right)}^{2/3}+\frac{u_0}{2}-\frac{3N\alpha }{2}\left[1-\ln \left(N^{4/3}\alpha \right)\right],$$ [25]

where $1/2N$ is neglected in comparison with the degree of ionization α. The mole fraction of m-mers follows from Eqs. 19 and 24 as

$$X_m=m{\left(X_1{e}^{\theta }\right)}^m{e}^{-\theta },$$ [26]

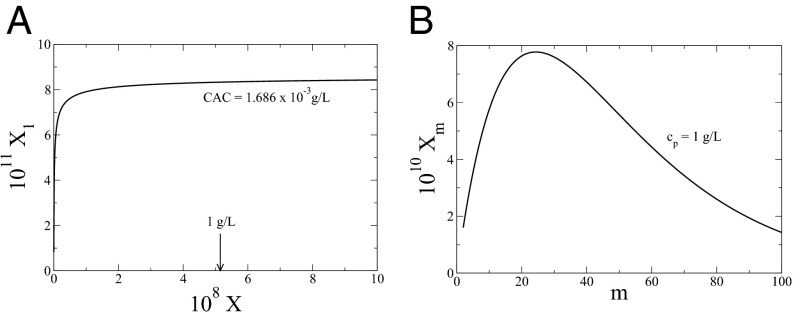
with the constraint $X={\displaystyle {\sum }_{m=1}^{\infty }{X}_m}.$ As well known (49), the above equation shows that there exists a critical aggregation concentration (CAC), $X_{\text{CAC}}=e^{-\theta },$ above which m-mers will form spontaneously. As a typical example, the dependence of $X_1$ on X is given in Fig. 3A for $\alpha =0.3,\hspace{0.5em}{\ell }_B/\ell =3,\hspace{0.5em}{u}_0=10,$ and $N=16.$ For this set of values, $X_{\text{CAC}}=8.68\times {10}^{-11}.$ If the molecular weight of the polyelectrolyte is $\mathrm{350,000}$ g/mol, then $X=5.148\times {10}^{-8}$ is equivalent to the polymer concentration of 1 g/L. Therefore, CAC is $1.686\times {10}^{-3}$ g/L. The distribution of $X_m$ is given in Fig. 3B for polymer concentrations of 1 g/L. It can be readily shown that the average size of the aggregate increases with polymer concentration. The functional form of Eq. 26, where θ is independent of m, enables several general conclusions on the size distribution (49). For $c>\text{CAC}$ and for large m,

$$X_m\sim m{e}^{-\left(m/\sqrt{X{e}^{\theta }}\right)}$$ [27]

$$m_{\max }=\sqrt{X}{e}^{\theta /2}$$ [28]

$$\langle m\rangle =2\sqrt{X}{e}^{\theta /2}$$ [29]

$$\langle m^2\rangle -\langle m^2\rangle =2X{e}^{\theta /2},$$ [30]

where $m_{\max }$ is the number of chains in the microgel at which $X_m$ is maximum, $\langle m\rangle$ is the average number of chains in the aggregate, and $\langle m^2\rangle -{\langle m\rangle }^2$ is the SD. By writing the volume fraction of the equilibrated microgel as $\langle m\rangle N{\ell }^3/\left(\left(4/3\right)\pi R_{\text{agg}}^3\right),$ it follows from Eqs. 21 and 29 that

$$R_{\text{agg}}={\left(\frac{3}{2\pi }\right)}^{1/3}N\sqrt{\alpha }{e}^{\theta /6}{X}^{1/6}\sim c^{1/6}.$$ [31]

Substituting this into the Stokes–Einstein expression for the self-diffusion coefficient of the aggregate gives

$$D_{\text{agg}}\sim \frac{T}{{\eta }_0{c}^{1/6}}.$$ [32]

This mean-field result is included in Fig. 1 as a theoretical expectation. Because the slow mode is here associated with diffusion of aggregates, the onset of the slow mode is correlated with the CAC. In other words, to observe the slow mode in DLS, it is necessary for the polymer concentration to be higher than the CAC.

Fig. 3.

(A) Dependence of mole fraction of unaggregated chains on the total mole fraction of the polymer in the salt-free solution for $\alpha =0,\hspace{0.5em}{\ell }_B/\ell =3,\hspace{0.5em}{u}_0=10,$ and $N=16.$ For $M=\mathrm{350,000}$ g/mol, $X=5.148\times {10}^{-8}$ is equivalent to the total polymer concentration of 1 g/L, which is orders of magnitude higher than the CAC of $1.686\times {10}^{-3}$ g/L. (B) Distribution function of the mole fraction of m-mers for polymer concentration of 1 g/L.

Discussion

The fast (ordinary) mode is shown to arise from the coupling between dynamics of polymer segments and their counterion cloud. Here, the diffusion coefficient $D_f$ is the sum of the cooperative diffusion coefficient $D_c$ (if there were no coupling as in uncharged polymers) and the contribution from coupling, which is simply the monomer diffusion coefficient $D_0$ with a prefactor of the effective degree of ionization α (Eq. 16). Because $D_c<\alpha D_0,$ $D_f$ is about one-fourth of the diffusion coefficient of an electrolyte ion. In the presence of added salt, the expression for $D_f$ is the same as Eq. 14 with ${\kappa }^2=4\pi {\ell }_B\left(\alpha c+2c_s\right)$ for monovalent counterions and salt ions. As $c_s$ increases the second term of Eq. 14 becomes weaker and $D_f$ approaches $D_c$ as seen in experiments. Even in the absence of deliberately added salt, a crossover from the asymptotic regime of $D_f\sim c^0{N}^0$ to $D_f\sim D_{SE}$ is seen as the polymer concentration is reduced to very low values. At such low polymer concentrations in aqueous media, there are always impurities and dissociated ions from water, etc., acting like salt. In addition, $D_c$ itself picks up $\sqrt{c}$ dependence because the static correlation length (exhibited by the polyelectrolyte peak) varies as $c^{-1/2}$ in dilute solutions. Our derived result is different from the classical Nernst–Hartley result (29) for coupled diffusion of electrolyte ions, with the difference arising from the fact that the electrophoretic mobility of a polyelectrolyte is independent of its molecular weight. The present theory is an extension of mode coupling (22) of mass and momentum fluctuations to include charge fluctuations.

The slow (extraordinary) mode is attributed to the formation of microgel-like aggregates where the physical cross-links arise from dipole–dipole pairings with each dipole originating from an adsorbed counterion to a charged monomer belonging to the polymer. By equilibrating such aggregates with Flory’s theory of ionic gels and implementing the theory of micellization, we have established the criterion for the onset of the slow mode as the CAC. The ordinary–extraordinary transition (splitting) point is identified with CAC. For $c>$ CAC, microgel-like aggregates form and the average number of chains in the aggregates increases with polymer concentration as $\sqrt{c}$ (Eq. 29). This in turn results in $D_{\text{app}}\sim c^{-1/6}$ as shown in Fig. 1. These results based on dipole–dipole-mediated microgel formation, originating from counterion adsorption, appear to be qualitatively consistent with the slow mode behavior. The discrepancy in quantitative details between the above law and experimental data can readily arise from polydispersity in the aggregate size, concentration dependence of cross-link density, and entanglement effects at higher polymer concentrations.

The above calculation can be repeated at high-salt concentrations. Now the equilibrium volume fraction inside the microgel is given by

$${\varphi }^{-1}=N^{4/5}{\left(\frac{1}{2}-\chi +\frac{{\alpha }^2}{4v_1{c}_s}\right)}^{3/5},$$ [33]

where $v_1$ is the volume of a solvent molecule. For the high-salt limit, $F_1$ is given by

$$\frac{F_1}{k_{B}T}=1.8{\left(\frac{1}{2}-\chi +\frac{{\alpha }^2}{2v_1{c}_s}\right)}^{2/5}{N}^{1/5}.$$ [34]

By combining Eqs. 19, 33, and 34, the expression for θ in Eq. 26 is replaced by (for $\chi =1/2$)

$$\theta =\frac{u_0}{2}+N^{1/5}{\left(\frac{{\alpha }^2}{4v_1{c}_s}\right)}^{2/5}\left[0.8752+\frac{3}{5}\ln \left(\frac{N^{4/3}{\alpha }^2}{4v_1{c}_s}\right)\right].$$ [35]

The general conclusions given in Eqs. 27–30 are still the same except that the CAC is very high. For example, for $\alpha =0.1,\hspace{0.5em}N=16,\hspace{0.5em}{\ell }_B/\ell =3,\hspace{0.5em}{u}_0=9,$ and $c_s=0.1$ M [by taking $v_1={\left(0.23\hspace{0.17em}\text{nm}\right)}^3$], CAC = 4.017 g/L. Even for the unphysically large polymer concentration of 100 g/L, $m_{\max }$ is only 4. In fact, this theory predicts that CAC($c_s$)/CAC($c_s=0$) = 15, 2,382, and 81,600 for $c_s$ = 0.05 M, 0.1 M, and 0.2 M, respectively. Full crossover formulas need to be used in comparing with experiments at moderate $c_s$ values, instead of the asymptotic formulas mentioned here. Nevertheless, such a strong increase in polymer concentration for the onset of slow mode as the salt concentration is increased is qualitatively consistent with experimental data.

It should be noted that the model presented here for the slow mode is analogous to the aggregation phenomenon in gelation of associating uncharged polymers (50–52). In these studies, the focus is the competition between sol-gel transition and liquid–liquid phase separation, whereas the present focus is far away from the macroscopic sol-gel transition. Also, using a combinatorics analysis of associating polymers, the authors of ref. 48 have shown that the system of reversibly associating polymers is correctly described by the Flory theory that is used here. Of particular relevance is the simulation study (49, 50) showing that micelle-like structures form if pairwise association energy is above a threshold value. However, for these structures to contribute dynamically, there is another threshold value beyond which chain dynamics are essentially frozen. Consistent with this picture, the present model assumes that the association energy is sufficiently strong such that micelle-like structures are allowed and at the same time the diffusion time of a chain in the aggregate is longer than the lifetime of the aggregate. Ermoshkin and de la Cruz (53, 54) have extended the theory of ref. 48 to treat polyelectrolyte gels created by divalent ions, with the main focus being sol-gel transition and liquid–liquid phase separation. Because the combinatorics treatment of associating bonds is equivalent to the Flory model, the new element is the concentration fluctuations, which are also treated in other works using replica formalism and charge regularization (55, 56). The relative merits of these advances are yet to be explored. In general, the slow mode treated here occurs at experimental conditions far from the sol-gel transition addressed in the abovementioned theories.

It must be mentioned that the mechanism proposed here for aggregation of similarly charged polymers, mediated by dipoles originating from adsorbed counterions, is of general applicability even beyond the presently treated charged homopolymers in polar solvents.

Materials and Methods

The derivations use well-established theoretical methods in polymer physics. The fast mode is addressed with a combination of the Onsager equation, Rouse–Zimm equations, field theory, and fluctuation–dissipation theory. The slow mode is addressed with a combination of dipole–dipole interaction energy, Flory’s theory of ionic gels, and micellization theory.