Significance
The influenza A M2 channel (AM2) transports protons into the influenza virus upon acid activation. It is an important pharmacological target as well as a prototypical case to study proton conduction through biological channels. The current work provides the most complete computational characterization to date of the physical basis for the acid activation mechanism of the AM2 proton channel. Our results show that lowering the pH value gradually opens the Trp41 gate and decreases the deprotonation barrier of the His37 tetrad, leading to channel activation. Our result also demonstrates that the C-terminal amphipathic helix does not significantly change the proton conduction mechanism in the AM2 transmembrane domain.
Keywords: ion channel, proton conduction, multiscale modeling, QM/MM, free-energy sampling
Abstract
The homotetrameric influenza A M2 channel (AM2) is an acid-activated proton channel responsible for the acidification of the influenza virus interior, an important step in the viral lifecycle. Four histidine residues (His37) in the center of the channel act as a pH sensor and proton selectivity filter. Despite intense study, the pH-dependent activation mechanism of the AM2 channel has to date not been completely understood at a molecular level. Herein we have used multiscale computer simulations to characterize (with explicit proton transport free energy profiles and their associated calculated conductances) the activation mechanism of AM2. All proton transfer steps involved in proton diffusion through the channel, including the protonation/deprotonation of His37, are explicitly considered using classical, quantum, and reactive molecular dynamics methods. The asymmetry of the proton transport free energy profile under high-pH conditions qualitatively explains the rectification behavior of AM2 (i.e., why the inward proton flux is allowed when the pH is low in viral exterior and high in viral interior, but outward proton flux is prohibited when the pH gradient is reversed). Also, in agreement with electrophysiological results, our simulations indicate that the C-terminal amphipathic helix does not significantly change the proton conduction mechanism in the AM2 transmembrane domain; the four transmembrane helices flanking the channel lumen alone seem to determine the proton conduction mechanism.
Visualizing the vectorial flow of protons through membrane proteins is a long-standing challenge in biophysics and chemistry, with manifold implications for understanding bioenergetics, active transport, and proton channel function. Multiscale modeling has become a full partner with experimental structural biology in addressing proton transport (PT), because it can connect the dots between the high-resolution but static pictures obtained from crystallography and the lower-resolution but dynamically informed structures seen in the ensemble averages by NMR and other spectroscopic approaches. In general, multiscale modeling connects three or more disparate but coupled scales of behavior. In the case of PT in proteins, there are usually four pertinent scales: (i) the quantum mechanical scale of bond breaking and bond making inherent in the Grotthuss proton shuttle mechanism; (ii) the molecular scale of the dynamical motions of the protein, membrane, ions, and water molecules; (iii) the “free energy” scale that arises from the statistical ensemble averaging of those molecular motions; and (iv) the “transport” scale that manifests as a macroscopic conductance, with associated gating and other possible behaviors tied to macroscopic experimental variables. The proper and rigorous connection of these various scales, in an overall multiscale computational simulation, is often a substantial challenge. Here, we turn our attention to understanding the mechanism of PT through a small proton channel encoded by an essential gene of influenza viruses (see reviews in refs. 1–4) and we demonstrate the outcomes and insights obtained from such a multiscale simulation.
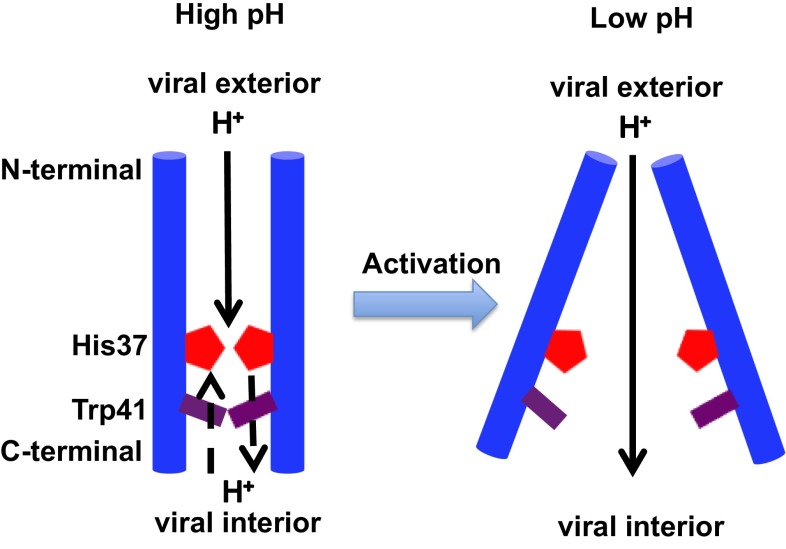
The influenza A M2 channel (AM2) is activated when the pH of the endosomally entrapped virus is lowered, resulting in proton flux into the virus interior, a crucial step in viral replication (5–7). M2 has a single transmembrane helix, which tetramerizes to form the conducting pore. The His37 tetrad (Fig. 1A), located near the center of the M2 transmembrane helix (M2TM), serves as a pH sensor that activates the channel as pH is lowered to near 6.0. His37 can also act as a shuttle that is sequentially protonated and deprotonated as an excess proton transits the activated channel. The Trp41 tetrad, next to the His37 tetrad toward the C terminus and virus interior, functions as a pH-dependent gate for proton conductance (8). The interplay between the protonation state of the His37 tetrad and conformations of the protein backbone and Trp41 side chains is essential for the pH activation mechanism of the channel (9–12). Under high-pH conditions the Trp41 side chains close the C-terminal pore below His37, forming a gate that blocks proton flow through the channel (referred to below as the “Cclosed” state).
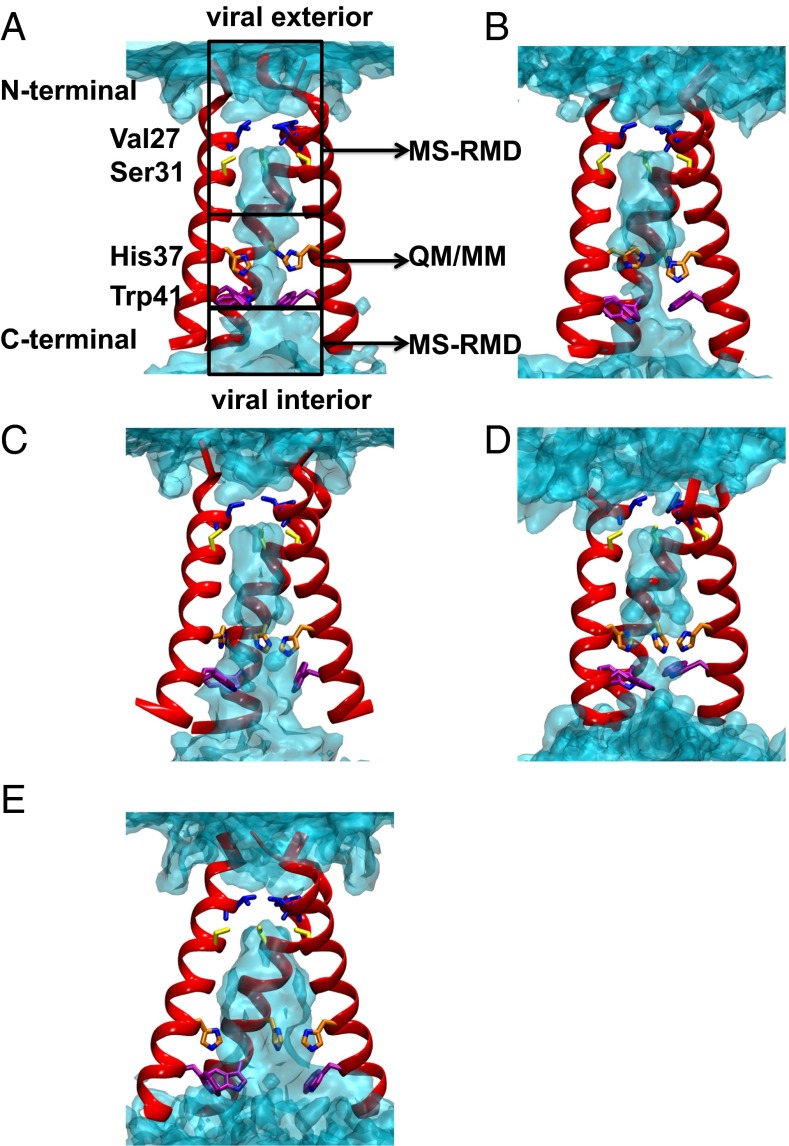
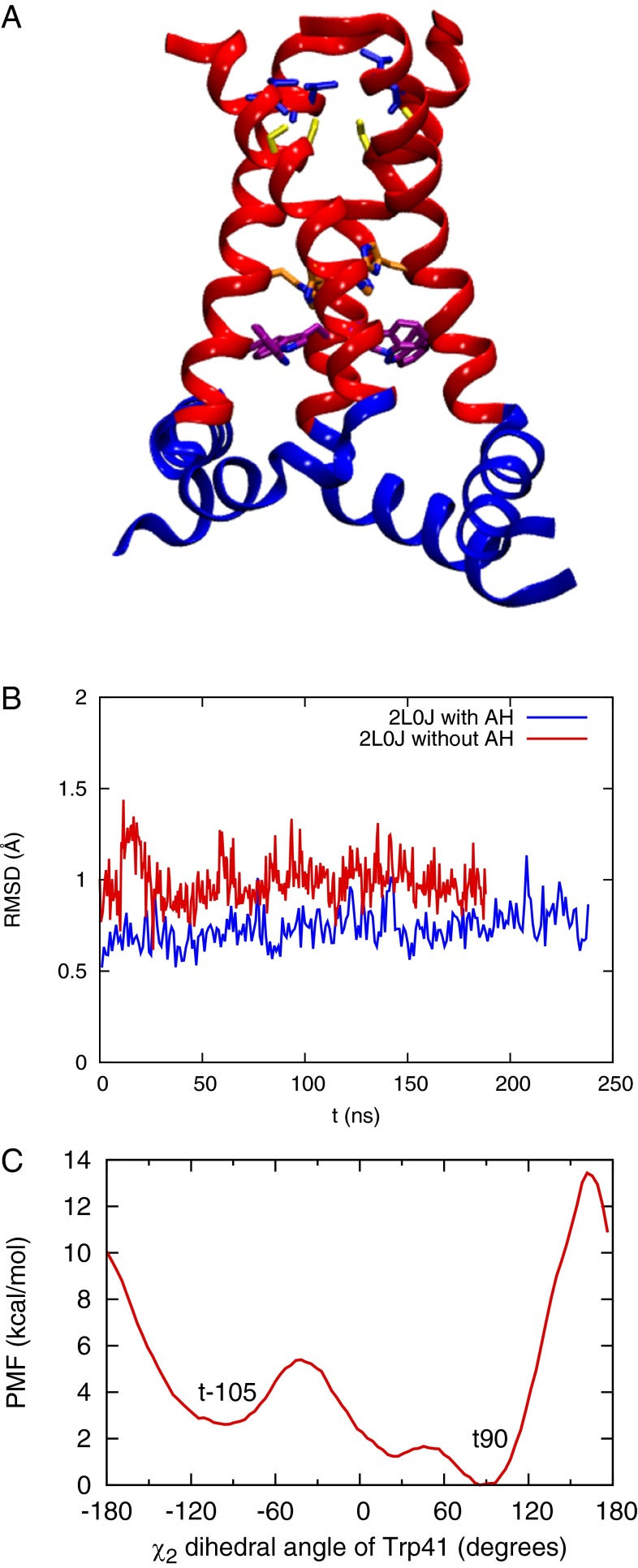
Fig. 1.
(A–C) Equilibrated structures of the Q0, Q1, and Q2 state AM2 channel from initial crystal structure 4QKL, respectively. The backbones of three helices are shown in red, and the side chains of pore-lining residues are shown as sticks. From N terminal to C terminal, Val27, Ser31, His37, and Trp41 are shown in blue, yellow, orange, and purple, respectively. The water oxygen density isosurface calculated from the simulation is shown as light blue shading. The regions sampled by QM/MM and MS-RMD simulations are labeled. One helix is removed for the purpose of clarity. (D) Equilibrated structure of the Q2 state AM2 channel from the initial crystal structure 3LBW (result from ref. 16). (E) Q0 state structure with backbone restrained to the 4QKL structure.
As the pH decreases to ∼6, the protonation state of the His37 tetrad reaches a critical level [likely Q2 (7)] and the channel becomes activated, able to enter the primary proton conduction cycle (4, 9, 13–17). (Herein the notation Qn denotes the state of the His37 tetrad, where n is the number of biprotonated histidines, ranging from 0 to 4.) In this cycle, a proton diffusing down its concentration gradient through the activated M2 channel transiently protonates His37, generating the Q3 state (assuming Q2 as the activated resting state). The high density of positive charge in the channel destabilizes the Cclosed state sufficiently to open an aqueous conduction path (8, 9, 16, 18). Diffusion of a proton into the interior of the virus could return the His37 tetrad back to the Q2 state, with accompanying conformational relaxation and reequilibration of the His37 tautomers, thereby completing the cycle (8, 13, 18).
Structures determined using X-ray crystallography, solution NMR, and solid-state NMR (SSNMR) support this acid-activated transporter-like mechanism (9, 10, 18–26). Near neutral pH the channel is closed in the Cclosed conformation (Fig. 1) with tight packing of His37 and Trp41 (10, 19, 23, 26). At lower pH the channel is more dynamic (26–28), which has precluded structure determination by solution or SSNMR. However, a series of crystallographic structures of the Copen states (Fig. 1) (23–25) have been determined, including high-resolution structures of the TM domain crystallized from lipidic cubic phase (24, 25). The Copen forms seen in these crystal structures (23–25) show more structural heterogeneity than the Cclosed forms, despite the Cclosed form’s having been crystallized over a range of pH values. These findings suggest that the allosteric coupling between protonation of His37 and opening of the C-terminal region is not absolute. In other words, a significant fraction of the protein in solution exists in multiple conformations, which can be captured within the crystal lattice over a range of pH values. This conclusion is in agreement with NMR measurements, which show a pH-dependent population of multiple conformational states (10–12, 26, 29, 30), as well as molecular dynamics (MD) simulations, which show graded increases in dynamics with increasing protonation state (16, 18, 31–38).
Classical MD has been very useful for examining the conformational relaxation that occurs following a change in the protonation state of the His37 tetrad during activation and conduction. However, a significant assumption of these classical MD analyses has been that the conformational changes are both computationally reversible and can be captured on the 100-ns to microsecond time scales that are readily accessible by MD (18, 31–37). Given the availability of a high-resolution structure for both the Copen and Cclosed forms of the protein it is now possible to determine the reversibility of the calculations and to determine whether the starting configurations substantially alter the conformational ensemble and computed energetics of proton translocation through the channel.
The major rate-limiting step for conduction (defined as conductance × [H+]) involves diffusion of protons to His37 at low permeant ion concentration (high pH). As the pH is lowered below the midpoint of the pH/flux curve, the chemical step of proton dissociation from His37 becomes rate-limiting (4, 16, 39). Because the conduction process involves bond making and breaking steps associated with excess proton diffusion (Grotthuss hopping) through water wires as well as protonation and deprotonation of His37, it is not possible to address the conduction mechanism directly using classical MD. However, as noted earlier the proton conduction process can be studied via multiscale simulation. For example, in our recent multiscale simulation study (16) we reported that during the transition from intermediate to low pH the C-terminal helices of the channel expand and the hydration level in the C-terminal pore is increased. This decreases the His37 deprotonation barrier and increases the proton conductance at low pH, which partially explains the acid activation mechanism of the channel. However, the acid activation mechanism for the transition from high to intermediate pH was not investigated in ref. 16. We note that recent experimental work by Cross and coworkers (27) confirmed (but did not cite) some of the results from ref. 16, such as the gating role of Trp41 and rapid equilibration of protons between His37 and the viral exterior originally observed electrophysiologically (8, 18).
Herein, we build upon our previous simulations of explicit PT in AM2 (16) and use recently published crystal structures (24) to probe the coupled scales and detailed mechanism of the AM2 acid activation behavior for the transition from high to intermediate pH. We have performed multiscale simulations starting from the high-pH room-temperature crystal structure in ref. 24 [Protein Data Bank (PDB) ID code 4QKL]. Our results show that, in lipid bilayers, the channel closes its C-terminal helices under high-pH conditions. Using permeation theory, we show that the resulting large deprotonation barrier of the His37 tetrad blocks the channel. Lowering the pH value increases the charge state of the His37 tetrad, which gradually opens the Trp41 gate and increases its hydration. This increases the channel conductance and leads to activation of the AM2 channel.
We also study here the importance of including the amphipathic helices of the AM2 channel by performing simulations starting from an earlier NMR structure (PDB ID code 2L0J) (10), which includes the transmembrane domain (M2TM; residues 26–46) and the amphipathic helices (residues 22–62 in total). The C-terminal amphipathic helix of M2 is essential for endosomal sorting complex required for transcription (ESCRT)-independent virus scission and filamentous virus formation (40), acting to stabilize the negative Gaussian curvature associated with the budding intermediate (41). Although the sequence and amphipathic character of this helix are essential to these processes, mutations that affect these parameters do not have a measurable effect on the conductance of the channel (41). Indeed, this C-terminal helix can be deleted entirely without greatly influencing the PT properties of the channel (42). This finding is also consistent with SSNMR structures of the channel (10, 26, 43), which show the amphipathic helix radiating away from the pore of the channel. For this reason our previous simulations (16, 34) and many other computational and experimental studies (9, 11, 30, 32, 44–46) have focused on the M2TM domain to investigate the AM2 proton conduction mechanism. However, it has recently been suggested, based on changes in the NMR signal, that the M2TM and full-length AM2 protein have different structure, dynamics, and function (including PT mechanism) (27). This rationale apparently led those authors to disregard previous work on the M2TM (16), despite the fact that it predicted several of their findings. Moreover, because the influence of the amphipathic helices has not yet been explicitly tested in simulations, we sought to verify whether they are or are not important for PT in the AM2 channel. Here we provide computational evidence confirming the structural and functional measurements (9, 11, 30, 32, 44–46) and demonstrating that the presence of these amphipathic helices does not significantly change the predicted conductivity of the channel.
Results
Our results are organized as follows. First, we discuss the structure of the AM2 channel under high-pH conditions obtained from classical MD simulations starting from the 4QKL crystal structure. Second, we discuss the pH activation mechanism of the AM2 channel based on the free energy profiles for the explicit PT across the channel obtained from a multiscale bridging of multiscale reactive molecular dynamics (MS-RMD) and quantum mechanics/molecular mechanics (QM/MM) MD simulations (Methods and Simulation Details).
AM2 Has Closed C-Terminal Helices Under High-pH Conditions.
The M2TM crystal structure 4QKL (residues 22–46), resolved at room temperature and high pH (pH 8.0) in the lipidic cubic phase, features open C-terminal helices. In contrast, the M2TM G34A mutant crystal structure 3LBW (residues 25–46) was resolved at an intermediate pH (pH 6.5) in detergent and features more closed C-terminal helices (Fig. 1D). Previous wild-type simulations starting from the 3LBW structure showed that the protein structure is stable in lipid bilayer at room temperature for the Q1 and Q2 states, which corresponds to the high to intermediate pH range (9). It was also shown by previous simulations that the C-terminal helices start to open in the Q3 state, which corresponds to an intermediate to low pH range (9, 16). Therefore, it was necessary to also test whether or not the 4QKL structure remains stable in the lipid bilayer under high to intermediate pH conditions. To do so, we inserted the 4QKL crystal structure into a 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC) lipid bilayer and equilibrated the protein structure for ∼500 ns for the Q0 state. Following this simulation, we increased the charge state of the His37 tetrad and equilibrated the system again for the Q1 and Q2 states, which mimics the activation of the channel upon lowering the pH to an intermediate value.
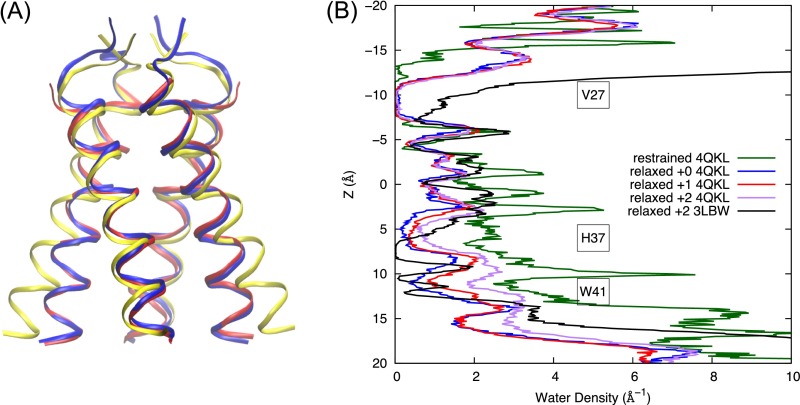
In the Q0 state, the C-terminal helices transition from the Copen to a canonical Cclosed conformation, with the protein backbone resembling that of the 3LBW crystal structure (Figs. S1A and S2A). The closing of the C-terminal helices brings the His37 and Trp41 side chains closer together and dehydrates the region between His37 and Trp41. The dehydration is dramatic when we compare the water density profile for the equilibrated Q0 state structure with that in which the backbone Cα atoms are restrained to the 4QKL structure (Fig. 1 A and E). In the C-terminal half of the channel (3 Å < z <16 Å) the pore hydration level is significantly reduced for the unrestrained equilibrated protein, compared with that with protein backbone restrained to the 4QKL structure (Fig. 1A vs. Fig. 1E). In the Q1 and Q2 states, the pore hydration is slightly increased, which induces larger backbone conformational flexibility (Fig. 1 B and C). However, the hydration level in the C-terminal pore is still lower than when the backbone is restrained to the 4QKL structure, especially in the His37 and Trp41 regions (Fig. 1E). Thus, 4QKL structure may represent a limiting case of a fully dilated Copen conformation that was trapped in the lipid cubic phase during crystallization. The differences in the Q2 water density profiles near the N-terminal helices between the 3LBW and 4QKL equilibrated structures (black and purple curves in Fig. S2B, respectively) are likely due to the fact that the 4QKL structure has three more residues (22–24) in the N-terminal region than the 3LBW. This addition causes the N-terminal helices in the equilibrated 4QKL structure to be more closely packed than in the equilibrated 3LBW structure in the Q2 state, resulting in lower water density in the N terminal for the former. This difference in the N-terminal packing propagates to the C-terminal helices, making the C-terminal helices in the equilibrated 4QKL structure slightly more open than those in the equilibrated 3LBW structure in the Q2 state (Fig. 1C vs. Fig. 1D). Regardless, the low hydration level in the C-terminal pore obtained after equilibration in a lipid bilayer at the high-pH condition (Q0 and Q1 states), as well as the close packing of the Trp41 side chains, contribute to large free energy barriers for His37 deprotonation, as discussed below.
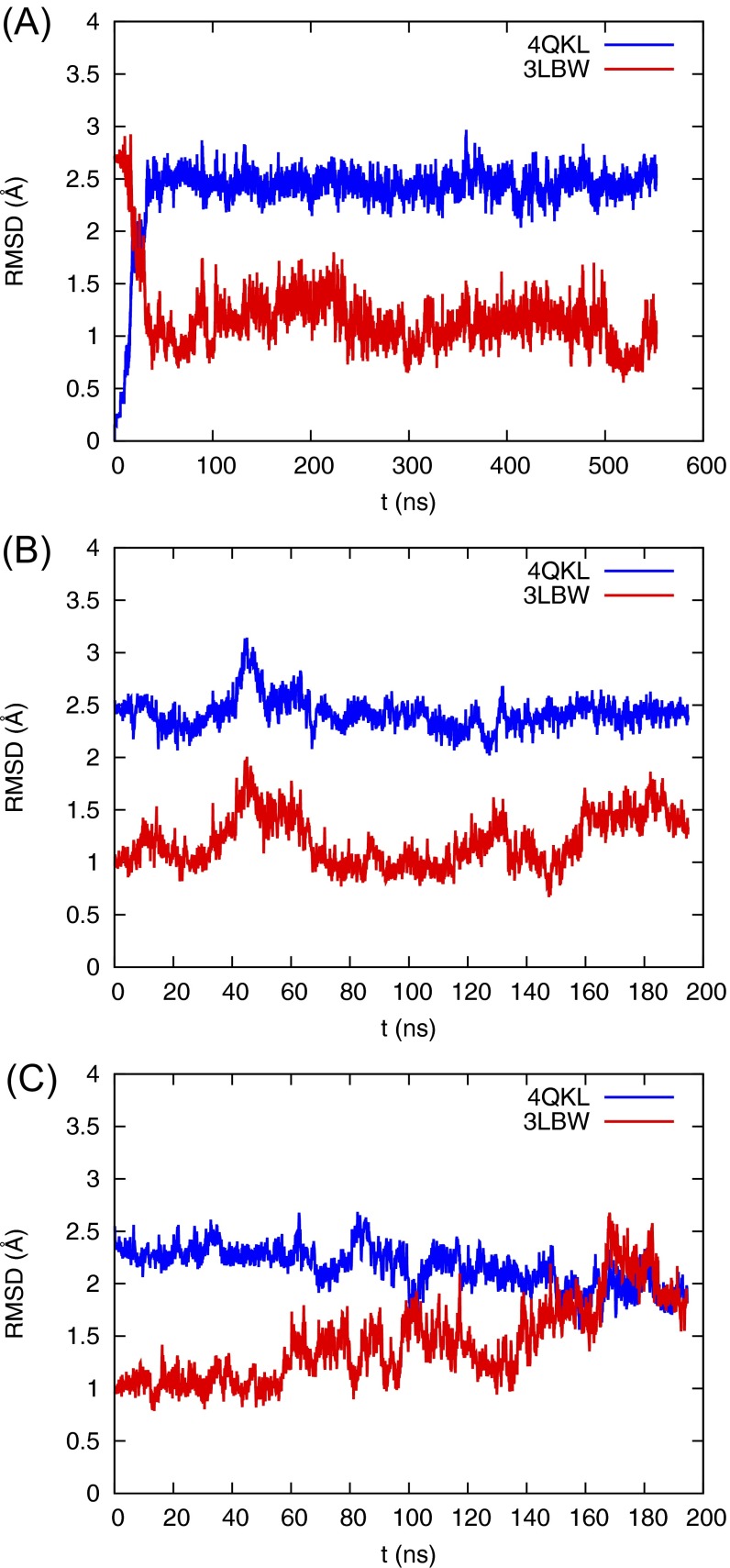
Fig. S1.
(A–C) rmsd of the Cα atoms of M2TM channel compared with crystal structures 4QKL (blue) and 3LBW (red) for (A) the Q0 state starting from the 4QKL crystal structure, (B) the Q1 state starting from the equilibrated Q0 state, and (C) the Q2 state starting from the equilibrated Q0 state.
Fig. S2.
(A) After equilibration in the lipid bilayer, the Q0 state of the AM2 channel relaxes from the initial crystal structure (yellow ribbon, PDB ID code 4QKL) that features open C-terminal helices to a structure that features a more closed C-terminal region (blue ribbon). The equilibrated structure is similar to the crystal structure 3LBW (red ribbon). (B) Water density profiles across the M2 channel for the Q0 state with the protein backbone restrained to the 4QKL structure (green), for the Q0, Q1, and Q2 states with backbones equilibrated in the membrane starting from crystal structure 4QKL (blue, red, and purple, respectively) and the Q2 state for simulations starting from crystal structure 3LBW (black).
AM2 Channel Has a Low Conduction Rate in the Inactivated Conformations Present at High pH.
We computed the free energy profile (or potential of mean force, PMF) for the charge defect associated with an excess proton to travel through the M2 channel (Fig. 2), including (i) diffusion from the N-terminal end of the pore into the outward-facing aqueous channel, (ii) protonation of the His37 tetrad, (iii) dissociation from the His37 tetrad, and (iv) diffusion to the C-terminal end of the pore. Thus, the +0 PMF describes the process where the Q0 state His37 tetrad is protonated by an excess proton from the viral exterior to transiently form the Q1 state, followed by a deprotonation of the excess proton to the viral interior to regenerate the Q0 state. The PMF was calculated as a function of a collective variable (hereafter referred to as the “CV”) that tracks the progress of the excess proton center of excess charge (CEC) during the PT process (Methods and Simulation Details). As the proton leaves the pore and enters into bulk solution on either side of the membrane, a cylindrical restraint (47) is used to quantify the free energy obtained by releasing the excess proton to the bulk proton concentration. Thus, the proton activity in bulk solution (i.e., pH), whether symmetric or asymmetric, does not enter into the calculation. Instead, these variables are considered via electropermeation theory following the construction of the PMF.
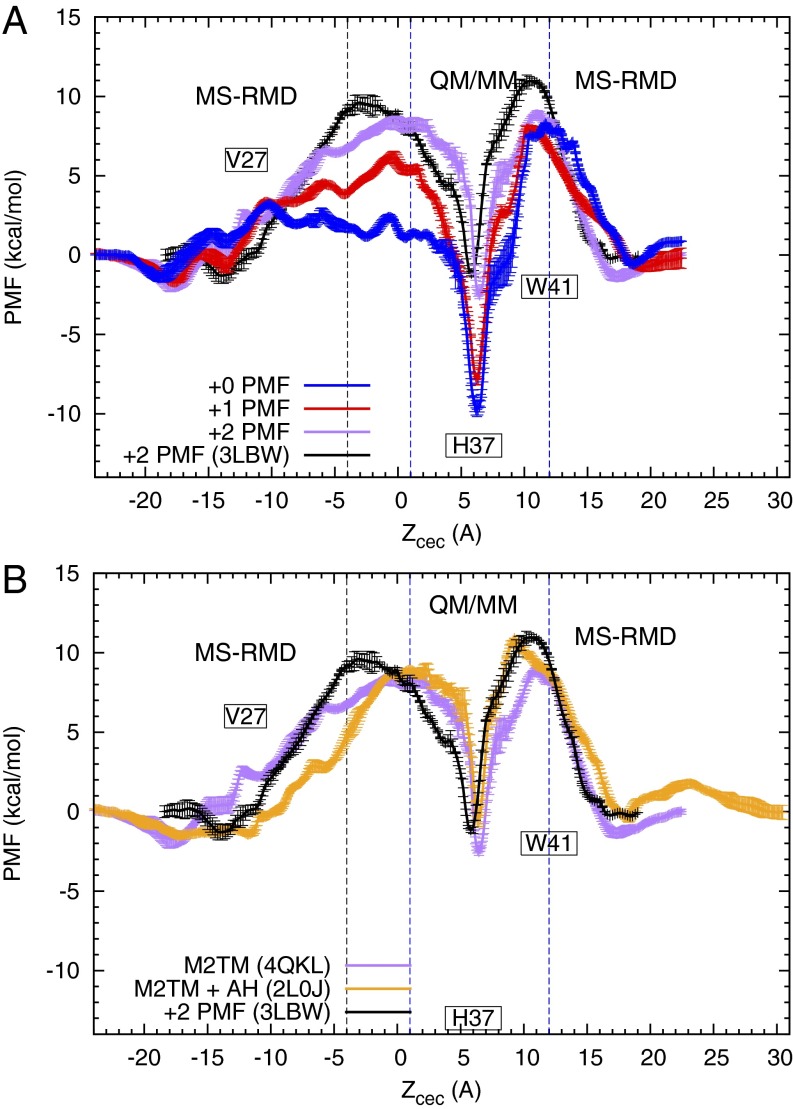
Fig. 2.
Free energy profiles (PMFs) for PT through the influenza A M2 channel. (A) The blue, red, and purple curves are the +0, +1, and +2 PMFs (defined in the text), respectively, calculated from simulations using 4QKL (without amphipathic helices) as the initial structure. The black curve is the +2 PMF calculated from simulations using 3LBW as initial structure and has been previously reported in ref. 16. The His37 deprotonation barrier is seen to be lowered in the +2 PMFs, and the minimum in the His37 tetrad is elevated, suggesting a pH-dependent activation mechanism. (B) The orange curve is the +2 PMF calculated from simulations using 2L0J (with amphipathic helices) as initial structure. The black and purple curves are the same as those in A. For all of the +2 PMFs, the similarities in the depth of the minima around His37 and the barriers of His37 deprotonation indicate that the proton conduction mechanism is not changed significantly by the amphipathic helices or by the initial structure used, as long as the protein is first well-equilibrated in the membrane.
The PMF profiles for the Q0 and Q1 states, which predominate at high pH, show that the protein is not sufficiently activated in these states to enable efficient proton flux. A proton passing through the channel in the +0 protonation state is influenced by a deep local free energy minimum, indicating that there is a strong preference for the proton to reside on His37 vs. other regions of the pore. The barrier for His37 deprotonating the excess proton to the viral interior (CV from 6 Å to 11 Å) is more than 15 kcal/mol. Application of permeation and kinetic theories of proton conduction to this PMF predicts a maximal possible conduction at a hypothetical saturating proton concentration for a given initial charge state of His37 (Q0 and Q1 for +0 and +1 PMFs, respectively). They are well below the experimentally measured conductance at intermediate pH when the AM2 channel is activated (Table 1). Thus, this conformational ensemble is not fit for proton conduction. Similar observations are also true for the +1 PMF. In both cases (i.e., the Q0 and Q1 states) the PMFs and calculated conductances indicate that the channel is inactive under high-pH conditions.
Table 1.
Comparison of calculated AM2 channel proton conductance from the simulations for the +0, +1, and +2 processes and experiments (10, 52, 53)
| PT process | Conductance, fs | His37 deprotonation rates, ms−1 | |
| Forward | Backward | ||
| +0 | 8.9 × 10−4 | 3.1 × 10−4 | 1.3 |
| +1 | 5.9 × 10−2 | 2.3 × 10−2 | 4.6 × 10−1 |
| +2 | 7.7 | 3.0 × 101 | 7.1 × 101 |
| +2 (with amphipathic helices) | 1.0 | 3.5 × 101 | 8.1 × 102 |
| +2 (3LBW)* | 1.2 | 7.0 | 6.4 × 101 |
| Experiment (intermediate pH)† | 0.4–4 | NA | NA |
Also shown are the estimated rates of deprotonation of the His37 in the various states in the two possible directions, based on transition state theory estimates (Supporting Information). NA, not assessed.
From ref. 16.
The large deprotonation barrier of His37 for the Q0 and Q1 states is caused by the lack of stable hydration between the His37 and Trp41 tetrads (Fig. 1 A and B). The close packing of the Trp41 side chains at high pH (Q0 and Q1 states) reduces the number of water molecules accessible for His37 deprotonation, causing a substantial barrier for the deprotonation of His37 to the first solvation shell of water molecules toward the viral interior (CV from 6 Å to 8 Å in Fig. 2A). Steric hindrance of the Trp41 side chains further increases the barrier when the hydrated excess proton moves from the first solvation shell to the second shell below His37 (CV from 8 Å to 11 Å). In addition to the high deprotonation barrier, the free energy minima in the His37 tetrad region are deep relative to bulk (∼ −10 kcal/mol) in the +0 and +1 PMFs, which is consistent with the estimated pKa values for the first two His37 residues (∼7.6 and 6.8 according to ref. 30). Thus, it is more energetically favorable for the His37 tetrad to bind the incoming proton in high-pH conditions (i.e., Q0 or Q1 states) than at low pH (i.e., Q2 state). This is in agreement with the higher pKa values for the first and second protonation of the His37 tetrad than the third and fourth (7, 30, 48, 49). Charge delocalization of the excess proton among the four His37 residues contributes to the stability of protonation for the Q0 and Q1 states.
The maximum proton conductance, calculated from Poisson–Nernst–Planck (PNP) electrodiffusion theory (Methods and Simulation Details), and the rates for His37 deprotonation in both directions of the channel, estimated from transition state theory (Supporting Information), are listed in Table 2. Differences between the total conductance and rate-limiting His37 deprotonation steps are predominantly due to the barrier for PT from the viral exterior to the His37 tetrad. An additional factor, though its impact is less, is the influence of varying proton diffusivity across the regions of the PMF, which is included in the conductance calculation but not included in rate calculations. Additional insight is gained by considering the rates of His37 deprotonation to just the first solvation shell, which are also listed in Table 2. For the Q0 and Q1 states, the rate constants for the forward proton deprotonation to the first solvation shell are much slower than those for the overall forward deprotonation. This is because the overall forward deprotonation process also includes PT from the hydronium below His37 through the Trp41 residues. This step results in additional barrier and much slower forward deprotonation rate in the Q0 and Q1 states (Tables 1 and 2).
Table 2.
Estimated rates of deprotonation of the His37 to the first solvation shell in the various states in the two possible directions, from transition state theory estimates (Supporting Information)
| PT process | His37 deprotonation rate, ms−1 | |
| Forward | Backward | |
| +0 | 4.1 × 101 | 3.8 × 101 |
| +1 | 5.0 × 101 | 2.0 × 101 |
| +2 | 3.1 × 102 | 1.8 × 102 |
| +2 (with amphipathic helices) | 6.7 × 101 | 1.4 × 103 |
| +2 (3LBW) | 2.2 × 102 | 1.7 × 103 |
| Experiment (intermediate pH)* | ∼4.5 × 102 | |
From ref. 30.
Mechanism for Rectification.
A particularly important and interesting feature of the PMFs in Fig. 2A is the pronounced asymmetry in the +0 PMF. The barriers for PT between the His37 tetrad and the viral exterior and interior are quite different. In particular, the forward protonation barrier (PT from the viral exterior to His37) is small (∼4.7 kcal/mol) relative to the forward deprotonation barrier (PT from His37 to the viral interior; ∼18.0 kcal/mol), whereas the backward protonation barrier (PT from viral interior to His37) is larger (∼8.9 kcal/mol) relative to the backward deprotonation barrier (∼12.9 kcal/mol). Including the approximate time for diffusion of an excess proton to the channel entrance slows down the kon (protonation) rates. This can be equivalently expressed in the context of transition state theory by increasing the protonation barriers. For example at a pH of 4.9 [the measured pKa of the third His37 residue (30), which should correspond to the pH at which the channel activates] diffusion would effectively add 6.7 kcal/mol () to the protonation barrier in either direction. Thus, the forward effective protonation barrier (∼11.4 kcal/mol) is lower than the forward deprotonation barrier (∼18.0 kcal/mol), such that kon outcompetes koff and the His37 tetrad jumps from the +0 to the +1 charge state. The equivalent happens for the +1 to +2 transition and the channel activates when the pH outside of the virus is low. In the opposite direction, however, the backward protonation barrier (∼15.6 kcal/mol) is larger than the deprotonation barrier (∼12.9 kcal/mol), such that koff outcompetes kon, and the channel remains in the +0 charge state. Although this introduces outward proton flow, it would be below the detectable limit. Thus, the channel activates and conducts inward current when pHout is low and pHin is high but stays inactive and does not conduct outward current when pHin is low and pHout is high. This property is called rectification (8, 50). Although the +0 PMF qualitatively explains the inward rectification mechanism, we note that the calculated difference between the backward kon and koff could be larger. This could be due to the calculated backward protonation barrier in the +0 PMF (∼8.9 kcal/mol) being underestimated, possibly due to an incompletely equilibrated transmembrane structure and/or from errors in the force-field representation of the Trp41 side-chain interactions. A Q0 state with an even more tightly packed Trp41 tetrad would likely increase the backward protonation barrier, thereby more effectively locking the system in the Q0 state and blocking outward conduction. Nevertheless, the asymmetry in the calculated +0 PMF is clearly evident and is qualitatively consistent with previous experimental results regarding the rectification behavior (8, 50).
It is also interesting to note that the M2 channel in the Weybridge strain of influenza virus (WM2) exhibits the rectification mentioned above, but the M2 in the Rostock strain (RM2) does not (50). This is because the RM2 has a D44N mutation compared with WM2. This mutation has the effect of breaking the hydrogen bond between Trp41 and Asp44 in WM2, opening the Trp41 gate at high pH value (18). Therefore, in RM2 the proton can reach His37 more easily from viral interior, eliminating the rectification.
Mechanism of Proton Conduction Through the Activated, Q2 State.
In the +2 PMF, the doubly protonated His37 tetrad is transiently protonated by another excess proton from the viral exterior to generate the Q3 state, then it deprotonates a proton to the viral interior to regenerate the Q2 state. The His37 deprotonation barrier for the Q2 state is decreased to ∼12 kcal/mol, (Fig. 2A) and the proton conductance is increased accordingly (Table 1). The rates for His37 deprotonation to the first solvation shell calculated from the +2 PMF are in good agreement with the proton exchange rate between water and histidine in intermediate pH condition measured by NMR experiment (30) (Table 2). The rates are faster than those in the Q0 and Q1 state, which is consistent with the experimental finding that high pH suppresses the histidine–water proton exchange rate in the S31N mutant (51). The conductance is in reasonable agreement with our previous result (16) and the experimental values (10, 52, 53). The difference between the present +2 PMF compared with our prior result is likely due to the three extra residues in the N-terminal helices in the new structure, which cause conformational changes in the backbone structure in both the N- and C-terminal regions (Fig. 1C vs. Fig. 1D), as discussed above.
The decrease in the His37 deprotonation barrier in the +2 PMF can be attributed to increased solvation between His37 and Trp41 (Fig. 1C), as well as increased flexibility of the Trp41 side chains. The more expanded C-terminal helices provide more space for the rotational motion of the Trp41 residues, and as a result the barrier for the excess proton to pass through the Trp41 is reduced (Fig. 2A, CV from 8 Å to 11 Å). This is consistent with the experimental finding that the Trp41 side-chain rotations are less restricted at lower pH (12). Importantly, as seen in Fig. 1C the free energy minimum in the His37 tetrad region for the Q2 state is raised compared with the +0 and +1 PMFs, which is consistent with the lower pKa value for the third His37 residue. The rise of the free energy minimum at the His37 tetrad is caused by the less favorable electrostatic interactions between the His37 tetrad and the excess proton in the Q2 state compared with Q0 and Q1 states. Specifically, upon increasing the charge of His37 tetrad from +0 to +2 the barrier from the viral exterior to His37 increases due to larger electrostatic repulsion between the excess proton and the His37 tetrad. At the same time, the barrier from His37 to the viral interior is decreased due to less charge delocalization in the more positively charged His37 tetrad. The combined effect is a shallower free energy minimum at His37 in the Q2 state.
AM2 Channel Activation Mechanism.
All of the above results and observations reveal the physical mechanism by which the M2 channel is activated in the Q2 state upon a lowering of pH. Although the forward PT barrier from viral exterior to His37 is increased in the Q2 state due to the larger electrostatic repulsion between His37 tetrad and the incoming proton, the forward PT barrier from His37 to viral interior is reduced due to the increased electrostatic repulsion between the His37 tetrad and the leaving excess proton, as well as the increased hydration and conformational flexibility of the Trp41 tetrad. The combined effect facilitates PT to the viral interior and enables proton conductance and channel activation by acidification (see Fig. 4). In addition, the solvation properties and conformation of the Val27 region remain almost the same upon acid activation from Q0 to Q2 state, whereas in the Q3 state the Val27 region is a bit more constricted. This is somewhat consistent with the transporter model proposed in ref. 33. Overall, our current mechanism is consistent with some of the predictions made in refs. 33 and 54.
Fig. 4.
Acid activation mechanism of the AM2 channel.
Effect of Amphipathic Helices.
Because the full-length M2 protein includes both M2TM and the amphipathic helices, as noted earlier we also investigated the influence of the amphipathic helices on the proton conductance mechanism for M2TM with the helices included in the calculations.
The +2 PMF for the system with amphipathic helices equilibrated from the modified NMR structure 2L0J (10) (discussed below) is, in general, very similar to that of the systems without amphipathic helices equilibrated from the 4QKL and 3LBW structures (Fig. 2B). Specifically, the His37 deprotonation process, which is the rate-limiting step, has a similar barrier in both cases, resulting in similar calculated conductances. Therefore, the existence of the amphipathic helices does not significantly influence the proton conductance mechanism. This is in line with the experimental measurements showing that the proton conductance is similar for the protein construct having only the M2TM and the construct having both the M2TM and the amphipathic helices (42).
Rotamer of the Trp41 Residue.
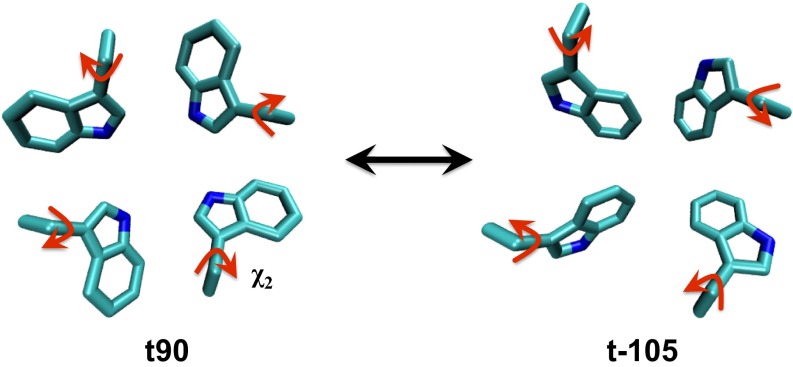
For the equilibration simulation starting from the NMR structure 2L0J (10), which includes both the M2TM and amphipathic helices, the structure stabilized only after adjusting the Trp41 side chains to a t90 rotamer configuration (Fig. 3 A and B and Fig. S3) (the equilibration starting from the t-105 rotamer of Trp41 because in the NMR structure 2L0J does not yield a stable protein structure within 200-ns simulation). Our decision to change to the t90 rotamer of Trp41 is supported by crystal structures (9, 24, 55), SSNMR measurements (12, 56), as well as long all-atom MD simulations (32), the latter showing that all four Trp41 residues flipped from the t-105 to the t90 rotamer after 500 ns. To further address this issue, we also calculated the PMF (Fig. 3C) for the rotation of the χ2 dihedral angle of one of the four Trp41 residues in the lipid bilayer, restraining the backbone of the M2TM to the initial 2L0J structure. The PMF in the figure indicates that the minimum at the t90 rotamer is more stable than that at the t-105 rotamer, which further supports our choice of the t90 rotamer. Once the t90 rotamers were in place, our simulations in the membrane were stable (Fig. 3 A and B). In addition, after removing the amphipathic helices from 2L0J structure and equilibrating only the M2TM in the membrane, the M2TM structure remained very similar to the initial 2L0J structure, suggesting that the amphipathic helices do not significantly change the M2TM structure.
Fig. 3.
(A) Equilibrated structure of the Q2 state starting from the initial crystal structure 2L0J. The M2TM and amphipathic helices are in red and blue, respectively. The Val27, Ser31, His37, and Trp41 are shown as sticks in blue, yellow, orange, and purple, respectively. (B) rmsd of the Cα atoms of the AM2 M2TM during the equilibration of NMR structure 2L0J (with amphipathic helices, blue) and the truncated 2L0J structure (without amphipathic helices, red) in a lipid bilayer. The reference structure is the M2TM of the 2L0J structure. The rmsd values indicate that the M2TM structure is stable and similar to the initial structure, both in the presence and absence of the amphipathic helices. This suggests that the amphipathic helices do no significantly change the structure of the M2TM structure in a POPC membrane. (C) The free energy profile for the rotation of the χ2 angle of one of the four Trp41 residues in the 2L0J structure in a lipid bilayer. The regions of the PMF corresponding to the t90 rotamer (in the crystal structures 3LBW and 4QKL) and t-105 rotamer (in the NMR structure 2L0J) are shown. The free energy for the t90 rotamer is ∼3 kcal/mol lower than that of the t-105 rotamer with a ∼2 kcal/mol barrier for conversion, indicating that the t90 rotamer is energetically more favorable than the t-105 rotamer in the 2L0J structure.
Fig. S3.
Illustration of the Trp41 t90 and t-105 rotamers from the top (N-terminal) view of the AM2 channel.
Molecular-Level Behavior of the His37 Tetrad.
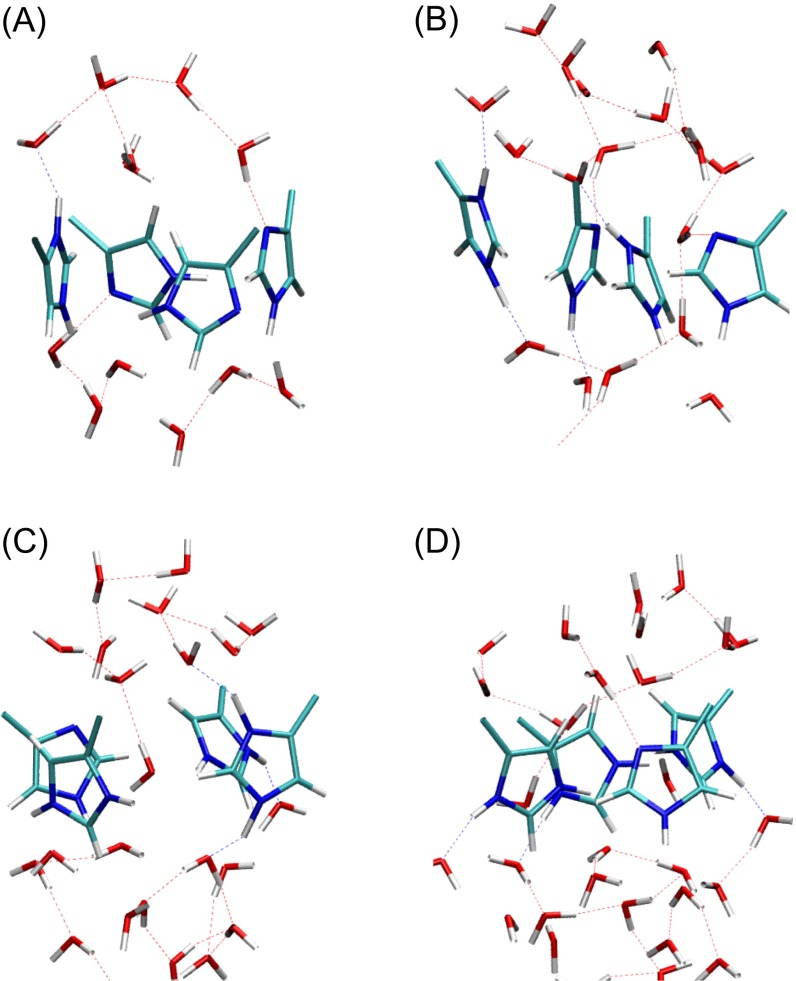
Finally, we comment on the hydrogen bonding in the His37 tetrad before and during proton permeation. In the QM/MM simulations of the +0 and +1 PMFs there are no direct hydrogen bonds between the His37 residues, as suggested by Cross and coworkers (10). This is consistent with the experimental finding of Hong et al. (57) that the His37 residues form hydrogen bond only with water instead of with one another. Typical snapshots of the configuration of the His37 tetrad and solvating water molecules are shown in Fig. S4 A and B. In the QM/MM simulations of the +2 PMFs we again did not observe direct hydrogen bonds between the His37 residues. In the 2L0J structure, the four His37 residues in the Q2 state have a dimer of dimers configuration via direct hydrogen bonds between His37 residues (10). However, it should be emphasized that this geometry resulted from hypothetical distance restraints, and there is no direct experimental spectroscopic evidence for the interaction. After only 100 ns of classical MD equilibration with the t90 rotamer of Trp41 all direct histidine–histidine hydrogen bonds are broken, and only water–histidine hydrogen bonds remain. Typical snapshots of the configuration of the His37 tetrad and solvating water molecules are shown in Fig. S4 C and D. The difference in the His37 hydrogen-bonding patterns between the simulation and NMR structures could be due to the difference in the Trp41 rotamer in the two structures, as discussed above.
Fig. S4.
Typical configurations of the His37 tetrad and its surrounding solvation structure corresponding to the free energy minimum in the (A) +0 PMF, (B) +1 PMF, (C) +2 PMF, and (D) +2 PMF with amphipathic helices. The hydrogen bonds between water molecules as well as those between water molecules and His37 tetrad are depicted as dotted lines. No direct hydrogen bonds between histidine residues are observed in any of the structures.
As the proton shuttles through the His37 tetrad, we observe in the QM/MM MD simulations the His37 residues undergo interconversion among τ, π, and cationic states via the protonation of a delta-N and deprotonation of an epsilon-N. Tautomer exchange within a His37 residue would require a very high energy unprotonated/negatively charged intermediate and is not expected to happen. However, interresidue tautomerization is likely given the water-mediated hydrogen bonding between τ and π tautomers. This is in agreement with the mechanism proposed by Williams et al. (figure 10 in ref. 51) based on their SSNMR measurements.
Conclusions
We find that under high-pH conditions the AM2 C-terminal helices adopt a Cclosed conformation. The closed Trp41 tetrad dehydrates the His37 tetrad and increases the His37 deprotonation barrier, thus blocking proton conduction at high pH. In contrast, the low charge state of the His37 tetrad at high pH reduces the electrostatic repulsion with the excess proton, lowering the barrier for proton permeation from the viral exterior. Thus, the protonation of His37 occurs more readily from the viral exterior than from the viral interior in the low charge state of His37 tetrad, and this asymmetry at least partly explains the rectification of proton flow observed in experiments (8, 50). As the pH decreases to intermediate values the positive charge on the His37 tetrad increases and the C-terminal helices are opened and more hydrated. This lowers the His37 deprotonation barrier and increases the proton conductance, thus activating the channel. Our previous multiscale simulation (16) has shown that as the pH further decreases from intermediate to low value (Q2 to Q3 state) the channel expansion and increased pore water dynamics further increase the proton conductance, despite the increased electrostatic repulsion between the His37 tetrad and the incoming proton. In combination with our previous work (16), the present results provide the most complete picture to date of the physical basis for the acid activation mechanism of the AM2 proton channel. The activation mechanism is summarized in Fig. 4. Additionally, our results indicate that the amphipathic helices do not significantly influence the proton conductance mechanism of the AM2 channel or its quantitative value.
Methods and Simulation Details
Classical MD Simulations.
The crystal structure resolved at room temperature and high pH (4QKL) (24) and the NMR structure obtained at intermediate pH (2L0J) (10) were used as initial structures for classical MD simulations. For the simulations starting from crystal structure the protein was inserted into a lipid bilayer membrane consisting of 170 POPC molecules and then solvated by a 25-Å-thick layer of water molecules on each side (Fig. 1A). Although a pure POPC bilayer is lacking the lipid heterogeneity of a real membrane, it is a reasonable choice for the sake of consistency [POPC has been has been used in most of the recently published M2 simulations (9, 16, 24)) and a widely used component of virus-mimetic membranes in experiments (12, 42, 49, 51)]. The protein’s principal axes were aligned with the z axis, and the lipid bilayer was aligned with the x–y plane. For the equilibration of Q0 state system all four His37 residues were singly protonated at the Nε atom (10, 11). In the first stage of equilibration, 100 kcal·mol−1·Å−2 harmonic restraints were first applied to the protein backbone Cα atoms and then gradually reduced to 0.01 kcal·mol−1·Å−2 over 30 ns, while the lipid and water molecules relaxed to stabilize the protein–lipid bilayer packing. Next, the harmonic restraints were removed, allowing all molecules in the system to relax for another 5 ns. Equilibration was followed by ∼500 ns of MD simulation. Equilibrations of the Q1 and Q2 state systems were initiated from the final structure of the Q0 state production simulation by protonating of one or two of the His37 residues, respectively. For the Q2 state, the two charged His37 residues were diagonal to each other (32). For both states, 1 kcal·mol−1·Å−2 harmonic restraints were applied to protein backbone Cα atoms and gradually reduced to 0.01 kcal·mol−1·Å−2 over ∼10 ns. Then all harmonic restraints were released and a production trajectory of ∼180 ns was sampled for each system.
For the simulations starting from the NMR structure that includes the amphipathic helices the protein was inserted into lipid bilayer membrane consisting of 207 POPC molecules and then solvated by a 30-Å-thick layer of water molecules on each side. The protein’s principal axes were aligned with the z axis, and the lipid bilayer was aligned with the x–y plane. Only the Q2 state was simulated, where the two doubly protonated His37 residues were in a diagonal position to each other (32), and the singly protonated His37 residues were protonated at the Nε atoms (10, 11). Importantly, the equilibration starting from the t-105 rotamers of the Trp41 residues, as found in the 2L0J NMR structure, did not a yield stable protein structure for over 200 ns. Moreover, one of the Trp41 residues flipped to the t90 conformer, as found in the crystal structures (9, 24, 55), during this simulation. This is consistent with another very long simulation study in which all four Trp41 residues eventually flipped to the t90 conformation (32), experimental support of the t90 conformation (9, 12, 24, 55, 56), and our own PMF calculation of the Trp41 χ2 dihedral angle rotation discussed earlier in this paper. Therefore, to facilitate the equilibration, the remainder of the Trp41 side chains were manually rotated from the t-105 rotamer to the t90 rotamer. In the first stage of the equilibration, 100 kcal·mol−1·Å−2 harmonic restraints were first applied to the all of the protein backbone’s Cα atoms for ∼30 ns, while the lipid and water molecules relaxed to stabilize the protein–lipid bilayer packing. In the second stage, the restraints on the Cα atoms of amphipathic helices were gradually reduced to 0.01 kcal·mol−1·Å−2 over 20 ns, while keeping the restraints on the M2TM Cα at 100 kcal·mol−1·Å−2. In the third stage, the amphipathic helices were allowed to move freely, while the restraints on the Cα atoms of M2TM helices were reduced to 0.01 kcal·mol−1·Å−2 over 65 ns. Then, all of the harmonic restraints were totally removed, allowing all molecules in the system to relax for another 10 ns. Equilibration was followed by ∼220 ns of MD simulation.
The protein and lipid were modeled using the CHARMM36 force field (58–61) and the water molecules were described using the TIP3P model (62). The electrostatic interactions were treated with particle mesh Ewald, using a spherical cutoff of 12.0 Å and an accuracy threshold of 10−6 (63). The Lennard-Jones (LJ) interaction cutoff was 12.0 Å using a switching function starting at 10 Å. Simulations were performed in the constant number, pressure, temperature ensemble at 308 K and 1 atm. For simulations starting from the crystal structure the classical MD simulations were performed with the NAMD package (64). The temperature and pressure were controlled by the Langevin temperature coupling and Langevin piston pressure coupling schemes (65), respectively. The equations of motion were integrated using the velocity Verlet integrator, with time step of 2.0 fs (66). For the simulations starting from NMR structure, the classical MD simulations were performed with GROMACS 5.0.4 software package (67, 68) to take advantage its graphics processing unit acceleration. The temperature and pressure were controlled by the V-rescale algorithm (69) and the Berendsen pressure coupling algorithm (70), respectively. The equations of motion were integrated using the leap-frog integrator, with time step of 2.0 fs.
QM/MM MD Simulations.
The free energy profile (or PMF) for PT through the His37-Trp41 tetrad region (Fig. 1A) was calculated with hybrid QM/MM umbrella sampling simulations (16). The PMF was calculated as a function of a collective variable (hereafter referred to as the “CV”) defined as the z coordinate difference between the center of mass of Cα atoms of Gly34 and that of the excess proton CEC. (The CV here is in essence a “reaction” or permeation coordinate for the PT process.) The excess proton CEC coordinate used in the QM/MM simulation was defined as (71)
| [1] |
where the Xj’s are the histidine nitrogen atoms and the water oxygen atoms in the QM region, and Hi’s are the hydrogen atoms bound to those heavy atoms in the QM region. The ’s are the hydrogen coordination number of a molecule in the least protonated state during the PT process. Therefore, for water oxygen atoms they were set to 2, and for His37 nitrogen atoms they were set to 0.50 in +0 PMF (four hydrogens shared by eight nitrogens in the Q0 state). Similarly, the ’s for the His37 nitrogen atoms were set to 0.625 in +1 PMF (five hydrogens shared by eight nitrogens in Q1 state) and 0.75 in +2 PMF (six hydrogens shared by eight nitrogens in the Q2 state). The is the distance between atom and atom , and reflects the coordination number of to , with the parameters chosen as Å, Å (72).
In addition, a correction term was introduced in the excess proton CEC definition in Eq. 1 (16) to correct for the contribution due to the presence of multiple protons around multiple protonatable sites in the His37 tetrad, such that
| [2] |
where X denotes the eight nitrogen atoms of the His37 tetrad, and
| [3] |
gradually switches from 1 to 0 as the nitrogen atom i is deprotonated. The excess proton CEC as defined in Eq. 1 describes the delocalized nature of the excess proton and has been shown to accurately locate the position of the excess proton charge defect in previous QM/MM simulations of biological PT channels (16, 71–73).
The last snapshots of Q0, Q1, and Q2 classical MD simulation trajectories were used as the initial structures for the QM/MM simulations for the +0, +1, and +2 PMFs, respectively. An excess proton was then added to a water molecule ∼6 Å above the His37 residue. The QM atoms included His37 side chains and up to three solvation shells of water molecules above and below His37. In all simulations, the QM box size was chosen to be 8 Å larger than the actual size of the QM atoms in each dimension. A quadratic confining potential was applied to restrain the QM atoms within the QM box, with the wall skin thickness being 2 Å × 2 Å × 2 Å. The QM region was treated by Becke–Lee–Yang–Parr level density functional theory (74, 75) with empirical dispersion corrections (76), under the Gaussian plane wave scheme (77). The Goedecker–Teter–Hutter pseudopotentials (78) were used and the Kohn–Sham orbitals were expanded in the Gaussian TZV2P basis set. The electron density was expanded by auxiliary plane wave basis set up to 360 Ry. The Gaussian expansion of the electrostatic potential scheme was used to treat the QM/MM electrostatic coupling with periodic boundary conditions (79, 80), and the spurious QM/QM periodic image interactions were decoupled as described in ref. 81. The equation of motion of the nuclei was integrated using a time step of 0.5 fs, and the wavefunction was optimized to the Born–Oppenheimer surface by an orbital transformation method (82) with a convergence criterion of 10−6. The temperature was controlled at 308 K by a Nosé–Hoover thermostat with a relaxation time constant of 0.1 ps. The initial configurations of all windows were prepared from the previous equilibrated window with smaller z value. With a ∼0.25-Å window spacing and force constants of 40 kcal⋅mol−1⋅Å−2, ∼40 umbrella windows were simulated for each of the QM/MM PMFs, respectively. All windows in this narrow region of the M2 channel had an equilibration time of ∼2 ps and production sampling of 5 ∼15 ps. The excess proton CEC position was collected every step (0.5 fs). All QM/MM simulations were performed using the CP2K package (83).
Reactive MD Umbrella Sampling.
The PT PMF in the regions outside the His37–Trp41 tetrad region (Fig. 1A) was calculated using the MS-RMD method (84–87) implemented with the LAMMPS MD package (lammps.sandia.gov) (88). Umbrella sampling was used and the same CV was used, except that in the MS-RMD simulation the excess proton CEC is given by (89)
| [4] |
where is the coordinates of the center of charge of the ith diabatic state. It was verified that the MS-RMD and QM/MM CEC definitions were essentially identical in the overlapping regions (i.e., when the CEC is nearly three solvation shells away from the His37–Trp41 tetrad).
The MS-RMD model 3.1 version (85) was used with SPC-Fw water model to describe the hydrated excess proton (90). The cutoffs for LJ and real-space electrostatic interactions were 12 Å, using a switching function starting at 10 Å for the LJ interactions. Long-range electrostatics were treated by the particle–particle particle–mesh method (91) with an accuracy threshold of 10−4. The integration time step was 1 fs. The temperature was controlled at 308 K by Nosé–Hoover thermostat with a relaxation time constant of 0.1 ps.
The initial configuration for each umbrella window was prepared by replacing a water molecule with a hydronium close to the center of the window. With a ∼0.5-Å window spacing and force constants of 10 kcal⋅mol−1⋅Å−2, 75–80 windows were simulated for each PMF. The replica-exchange umbrella sampling (REUS) method (92) was used to facilitate convergence, with an exchange attempt frequency of 1 ps−1. All windows were equilibrated for ∼100 ps and sampled with REUS for 1∼2 ns. It should be noted that in the wider regions of the M2 channel longer sampling times are required in the umbrella windows. The CV value was collected every 10 fs.
Calculation of Proton Conductance.
The final PMFs for PT across the entire channel were generated by combining the umbrella windows in the MS-RMD and the QM/MM zones (Fig. 1A) using the weighted histogram analysis method (93–95), similar to what was done in ref. 16. The statistical errors were estimated by a block-average analysis.
The maximum proton conductance, , for proton permeation through M2 in different charge states was calculated from PNP electrodiffusion theory (96–98) via the formula
| [5] |
where e is the elementary charge, is Boltzmann’s constant, T is the temperature, L is the length of the M2 channel (L = 45 Å for systems setup with crystal structure and L = 54 Å for system setup with NMR structure because the amphipathic helices of the latter extends the proton pathway within the protein), and and are, respectively, the diffusion coefficient and the PMF as a function of the CV for proton translocation through the channel. The brackets in Eq. 5 denote spatial averaging over the length of the channel in the direction of the channel axis (z axis). The position-dependent diffusion coefficient for the excess proton was evaluated by the Woolf–Roux equation (99):
| [6] |
where is the velocity autocorrelation function for the CV calculated based on the data from window i, is the reference point for the harmonic restraint potential in window i, and is the Laplace transform of this function. To estimate the value of the limit as s → 0, we linearly extrapolate from the range 5 ≤ s ≤15. To obtain more converged diffusion constants in the His37–Trp41 region, the computationally more efficient MS-RMD simulation was used instead of the more expensive and time scale-limited QM/MM simulation. Due to space constraints, we refer to our previous paper (16) for the discussion on the limitations of the method used to calculate the PMFs and conductions.
His37 Deprotonation Rate Calculations
Based on the PMFs shown in Fig. 2 of the main text, the rate constants for His37 deprotonation in forward (to C-terminal) and backward (to N-terminal) directions were estimated using transition state theory:
| [S1] |
where is the free energy barrier height for the His37 forward or backward deprotonation, is Boltzmann’s constant, and T is the simulation temperature. The preexponential factor is the fundamental frequency of the collective variable (CV) around the His37 minimum in the PMF, which is calculated as
| [S2] |
where the second derivative of the PMF is evaluated at the His37 minimum, and by virtue of equipartition theorem. The are evaluated from the CV trajectories of the QM/MM umbrella windows near the His37 minimum of the PMF. The calculated His37 forward deprotonation rate is different from the calculated conductance using PNP theory (Table 1). The likely reason is that transition state theory will always overestimate the rate (the His37 deprotonation in this case), and also that the free energy barrier to protonate His37 from the N terminal (Fig. 2) is not taken into account in the transition rate theory. This barrier can influence the conductance through the channel, as was shown for the V27A mutant where the reduced proton entrance barrier near the N terminal increases the overall proton conductance.
Acknowledgments
This research was supported by National Institutes of Health Grants R01-GM053148 (to G.A.V., J.M.J.S., and R.L.), R01-GM056432 (to W.F.D.), and R01-GM088204 (to M.H.) and a Carlsberg Foundation International Fellowship (J.J.M.). The researchers used computing facilities provided by the Extreme Science and Engineering Discovery Environment, which is supported by National Science Foundation Grant OCI-1053575, as well as by the University of Chicago Research Computing Center and the US Department of Defense High Performance Computing Modernization Program.
Footnotes
The authors declare no conflict of interest.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1615471113/-/DCSupplemental.
References
- 1.Pinto LH, Holsinger LJ, Lamb RA. Influenza virus M2 protein has ion channel activity. Cell. 1992;69(3):517–528. doi: 10.1016/0092-8674(92)90452-i. [DOI] [PubMed] [Google Scholar]
- 2.Lamb RA, Holsinger LJ, Pinto LH. Cellular Receptors for Animal Viruses. Cold Spring Harbor Lab Press; Cold Spring Harbor, NY: 1994. The influenza A virus M2 ion channel protein and its role in the influenza virus life cycle; pp. 303–321. [Google Scholar]
- 3.Pinto LH, Lamb RA. The M2 proton channels of influenza A and B viruses. J Biol Chem. 2006;281(14):8997–9000. doi: 10.1074/jbc.R500020200. [DOI] [PubMed] [Google Scholar]
- 4.Polishchuk AL, et al. A pH-dependent conformational ensemble mediates proton transport through the influenza A/M2 protein. Biochemistry. 2010;49(47):10061–10071. doi: 10.1021/bi101229m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Wang C, Lamb RA, Pinto LH. Activation of the M2 ion channel of influenza virus: A role for the transmembrane domain histidine residue. Biophys J. 1995;69(4):1363–1371. doi: 10.1016/S0006-3495(95)80003-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Chizhmakov IV, et al. Selective proton permeability and pH regulation of the influenza virus M2 channel expressed in mouse erythroleukaemia cells. J Physiol. 1996;494(Pt 2):329–336. doi: 10.1113/jphysiol.1996.sp021495. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Hu J, et al. Histidines, heart of the hydrogen ion channel from influenza A virus: Toward an understanding of conductance and proton selectivity. Proc Natl Acad Sci USA. 2006;103(18):6865–6870. doi: 10.1073/pnas.0601944103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Tang Y, Zaitseva F, Lamb RA, Pinto LH. The gate of the influenza virus M2 proton channel is formed by a single tryptophan residue. J Biol Chem. 2002;277(42):39880–39886. doi: 10.1074/jbc.M206582200. [DOI] [PubMed] [Google Scholar]
- 9.Acharya R, et al. Structure and mechanism of proton transport through the transmembrane tetrameric M2 protein bundle of the influenza A virus. Proc Natl Acad Sci USA. 2010;107(34):15075–15080. doi: 10.1073/pnas.1007071107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Sharma M, et al. Insight into the mechanism of the influenza A proton channel from a structure in a lipid bilayer. Science. 2010;330(6003):509–512. doi: 10.1126/science.1191750. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Hu F, Luo W, Hong M. Mechanisms of proton conduction and gating in influenza M2 proton channels from solid-state NMR. Science. 2010;330(6003):505–508. doi: 10.1126/science.1191714. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Williams JK, Zhang Y, Schmidt-Rohr K, Hong M. pH-dependent conformation, dynamics, and aromatic interaction of the gating tryptophan residue of the influenza M2 proton channel from solid-state NMR. Biophys J. 2013;104(8):1698–1708. doi: 10.1016/j.bpj.2013.02.054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Pinto LH, et al. A functionally defined model for the M2 proton channel of influenza A virus suggests a mechanism for its ion selectivity. Proc Natl Acad Sci USA. 1997;94(21):11301–11306. doi: 10.1073/pnas.94.21.11301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Salom D, Hill BR, Lear JD, DeGrado WF. pH-dependent tetramerization and amantadine binding of the transmembrane helix of M2 from the influenza A virus. Biochemistry. 2000;39(46):14160–14170. doi: 10.1021/bi001799u. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Lear JD. Proton conduction through the M2 protein of the influenza A virus; a quantitative, mechanistic analysis of experimental data. FEBS Lett. 2003;552(1):17–22. doi: 10.1016/s0014-5793(03)00778-6. [DOI] [PubMed] [Google Scholar]
- 16.Liang R, Li H, Swanson JMJ, Voth GA. Multiscale simulation reveals a multifaceted mechanism of proton permeation through the influenza A M2 proton channel. Proc Natl Acad Sci USA. 2014;111(26):9396–9401. doi: 10.1073/pnas.1401997111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.DiFrancesco ML, Hansen U-P, Thiel G, Moroni A, Schroeder I. Effect of cytosolic pH on inward currents reveals structural characteristics of the proton transport cycle in the influenza A protein M2 in cell-free membrane patches of Xenopus oocytes. PLoS One. 2014;9(9):e107406. doi: 10.1371/journal.pone.0107406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Ma C, et al. Asp44 stabilizes the Trp41 gate of the M2 proton channel of influenza A virus. Structure. 2013;21(11):2033–2041. doi: 10.1016/j.str.2013.08.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Cady SD, et al. Structure of the amantadine binding site of influenza M2 proton channels in lipid bilayers. Nature. 2010;463(7281):689–692. doi: 10.1038/nature08722. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Wang J, et al. Structure and inhibition of the drug-resistant S31N mutant of the M2 ion channel of influenza A virus. Proc Natl Acad Sci USA. 2013;110(4):1315–1320. doi: 10.1073/pnas.1216526110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Wu Y, et al. Flipping in the pore: Discovery of dual inhibitors that bind in different orientations to the wild-type versus the amantadine-resistant S31N mutant of the influenza A virus M2 proton channel. J Am Chem Soc. 2014;136(52):17987–17995. doi: 10.1021/ja508461m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Hong M, DeGrado WF. Structural basis for proton conduction and inhibition by the influenza M2 protein. Protein Sci. 2012;21(11):1620–1633. doi: 10.1002/pro.2158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Stouffer AL, et al. The interplay of functional tuning, drug resistance, and thermodynamic stability in the evolution of the M2 proton channel from the influenza A virus. Structure. 2008;16(7):1067–1076. doi: 10.1016/j.str.2008.04.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Thomaston JL, et al. High-resolution structures of the M2 channel from influenza A virus reveal dynamic pathways for proton stabilization and transduction. Proc Natl Acad Sci USA. 2015;112(46):14260–14265. doi: 10.1073/pnas.1518493112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Thomaston JL, DeGrado WF. Crystal structure of the drug-resistant S31N influenza M2 proton channel. Protein Sci. 2016;25(8):1551–1554. doi: 10.1002/pro.2937. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Schnell JR, Chou JJ. Structure and mechanism of the M2 proton channel of influenza A virus. Nature. 2008;451(7178):591–595. doi: 10.1038/nature06531. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Miao Y, Fu R, Zhou HX, Cross TA. Dynamic short hydrogen bonds in histidine tetrad of full-length M2 proton channel reveal tetrameric structural heterogeneity and functional mechanism. Structure. 2015;23(12):2300–2308. doi: 10.1016/j.str.2015.09.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Hu F, Luo W, Cady SD, Hong M. Conformational plasticity of the influenza A M2 transmembrane helix in lipid bilayers under varying pH, drug binding, and membrane thickness. Biochim Biophys Acta. 2011;1808(1):415–423. doi: 10.1016/j.bbamem.2010.09.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Li C, Qin H, Gao FP, Cross TA. Solid-state NMR characterization of conformational plasticity within the transmembrane domain of the influenza A M2 proton channel. Biochim Biophys Acta. 2007;1768(12):3162–3170. doi: 10.1016/j.bbamem.2007.08.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Hu F, Schmidt-Rohr K, Hong M. NMR detection of pH-dependent histidine-water proton exchange reveals the conduction mechanism of a transmembrane proton channel. J Am Chem Soc. 2012;134(8):3703–3713. doi: 10.1021/ja2081185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Zhong Q, Newns DM, Pattnaik P, Lear JD, Klein ML. Two possible conducting states of the influenza A virus M2 ion channel. FEBS Lett. 2000;473(2):195–198. doi: 10.1016/s0014-5793(00)01522-2. [DOI] [PubMed] [Google Scholar]
- 32.Wei C, Pohorille A. Activation and proton transport mechanism in influenza A M2 channel. Biophys J. 2013;105(9):2036–2045. doi: 10.1016/j.bpj.2013.08.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Khurana E, et al. Molecular dynamics calculations suggest a conduction mechanism for the M2 proton channel from influenza A virus. Proc Natl Acad Sci USA. 2009;106(4):1069–1074. doi: 10.1073/pnas.0811720106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Chen H, Wu Y, Voth GA. Proton transport behavior through the influenza A M2 channel: Insights from molecular simulation. Biophys J. 2007;93(10):3470–3479. doi: 10.1529/biophysj.107.105742. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Yi M, Cross TA, Zhou HX. A secondary gate as a mechanism for inhibition of the M2 proton channel by amantadine. J Phys Chem B. 2008;112(27):7977–7979. doi: 10.1021/jp800171m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Yi M, Cross TA, Zhou HX. Conformational heterogeneity of the M2 proton channel and a structural model for channel activation. Proc Natl Acad Sci USA. 2009;106(32):13311–13316. doi: 10.1073/pnas.0906553106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Wu Y, Voth GA. A computational study of the closed and open states of the influenza a M2 proton channel. Biophys J. 2005;89(4):2402–2411. doi: 10.1529/biophysj.105.066647. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Dong H, Fiorin G, DeGrado WF, Klein ML. Proton release from the histidine-tetrad in the M2 channel of the influenza A virus. J Phys Chem B. 2014;118(44):12644–12651. doi: 10.1021/jp5102225. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Zhou HX. A theory for the proton transport of the influenza virus M2 protein: Extensive test against conductance data. Biophys J. 2011;100(4):912–921. doi: 10.1016/j.bpj.2011.01.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Roberts KL, Leser GP, Ma C, Lamb RA. The amphipathic helix of influenza A virus M2 protein is required for filamentous bud formation and scission of filamentous and spherical particles. J Virol. 2013;87(18):9973–9982. doi: 10.1128/JVI.01363-13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Schmidt NW, Mishra A, Wang J, DeGrado WF, Wong GCL. Influenza virus A M2 protein generates negative Gaussian membrane curvature necessary for budding and scission. J Am Chem Soc. 2013;135(37):13710–13719. doi: 10.1021/ja400146z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Ma C, et al. Identification of the functional core of the influenza A virus A/M2 proton-selective ion channel. Proc Natl Acad Sci USA. 2009;106(30):12283–12288. doi: 10.1073/pnas.0905726106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Wang T, Hong M. Investigation of the curvature induction and membrane localization of the influenza virus M2 protein using static and off-magic-angle spinning solid-state nuclear magnetic resonance of oriented bicelles. Biochemistry. 2015;54(13):2214–2226. doi: 10.1021/acs.biochem.5b00127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Wang J, et al. Molecular dynamics simulation directed rational design of inhibitors targeting drug-resistant mutants of influenza A virus M2. J Am Chem Soc. 2011;133(32):12834–12841. doi: 10.1021/ja204969m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Dong H, Fiorin G, Degrado WF, Klein ML. Exploring histidine conformations in the M2 channel lumen of the influenza A virus at neutral pH via molecular simulations. J Phys Chem Lett. 2013;4(18):3067–3071. doi: 10.1021/jz401672h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Carnevale V, Fiorin G, Levine BG, Degrado WF, Klein ML. Multiple proton confinement in the M2 channel from the influenza A virus. J Phys Chem C Nanomater Interfaces. 2010;114(48):20856–20863. doi: 10.1021/jp107431g. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Allen TW, Andersen OS, Roux B. Energetics of ion conduction through the gramicidin channel. Proc Natl Acad Sci USA. 2004;101(1):117–122. doi: 10.1073/pnas.2635314100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Colvin MT, Andreas LB, Chou JJ, Griffin RG. Proton association constants of His 37 in the Influenza-A M218-60 dimer-of-dimers. Biochemistry. 2014;53(38):5987–5994. doi: 10.1021/bi5005393. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Liao SY, Yang Y, Tietze D, Hong M. The influenza M2 cytoplasmic tail changes the proton-exchange equilibria and the backbone conformation of the transmembrane histidine residue to facilitate proton conduction. J Am Chem Soc. 2015;137(18):6067–6077. doi: 10.1021/jacs.5b02510. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Chizhmakov IV, et al. Differences in conductance of M2 proton channels of two influenza viruses at low and high pH. J Physiol. 2003;546(Pt 2):427–438. doi: 10.1113/jphysiol.2002.028910. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Williams JK, et al. Drug-induced conformational and dynamical changes of the S31N mutant of the influenza M2 proton channel investigated by solid-state NMR. J Am Chem Soc. 2013;135(26):9885–9897. doi: 10.1021/ja4041412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Leiding T, Wang J, Martinsson J, DeGrado WF, Arsköld SP. Proton and cation transport activity of the M2 proton channel from influenza A virus. Proc Natl Acad Sci USA. 2010;107(35):15409–15414. doi: 10.1073/pnas.1009997107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Mould JA, et al. Mechanism for proton conduction of the M(2) ion channel of influenza A virus. J Biol Chem. 2000;275(12):8592–8599. doi: 10.1074/jbc.275.12.8592. [DOI] [PubMed] [Google Scholar]
- 54.Khurana E, Devane RH, Dal Peraro M, Klein ML. Computational study of drug binding to the membrane-bound tetrameric M2 peptide bundle from influenza A virus. Biochim Biophys Acta. 2011;1808(2):530–537. doi: 10.1016/j.bbamem.2010.03.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Stouffer AL, et al. Structural basis for the function and inhibition of an influenza virus proton channel. Nature. 2008;451(7178):596–599. doi: 10.1038/nature06528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Luo W, Mani R, Hong M. Side-chain conformation of the M2 transmembrane peptide proton channel of influenza a virus from 19F solid-state NMR. J Phys Chem B. 2007;111(36):10825–10832. doi: 10.1021/jp073823k. [DOI] [PubMed] [Google Scholar]
- 57.Hong M, Fritzsching KJ, Williams JK. Hydrogen-bonding partner of the proton-conducting histidine in the influenza M2 proton channel revealed from 1H chemical shifts. J Am Chem Soc. 2012;134(36):14753–14755. doi: 10.1021/ja307453v. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.MacKerell AD, et al. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J Phys Chem B. 1998;102(18):3586–3616. doi: 10.1021/jp973084f. [DOI] [PubMed] [Google Scholar]
- 59.MacKerell AD, Jr, Feig M, Brooks CL., 3rd Improved treatment of the protein backbone in empirical force fields. J Am Chem Soc. 2004;126(3):698–699. doi: 10.1021/ja036959e. [DOI] [PubMed] [Google Scholar]
- 60.Best RB, et al. Optimization of the additive CHARMM all-atom protein force field targeting improved sampling of the backbone φ, ψ and side-chain χ(1) and χ(2) dihedral angles. J Chem Theory Comput. 2012;8(9):3257–3273. doi: 10.1021/ct300400x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Klauda JB, et al. Update of the CHARMM all-atom additive force field for lipids: Validation on six lipid types. J Phys Chem B. 2010;114(23):7830–7843. doi: 10.1021/jp101759q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW, Klein ML. Comparison of simple potential functions for simulating liquid water. J Chem Phys. 1983;79:926–935. [Google Scholar]
- 63.Darden T, York D, Pedersen L. Particle mesh Ewald: An N-log(N) method for Ewald sums in large systems. J Chem Phys. 1993;98:10089–10092. [Google Scholar]
- 64.Phillips JC, et al. Scalable molecular dynamics with NAMD. J Comput Chem. 2005;26(16):1781–1802. doi: 10.1002/jcc.20289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Feller SE, Zhang Y, Pastor RW, Brooks BR. Constant pressure molecular dynamics simulation: The Langevin piston method. J Chem Phys. 1995;103(11):4613–4621. [Google Scholar]
- 66.Verlet L. Computer “experiments” on classical fluids. I. Thermodynamical properties of Lennard-Jones molecules. Phys Rev. 1967;159(1):98–103. [Google Scholar]
- 67.Berendsen HJC, Vanderspoel D, Vandrunen R. GROMACS: A message-passing parallel molecular dynamics implementation. Comput Phys Commun. 1995;91(1–3):43–56. [Google Scholar]
- 68.Abraham MJ, et al. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX. 2015;1–2:19–25. [Google Scholar]
- 69.Bussi G, Donadio D, Parrinello M. Canonical sampling through velocity rescaling. J Chem Phys. 2007;126(1):014101. doi: 10.1063/1.2408420. [DOI] [PubMed] [Google Scholar]
- 70.Berendsen HJC, Postma JPM, Vangunsteren WF, Dinola A, Haak JR. Molecular dynamics with coupling to an external bath. J Chem Phys. 1984;81(8):3684–3690. [Google Scholar]
- 71.König PH, et al. Toward theoretical analysis of long-range proton transfer kinetics in biomolecular pumps. J Phys Chem A. 2006;110(2):548–563. doi: 10.1021/jp052328q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Riccardi D, et al. “Proton holes” in long-range proton transfer reactions in solution and enzymes: A theoretical analysis. J Am Chem Soc. 2006;128(50):16302–16311. doi: 10.1021/ja065451j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Liang R, Swanson JMJ, Voth GA. Benchmark study of the SCC-DFTB approach for a biomolecular proton channel. J Chem Theory Comput. 2014;10(1):451–462. doi: 10.1021/ct400832r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Becke AD. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys Rev A Gen Phys. 1988;38(6):3098–3100. doi: 10.1103/physreva.38.3098. [DOI] [PubMed] [Google Scholar]
- 75.Lee C, Yang W, Parr RG. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys Rev B Condens Matter. 1988;37(2):785–789. doi: 10.1103/physrevb.37.785. [DOI] [PubMed] [Google Scholar]
- 76.Grimme S, Antony J, Ehrlich S, Krieg H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J Chem Phys. 2010;132(15):154104. doi: 10.1063/1.3382344. [DOI] [PubMed] [Google Scholar]
- 77.Lippert G, Hutter J, Parrinello M. A hybrid Gaussian and plane wave density functional scheme. Mol Phys. 1997;92(3):477–487. [Google Scholar]
- 78.Hartwigsen C, Goedecker S, Hutter J. Relativistic separable dual-space Gaussian pseudopotentials from H to Rn. Phys Rev B. 1998;58:3641–3662. doi: 10.1103/physrevb.54.1703. [DOI] [PubMed] [Google Scholar]
- 79.Laino T, Mohamed F, Laio A, Parrinello M. An efficient linear-scaling electrostatic coupling for treating periodic boundary conditions in QM/MM simulations. J Chem Theory Comput. 2006;2(5):1370–1378. doi: 10.1021/ct6001169. [DOI] [PubMed] [Google Scholar]
- 80.Laino T, Mohamed F, Laio A, Parrinello M. An efficient real space multigrid QM/MM electrostatic coupling. J Chem Theory Comput. 2005;1(6):1176–1184. doi: 10.1021/ct050123f. [DOI] [PubMed] [Google Scholar]
- 81.Blöchl PE. Electrostatic decoupling of periodic images of plane-wave-expanded densities and derived atomic point charges. J Chem Phys. 1995;103(17):7422–7428. [Google Scholar]
- 82.VandeVondele J, Hutter J. An efficient orbital transformation method for electronic structure calculations. J Chem Phys. 2003;118(10):4365–4369. [Google Scholar]
- 83.VandeVondele J, et al. QUICKSTEP: Fast and accurate density functional calculations using a mixed Gaussian and plane waves approach. Comput Phys Commun. 2005;167(2):103–128. [Google Scholar]
- 84.Knight C, Lindberg GE, Voth GA. Multiscale reactive molecular dynamics. J Chem Phys. 2012;137(22):22A525. doi: 10.1063/1.4743958. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Nelson JG, Peng Y, Silverstein DW, Swanson JMJ. Multiscale reactive molecular dynamics for absolute pK a predictions and amino acid deprotonation. J Chem Theory Comput. 2014;10(7):2729–2737. doi: 10.1021/ct500250f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Lee S, Liang R, Voth GA, Swanson JMJ. Computationally efficient multiscale reactive molecular dynamics to describe amino acid deprotonation in proteins. J Chem Theory Comput. 2016;12(2):879–891. doi: 10.1021/acs.jctc.5b01109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Yamashita T, Peng Y, Knight C, Voth GA. Computationally Efficient Multiconfigurational Reactive Molecular Dynamics. J Chem Theory Comput. 2012;8(12):4863–4875. doi: 10.1021/ct3006437. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Plimpton S. Fast parallel algorithms for short-range molecular dynamics. J Comput Phys. 1995;117(1):1–19. [Google Scholar]
- 89.Day TJF, Soudackov AV, Cuma M, Schmitt UW, Voth GA. A second generation multistate empirical valence bond model for proton transport in aqueous systems. J Chem Phys. 2002;117(12):5839–5849. [Google Scholar]
- 90.Wu Y, Tepper HL, Voth GA. Flexible simple point-charge water model with improved liquid-state properties. J Chem Phys. 2006;124(2):024503. doi: 10.1063/1.2136877. [DOI] [PubMed] [Google Scholar]
- 91.Hockney RW, Eastwood JW. Computer Simulation Using Particles. McGraw-Hill; New York: 1981. p. 540. [Google Scholar]
- 92.Sugita Y, Kitao A, Okamoto Y. Multidimensional replica-exchange method for free-energy calculations. J Chem Phys. 2000;113(15):6042–6051. [Google Scholar]
- 93.Roux B. The calculation of the potential of mean force using computer simulations. Comput Phys Commun. 1995;91(1–3):275–282. [Google Scholar]
- 94.Allen MP, Tildesley DJ. Computer Simulation of Liquids. Oxford Univ Press; New York: 1990. [Google Scholar]
- 95.Kumar S, Bouzida D, Swendsen RH, Kollman PA, Rosenberg JM. The weighted histogram analysis method for free-energy calculations on biomolecules. 1. The method. J Comput Chem. 1992;13(8):1011–1021. [Google Scholar]
- 96.Levitt DG. Interpretation of biological ion channel flux data--reaction-rate versus continuum theory. Annu Rev Biophys Biophys Chem. 1986;15:29–57. doi: 10.1146/annurev.bb.15.060186.000333. [DOI] [PubMed] [Google Scholar]
- 97.Roux B, Karplus M. Ion-transport in a gramicidin-like channel: Dynamics and mobility. J Phys Chem. 1991;95(12):4856–4868. [Google Scholar]
- 98.Levitt DG. General continuum theory for multiion channel. I. Theory. Biophys J. 1991;59(2):271–277. doi: 10.1016/S0006-3495(91)82220-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.Woolf TB, Roux B. Conformational flexibility of o-phosphorylcholine and o-phosphorylethanolamine: A molecular dynamics study of solvation effects. J Am Chem Soc. 1994;116(13):5916–5926. [Google Scholar]