Geometry-induced capillary emptying

Significance

We present a precise mathematical criterion that determines whether the liquid in a capillary of arbitrary cross-section will remain in it or will flow out when the capillary is at a horizontal position. The rich phenomenology found can be used to construct very sensitive microfluidics devices.

Abstract

When a capillary is half-filled with liquid and turned to the horizontal, the liquid may flow out of the capillary or remain in it. For lack of a better criterion, the standard assumption is that the liquid will remain in a capillary of narrow cross-section, and will flow out otherwise. Here, we present a precise mathematical criterion that determines which of the two outcomes occurs for capillaries of arbitrary cross-sectional shape, and show that the standard assumption fails for certain simple geometries, leading to very rich and counterintuitive behavior. This opens the possibility of creating very sensitive microfluidic devices that respond readily to small physical changes, for instance, by triggering the sudden displacement of fluid along a capillary without the need of any external pumping.

The interaction of liquids with solids has been a fertile topic for physicists, chemists, mathematicians, and engineers, providing fundamental insights into the properties of matter, for example, the necessity of attractive molecular forces (1–3), explaining the rich phenomenology of wetting (4–7) and superhydrophobicity (8–11), and leading to the development of modern microfluidic devices (12–15). One of the prototypical examples of this is the capillary rise of a liquid in a vertical tube, where the shape and location of the meniscus (the interface separating the liquid from the gas) are determined by the surface tensions, the geometry of the capillary, and the strength of the gravitational force, as firmly established by comprehensive studies spanning several centuries (16). It is somehow surprising that, in contrast, the simplest question that may be asked when a capillary is turned to the horizontal, namely, “Does the liquid spill out?,” has so far remained unanswered. Here, we answer this question providing an appropriate mathematical criterion for spilling, and show that the phenomenology of a horizontally oriented capillary is distinctively richer than that of its vertical counterpart because, in this configuration, the meniscus undergoes an unbound deformation triggered by the effect of gravity that precedes the emptying of the capillary. This effect is absent in previous studies of capillarity in “horizontal” systems, like fibers (17) or grooves (18), where gravity is neglected.

Emptying

It is common experience that when a wide container, like a cylindrical glass, is partially filled with liquid and tilted slowly to the horizontal, the liquid spills out, and the glass inevitably empties. In contrast, if the container is narrow enough, like a drinking straw, the liquid remains in the container even in the horizontal position. For lack of a better criterion, the standard assumption is that the liquid will remain in a capillary of narrow cross-section and will flow out otherwise, but can one provide a definite answer that takes into account the cross-sectional shape of the capillary? To answer this question, we turn to macroscopic thermodynamics, which states that the liquid adopts the shape that minimizes the total free energy. This energy has three terms, each dependent on the shape $\ell$ of the meniscus:

$$E\left[\ell \right]/\gamma =\mathcal{A}-\cos \theta \hspace{0.17em}\mathcal{S}+\mathcal{G}/a^2.$$ [1]

Here, γ is the surface tension of the liquid–gas interface and θ is the contact angle (indicative of the affinity of the liquid toward the solid). The capillary length $a=\sqrt{\gamma /\mathrm{\Delta }\rho \hspace{0.17em}g}$ is defined in terms of the mass density difference between the liquid and the gas $\mathrm{\Delta }\rho$, and the gravitational acceleration g; for pure water at room temperature, $a\approx 2.7\hspace{0.5em}\text{mm}$. The functional dependence of the free energy on the meniscus shape $\ell$ enters through three geometrical quantities: the area of the meniscus $\mathcal{A}$, the surface area of the container walls in contact with the liquid $\mathcal{S}$, and the position of the center of mass of the fluid multiplied by its volume $\mathcal{G}$. The equilibrium shape of the fluid can be obtained from minimization of [1], which amounts to balancing the three competing terms, subject to a constant volume condition. This can be done formally and leads to the renowned Young–Laplace equation for $\ell$, which must be solved requiring the meniscus to touch the container walls at an angle θ. However, obtaining the shape of the liquid meniscus is a very demanding task in practice. Despite enormous efforts (16), hardly any analytical solutions to the Young–Laplace equation are known, except for simple containers without gravity. Here, we concentrate on the solutions to this equation when the container is a horizontal capillary of arbitrary cross-section. These show a number of remarkable features:

• i)The Young–Laplace equation may or may not have a solution. The absence of a solution indicates that no meniscus can hold the liquid and, therefore, the liquid must necessarily flow out of the capillary. This contrasts with vertical (or, in general, upward-oriented) capillaries, for which the Young–Laplace equation always has a solution, except in the complete absence of gravity (16). Without gravity, the orientation is clearly irrelevant and therefore both the vertical and horizontal capillaries behave identically.
• ii)For a given capillary geometry (cross-sectional shape and orientation), one may identify an emptying line in the $\left(\theta ,a\right)$ plane which corresponds to the values of the parameters for which solutions cease to exist. This line separates two regions, which we refer to as “filled” and “empty.”
• iii)The emptying line is a critical line. All existing solutions in the filled region disappear when this line is crossed. In general, the meniscus obtained from solving the Young–Laplace equation spreads out progressively along the capillary as this line is approached and, close to it, small changes in the parameters produce large changes in the length of the meniscus, which becomes infinitely (arbitrarily) long when the line is reached. See 1–4 in Fig. 1.
• iv)Crucially, there are different mechanisms by which the meniscus spreads out, arising from the competition between gravity (that wants the liquid to be at the lowest point of the capillary) and capillary forces (that prefer the meniscus to be near the points of highest curvature of the capillary). As a consequence, the emptying line can have different sections corresponding to different emptying mechanisms.

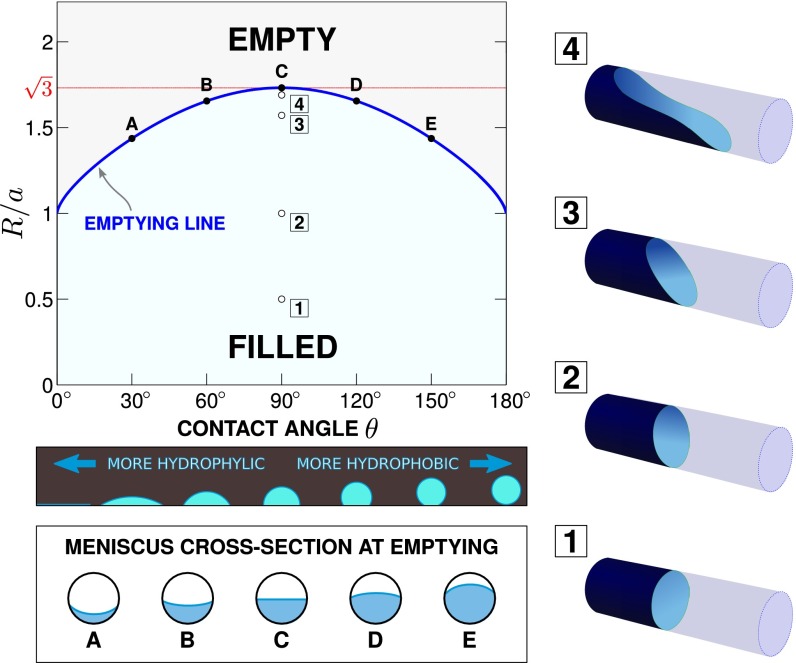
Fig. 1.

Emptying line for a cylindrical capillary of radius R as a function of the contact angle θ of the liquid with the walls. The cross-section of a 3D drop of constant volume is included to illustrate the interaction of the liquid with a flat wall for different contact angles, from very hydrophilic ($\theta =0\mathrm{°}$) to very hydrophobic ($\theta =180\mathrm{°}$). The emptying line separates the filled region (where a meniscus exists) from the empty region (where no meniscus exists, which prompts the emptying of the capillary). Plots 1– 4 show the deformation of the meniscus for $\theta =90\mathrm{°}$ as the emptying line is approached (by increasing the value of $R/a$), and the appearance of a liquid tongue before emptying. Plots A–E illustrate the cross-section of the (infinitely long) liquid tongue at emptying for five different contact angles.

Computing the emptying line by the direct numerical determination of 3D menisci is impracticable due to the critical nature of capillary emptying. To avoid this, we have devised an exact reduction of the problem: Instead of minimizing the 3D functional [1] subject to a constant volume constraint, we minimize a 2D functional defined for the cross-section of the capillary but with variable volume. Physically, this functional represents the energy cost per unit length of a translationally invariant meniscus that extends along the horizontal capillary (Supporting Information). The minimizing 2D shape corresponds to the section of the (arbitrarily long) 3D meniscus that prompts the emptying of the capillary. Mathematically, this method represents a physically motivated generalization of the pioneering work of Finn on capillaries without gravity (16), and is ultimately based on the recent application of generalized Poincaré inequalities to functions of bounded variation (19).

Results

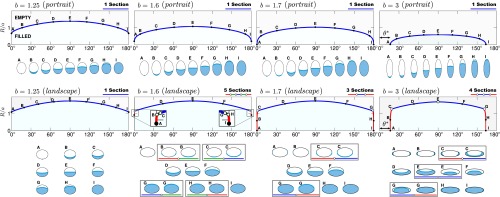
When this method is applied to a capillary with a circular cross-section of radius R, the simple emptying line of Fig. 1 is obtained. From this, we see that any circular capillary, made of any material and containing any liquid, whose radius is larger than $\sqrt{3}\hspace{0.17em}a$, will empty in the horizontal position. Likewise, any circular capillary whose radius is smaller than a will remain filled in that position, irrespective of the contact angle. Only in a narrow range of sizes $a<R<\sqrt{3}\hspace{0.17em}a$ does the contact angle θ (i.e., the choice of liquid and capillary material) exert an influence on the final outcome. This is similar to what happens to a liquid confined in a horizontal capillary slit made of two parallel walls, which is essentially a 2D phenomenon (20). Although these results roughly confirm the intuitive idea that wide capillaries empty and narrow capillaries remain filled when turned to the horizontal, the reality is very different for capillaries with noncircular cross-sections. For example, Fig. 2 shows the emptying line for capillaries whose cross-sections are ellipses of semiaxes R and $bR$. The emptying line is computed for progressively more eccentric ellipses and for two different orientations (portrait and landscape-like), which illustrate the extremely sensitive interplay between the different energetic contributions in [1]. Two features emerge that are worth emphasizing: (i) For sufficiently eccentric capillaries ($b>b^{\ast }\approx 1.635$), the emptying line touches the line $R/a=0$ at contact angles ${\theta }^{\ast }\left(b\right)$ and $180\mathrm{°}-{\theta }^{\ast }\left(b\right)$. This means that, contrary to intuition, those capillaries will empty if the contact angle θ is smaller than ${\theta }^{\ast }\left(b\right)$ or larger than $180\mathrm{°}-{\theta }^{\ast }\left(b\right)$, no matter how small they are. The line $R/a=0$ also represents the limit of vanishing gravity and, therefore, any result for that line is necessarily independent of the orientation of the capillary. (ii) For landscape-like elliptical cross-sections (Fig. 2), the emptying line is divided into sections corresponding to different emptying mechanisms with distinct meniscus shapes, including those that spread along the sides of the capillary rather than its bottom. At the common point of two adjacent sections, two different (yet equivalent) emptying mechanisms coexist. These common points need to be the starting points of lines of coexisting solutions in the filled region, which the present 2D-reduction approach cannot describe. All these features represent a radical departure from the simple case of the circular capillary, where emptying is essentially determined by the size R (wide or narrow containers), and there is only a single emptying mechanism.

Fig. 2.

Emptying line as a function of the contact angle θ for a capillary with an elliptical cross-section of semiaxes R and $bR$ in two different orientations: portrait (Top) and landscape (Bottom). The meniscus cross-section at different points of the emptying line (circles) is shown under each diagram (A–I). In the portrait orientation, the emptying line lowers as b increases, and touches the line $R=0$ for $b\ge b^{\ast }\approx 1.635$. This creates gaps of width ${\theta }^{\ast }\left(b\right)$ at both ends of the diagrams (not visible for $b=1.7$, but apparent for $b=3$) representing values of the contact angle for which the capillary empties for any size R. In the landscape orientation, gravity and capillary forces compete to place the liquid, respectively, at the lowest position or near the point of highest curvature of the capillary. This competition causes the emptying line to break into sections, each corresponding to a different emptying mechanism, including those with unconnected interfaces (red lines). At the common point of two sections (white circles), two different emptying mechanisms coexist (represented in a common box under the diagrams). The number of sections of the emptying line depends strongly on the geometry, and does not follow a simple pattern.

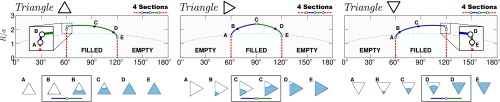
Additional features also emerge when capillary cross-sections with edges are considered. For example, Fig. 3 shows the emptying lines of a horizontal capillary of triangular cross-section. The presence of an opening angle β in the cross-section of the capillary gives rise to a distinct emptying mechanism that takes place close to the corner. Any capillary with such an angle will empty for $\theta <\left(180\mathrm{°}-\beta \right)/2$ and $\theta >\left(180\mathrm{°}+\beta \right)/2$, no matter how small the cross-section is. Although this phenomenon, closely related to wedge filling (21), has already been described in the absence of gravity (22), we see here that, quite unexpectedly, it extends unaltered to appreciable values of the gravitational field (dashed red lines) that depend on the geometrical details of the capillary. Approaching these vertical sections of the emptying line, the meniscus does not develop a tongue. This is consistent with the vanishing of the meniscus cross-section on approaching the points “A” in Fig. 3 along the (blue) emptying line. In practice, upon crossing these vertical sections of the emptying line, the capillary will simply empty because all of the liquid in the capped end will flow out along the wedge. This has been observed in experiments at zero gravity (corresponding to $R/a=0$) (16). Note also that, as the cross-section of this triangular capillary lacks symmetry under 180° rotations, the emptying line is no longer symmetric about $\theta =90\mathrm{°}$, as it was in the previous examples.

Fig. 3.

Emptying line for a capillary of triangular cross-section inscribed in a circle of radius R in three different orientations as a function of the contact angle θ. The meniscus cross-section at different points of the emptying line (circles) is shown under each diagram (A–E). The existence of corners in the cross-section creates a gap in the emptying line, for which the capillary empties for any size R, similar to that of very eccentric elliptical capillaries of Fig. 2. However, unlike this latter case, the emptying line rises vertically from $R/a=0$ (dashed red lines) and, upon approaching this line from the filled region, no tongue is formed in the meniscus. The emptying line of a circular capillary of radius R is included for comparison (dotted line).

With the exception of the vertical sections of the emptying line that appear in capillaries with edges, the 3D meniscus develops a tongue that grows in size whenever an emptying line is approached from the filled region. This can be achieved in a number of ways: changing the contact angle [for instance, varying the temperature or using electrowetting (18, 23)], changing the gravitational acceleration (24), or simply rotating the capillary around its axis. In this way, a number of microfluidic devices can be constructed (including, for instance, those with immiscible fluids or other coexisting phases that could play the role of liquid and gas) that exploit the sharp change in the meniscus shape in response to very small physical changes, for instance, by triggering the sudden displacement of fluid along the capillary without the need of any external pressure, or by increasing the meniscus area for catalytic purposes. As we focus here only on equilibrium properties, contact angle hysteresis has not been addressed. However, earlier experimental studies in zero gravity indicate that even in the presence of large contact angle hysteresis, the meniscus behavior is consistent with the discontinuities predicted by the mathematical solution of the idealized Young–Laplace theory (24). Regarding the dynamics of capillary emptying, note that, in the growth of the tongue, the front and rear of the meniscus will be characterized by the advancing and receding contact angles, respectively. Further consequences of capillary emptying could also be envisaged for the localization of fluids in porous media.

Equation for the Emptying Line

The Young–Laplace Equation.

The free energy of a liquid droplet in a capillary can be written as the following functional of the meniscus shape $\ell \hspace{0.17em}$:

$$E\left[\ell \right]/\gamma =\mathcal{A}-\cos \theta \hspace{0.17em}\mathcal{S}+\mathcal{G}/a^2.$$ [S1]

Here, γ is the liquid–gas surface tension, θ is the contact angle of the liquid with the capillary material, and $a=\sqrt{\gamma /\mathrm{\Delta }\rho \hspace{0.17em}g}$ is the capillary length, defined in terms of the mass density difference between the liquid and the gas $\mathrm{\Delta }\rho$, and the gravitational acceleration g. The functional dependence of the free energy on the meniscus shape $\ell$ enters through three geometrical quantities: the area of the meniscus $\mathcal{A}\hspace{0.17em}$, the surface area of the container walls in contact with the liquid $\mathcal{S}$, and the position of the center of mass of the fluid multiplied by its volume $\mathcal{G}$.

In turn, the equilibrium shape of the liquid drop is obtained from minimization of $E\left[\ell \right]$, subject to the condition that the liquid volume $\mathcal{V}$ is fixed. Therefore, the functional to be minimized is

$$F\left[\ell \right]=\mathcal{A}-\cos \theta \hspace{0.17em}\mathcal{S}+\mathcal{G}/a^2+\lambda \mathcal{V},$$ [S2]

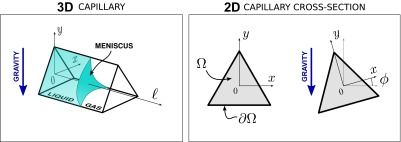
where λ is the Lagrange multiplier. With an appropriate choice of coordinates (Fig. S1), the meniscus can be represented as a function $\ell \left(x,y\right)$ and the above terms can be written for a horizontal capillary:

$$\begin{array}{l}\mathcal{A}={\displaystyle {\int }_{\mathrm{\Omega }}dx\hspace{0.17em}dy}\hspace{0.17em}\sqrt{1+{\left(\nabla \ell \right)}^2},\\ \mathcal{S}={\displaystyle {\oint }_{\partial \mathrm{\Omega }}ds}\hspace{0.17em}\ell ,\\ \mathcal{G}={\displaystyle {\int }_{\mathrm{\Omega }}dx\hspace{0.17em}dy}\hspace{0.17em}\left(x\sin \varphi +y\cos \varphi \right)\hspace{0.17em}\ell ,\\ \mathcal{V}={\displaystyle {\int }_{\mathrm{\Omega }}dx\hspace{0.17em}dy}\hspace{0.17em}\ell ,\end{array}$$ [S3]

where $\mathrm{\Omega }$ represents the cross-section of the capillary, and $\partial \mathrm{\Omega }$ its perimeter. A formal minimization of [S2] produces the Young–Laplace equation:

$$\nabla \cdot \left(\frac{\nabla \ell }{\sqrt{1+{\left(\nabla \ell \right)}^2}}\right)=\hspace{0.17em}\frac{1}{a^2}\left(x\sin \varphi +y\cos \varphi \right)+\lambda ,$$ [S4]

together with the boundary condition that the angle formed by the meniscus with the capillary walls must be θ at all points. In physical terms, the left side of this equation is (twice) the mean curvature of the meniscus at each point which, in the absence of gravity ($a\to \infty$), needs to be a constant.

Fig. S1.

Schematic drawing of a capillary and its cross-section, indicating the choice of coordinates. The variable $\varphi$ represents the rotation angle of the capillary around its longitudinal axis.

The Lagrange multiplier λ is itself determined by the constant volume condition. However, for capillaries (containers with a constant cross-section), λ is independent of the volume of liquid, provided the meniscus does not touch the end cap. This follows immediately from integration of [S4] over $\mathrm{\Omega }$, yielding

$$\lambda =\frac{\partial {\mathrm{\Omega }}_0\cos \theta }{{\mathrm{\Omega }}_0},$$ [S5]

where ${\mathrm{\Omega }}_0$ is the area of the capillary cross-section, and $\partial {\mathrm{\Omega }}_0$ the length of its perimeter. In writing [S5], we have assumed that the origin of the coordinates x and y lies along the line of the center of mass of $\mathrm{\Omega }$; this choice means that λ does not depend on the turning angle ϕ. The independence of the Lagrange multiplier on volume implies that the meniscus shape is also independent of the volume of liquid, which is in accord with experience. In the following, we assume that the length of the capillary and volume of liquid are effectively infinite, which prevents the uninteresting influence of finite size effects in our results.

Emptying Tongue.

Upon approaching any point on the emptying line from the filled region, the meniscus will, in general, develop a tongue of length L which diverges when the emptying line is reached (Fig. S2). Note that, because the total energy of the meniscus, given by [S1], is finite, the energy cost per unit length of this (in that limit, infinitely long) tongue must necessarily be zero. In other words, the emptying line must correspond to the condition that there is a translationally invariant solution to [S4] with zero energy. Note that this condition applies even if no tongue develops: if there exists any translationally invariant solution to [S4] with negative energy, the total energy of the system, which must attain the minimum possible value, would decrease unboundedly by simply making a meniscus tongue with the shape of that solution progressively longer; if the total energy is negatively unbound, no meniscus shape exists that can hold the liquid in the capillary, and this must empty.

Fig. S2.

Schematic drawing of menisci in a horizontal capillary approaching the emptying line as the capillary length a is decreased progressively (from left to right). When the emptying line is reached (for a particular value of a), the length L diverges. Although the liquid volume is conserved, the menisci have been shifted along the capillary to facilitate representation.

Emptying Line.

The existence of a translationally invariant solution to [S4] with zero energy may be formulated as

$$\underset{\eta }{\min }{E}^{2\text{D}}\left[\eta \right]=0,$$ [S6]

where $E^{\hspace{0.17em}2\text{D}}$ is a 2D reduction of the functional S2:

$$E^{\hspace{0.17em}2\text{D}}\left[\eta \right]={\mathcal{A}}^{\hspace{0.17em}2\text{D}}-\cos \theta \hspace{0.17em}{\mathcal{S}}^{\hspace{0.17em}2\text{D}}+{\mathcal{G}}^{\hspace{0.17em}2\text{D}}/a^2+\lambda {\mathcal{V}}^{\hspace{0.17em}2\text{D}}.$$ [S7]

This functional represents the energy of a 2D drop of liquid η placed inside the cross-section $\mathrm{\Omega }$, in the grand canonical ensemble. The 2D drop η corresponds to the cross-section of the translationally invariant meniscus tongue, which is assumed to be of infinite length. In expression S7, λ is still given by Eq. S5 and therefore does not impose a constraint on the volume ${\mathcal{V}}^{\hspace{0.17em}2\text{D}}$. In fact, in this interpretation, [S5] is a generalized Kelvin equation (25), and the value of λ is essentially the pressure at which there is thermodynamic coexistence between two phases: capillary liquid (a completely full capillary) and capillary gas (a completely empty capillary).

The above physical argument implies that there is no absolute minimum of the functional [S2] when the functional [S7] attains negative values. It is, therefore, sufficient condition for the non-existence of equilibrium solutions. The fact that it is indeed a necessary and sufficient condition for the nonexistence of any solution of Eq. S4 has been proved recently in the more mathematical context of functions of bounded variation by Obersnel et al. (19).

Note that, owing to the symmetries of Eq. S1, the emptying line is always symmetric about $\theta =90\mathrm{°}$ for capillary cross-sections invariant under a $180\mathrm{°}$ rotation (e.g., ellipses, rectangles,…), and for any up–down symmetric configuration (e.g., an equilateral triangle with a vertical side).

Numerical Method

To obtain the emptying line for a given capillary geometry ($\mathrm{\Omega }$ and ϕ), we must solve Eq. S6 for each value of the contact angle θ. To do this, we find first the minimum of [S7] for a given value of the capillary length a, and compute its energy. The emptying line corresponds to the value of a for which this energy is zero. This is a deceptively difficult task for two main reasons:

• i)A formal minimization of the functional [S7] yields the differential equation of a 2D drop inside the capillary cross-section under gravity, with the anticipated boundary condition that the drop must touch the capillary walls with the contact angle θ. In Cartesian coordinates, this equation reads

$$\frac{\eta ″\left(x\right)}{{\left(1+\eta \prime {\left(x\right)}^2\right)}^{3/2}}\hspace{0.17em}=\hspace{0.17em}\pm \hspace{0.17em}\frac{1}{a^2}\left(x\sin \varphi +\eta \cos \varphi \right)+\lambda ,$$ [S8]

where the sign refers to the liquid being below ($+$) or above ($-$) the gas at the point $\left(x,\eta \left(x\right)\right)$. In general, the presence of gravity precludes any analytical solution, and numerical methods must be adopted. Additionally, this equation is known to exhibit multiple solutions (26). The emptying line corresponds to the smallest value of the gravity acceleration (the largest value of a) for which Eq. S6 is verified. If the energies of two different solutions vanish for the same value of a, this means that there exist two equivalent (yet different) emptying mechanisms for the capillary.

• ii)In addition to their shape, the location of the drops (the starting point of integration) is not known a priori, which increases the complexity of the problem.

To solve these problems, we parametrize the perimeter of the capillary cross-section $\partial \mathrm{\Omega }$ with a variable t. Each value of the parameter $t\in \left[-\pi ,\pi \right)$ refers to a unique point in the perimeter $\left(x_{\partial \mathrm{\Omega }}\left(t\right),y_{\partial \mathrm{\Omega }}\left(t\right)\right)$. Next, we define a function $\mathrm{\Psi }\left(t\right)$ as the value of [S7] that is obtained from integration of the drop equation starting at the point $\left(x_{\partial \mathrm{\Omega }}\left(t\right),y_{\partial \mathrm{\Omega }}\left(t\right)\right)$ making the correct angle θ with the capillary wall. As the initial point of integration and the derivative are known, the integration can be performed, akin to a shooting method, ending when the drop reaches another point on the wall. In general, the contact angle condition is not verified at this second point of contact. However, because the parameter t spans the entire perimeter, all drops satisfying the contact angle condition at both points of contact are necessarily included, and occur at specific values of t. These drops correspond to the stationary points of the functional $E^{\hspace{0.17em}2\text{D}}\left[\eta \right]$, and appear as extrema of the function $\mathrm{\Psi }\left(t\right)$. Note, however, that not every extremum of $\mathrm{\Psi }\left(t\right)$ corresponds necessarily to a stationary point of $E^{\hspace{0.17em}2\text{D}}\left[\eta \right]$, with the exception of the global minimum of $\mathrm{\Psi }\left(t\right)$, which is a guaranteed minimizer of $E^{\hspace{0.17em}2\text{D}}\left[\eta \right]$ and, indeed, its global minimum.

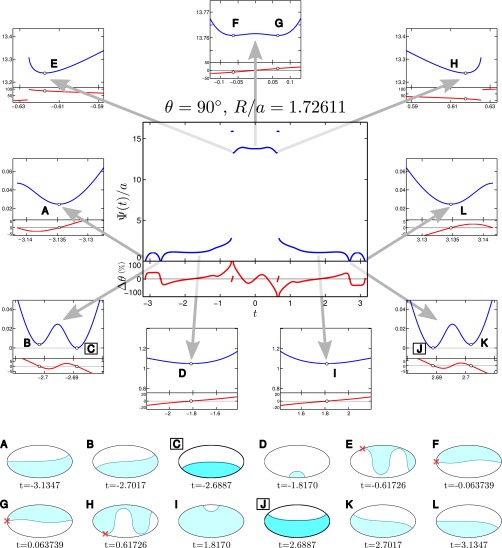
What makes the phenomena of capillary emptying so rich is that solutions to the Young–Laplace equation may disappear abruptly, as pointed out by Finn (26). This means that the function $\mathrm{\Psi }\left(t\right)$ is discontinuous, and displays an extraordinary sensitivity to the capillary geometry and to changes of the variables θ and a. This is illustrated in Fig. S3, where the two global minima of $\mathrm{\Psi }\left(t\right)$ represent different emptying mechanisms.

Fig. S3.

Blue line: Function $\mathrm{\Psi }\left(t\right)$ for the point ($\theta =90\mathrm{°}$, $R=1.72611a$) on the emptying line of a horizontal capillary with an elliptical cross-section ($x_{\partial \mathrm{\Omega }}^2+\left(1/4\right)y_{\partial \mathrm{\Omega }}^2=R^2$) oriented at an angle $\varphi =90\mathrm{°}$. Red line: Relative error in the contact angle condition $\mathrm{\Delta }\theta$ at the second point of contact [check the definition of $\mathrm{\Psi }\left(t\right)$ in the main text]. This error vanishes at all stationary points of the functional [S7]. Blowups: Details of $\mathrm{\Psi }\left(t\right)$ and $\mathrm{\Delta }\theta$ for all minima of the function $\mathrm{\Psi }\left(t\right)$. A–L: Drop shapes corresponding to each of the minima of $\mathrm{\Psi }\left(t\right)$. Drops C and J correspond to the absolute minima of $\mathrm{\Psi }\left(t\right)$ and, hence, of the functional [S7]; as $\mathrm{\Psi }\left(t\right)$ vanishes at these two minima, they verify Eq. S6 and, therefore, represent equivalent (yet different) cross-sections of the (infinitely long) meniscus at capillary emptying. Drops A, B, D, I, K, and L are stationary points of the functional [S7]; they do not represent emptying mechanisms, as their value of $\mathrm{\Psi }$ is positive. Drops E–H are minima of $\mathrm{\Psi }\left(t\right)$ but not stationary points of [S7], because the second point of contact of these drops with the capillary walls (red crosses) does not display the correct contact angle.