Adaptive integration of habits into depth-limited planning defines a habitual-goal–directed spectrum

Significance

Solving complex tasks often requires estimates of the future consequences of current actions. Estimates could be learned from past experience, but they then risk being out of date, or they could be calculated by a form of planning into the future, a process that is computationally taxing. We show that humans integrate learned estimates into their planning calculations, saving mental effort and time. We also show that increasing time pressure leads to reliance on learned estimates after fewer steps of planning. We suggest a normative rationale for this effect using a computational model. Our results provide a perspective on how the brain combines different decision processes collaboratively to exploit their comparative computational advantages.

Abstract

Behavioral and neural evidence reveal a prospective goal-directed decision process that relies on mental simulation of the environment, and a retrospective habitual process that caches returns previously garnered from available choices. Artificial systems combine the two by simulating the environment up to some depth and then exploiting habitual values as proxies for consequences that may arise in the further future. Using a three-step task, we provide evidence that human subjects use such a normative plan-until-habit strategy, implying a spectrum of approaches that interpolates between habitual and goal-directed responding. We found that increasing time pressure led to shallower goal-directed planning, suggesting that a speed-accuracy tradeoff controls the depth of planning with deeper search leading to more accurate evaluation, at the cost of slower decision-making. We conclude that subjects integrate habit-based cached values directly into goal-directed evaluations in a normative manner.

Behavioral and neural evidence suggest that the brain uses distinct goal-directed and habitual systems for decision-making (1–5). A goal-directed system exploits an individual’s model, i.e., their knowledge of environmental dynamics, to simulate the consequences that will likely follow a choice (6) (Fig. 1A). Such evaluations, which assess a decision-tree expanding into the future to estimate the total reward, adapt flexibly to changes in environmental dynamics or the values of outcomes. Evaluating deep trees, however, is computationally expensive (in terms of time, working memory, metabolic energy, etc.) and potentially error-prone. By contrast, the habitual system simply caches the rewards received on previous trials conditional on the choice (Fig. 1C) without a representational characterization of the environment (hence being called “model-free”) (6, 7). This process hinders adaptation to changes in the environment, but has advantageous computational simplicity. Previous studies show distinct behavioral and neurobiological signatures of both systems (8–18). Furthermore, consistent with the theoretical strengths and weaknesses of each system (2, 19), different experimental conditions influence the relative contributions of the two systems in controlling behavior according to their respective competencies (20–23).

Fig. 1.

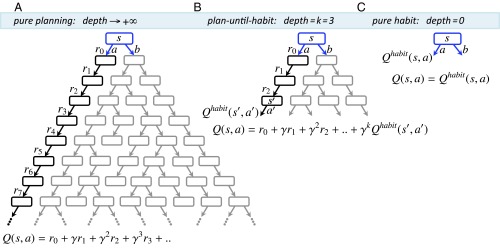
Schematic of the algorithm in an example decision problem (see SI Appendix for the general formal algorithm). Assume an individual has a “mental model” of the reward and transition consequent on taking each action at each state in the environment. The value of taking action $a$ at the current state $s$ is denoted by $Q(s,a)$ and is defined as the sum of rewards (temporally discounted by a factor of $0\le \gamma \le 1$ per step) that are expected to be received upon performing that action. $Q(s,a)$ can be estimated in different ways. (A) “Planning” involves simulating the tree of future states and actions to arbitrary depths ($k\to \infty )$ and summing up all of the expected discounted consequences, given a behavioral policy. (B) An intermediate form of control (i.e., plan-until-habit) involves limited-depth forward simulations ($k=3$ in our example) to foresee the expected consequences of actions up to that depth (i.e., up to state $s\text{'}$). The sum of those foreseen consequences ($r_0+\gamma r_1+{\gamma }^2{r}_2$) is then added to the cached habitual assessment [${\gamma }^k{Q}_{habit}(s\text{'},a\text{'})$] of the consequences of the remaining choices starting from the deepest explicitly foreseen states ($s\text{'}$). (C) At the other end of the depth-of-planning spectrum, “habitual control” avoids planning ($k=0$) by relying instead on estimates $Q_{habit}(s,a)$ that are cached from previous experience. These cached values are updated based on rewards obtained when making a choice.

Here, we suggest that individuals, rather than simply showing greater reliance on the more competent system in each condition, combine the relative strengths of the two systems in a normative manner by integrating habit-based cached values directly into goal-directed evaluations. Specifically, we propose that given available resources (time, working memory, etc.), individuals decide the depth k up to which they can afford full forward simulations and use cached habitual values thereafter. That is, individuals compute the value of a choice by adding the first k rewards, predicted by the explicit simulation, to the value of the remaining actions, extracted from the cache. We call this process an integrative “plan-until-habit” system (Fig. 1B).

The greater flexibility of planning implies that a larger $k$ in the plan-until-habit system leads to more accurate evaluations. This accuracy comes at the cost of spending more time and using more cognitive resources. If the depth is zero ($k=0$), for example because of severe time constraints, the overall plan-until-habit system would appear purely habitual. In contrast, given a sufficiently great depth ($k\to \infty$), it would appear purely goal-directed. Intermediate integer values of $k$ could permit a normative balance, whereby depth of planning is optimized with respect to available resources.

Previous studies of planning have used shallow tasks (8–18, 20–23) and have found evidence for the two extreme values of $k$. Rather than this dichotomous dependence on either goal-directed or habitual systems, we hypothesize that individuals use an integrative plan-until-habit system for decision making with intermediate values of $k$. We further hypothesize that the choice of $k$ is a covert internal decision that is influenced by the availability of cognitive resources.

To test these hypotheses, we designed a three-step task that was adapted from a popular methodology for assessing model-based and model-free control (12). Our version involves a deeper planning problem that provides the opportunity for subjects to exhibit a plan-until-habit strategy with an intermediate value of $k$. In brief, our human behavioral data demonstrate that individuals indeed used intermediate depths in the plan-until-habit system and that limiting the time allowed to make a decision led to significantly smaller values of $k$ (i.e., shallower goal-directed planning).

Results

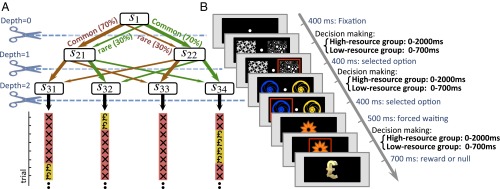
Two groups of subjects performed ∼400 trials of a three-stage task (Fig. 2). The first stage involved two choices, represented by different fractal images, each of which led commonly to one, and rarely to the other, of two second-stage states. These states were distinguished by the particular pairs of choices they afforded (again represented by distinct fractals), each of which led commonly to one, and rarely to a second, of four terminal third-stage states, as depicted in Fig. 2A. These states were again identified with distinct fractals and subjects made a forced-choice response to reveal whether or not the particular state contained a rewarding point. In this task, subjects were motivated to collect as many points as they could. The reward was deterministically present in just one terminal state at a time, staying put for a random number of trials [drawn from a suitably discretized normal distribution $X\sim N(\mu =5,{\sigma }^2=2)$] and then hopping randomly to one of the other three terminal states, and so on. Critically, subjects in the two groups were different in terms of the time subjects were allowed for responding at each stage. The high-resource group (n = 15) had 2 s to respond, whereas the low-resource group (n = 15) performed under an imposed time pressure of 700 ms (see Methods and Figs. S1–S3 for further details).

Fig. 2.

Schematic and implementation of the experimental design. (A) Each trial started from state $s_1$, which afforded two actions (illustrated by red and green arrows here). Depending on the chosen action, a common ($P=0.7$) or rare ($P=0.3$) transition was made to one of two second-stage states. Again, the subject had two choices, each associated with common ($P=0.7$) or rare ($P=0.3$) transitions to two of four third-stage states. After performing a forced-choice action at this terminal state, the subject observed whether or not the resulting third-stage state contained a reward point. In each trial, only one of the four terminal states contained reward. The reward stayed in one terminal state for a random number of trials and then transitioned randomly into one of the three other terminal states. (B) Two groups of subjects performed the task for around 400 trials: a high-resource group (n = 15) and a low-resource group (n = 15) had 2 s and 700 ms, respectively, to react at each of the three stages. See SI Appendix and Figs. S1–S3 for further details.

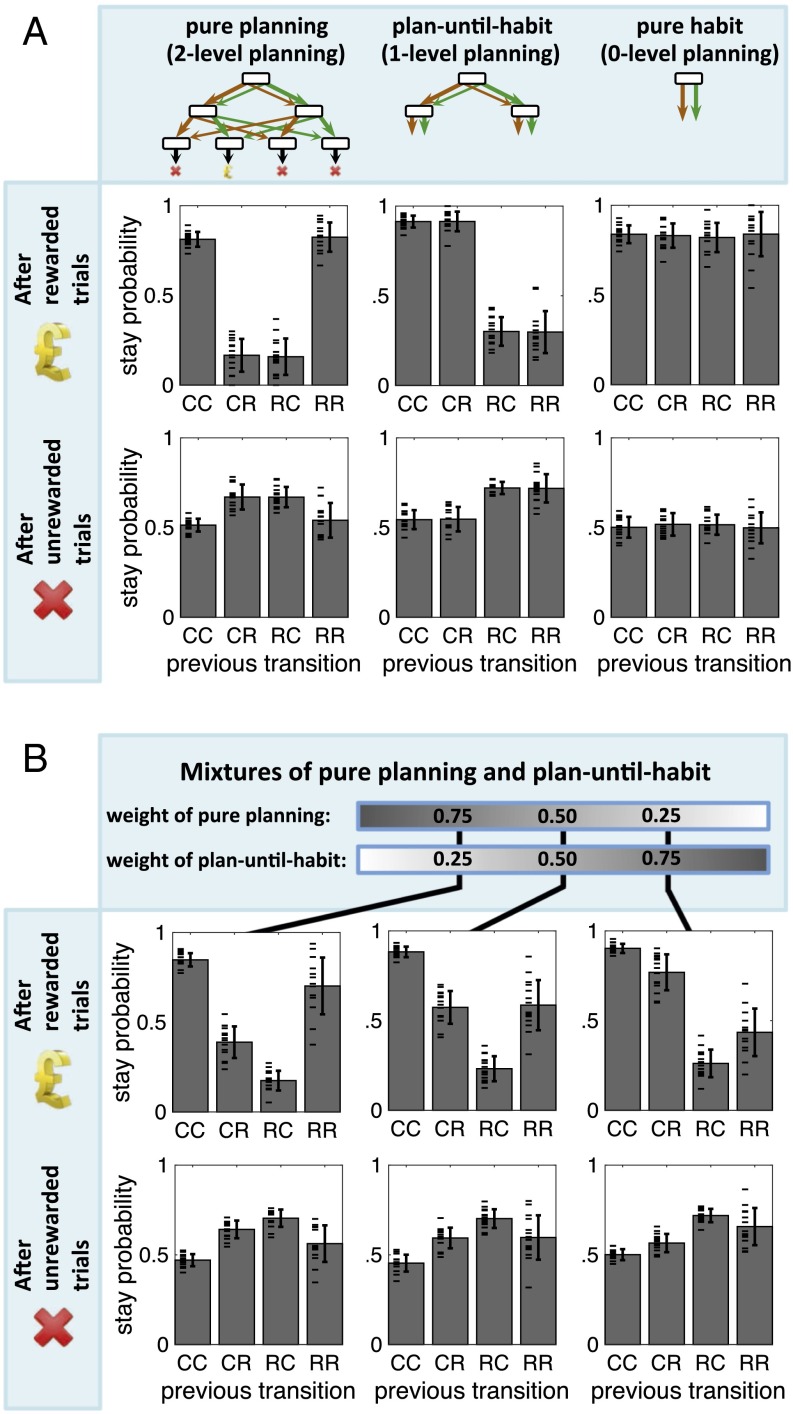
The depth of planning $k$ in this task can take on values $k=0$, $k=1$, or $k=2$, equivalent to adopting pure habitual, plan-until-habit, and pure planning strategies, respectively. Simulations showed that different agents using different depths of planning demonstrate distinctive behavioral patterns in this task (Fig. 3A). One way to examine the behavioral pattern associated with using each strategy is to classify the transitions on each trial into one of four categories: CC, CR, RC, or RR (where C and R stand for “common” and “rare,” respectively, and the first and the second letters represent the types of the first- and second-stage transitions); and the outcome of each trial into one of two categories: rewarded and unrewarded. Together, these produce 4 × 2 = 8 categories of trials. The behavioral pattern for each simulated agent was measured in terms of stay-probability profile (12), defined as the probability of repeating the same first-stage action that was chosen in the previous trial, given the category (one out of eight) of the previous trial.

Fig. 3.

Results of simulating artificial agents with different depths of planning in the task described in Fig. 2A. (A) Probabilities, predicted by the three different strategies, for repeating the first-stage choice (“stay probability”) after experiencing common (C) or rare (R) transitions for the first- and second-stage choices (concatenating the letters) and given reward (top row) or its absence (bottom row). The three different strategies (columns, from left to right) are, respectively, pure planning ($k=2$), planning-until-habit ($k=1$; planning only one step ahead, and using habitual values at the second stage), and a pure habitual system ($k=0$; implemented by a model-free temporal-difference learning). Each plot was averaged over 15 agents, each having 500 trials. (B) Mixtures (action selection based on weighted average values) of the first and second strategies, with three different weights. See SI Appendix for details of the simulations and the rationale for the parameters used.

A difference between stay-probability profiles arises from the fact that a pure planning strategy, after a rewarded trial, would target the terminal (i.e., third-stage) state that had just been visited and rewarded. Planning, therefore, would require choosing the same first-stage action as in the previous trial, if the previous trial was of the types CC or RR, but choosing the other action if the previous trial was CR or RC. The plan-until-habit strategy after a rewarded trial, however, would target the “second-stage” state that was visited, overlooking the ensuing terminal state or whether it was reached after a common or rare second-stage transition. This strategy would imply choosing the same first-stage action as in the previous trial, only if the first transition in the previous trial was of type C. Finally, the purely habitual strategy after a rewarded trial would simply repeat the choice that was made and thus reinforced in the previous trial (see Methods and Fig. S4 for details of simulations, and Fig. S5 for the effect of using different eligibility traces in the Q-learning algorithm used for implementing the habitual strategy).

We also simulated mixture strategies in which the values of the first-stage choices were weighted averages of values computed separately by pure planning and plan-until-habit strategies. As expected, the stay-probability profiles of such mixture strategies were mixtures of the stay-probability profiles of the two separate strategies, proportional to the weights given to each strategy (Fig. 3B).

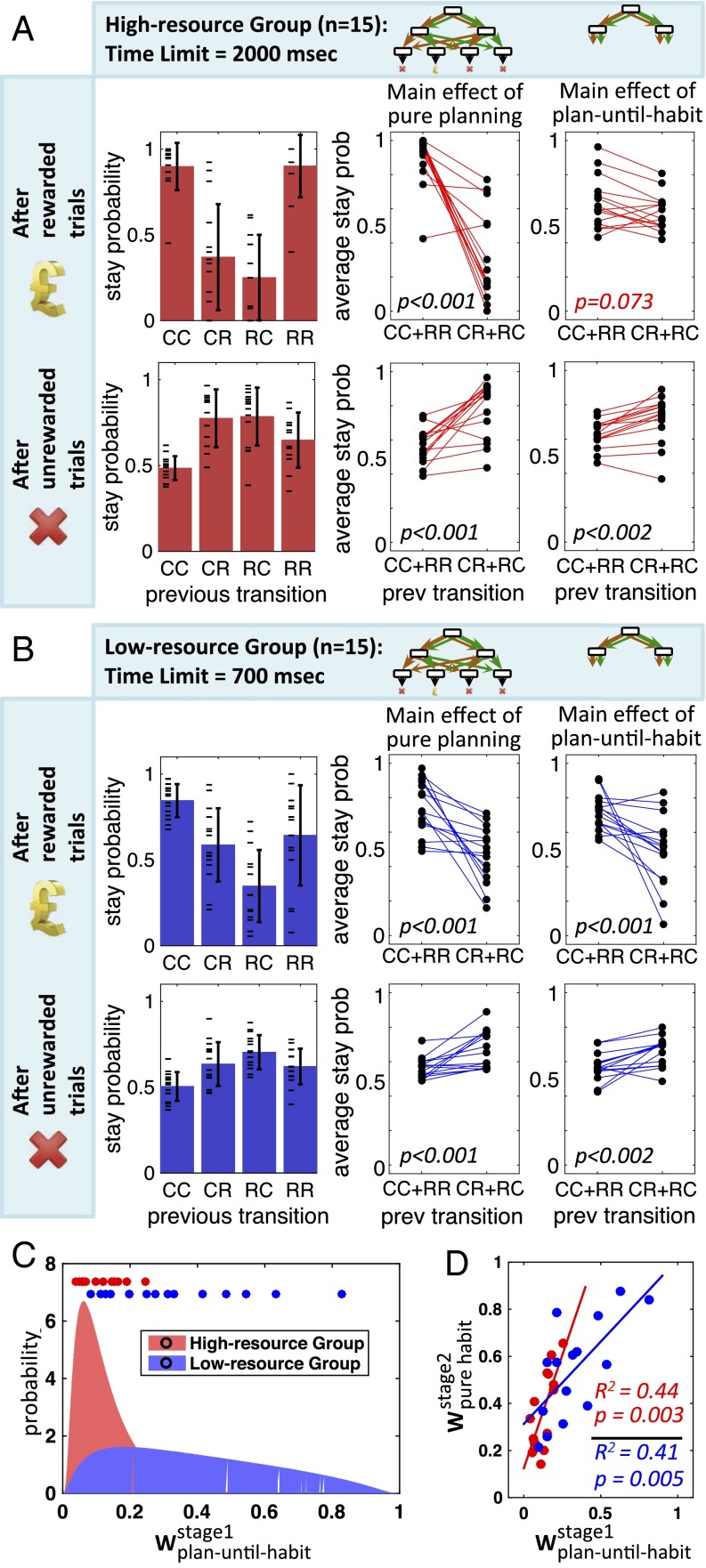
We tested patterns of stay-probability in participants. As expected, the stay probability profile in the high-resource group showed a significant pure planning effect after both rewarded ($P<0.001$, nonparametric Wilcoxon signed-rank test was used for this and all following stay-probability tests) and unrewarded trials ($P<0.001$) (Fig. 4A). By contrast, the planning-until-habit effect was only significant after unrewarded trials ($P<0.002$) and not rewarded ones ($P=0.073$) (see Methods for details of statistical analyses). For the low-resource group of subjects, the main effects of both pure planning and plan-until-habit strategies were significant after both rewarded and unrewarded trials ($P<0.001$ for both strategies after rewarded trials, and $P<0.002$ for both strategies after unrewarded trials) (Fig. 4B).

Fig. 4.

Behavioral results. Both high-resource (A) and low-resource (B) groups show significant effects of using pure planning (middle column), but only the low-resource group shows a significant effect of using the plan-until-habit strategy (right column) after both rewarded and unrewarded trials. Each black circle represents the average stay probability for one subject, after the indicated types of trial. (C) Model-fitting results show that the weight $W_{plan-until-habit}^{stage1}$ of using the plan-until-habit strategy at the first stage of the task is significantly smaller in the high-resource group than that in the low-resource group ($P<0.01$). The two curves show the probability distribution of $W_{plan-until-habit}^{stage1}$ in the two groups. Circles show the median of the distribution of $W_{plan-until-habit}^{stage1}$ for each of the subjects. (D) Within both groups, there is a strong correlation across subjects between $W_{plan-until-habit}^{stage1}$ and the weight $W_{habit}^{stage2}$ of using the pure habit strategy (against using the planning strategy) at the second stage. Each circle represents the medians of $W_{plan-until-habit}^{stage1}$ and $W_{habit}^{stage2}$ for a single subject. Wilcoxon signed-rank test (nonparametric) was used in A and B. Spearman’s rank correlation coefficient test (nonparametric) was used in D.

We further predicted that increased time pressure would decrease the depth of planning, resulting in a weaker reliance on the planning, but stronger reliance on the plan-until-habit strategy. Supporting this prediction, the planning effect was stronger in the high- compared with the low-resource group, after both rewarded ($P=0.011$) and unrewarded ($P=0.027$) trials. Conversely, the plan-until-habit effect was stronger in the low- compared with the high-resource group after rewarded trials ($P=0.034$). This latter difference, however, was not significant after unrewarded trials ($P=0.9$) (see Methods for details).

Together, these model-agnostic stay-probability analyses show that when under time pressure, human subjects choose a limited depth for forward simulation by integrating habits into planning. Further analysis, using mixed-effect lagged logistic regression analysis (24), corroborated these results showing a decaying effect on choice probability, of events (i.e., transition types and reward) at several lags relative to the current trial (see Figs. S6 and S8 for simulations and Fig. S7 for empirical data).

Note that switching to habitual values at the pruned branches is essential in our task. That is, simply pruning the decision tree after one level of planning and not switching to habitual values, as suggested in previous work (25, 26), would estimate zero values for both first-stage choices, because there is no reward available at the first stage of the task. This strategy would predict indifference between the two first-stage choices, as opposed to the distinctive stay-probability pattern that is predicted by the plan-until-habit strategy and evident in our experimental data.

To confirm our results, we used a hierarchical Bayesian method to fit a comprehensive collection of hybrid models to the experimental data to find the model that best explained the data from each group. Each hybrid model incorporated a weighted combination of one or more of the planning, plan-until-habit, and habitual strategies, such that all possible combinations were considered. As part of inference, the combination weights were fitted to data from each group (see Methods for details). In both groups of subjects, the best hybrid models (in terms of integrated Bayesian information criterion) consisted just of the pure planning and plan-until-habit strategies (Fig. S9). That is, both groups of subjects used both pure planning and plan-until-habit strategies, but not the pure habitual strategy, for making their choices at the first stage of the task. The weight of the plan-until-habit strategy, however, was significantly smaller in the high-resource than the low-resource group (permutation test; $P<0.01$) (Fig. 4C and Fig. S10), corroborating the model-agnostic, stay-probability analysis that showed only a weakly significant presence of the plan-until-habit strategy in the high-resource group (Fig. 4A). Combined, these analyses demonstrate the use of both planning and plan-until-habit strategies in both groups of subjects, with plan-until-habit being more pronounced under increased time pressure (for classification performance, see confusion matrix in Fig. S11). Synthetic data generated by simulating the best-fit model to data captured qualitative and quantitative patterns of stay-probabilities reported in Fig. 4 (Fig. S12).

When arriving at the second stage of the task, only one step remains before the terminal states. Thus, subjects can adopt a depth of planning of either zero or one, corresponding to pure habitual and pure planning strategies, respectively. Model-fitting results showed a combination of both these strategies at the second stage, in both groups of subjects (with the weight of the habitual system being 0.37 ± 0.18 for the high-resource group, and 0.59 ± 0.23 for the low-resource group). This result confirms previous demonstrations of habitual and goal-directed strategies in depth-limited tasks (8–18, 20–23). Furthermore, across subjects within both groups, the weight of using the plan-until-habit strategy at the first stage was correlated with the weight of using the pure habitual strategy at the second stage (Fig. 4D). This finding implies that subjects with more limited planning capacities demonstrate this trait at both stages of the task.

Discussion

Our results imply an adaptive integration of planning and habit-based decision processes. Previous accounts of interaction between the two processes have mostly focused on competition (2, 12, 22), where one of the two processes that is more competent in a condition takes control over behavior. Here, we showed that the integrative plan-until-habit framework sometimes masquerades as two dichotomous systems when the task design only allows for pure habitual or pure planning strategies. Our task was specifically designed so that a nonboundary depth that requires integration of the two systems can also be adopted, rendering habitual and goal-directed responding as two extremes of a spectrum. Our results show that humans are equipped with a much richer repertoire of strategies, than just two dichotomous systems, for coping with the complexity of real-life problems as well as with limitations in their cognitive resources. Therefore, the factors that have been shown or suggested to influence competitive combination in favor of habitual responding, such as working memory load (13), opportunity cost (27, 28), stress (22), or the one we examined directly, namely time (19, 29), would all be expected to favor shallower trees and thus relatively greater dominance of habits.

Another recent study suggests that humans plan (18) toward goals and that targeted goals are reinforced when subjects are rewarded, resulting in higher tendency of targeting those goals in the future. This model, too, cannot explain the behavioral profiles in our results, and predicts a stay-probability pattern similar to that of a pure habitual system (Fig. 1A, right column). In fact, targeting the state (either on the second or third stage of our task) that was targeted in the previous trial would require taking the same action that was chosen in that trial. This strategy predicts a high stay probability after rewarded trials, regardless of the transition category.

The previous, discrete, distinction between goal-directed and habitual decision making has been used to illuminate several psychiatric disorders such as addiction (30) and obsessive-compulsive disorder (31, 32). Recent interpretations in psychiatry (33) favor the notion that these and other diseases are best considered in terms of spectra rather than binary distinctions. It will be most interesting to see whether classifying individuals according to their preferred depths of planning (i.e., on a gradient between goal-directed and habitual decision-making) provides a richer and more accurate correlate of dysfunction.

Our task’s simple dissociation of different forms of habitual and goal-directed interaction leaves for future work richer possibilities, including different depths of planning in different parts of the tree, or indeed using other heuristic value-estimation methods other than model-free learning, such as a rollout mechanism as in Monte Carlo tree search (34) or using social advices. There are also more extreme forms of habits than the sort of cached values that we considered (35). A more general question concerns individuating the operations associated with building trees of possible future states, populating leaves or branches with habitual values, or simulated steps or rewards, and propagating the results up the tree to estimate the future worth of current possible actions. Examining these metacontrolling internal evaluative actions (36), and indeed their neural substrates in versions of cortico–amygdala–striatal interactions that realize more straightforward habitual and goal-directed control of external actions, offers the prospect of enriching our understanding of normative control and providing a more comprehensive picture of the normative control of control.

Methods

Subjects.

Thirty subjects (17 female, 13 male) were recruited form the SONA subject pool (https://uclpsychology.sona-systems.com/Default.aspx?ReturnUrl=/) with the restrictions of being London-based university students and aged between 20 and 30 y. The study was approved by the University College London Research Ethics Committee (Project ID 3450/002). Subjects gave written informed consent before the experiment.

Experimental Procedure.

The subjects were randomly divided into two groups of 15. The only difference in the task setup between the two groups was that the reaction-time limitations during both practice and test sessions were 2,000 ms and 700 ms for the high-resource and the low-resource groups, respectively.

All subjects first experienced a practice session, consisting of 60 trials. To make it easier for subjects to understand the task, the probability of common and rare transition during this session were P = 0.8 and P = 0.2, respectively. Subjects then performed the test session during which, a new set of fractal images were used for representing state-action pairs. The number of trials performed during the test session was 350 and 500 for the subjects in the high-resource and the low-resource groups, respectively, because of the difference in time constraints. Fractal images associated with states and state-action pairs were counter balanced across subjects. Also, the motor-level actions (pressing the right vs. left shift keys on a computer keyboard) required for choosing each option (i.e., the two fractal images) at each state was counterbalanced across trials.

Subjects were instructed that they would be compensated with a payment between £7 to £30, depending on the total number of points they collected during the test session. See SI Appendix for further details.

Model.

A Markov decision process (MDP) is defined by a quintuple $\left(S,A,P_{.}\left(.,.\right),R_{.}\left(.,.\right),\gamma \right)$, where $S$ is a finite set of states, $A$ is a finite set of actions, $P_a\left(s,s\text{'}\right)=p\left(s_{t+1}=s\text{'}|s_t=s,a_t=a\right)$ is the probability that taking action $a$ in state $s$ at time $t$ will lead to state $s\text{'}$ at time $t+1$, and $R_a\left(s,s\text{'}\right)$ is the expected immediate reward received after transition to state $s\text{'}$ from state $s$ and action $a$. Finally $\gamma \in \left[\mathrm{0,1}\right]$ is the discount factor.

The goal, in our case, is to choose a policy $\pi$ that maximizes the expected discounted sum over a potentially infinite time-horizon:

$${\langle {\displaystyle \sum _{t=0}^{\infty }{\gamma }^t{R}_{a_t}\left(s_t,s_{t+1}\right)}\rangle }_{\pi }$$ [1]

by choosing actions $a_t=\pi \left(s_t\right)$.

To achieve this goal, reinforcement learning (RL) (6) algorithms define a further function, $Q\left(s_t,a_t\right)$, which estimate the expected sum of discounted rewards for taking action $a_t$ at state $s_t$, and then continuing optimally (or according to a given policy). Two putative variants of the RL algorithm are model-free (MF) and model-based (MB) RL, equivalent to habitual system and goal-directed planning system, respectively.

One MF algorithm (Q-learning), when at state $s_t$, uses prior Q-values $Q^{habit}(s_t,a)$ of all possible actions $a$ for making a choice. Upon performing the chosen action, $a_t$, the agent receives an instantaneous reward $r_t$ from the environments and arrives in a new state $s_{t+1}$. Based on these observations, the agent computes a reward prediction error, ${\delta }_t$:

$${\delta }_t=r_t+\gamma \underset{a\text{'}}{\max }{Q}_t^{habit}(s_{t+1},a\text{'})-Q_t^{habit}(s_t,a_t).$$ [2]

This prediction error is then used to update the prior Q-value of the experienced state-action pair:

$$Q_{t+1}^{habit}\left(s_t,a_t\right)=Q_t^{habit}\left(s_t,a_t\right)+\alpha {\delta }_t,$$ [3]

where $0<\alpha \le 1$ is learning rate.

One MB algorithm, by contrast, learns the reward ${\widehat{R}}_{a_t}\left(s_t,s^{\text{'}}\right)$ and transition ${\widehat{P}}_{a_t}(s_t,s\text{'})$ functions of the MDP and on the basis of those, computes Q-values in a recursive value-iteration process:

$$Q_t^{plan}\left(s_t,a_t\right)={\displaystyle \sum }_{s\text{'}}{\widehat{P}}_{a_t}(s_t,s\prime )\left({\widehat{R}}_{a_t}\left(s_t,s\prime \right)+\gamma \underset{a\text{'}}{\max }{Q}_t^{plan}(s\prime ,a\prime )\right).$$ [4]

No matter whether a MB or a MF algorithm is used for estimating the value of actions, a “soft-max” rule can be used to choose among possible actions, with probabilities proportional to the exponential of the Q-values:

$$\pi :\hspace{0.17em}p\left(a_t=a|s_t\right)\propto e^{\beta Q\left(s_t,a\right)},$$ [5]

where $\beta$ is the rate of exploration.

Because both MF (habit) and MB (planning) systems have previously been shown to be involved in decision-making in animals and humans, Eq. 4 suggests the obvious possibility of limiting the depth of recursive value-iteration to a certain value (terminating tree expansion), and substituting the term $Q_t^{plan}(s\text{'},a\text{'})$ at that depth with the MF estimation $Q_t^{habit}(s\text{'},a\text{'})$. This model is an alternative to previous suggestions of calculating the two values separately and then finding a weighted average. We call these a plan-until-habit model.

For the specific case of our experiment, choosing a depth of two in the integrative plan-until-habit algorithm is equivalent to a pure MB system (Fig. S4A). Choosing a depth of zero, on the other hand, is equivalent to a pure MF system (Fig. S4C).

As an intermediate strategy, choosing a depth of one is equivalent to using Eq. 4, but replacing the term $Q_t^{plan}(s\text{'},a\text{'})$ with $Q_t^{habit}(s\text{'},a\text{'})$ (Fig. S4B). That is:

$$Q_t^{plan-until-habit}\left(s_t,a_t\right)={\displaystyle \sum }_{s\text{'}}{\widehat{P}}_{a_t}(s_t,s\prime )\left(R_{a_t}\left(s_t,s\prime \right)+\gamma \underset{a\text{'}}{\max }{Q}_t^{habit}(s\prime ,a\prime )\right).$$ [6]

Simulations.

In our task, the habitual Q-values can be computed by a temporal difference learning alogorithm with an eligibility trace of zero (λ = 0) or one (λ = 1). The values of the free parameters in simulations were the mean value of the parameters recovered from the low-resource group of human subjects. That is, ${\alpha }_{plan}=0.8$, ${\alpha }_{habit\left(\lambda =1\right)}={\alpha }_{habit\left(\lambda =0\right)}={\rho }_{habit\left(\lambda =1\right)}={\rho }_{habit\left(\lambda =0\right)}=0.55,{\omega }_2=0.59$, and $\beta 1=8.2$, $\beta 2=4.2$. $\beta 1$ and $\beta 2$ are the rates of exploration at the first and the second stages of the task, respectively. Also, $\alpha$ denotes learning rate. See SI Appendix for further details.

Stay-Probability Analysis.

To test the main effect of the planning model we first computed a variable $E_{p,\hspace{0.17em}Rew}$ as:

$$E_{p,\hspace{0.17em}Rew}=p\left(a_{1,t}=a_{1,t-1}|T_{t-1}=CC,R_{t-1}=1\right)+p\left(a_{1,t}=a_{1,t-1}|T_{t-1}=RR,R_{t-1}=1\right)-p\left(a_{1,t}=a_{1,t-1}|T_{t-1}=CR,R_{t-1}=1\right)-p\left(a_{1,t}=a_{1,t-1}|T_{t-1}=RC,R_{t-1}=1\right).$$

We then used the nonparametric Wilcoxon signed-rank test on $H_0:E_{p,\hspace{0.17em}Rew}>0$. This method tests whether stay-probability [$p(a_{1,t}=a_{1,t-1})$] after rewarded trials ($R_{t-1}=1$) was higher when the transition type in the previous trial ($T_{t-1}$) was CC or RR, compared with when it was CR or RC. A similar procedure was used to test the main effect of planning after “nonrewarded” trials by replacing $R_{t-1}=1$ with $R_{t-1}=0$.

Similarly, to test the main effect of the plan-until-habit strategy, we first computed a variable $E_{p-h,Rew}$ as:

$$E_{p-h,Rew}=p\left(a_{1,t}=a_{1,t-1}|T_{t-1}=CC,R_{t-1}=1\right)+p\left(a_{1,t}=a_{1,t-1}|T_{t-1}=CR,R_{t-1}=1\right)-p\left(a_{1,t}=a_{1,t-1}|T_{t-1}=RC,R_{t-1}=1\right)-p\left(a_{1,t}=a_{1,t-1}|T_{t-1}=RR,R_{t-1}=1\right).$$

We used Wilcoxon signed-rank test on $H_0:E_{p-h,\hspace{0.17em}Rew}>0$. A similar procedure was used to test the plan-until-habit effect after nonrewarded trials by replacing $R_{t-1}=1$ with $R_{t-1}=0$.

As explained in Results, the plan-until-habit effect in the first group is only significant after nonrewarded and not after rewarded trials. This effect could be simply due to the low number of samples in the latter condition compared with the former.

To compare between the two groups, we used the nonparametric Mann–Whitney U test on $H_1:E_{p,\hspace{0.17em}Rew}(\text{high}-\text{resource}\hspace{0.17em}\text{group})>E_{p,\hspace{0.17em}Rew}(\text{low}-\text{resource}\hspace{0.17em}\text{group})$ and also on $H_1:E_{p-h,\hspace{0.17em}Rew}\left(\text{high}-\text{resource}\hspace{0.17em}\text{group}\right)<E_{p-h,\hspace{0.17em}Rew}(\text{low}-\text{resource}\hspace{0.17em}\text{group})$. We used similar procedures for testing the same effects after nonrewarded trials.

Model-Fitting.

Different combinations of the four models mentioned in Simulations were fit to data. For the hybrid model that contained all of the four individual models, the Q-values for the two top-stage action were computed as follows:

$$\text{for}\hspace{0.17em}\text{all}\hspace{0.17em}{a}_1\hspace{0.17em}\in \left\{a,b\right\}\hspace{0.17em}:$$

$$Q_t^{mix}\left(s_1,a_1\right)={\omega }_{\mathrm{1,1}}{Q}_t^{plan}\left(s_1,a_1\right)+{\omega }_{\mathrm{1,2}}{Q}_t^{plan-until-habit}\left(s_1,a_1\right)+{\omega }_{\mathrm{1,3}}{Q}_t^{habit\left(\lambda =1\right)}\left(s_1,a_1\right)+{\omega }_{\mathrm{1,4}}{Q}_t^{habit\left(\lambda =0\right)}\left(s_1,a_1\right)+{\omega }_{1,stayBias}\phi \left(a_1,a_{1,t-1}\right),$$

where ${\omega }_{1,stayBias}$ is a stay bias, and the function $\phi (.,.)$ returns 1, if the action in consideration is the same action that was taken in the previous trial, and returns 0, otherwise. The stay bias, as also used in previous similar works (12), captures choice perseveration/switching bias in behavior.

The other n = 4 weights for the n = 4 individual models were computed as follows:

$${\omega }_{1,i}=\{\begin{array}{cc}\frac{e^{{\varpi }_i}}{e+{{\displaystyle \sum }}_{i\in \left\{1,..,n-1\right\}}{e}^{{\varpi }_i}}& if\hspace{0.17em}i\in \left\{\mathrm{1,2,3}\right\}\\ \frac{e}{e+{{\displaystyle \sum }}_{i\in \left\{1,..,n-1\right\}}{e}^{{\varpi }_i}}& if\hspace{0.17em}i=4\end{array},$$

where ${\varpi }_i\hspace{0.17em}(i\in \left\{\mathrm{1,2,3}\right\})$ were the free parameters of the model. SI Appendix, Eq. 19 guarantees that all of the weights, ${\omega }_{1,i}\hspace{0.17em}(i\in \left\{\mathrm{1,2,3,4}\right\})$, of the individual models are greater than zero, and they sum to one.

The same logic used in the two above equations was also used for fitting other hybrid models were only three, two, one, or zero, out of the four individual models were available.

The expectation-maximization method was used, separately for each group, to infer group-level distributions over each of the free parameters of a given hybrid model. That is, for each free parameter a distribution was inferred by estimating two hyperparameters: mean and variance of a Gaussian distribution (Laplace approximation of the parameter values).