Lability of secondary organic particulate matter

Significance

Mass lability of atmospheric organic particulate matter, meaning its tendency to evaporate, is an important property in the mechanisms governing the climate and health effects. This property can be governed by both the volatility and the molecular diffusivity of the constituent organic species. An experimental approach presented herein highlights a nonlabile-to-labile transition at a threshold humidity for material representative of anthropogenic particulate matter. The behavior differs markedly from materials representing biogenic sources, which lack such a transition. Accounting for this transition in the interpretation of laboratory datasets collected at low relative humidity can potentially reduce discrepancies between modeled and observed concentrations of particulate matter in urban regions.

Abstract

The energy flows in Earth’s natural and modified climate systems are strongly influenced by the concentrations of atmospheric particulate matter (PM). For predictions of concentration, equilibrium partitioning of semivolatile organic compounds (SVOCs) between organic PM and the surrounding vapor has widely been assumed, yet recent observations show that organic PM can be semisolid or solid for some atmospheric conditions, possibly suggesting that SVOC uptake and release can be slow enough that equilibrium does not prevail on timescales relevant to atmospheric processes. Herein, in a series of laboratory experiments, the mass labilities of films of secondary organic material representative of similar atmospheric organic PM were directly determined by quartz crystal microbalance measurements of evaporation rates and vapor mass concentrations. There were strong differences between films representative of anthropogenic compared with biogenic sources. For films representing anthropogenic PM, evaporation rates and vapor mass concentrations increased above a threshold relative humidity (RH) between 20% and 30%, indicating rapid partitioning above a transition RH but not below. Below the threshold, the characteristic time for equilibration is estimated as up to 1 wk for a typically sized particle. In contrast, for films representing biogenic PM, no RH threshold was observed, suggesting equilibrium partitioning is rapidly obtained for all RHs. The effective diffusion rate D_org for the biogenic case is at least 10³ times greater than that of the anthropogenic case. These differences should be accounted for in the interpretation of laboratory data as well as in modeling of organic PM in Earth’s atmosphere.

Atmospheric particulate matter (PM) has significant effects on climate, air quality, and human health (1). Globally, organic compounds constitute 20 to 90% of the submicron PM mass. Most of this mass is produced by the oxidation and subsequent condensation of biogenic and anthropogenic gaseous precursors as secondary organic material (SOM) (2). Parameterizations of produced mass have been developed based on the oxidation of different types of volatile organic compounds (VOCs) in environmental chambers (3, 4). Chemical transport models (CTMs) based on these parameterizations, however, do not successfully account for the PM concentrations measured in the atmosphere (5, 6), and closing the gap between model and measurements is a major research goal (7–10).

The parameterizations embedded in the CTMs largely assume rapid mass transfer for the partitioning of semivolatile organic compounds (SVOCs) between the particle and vapor phases (11, 12). Without considering the kinetic factors, this equilibrium approach may not, however, always accurately represent processes on the timescales of the laboratory experiments or of atmospheric transformations. Observations suggest that atmospheric organic PM and laboratory-generated SOM can be liquid, semisolid, or solid, depending on many factors (13–15), such as the VOC precursor (16, 17), temperature (18, 19), and relative humidity (RH) (20–23). The current debate focuses on whether viscosities might be high enough and consequently diffusivities low enough that, under some conditions, mass transfer shifts from rapid to kinetically limited (24–29). The approach to equilibrium for some atmospheric and laboratory scenarios might extend to many hours or even days (30), in some cases exceeding the typical lifetime of PM in the atmosphere. Predictions of atmospheric PM concentrations, implemented in many CTMs for an assumption of equilibrium within an hourly time step, might become inaccurate.

Herein, the evaporation rates of organic films were used to address the foregoing topics, especially the dependence on RH. A quartz crystal microbalance (QCM; SI Appendix, Fig. S1) was used to measure the time course of film mass. Evaporation rates (nanograms per minute) and vapor mass concentrations (micrograms per cubic meter) were obtained from these datasets. RH was regulated inside the QCM cell to affect the water content of the film. Greater water content, in turn, acted as a plasticizer to increase the molecular diffusivities and hence evaporation rates of film constituents (15, 16, 20, 21, 31, 32). The datasets of evaporation rates were inverted by a physical model to infer corresponding molecular diffusivities.

Results

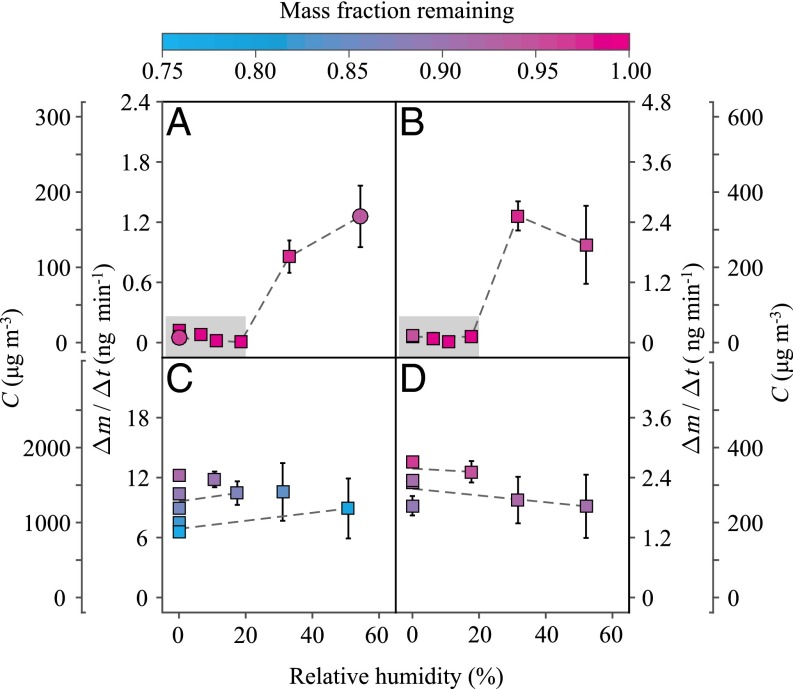
QCM-determined evaporation rates are plotted in Fig. 1 for several different values of RH. Ordinate axes show the observed evaporation rates (Δm/Δt; nanograms per minute) and the corresponding vapor mass concentrations (C; micrograms per cubic meter) (SI Appendix). For films derived from aromatic precursors such as toluene and m-xylene, which are both representative of anthropogenic sources, the evaporation rates were low below 20% RH (Fig. 1 A and B). For this RH regime, the film/vapor interface was isolated from the interior region of the film because of slow species diffusivity in the condensed phase. As a result, after a transient period, the remaining surface species were depleted of high-volatility compounds, and the vapor mass concentration over the film was low. The overlying vapor was limited to dynamic exchange with the depleted surface region because species diffusion from the interior to the surface was negligible. This kinetic constraint implies that only local thermodynamic equilibrium was established between the vapor and the depleted surface region, rather than global equilibrium between the vapor and the entirety of the film. The inferred slow species diffusivity is also consistent with the shattering of toluene-derived particles after poking by a sharp needle at low RH, indicating a glassy state and high viscosity (33).

Fig. 1.

Evaporation rates (Δm/Δt) over different organic films as a function of increasing RH. Secondary axes show the vapor mass concentrations C associated with the evaporation rates. The VOC precursors and the oxidants used to grow the film are (A) toluene + OH, (B) m-xylene + OH, (C) isoprene + OH, and (D) α-pinene + O₃. Replicate experiments are represented by different marker types. Error bars correspond to 1σ of uncertainty in the QCM measurements. During the course of measurement, the films evaporated. The beginning of the evaporation curves is displayed in this figure, and the full dataset is shown in Fig. 2. The data points are colored (see overbar) by the mass fraction of the organic film remaining at the time that C was measured. The dashed lines connect data points of similar mass fractions to guide the eye. Gray shading represents conditions of slow species diffusivity in the organic film and corresponds to conditions where C was kinetically controlled.

The evaporation rate abruptly increased between 20% and 30% RH (Fig. 1 A and B). This result, obtained on increasing RH, was unexpected based on thermodynamic considerations alone. A higher film water content caused by exposure to increased RH decreases the intrinsic thermodynamic volatility of the film. Both dilution (i.e., Raoult’s law) and increased hydrogen bonding drive this thermodynamic effect (23). The increase in evaporation rate was, instead, a consequence of shifting from slow to fast kinetic factors. The rate of species diffusion from the interior to the surface became competitive with the rate of evaporation from the surface to the vapor.

For RH above 30%, the uptake of water into the film increased species diffusivity in the film sufficiently that fast kinetic factors prevailed. As a result, the evaporation rates were independent of RH (Fig. 1 A and B). In this regime, the diffusion of high-volatility compounds from the interior to the surface was faster than evaporation, so that a homogeneous composition was maintained throughout the film. Global thermodynamic equilibrium was established for the vapor, the surface region, and the interior region. As a result, higher vapor concentrations were observed.

For films derived from α-pinene and isoprene, which are representative of biogenic sources, changes in RH did not strongly affect evaporation rates (Fig. 1 C and D). This result indicates that species diffusivity remained high, even at low RH. Vapor mass concentrations represented global equilibrium. In agreement, SOM particles derived from α-pinene and isoprene did not shatter after poking, even at the low RH (22, 34), implying low viscosities and high species diffusivities.

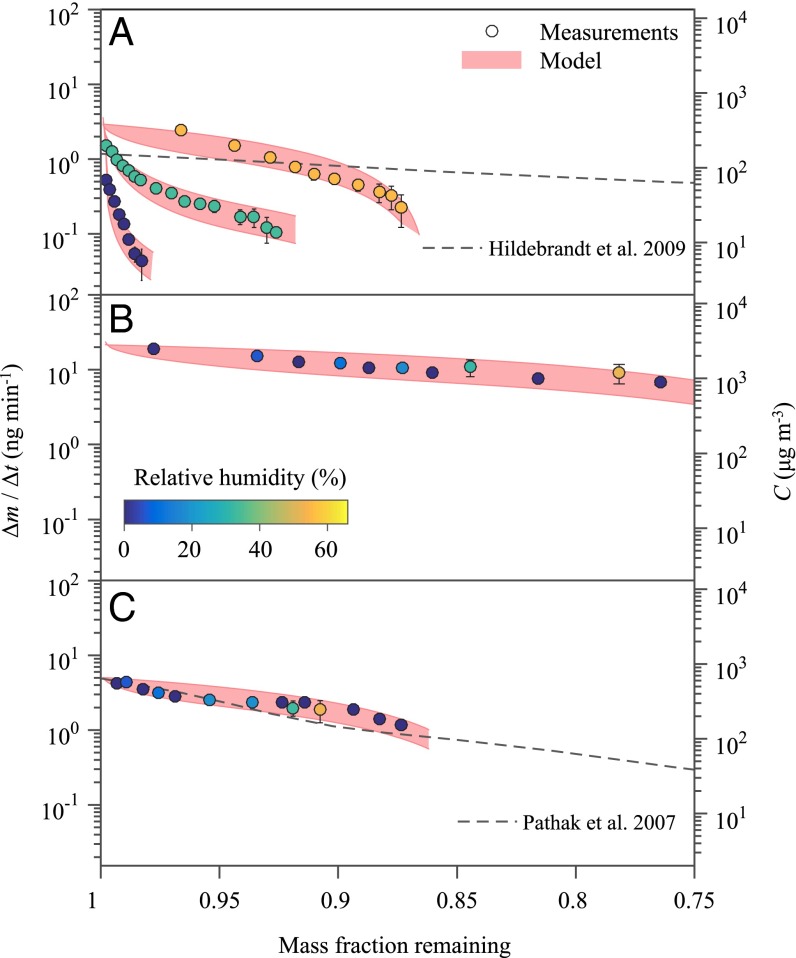
In line with the foregoing understanding, evaporation rates slowed as the remaining mass fraction decreased (Fig. 2). The most-volatile components evaporated early. For the aromatic-derived films, the vapor mass concentration over the film decreased at low RH (Fig. 2A). Even as the overall remaining mass fraction was high at low RH, the surface region was nevertheless highly depleted of volatile species, and these species were unable to diffuse from the interior to the surface region of the film. For SOM derived from α-pinene and isoprene, because of the high evaporation rates, changes in film composition were significant enough that the overall volatility of the film decreased during the observation time (Fig. 2 B and C). The vapor mass concentrations represented the most-volatile fraction (10 to 25%) of the SOM. Water content did not have an observable effect on the volatility of the biogenic films, at least for the range of experimental conditions from <5% RH to 50% RH.

Fig. 2.

Evaporation rates (Δm/Δt) and vapor mass concentrations C for decreasing remaining mass fraction of different organic films. The VOC precursors and the oxidants used to grow the film, the mass concentrations M_org of the organic PM from which the film was grown, and the initial masses m₀ of the film are (A) toluene + OH, M_org = 90 μg m⁻³, m₀ = 6,100 ng; (B) isoprene + OH, M_org = 90 μg m⁻³, m₀ = 15,300 ng; and (C) α-pinene + O₃, M_org = 90 μg m⁻³, m₀ = 19,100 ng. Experiments conducted at different RH are separated by coloring of the data points. Red shading shows the results of model 1 for describing the observations (Results). For comparison, different lines represent parameterizations reported in the literature (SI Appendix, Table S3). The parameterizations were developed in a framework that assumed lability, meaning equilibrium between the gas and particle phases.

The results of Fig. 2 were modeled for each film to retrieve the effective diffusivity D_org of the constituent organic molecules of the films. To do so, modeled evaporation rates were constrained to the measured evaporation rates in a diffusive multislab model (SI Appendix). The slab representing the surface region was taken as in local thermodynamic equilibrium with the overlying vapor. The compositions of the surface slab and the interior slabs depended on species diffusion. For initialization, model parameters of intrinsic volatility were constrained by the vapor mass concentrations when global thermodynamic equilibrium prevailed at high RH (SI Appendix, Table S1). These intrinsic volatilities were assumed to hold also at low RH. The assumption is that the effects of shifting water content on intrinsic volatility were not important across the range of investigated RH values. Effective diffusivity was held constant with remaining mass fraction. The model obtained values of D_org when kinetic factors slowed evaporation at low RH for the aromatic-derived films. At high RH, the model obtained lower limits of D_org for both the anthropogenic and biogenic films.

The modeling framework considered two possibilities for describing intrinsic volatility. Model 1 approximated the composition of the organic film as one volatile component and one nonvolatile component. Model 2 considered a more complex description that the film consisted of one nonvolatile component and four components of decadal volatility from 10¹ µg m⁻³ to 10⁴ µg m⁻³ (4). The results of model 1, represented by the shaded region in Fig. 2, capture the experimental observations within measurement uncertainty. The associated values of D_org vary with film type and RH (SI Appendix, Table S2). These values represent an effective diffusivity between the volatile and nonvolatile components. The values obtained for model 2 were the same within the uncertainty ranges as those of model 1 (SI Appendix, Fig. S2 and Table S2), and model 1, as the simpler of the two models, was selected herein for further presentation.

A comparison between the volatilities measured in this study and those predicted based on model l parameterizations reported in the literature is shown in Fig. 2 (points and lines, respectively; see SI Appendix, Table S3 for additional information). For appropriateness to the present study, possible literature sources were screened for comparable RH, M_org, NO_x concentration, and temperature. In the classical approach, the parameterizations are formulated based on the relative mass yield of each species taken to have decadal volatility to infer volatility (4). In this formalism, species are partitioned between the gas and particle phases, depending on particle organic mass concentration M_org. The parameterizations can lead to inaccurate predictions when the underlying assumption of global equilibrium between the vapor and the particles does not hold (25). This approach also fails mechanistically when the condensed-phase reactions significantly alter SOM composition and thus volatility (12, 35). By comparison, the QCM-based approach has the advantage that direct measurements of volatility, without inference, are made.

The lines in Fig. 2 representing the literature formalism were initialized by using the M_org value listed in each panel. For comparison with these values of M_org, mass concentrations of organic PM are typically under 10 µg m⁻³ over relatively unpolluted forested regions (36) but can approach more than 100 µg m⁻³ in polluted megacity regions around the globe (37). The listed values of M_org, in conjunction with the relative mass yields of the different species of decadal volatility (SI Appendix, Table S3), were used to calculate the associated values of vapor mass concentration C for an initial mass fraction of unity. The lines were then drawn by plotting the corresponding value of C as the mass evaporated in clean air of infinite volume (SI Appendix).

For the toluene-derived film, for RH < 30%, the literature formalism overestimates the observed evaporation rate or, equivalently, the vapor mass concentration (Fig. 2A). For the highest RH of the present study (55%), the vapor mass concentrations were in the volatility-limited regime, but the literature formalism still overestimates the measured evaporation rates for a remaining mass fraction below 0.9. The explanation can be that the presented literature was developed for RH < 20%; parameters for comparison at higher RH do not appear to be available in the literature. The direct measurements of volatility reported herein suggest that the literature formalism developed under the assumption of rapid mass transfer is not an accurate predictor of actual evaporation rates when kinetic factors regulate rates of dynamic exchange between the vapor and condensed phases. The toluene-derived film has a larger fraction of low-volatility products than that predicted by the literature formalism (SI Appendix, Tables S1 and S3).

Based on the review article of Carlton et al. (38) and a survey of more recent literature carried out as part of the present study, there appears to be no literature parameterization available for isoprene photooxidation under low-NO_x conditions for the high M_org values (90 μg m⁻³) of the present study. In this case, no comparison is shown in Fig. 2B between observations and a literature formalism. Although there are parameterizations in the literature for lower M_org, extrapolation has large uncertainties because the relative mass yields of higher volatility bins are not well constrained by datasets collected at lower M_org.

In contrast to the results for the toluene-derived film, the literature formalism predicts well the observed volatility of the α-pinene–derived film (Fig. 2C). The agreement is consistent with an absence of kinetic limitations on evaporation, both in the observations of this work and in the rapid mass transfer assumed in the literature formalism. In regard to related studies, Vaden et al. (24) reported that the evaporation of α-pinene–derived SOM particles was slower than the literature formalism. The initial interpretation was a kinetic limitation, which would be contrary to the findings herein. A follow-up study by the same group, however, showed that the evaporation did not depend on RH (39), and a revised interpretation was offered that oligomerization, rather than diffusion, may reduce the evaporation rate below that expected by the literature formalism (40).

Some caveats to the comparisons between observations and parameterizations in Fig. 2 are as follows. The comparisons are based on using M_org as the singular normalization quantity between the organic films and the chamber-based results. Factors other than M_org can also influence chemical composition and hence volatility. The extent of oxidation, for example, can vary depending on conditions of production and processing, and these factors can be expected to affect composition and volatility (12, 41, 42). The comparative analysis to the literature formalism also assumes that the film composition corresponds to the particle composition when still suspended as an aerosol at the M_org values listed in the panels of Fig. 2. The requirement is that significant evaporation does not take place before the QCM measurements. In this regard, experiments were begun within 10 min of film preparation (SI Appendix), which can be compared with timescales of 10 h to 24 h over which the curves in Fig. 2 were collected, suggesting that most of the evaporation did indeed occur within the QCM cell. Another possible confounding factor for the interpretation herein could be oligomer decomposition associated with the RH changes, which would influence the intrinsic volatility. This possibility is excluded based on the analysis of infrared spectroscopy data (SI Appendix).

Discussion

When considered together, volatility as a thermodynamic parameter and diffusivity as kinetic parameter delineate the lability of atmospheric organic PM. The implications can be considered for a scenario representative of the atmospheric dilution of anthropogenic organic particles accompanying the dispersion of an urban pollution plume. At time zero, the volatile and nonvolatile components of an individual particle are completely mixed with one another throughout both the interior and surface regions of the particle, and the surrounding air is clean and of infinite extent. As time evolves, the evaporation of molecules from the particle consists of a sequence of events: diffusion from the interior region to the surface region of the particle; evaporation from the surface region into the vapor; and transport through the boundary layer surrounding the particle into the infinite extent of the gas, among other possible processes (43). Any one of these processes, as a slow step, can limit the overall evaporation rate.

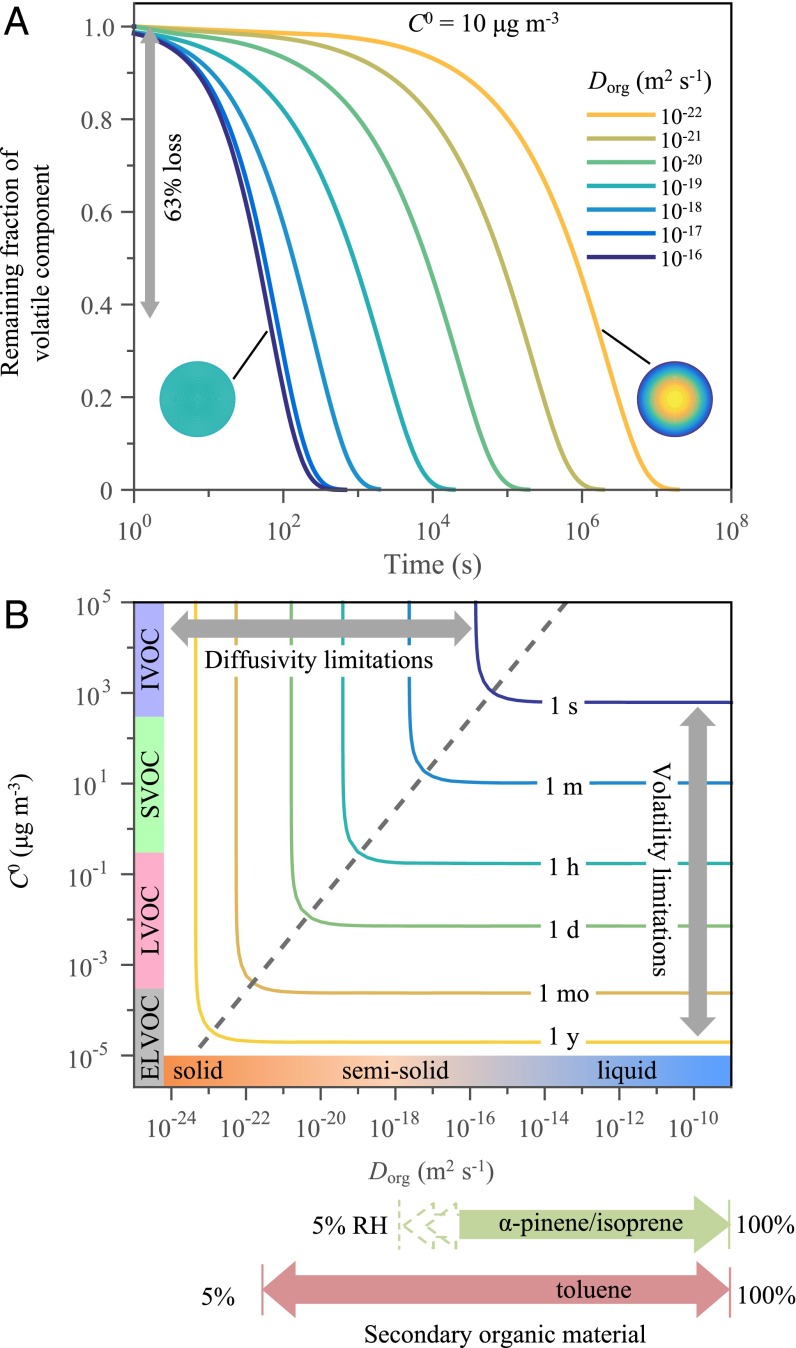
A numerical approach, using the framework of model 1 for a spherical geometry (SI Appendix), is used herein to simulate these linked processes and respond to the slow step. A characteristic time of evaporation is defined as the time required for depletion of 63% of the volatile component. Fig. 3A displays the temporal evolution of the remaining mass fraction of the volatile component for several different values of D_org. The curves are drawn for a vapor mass concentration C⁰ of 10 μg m⁻³ for the volatile component in pure form, denoted by the superscript 0. The diameter of the particle is 100 nm. The characteristic time for 63% loss increases from 10² s to 10⁶ s as effective diffusivity decreases from 10⁻¹⁶ m² s⁻¹ to 10⁻²² m² s⁻¹. In the limit that particle diameter does not significantly change during the course of evaporation, the simulation results are independent of the relative initial concentrations of the two components.

Fig. 3.

Simulated evaporation of a mixed particle of volatile and nonvolatile components. (A) Simulated remaining fraction of the volatile component during evaporation for different values of effective diffusivity D_org between components in the particle phase. Data are shown for a volatile component having a vapor mass concentration C⁰ in its pure form of 10 µg m⁻³. The initial particle diameter is 100 nm. The coloring of the inset cartoon circles represents either the absence of chemical gradients (i.e., in a particle having high diffusivity and corresponding to the maximum rate of evaporation) or the presence of chemical gradients (i.e., in a particle having low diffusivity and limiting the overall rate of evaporation). The characteristic time for evaporation is defined for 63% loss of the volatile component (gray arrow). (B) Contour plot of the characteristic time for evaporation as a function of D_org and C⁰. Characteristic volatilities associated with intermediate volatility species (IVOC), SVOC, LVOC, and ELVOC are labeled on the ordinate. Ranges of diffusivities typically associated with solids, semisolids, and liquids are labeled on the abscissa (20). For comparison, the ranges estimated in this study for the RH-dependent effective diffusivities of α-pinene–derived and toluene-derived SOM are shown in heavy arrows along the abscissa.

Additional simulations of the characteristic time for evaporation were systematically performed across a matrix of D_org and C⁰ values for a 100-nm particle. Fig. 3B shows a contour plot of the results. For sufficiently low diffusivity (i.e., to the left of the dashed line), the slow diffusion of molecules within the particle limits the overall evaporation rate. The characteristic time for evaporation decreases for greater D_org. A gradient in composition develops inside the particle, and the concentration of the volatile component in the surface region becomes small (right circle in Fig. 3A). The compositional gradient develops because diffusion from the interior region to the surface region is not fast enough to replace molecules that are evaporating from the surface region.

At a critical juncture, represented by the dashed line Fig. 3B, diffusion becomes fast enough that a different process limits the overall rate of evaporation. This process is transport through the boundary layer surrounding the particle, and it represents the maximum rate of evaporation. This rate is proportional to the vapor mass concentration C⁰ of the volatile component in pure form. Concentrations of the volatile and nonvolatile components remain homogeneously mixed throughout both the interior and surface regions during evaporation (left circle in Fig. 3A).

Delineating the boundary between diffusivity and volatility limitations is important for correctly understanding and accurately modeling the lifecycle of atmospheric particles. The boundary occurs at a critical value ξ* for the parameter ξ defined by ξ = D_org/C⁰. Riipinen et al. (44) used this parameter to delineate the relative importance of diffusivity in particle growth, but it also holds for evaporation. The dashed line in Fig. 3B corresponds to C⁰ = D_org/ξ*. For ξ < ξ*, diffusivity must be explicitly considered for accurate modeling of evaporation and molecular partitioning between the gas and particle phases. For submicron particles, ξ* values range from 10⁻⁹ m⁵ s⁻¹ kg⁻¹ to 10⁻¹¹ m⁵ s⁻¹ kg⁻¹ (SI Appendix) depending on the Knudsen number and the mass accommodation coefficient (SI Appendix, Fig. S3). A value of ξ* of 3.78 × 10⁻¹⁰ m⁵ s⁻¹ kg⁻¹, representing unity mass accommodation and 100-nm particles for the pressures and temperatures of the atmospheric boundary layer, applies to Fig. 3B.

For the scenario of accumulation-mode particles in polluted suburban regions, SVOC species having volatilities of 1 µg m⁻³ to 100 µg m⁻³ are of most interest for gas−particle partitioning. Partitioning includes both evaporation and condensation. For SVOC species, the characteristic timescales for these two processes are typically similar, although condensation can be more complex than evaporation in some cases (30). For D_org of 10⁻¹⁶ m² s⁻¹ to 10⁻¹⁸ m² s⁻¹ or less, the characteristic time for evaporation of SVOC species becomes limited by diffusion (Fig. 3B). Similar transition values have been suggested in previous theoretical studies using more detailed models (30, 45). Associated characteristic times are up to several minutes (Fig. 3B). For comparison, most CTMs have time steps on the order of tens of minutes or longer. The 1-h contour, implying errors in any models making predictions that assume equilibration of reversible vapor−particle partitioning within each model time step, occurs in Fig. 3B for species having volatilities C⁰ of less than 1 μg m⁻³ (i.e., LVOC species) or with in-particle diffusivities of less than 10⁻¹⁹ m² s⁻¹.

For SVOC species, the foregoing results indicate that the equilibration assumption prescribed in many CTMs is valid when moderate or high RH prevails in the atmospheric boundary layer. Low RH prevails in several megacities during certain times of the year (33). At these times, the gas-to-particle mass transfer of SVOCs can be impeded, and associated oxidation pathways and, ultimately, atmospheric fates can become altered. For extremely low VOC (ELVOC) and some low VOC (LVOC) species, evaporation can generally be considered slow compared with diffusivity for the characteristic timescales relevant to atmospheric processes (Fig. 3B). Condensation, however, can be fast, depending on the species production rates in the gas phase (30), and, in these cases, irreversible uptake should be an appropriate description. Even in these cases, however, diffusivity determines whether the interior composition of the particle becomes well mixed or not, which can influence physical properties and chemical reactivity (16).

The results reported herein, in conjunction with other recent work (16, 21), provide an opportunity to test for possible relationships among transitions with RH in mechanical properties, chemical reactivity, and mass lability. Properties of organic PM can vary with many factors. For example, the viscosity of α-pinene–derived SOM can vary by two orders of magnitude for shifting M_org (46). Comparison of properties for organic PM produced within the same research group, suggesting a possible decrease in variability caused by extrinsic factors, provides one important perspective. Three comparative studies in that regard are summarized herein. For the toluene-, α-pinene–, and isoprene-derived organic PM, Bateman et al. (21) reported transitions in mechanical properties from semisolid to liquid at 60 to 80%, 70 to 90%, and 40 to 60% RH, respectively. For these same three systems, Li et al. (16) reported transitions in chemical reactivity of 35 to 45%, 35 to 45%, and <5% RH, respectively, meaning that reactivity greatly increased although the particles were not yet liquid. The present study directly measured evaporation rates to infer the diffusion limitations in gas−particle partitioning. For the three systems, transitions in evaporation rates occurred at 20 to 30%, <5%, and <5% RH, respectively, implying that mass lability greatly increased even though the particles were not yet liquid and not yet reactive. A comparison of these RH ranges suggests that correlations among transitions of mechanical properties, chemical reactivity, and mass lability are weak. Hence, based on the collected datasets, using any one of these as a surrogate to predict another is not recommended.

The present study highlights the low evaporation rates and hence low effective diffusivity for organic PM derived from aromatic precursors. By implication, aromaticity of the precursor and, by extension, of highly conjugated products appears to be important. Many chamber experiments for aromatic-derived SOMs were conducted at low RH and with observation times measured in hours (3, 9, 47–50). For toluene-derived material for RH < 5%, the characteristic time for SVOC equilibration is estimated as on the order of 1 wk for a 100-nm particle, based on the results of the present study (Fig. 3B). The estimated value of 3.0 × 10⁻²² m² s⁻¹ for D_org is at least 10³ times smaller than that of the isoprene- and α-pinene–derived PM at low RH (SI Appendix, Table S2). The mechanism of particle growth from aromatic precursors can then be inferred as adsorptive partitioning and layer-by-layer growth (51). By comparison, for biogenically derived organics, particles tended to grow by absorptive partitioning, although some in-particle diffusion limitation remained possible in large particles at low RH. All other factors being equal, growth by absorptive partitioning tends to be faster than by adsorptive partitioning. Parameterizations based on an assumption of equilibrium in absorptive partitioning for datasets that were collected when adsorptive or diffusion-limited partitioning prevailed can be biased. When used in CTMs, these parameterizations may erroneously represent partitioning and PM production at elevated RH. Atmospheric measurements appear to suggest that models are most inaccurate in urban regions for which aromatic species contribute significantly to the production of atmospheric organic PM (6).

The solidity of aromatic-derived SOMs at low RH may also bias the measured particle mass yield in chamber experiments. In chamber experiments, wall loss competes with the growth of particles for the scavenging of low-volatility oxidation products from the vapor phase (9). The possible importance of wall loss compared with particle growth depends on relative mass transfer rates, which determine the timescales for vapor−particle and vapor−wall interactions. In agreement with the low effective diffusivity reported in the present study, Zhang et al. (9) reported slow mass transfer of vapor species to the particles relative to the wall for toluene photooxidation, resulting in more pronounced vapor wall loss, and particle mass yield was underestimated by a factor of 2 to 4. Because of the kinetic limitations of species diffusion inside the particles, the low-volatility oxidation products in the vapor preferably deposited on the chamber walls instead of contributing to the mass concentration of organic PM. In contrast, for α-pinene ozonolysis, Nah et al. (52) reported that condensation of organic vapors is dominated by quasi-equilibrium growth, and the extent of wall loss is smaller than that of the toluene system. The findings of the present study are consistent with this report.

In summary, the results presented herein suggest that effective diffusivity can influence the lability of atmospheric organic PM in different ways for particle types derived from Earth’s different natural biomes compared with particles associated with regions of urban and industrial development. An RH-dependent behavior was observed for the toluene-derived SOM, indicating that diffusion limitations strongly influence this model system of anthropogenic PM. A study by Ye et al. (53), carried out independently at the same time as this work, reached a similar conclusion by a much different methodology, and the two studies thus complement and reinforce one another. For RH below 20%, organic PM produced from aromatic precursors in urban atmosphere is effectively nonlabile, implying extended residence times for semivolatile species in this type of organic PM. The behavior can be delineated within regional and global CTMs by consideration of the presented ratio quantity ξ* to simplify prediction of diffusivity compared with volatility-limited regimes. This quantity can be used in simulations of gas−particle partitioning of SVOCs to take into account the diffusivity of organic PM (30, 45). The simulated mass concentrations, particle sizes, and physiochemical properties of atmospheric organic PM can change, ultimately influencing predictions of associated climate and health effects. Quantifying the effective diffusivity of organic PM, as a key factor for kinetic modeling, can potentially reduce uncertainties in the assessment of these effects. More broadly, the QCM technique used in this study provides an approach for measuring volatility and diffusivities for thin-film samples of tens of nanometer thickness, and this approach can be useful in various fields of research, such as material science, biomedical science, and physical chemistry.

Materials and Methods

Different types of SOM were produced in aerosol form through oxidation reactions of gaseous biogenic and anthropogenic SOM precursors in an oxidation flow reactor (OFR) (SI Appendix, Table S4) (54, 55). The aerosol particle populations were characterized by a scanning mobility particle sizer (SMPS; TSI Inc.) and an aerosol mass spectrometer (HR-ToF-AMS; Aerodyne Research Inc.). Organic films were grown by electrostatic precipitation of aerosol particles exiting the OFR onto QCM substrates (TSI 3089) (56). The evaporation rates and vapor mass concentrations of the organic films were analyzed by a QCM (Q-sense E4) equipped with a flow cell (Q-sense QSX 303). RH-regulated nitrogen gas flowed across the surface of the film. The plug flow residence time of the gas inside the QCM cell varied between 0.3 s and 0.4 s. Detailed additional information about the measurements and associated modeling is provided in SI Appendix.