From Whole-Brain Data to Functional Circuit Models: The Zebrafish Optomotor Response

SUMMARY

Detailed descriptions of brain-scale sensorimotor circuits underlying vertebrate behavior remain elusive. Recent advances in zebrafish neuroscience offer new opportunities to dissect such circuits via whole-brain imaging, behavioral analysis, functional perturbations, and network modeling. Here, we harness these tools to generate a brain-scale circuit model of the optomotor response, an orienting behavior evoked by visual motion. We show that such motion is processed by diverse neural response types distributed across multiple brain regions. To transform sensory input into action, these regions sequentially integrate eye- and direction-specific sensory streams, refine representations via interhemispheric inhibition, and demix locomotor instructions to independently drive turning and forward swimming. While experiments revealed many neural response types throughout the brain, modeling identified the dimensions of functional connectivity most critical for the behavior. We thus reveal how distributed neurons collaborate to generate behavior and illustrate a paradigm for distilling functional circuit models from whole-brain data.

Graphical Abstract

INTRODUCTION

How neurons across the brain collaborate to process information that ultimately guides behavior is not well understood. Most progress toward understanding comprehensive sensorimotor circuits has been made in invertebrates (Kato et al., 2015; Ohyama et al., 2015). For example, the processes by which environmental stimuli drive specific motor patterns in C. elegans (Bounoutas and Chalfie, 2007; Chalasani et al., 2007) and Drosophila (Borst et al., 2010; Ruta et al., 2010; Silies et al., 2014) have been dissected at the level of individual neurons and their synapses. In these cases, the stereotypy and small size of the invertebrate brain and the identifiability of its neurons were indispensable for precisely measuring neural circuit structure and dynamics.

With a few notable exceptions (Heiligenberg and Konishi, 1991; Lisberger, 2010), isolating the neural circuits implementing vertebrate behavior has only been successful for peripheral reflexes (Fink et al., 2014; Korn and Faber, 2005). This is partly due to technical limitations, as information processing in vertebrates is typically coordinated by many neurons in various brain regions (Felleman and Van Essen, 1991). Consequently, most research has focused on microcircuits that are spatially localized and functionally coherent, e.g., within the retina (Masland, 2012) or cortex (Ko et al., 2011). This leaves the understanding of central brain mechanisms linking sensation to action incomplete. Moreover, neural response properties in vertebrates appear heterogeneous and redundant (Bianco and Engert, 2015; Rigotti et al., 2013), yet the origins and significance of this redundancy and response variability remain poorly understood (Sompolinsky, 2014). Without access to brain-scale neuronal activity in well-defined behavioral contexts, it seems unlikely that we will understand why the vertebrate brain has, despite immense energy constraints, evolved its heterogeneous, multilayered architecture.

The larval zebrafish is a small and translucent vertebrate, permitting cellular resolution optical imaging of nearly all its ~100,000 neurons (Ahrens et al., 2013a). Recent studies using brain-wide imaging have revealed that sensorimotor processing is indeed widely distributed across the entire zebrafish brain (Ahrens et al., 2012, 2013a; Portugues et al., 2014). However, the overwhelming complexity of whole-brain imaging data has made it difficult to establish links between brain- and circuit-level descriptions of behavior. Such links must be established by applying both experimental and theoretical approaches to behaviors that are simple enough to characterize in mechanistic detail but sophisticated enough to engage complex sensorimotor transformations.

The zebrafish optomotor response (OMR), a position-stabilizing reflex to whole-field visual motion, offers an opportunity to dissect the central circuits underlying such a behavior using closed-loop stimulus delivery, detailed behavioral analysis, whole-brain imaging, functional perturbations, and network modeling. These approaches allowed us to follow the flow of visual information through nuclei that integrate binocular retina input to motor centers that drive turning and forward swims, resulting in a functional whole-brain circuit model that describes the sensorimotor transformation in terms of experimentally observed neural response types.

RESULTS

The Optomotor Response Is Driven by Egocentric Processing of Optic Flow

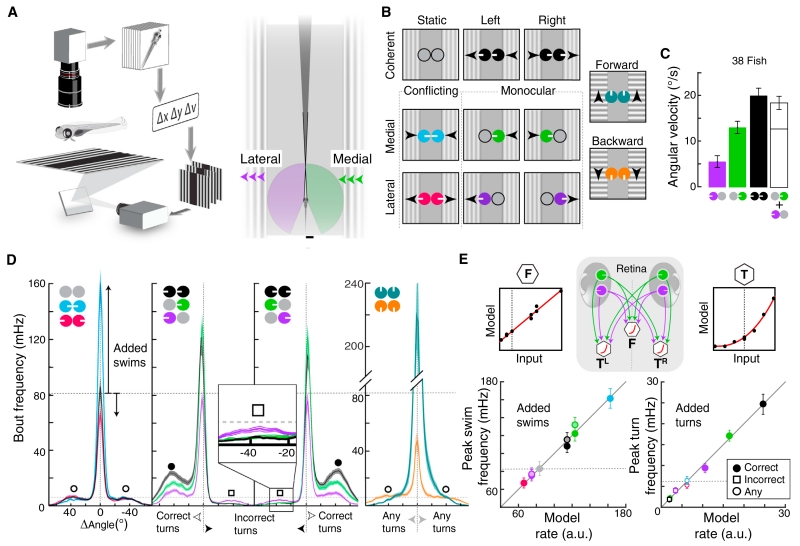
For binocular animals to perform the OMR, the brain must integrate motion signals from each eye. We thus sought to dissect this sensorimotor transformation using independent stimulus presentation to each eye. A closed-loop system allowed us to continuously update the stimulus in each monocular visual field (Figure 1A; Movie S1), ensuring that fish continually experienced a particular motion pattern relative to the body axis. For leftward or rightward motion, we labeled these component monocular stimuli egocentrically, with medial motion going toward the midline and lateral motion going away from the midline (Figure 1A, right). Following a psychophysics approach, we presented stimuli from a matrix of all possible combinations of static (no motion), medial, and lateral motion, along with forward and backward motion (Figure 1B). By comparing the behavioral responses to monocular (i.e., motion to one eye only), coherent (e.g., leftward motion comprising medial “approaching” motion to the right eye and lateral “leaving” motion to the left eye), and conflicting stimuli (i.e., “inward” medial-medial motion or “outward” lateral-lateral motion to both eyes), we quantified basic algorithmic properties by which the brain combines binocular inputs to generate a motor output.

Figure 1. Eye- and Direction-Specific Optic Flow Evoke Distinct Orienting and Locomotion Patterns.

(A) Behavioral setup. Left, freely swimming fish are monitored with a camera while moving gratings are presented. Heading (Δν) and position (Δx, Δy) are extracted to lock visual motion direction to body axis. Right, illustration of each monocular visual field (purple, green, 163°) and the small binocular overlap (dark gray, 12°). Scale bar, 500 μm.

(B) Stimulus set composed of static, medial and lateral motion, and forward and backward stimuli. Arrowheads indicate motion direction. Circular icons represent eyes, and white tick marks show the direction of motion. These icons and colors are used throughout the paper.

(C) Bar graph of average angular velocity (heading direction change per second) during behavioral responses. The white bar represents the linear combination of monocular medial and lateral motion. Error bars are SEM across fish (n = 38).

(D) Average histograms of absolute frequency per swim bout angle. Left, conflicting stimuli affect forward swim frequency (center peak, added “swims”) relative to the static condition (inward versus static, p = 6.6 × 10⁻⁶; outward versus static, p = 7.7 × 10⁻⁸, paired Wilcoxon). Inward reciprocally suppressed turns (open circles). Middle, left/right stimuli increased correct (in motion direction, filled circles) and decreased incorrect (opposite of motion direction, open squares) turn frequency (inset). Medial enhanced but monocular lateral stimuli suppressed swimming (lateral versus static, p = 0.006). Shaded error is SEM, n = 38. Right, forward stimuli increased, backward stimuli significantly reduced forward swim frequency (versus static, p = 2.1 × 10⁻⁶). n = 30.

(E) Comparison of measured bout frequencies and minimal model output. DSRGCs connect to motor centers for forward swimming (F) and left (T^L) and right turning (T^R). Left, forward swimming. Each point is the mean peak response to a stimulus; lighter center indicates leftward motion. Right, turning behavior. correct turns, filled circles; incorrect turns, open circles; non-directional stimuli, open squares. Model input-output functions for each behavioral component, top right and left. Dotted lines indicate baseline rates.

As expected, leftward and rightward coherent stimuli led to leftward and rightward turning, respectively (Figures 1C and S1A–S1C). In addition, average turning was larger to coherent motion than to monocular stimuli and were similar to the sum of the responses to each monocular component (Figure 1C). Interestingly, the contributions of medial and lateral components were not equal; medial contributed substantially more to turning than lateral. Furthermore, response latencies to stimuli containing medial motion were shorter than to stimuli containing only lateral motion (Figure S1D). Together, these observations reveal several algorithmic properties of the OMR, which are necessarily implemented in the brain: (1) the direction of whole-field coherent motion dictates the direction of behavioral output; (2) the average turning response to coherent motion approximates the sum of responses to medial plus lateral motion; and (3) despite representing environmentally equivalent motion cues, medial and lateral motion are differentially processed by the zebrafish brain to generate different behaviors.

Eye- and Direction-Specific Motion Differentially Affect Forward Swimming and Turning

Examination of discrete swim bouts (Figures S1E and S1F) revealed that histograms of individual bout angles in response to each stimulus were typically trimodal (Figures 1D, S1G, and S1H), with a central peak corresponding to forward swimming and left/right peaks corresponding to left/right turning. As these peaks changed dramatically across the stimulus set, we focused our analyses on their amplitude changes. Coherent stimuli enhanced turning in the direction of motion (“correct”) relative to the baseline static condition, while turning in the opposite direction of motion (“incorrect”) was suppressed. Similar to coherent stimuli, monocular medial stimuli increased forward swims and correct turns while suppressing incorrect turns (Figure 1D, inset). In contrast, monocular lateral stimuli slightly decreased forward swimming and modulated turning less than medial stimuli. Hidden by averaged turning responses (Figures S1B and S1C), this analysis revealed fundamental differences in the behavioral responses to conflicting stimuli. While each conflicting stimulus eliminated the turning responses observed under monocular stimulation (Figure 1D), inward stimuli enhanced forward swimming, resulting in behavior that looked much like that in response to forward motion, and outward stimuli suppressed forward swimming, mirroring backward motion responses. These data thus establish two additional algorithmic properties of the OMR. First, visual motion drives correct turns and suppresses incorrect turns, and these effects are both stronger for medial than for lateral motion. Second, turning and forward swimming are modulated separately, with medial motion driving swimming, akin to forward motion, and lateral motion suppressing swimming, akin to backward motion.

To illustrate the minimal computational requirements for these observed sensorimotor transformations, we implemented a neural circuit architecture in which direction-selective retinal ganglion cells (DSRGCs) send monocular motion signals to premotor neurons presumed to independently drive peak frequencies of turning (T) and forward swimming (F, central diagram, Figure 1E). These premotor neurons represent ventromedial spinal projection neurons (vSPNs, T) (Huang et al., 2013) and the nucleus of the medial longitudinal fasciculus (nMLF, F) (Orger et al., 2008). Forward swimming was well modeled in this architecture as the sum of monocular components (left panels, Figure 1E), with medial motion driving swimming and lateral motion suppressing it. Although turning frequencies depended nonlinearly on monocular components, a biologically plausible input-output nonlinearity could reproduce the required transformation (right panels, Figure 1E). Thus, as few as three dedicated neurons could conceivably transform direct monocular inputs into the observed pattern of forward swimming and turning, concretely instantiating the aforementioned algorithmic properties of the OMR (Figures S1H and S1I).

Whole-Brain Imaging Identifies Regions Activated during the OMR

To map brain areas for response features consistent with revealed algorithmic properties, we measured neural activity to visual motion using two-photon calcium imaging in transgenic Tg(elavl3:GCaMP5G) zebrafish. Though animals were restrained during imaging, we made motor nerve recordings (Ahrens et al., 2013b) in a subset of fish and observed a pattern of bout frequency modulation that matched freely swimming fish (Figures S2A and S2B).

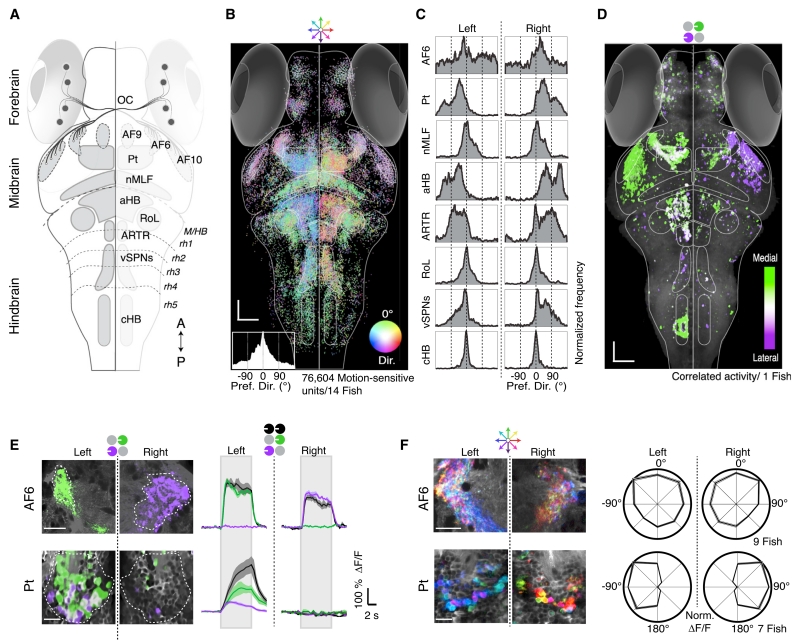
Combined with known zebrafish neuroanatomy (Figure 2A) (Burrill and Easter, 1994), these whole-brain maps highlight the route of information flow. Because the OMR was modulated by the overall direction of motion (Figures 1C, 1D, S1A–S1C), we first examined the spatial distribution of direction-selective neural units (Figure 2B), which revealed that motion information was distributed and segregated across a handful of brain areas (Figure 2C). Of the ten arborization fields (AFs) of retinal axons (Robles et al., 2014), AF6 and 10 were strongly activated by motion stimuli (Figures 2B, S2C, and S2D). Near AF6, responses in the pretectum (Pt) (Figures 2B and 2C) were lateralized, with the left Pt responding primarily to leftward motion, and the right Pt responding to rightward motion. Responses to forward motion were bilaterally distributed across the Pt. Directional signals were demixed in the hindbrain and midbrain. In particular, forward-selective neurons were anatomically segregated from lateralized left- and right-selective neurons. This response segregation is reminiscent of the behavioral segregation of forward swimming and turning.

Figure 2. Whole-Brain Activity Maps Reveal Processing Stages Underlying the OMR.

(A) Dorsal overview of zebrafish neuroanatomy. DSRGCs (black dots) project via the optic chiasm (OC) to ten contralateral retinal arborization fields (AFs). Pt, pretectum; nMLF, nucleus of the medial longitudinal fasciculus; aHB, anterior hindbrain; RoL, neurons in rhombomere 1; ARTR, anterior rhombencephalic turning region; vSPNs, ventromedial spinal projection neurons; cHB, caudal hindbrain; M/HB, midbrain-hindbrain border; rh1–5, rhombomeres 1–5. A, anterior; P, posterior.

(B) Distribution of all motion-sensitive units (n = 76,604) across 14 Tg(elavl3:GCaMP5G) fish. Each unit is a dot, color coded for preferred motion direction (see Dir. color wheel). Bottom left, histogram of direction preference. Scale bars, 50 μm.

(C) Histograms of direction preference for specific brain regions.

(D) Binocular activity map generated from sequential presentation of monocular leftward motion to each eye. Pixels are colored for medial versus lateral preference (STAR Methods). Binocular regions appear white. Anatomy in gray.

(E) Left, two-photon micrographs from single AF6 and Pt planes. Right, average ΔF/F for regions of interest (ROIs) (dashed white lines). Gray rectangles indicate stimulus presentation periods. Shaded areas are SEM over n = 10 stimulus repetitions.

(F) Left, responses to eight whole-field motion stimuli, see color wheel, top. Right, polar plots (±SEM, shaded area) of average normalized ΔF/F in n = 7 fish.

To visualize binocular integration of coherent monocular signals, we generated maps overlaying responses to monocular medial and lateral stimuli presented sequentially to the eyes (Figures 2D and S2D). While responses in the AFs were exclusively monocular, neurons in the Pt exhibited the binocular integration required of the OMR, and downstream neurons in the anterior hindbrain (aHB) and vSPNs displayed qualitatively similar binocular responses (Figures S2D and S2E). These response maps suggest a qualitative brain-scale functional-anatomical model underlying the zebrafish OMR (Figure S2F).

To move beyond map-making and characterize the local computations, we focused analyses within specific brain regions. STARting at the sensory end, we extracted fluorescence time series from motion-sensitive regions containing retinal terminals. As AF10 ablations spare the OMR (Roeser and Baier, 2003), we concentrated on AF6. Consistent with completely decussated retinal projections, responses in AF6 were exclusively monocular (Figure 2E, top). AF6 also showed localized regions of highly tuned directional responses for all direction of motion, roughly matching the size of synaptic boutons (>1 μm²) (Figure 2F, top). To test whether information arriving in AF6 is necessary for the OMR, we ablated it unilaterally and found behavioral deficits specific to contralateral eye stimulation (Figures S3A–S3C). Thus, AF6 is an important site of retinal input to the OMR circuit.

To generate the OMR, neurons must integrate this monocular information to form binocular representations. We observed neurons in the Pt (Figure 2E, bottom) that showed sustained, binocular responses and sent neurites into the ipsilateral AF6 (Figure S3D). In addition, average Pt activity reflected several algorithmic properties of the behavior, including ipsilateral inhibition to medial stimuli (Figures S3E–S3G). Moreover, the Pt showed enhanced and lateralized direction selectivity (Figure 2F, bottom; Figure S3F) and receives direct retinal input in other species (Gamlin, 2006). The Pt is thus well positioned to support the sensorimotor transformation underlying the OMR.

Pretectal Activity as a Neural Correlate of Optomotor Behavior

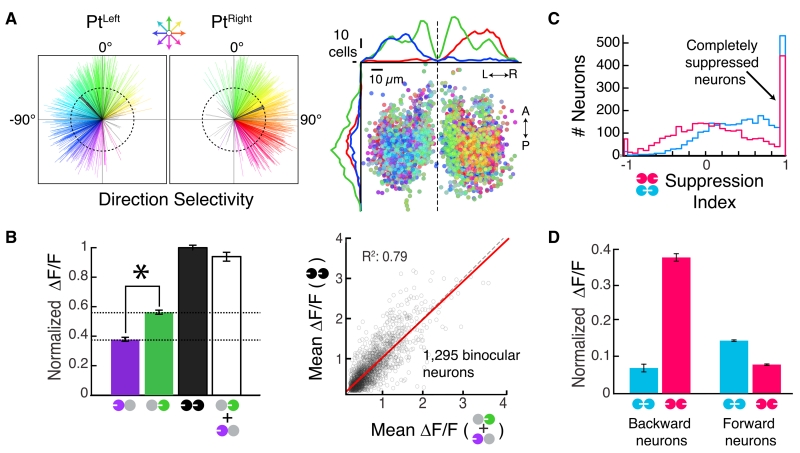
The Pt exhibited considerable diversity at the neuronal level, with individual neurons responding in various patterns to monocular, coherent, and conflicting motion (Movie S2; Figure S3F). To investigate the representation, we analyzed individual neurons (3,070 Pt neurons, 12 fish). If the Pt coordinates the OMR, it must encode all directions of motion (Orger et al., 2008). Consistent with this, most neurons were strongly tuned to a particular direction of motion (Figure 3A, left), with forward-tuned neurons clustered near the midline (Figure 3A, right). Most neurons were binocularly excited (Figure S3H). These binocular neurons preferred medial to lateral motion and linearly integrated the monocular components of whole-field motion (Figure 3B). Most Pt neurons showed at least partial suppression to conflicting motion (Figure 3C, left), mirroring the reciprocal suppression of turns seen behaviorally. Finally, we found that, much like the behavior, Pt neuron responses to forward and inward motion were associated (Figure 3D). Similar associations were seen between backward and outward motion. Together, these data provide neural correlates for many OMR algorithmic properties, suggesting that the Pt links motion information from the retina to appropriate motor actions.

Figure 3. Population Activity in the Pretectum.

(A) Left, direction selectivity vectors for neurons in the Pt (see color wheel, top). Gray, magnitudes smaller than 0.4; black, population average vectors. Right, anatomical distribution of direction preference. A, anterior; P, posterior; L, left; R, right. Dashed line, brain midline.

(B) Left, Linear binocular integration of normalized ΔF/F responses. *p = 1.2 × 10⁻³⁷, paired Wilcoxon. Bars are mean ± SEM across all neurons. Right, scatterplot of individual Pt neuron responses. Red, least-squares regression line; dashed black, unity line.

(C) Histogram of Pt neuron suppression indices (STAR Methods).

(D) Normalized ΔF/F to conflicting motion for neurons preferring either backward (−135° to +135°, n = 191) or forward (−45° to +45°, n = 678) motion.

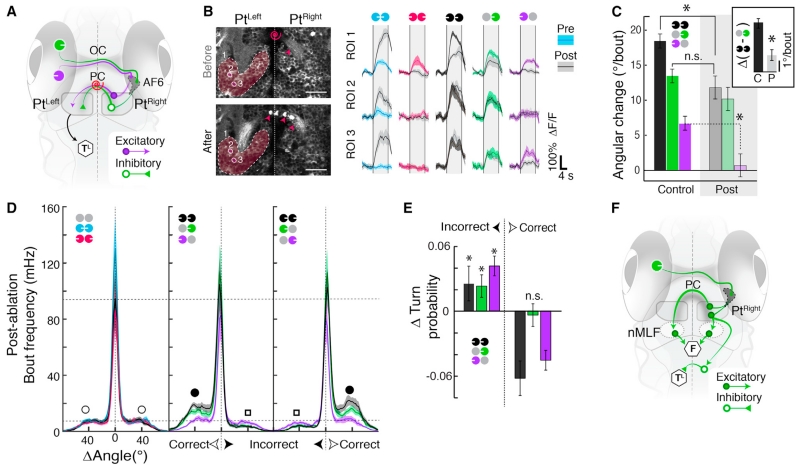
Posterior Commissure Ablation Disrupts Binocular Integration

As retinal input is exclusively monocular, binocular Pt response properties (Figures 3B and 3C) require both excitatory and inhibitory signals to re-cross the midline. In particular, coherent motion responses require interhemispheric excitation from lateral motion, and negated responses to inward stimuli require interhemispheric inhibition from medial motion. A strong anatomical candidate for these connections is the posterior commissure (PC) (Figure 4A), which passes between the left and right Pt and has been proposed to carry motion information in rodents (Giolli et al., 1984).

Figure 4. Laser Ablation of Posterior Commissure Disrupts Binocular Integration.

(A) The posterior commissure (PC) connects the left and right Pt, providing a putative conduit for lateral excitation (purple arrow) and medial inhibition (green triangle). Red spiral, target for laser ablation. (OC) optic chiasm. (T^L) motor center for turning.

(B) Left, anatomy before (top) and after (bottom) PC ablation. Red spiral, ablation site. Red arrowheads, bottom, tissue debris (compare to top). Right, average ΔF/F before (colored) and after (gray) PC ablation for the three ROIs. n = 6 stimulus repetitions. Vertical lines represent stimulus presentation periods.

(C) Average orientation change per bout in control (n = 38 fish) and ablated (post, n = 14 fish) animals. Inset, difference between coherent binocular and monocular medial responses (p = 6.2 × 10⁻⁵, unpaired Wilcoxon). C, control; P, post. Post-ablation monocular lateral versus static baseline, p = 0.2; Post-ablation coherent versus control monocular medial, p = 0.08. (*) p < 10⁻⁴, n.s., not significant, p > 0.05.

(D) Average histograms of absolute frequency per bout angle post-ablation (n = 14 fish).

(E) Change in peak turn probability (post-ablation minus control) for incorrect and correct turns. *p < 0.05.

(F) PC ablation reveals effect of medial motion on behavior. Medial motion activates the contralateral nMLF directly and the ipsilateral nMLF indirectly via the PC to drive forward swimming (F). Medial motion suppresses incorrect turns (T^L) via the PC but also via other interhemispheric connections, potentially in the hindbrain.

After confirming that Pt neurons project through the PC (Figure S4A), we laser-ablated the commissure (Figure 4B, left; Figure S4B). As expected, when we imaged Pt responses before and after PC ablation, both average Pt and single neuron Pt responses to inward motion were enhanced (Figure 4B, right), and responses to stimuli with lateral components were attenuated. We also measured behavior following PC ablation and found that contributions of lateral motion to average turning diminished (Figure 4C), as responses to monocular lateral were eliminated, and differences between coherent and monocular medial were reduced (Figure 4C, inset). This was not a non-specific perturbation, as overall bout frequencies were indistinguishable from controls (Figure S4C). Instead, these deficits resulted from a reduction in both correct and incorrect turn modulation in PC-ablated fish (Figures 4D and 4E). In response to inward motion, PC-ablated fish did not exhibit behavioral alternation between leftward and rightward turning, as might be expected from two lateralized medial turning signals that could not inhibit each other. Thus, although the PC carries some medial inhibition, additional inhibition must be communicated elsewhere. Moreover, we observed that forward swimming in response to medial was reduced (Figure S4C, inset). This suggests that some forward swim drive is relayed through the PC. Simulating PC ablation in the minimal model (Figure 1E) further supported these hypotheses (Figure S4E). Combining the PC ablation results with anatomy (Figure S4F) suggests that medial signals bilaterally activate, via the PC, the downstream region known to drive swimming (i.e., the nMLF) and that the suppression of incorrect turns by medial motion should occur via additional interhemispheric connections (Figure 4F).

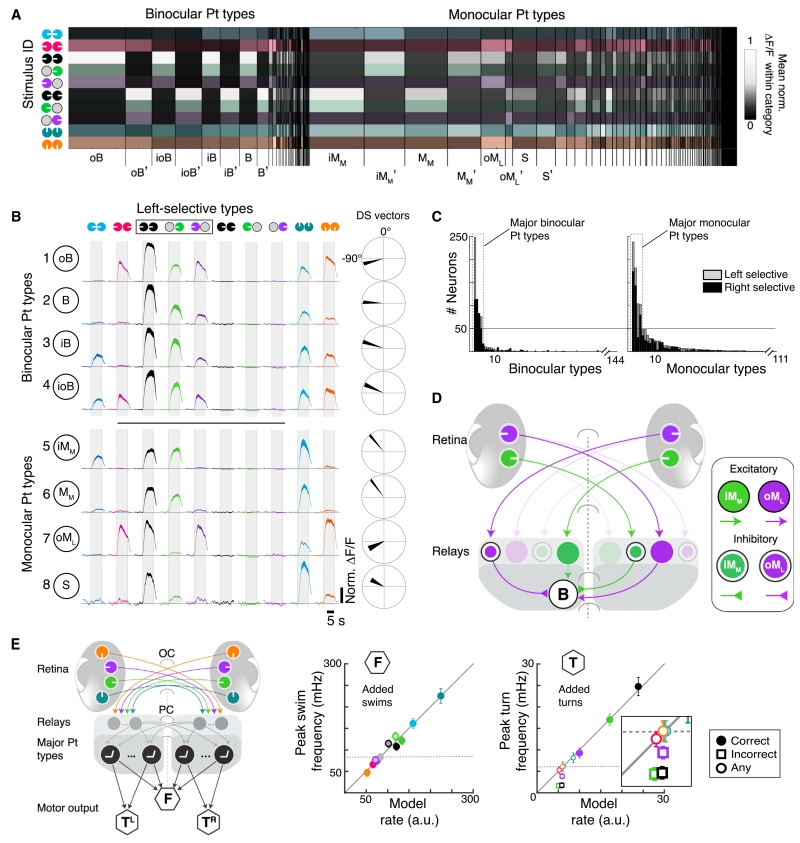
Most Pt Neurons Can Be Classified into a Few Functional Response Types

Our results suggest that Pt neurons separately drive downstream circuits that control forward swimming and turning. To investigate how response heterogeneity across the Pt population might support these parallel functions, we first classified Pt neurons into functional response types (Figures 5A and S5A–S5C; Table S1; STAR Methods). Eight bilaterally symmetric (Figure S5D) response types occurred with elevated frequency, together comprising more than 66% of the Pt population.

Figure 5. Pretectal Neurons Cluster into Distinct Functional Response Types.

(A) Heatmap of mean normalized ΔF/F within monocular and binocular response categories (STAR Methods). Column width, relative frequency neuron types; brightness, mean normalized ΔF/F. Top types: oB, outward-responsive binocular neuron; B, binocular; iB, inward-responsive binocular; ioB, inward- and outward-responsive binocular; iM_M, inward-responsive monocular (medial-selective); M_M, monocular (medial-selective); oM_L, outward-responsive monocular (lateral-selective); S, selective for coherent motion. (‘) matching right-selective types.

(B) Left, average normalized ΔF/F for the top 8 left-selective response types, ranked by frequency. Shaded area, SEM across neurons. Mirror-symmetric right-selective types in Figure S5D. Right, average direction selectivity. Vector width is bootstrapped standard error for each x and y vector component.

(C) Sorted histograms of response type frequency. Major Pt types (dashed boxes) lie above the indicated discontinuity threshold (gray line, STAR Methods).

(D) Hypothesized circuit for generating Pt types via monocular relay neurons. In this example, the B neuron is activated by leftward medial and lateral but inhibited by rightward medial and lateral motion.

(E) Left, Model using overrepresented Pt response types generated from relay neurons that integrate DSRGCs signals. Pt neurons project ipsilaterally to left and right turning centers (T^L, T^R) and to a forward swimming center (F). Right, comparison of measured bout frequencies and minimal model output. Insufficient suppression of Pt neurons caused model failure for incorrect turns (open squares, inset).

Four of these eight classes were binocularly activated by both medial and lateral stimuli (Figures 5B, top, 5C, left), and the remaining “monocular” classes responded to at most one monocular stimulus (Figures 5B, bottom, 5C, right). Within the binocular group, all classes responded most strongly to coherent stimuli (Figure 5B), but they were distinguishable by patterns of inhibition revealed only by their responses to conflicting stimuli. For example, response type ioB, a binocular neuron (ioB) exhibiting responses to conflicting inward (ioB) and outward (ioB) motion, responded to both conflicting stimuli. On the other hand, response type B (binocular neuron) did not respond to either conflicting stimulus, despite responding to both monocular stimuli. This suggests that the left-selective B type might play a specific role in generating left turns, as conflicting stimuli do not enhance turning. Consistent with this role, the B type was selective for directions of motion associated with turning (Figure 5B, far right).

The monocular classes were distinguished both by patterns of excitation in response to monocular medial or lateral stimuli and by inhibition in response to conflicting motion. For example, response class iM_M was a monocular (iM_M) neuron, responsive to medial motion (iM_M), and activated by inward motion (iM_M). Because it showed a strong preference for forward motion and responded to all stimuli that promoted forward swimming, it is a good candidate to drive this behavioral module.

In order to generate all of the observed Pt response types, we predict the existence of at least three types of relay units (Figure 5D). First, excitatory oM_L neurons might cross the midline to generate binocular responses. Second, inhibitory oM_L neurons could suppress responses to conflicting outward motion in B and iB neurons. Third, inhibitory iM_M neurons could project across the midline to suppress responses to conflicting inward stimuli. Finally, an excitatory iM_M neuron may relay retinal signals within the Pt, as suggested by inhomogeneous retinal innervation across the Pt in other species (Gamlin, 2006). Altogether, the overrepresented response types compactly summarize the neural correlates of forward swimming and turning behaviors.

Network Modeling Demonstrates Requirements of Downstream Processing

With this response diversity, the Pt could, in theory, implement the minimal model derived from behavior (Figure 1E). However, no single overrepresented response class exhibited an activity profile that precisely matched the behavior. For instance, neurons directly driving turning should not respond to backward and forward motion, as neither of these stimuli significantly increased turning, yet every Pt response type was activated by backward and/or forward stimuli. Furthermore, although the B type responded most similarly to the turning behavior, many other response types reproduced features of turning, and no type predicted the suppression of incorrect turns. This reinforces our hypothesis that turning opponency occurs downstream of the Pt.

The observed response heterogeneity, together with the lack of a single response type that could explain the behavior, motivated an interpretation of the data wherein a combination of several response types underlies the OMR. To quantitatively formulate this hypothesis, we applied neuronal network modeling. Since the major Pt neural types correlated strongly with each other and with behavior, it is a priori possible that any of them contributed to the behaviors. We thus included all overrepresented classes in the model network (Figure 5E, left). Because representations were lateralized, we assumed that the left and right Pt drove leftward and rightward turning, respectively. However, since none of the major Pt response types were appreciably suppressed below baseline levels by opposing motion signals, we did not force the Pt network to suppress incorrect turns (Figure 5E, right). Aside from this limitation, the model architecture was able to account for the behavior.

Hindbrain Circuitry Refines Pt Representations

To complete the model, we examined other brain regions revealed by whole-brain imaging (Figures 2B and S6) and investigated how Pt signals are refined. Recall that neurons preferring stimuli that promote forward swimming were anatomically segregated in the nMLF, RoL, and cHB (Figures 2A–2C andS7A). We found that monocular medial stimuli bilaterally recruited these regions (Figure S7B), explaining the reduction in forward swim frequency observed after PC ablation. Neurons responding to swim-promoting stimuli were sparsely distributed within these regions (Figure S7C) and could ultimately drive forward swimming.

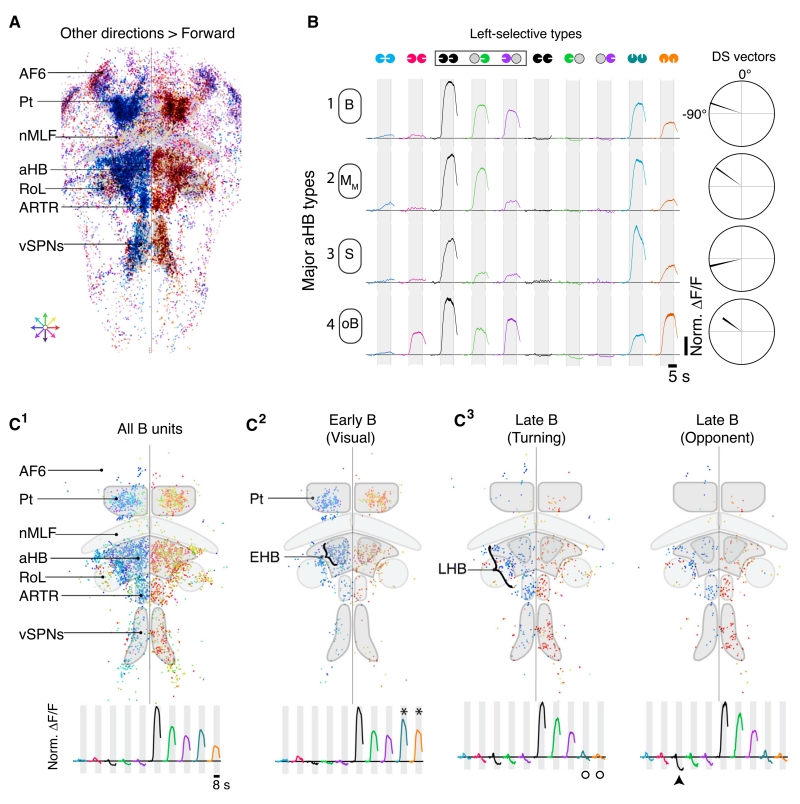
Elsewhere in the hindbrain, especially in the aHB and vSPNs, neurons preferred stimuli associated with turning (Figure 6A). Neurons in the aHB are anatomically positioned between visual neurons in the Pt and premotor vSPNs and were thus good candidates for mediating the additional interhemispheric inhibition necessary to suppress incorrect turns. To test this hypothesis, we first classified aHB neurons into functional response types. We found four overrepresented types that were a subset of the Pt types (Figures 6B and S7D–S7F; Table S2) and hypothesize that only this subset of Pt neurons sends projections to the aHB. Intriguingly, the aHB representation enhanced the B type, the strongest functional candidate for driving turns. Furthermore, the B type clustered within the Pt and aHB (Figure 6C1).

Figure 6. Hindbrain Circuitry Refines Turning Behavior.

(A) Distribution of all motion-sensitive units with higher peak ΔF/F responses to any direction over forward (n = 44,047, n = 14). Each unit is color coded for preferred direction of motion. Anatomical labels as in Figure 2.

(B) Average normalized ΔF/F in response to each stimulus for the four overrepresented aHB response types (left selective). Right, average direction selectivity vectors for each respective class (cf. Figure 5B). Neurons named as in Figure 5.

(C) C¹ Distribution of all binocular units (B), colored for preferred motion direction. C² B units activated by forward and backward motion. C³ Left, B units without significant responses to forward and backward motion. Right, motion-opponent B units suppressed by the opposite direction of motion. Traces show mean normalized ΔF/F traces for each population of B units. (*), active above baseline (>1.8*STD); arrowhead, suppressed below baseline (< −1.8*STD); circles, no significant response.

Neurons ultimately driving turning should not respond to either forward or backward motion. We found that B neurons responding to forward and backward motion were enriched in the Pt (Figure 6C2), and B neurons lacking these responses were enriched in the vSPN region (Figure 6C3). More interestingly, anatomically organized subpopulations of aHB and anterior rhombencephalic turning region (ARTR) neurons were associated with the Pt or vSPN representation (Figures 6C2 and 6C3). We refer to these sub-regions as the early (EHB) and late (LHB) hindbrain, respectively, as the EHB is functionally associated with visual areas (i.e., Pt) and the LHB is associated with motor areas (i.e., vSPNs). Many of the B neurons in the LHB were suppressed to levels not seen in the Pt but expected from the behavioral output (Figure 6D3, right), indicating that necessary interhemispheric inhibition lies within the hindbrain. By dissecting these hindbrain circuits, we provide a critical link between visual processing in the Pt and behavior.

Quantitative Model for Pt and aHB Control of Behavior

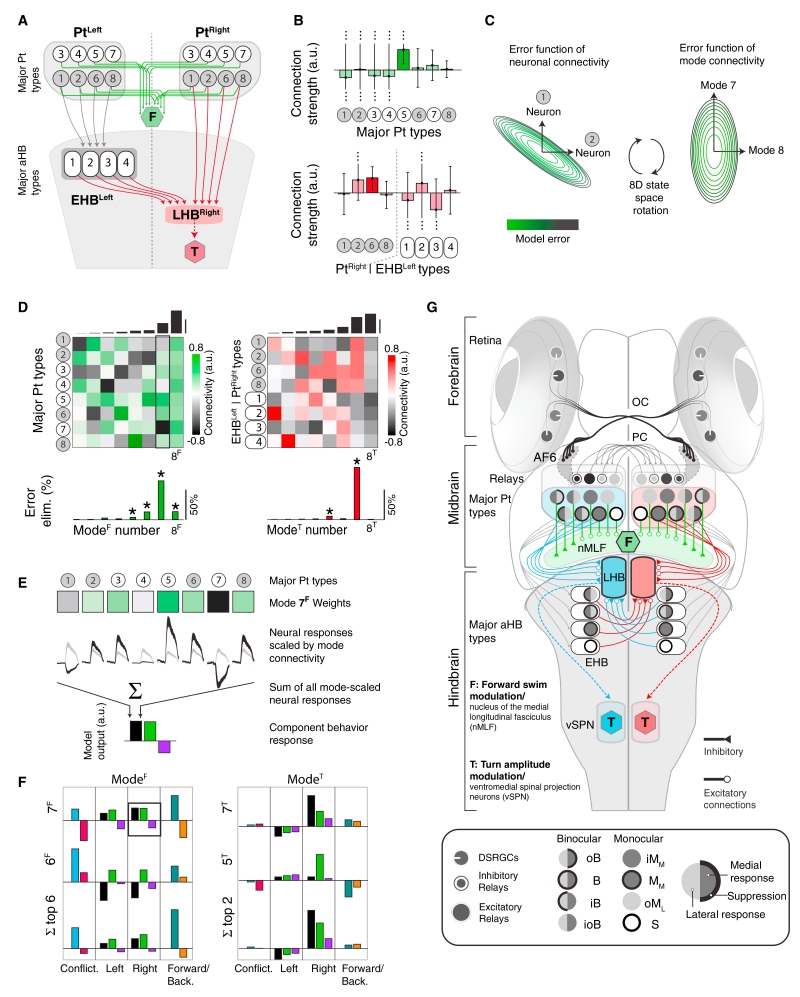
These considerations lead us to a model of how the Pt generates forward swimming and the Pt and aHB cooperate to generate turning (Figure 7A). Neurons in each major Pt response category drive premotor neurons controlling forward swimming. Since brain responses associated with forward swimming are bilaterally symmetric (Figure S7A), we assume that the left and right Pt contribute symmetrically (green lines, Figure 7A). Thus, the transformation of Pt signals into forward swimming behavior consists of eight functional connection weights, from each Pt response type to premotor nMLF units. To refine turn-related signals, we suppose that a subset of Pt neurons project to aHB. Both EHB and LHB receive ipsilateral inputs from the four Pt types common to the aHB (Figure 6B). LHB also receives contralateral input from EHB. Thus, the transformation of right Pt and left EHB signals into rightward turning consists of eight functional connection weights onto neurons in right LHB, which then drives turn generation (Figure 7A). The model is symmetric across the midline for leftward turning and accounts for the missing turn suppression (Figure S7G, cf. Figure 5E).

Figure 7. Neural Network Modeling Identifies Significant Dimensions of Functional Connectivity.

(A) Model incorporating hindbrain circuitry. Green, F, forward premotor units. Gray circles, Pt neurons projecting to the ipsilateral early hindbrain (EHB, ovals) and late hindbrain (LHB). Red, T, turn premotor circuitry. Neurons numbered as in Figures 5B and 6B.

(B) Best-fit connection strengths (95% confidence intervals) between neuron types and premotor units. Only two types predict significant non-zero connections (darker bars).

(C) Left, model error as a function of connectivity strength between neuron type 1 and F and neuron type 2 and F; all others connected by best-fit connection strengths. Right, while Pt neurons do not behave independently, we identified independent dimensions of population connectivity (functional modes) by rotating the error surface. Each axis now corresponds to a pattern of activation and suppression across neuron types (STAR Methods).

(D) Top, independent connectivity patterns for neuronal response types (rows) within each functional mode (columns), sorted according to the model’s sensitivity to perturbations in the direction of each mode (black bars, top). Bottom, fraction of error eliminated by each mode. (*) modes with a reliable influence on behavior (STAR Methods).

(E) Illustration of how modes contribute to model output in response to stimuli (here shown only for coherent rightward motion).

(F) The behavioral output associated with individual swimming modes (Mode^F) and turning modes (Mode^T). Top two rows show output for the two most significant swimming (left) and turning (right) modes. Bottom row shows collective output for the six most and two most significant swimming and turning modes, respectively. Bars are colored by stimulus identity.

(G) Quantitative whole-brain model for the OMR, reflecting the best-fit connectivity in Figure 7B. Neuron types are represented by symbols illustrating activation and suppression by motion stimuli (see legend).

Identifying Critical Dimensions of Functional Connectivity

The experimentally informed circuit architecture (Figure 7A) can account for the behavioral responses. However, one would not expect the model to predict every feature of the functional connectivity that might be revealed by future experiments, as current experiments only provide a low-dimensional view of the brain (Gao and Ganguli, 2015). For example, our stimuli did not isolate behavioral drive to individual functional response types, as multiple sets of connections (Figure S7H, top) lead to similar behavioral predictions (Figure S7H, bottom). Nevertheless, a successful model should accurately predict behavior in experiments probing functional elements well-constrained by the current data. To identify critical determinants of model performance, we examined the full ensemble of models that linearly generate sensorimotor transformations via the circuit architecture of Figure 7A (STAR Methods). The model architecture could accurately predict the behavioral data using a range of functional connections (Figure 7B), and even the signs of connections were ambiguous.

Such flexibility is common in multiparameter models when correlated parameter changes compensate to avoid error (Fisher et al., 2013; O’Leary et al., 2015). Individual connections could compensate in our model (Figure 7C, left), so we identified connectivity patterns that independently affect model accuracy (Figure 7C, right). We term these patterns functional modes. Figure 7D represents the functional modes as columns in a matrix, where each row represents a response type in Pt for forward swims (Figure 7D, left) and in Pt or EHB for turns (Figure 7D, right). For example, the eighth functional mode of swimming (8^F) positively weighted connections from every response type (Figure 7D, left). The modes are ordered so that parameter changes along high-numbered modes induce large errors (Figure 7D, top). The models in Figure S7H performed similarly because they differed along the first mode.

The functional modes can also be interpreted as population activity patterns that contribute independently to the accuracy of the sensorimotor transformation, so we could calculate the fraction of error eliminated by each mode (Figure 7D, bottom). A few modes eliminated the vast majority of model error, and the signs of abstract functional connections from these modes were reliably determined and positive. The seventh functional mode of swimming (7^F) eliminated the most error, while 6^F and 8^F repaired discrepancies. Similarly, the seventh mode of turning (7^T) was most important, while 5^T refined model predictions. Thus, one significant mode mostly explained each behavior, but secondary modes helped shape detailed behavioral patterns.

Similar considerations reveal reliable optogenetic predictions. The model predicts that activation of a response type or functional mode will cause a behavioral response if there was a significant functional connection between them. The model also predicts that uniform activation of left Pt would drive forward swimming (p = 0.002), drive leftward turning (p = 2.7 × 10⁻¹³), and suppress rightward turning (p = 0.0018). Selective activation of all binocular response classes in left Pt would likely suppress swimming (p = 0.11), drive left turning (p = 4.8 × 10⁻¹²), and have no effect on right turning (p = 0.41). Selective activation of all monocular classes in left Pt would likely drive swimming (p = 0.051), suppress left turning (p = 0.0069), and have no effect on right turning (p = 0.48).

Finally, our model predicts that Pt is functionally multiplexed, with different aspects of the population response driving the behaviors. For example, mode 7^F weighted response types according to their preference for inward versus outward motion (Figure 7E), which made this mode a component of the population response that was activated by stimuli promoting forward swimming and suppressed by stimuli reducing forward swimming (Figure 7F). Importantly, the model also predicts that certain aspects of the population response are functionally irrelevant. The irrelevance of 8^T (Figure 7D, right) means that matched responses in right Pt and left aHB do not drive behavior. Nevertheless, such activity characterized several stimulus conditions (e.g., forward motion). Unsupervised techniques for parsing population activity risk equating response frequency with relevance. Since brains must multiplex their functions in ethological conditions, it is critical that future work integrate model and experiment to align responses to specific functions.

DISCUSSION

Here, we combine experiment and theory to delineate a sensorimotor transformation within the zebrafish brain, from sensory input to locomotor output. By sequentially evaluating possible models with behavioral, functional, and anatomical data, we arrived at a quantitative whole-brain circuit model that accounts for the observed aspects of the OMR using experimentally identified neural response types. We note that analyses at the behavioral, whole-brain, and systems levels were critical for defining a biologically plausible and functionally relevant circuit architecture. Yet, we acknowledge that our treatment ignores processing in the retina and spinal cord. Dedicated experiments to decipher these peripheral mechanisms will complement our model of central processing. Overall, our methodology establishes a roadmap for digesting large-scale neural data from vertebrate brains and raises fundamental questions that are broadly relevant to whole-brain descriptions of function and behavior.

Relevance of Eye-Specific Motion Processing

We dissected the routes of sensory input by decomposing motion egocentrically. For a given eye, left- and rightward motion should, a priori, be perceptually symmetric. Yet, sensorimotor circuitry maintained asymmetries (i.e., lateral versus medial) throughout. These functional asymmetries might survive from an evolutionary past in which eye-specific pathways did not converge, reflecting vestigial functional inefficiencies: only lateral signals must re-cross the midline to drive turning behavior. The large inhibitory influence of medial motion on contralateral turning might be a corresponding consequence of the early emphasis on medial pathways. Instead, medial motion might be privileged due to the ethologically relevance of approaching motion in other behaviors, and reciprocal inhibition from opponent motion signals may help stabilize motor outputs in noisy environments (Mauss et al., 2015).

Homologs of Optomotor Response Circuitry

Several features of the zebrafish OMR likely translate to processing in higher-order vertebrates. The mammalian anatomy of retinal projections and the Pt suggests that binocular integration may occur via the PC (Sun and May, 2014). The zebrafish OMR is established by separate visual channels controlling multiple behavioral parameters. As visual information is organized into channels in other brains (Gollisch and Meister, 2010; Huberman et al., 2009; Yonehara et al., 2009), we hypothesize that distinct channels may activate segregated motor nuclei to generate flexible behavior in other vertebrates. In particular, the nMLF or neighboring neurons may be functional homologs of the mesencephalic locomotor region in mammals (Dunn et al., 2016; Ryczko and Dubuc, 2013; Severi et al., 2014), whereas the vSPNs are functionally and anatomically similar to neurons in the mammalian reticular formation (Armstrong, 1988). Furthermore, the prevalence of caudal interhemispheric connections in the mammalian brain (Chédotal, 2014) is reminiscent of the zebrafish hindbrain, and these connections might also refine lateralized motor streams in higher-order vertebrates.

In zebrafish, OMR circuitry overlaps with circuits activated in other stabilizing reflexes, such as the optokinetic reflex (OKR) of the eyes (Kubo et al., 2014; Portugues et al., 2014). In particular, neurons in the Pt are consistently recruited by stimuli that evoke the OKR, but binocular neural activation is far less common than during the OMR, perhaps suggesting that different subpopulations coordinate each behavior. Notably, Kubo et al. also identified frequent response types in the Pt and hypothesized a Pt circuit that could generate the response types (cf.Figure 5D).

Quantitative Modeling

To understand the requirements of the system, we first built a minimal model to explain the measured sensorimotor transformation (Figure 1E). As this model conflicts with anatomical and functional details of the brain, we reassessed the model with each new result to eventually obtain a candidate whole-brain description (Figure 7G). This iterative migration between experiment and theory will be necessary to illuminate the mechanisms of complex sensorimotor transformations, which are underconstrained by conceivable experiments (Gao and Ganguli, 2015).

Functional similarity between neurons resulted in a model whose output was insensitive to some aspects of connectivity. This will be common going forward, as neuroscientists typically characterize high-dimensional systems using a few stimuli and behaviors (Fisher et al., 2013; Gao and Ganguli, 2015; O’Leary et al., 2015). Nevertheless, a few combined parameters were critical to explain the behavior, thereby distilling the behaviorally relevant features of the population response. Thus, although we did not assign unique functional roles to each response class, we could identify model features that were well constrained by the data to make testable predictions for collective encoding. The model architecture also makes predictions for connectivity between Pt response classes, aHB classes, and premotor nuclei that can be tested with viral tracing, connectomics, channelrhodopsin-assisted circuit mapping, and electrophysiology.

Validation of Microcircuitry

Our model uses DSRGCs and monocular relays to construct the overrepresented Pt response types. All retinal input arrives in AF6 from the contralateral visual field, so excitatory and inhibitory relays are necessary for binocular integration and reciprocal suppression. Not all Pt neurons receive direct retinal input in other animals (Fite, 1985; Koontz et al., 1985; Scalia, 1972; Vanegas and Ito, 1983), and relays might distribute input signals throughout the Pt. Future experiments measuring coarse projections, detailed connectivity, and neurotransmitter identity of candidate relay are necessary. We predict that lateral relay neurons (oM_L) exist in excitatory and inhibitory forms that differ in their projection patterns. One could use transgenic lines specifically labeling glutamatergic and GABAergic populations to test this hypothesis.

Our model also predicts that LHB neurons are excited by specific ipsilateral Pt response types and inhibited by contralateral EHB neurons. The latter prediction is consistent with known organization in the zebrafish hindbrain (Kinkhabwala et al., 2011; Randlett et al., 2015; Sassa et al., 2007) and with the prevalence of commissures in the rhombencephalon (Koyama et al., 2011; Lee et al., 2015), but the detailed organization proposed here must be verified. Furthermore, a rigorous definition of EHB and LHB requires further experiments to distinguish each structure anatomically and functionally.

A Generalizable Framework

We provide an eminently testable framework for future studies and a detailed description of the neural circuitry underlying the OMR. We chose the OMR because it is an accessible gateway to a fundamental sensorimotor transformation layered with rich complexity. While we address the feed-forward foundation of the OMR with a simple stimulus set, the circuit properties revealed here provide a basis for future studies. Indeed, complementary studies of visuomotor behaviors that aim to explain learning, decision making, and multimodal processing must first ground themselves in the circuits controlling basic behaviors. More generally, our study establishes a computational and experimental scaffold for generating testable circuit models on large scales. Our work in larval zebrafish provides a critical link between efforts in smaller model organisms and those in vertebrates, an essential step toward tackling the complexity of mammalian brains.

STAR*METHODS

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Chemicals, Peptides, and Recombinant Proteins
Alpha-Bungarotoxin	Life Technologies	B1601
Deposited Data
Pretectal Response Distribution. See Table S1	This study	N/A
Anterior Hindbrain Response Distribution. See Table S2	This study	N/A
Experimental Models: Organisms/Strains
Tg(elavl3:GCaMP5G)	(Ahrens et al., 2013a)	N/A
Tg(elavl3:GCaMP2)	(Ahrens et al., 2013b)	N/A
Tg(alpha-tubulin:C3PA-GFP)	(Ahrens et al., 2013b)	N/A
Software and Algorithms
Labview (Behavioral acquisition framework)	National Instruments	http://www.ni.com/en-us.html
MATLAB (Behavioral and imaging analysis, modeling)	MathWorks	http://www.mathworks.com/?requestedDomain=www.mathworks.com
Open GL (Stimulus rendering)	OpenGL	https://www.opengl.org/
C# (.NET Framework 3.5) (Two-photon acquisition)	Microsoft/ (Ahrens et al., 2013b)	http://www.microsoft.com/en-us/
FIJI (ImageJ) (Neural tracing)	NIH	http://fiji.sc
Automatic ROI segmentation	(Portugues et al., 2014) / This study	N/A

CONTACT FOR REAGENTS AND RESOURCE SHARING

Further information and requests for resources and reagents should be directed to the Lead Contact Florian Engert (florian@mcb.harvard.edu).

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Zebrafish

For all experiments, we used 5-7 days post-fertilization (dpf) wild-type (AB or TL) or transgenic nacre −/− zebrafish; nacre −/− mutants lack pigment in the skin but retain wild-type eye pigmentation. All measured behavioral variables in nacre −/− fish were similar to wild-type, heterozygous siblings. Zebrafish were maintained on a 14 hr. light /10 hr. dark cycle and fertilized eggs were collected and raised at 28.5 °C. Embryos were kept in E3 solution (5 mM NaCl, 0.17 mM KCl, 0.33 mM CaCl2, 0.33 mM MgSO4). All experiments were approved by Harvard University’s standing committee on the use of animals in research and training. All imaging experiments in this study were performed on transgenic zebrafish Tg(elavl3:GCaMP5G), a generous gifts from Drs. Michael Orger, Drew Robson and Jennifer Li or in double transgenic Tg(elavl3:GCaMP5G); Tg(α-tubulin:C3PA-GFP). The Tg(α-tubulin:C3PA-GFP) was kindly provided by Dr. Michael Orger. Tg(elavl3:GCaMP2), also a gift from Drs. Michael Orger, Drew Robson and Jennifer Li was used as anatomical reference in laser ablation of the posterior commissure.

METHOD DETAILS

Behavior in freely swimming zebrafish

Zebrafish swam freely in a clear 5 cm diameter petri dish (VWR) in filtered E3 solution at 3-5 mm height, minimizing variability of visual angle. Illumination of the fish was achieved by a circular array of infrared light-emitting diodes (810 nm) directed from below. Fish behavior to various motion stimuli was recorded at 200 Hz using an infrared-sensitive, high-speed, monochrome charge coupled device (CCD) camera (Pike F-032, 1/3,” Allied Vision Technology, Germany). A zoom lens (Edmund Optics, USA) was used with an infrared pass filter (RG72, Hoya, Japan). The center of the dish was aligned with the center of an appropriately zoomed camera image such that the edge of the dish was not visible in the field of view; this simplifies the fish detection algorithm by not having to handle sidewall reflections. Stimuli were projected onto a 12 by 12 cm diffusing screen after reflection by a 4 × 4 inch cold mirror (both Edmund optics, USA) 5 mm directly below the fish using a commercial DLP projector (Optoma, USA). Custom image processing software (Labview, National Instruments, USA and Visual C++, Microsoft, USA) extracted the position (center of mass) and orientation (vector anchored by detection of swim bladder and center of mass between eyes) of the fish at the camera acquisition frame rate (200 Hz) from a background-subtracted frame. This information was used to continuously update a stimulus rendered in real-time using OpenGL to provide consistent motion stimulation with respect to the body axis. To begin each trial, fish were induced to swim to the center of the camera field of view by concentric circular, converging sinusoidal gratings (Movie S1). Detection of the fish near the center triggered a trial. Each trial began with a 500 ms static period in which gratings (running parallel relative to the fish body axis, spatial period of 1 cm) were locked to fish orientation in a closed loop configuration. These orientation-locked gratings then began to move at 10 mm/s (or remained stationary throughout the trial, depending on the particular stimulus identity, Movie S1). Stimulus presentation continued until either the fish aborted the trial early by leaving the active area or the maximum trial duration (30 s) was reached. To independently stimulate each eye, a 0.8 cm area was blanked (black) directly underneath the fish. In control experiments, we widened the blanked area and did not observe any effect on behavioral outcome (data not shown); this is consistent with independent stimulation of each eye. Only fish that completed at least 10 repetitions in less than 3 hr were included in further analysis or ablation experiments. Extracted the position and orientation were further analyzed as described in Quantification and Statistical Analysis.

Fictive behavior

Transdermal motor nerve recordings of fictive behavior were performed as outlined in (Ahrens et al., 2013b). Larval zebrafish (5-7 dpf) were paralyzed by immersion in a drop of fish water with 1 mg/ml alpha bungarotoxin (Sigma-Aldrich) and embedded in a drop of 2% low melting point agarose, after which the tail was freed by cutting away the agarose around it. Two suction pipettes were placed on the tail of the fish at intersegmental boundaries, and gentle suction was applied until electrical contact with the motor neuron axons was made, usually after about 10 min. These electrodes allowed for the recording of multi-unit extracellular signals from clusters of motor neuron axons, and provided a readout of intended locomotion. Extracellular signals were amplified with a Molecular Devices Axon Multiclamp 700B amplifier and fed into a computer using a National Instruments data acquisition card. Custom software written in C# (Microsoft) recorded the incoming signals. These signals were then analyzed offline in MATLAB (Mathworks, USA). Please seeQuantification and Statistical Analysis for detailed analysis.

Two-photon Ca²⁺ imaging

In-vivo two-photon fluorescence imaging of neural activity was performed in 5-7 dpf Tg(elavl3:GCaMP5G) zebrafish larvae. Prior to imaging, larvae were paralyzed in α-Bungarotoxin (1 mg/ml, Sigma, USA) and embedded in low melting point agarose (2% w/v), which prevented movement artifacts. Viability was monitored before and after imaging by observing the heartbeat and blood flow through brain vasculature. All data acquisition and analysis was performed using custom Labview (National Instruments, USA), MATLAB (Mathworks, USA) and C# software. Imaging was performed with a custom two-photon laser-scanning microscope, using a pulsed Ti-sapphire laser tuned to 920 nm (Spectra Physics, USA). Stimuli were projected from below with a DLP or LCOS projector (Optoma, USA or AAXA Technologies, USA, respectively) using only the red channel, which allowed for simultaneous visual stimulation and detection of green fluorescence. Visual stimuli were blanked with a black bar underneath the fish, as in free behavior experiments. Stimuli were 8.5 s in duration, which was long enough for neural activity to reach characteristic peaks (for transient responses) or plateaus (for sustained responses, see Figure 5B), and were separated by 11.5 s of static (no motion) gratings. For brain-wide mapping experiments, images were acquired at 2 Hz. For pretectal imaging, frames were acquired at 3.6 Hz, as afforded by the smaller field of view. For experiments spanning smaller brain volumes (e.g., specific pretectal imaging), 10 stimulus repetitions were presented per z-plane. For experiments across large brain volumes (e.g., whole-brain experiments), 3 stimulus repetitions were presented per z-plane. The resulting image time and depth series were analyzed in MATLAB (Mathworks, USA). Subsequent analysis was performed as described in Quantification and Statistical Analysis.

Tracing pretectal projection patterns

Double Tg(α-tubulin:C3PA-GFP); Tg(elavl3:GCaMP5G) fish at 6 dpf were embedded in 2% agarose in a 35 mm petri dish. We modified the tracing protocol developed by Datta et al. (Datta et al., 2008) to trace projections from a subset of Pt neurons (Figure S3D). While presenting whole-field motion stimuli from below, fish were first imaged under a two-photon microscope at 925 nm to identify motion-sensitive neurons. Then, after taking anatomical stacks of the region, individual motion-sensitive Pt neurons were selected on one side of the brain. PA-GFP in selected neurons was then activated using 5-10 pulses (100 ms – 2 s) of 770 nm pulsed infrared laser light. Selective photoconversion was confirmed by switching to 925 nm and imaging the selected plane for increased fluorescence. The activation protocol was repeated until photoconverted fluorescence no longer increased significantly. Anatomical stacks of projection patterns were acquired 2 hr post-activation. The pre and post activation two-photon stacks were then aligned and analyzed using FIJI (ImageJ) software. For highlighting of the posterior commissure (Figure S4A and S4F, right), anatomical pre-activation stacks of Tg(α-tubulin:C3PA-GFP) were acquired, before activating a small region with the same protocol as described above. The pre and post activation two-photon stacks were then aligned and analyzed using FIJI (ImageJ) software in separate color channels.

Two-photon laser ablations

After embedding zebrafish in low melting agarose, areas were targeted using neuroanatomical landmarks, stereotypical blood vasculature, and/or neuronal activity patterns in Tg(elavl3:GCaMP2) or Tg(elavl3:GCaMP5G) larvae. Mode-locked laser power (885 nm, 120-135 mW maximum at sample) was linearly increased while the beam was scanned in a spiral pattern over the targeted region (typically 0.5 – 10 s). The laser scan was immediately terminated upon the detection of fluorescence saturation, which is presumed to result from the creation of highly localized plasma via multi-photon absorption. For single cells, this method resulted in the complete destruction of the target cell without affecting adjacent cells. Ablations in neuropil regions (like the PC) required additional validation. Due to the depth and anatomical position of the PC, nearly 50% of ablated fish showed non-specific side effects such as nearby necrotic tissue or changes in the optical density of the optic tectum, likely due to blood vessel cauterization from out-of-focus heating. These fish were excluded from post-ablation analysis. Before and after PC ablation imaging was performed in only a subset of fish. After freeing fish from agarose and a recovery period (10-120 min, until fish were swimming spontaneously), fish were tested in the behavioral assay. For the AF6 ablation, we specifically monitored fluorescence before and after ablation across AFs. Only fish that exhibited functional perturbations specific to AF6 were further analyzed.

Quantitative modeling

Behavior-only modeling

We built the model in Figure 1E to illustrate that a simple circuit architecture could account for the observed binocular visuomotor transformation. For all behavioral model results error bars are SEM across fish (N = 38). The synaptic inputs onto the forward swimming center were 0.0395 from the medial responsive RGCs and −0.0088 from the lateral responsive RGCs. The magnitudes of synaptic inputs onto the two turning centers were 0.0133 from the medial responsive RGCs and 0.0068 from the lateral responsive RGCs. The sign of each connection onto a turning center was positive when the direction of the RGC matched the direction of the turning center. After summing the monocular components of the motion stimuli, we converted the resultant retinal input signals into the model rate through a transfer function. For forward swimming, this transfer function was the sum of the retinal input and the baseline static swimming rate (0.0836). For turning, we fit a cubic transfer function to generate the behavioral turning rates from the retinal input signals. The resulting transfer function was f(x) = 114.6x³ + 17.48x² + 0.5168x + 0.006175, where x denotes the retinal input signal. To simulate the ablation experiment in Figure S4E, we removed those synaptic inputs that could not reach the lateralized turning centers without an interhemispheric connection within the zebrafish brain.

Quantifying the visuomotor transformation

Larval zebrafish responded to optomotor stimuli by modulating at least three elements of behavior: forward swimming; turning to the left; and turning to the right (Figure 1D). For each stimulus condition and element of behavior, we quantified the response magnitude as the amplitude of the associated peak of the mean bout frequency histogram. We similarly quantified the uncertainties of each mean response magnitude using the SEM of the histogram. Since neuronal fluorescence responses were measured relative to the background set by the static stimulus, we shifted the behavioral responses to also be relative to the static stimulus. We accordingly corrected the uncertainty of each stimulus response to account for the uncertainty of the static response. Since the static stimulus is zero by construction, we are left with ten non-trivial stimulus conditions.

For each of the three behavioral classes, we construct a 10-dimensional vector y whose components are the experimental motor response magnitudes for the 10 stimulus conditions. We also define the 10×10 diagonal matrix C whose diagonal elements, ${\sigma }_i^2$, are the squares of the response uncertainties. Suppose that $\widehat{y}$ is a 10-dimensional vector of predicted response magnitudes by some circuit model. We quantify the error of the model as

$$e={(y-\widehat{y})}^T{C}^{-1}(y-\widehat{y})=\sum _{i=1}^{10}\frac{{(y_i-{\widehat{y}}_i)}^2}{{\sigma }_i^2}$$

where the superscript T denotes the matrix transpose, and i indexes the stimulus condition. Note that e is simply the squared error weighted by the uncertainty in each stimulus condition.

Linear regression framework for functional connectivity

As discussed in the main text and illustrated by Figure 7A, our model uses functional connections from neurons in the major Pt and aHB response categories to premotor neurons to generate each element of behavior. For example, eight functional connection strengths, from the {oB, B, iB, ioB, iM_M, M_M, oM_L, S} major Pt neuron categories (and their rightward selective counterparts) to nMLF neurons, parameterize the forward swimming component of the visuomotor transformation (green lines, Figure 7A). The model parameters for the rightward turning component of the visuomotor transformation also consists of eight functional connection weights, now from the {oB’, B’, iM_M’, S’} major right-selective Pt neuron categories and the {oB, B, iM_M, S} major left-selective aHB neuron categories to right LHB units. The circuit driving leftward turning is the mirror-reflection of the circuit driving rightward turning.

Our task is to understand how the choice of these functional connection weights affects the accuracy of the modeled visuomotor transformation. Since the formalism does not depend on the element of behavior under consideration, we henceforth use abstract notation to describe the general method. Let X denote the n×p response matrix, which comprises the mean fluorescence response of p neurons to each of n stimuli. Note that n = 10 and p = 8 for each type of behavior considered here. For example, the columns of X correspond to the responses of the {oB’, B’, M_M’, S’} major right-selective Pt neuron categories and the {oB, B, M_M, S} major left-selective aHB neuron categories to the 10 stimulus conditions, when considering rightward turning behavior. We model the visuomotor transformation as a linear combination of these responses

$$\widehat{y}=X\beta ,$$

where β denotes the p-dimensional weight vector of functional connection weights.

Choosing the weight vector to minimize e is mathematically equivalent to performing maximum likelihood parameter estimation with the generative model

$$y=X\beta +\eta ,$$

where η is an n-dimensional vector of zero-mean Gaussian noise with covariance matrix C. In particular, the log-likelihood function for this model is

$$l\left(\beta \right)=-\frac{1}{2}e\left(\beta \right)+A,$$

where A is a constant that does not depend on the model parameters. We thus applied standard techniques from maximum likelihood parameter estimation to compute confidence intervals for the best-fit model parameters (Figures 7B–7D). Similarly, we computed p-values for the model’s predictions regarding the effects of optogenetic activation of a neural activity pattern, x, by considering the null hypothesis that x^Tβ = 0.

Structure of the error function

With the assumptions described in the previous sections, the error associated with the visuomotor transformation is a quadratic function of the functional connection strengths

$$e\left(\beta \right)=e_{\mathit{min}}+{\left(\beta -\widehat{\beta }\right)}^{T}H\left(\beta -\widehat{\beta }\right),$$

where

$$\widehat{\beta }=H^{-1}U$$

is the best fit functional connection strengths (colored bars in Figure 7B),

$$H=X^T{C}^{-1}X$$

is proportional to the Hessian matrix of the error function, and U is defined by

$$U=X^T{C}^{-1}y.$$

The minimal error achievable by the model architecture is

$$e_{\mathit{min}}=y^T{C}^{-1}y-U^T{H}^{-1}U,$$

Let V denote the p×p matrix in which each column is a right eigenvector of H. Then VV^T = V^TV = I, where I is the identity matrix, Λ = V^THV is a diagonal matrix whose diagonal contains the eigenvalues of H, and V^Tβ is the weight vector in the basis of eigenvectors of H. The matrices in Figure 7D simply show V for both swimming and right turning behavior. The eigenvectors of H correspond to the principal axes of the quadratic error surface, and we refer to each eigenvector of H as a functional connectivity mode.

The basis of functional modes is useful because the error function receives independent contributions from the component of the weight vector along each functional mode,

$$e\left(\beta \right)=e_{\mathit{min}}+\sum _{i=1}^p{\lambda }_i{({\gamma }_i-{\widehat{\gamma }}_i)}^2,$$

where the λ_i are eigenvalues of H,

$${\gamma }_i={\left(V^T\beta \right)}_i=\sum _{j=1}^p{V}_{ji}{\beta }_j$$

is the projection of β onto the i^th mode, and ${\widehat{\gamma }}_i$ is the projection of the optimal weight vector onto the i^th mode. Note that the black bar plots in Figure 7D show the eigenvalue associated with each functional mode. Departures of β from when the optimal weight induce large errors they project onto modes that are associated with large eigenvalues. Thus, the confidence interval for ${\widehat{\gamma }}_i$ is narrow for the modes associated with large eigenvalues.

This basis transformation is also useful because the projections of the optimal weight vector along each mode contribute independent error reduction to model. In particular, note that we can rewrite the minimal error as

$$e_{\mathit{min}}=y^T{C}^{-1}y-\sum _{i=1}^p\frac{{\left(V^{T}U\right)}_i^2}{{\lambda }_i}=y^T{C}^{-1}y\left(1-\sum _{i=1}^p{r}_i^2\right),$$

where

$$r_i^2=\frac{1}{y^T{C}^{-1}y}\frac{{\left(V^{T}U\right)}_i^2}{{\lambda }_i}.$$

Because the error of the fully disconnected model is y^TC⁻¹y, $r_i^2$ is the fraction of error eliminated by each mode. The bottom panels in Figure 7D shows $r_i^2$ for each mode.

Interpreting the functional modes as neural activity patterns

In the previous section, we defined V as the p×p matrix in which each column is a right eigenvector of H. If x is a p-dimensional pattern of neural activation across a population of behaviorally relevant major neuron categories, then V^Tx represents the same activity pattern in the basis defined by the columns of V, and any activity pattern can be written as a linear combination of the columns of V. Thus, we can thus think of the columns of V as defining functional modes of activity. Thus, an activity mode is the pattern of activation that maximizes the projection of the response vector onto the corresponding vector of connectivity weights. In this framework, the functional modes replace the major neuron categories as the elemental components of neural population activity. Figure 7F displays the stimulus response profiles of several functional modes (6^F, 7^F, 5^T, 7^T). Each component of the functional connectivity, γ_i, corresponds to a functional connection strength from one functional mode of activity to a premotor neuron driving behavior. The characterization of the error surface provided in the previous section implies that the functional modes define patterns of activity from which functional connections contribute independently to the accuracy of the modeled visuomotor transformation. The bottom panels of Figure 7D show that the functional modes provide a description of neural activity in which only a few dimensions contribute to the model’s ability to generate appropriate motor activity under the experimental stimulus conditions.

QUANTIFICATION AND STATISTICAL ANALYSIS

Quantification of swim kinematics

Offline behavioral analysis was performed using custom MATLAB scripts (Mathworks, USA). Because we did not assume that data were normally distributed, we used non-parametric statistics for all hypothesis testing. Angular velocity for each fish was calculated as total angle turned over total stimulus presentation time. Single swim bouts were extracted by peak detection in traces obtained via multiplication of orientation change records by box-smoothed (20 ms) swim velocity records (calculated from fish center-of-mass). Latency was calculated as time between motion onset of moving gratings and first detected swim bout. Bout frequency was computed as the total number of detected swim bouts over total stimulus time. Heading angle change for each bout was calculated as orientation directly before (2 ms) and after (10 ms) a detected swim bout. By convention, negative values indicate rightward (or clockwise) and positive values indicate leftward (or counterclockwise) heading angle change. For Figure S1C, we corrected for innate turn biases by subtracting the angular velocity measured during the static stimuli from all other measurements on a fish-by-fish basis before averaging. For all behavioral bar graphs (Figures 1C, 4C, and 4E) error bars represent standard error of the mean (SEM) across fish. For histograms, shaded error is SEM across fish for angle bout type (Figures 1C and 4D). For supplemental figures, consult associated legends.

Fictive behavior analysis

Analysis of fictive behavior was performed on filtered signals, which consist of the standard deviation of the raw signal in 17 ms time bins. For fictive bout frequency analysis, bouts were marked at peaks in the filtered signal separated by at least 100 ms and crossing an amplitude threshold (adjusted for signal noise: 1 fish at 4.35, 2 fish at 1.95 times the peak baseline noise, as assayed by frequency histogram). Visual stimuli were presented as outlined in two-photon Ca²⁺ imaging, below. Because baseline fictive swim frequency was reduced relative to freely swimming experiments, we restricted our analyses only to active stimulus epochs (at least 0.1 Hz bout frequency).

Functional imaging analysis

To generate activity maps (Figures 2E, 2F, S3E, and S3F), fluorescence movies were averaged separately across all frames corresponding to each individual stimulus. A baseline image, the average of all frames during interstimulus periods, was then subtracted from these average images, which were masked to exclude regions outside of the brain. The resulting images, which were thresholded at 0.5* standard deviation (STD) above the mean and eroded and dilated to reduce noise, reflected normalized activity for each stimulus that was less polluted from noise in regions of low baseline fluorescence than traditional ΔF/F maps. These activity images, specific to each individual stimulus, were then combined to produce each type of map. For maps of direction selectivity, activity images for each of the 8 directions of whole-field motion were linearly combined using weighted projections into HSV color space, such that the combined color is related to the vector sum of activity elicited in response to each direction of motion: ultimately, the hue indicates directionality, the value reflects overall motion sensitivity, and the saturation represents the vector magnitude (strength of direction selectivity). For maps of medial/lateral selectivity, activity images for medial and lateral stimulus epochs were combined similarly, with the medial activity image represented in the green channel and the lateral activity image represented in the magenta channel. All other maps were generated analogously, with colors adjusted as indicated.

To generate whole-brain activity maps, Figures 2D and S2D, we used a method that better captured correlated activity in neuropil regions, as follows. First, we constructed an average regressor based on strongly responding voxels, as extracted from manual ROIs in persistently active regions, which we deduced were more related to the OMR, given the persistent properties of the behavior. We used this regressor to calculate the correlation coefficient for each pixel time series in every plane of the acquired image stack for each individual stimulus. Maps were then generated by assigning the resulting correlation images to appropriate color channels and combining as in the activity maps above. Map shown in Figure 2D is a maximum intensity projection through 135 μm of brain tissue, with ventral AF10 as the most dorsal plane.

The quantifications of pretectal data presented in Figure 3 were based on ROI selection using a method adapted from Ahrens et al. (2013a). For this analysis, an activity map for each imaged plane was first extracted by sweeping a square ROI roughly equal to half the size of a cell body across the spatial extent of an imaging movie. For each swept ROI, the spatially averaged fluorescence time series was normalized by the ROI’s mean fluorescence across time and the average fluorescence of all pixels across space and time. This signal was then cubed to amplify peaks, and each square’s average processed signal was assigned to each square’s spatial location. This analysis produced maps of activity that were robust to noise in regions of low baseline fluorescence. These activity maps were then overlaid on mean fluorescence images (reflecting anatomy) and used to guide manual neuron ROI selection. To make composite maps of the pretectal population across fish, all imaged planes were registered to a standard Tg(elavl3:GCaMP2) brain, which has an expression pattern indistinguishable from Tg(elavl3:GCaMP5G), using cross-correlation.

Fluorescence traces from these ROIs were then divided by a stable baseline amplitude averaged across all interstimulus intervals to generate ΔF/F traces. The means of trial-averaged ΔF/F for individual stimuli were then used to calculate functional indices. Binocularity index was calculated as [(xM or xL)_max – (Mx or Lx)_max]/[(xM or xL)_max + (Mx or Lx)_max], where xM and xL are right-eye monocular medial and lateral responses, respectively, and Mx and Lx are left-eye monocular medial and lateral responses, respectively. By construction, a value of 0 corresponds to equal activation by left and right eyes, and −1 and 1 correspond to exclusive activation by the left or right eye, respectively. The inward medial-medial suppression index was computed as [(xM or Mx)_max – MM]/[(xM or Mx)_max + MM], where MM is the response to inward motion. By construction, an index of 0 corresponds to no suppression and an index of 1 indicates that medial motion in the contralateral eye completely suppresses the response to medial motion in the other. The outward lateral-lateral suppression index was calculated analogously. To restrict indices to the [−1 1] range, all values were thresholded at 10% ΔF/F (calculated noise floor) to exclude negative ΔF/F deflections (or suppressed responses), which we did not integrate into our indices. To calculate direction selectivity vectors, we performed a vector sum of responses to the 8 directions of motion after normalizing to the maximum response across all directions.

For automatic ROI segmentation (Figures 2 and 6), we adapted a method from Portugues et al. (Portugues et al., 2014). In brief, we performed a neighborhood correlation analysis for each pixel in each plane of the fluorescence movie to generate maps of local correlation. This metric was typically high for pixels within the same cell body and discrete, local regions of high local correlation were easily segmented into individual ROIs automatically by seeding an ROI at a pixel with a local correlation maximum and growing the ROI spatially until the correlation dropped below a fixed threshold (0.15). To support ROI selection at the single cell level, ROIs were also limited in size between 30 and 200 pixels, or cells approximately 1.7 to 4.3 microns in radius at standard imaging resolution. Because this method was blind to the underlying anatomy, this automatic ROI segmentation also selected correlated regions of neuropil that met the stated size requirements.

Classification of functional response types

As we were confronted with complex response patterns in each brain region (Figure S6; Movie S2), we classified neural response types with barcode analysis. We assigned each neuron an 8-bit barcode (Kubo et al., 2014), which encodes whether or not the neuron significantly increased its fluorescence upon motion onset for each of the coherent, monocular, and conflicting stimuli. ΔF/F fluorescence traces for ROIs were trial-averaged for each individual stimulus (Figure 1B) but excluding forward and backward epochs, as we were primarily interested in how information from both eyes was combined. The resulting traces were then baseline corrected with a first-degree polynomial fit to the baseline period. We then assessed whether activity during stimulus periods was significantly different from its baseline. For a given neuron and stimulus, if the mean of the trial-averaged signal exceeded 1.8*STD above its baseline, then the neuron was assigned a ‘1’ for that particular stimulus; otherwise, it was assigned a ‘0.’ This resulted in a binary barcode for each neuron across all stimuli in the orthogonal set. Based on these 8 stimuli, neurons could fall into 256 (2⁸) different response combination classes. This method, and the associated significance threshold, provided the most consistent classification across fish during visual inspection of individual neurons, and deviations from this threshold did not markedly change relative frequency distributions. While we tried other clustering methods, our barcode technique provided the most intuitive results reflecting the stimulus-behavior relationship. Other methods we tested, like k-means clustering, required arbitrary parameterizations of the data (like estimated number of clusters). We labeled a response class as over-represented if, in sorted histograms of class frequency, the class (or its mirror-symmetric partner) was separated from the others by a graphical non-linearity (see Figure 5C) and was present in all fish. These functional response types allowed us to summarize this heterogeneity in our model. Although studies have analyzed heterogeneous population responses without classifying neurons, our classification helped us in several ways. First, a model that references response types rather than individual neurons can make predictions for how activity of sub-populations of neurons will translate into behavior. Second, Kubo et al. classified Pt responses during the OKR using this scheme (Kubo et al., 2014), permitting a comparison of Pt responses across behaviors. Third, response type classification helped us to identify elements of the representation that transformed across brain areas. Fourth, certain response types had a natural interpretation (e.g., Pt relay neurons). These neuronal response classes could have subtypes that are crucial to more complex behaviors and stimuli.

For analyses where relative differences in activity across stimuli were most meaningful (e.g., Figure 2F, right, Figure 3B, left, Figure 5B), we used normalized ΔF/F metrics. In these cases, we calculated trial-averaged ΔF/F traces for each ROI and then divided by the maximum ΔF/F value across all time points and stimuli. These normalized traces were then averaged across ROIs (where indicated). All ΔF/F metrics using single values from stimulus epochs (Figure 2F, right, Figure S3E, bottom, Figure S3F, bottom, Figure S3G, Figure 3B, left, Figure 3D) were calculated as mean normalized ΔF/F across all time points during each respective stimulus presentation.

DATA AND SOFTWARE AVAILABILITY

Data Resources

We are providing two supplemental data files (Tables S1 and S2) containing information for the pretectum and anterior hindbrain for each response type, including frequency, average peak calcium response, and identifying metadata (e.g., monocular versus binocular, barcode representation). Other data on behavior or imaging will be made available upon request.

Software

Software for data acquisition, analysis and quantitative modeling will be made available upon request.

Highlights.

• Optomotor response is driven asymmetrically but linearly by visual motion to each eye

• Dedicated circuits differentially process eye- and direction-specific motion

• Neural representations are distributed over select overrepresented response types

• Behavior as well as neural activity is captured by realistic whole-brain circuit model

In Brief.

Whole-brain imaging and behavioral analysis combined with network modeling reveal key circuit elements contributing to a complex sensorimotor behavior in zebrafish larvae and provide a framework for building brain-level circuit models.