Temperature-robust neural function from activity dependent ion channel regulation

Summary

Many species of cold-blooded animals experience substantial and rapid fluctuations in body temperature. Because biological processes are differentially temperature-dependent, it is difficult to understand how physiological processes in such animals can be temperature-robust. [1-8]. Experiments have shown that core neural circuits such as the pyloric circuit of the crab Stomatogastric Ganglion (STG) exhibit robust neural activity in spite of large (20 °C) temperature fluctuations [3, 5, 7, 8]. This robustness is surprising because the temperature dependencies of ionic currents in the STG are not tuned [7]. This is apparently paradoxical because: a) each neuron has many different kinds of ion channels with different temperature dependencies (Q₁₀s) that interact in a highly nonlinear way to produce firing patterns; b) across animals there is substantial variability in conductance densities that nonetheless produce almost identical firing properties. The high variability in conductance densities in these neurons [9, 10] appears to contradict the possibility that robustness is achieved through precise tuning of key temperature-dependent processes. In this paper we develop a theoretical explanation for how temperature robustness can emerge from a simple regulatory control mechanism that is compatible with highly variable conductance densities [11-13]. The resulting model suggests a general mechanism for how nervous systems and excitable tissues can exploit degenerate relationships among temperature-sensitive processes to achieve robust function.

Results

Temperature sensitivity of physiological processes such voltage-dependent ion channel gating are described by an approximate, empirical measure, the Q₁₀, defined as the fold-change per 10 °C from some reference temperature:

$$\frac{R_T}{R_{\mathrm{ref}}}={Q_{10}}^{(T-T_{\mathrm{ref}})∕10}$$ (1)

Here R_T is the rate (or magnitude) of the process at temperature T and R_ref is the reference value at temperature T_ref. A Q₁₀ of 1.0 therefore means that a process is temperature-independent. Experimentally, Q₁₀s for single-channel conductance tend to lie in the range of 1.2-1.5. On the other hand, Q₁₀s for ion channel gating or inactivation are typically in the range 2.0 – 4.0 [14], meaning that the rate of channel opening, for example, can speed up more than two-fold per 10 °C increase.

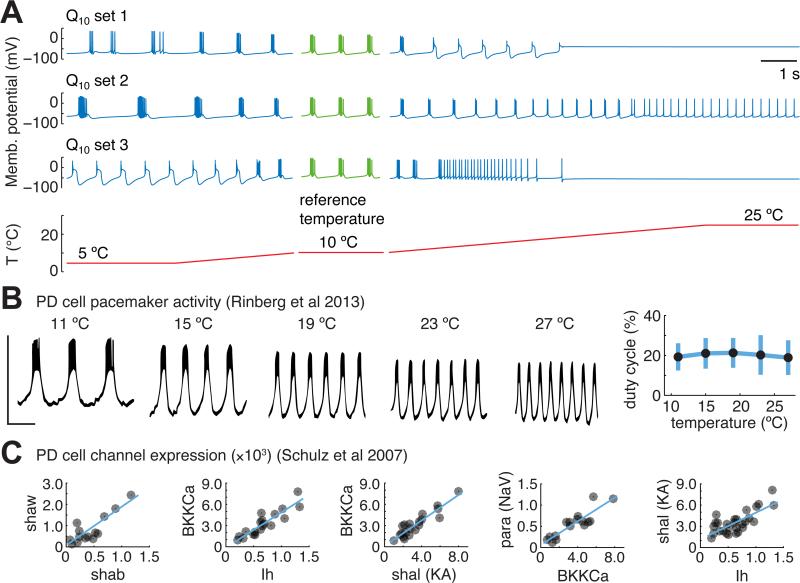
Activity in single neurons and circuits results from the interaction of many nonlinear voltage-gated conductances, and is therefore generically very sensitive to changes in kinetic properties of conductances [4]. This is evident in warm-blooded homeotherms such as humans, where changes in brain temperature of only a few degrees can result in seizures, loss of consciousness or death. Figure 1A illustrates temperature sensitivity in model pacemaker neurons that have been assigned random Q₁₀s over a realistic range (2 - 4). Each neuron has the same set of 8 conductances with fixed densities. At the reference temperature (10 °C) the neurons show identical bursting activity (green traces in Figure 1A). However, this activity is severely disrupted as temperature is varied from 5-25 °C, with each different assignment of Q₁₀s causing qualitatively different changes. In contrast, the biological data reproduced in Figure 1B shows temperature robust pacemaker activity in isolated PD cells of the STG [3]. Notably, the duty cycle of these neurons (the percentage of time the neuron is firing during a burst cycle), which is important for coordinating relative muscle contraction timing, is tightly preserved even though the cycle frequency increases with temperature. Pacemaker duty cycle robustness, in concert with synaptic and intrinsic mechanisms of the follower cells [7], allows temperature compensation of phase relationships in the wider circuit.

Figure 1. Temperature robust neural activity is non-trivial but observed biologically in neurons with highly variable conductance expression.

(A) Three example model neurons with identical conductance densities and randomly assigned Q₁₀s for all kinetic parameters (values and ranges in Supplemental Table S1). Conductance densities were chosen to produce bursting pacemaker activity at the reference temperature (green traces). All models are subjected to an identical acute temperature ramp between 5 and 10 °C and between 10 and 25 °C (blue traces); temperature ramp is shown on the same timescale (red trace). (B) Example traces of a pharmacologically isolated PD pacemaker cell in the STG, subjected to acute changes in temperature, reproduced from [2]. Scale bar spans −75 to −25 mV (vertical) and 1 second (horizontal). (Right) summary measurements of PD duty cycle as a function of temperature across 12 different preparations [1]. (C) Single-cell ion channel gene expression data from PD pacemaker neurons, reproduced from [9]. Units are mRNA copy numbers from single cell real-time PCR, normalized to ribosomal RNA. Blue lines are linear fits where significant correlations were found.

Together with other studies [7, 15] the extreme sensitivity of the models in Figure 1A shows that temperature robust behavior is not expected for ion channel Q₁₀s selected from a biologically realistic range. Therefore, some tuning of either the Q₁₀s or the channel densities must occur in temperature-robust biological systems. It is conceivable that ion channel Q₁₀s can be tuned on an evolutionary timescale or on short timescales as a result of protein modification. On the other hand, channel densities are known to be under regulatory control [11-13] and biological data show that conductance expression is highly variable in neurons, including the pacemaker cells of the STG (Figure 1C). This is consistent with theoretical studies that show there are many possible combinations of neuronal parameters consistent with a given type of activity [16-20], suggesting that neurons can somehow find entire families of temperature robust combinations of channel densities.

Temperature robustness via channel density regulation

Consider a physiological property, P, of a neuron – this could be spike frequency, burst duty cycle or any other relevant property. Temperature robustness of P arises when the derivative of P with respect to temperature, T, is close to zero over some temperature range:

$$\frac{dP}{dT}\approx 0$$

For convenience we restrict attention to a single compartment neuron model with fixed capacitance. In this case, all physiological properties depend on the dynamics of the ionic currents in the cell. We can thus write the temperature dependence of P in terms of the temperature-dependence of each current, I_i, using the chain rule [2, 21, 22]:

$$\frac{dP}{dT}=\sum _i\frac{dP}{d{I}_i}\frac{d{I}_i}{dT}$$

The contribution of each current, I_i, to P is weighted by the corresponding channel density, ḡ_i. Thus,

$$\frac{dP}{dT}=\sum _i{\stackrel{‒}{g}}_i\frac{dP}{d{x}_i}\frac{d{x}_i}{dT}$$ (2)

where x_i is the unit current due to each channel type (so that I_i = ḡ_ix_i). Informally, this relationship can be summarized as:

$$\text{temperature dependence of property}P=\sum _{\text{all currents}}\left(\text{expression level of current}i\right)\times \left(\text{change in}P\text{due to temperature dependence of current}i\right)$$

Within some range of the ḡ_i, each current affects membrane potential dynamics to either increase or decrease property P (or it has no effect, in which case it is irrelevant). Therefore, the dP/dx_i terms in (2) are either positive or negative. The dx_i/dT terms depend only on the Q₁₀ s corresponding to current i, which are always positive and monotonic. Re-writing equation (2) and setting dP/dT = 0, gives:

$$0=\sum _{i=1}^{n-k}{\stackrel{‒}{g}}_i\mid \frac{dP}{d{x}_i}\mid \frac{d{x}_i}{dT}-\sum _{i=n-k+1}^n{\stackrel{‒}{g}}_i\mid \frac{dP}{d{x}_i}\mid \frac{d{x}_i}{dT}$$ (3)

Here we have split the currents according to whether dP/dx_i is positive or negative. For a large number, n, of different conductances with a mixture of positive and negative contributions (1 < k < n), condition (3) is easily satisfied at a single temperature by solving for ḡ_i. If, in addition, the dP/dx_i terms are sufficiently smooth, P will be approximately temperature invariant over an extended temperature range. Most importantly, if (3) is satisfied for one set of conductance densities, {ḡ_i}, then linearly scaled densities {αḡ_i} also satisfy (3), where α is a scaling factor. This shows that a single temperature robust solution can extend to entire families of temperature-robust solutions with linearly correlated conductance densities.

Intuitively, the above argument says that temperature robustness is achieved when the temperature dependencies of multiple processes that negatively and positively affect P approximately cancel. This approximate cancelling has been called ‘antagonistic balance’ [2, 22]. The important point to take from equation (2) is that the weighting of each contribution to overall temperature dependence is controlled by conductance density, equivalently, the expression levels of channel proteins in a biological neuron. Clearly, non-permissive situations can exist, for example if a property depends on only one gating variable of a temperature sensitive conductance.

Equation (3) says that if a property is influenced positively and negatively by multiple temperature-sensitive currents, then temperature robustness can be achieved by controlling conductance densities alone. Furthermore, whenever such solutions exist, linearly correlated temperature-robust sets of conductances will also exist. In neurons that express many types of conductance, there will generally be many positive and negative contributions to a given property, making equation (3) easier to satisfy. Together, this shows that regulation that gives linearly correlated conductances can be sufficient for temperature robustness.

Existence of temperature robust channel density configurations in models with mismatched Q₁₀s

We examined the temperature robustness of duty cycle (fraction of cycle period that the neuron is active) in model bursting pacemaker neurons. Duty cycle is important for coordinating rhythms in central pattern generating circuits, such as in the pyloric circuit of the STG. Moreover, temperature robustness of this property is far from trivial to achieve, as Figure 1A illustrates.

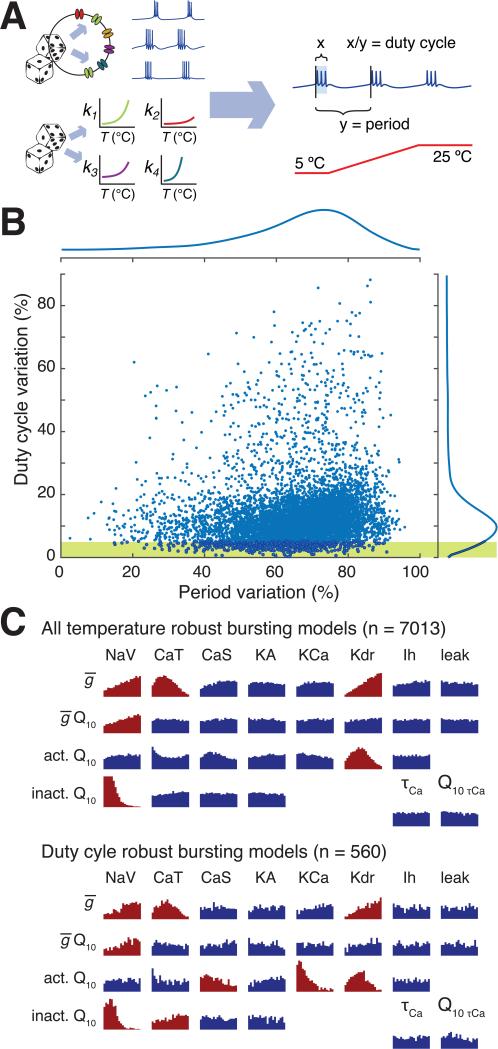
To provide an initial set of candidate models, we randomly sampled conductance densities as well as Q₁₀s in a single compartment conductance based model (Figure 2A). For each sample, all of the voltage-dependent gating variables as well as the unitary conductances and calcium dynamics were assigned random Q₁₀ values over a realistic range. Q₁₀s for each gating variable were randomised uniformly in the range (1< Q₁₀ <4) and unitary conductances in the range (1< Q₁₀ < 1.5). As expected, most (94%) of the 116,400 models we sampled failed to maintain bursting activity over a temperature range (5-25 °C).

Figure 2. Many sets of conductance densities can produce temperature robust neurons with mismatched Q₁₀s.

(A) Strategy for sampling temperature-robust combinations of channel densities and Q₁₀s. Both channel densities and Q₁₀s were randomly assigned to 116,400 single compartment models, which were then screened to find temperature robust pacemaking activity by measuring duty cycle and burst period during acute temperature ramps (parameters in Supplemental Table S1). (B) Total variation in cycle period and duty cycle over the temperature range 5 – 25 °C for all 7013 models that maintained bursting across temperature. Total variation is defined as the difference between maximum and minimum cycle period/duty cycle across the temperature range. Marginal distributions of period variation and duty cycle variation are shown to the top and right of the plots. Yellow shaded region shows the subset of models that maintained duty cycle within 5% over the temperature range. (C) (Top panel) Histograms of Q₁₀s for all channel gating variables and maximal conductances, and for calcium buffering time-constant and Q₁₀. For maximal conductances, the horizontal axis ranges from 1.0 to 1.5. For calcium buffer time-constant the range is 20-100 ms. For all other Q₁₀ histograms the range is 1.0 to 4.0.

Distributions that deviate substantially from the original uniform sampling distribution are shaded red (Kolmogorov-Smirnov statistic > 0.1.) Conductance abbreviations: NaV = fast sodium, CaT = transient calcium, CaS = slow calcium, KA = A-type potassium, KCa = calcium-activated potasium, Kdr = delayer rectifier potassium, Ih = hyperpolarization-activated mixed cation conductance. (Bottom panel) as for Top panel, but for the subset of 560 models that maintained duty cycle within 5%, as depicted in yellow shaded region of (B).

However, among the 7013 models that did maintain bursting activity across temperature, 560 (0.5%) of the models maintained duty cycle within a 5% range. The distribution of duty cycle variation in all models over 5-25 °C is shown in Figure 2B, along with the distribution of variation in cycle period. Notably, period is less temperature-robust than duty cycle in these models. Biologically, most neurons and neural circuits, including those found in the pyloric circuit exhibit increases in frequency of bursting or spiking as temperature increases [6-8]. Interestingly, the distribution in duty cycle total variation peaks at 10.5%, very close to the biologically observed value of 13% in isolated pacemaker neurons of the crab pyloric rhythm [3]. Thus, in a neuron with only 8 conductances it is relatively easy to find combinations of Q₁₀s and conductance densities that are temperature robust.

Which conductance parameters contribute to duty cycle robustness? Figure 2C shows histograms of Q₁₀ values for which temperature robust bursting (top panel) and temperature robust duty cycle (bottom panel) exist. Permissible Q₁₀s for bursting are broadly distributed, indicating that individual Q₁₀ values are relatively unimportant. Some Q₁₀s (colored red) show detectable deviations from uniform distributions, indicating that bursting is sensitive to the corresponding kinetic parameter. These distributions did not alter markedly when we selected parameter sets with robust duty cycles (Fig 2C, lower panel), except for the calcium-dependent potassium conductance, (g_KCa), which favored lower Q₁₀ values. Therefore, in this model, many combinations of conductances can offset temperature-dependent deviations in kinetics as expected from the previous analysis (Equation 3). As reported previously [15], there was no obvious correlation among the parameters of robust models (data not shown).

Although many sets of conductance densities give rise to temperature robust duty cycle, these represent a small fraction of densities that give temperature robustness of a bursting rhythm to begin with, which in turn occupy a small volume of all feasible conductance densities. Moreover, it is clear that a smaller fraction still (solutions toward the left-hand region of the shaded region of Figure 2B) have temperature robust period as well as duty cycle. In this sample, only two parameter sets can maintain both properties within 10%. Thus, robustness to one property imposes a strong constraint on the ability to be robust to additional properties.

Activity-dependent channel regulation can generate temperature robust neuronal properties

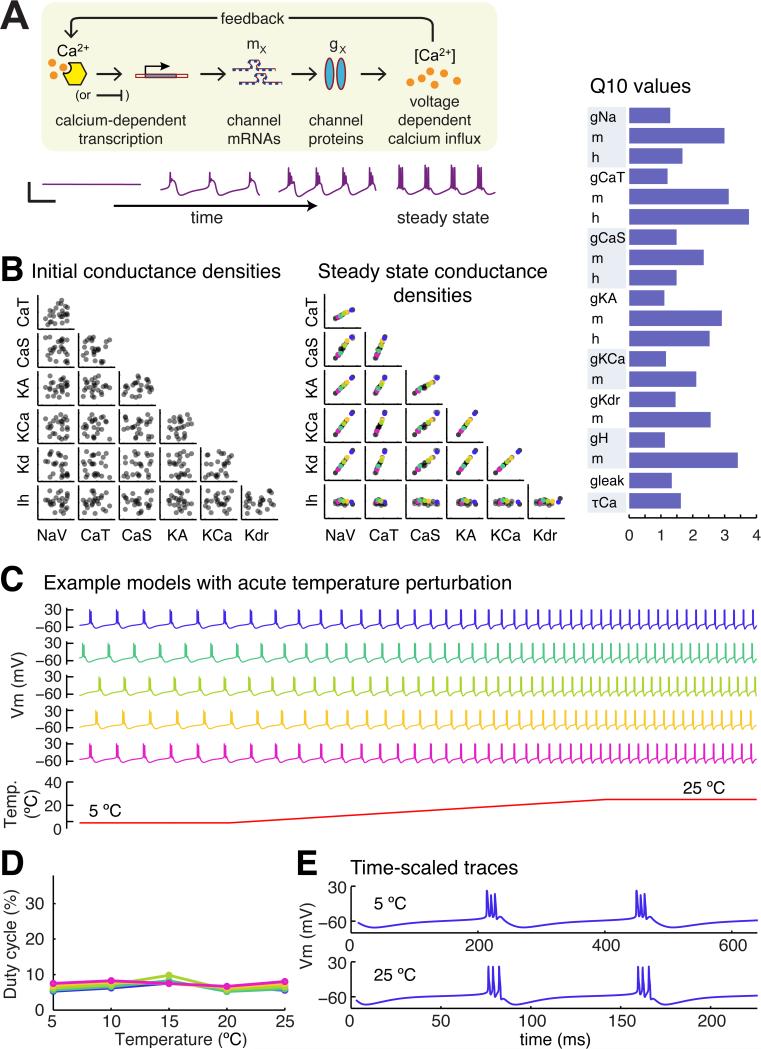
The fixed conductance densities of the models in Figure 2 allowed us to construct models that regulate their conductances using activity-dependent feedback. We recently showed [11, 12] how a simple model of gene regulation can be coupled to a single, global activity sensor, such as a putative calcium-activated pathway depicted in Figure 3A. Briefly, the expression rates of each gene, m_i, is proportional to the deviation of calcium concentration, [Ca], from an equilibrium value, Ca_eq:

$$\frac{d{m}_i}{dt}=K_i({\mathrm{Ca}}_{eq}-\left[\mathrm{Ca}\right])$$ (4)

The origin of Ca_eq is discussed extensively in [11] and arises when one considers the interaction between calcium-dependent processes that interact to control gene expression. Together, Ca_eq, and the expression rate constants, K_i, constitute a regulation parameter set for a model, which is assumed to be fixed for a particular cell type [11, 12]. For example, cells with a constitutively repressed channel gene would have a correspondingly low expression rate. We note that these rates are very slow relative to spikes and calcium oscillations, so these equations effectively average out calcium concentration. Channel densities in the model evolve in proportion to the expression levels of the corresponding genes:

$$\frac{d{\stackrel{‒}{g}}_i}{dt}=A(m_i-{\stackrel{‒}{g}}_i)$$ (5)

where A is some constant representing channel turnover rate. From random initial conditions, the model settles to a steady-state (ss) in which the channel genes, and thus channel density, are linearly correlated, as can be seen by integrating equations (4-5) and calculating the approximate ratios of the steady state densities, ${\stackrel{‒}{g}}_i^{ss}$:

$${\stackrel{‒}{g}}_i^{ss}∕{\stackrel{‒}{g}}_j^{ss}\approx K_i∕K_j$$ (6)

further analysis in [11, 12] shows further that this model converges.

Figure 3. An example of a self-regulating population of model neurons that establish temperature-robust sets of conductance densities.

(A) Cartoon of the conductance regulation model used in this paper. Calcium concentration directly modulates the expression rates of all conductances densities by altering the rate of production of a channel intermediate (‘mRNA’) on an appropriately slow timescale (orders of magnitude slower than fluctuations in calcium due to spikes and membrane potential oscillations). (Lower panel) Example traces showing convergence of the model. Scale bar: 50 mV (vertical), 500 ms (horizontal). See ref [11] for full model details. (B) (Left panel) Random initial conductance densities in 25 model neurons. (Middle panel) Steady-state conductance densities in the same 25 model neurons in the left panel following convergence under the control of one example parameter set from the 2028 parameter sets that produced temperature-robust self-regulating neurons. (Right panel) Q₁₀ values of the conductances in the model neurons in the left and middle panels. (C) Acute temperature ramps in five example model neurons selected from the steady-state population in (B). (D) Quantification of duty cycle in the five example neurons in (C) as a function of temperature. (E) Time-stretched membrane potential traces from the blue model neuron in (C).

Equation (6) provides a way to estimate regulation parameters from fixed models. We used the subpopulation of 560 fixed models in Figure 2 that maintained duty cycle within 5% to derive initial guesses for the K_i and the average calcium concentration, Ca_eq.

Equation (6) is approximate due to nonlinearities between steady-state average calcium and conductance density [11]. We thus sampled regulation parameters in a neighborhood and subjected the resulting self regulating models to temperature perturbations (400 samples for each of the 560 candidate parameter sets, 235,600 in total). In this sample, models are not only required to maintain duty cycle within a 5% range over 5-25 °C, they must also, by necessity, maintain average calcium concentration as temperature changes. A fraction (<1%; 2098 parameter sets) satisfied these criteria and generated self-regulating duty cycle-robust neurons.

Figure 3B shows the initial and steady-state conductances of an example self-regulating model and its corresponding set of assigned Q₁₀ values. Multiple runs of the model generates a population of cells with variable underlying conductances that are linearly correlated [12], as predicted by quation (6). These correlations recapitulate direct measurements of mRNA expression and conductance densities in identified neurons of the STG [9, 10, 13, 23] (Figure 1C).

Figure 3C shows membrane potential traces during acute temperature ramps, for five different neurons indicated in Figure 3B (color coded). Figure 3D quantifies duty cycle robustness with respect to temperature in this population of cells. Scaled membrane potential traces of the top cell in Figure 3C are shown in Figure 3E. The action potential waveform in the scale traces deviates with temperature, indicating temperature induced changes in the gating kinetics of the underlying conductances, which is to be expected given the substantial mismatch among the underlying Q₁₀s (Figure 3B). Nonetheless, this set of regulation parameters, along with the other 2098 parameter sets, drives conductance densities toward regions of parameter space where temperature effects are balanced to maintain duty cycle.

Discussion

While many sets of conductances and Q₁₀s are temperature robust over some range, these represent a very small fraction of a random sampling of parameter space. Indeed, the conductance densities of successful self-regulating models form a very specific slice through parameter space. The general form of the model we present here demonstrates how a simple, biologically plausible control rule can allow neurons to land in these spaces of “good solutions” where temperature compensation occurs automatically. The signature of this control rule is found in the tight correlations in channel expression that is seen experimentally in temperature robust neurons. We speculate that over evolutionary timescales, the gene sequences and resulting enzymatic interactions that control gene expression have been shaped to make some organisms, tissues and cells acutely temperature robust by similarly constraining the underlying regulatory balance of multiple temperature-dependent components. Although we have focused on the context of rhythmic neuronal activity that is observed to be robust in crustaceans, the principle of how multiple, degenerate temperature-dependent processes can be co-regulated to ensure robustness likely generalizes. For example, many species of cold-blooded homeotherms need to be robust to acute temperature fluctuations in the nervous system so as to maintain thermal homeostasis through the behaviors they employ that demonstrate their temperature preferences [24]. Even commonly used warm-blooded model organisms, such as rodents, exhibit remarkably robust nervous system function in the face of large temperature fluctuations [25]. What remains an open question is how robustness to one perturbation, in this case temperature, can coexist with robustness to other environmental challenges, each of which will potentially impose a new constraint on the available parameters, and thus on the regulatory mechanisms themselves.

Experimental Procedures

Single compartment pacemaker model neurons were constructed using channel kinetics described in [12]. The models had 7 voltage-dependent conductances: fast sodium (NaV), transient and slow calcium (CaT, CaS), A-type potassium (KA), calcium-activated potassium (KCa), delayed rectified potassium (Kdr), hyperpolarization-activated mixed cation (Ih) and a leak. Calcium dynamics has a first order decay as described in [12].

Temperature dependence was modeled in the time-constants of the channel gating variables, the maximal conductance and the time-constant of calcium buffering. For example, for a conductance g with gating variables, m and h, we have standard kinetic equations g = ḡm^ph^q; τ_mṁ = m_∞(V) – m; τ_hḣ = h_∞(V) – h, where ḡ is maximal conductance, p, q are gating exponents, τ_x are gating time constants, x_∞(V) are steady-state voltage dependencies and V is membrane potential. The temperature dependence is modeled as g = R_g(T)ḡm^ph^q and R_m(T)⁻¹τ_mṁ = m_∞(V) – m, (with the same form for h), where T is temperature (in Kelvin) and R_x(T) = Q_10,x^{(T–T_ref)/10}. In the case of calcium buffering, the corresponding equation is R_Ca(T)⁻¹τ_Ca[Ċa] = 0.94I_Ca – [Ca] + 0.05. The coefficient of 0.94 (in units of μM nF / pA) is a geometric factor converting calcium current to concentration assuming the cell is approximated as a cylinder of 50 μm in diameter and 400 μm long and the steady-state value of 0.05 (in μm) corresponds to approximate resting cytosolic calcium concentration [12].

Models that use calcium dependent channel regulation (Figure 3) are exactly as described previously [12]. Regulation parameters were chosen as described in the main text. The conductance densities, regulation parameters and Q₁₀ values for all simulations are given in table S1 in the supplemental data. Duty cycle measurements were made using a spike threshold of −10mV. Simulation code is available at https://github.com/marderlab/oleary_marder_2016

Highlights.

• - Neural activity is generically highly temperature sensitive

• - Neurons achieve temperature robustness with highly variable conductance densities

• - Feedback regulation shapes variability to permit temperature robust neural activity

• - Robustness to global perturbations constrains cellular regulation mechanisms