Noise Shaping in Neural Populations with Global Delayed Feedback

Abstract

The interplay between intrinsic and network dynamics has been the focus of many investigations. Here we use a combination of theoretical and numerical approaches to study the effects of delayed global feedback on the information transmission properties of neural networks. Specifically, we compare networks of neurons that display intrinsic interspike interval correlations (nonrenewal) to networks that do not (renewal). We find that excitatory and inhibitory delays can tune information transmission by single neurons but not by the entire network. Most surprisingly, addition of a delay can change the dependence of the information on the coupling strength for renewal neurons and not for nonrenewal neurons. Our results show that intrinsic ISI correlations can have nontrivial interactions with network-induced phenomena.

1. Introduction

There is considerable interest in understanding the properties of excitable systems [5, 25, 54, 73, 75] and in particular neural spike trains. The study of experimental data from neurons in the brain is complicated by the fact that these display variability to repeated presentations of the same stimulus [46]. The role of this noise is still unclear: noise can increase information transmission through stochastic resonance [5, 25, 54] in the subthreshold regime at the single neuron level. In the suprathreshold regime, noise is only detrimental at the single neuron level but can increase information transmission by a population [71]. Studies of neural systems are furthermore complicated by the fact that many neurons display intrinsic dynamics such as burst firing [33, 68, 69], oscillations [32, 28, 34, 45, 66, 72], correlations in the activity of many neurons or correlations between successive interspike intervals (ISIs) [7, 17, 18, 36, 37, 39, 43, 61] as reviewed in [24]. Finally, anatomical studies in several systems have shown that feedback projections from higher centers often vastly outnumber feedforward projections from the periphery [6, 31, 57, 69]. Finite conduction speeds through axons will induce delays in this input and can have important consequences on information processing by neurons [12, 20, 21, 26, 34, 41, 45]. Understanding the interaction between intrinsic and network induced dynamics and their role in regulating information transmission by neural assemblies is therefore of critical interest.

Electrophysiological experiments have shown that many neurons displayed a single negative ISI correlation at lag one [7, 17, 24, 36, 37, 39, 43, 61] implying that ISIs shorter than average are followed by ISIs longer than average and vice-versa. Other studies have shown that some neurons can display temporal anti-correlations in which the ISI correlation coefficients alternate in sign and decay over long lags [2]. Finally, many neurons display increased variability at very long time scales (e.g. minutes) [9, 43, 52] which are caused by weak positive ISI correlations that decay over many lags [52]. We do not consider these correlations here because their effects are felt at time scales that are often much greater than those seen in animal behavior [55]. It has been shown that both a single negative ISI correlations [9, 27, 44, 61] as well as temporal anti-correlations [23] can enhance signal detection and information transmission in isolated single neurons. In the case of a single negative ISI correlation at lag one, this process occurs through noise shaping [8, 9, 10, 11, 40]: a process by which the noise power of a neurons is shifted from a certain frequency range to another and thereby increasing information transmission in the former [56, 70]. However, noise shaping can also occur at the network level as a result of inhibitory coupling [49]. How does noise shaping occurring at the single neuron level interact with noise shaping resulting from all-to-all inhibitory coupling? Recent work has shown that it was excitatory coupling, and not inhibitory coupling, that would lead to increased information transmission in networks of neurons that display intrinsic ISI correlations [1]. However, this previous study assumed that the interactions occurred instantaneously and did not include temporal delays.

Here we explore and compare the effects of adding delayed all-to-all coupling in networks composed of neurons with and without intrinsic ISI correlations. We note that such network geometry has been previously used with success to reproduce experimental results [12, 20, 21]. Further, anatomical studies have shown that the number of neurons in the brain that are connected in such a manner can range from a few to many [47, 48]. We thus believe that our approach is realistic and can thus give results that are relevant to experimentalists.

The paper is organized as follows. The models are presented in section 2. Based on linear response theory [63], section 3 shows the theoretical calculations for information transmission [62] in neural networks with delayed feedback [12]. Section 4 shows the results, where we explore the effects of varying network size, delay time and network connectivity on the coherence and mutual information rate. We finally discuss the implications of our results in section 5.

2. The models

2.1. Renewal and nonrenewal models

As before, we use two neuron models: one that displays intrinsic ISI correlations (and therefore noise shaping) and one that does not [1, 10, 40]. The neuron model that displays intrinsic ISI correlations is referred as nonrenewal and the one that does not is referred to as renewal. Both are perfect integrate-and-fire models [30] where the observable output v (i.e. the membrane voltage) is given by [10, 40]:

$$\stackrel{.}{v}=\mu +s(t)$$ (2.1)

where μ is a positive bias current and s(t) is a time-dependent stimulus. Every time the voltage v reaches a threshold θ it is said that an action potential has occurred and v is is reset to a value θ_R. A new threshold value is then drawn uniformly within the interval [θ₀ − D, θ₀ + D] thereby introducing variability in the firing sequence if D > 0.

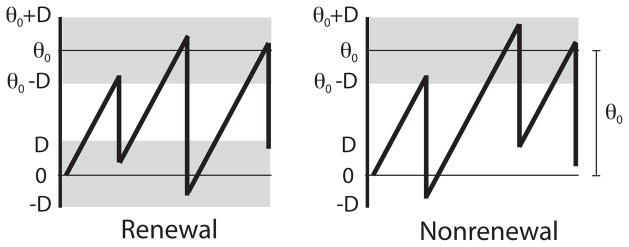
The difference between the two models relies on the reset rule: in the nonrenewal model, we have θ_R = θ − θ₀ and thus θ_R ∈ [−D, D] (fig. 1). This reset rule introduces a correlation between the threshold value θ and its subsequent reset value θ_R, thereby negatively correlating successive interspike intervals (ISI) in the absence of a time-dependent signal s(t) [10, 40]. On the other hand, in the renewal model, θ_R is drawn uniformly within the interval [−D, D]. This makes the threshold θ and the reset value θ_R independent and, as a consequence, consecutive ISIs will not be correlated [10, 40]. Both the renewal and the nonrenewal models share the same first order statistics of threshold and reset values and therefore will share the same first order ISI statistics [10, 40]. In particular, the mean ISI is given by 〈I〉 = θ₀/μ. The mean firing rate r₀ = 1/〈I〉 is then the same for both models and given by:

$$r_0=\frac{\mu }{{\theta }_0}$$ (2.2)

Figure 1.

Example time series from the renewal (left) and nonrenewal (right) integrate and fire models. In both models, the threshold value between two consecutive firings is drawn uniformly within the interval [θ₀ − D, θ₀ + D]. The difference is in the reset rule whenever v reaches θ: for the renewal model, the reset value of the voltage immediately after an action potential is drawn uniformly within the interval [−D, D]. In contrast, the voltage v is decremented by a fixed amount θ₀ in the nonrenewal model.

2.2. Network architecture

The N model neurons are then coupled to each other through their spiking activity, in a way such that whenever any neuron fires an action potential all the neurons within the network will receive a post synaptic current after a time delay τ_d ≥ 0 (fig. 2). The activity of neuron k in a given network is then given by:

$$\stackrel{.}{v_k}={\mu }_k+s(t)+\frac{1}{N}\sum _{j=1}^N\sum _{m=1}^{M_j(t)}{K}_{kj}\gamma (t-t_j^m-{\tau }_d)$$ (2.3)

where μ_k is the constant bias current to neuron k, $t_j^m$ is the m^th spike of neuron j, τ_d is the delay and M_j(t) is the spike count of neuron j at time t (i.e. the total number of action potentials fired by neuron j at time t). K_kj represents the coupling strength between neurons j and k and γ(t) is the post-synaptic current waveform given by [1, 12]:

$$\gamma (t)=\mathrm{\Theta }(t)e^{-t/{\tau }_s}$$ (2.4)

where Θ(t) is the Heaviside function (Θ(t) = 1 if t ≥ 0; Θ(t) = 0 if t < 0) and τ_s determines the rate of decay of the post-synaptic current. Throughout this study we will consider homogeneous networks and take K_kj = K and μ_k = μ.

Figure 2.

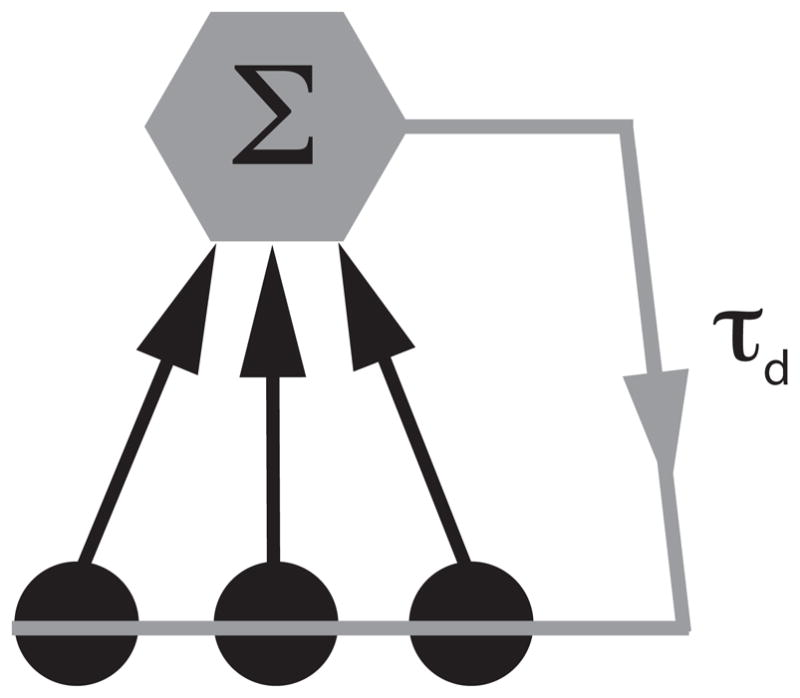
Network architecture. Each neuron projects to an integrator neuron which in turn feeds back to all the neurons with delay τ_d. Note that, mathematically, this is equivalent to all-to-all coupling with a delay [21, 41]. We further note that anatomical studies have shown that such a geometry occurs in the brain and that the number of neurons that actually project to the integrator can vary from a few to many [47, 48].

3. Theory of signal processing by networks of renewal and nonrenewal neurons

We now present information theory which relies on computing the mutual information rate between the stimulus s(t) and the spike train activity of either a single neuron k in the network, x_k(t), or the average spike train activity of all the neurons in the network $X(t)=\frac{1}{N}{\sum }_{k=1}^N{x}_k(t)$. We first introduce information theory and then present calculations based on linear response theory that will give an approximate expression for the mutual information rate that is valid if both the stimulus s(t) and the fluctuations in the average network activity $\frac{1}{N}{\sum }_{k=1}^N{x}_k(t)$ are weak.

Throughout this study, we assume that the spike train activity of neuron k is represented by a sum of Dirac delta functions centered on the spiking times ${\{t_k^j\}}_{j=1}^{M_k(t)}$:

$$x_k(t)=\sum _{j=1}^{M_k(t)}\delta (t-t_k^j)$$ (3.1)

where M_k(t) is the spike count of neuron k at time t. We also take the stimulus s(t) to be a zero mean Gaussian white noise with spectral height α that is lowpass filtered by a fourth-order Butterworth filter with cutoff frequency f_c. We note that the stimulus s(t) is not correlated with the sequence of threshold and/or reset values used in each model. Therefore, the different threshold and reset values is considered as a source of noise that introduces variability in the responses of both models. The strength of this noise is controlled by the parameter D ≥ 0 [1].

3.1. Information theory

Information theory was developed by Shannon [19, 67] in the context of telecommunications and has been widely applied in neuroscience [3, 8, 12, 13, 14, 15, 16, 17, 18, 38, 50, 58, 62, 65]. If the stimulus s(t) has a Gaussian probability distribution, then a lower bound on the mutual information rate MI is given by [3, 62]:

$$MI={\int }_0^{f_c}I(f)df$$ (3.2)

Note that the mutual information rate is expressed in bits/(unit time) and quantifies the system’s ability to distinguish between different stimuli: X bits/(unit time) implies that 2^X stimuli can be distinguished by looking at the activity over one time unit [3, 19]. As time is dimensionless in our study, the mutual information rate MI is thus expressed in bits. Here I(f) is the mutual information rate density given by:

$$I(f)=-{log}_2[1-C(f)]$$ (3.3)

and C(f) is the coherence function given by:

$$C(f)=\frac{{\mid P_{xs}(f)\mid }^2}{P_{xx}(f)P_{ss}(f)}$$ (3.4)

where P_yy(f) = 〈|x̂(f)|²〉 is the power spectrum of the neuronal response x(t) to the stimulus s(t) with x̂(f) the Fourier transform of x(t), P_ss(f) = 〈|ŝ_t(f)|²〉 is the power spectrum of the stimulus s(t) with ŝ_t(f) the Fourier transform of s(t), and P_xs(f) = 〈x̂^*(f)ŝ_t(f)〉 is the cross spectrum between x(t) and s(t), where x̂^*(f) denotes the complex conjugate of x̂(f). Here the 〈…〉 denotes averaging of realizations. We note that the lower bound given by equation (3.2) is equal to the actual mutual information rate in the case of a linear system [3, 64].

3.2. Linear response theory

According to linear response theory, the activity of a neuron in the network in the presence of a time-varying stimulus can be approximated by the baseline activity (i.e. s(t) = 0 and K = 0) of an isolated neuron, x₀(t), plus a small perturbation [63]. Linear response theory has been applied before to describe the behavior of neurons in response to weak input [1, 10, 12, 21, 40, 41].

The spike train of a single neuron k in response to a small time dependent perturbation A_k(t) is then given by:

$$x_k(t)=x_{0k}(t)+({\chi }_k\ast A_k)(t),$$ (3.5)

were χ_k(t) is the susceptibility of neuron k in response to the input. The “*” operation represents a convolution. We note that for a stochastic linear system, equation (3.5) is usually 〈x_k(t)〉 = 〈x_0k(t)〉 + (χ_k * A_k)(t), where 〈…〉 denotes an average over realizations. However, equation (3.5) will hold approximately for large D [1, 21, 40, 41]. As before [1, 12, 21, 41], we take the perturbation A_k(t) to be composed of the common time varying stimulus as well as the average network activity received by neuron k:

$$A_k(t)\equiv A(t)=s(t)+\frac{1}{N}\sum _{j=1}^N\sum _{m=1}^{M_j(t)}K\gamma (t-t_j^m-{\tau }_d)$$ (3.6)

Taking the Fourier transform of equation (3.5) gives:

$${\widehat{x}}_k(f)={\widehat{x}}_{0k}(f)+{\widehat{\chi }}_k(f)\widehat{A}(f)$$ (3.7)

where x̂_k(f), Â(f), x̂_0k(f), and χ̂_k(f) are the Fourier transforms of x_k(t), A(t), x_0k(t), and χ_k(t), respectively. Applying equation (3.6) into equation (3.5) and taking the Fourier transform on both sides yields:

$${\widehat{x}}_k(f)={\widehat{x}}_{0k}(f)+{\widehat{\chi }}_k(f){\widehat{s}}_t(f)+{\widehat{\varphi }}_k(f)\frac{1}{N}\sum _{n=1}^N\widehat{x_n}(f)$$ (3.8)

$${\widehat{\varphi }}_k(f)=K{\widehat{\chi }}_k(f)\widehat{\gamma }(f)exp(-2\pi if{\tau }_d)$$ (3.9)

where ŝ_t(f) is the Fourier transform of s(t) and γ̂(f) is the Fourier transform of γ(t) given by:

$$\widehat{\gamma }(f)=\frac{1}{1/{\tau }_s+i2\pi f}$$ (3.10)

Previous studies have found that the susceptibilities of both the renewal and the nonrenewal models are equal and given by [10, 40]:

$${\widehat{\chi }}_k(f)\equiv \widehat{\chi }(f)=\frac{1}{{\theta }_0}$$ (3.11)

we thus have:

$${\widehat{\varphi }}_k(f)\equiv \widehat{\varphi }(f)=K\widehat{\chi }(f)\widehat{\gamma }(f)exp(-2\pi if{\tau }_d)$$ (3.12)

3.2.1. Mutual Information rate density between the average network activity and the stimulus

In this section, we derive an expression for the coherence between the average network activity and the stimulus s(t). The average network activity can be found by summing equation (3.8) from k = 1 to N and dividing by N. After rearranging terms we obtain:

$$\frac{1}{N}\sum _{k=1}^N{\widehat{x}}_k(f)=\frac{\frac{1}{N}{\sum }_{k=1}^N{\widehat{x}}_{0k}+\widehat{\chi }(f){\widehat{s}}_t(f)}{1-\widehat{\varphi }(f)}$$ (3.13)

From this we can find the average network activity spectrum. If we set $\widehat{X}(f)=\frac{1}{N}{\sum }_{k=1}^N{\widehat{x}}_k(f)$ and denote its complex conjugate by X̂(f)^★, then the power spectrum of the average activity P_XX(f) = 〈X̂(f)X̂(f)^★〉, where the 〈…〉 denotes an average over realizations, is given by:

$$P_{XX}(f)={\left|\frac{1}{1-\widehat{\varphi }(f)}\right|}^2\left[\frac{1}{N}{P}_{00}(f)+{\mid \widehat{\chi }(f)\mid }^2{P}_{ss}(f)\right]$$ (3.14)

Here P₀₀(f) is the power spectrum of a single neuron in the absence of coupling and stimulation. Expressions have already been derived for the power spectra P_00r(f) and P_00n(f) of renewal and nonrenewal model single neurons, respectively [10, 40]:

$$\begin{array}{lll}\hfill P_{00r}(f)& =\hfill & r_0[{(\beta f)}^4-{sin}^4(\beta f)]/\mathrm{\Gamma }\hfill \\ \hfill \mathrm{\Gamma }& =\hfill & {(\beta f)}^4-2{(\beta f)}^2{sin}^2(\beta f)cos(2\pi f/r_0)+{sin}^4(\beta f)\hfill \end{array}$$ (3.15)

$$P_{00n}(f)=r_0-\frac{{sin}^2(\beta f)}{{(\beta f)}^2}\left(r_0-r_0^2\sum _{n=-\infty }^{\infty }\delta (f-n{r}_0)\right)$$ (3.16)

where $\beta =\frac{2\pi D}{\mu }$, and r₀ is the baseline firing rate given by equation (2.2).

The cross-spectrum, P_Xs(f), between the average network activity X(t) and the time-varying stimulus s(t) is obtained by evaluating P_Xs(f) = 〈X̂(f)ŝ_t(f)^★〉, where ŝ_t(f)^★ is the complex conjugate of ŝ_t(f). This yields:

$$P_{Xs}(f)=\frac{\widehat{\chi }(f)}{1-\widehat{\varphi }(f)}{P}_{ss}(f)$$ (3.17)

where P_ss(f) is the power spectrum of the time-varying stimulus. Finally, the coherence between the average network activity and the stimulus can be obtained by equation (3.4):

$$C_{Xs}(f)\equiv C_{\mathit{network}}(f)=\frac{{\mid \widehat{\chi }(f)\mid }^2{P}_{ss}(f)}{\frac{1}{N}{P}_{00}(f)+{\mid \widehat{\chi }(f)\mid }^2{P}_{ss}(f)}$$ (3.18)

The mutual information rate can then be obtained from equation (3.18) using equations (3.2) and (3.3). Note that the expression for the coherence between the average network activity and the time-varying stimulus given by equation (3.18) does not depend on the term ϕ̂(f) and therefore it does not depend directly on the coupling strength K and the delay τ_d [1]. Instead, the dependence of the coherence on the coupling comes indirectly through the dependence of P₀₀(f) on the bias current μ. We note that this does not mean that the delay does not affect the firing dynamics as both power spectrum given by equation (3.14) and the cross-spectrum given by equation (3.17) of the average network activity both strongly depend on the delay τ_d through ϕ̂(f) and this effect has been seen previously [12, 42]. It has been shown in previous studies that in a network of LIF neurons the input to each neuron can be decomposed into a constant and time-dependent components [12, 21, 41]. The new bias current μ′ is composed of the bias current μ in the absence of coupling plus a contribution from the average network activity [1, 12, 21, 41]:

$${\mu }^{\prime }=\mu +K{\tau }_s{r}_0({\mu }^{\prime })$$ (3.19)

where r₀(μ′) is the firing rate of a single uncoupled integrate-and fire neuron with bias μ′. Substituting r₀(μ′) = μ′/θ₀ in equation (3.19) and solving for μ′ gives [1]:

$${\mu }^{\prime }=\frac{\mu }{1-\frac{K{\tau }_s}{{\theta }_0}}$$ (3.20)

Thus, while the average network activity depends on the coupling strength K, it does not depend on the delay τ_d. The situation is however different if one computes the information rate from a single neuron within the network.

3.2.2. Mutual Information rate density between a single neuron within the network and the stimulus

In this section, we derive an expression for the coherence between the spike train of a single neuron x_k(t) and the stimulus s(t). An expression for the power spectrum of x_k(t) can be found by substituting equation (3.13) into equation (3.8):

$${\widehat{x}}_k(f)={\widehat{x}}_{0k}(f)+\widehat{\chi }(f){\widehat{s}}_t(f)+\widehat{\varphi }(f)\frac{\frac{1}{N}{\sum }_{n=1}^N{\widehat{x}}_{0n}(f)+\widehat{\chi }(f){\widehat{s}}_t(f)}{1-\widehat{\varphi }(f)}$$ (3.21)

The power spectrum of the output spike train of neuron k can be obtained by computing $P_{x_k{x}_k}(f)=\langle \widehat{x_k}{(f)}^{★}\widehat{x_k}(f)\rangle$, which gives:

$$P_{x_k{x}_k}(f)=P_{00}(f)\left\{\frac{N-1}{N}+\frac{1}{N}{\left|\frac{1}{1-\widehat{\varphi }(f)}\right|}^2\right\}+{\mid \widehat{\chi }(f)\mid }^2{P}_{ss}(f){\left|\frac{1}{1-\widehat{\varphi }(f)}\right|}^2$$ (3.22)

We next have to evaluate the cross-spectrum between neuron k and the stimulus given by P_xks(f) = 〈x̂_k(f)ŝ_t(f)^★〉, which yields:

$$P_{x_{k}s}(f)=\frac{\widehat{\chi }(f)}{1-\widehat{\varphi }(f)}{P}_{ss}(f)$$ (3.23)

we note that the expression for P_xkxk(f) given by equation (3.22) and the expression for P_xks given by equation (3.23) do not depend on k. Thus, all neurons in the network will have the same power spectra and cross-spectra and will thus have the same coherence C_xks(f) ≡ C(f) which can be obtained by substituting equations (3.22) as well as (3.23) into equation (3.4) [12]:

$$C(f)=\frac{{\mid \widehat{\chi }(f)\mid }^2{P}_{ss}(f){\left|\frac{1}{1-\widehat{\varphi }(f)}\right|}^2}{{\mid \widehat{\chi }(f)\mid }^2{P}_{ss}(f){\left|\frac{1}{1-\widehat{\varphi }(f)}\right|}^2+P_{00}(f)\left\{\frac{N-1}{N}+\frac{1}{N}{\left|\frac{1}{1-\widehat{\varphi }(f)}\right|}^2\right\}}$$ (3.24)

The mutual information rate can then be obtained from equation (3.24) using equations (3.2) and (3.3). It is worth noting that when the network is composed of one neuron (i.e. N = 1), we have C(f) = C_network(f) and C(f) furthermore does not depend on the delay τ_d.

We note that the only difference between the coherence of single renewal and nonrenewal neurons and the stimulus in a homogeneous network comes from the baseline powerspectrum P₀₀(f). Equations (3.15) or (3.16) can be substituted into equation (3.24) in order to obtain the coherence between single renewal or nonrenewal neurons and the stimulus, respectively.

4. Noise shaping by global delayed feedback

It was previously shown that suitable scaling of the noise parameter D would lead to similar mutual information rates in both models [1]. Thus, in order to better compare the effects of the delay on the two models we chose the noise intensities D_n and D_r for the nonrenewal and renewal model neurons, respectively, such that both models would have the same mutual information rates.

4.1. Network size

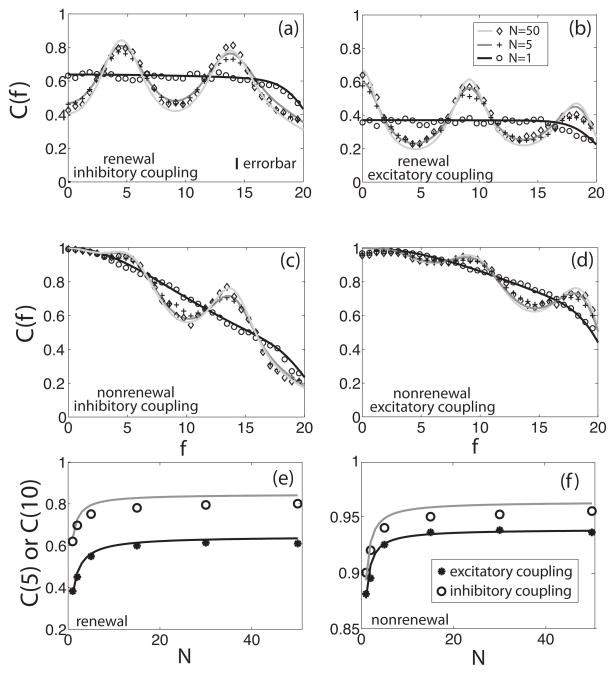
We first examined the dependence of the coherence of a single neuron in a network C(f) on the network size N. Figure 3 shows the coherence C(f) for networks of renewal (figures 3a and 3b) and nonrenewal (figures 3c and 3d) models as a function of frequency for different network sizes N. The simulations are shown as symbols and the theoretical result, given by equation (3.24), are shown as a continuous line. Note that we have C(f) = 1 of the nonrenewal model at f = 0, this is due to the fact that the power spectrum P_00n(0) = 0 for this model [10, 40]. For the renewal model, we have $P_{00r}(0)=2D^2\mu /(3{\theta }_0^3)>0$ and thus C(f) < 1 [1]. When N = 1 there is no resonance in the coherence due to the fact that it doesn’t depend on ϕ(f) which can be seen by substituting N = 1 in equation (3.24). For N > 1 a resonance appears at approximately the inverse of the delay τ_d for positive coupling (i.e. K > 0) and at the inverse of 2τ_d for negative coupling (i.e. K < 0). In both models the resonances in the coherence C(f) become more prominent as the network size increases but converge to limit values as N → ∞. It can be seen that the coherence value at given frequencies saturates as N increases in figures 3e and 3f for renewal and nonrenewal networks, respectively.

Figure 3.

Coherence C(f) between a single neuron and the stimulus as a function of frequency f for different network sizes, N. (a) Coherence for a network composed of renewal neurons with inhibitory coupling in a network of 1 (circle, black), 5 (cross, dark gray), and 50 (diamond, light gray) neurons. The symbols are the numerical simulations and the solid lines are obtained from the theory. (b) Coherence for the same network but with excitatory coupling. (c) Coherence for a network composed of nonrenewal neurons with inhibitory coupling. (d) Coherence for a network composed of nonrenewal neurons with excitatory coupling. (e) Coherence value at f = 10 for excitatory coupling (solid circles) and coherence value at f = 5 for inhibitory coupling (hollow circles) as a function of the network size N for a network composed of renewal neurons. Theoretical values are shown as solid lines for both cases and agree very well with numerical simulations. (f) Coherence value at f = 10 for excitatory coupling (solid circles) and coherence value at f = 5 for inhibitory coupling (hollow circles) as a function of the network size N for a network composed of nonrenewal neurons. Theoretical values are shown as solid lines for both cases and agree very well with numerical simulations. Parameter values used for all the simulations were θ₀ = 2, μ = 300, τ_d = 0.1, τ_s = 0.01, f_c = 20, σ = 27, D_n = 1, D_r = 0.4, and K = −100 (inhibitory coupling) or 100 (excitatory coupling). In this and subsequent figures, the errorbar gives the standard error from 10 numerical simulations of the networks.

It was previously shown in [12] that the coherence increases at the resonant frequency as the network size increases and that this effect is due to a decrease in the power spectrum of a single neuron P_xx(f), while the cross-spectrum P_xs(f) remains constant. Since the coherence C(f) is proportional to the ratio |P_xs(f)|²/P_xx(f) for fixed f, the coherence C(f) increases whenever P_xx(f) decreases and P_xs(f) remains constant [12]. Intuitively, this occurs because, as N increases, the variance of the average network activity decreases and therefore contributes less power to the power spectrum of an individual neuron. The difference between excitatory and inhibitory coupling can be understood as follows. For excitatory coupling, the single neuron will tend to oscillate with a period equal to the delay τ_d. However, for inhibitory coupling, the single neuron will tend to oscillate with a period equal to twice the delay τ_d: the neuron fires at t = 0, it is then inhibited around t = τ_d, and the release from inhibition causes another firing near t = 2τ_d [12, 21, 41]. These oscillations translate to peaks in the power spectrum at integer multiples of 1/τ_d for excitatory coupling and 0.5/τ_d for inhibitory coupling [12].

Adding a delay will thus differentially affect the mutual information rate MI depending on the frequency content of the stimulus s(t). For excitatory coupling, adding a delay will increase the coherence (and thus the mutual information rate density) in the frequency ranges [0, $0.5{\tau }_d^{-1}$] and [ $(0.5n-0.25){\tau }_d^{-1},(0.5n+0.25){\tau }_d^{-1}$] for integer n > 0 even. In contrast, the coherence will decrease in the frequency ranges [ $(0.5n-0.25){\tau }_d^{-1},(0.5n+0.25){\tau }_d^{-1}$] for integer n > 0 odd. In contrast, adding a delay with inhibitory coupling will increase the coherence in the frequency ranges [ $(0.25n-0.125){\tau }_d^{-1},(0.25n+0.125){\tau }_d^{-1}$] for integer n > 0 odd and decrease the coherence in the frequency ranges [0, $0.25{\tau }_d^{-1}$] and [ $(0.25n-0.125){\tau }_d^{-1},(0.25n+0.125){\tau }_d^{-1}$] for integer n > 0 even.

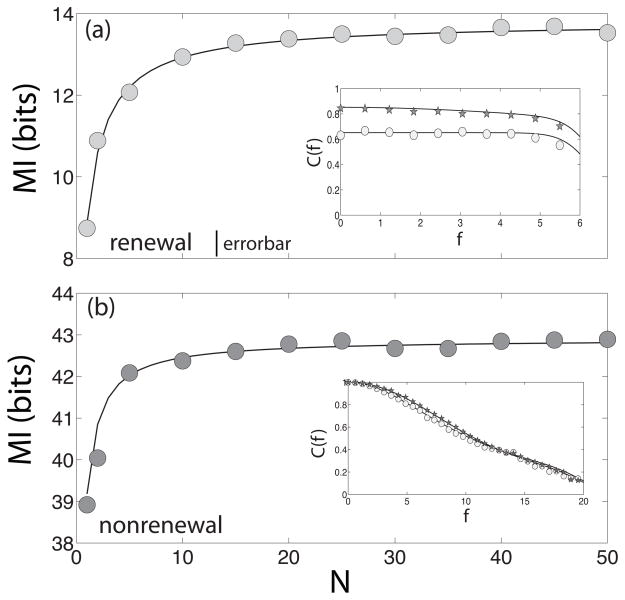
Figure 4 shows the mutual information rate MI as a function of network size, N for both models. For the renewal model, we chose f_c = 6 and τ_d = 0.01 such that increasing N increases the coherence over the frequency range [0, 6] (figure 4a, inset). For the nonrenewal model, we chose f_c = 20 and τ_d = 0.025 such that increasing N also increases the coherence over the frequency range [0, 20] (figure 4b, inset). It can be seen that the mutual information rate MI increases as a function of N and saturates for large N. Figure 4 shows that for both models the biggest change in MI happens when the network is composed from N = 1 to N = 10. It can be seen that the qualitative behavior of both graphs is essentially the same although the nonrenewal model has a larger mutual information rate MI due to the fact that the coherence is unity for f = 0.

Figure 4.

Mutual information rate MI transmitted by a single neuron as a function of network size N for a network composed of renewal (a) and nonrenewal (b) model neurons. The numerical simulations are shown as symbols while the theory is shown as a solid line. In (a), parameters are the same as in fig. 3 except τ_d = 0.01 and f_c = 6. The inset shows the coherence for N = 1 (circles) and N = 10 (stars) for these parameters. In (b), parameters are the same as in fig. 3 except τ_d = 0.025. The inset shows the coherence for N = 1 (circles) and N = 10 (stars) for these parameters.

We conclude that adding a delay has qualitatively the same effect in both models and will create resonances in the coherence in frequency ranges that will depend on the sign of the coupling strength K. The differences observed for both models are largely due to the differences in their coherence curves with K = 0 that have been previously explained in detail [10, 40]. The fact that the coherence C(f) is unity for f = 0 for the nonrenewal model will attenuate the relative effects of delayed feedback near f = 0 since 0 ≤ C(f) ≤ 1 by definition.

4.2. Delay time

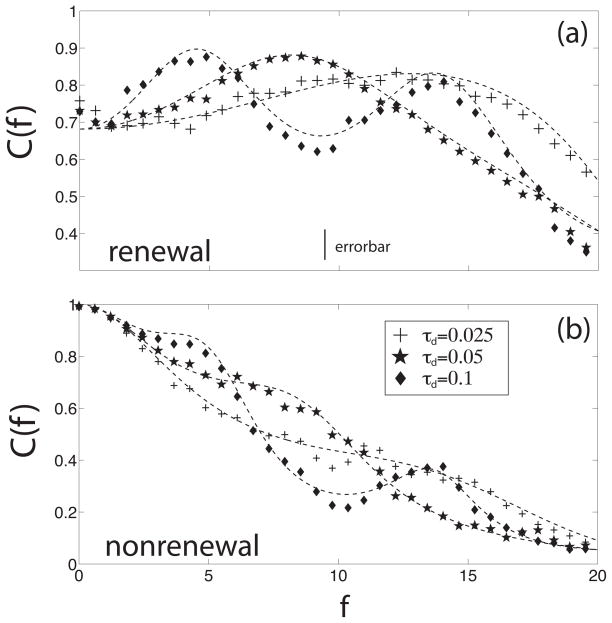
We now explore the consequences of varying the delay τ_d on the resonance in the coherence C(f) of both models. Figure 5 shows the coherence C(f) for both renewal and nonrenewal models as a function of frequency f for different delay times: τ_d = 0.1 (diamonds), 0.05 (stars) and 0.025 (crosses).

Figure 5.

Coherence C(f) of a single neuron in a network of renewal (a) and nonrenewal (b) neurons with inhibitory coupling for different delay times: 0.1 (diamonds), 0.05 (stars), 0.025 (crosses). The symbols represent the numerical simulations and the dashed lines the theoretical results. It can be seen there is good agreement between the simulations and the theory. Other parameters have the same value as in fig. 3 except θ = 5 and K = −100. We also used N = 10. The parameters used are such that the MI is the same for both models when K = 0.

It can be seen in figure 5 that varying the delay τ_d changes the frequency at which the coherence C(f) has a resonance for both renewal (figure 5a) and nonrenewal (figure 5b) networks. As mentioned above, inhibitory coupling is expected to create local maxima in the coherence located near integer multiples of $0.5{\tau }_d^{-1}$ which is approximately true. The main difference with the models relies in that coherence C(f) decreases as f increases for the nonrenewal model (figure 5b) whereas it is approximately constant for the renewal model in the absence of feedback (figure 5a). Due to this effect, the local maxima in the coherence of the nonrenewal model neuron decrease in height with increasing f (see for instance when τ_d = 0.1) whereas the first two local maxima in the coherence C(f) created by the same delay have approximately the same height for the renewal model neuron.

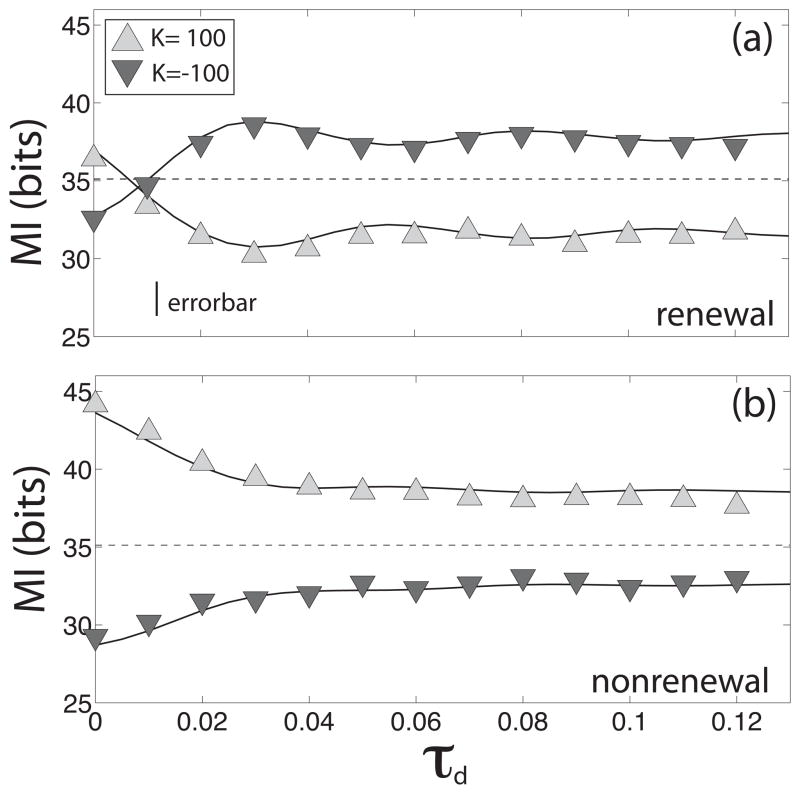
An alternative way to see the effects of the feedback delay time on the information transmission is through the mutual information rate MI for different values of the delay τ_d. Figure 6 shows the mutual information rates MI for both models as a function of the delay τ_d for a single neuron in a network composed of renewal (figure 6a) and nonrenewal (figure 6b) model neurons when they are coupled with excitation (triangles up) or inhibition (triangles down). The solid lines represent the theory for both cases and the dashed line show the value of the mutual information rate MI when the networks are uncoupled. The noise level was adjusted such that both model neurons display the same mutual information rate MI when uncoupled. It can be seen that, with excitatory coupling, the mutual information rate MI decreases with increasing delay in both models. The situation is opposite, however, when the networks are coupled with inhibition: the MI has a minimum value when τ_d = 0 from which it increases until reaching a constant value.

Figure 6.

Mutual information rate MI as a function of delay time for a neuron in a renewal network, (a), and one in a nonrenewal network (b). Symbols show the numerical simulations and the solid line the theoretical results. Triangles up represent excitatory coupling and triangles down inhibitory coupling. Dashed line represents the value of the MI when the network is uncoupled. Other parameters have the same value as in figure 5.

The main difference between both models is the value to which the mutual information rate MI converges to for large delay with respect to the value for uncoupled networks. For the nonrenewal model, the mutual information rate MI is always lesser/greater than its value for no coupling for inhibitory/excitatory coupling for any value of the delay τ_d. For the renewal model, the mutual information rate MI increases/decreases to a value that is greater/lesser than value for no coupling for inhibitory/excitatory coupling. In order to understand why this effect happens it is necessary to explore the effects of different couplings on the coherence and MI.

4.3. Network connectivity

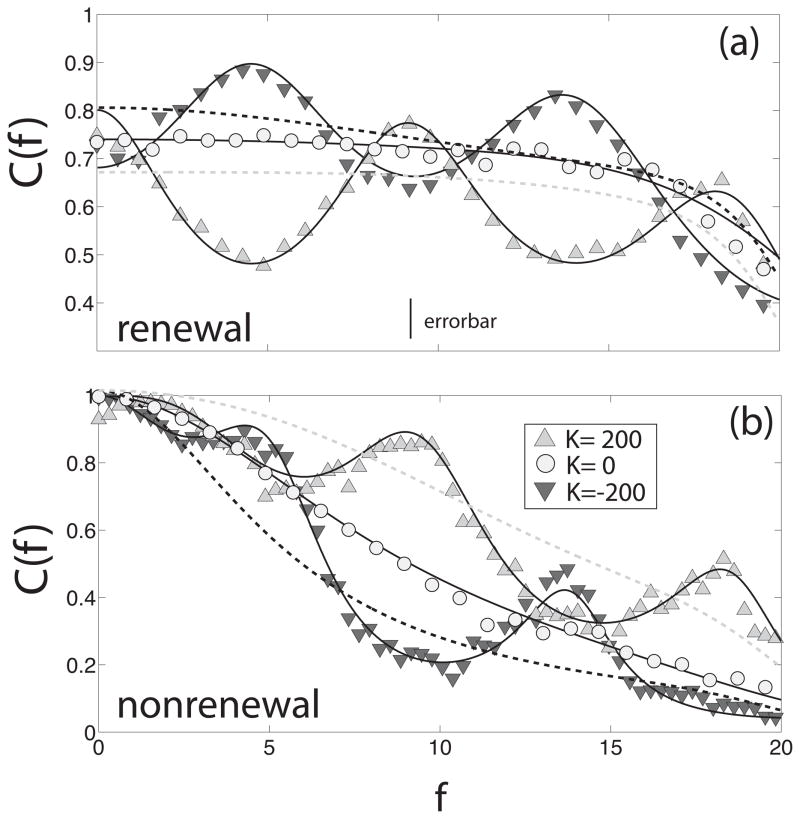
We finally explore the role of the network coupling strength K. Figure 7 shows the coherence C(f) for single neurons in networks of renewal (figure 7a) and nonrenewal (figure 7b) neurons with different connectivities: inhibitory (triangles down), excitatory (triangles up) and no coupling (circles). As in the previous examples one of the differences between the models relies on the fact that the coherence for the nonrenewal model is one at f = 0 while for the renewal model it reaches a fixed value less than one at f = 0. It can also be seen that the resonances caused by the delayed feedback appear at the same frequencies for both models.

Figure 7.

Coherence C(f) of a single neuron in a network of renewal (a) and nonrenewal (b) neurons with a fixed delay τ_d = 0.1 for different values of the coupling strength K, inhibitory coupling (dark triangles down), zero coupling (circles) and excitatory coupling (light triangles up). Other parameters have the same value as in fig 5. In both (a) and (b), the dashed lines show the coherence for τ_d = 0 and inhibitory (black) and excitatory (gray) coupling. Whereas the resonance due to the coupling happens at the same frequency for both models, excitatory coupling tends to increase the coherence for the nonrenewal model as compared to zero coupling whereas the coherence decreases for the renewal model when coupled with excitation. The story is opposite for inhibitory coupling.

However, an interesting difference between both models is that compared to the situation where the networks are not connected (represented in circles), excitatory coupling lowers the coherence in the renewal model and it increases it in the nonrenewal. The situation is opposite for inhibitory coupling: the mean value of the coherence C(f) over the frequency range [0, f_c] increases compared to the uncoupled situation for the renewal model neuron and decreases for the nonrenewal model neuron.

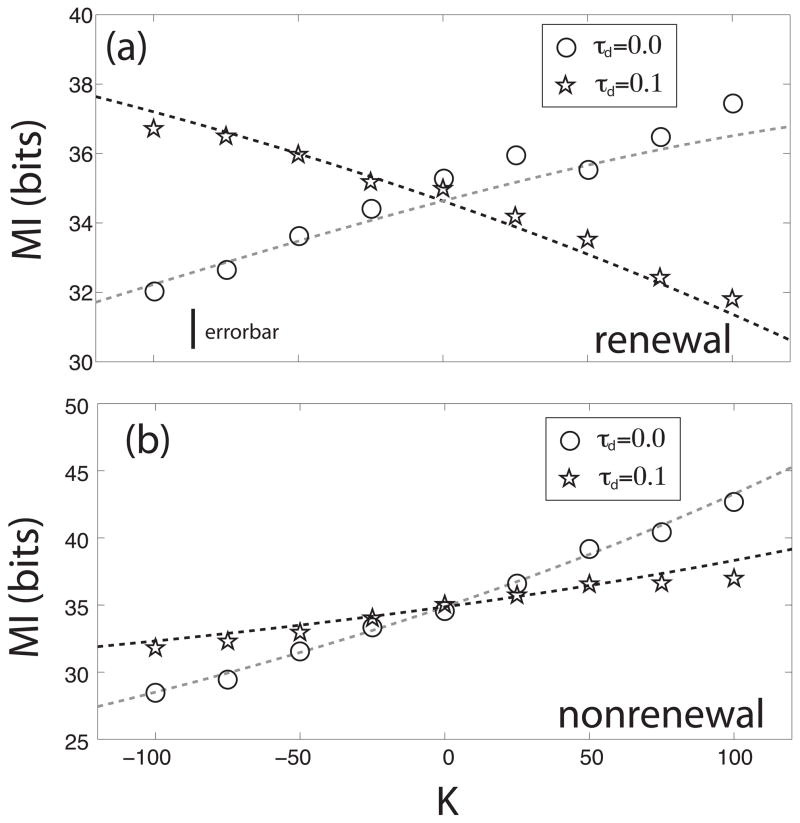
This situation can be better visualized when computing the mutual information rate MI for different coupling. Figure 8 shows the mutual information rate as a function of K when the networks have no delay (represented as hollow circles) and with a delay (stars) for renewal (figure 8a) and nonrenewal (figure 8b) models. For τ_d = 0, both models show an increase in the mutual information rate MI as a function of increasing coupling strength K. However, adding a delay τ_d = 0.1 causes the mutual information rate MI to decrease with increasing coupling strength K for the renewal model only (figure 8a) and not for the nonrenewal model (figure 8b). These results show that intrinsic ISI correlations can have a profound effect on how delayed feedback can alter information transmission by neural networks.

Figure 8.

Effects of adding a delay on the mutual information rate MI as a function of coupling strength K for a neuron in a renewal network (a) and a neuron in a nonrenewal network (b) with τ_d = 0 (circles) and τ_d = 0.1 (stars). Other parameters have the same values as in fig. 5.

5. Discussion

We have explored the effects of delayed global feedback on information transmission in networks of renewal and nonrenewal neurons. Specifically, we found that adding a delay τ_d can cause local maxima and minima in the coherence function between a single neuron’s spike train and the stimulus. The value of the delay τ_d as well as the sign of the coupling coefficient K both determine the location of these maxima/minima. Most interestingly, we found that delays could have differential effects on the mutual information rate MI transmitted by individual renewal and non-renewal neurons embedded in a network. Specifically, we found that increasing the delay τ_d will increase/decrease the overall coherence for excitatory/inhibitory coupling in nonrenewal/renewal model neurons. However, we note that, for τ_d = 0, the coherence increases/decreases for excitatory/inhibitory coupling for both model neurons. Thus, for renewal neurons, the delay qualitatively changed the effect of coupling in the mutual information rate. In contrast, adding a delay did not qualitatively change the effects of coupling on the mutual information rate for nonrenewal neurons.

Our results complement those of [1] where information transmission by networks of renewal and nonrenewal neurons was investigated using methods similar to our own. However, our results focus on the activity of single neurons in the presence of delays whereas [1] only looked at the average network activity in the absence of delays. Our theoretical calculations show in fact that addition of a delay τ_d will surprisingly not affect information transmission by the average network activity, thereby generalizing the results found in [1]. In contrast, the delay τ_d can significantly alter information transmission by single neurons. It was found previously that delays could cause resonances in the coherence and mutual information rate in networks of neurons that may be exploited by sensory systems [12]. However, the model used was a renewal process that did not display any intrinsic noise shaping. More generally, addition of a delay τ_d has been shown to cause oscillatory dynamics in neuronal networks [20, 21, 41, 74]. Our results are consistent with these as the power spectra and cross-spectra of the average network activity will depend on the delay (i.e. addition of the delay will cause changes in the dynamics). However, these effects are not seen when one considers the mutual information density which normalizes the cross-spectrum by the power spectrum of the response as was recently reported [42]. As such, these oscillations may or may not affect information transmission depending on whether one considers the average network activity or the activity of a single neuron as was previously pointed out [12]. We note that the notion that higher order neurons simply sum the activity of their afferent neurons is at best questionable given recent results. Moreover, experimental recordings can only be currently achieved from a infinitesimal percentage of neurons in the brain. As such, we believe that our results using single neurons are more likely to be directly applicable to experimental data.

Our results have shown that the addition of a delay can significantly alter the effects of coupling on information transmission for renewal but not nonrenewal neurons. Whereas information increased with increasing coupling for no delay for renewal neurons, a non-zero delay could cause the information to now decrease with increasing coupling. Since the majority of synaptic connections in cortex are excitatory and are associated with a non-zero delay due to finite conduction speeds in neural tissue [4, 35], our results imply that such coupling would only decrease information transmission by single neurons if they display renewal dynamics. However, our results also imply that such coupling would increase information transmission by single neurons if they display nonrenewal dynamics. Experimental data has shown that many neurons both peripheral and central can display a single negative ISI correlation at lag one and thus nonrenewal dynamics similar to that shown in our nonrenewal model [7, 17, 24, 36, 37, 39, 43, 61]. Moreover, a recent study has shown that temporal anti-correlations appear to improve signal detection in a manner analogous to that seen for a single negative ISI correlation coefficient at lag one [23]. While the consequences of negative ISI correlations on information transmission by single uncoupled neurons is generally well understood [9, 10, 17, 27, 40, 44, 52, 61], our results provide a potential explanation for experimental data showing that these ISI correlations are found in more central neurons [37, 39, 43] that often make and receive thousands of synaptic connections [4, 35]. Our results also complement those of [1] who showed that excitatory coupling will also increase information transmission in networks of nonrenewal neurons when considering the average network activity and thus appear to be robust.

Our results using renewal models are similar to those of others [12, 29, 51, 59, 60]. However, such studies are carried for infinite size networks or using corrections to the thermodynamic limit [51]. Other studies use approximations for small or large delays [59], or very restrictive forms for the feedback input [60], or have been carried out solely in renewal neurons [12]. In contrast, our approach can be carried out for arbitrary values of the networks size or the delay and can be furthermore applied to nonrenewal processes that can display behaviors that are quite different than those displayed by renewal processes [7, 8, 9, 10, 11, 20, 40, 41, 43, 52].

We note that our nonrenewal model displays zero power at zero frequency and has infinite phase coherence [1, 10, 40]. These features are of course not found experimentally. Nevertheless, our nonrenewal model successfully reproduced and explained the mechanism that increases information transmission in neurons: noise shaping [10, 40]. This phenomenon was then verified experimentally [8]. Moreover, predictions made previously as to the opposite effect of the bias μ on the zero frequency power spectrum in renewal and nonrenewal models appear to agree with experimental results [1]. It is thus likely that our predictions would apply to more realistic neuron models that more closely mimic the negative ISI correlations seen experimentally.

We note that many neurons can display weak positive ISI correlations that decay slowly as a function of lag [43]. Such correlations lead to increased variability in the spike train at long timescales and thus worse signal detection [9, 43, 52, 61]. However, as mentioned above, these effects are mostly seen at time scales that are much longer than those observed in animal behavior [55]. We note however that these positive ISI correlations can interact with a single negative ISI correlation at lag one in order to give a time scale at which spike train variability is minimal [9, 43, 52, 61] which corresponds to the behavioral timescale [55].

In conclusion, our results show that delayed feedback and intrinsic ISI correlations can interact in a non-trivial manner to shape information transmission. Future studies of interactions amongst neurons should therefore consider the effects of intrinsic dynamics as these may have important effects. Future studies could extend our results by considering the effects of positive ISI correlations, distributions of delays, or heterogeneous networks.