A measure of association for ordered categorical data in population-based studies

Abstract

Ordinal classification scales are commonly used to define a patient’s disease status in screening and diagnostic tests such as mammography. Challenges arise in agreement studies when evaluating the association between many raters’ classifications of patients’ disease or health status when an ordered categorical scale is used. In this paper, we describe a population-based approach and chance-corrected measure of association to evaluate the strength of relationship between multiple raters’ ordinal classifications where any number of raters can be accommodated. In contrast to Shrout and Fleiss’ intraclass correlation coefficient, the proposed measure of association is invariant with respect to changes in disease prevalence. We demonstrate how unique characteristics of individual raters can be explored using random effects. Simulation studies are conducted to demonstrate the properties of the proposed method under varying assumptions. The methods are applied to two large-scale agreement studies of breast cancer screening and prostate cancer severity.

1 Introduction

Ordered categorical scales are commonly utilized in screening and diagnostic tests such as mammography to assess a patient’s disease status or health outcome. Some examples include the Kellgren/Lawrence five-category scale which grades radiographic changes of osteoarthritis,¹ the Dermatology Index of Skin Disease Severity (DIDS) scale used to classify severity of inflammatory skin disease in patients with psoriasis and dermatitis,^2,3 and the Gustilo and Anderson scale for grading severity of open fractures.⁴ In the cancer setting, breast cancer status is classified from mammograms using the BI-RADS scale,⁵ and the severity of prostate cancer using the Gleason grading scale.^6,7 Usually some degree of subjectivity in interpretation is required on the part of the rater, which often leads to substantial inconsistencies between raters’ classifications of the same subject, as has been demonstrated in widely used testing procedures including mammography.^8–11 Discrepancies may be due to either a different interpretation of the ordered categorical scale, or if the rater perceives the subject’s disease status to be more or less severe than another rater based upon the X-ray, mammogram, or biopsy. These inconsistencies have motivated several large-scale studies to assess accuracy and agreement between raters’ classifications and factors that may influence these properties, including cancer,^9–12 rheumatology, and bone fractures.^1,4,13

Measures of association are frequently reported in inter-rater agreement studies in conjunction with measures of agreement when an ordered categorical scale is used to assess a patient’s disease status or health outcome. Both measures provide a useful summary of the strength of relationship between raters’ classifications.^14–16 However, due to the ordinal nature of the data and limited availability of statistical methods, it can be challenging to evaluate levels of association and agreement between raters, and especially so when multiple raters (more than two or three) are participating in the study.

Whereas agreement measures focus on quantifying levels of exact agreement between raters, measures of association incorporate additional valuable information about the extent of disagreement between raters’ classifications. For example, two raters’ classifications of a patient’s test result two or three categories apart implies stronger disagreement than if their classifications were only one category apart. Values of association measures can differ substantially from measures of agreement in the same setting since strong association and yet poor agreement between raters’ classifications may occur.^16,17 In this paper, we focus on developing a population-based modeling approach and measure of association that easily incorporate the ordinal classifications of any number of raters (at least three) and patients’ test results, where missing classifications can be accommodated.¹⁸ When raters and test results in the study are random samples from their respective populations, inferences can be made regarding the underlying populations under study.

Existing approaches for evaluating levels of association between a single pair of raters’ ordinal classifications include Cohen’s weighted kappa,¹⁹ a nonparametric rank-invariant approach which treats classifications as ranks,^17,20 an odds ratio smoothing procedure,²¹ latent trait, and log-linear models.^22–25

Methods that can be used to assess association between multiple raters include a modeling approach³ using generalized estimating equations with a weighted kappa measure formulated in a similar manner to Cohen’s kappa.¹⁹ Nelson and Pepe²⁷ describe an exploratory graphical approach to examine the variability between raters’ ordinal ratings. However, these approaches generally do not extend easily to assessing association between more than a few raters, where Gonin et al.’s approach includes a fixed term for each rater with increasing complexity as the number of raters grows larger. Shrout and Fleiss’s intraclass correlation coefficient (ICC)[2,1] is a commonly used summary statistic to assess reliability between multiple raters’ ordinal classifications and Mielke et al. discuss Cohen’s weighted kappa for multiple raters.^28–30 Extensions of Cohen’s kappa statistic tend to be sensitive to the same flaws as Cohen’s original kappa statistic.^31,32 Other researchers have explored Bayesian approaches using generalized linear mixed models (GLMMs) with nested random effects to assess agreement for ordinal classifications and binary classifications.^33–35 Many of these approaches are not easily implemented in standard statistical software packages. Our proposed approach flexibly includes the ordinal ratings of any number of raters without increasing complexity and accommodates missing data. We provide freely available functions in the R software package for the implementation of the methods.³⁶

In section 2, the proposed model and framework for assessing association between multiple raters’ ordinal classifications are defined. The proposed model-based measure of association is developed in section 3 with a brief overview of existing approaches. Simulation studies are conducted in section 4 to investigate the properties of the proposed approach. Applications to two large-scale medical studies are presented in section 5, and a description of how to assess unique traits of individual raters and test results in an agreement study in this population-based setting is presented in section 6. A brief discussion follows in section 7.

2 An ordinal model of association

2.1 Introduction

We assume that a subject’s true disease or health outcome can be modeled as a continuous unobserved latent trait variable.^33,37,38 In our setting, each of J raters independently grades the same sample of I subjects’ test results by assigning classifications Y_ij = c (i = 1,…., I; j = 1,…, J; c = 1,…, C) according to an ordered categorical scale with C categories based upon their personal assessment of the subject’s true underlying continuous disease status W_ij. The latent variable W_ij can be written in the form of a linear model as W_ij = β₀ + u_i + v_j + ε_ij with intercept β₀ and a crossed random effects structure with subject random effects u_i, (i = 1,…, I) and rater random effects v_j, (j = 1,…, J), assumed mutually independent with $\mathrm{N}(0,{\sigma }_u^2)$ and $\mathrm{N}(0,{\sigma }_v^2)$ distributions respectively, and errors ε_ij distributed as N(0, σ²). The classifications Y_ij = c are equivalent to α_c−1 ≤ W_ij ≤ α_c where the set of strictly monotonically increasing thresholds α₀,…,α_C divides the underlying continuous latent variables W_ij into C + 1 intervals with α₀ = −∞ and α_C = +∞.³⁷

The ordinal GLMM provides an ideal framework for modeling the ordinal classifications of multiple raters.^37,39,40 It flexibly incorporates missing data since every rater may not classify every subject in the sample. A crossed random effect structure of raters and subjects’ test results appropriately accounts for the dependency between classifications due to all raters grading the same sample of subjects. An issue arises with ordinal data where the absolute location β₀ and scale σ of the latent variable are not identifiable. This is dealt with here wlog by setting β₀ = 0 and σ = 1.³⁷ A variety of link functions can be used as part of the ordinal GLMM framework. In our setting, the probit link function is especially appealing due to the continuous latent disease status assumption underlying the model and for the ease of mathematics and is our choice of link function. It has been previously demonstrated that nearly identical results are obtained when a logistic link is used in the GLMM.^41,42

The ordinal GLMM with a probit link function models the cumulative probability that a subject’s test result is classified into category c or lower (c = 1,…,C)

$${\mathrm{\Phi }}^{-1}\left(\mathrm{Pr}\left(Y_{ij}\le c|u_i,v_j\right)\right)={\alpha }_c-(u_i+v_j)$$ (1)

This can also be rewritten as the probability of a subject’s test result being classified into any particular category $\mathrm{Pr}\left(Y_{ij}=c|u_i,v_j\right)=\mathrm{\Phi }\left({\alpha }_c-\left(u_i+v_j\right)\right)-\mathrm{\Phi }\left({\alpha }_{c-1}-\left(u_i+v_j\right)\right)$, where Φ is the cumulative distribution function (cdf) of the standard normal distribution.

Rater random effects v_j (j = 1,…, J) account for the uniqueness of each rater’s classifications, where a large rater random effects variance component ${\sigma }_v^2$ indicates a more heterogeneous group of raters. Similarly, a large variance component ${\sigma }_u^2$ for the subject random effects u_i (i = 1,…, I) suggests a set of test results displaying a broad range of clarity of disease status. In section 6, we show how random effects can be estimated for raters and subjects included in a study, which can provide useful information and feedback for training purposes of individual raters.

To obtain estimates of the parameter vector $\mathit{\theta }=\left({\alpha }_1,\dots ,,{\alpha }_{C-1},{\sigma }_u^2,{\sigma }_v^2\right)$ for the ordinal GLMM in equation (1) we fit the GLMM model using an approximate maximum likelihood approach. The marginal likelihood function takes the form

$$\begin{array}{l}L(\mathit{\theta };\mathbf{Y})={\displaystyle {\int }_{\mathbf{u},\mathbf{v}}L(\mathit{\theta };\mathbf{u},\mathbf{v},\mathbf{y})}\mathrm{d}\mathbf{u}\mathrm{d}\mathbf{v}={\displaystyle {\int }_{\mathbf{u},\mathbf{v}}{f}_{Y|u,v}}(\mathbf{y};\mathbf{u},\mathbf{v}){\mathbf{f}}_{\mathbf{u}}(\mathbf{u};{\sigma }_u^2)f_v(\mathbf{v};{\sigma }_v^2)\mathrm{d}\mathit{u}\mathrm{d}\mathbf{v}\\ ={\displaystyle {\int }_{\mathbf{u}}{\displaystyle {\int }_{\mathbf{v}}\left[\begin{array}{ccc}I& J& C\\ \prod & \prod & \prod \\ i=1& j=1& c=1\end{array}{\left[\mathrm{\Phi }({\alpha }_c-(u_i+v_j))-\mathrm{\Phi }({\alpha }_{c-1}-(u_i+v_j))\right]}^{d_{\mathit{ijc}}}\right]\left[{{\displaystyle \prod _{i=1}^I\frac{1}{\sqrt{2\pi {\sigma }_u^2}}e}}^{\frac{-u_i^2}{2{\sigma }_u^2}}\right]\left[{{\displaystyle \prod _{j=1}^J\frac{1}{\sqrt{2\pi {\sigma }_v^2}}e}}^{\frac{-v_j^2}{2{\sigma }_v^2}}\right]\mathrm{d}\mathbf{u}\mathrm{d}\mathbf{v}}}\end{array}$$

with indicator function d_ijc = 1 if y_ij = c and 0 otherwise. Due to the high dimensionality of the crossed random effects, no closed-form solution for maximizing the likelihood function is available. However, multivariate Laplacian approximation provides an attractive and viable solution to obtaining approximate maximum likelihood estimates $\widehat{\mathit{\theta }}$.⁴³ Large-sample approximate standard errors are estimated by taking the square-roots of the diagonals of matrix H at convergence $se(\widehat{\mathit{\theta }})=\sqrt{\text{diag}\left[-{\left\{\mathbf{H}(\widehat{\mathit{\theta }})\right\}}^{-1}\right]}$, where $\mathit{H}=\frac{{\partial }^{2}l(\mathit{\theta };\mathbf{u},\mathbf{v},\mathbf{y})}{\partial \mathit{\theta }\partial {\mathit{\theta }}^t}$ is the second-order derivative of the log-likelihood function l(θ; u, v, y) evaluated at the approximate maximum likelihood estimates of θ and is generated during the model-fitting process. This fitting approach is available in the ordinal package in R for fitting ordinal GLMM models with crossed random effects, one of the few statistical software packages currently able to do so. Also explored were adaptive quadrature methods for fitting the ordinal GLMM model, but these were not feasible for our ordinal GLMM model due to the large number of random effects.^38,44,45 Simulation studies presented in section 4 demonstrate that reasonably unbiased estimates are obtained using the ordinal package under a wide range of varying conditions.

In the following section, we develop a chance-corrected model-based measure of association which is based upon the ordinal GLMM parameters $\mathit{\theta }=\left({\alpha }_1\dots ,,{\alpha }_{C-1},{\sigma }_u^2,{\sigma }_v^2\right),{\alpha }_0=-\infty$ and α_C = +∞ in equation (1).

3 A measure of association in the population-based setting

Measures of association are a popular choice for comparing raters’ ordinal classifications, incorporating information about agreement and disagreement into a comprehensive summary measure. While measures of exact agreement can be used for both nominal (unordered) and ordinal classifications, measures of association are appropriate only for classifications based upon an ordered categorical scale. Here, we develop a chance-corrected measure of association based upon the ordinal GLMM in equation (1). We first define two probabilities which are instrumental in the development of a chance-corrected measure of association—observed and chance association.

3.1 Observed and chance association

Observed association, p_0a is the proportion of time raters j and j^′ (j ≠ j^′) classify the same patient’s test result into the rth and sth categories respectively (r, s = 1,…, C), weighted by how many categories apart they are. While any weighting scheme can be applied, two conventional choices are: linear (absolute error) weights w_rs = 1− |r − s |/(C − 1); and quadratic (squared-error) weights w_rs = 1− (r − s)²/(C − 1)² for pairs of classifications in the rth and sth categories respectively (r, s = 1,…, C) by two raters j and j^′ (j ≠ j^′). Based upon the ordinal GLMM in the population-based setting p_0a takes the form (derivation in Appendix 1)

$$\begin{array}{l}{p}_{0a}={\displaystyle \sum _{r=1}^C{\displaystyle \sum _{s=1}^C{w}_{rs}[\mathrm{Pr}(Y_{ij}=r\cap Y_{ij\prime }=s)]}}\text{in the general population – based setting}\\ ={\displaystyle {\int }_{-\infty }^{+\infty }{\displaystyle \sum _{r=1}^C{\displaystyle \sum _{s=1}^C{w}_{rs}}}}[\mathrm{\Phi }\left(\frac{{\alpha }_r^{\ast }-z\sqrt{\rho }}{\sqrt{1-\rho }}\right)-\mathrm{\Phi }\left(\frac{{\alpha }_{r-1}^{\ast }-z\sqrt{\rho }}{\sqrt{1-\rho }}\right)]\times \left[\mathrm{\Phi }\left(\frac{{\alpha }_s^{\ast }-z\sqrt{\rho }}{\sqrt{1-\rho }}\right)\right]-\mathrm{\Phi }\left(\frac{{\alpha }_{s-1}^{\ast }-z\sqrt{\rho }}{\sqrt{1-\rho }}\right)\\ \times \varphi (z)\mathrm{d}z0.5\le p_{0a}\le 1,\end{array}$$ (2)

where ${\alpha }_c^{\ast }={\alpha }_c/\sqrt{{\sigma }_u^2+{\sigma }_v^2+1}$ and $\rho ={\sigma }_u^2/({\sigma }_u^2+{\sigma }_v^2+1)$, which itself is a natural measure comparing the variability amongst subjects’ test results, ${\sigma }_u^2$, relative to the overall variability present between classifications. Large variability between test results relative to the variability between the raters will yield a value of ρ close to 1. In this population-based setting over many raters, observed association p_0a takes values between 0.5 and 1 (proof in Appendix 3).

Chance association p_ca is the proportion of time rater j classifies subject i into the rth category and rater j^′ (j ≠ j^′) classifies subject i^′ (i ≠ i^′) into the sth category (r, s = 1,…, C) simply due to coincidence, weighted according to how many categories apart the ratings are. For the ordinal GLMM p_ca takes the form (derivation in Appendix 2)

$$\begin{array}{l}{p}_{ca}={\displaystyle \sum _{r=1}^C{\displaystyle \sum _{s=1}^C{w}_{rs}}}[\text{Pr}(Y_{ij}=r)\times \text{Pr}(Y_{i^{\prime }{j}^{\prime }}=s)]\\ ={\displaystyle \sum _{r=1}^C{\displaystyle \sum _{s=1}^C{w}_{rs}[\mathrm{\Phi }({\alpha }_r^{\ast })-\mathrm{\Phi }({\alpha }_{r-1}^{\ast })]}}\times [\mathrm{\Phi }({\alpha }_s^{\ast })-\mathrm{\Phi }({\alpha }_{s-1}^{\ast })],0.5\le p_{ca}\le 1\end{array}$$ (3)

It can be shown in this population-based setting that p_oa ≥ p_ca ≥ 0:5 (see Appendix 3 for proof). Estimates ${\widehat{p}}_{0a}$ and ${\widehat{p}}_{ca}$ can be obtained from fitting the corresponding ordinal GLMM in equation (1) as outlined in section 2.

3.2 A proposed population-based measure of association

The proposed model-based measure of association κ_ma is a linear function of observed association p_0a in equation (2). Two adjustments that we make to this linear function to derive the proposed measure κ_ma are to minimize the effects of chance association on κ_ma so that the measure is chance-corrected, and to ensure that κ_ma is scaled to take values between 0 and 1 so that it is easily interpretable in a similar manner to Cohen’s weighted kappa statistic.¹⁹ First, we minimize the effects of chance association on κ_ma by finding the values of the fixed threshold terms $\left({\alpha }_1^{\ast },\dots ,{\alpha }_{C-1}^{\ast }\right)$ with ${\alpha }_0^{\ast }=-\infty \text{and}{\alpha }_C^{\ast }=+\infty$ which minimize the expression for chance association in equation (3). The expression for p_ca takes a minimum value of 0.5 when the monontonically increasing threshold values denoted as $({\alpha }_{min,1}^{\ast },{\alpha }_{min,2}^{\ast },\dots ,{\alpha }_{min,C-1}^{\ast })$ take the values (0.00001, 0.000002,…) (see Appendix 3). We then substitute these threshold values into the expression for κ_ma. Finally, we scale κ_ma to lie between 0 and 1 for similar interpretability to Cohen’s weighted kappa statistic. Since 0.5 ≤ p_0a ≤ 1, multiplying the expression for κ_ma by 2 and subtracting 1 scales κ_ma so that 0 ≤ κ_ma ≤ 1. The form of κ_ma (4) is thus

$$\begin{array}{l}{\kappa }_{ma}=2\ast p_{0a}\left(\left(-\infty ,{\alpha }_{min,1}^{\ast },\dots ,,{\alpha }_{min,C-1}^{\ast },+\infty \right),\rho \right)-1\\ =2\ast {\displaystyle {\int }_{-\infty }^{+\infty }{\displaystyle \sum _{r=1}^C{\displaystyle \sum _{s=1}^C{w}_{rs}}}}\left[\mathrm{\Phi }\left(\frac{{\alpha }_{min,r}^{\ast }-z\sqrt{\rho }}{\sqrt{1-\rho }}\right)-\mathrm{\Phi }\left(\frac{{\alpha }_{min,r-1}^{\ast }-z\sqrt{\rho }}{\sqrt{1-\rho }}\right)\right]\times [\mathrm{\Phi }\left(\frac{{\alpha }_{min,s}^{\ast }-z\sqrt{\rho }}{\sqrt{1-\rho }}\right)-\mathrm{\Phi }\left(\frac{{\alpha }_{min,s-1}^{\ast }-z\sqrt{\rho }}{\sqrt{1-\rho }}\right)]\\ \times \varphi (z)\text{dz}-10\le {\kappa }_{ma}\le 1\end{array}$$ (4)

A value of κ_ma near 0 indicates poor chance-corrected association between raters, while a value closer to 1 suggests very strong chance-corrected association between raters. We demonstrate in section 4 that, in contrast to Cohen’s weighted kappa, κ_ma is unaffected by changes in the underlying disease prevalence.

Estimation of κ_ma for a dataset involves first fitting the GLMM in equation (1) and obtaining estimates ${\widehat{\sigma }}_u^2$ and ${\widehat{\sigma }}_v^2$. These values are used to calculate the coefficient $\widehat{\rho }={\widehat{\sigma }}_u^2/({\widehat{\sigma }}_u^2+{\widehat{\sigma }}_v^2+1)$ which in turn is incorporated into the estimate ${\widehat{\kappa }}_{ma}$.

The variance var $({\widehat{\kappa }}_{ma})$ is derived using the multivariate delta method as a function of the rater and subject random effects variance components (assumed independent) where $\mathrm{var}({\widehat{\sigma }}_u^2)=2{({\sigma }_u^2)}^2/I$ and $\mathrm{var}({\widehat{\sigma }}_v^2)=2{({\sigma }_v^2)}^2/J$ for large I and J. The variance of $\widehat{\rho }$ is calculated as

$$\mathrm{var}(\widehat{\rho })=\frac{2{\left({\sigma }_u^2\right)}^2{\left({\sigma }_v^2+1\right)}^2}{I{\left({\sigma }_u^2+{\sigma }_v^2+1\right)}^4}+\frac{2{({\sigma }_v^2)}^2{({\sigma }_u^2)}^2}{J{\left({\sigma }_u^2+{\sigma }_v^2+1\right)}^4}$$

Since κ_ma is a function of ρ, the delta method is again applied

$$\begin{array}{l}\mathrm{var}({\widehat{\kappa }}_{ma})=4\times \mathrm{var}(\widehat{\rho })\times \left[{\displaystyle {\int }_{-\infty }^{+\infty }{\displaystyle \sum _{r=1}^C{\displaystyle \sum _{s=1}^C{w}_{rs}\times ([\mathrm{\Phi }\left(\frac{{\alpha }_{min,r}^{\ast }-z\sqrt{\rho }}{\sqrt{1-\rho }}\right)-\mathrm{\Phi }\left(\frac{{\alpha }_{min,r-1}^{\ast }-z\sqrt{\rho }}{\sqrt{1-\rho }}\right)}}}\right]\\ \times [\varphi \left(\frac{{\alpha }_{min,s}^{\ast }-z\sqrt{\rho }}{\sqrt{1-\rho }}\right)\left(\frac{-z}{2\sqrt{\rho (1-\rho )}}+\frac{{\alpha }_{min,s}^{\ast }-z\sqrt{\rho }}{2{\left(1-\rho \right)}^{3/2}}\right)-\varphi \left(\frac{{\alpha }_{min,s-1}^{\ast }-z\sqrt{\rho }}{\sqrt{1-\rho }}\right)\\ \times \left(\frac{-z}{2\sqrt{\rho (1-\rho )}}+\frac{{\alpha }_{min,s-1}^{\ast }-z\sqrt{\rho }}{2{\left(1-\rho \right)}^{3/2}}\right)]+[\mathrm{\Phi }\left(\frac{{\alpha }_{min,s}^{\ast }-z\sqrt{\rho }}{\sqrt{1-\rho }}\right)-\mathrm{\Phi }\left(\frac{{\alpha }_{min,s-1}^{\ast }-z\sqrt{\rho }}{\sqrt{1-\rho }}\right)\\ \times [\varphi \left(\frac{{\alpha }_{min,r}^{\ast }-z\sqrt{\rho }}{\sqrt{1-\rho }}\right)\left(\frac{-z}{2\sqrt{\rho (1-\rho )}}+\frac{{\alpha }_{min,r}^{\ast }-z\sqrt{\rho }}{2{\left(1-\rho \right)}^{3/2}}\right)-\varphi \left(\frac{{\alpha }_{min,r-1}^{\ast }-z\sqrt{\rho }}{\sqrt{1-\rho }}\right)\\ {\times \left(\frac{-z}{2\sqrt{\rho (1-\rho )}}+\frac{{\alpha }_{min,r-1}^{\ast }-z\sqrt{\rho }}{2{\left(1-\rho \right)}^{3/2}}\right)])\varphi (z)\mathrm{d}z]}^2\end{array}$$

For practical purposes, functions in R to fit the ordinal GLMM in equation (1) and to estimate κ_ma and var $({\widehat{\kappa }}_{ma})$ for an inter-rater agreement dataset are available from the first author and in supplemental material on the journal’s website. Figure 1 demonstrates the effects of the rater random effect variance ${\sigma }_v^2$ on the proposed measure of association κ_ma as the subject random effects variance ${\sigma }_u^2$ increases. The strongest association is observed for small values of the rater variance ${\sigma }_v^2$. The association measure κ_ma increases with ${\sigma }_u^2$; this is due to more clearly defined disease status observed in a more heterogeneous group of subject test results.

Figure 1.

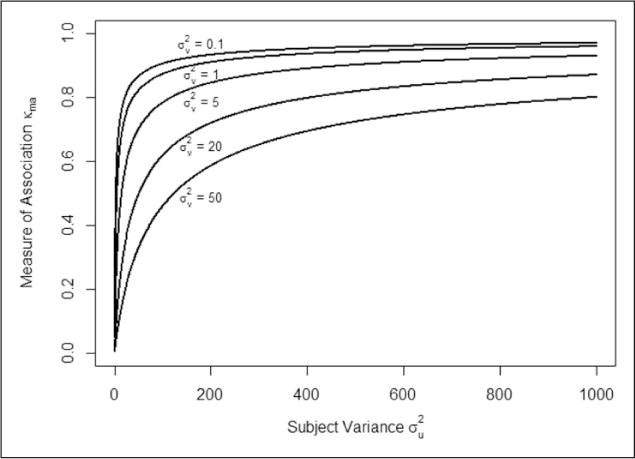
The effects of varying rater random effects variance ${\sigma }_v^2$ and subject random effects variances ${\sigma }_u^2$ on the proposed measure of association κ_ma with quadratic weights.

3.3 Cohen’s weighted kappa with model-based parameters

Cohen’s weighted kappa statistic is a chance-corrected statistic for assessing association between two raters, based upon the observed weighted proportion of pairs in agreement and chance weighted proportion of pairs in agreement expected under a statistical model of independence.^16,19 Here, we generate a population-based Cohen’s weighted kappa statistic for multiple raters incorporating ordinal GLMM probabilities of observed and chance association p_0a and p_ca (defined in section 3.1) for comparison with our proposed measure of association κ_ma (4). This statistic will be referred to as κ_GLMM,a and takes the following form, with choice of weights described in section 3.1

$${\kappa }_{\mathit{\text{GLMM}},a}=\frac{p_{0a}-p_{ca}}{1-p_{ca}}\text{estimated as}{\widehat{\kappa }}_{\mathit{\text{GLMM}},a}=\frac{{\widehat{p}}_{0a}-{\widehat{p}}_{ca}}{1-{\widehat{p}}_{ca}}\text{with}0\le {\kappa }_{\mathit{\text{GLMM}},a}\le 1$$

3.4 Shrout and Fleiss’ ICC[2,1]

Shrout and Fleiss’ [2,1] statistic is derived from a two-way ANOVA model and is commonly used as a measure of association to assess reliability between raters.²⁸ While six forms of the ICC are described in their paper, the ICC[2,1] is an appropriate statistic when all subjects are graded by the same set of raters who are assumed to be a random subset of all possible raters. This statistic has been demonstrated to be equivalent to Cohen’s weighted kappa with quadratic weights when comparing two raters’ classifications.⁴⁶

4 Simulation studies

Simulation studies were conducted under a varying range of scenarios as presented in Table 1 to investigate the behavior of the proposed measure of association κ_ma and the parameters of the ordinal GLMM in equation (1). Simulation scenarios included increasing rater and subject-level random effect variances and numbers of raters and items (sample size) and assessing their impact on estimation of the parameter vector $\mathit{\theta }=\left({\alpha }_1,\dots ,,{\alpha }_{C-1},{\sigma }_u^2,{\sigma }_v^2\right)$ and κ_ma when estimated using the ordinal package in R. Effects of non-normally distributed random effects parameter estimation were also explored.

Table 1.

Parameter values for the simulation scenarios examined.

Variance components $\left({\sigma }_u^2,{\sigma }_v^2\right)$	Random effects distributions	Number of items I, Number of raters J
(1, 5)
(5, 1)	ui ~ Exp(λ) and vj ~ Unif(a, −a)	(I=100, J=10)
(5, 20)	$u_i~\mathrm{N}\left(0,{\sigma }_u^2\right)\text{and}{v}_j~\mathrm{N}\left(0,{\sigma }_v^2\right)$	(I=250, J=100)
(20, 5)
(10, 10)

Sets of 1000 simulated datasets based upon the ordinal GLMM in equation (1) were generated for each simulation scenario in the following manner. A parameter vector containing true values $\mathit{\theta }=({\alpha }_1,{\alpha }_2,{\alpha }_3,{\alpha }_4,{\sigma }_u^2,{\sigma }_v^2)$ for C = 5 and the number of raters J and subjects I was specified for each set of simulations according to Table 1 (every combination). Random subject effects u_i (i = 1,…, I) and rater effects v_j (j = 1,…, J) were generated using R functions rnorm, rexp, and runif depending on the scenario and centered and scaled after choosing parameters λ and a to achieve the specified ${\sigma }_u^2$ and ${\sigma }_v^2$. A sample of n = IJ ordinal classifications Y_ij = c (c = 1,…, C) was then randomly generated from a multinomial distribution using the R function rmultinom according to the probability mass function

$${{\displaystyle \prod _{c=1}^C[\text{Pr}(Y_{ij}=c|u_i,v_j]}}^{d_{\mathit{ijc}}}={{\displaystyle \prod _{c=1}^C[\mathrm{\Phi }({\alpha }_c-(u_i+v_j\left)\right)-\mathrm{\Phi }({\alpha }_{c-1}-(u_i+v_j\left)\right)]}}^{d_{\mathit{ijc}}}$$

where d_ijc = 1 if Y_ij = c and 0 otherwise. The clmm function in the ordinal package in R was used to fit the ordinal GLMM (1) and obtain parameter estimates $\widehat{\mathit{\theta }}=({\widehat{\alpha }}_1,{\widehat{\alpha }}_2,{\widehat{\alpha }}_3,{\widehat{\alpha }}_4,{\widehat{\sigma }}_u^2,{\widehat{\sigma }}_v^2)$ with their estimated standard errors for each simulated dataset.

Table 2((a) and (b)) displays simulation results for the proposed chance-corrected measure of association, κ_ma. The true value of κ_ma is presented for each simulation scenario along with the mean of the estimates ${\widehat{\kappa }}_{ma}$ from the one thousand simulated datasets. The standard error (S.E.) is presented as the average of the one thousand standard error estimates $se({\widehat{\kappa }}_{ma})$. Slight bias is observed in the estimation of the proposed association measure κ_ma for the smaller sample size (I = 100, J = 10) especially when the rater random effect variance ${\sigma }_v^2$ is large. This bias diminished at the larger sample size (I = 250, J = 100). Slightly increased levels of bias in the estimation of κ_ma were observed in both small and large sample sizes when the random effects were not normally distributed, though corresponding standard errors were similar to those for normally distributed random effects. These results indicate the proposed association measure is estimated in a reasonably unbiased manner for large and smaller sample sizes, varying random effects variances, and certain departures from the distributional assumptions such as normality of the random effects’ distributions.

Table 2.

True values and mean estimates (mean standard error) of the proposed measure of association κ_ma for each of the 20 simulation studies. Each set of simulations is based upon 1000 simulated datasets with C=5 categories.

(a) Normally distributed random effects
		I=100, J=10	I=250, J=100
$\left({\sigma }_u^2,{\sigma }_v^2\right)$	True κma	Mean ${\widehat{\kappa }}_{ma}$ (S.E.)	Mean ${\widehat{\kappa }}_{ma}$ (S.E.)
(1, 5)	0.091	0.110 (0.033)	0.094 (0.012)
(5, 20)	0.123	0.153 (0.050)	0.127 (0.017)
(10, 10)	0.316	0.347 (0.075)	0.320 (0.028)
(5, 1)	0.506	0.508 (0.046)	0.503 (0.021)
(20, 5)	0.559	0.560 (0.066)	0.551 (0.026)

(b) Non-normally distributed random effects
		I=100, J=10	I=250, J=100
$\left({\sigma }_u^2,{\sigma }_v^2\right)$	True κma	Mean ${\widehat{\kappa }}_{ma}$ (S.E.)	Mean ${\widehat{\kappa }}_{ma}$ (S.E.)
(1, 5)	0.091	0.104 (0.033)	0.091 (0.012)
(5, 20)	0.123	0.128 (0.044)	0.118 (0.016)
(10, 10)	0.316	0.312 (0.073)	0.293 (0.027)
(5, 1)	0.506	0.499 (0.047)	0.476 (0.021)
(20, 5)	0.559	0.540 (0.068)	0.504 (0.027)

Tables 3 and 4 present results for a selected range of the simulation studies, with further sets of simulations (Tables 3(c) and 3(d)) presented in the Supplemental Material online. Parameter estimates $\widehat{\mathit{\theta }}=({\widehat{\alpha }}_1,{\widehat{\alpha }}_2,{\widehat{\alpha }}_3,{\widehat{\alpha }}_4,{\widehat{\sigma }}_u^2,{\widehat{\sigma }}_v^2)$, a model-based measure of agreement ${\widehat{\kappa }}_{ma}$ and proposed measure of association ${\widehat{\kappa }}_{ma}$ are presented in these tables.⁴² The standard deviation of the observed 1000 estimates is presented for each parameter, with standard error reported as the mean of the 1000 standard error estimates.

Table 3.

Results from five simulation studies. Each is based upon 1000 datasets simulated from an ordinal GLMM with five categories (C=5), with thresholds α₀ = −∞ and α₅ = + ∞ and I= 100 items and J= 10 raters. Random effects $u_i\sim \mathrm{N}(0,{\sigma }_u^2)$, and $v_j\sim \mathrm{N}(0,{\sigma }_v^2)$.

C = 5 Categories, I= 100 items, J = 10 raters
Parameter	Simulation set #1			Simulation set #2			Simulation set #3			Simulation set #4			Simulation set #5
	Truth	Est. mean	Est. S.E. (obs.)	Truth	Est. mean	Est. S.E. (obs.)	Truth	Est. mean	Est. S.E. (obs.)	Truth	Est. mean	Est. S.E. (obs.)	Truth	Est. mean	Est. S.E. (obs.)
${\sigma }_u^2$	1	1.008	0.195 (0.202)	5	4.798	0.878 (0.867)	5	5.019	0.971 (1.063)	20	17.465	3.467 (3.324)	10	9.778	1.816 (1.866)
${\sigma }_v^2$	5	4.555	2.221 (2.375)	1	0.910	0.423 (0.441)	20	18.654	9.631 (12.617)	5	4.442	2.059 (2.234)	10	9.057	4.243 (4.723)
α1	0	−0.006	0.673 (0.745)	0	−0.010	0.378 (0.405)	0	0.026	1.360 (1.647)	0	−0.046	0.795 (0.855)	0	−0.026	0.984 (1.083)
α2	1	0.998	0.675 (0.748)	1	0.989	0.380 (0.409)	1	1.030	1.362 (1.651)	1	0.941	0.797 (0.857)	1	0.973	0.985 (1.083)
α3	2	2.000	0.678 (0.754)	2	1.988	0.385 (0.410)	2	2.034	1.365 (1.649)	2	1.936	0.801 (0.858)	2	1.973	0.989 (1.088)
α4	3	3.005	0.684 (0.755)	3	2.988	0.394 (0.421)	3	3.036	1.370 (1.654)	3	2.931	0.807 (0.864)	3	2.982	0.994 (1.093)
ρ	0.143	0.171	0.051 (0.063)	0.714	0.714	0.051 (0.05)	0.192	0.236	0.075 (0.094)	0.769	0.766	0.067 (0.069)	0.476	0.514	0.099 (0.111)
var(ρ)	0.002	0.004		0.003	0.003		0.0049	0.0088		0.005	0.005		0.0115	0.0123
κm	0.035	0.043	0.014 (0.017)	0.264	0.267	0.032 (0.038)	0.048	0.062	0.023 (0.029)	0.306	0.312	0.050 (0.059)	0.141	0.162	0.042 (0.050)
var(κm)	0.0002	0.0002 (0.0003)		0.001	0.001 (0.001)		0.0004	0.0006 (0.0008)		0.0029	0.0025 (0.0035)		0.0018	0.0018 (0.0025)
κma	0.091	0.110	0.033 (0.041)	0.506	0.508	0.046 (0.050)	0.123	0.153	0.050 (0.062)	0.559	0.560	0.066 (0.068)	0.316	0.347	0.075 (0.084)
var(κma)	0.001	0.0011 (0.0017)		0.002	0.002 (0.002)		0.002	0.003 (0.004)		0.005	0.004 (0.005)		0.0060	0.006 (0.007)

Table 4.

Results from five simulation studies. Each is based upon 1000 datasets simulated from an ordinal GLMM with five categories (C = 5), with thresholds α₀ = −∞ and α₅ = + ∞ and (I= 250 items and J= 100 raters. Random effects $u_i\sim \mathrm{N}(0,{\sigma }_u^2)$, and $v_j\sim \mathrm{N}(0,{\sigma }_v^2)$.

C = 5 Categories, I = 250 items, J = 100 raters
Parameter	Simulation set #1			Simulation set #2			Simulation set #3			Simulation set #4			Simulation Set #5
	Truth	Est. mean	Est. S.E. (obs.)	Truth	Est. mean	Est. S.E. (obs.)	Truth	Est. mean	Est. S.E. (obs.)	Truth	Est. mean	Est. S.E. (obs.)	Truth	Est. mean	Est. S.E. (obs.)
${\sigma }_u^2$	1	1.001	0.093 (0.093)	5	4.942	0.473 (0.454)	5	5.002	0.460 (0.444)	20	19.226	1.896 (1.785)	10	9.997	0.925 (0.934)
${\sigma }_v^2$	5	4.879	0.721 (0.713)	1	1.006	0.144 (0.142)	20	19.566	2.958 (2.922)	5	5.016	0.718 (0.721)	10	9.844	4.414 (4.436)
α1	0	−0.003	0.231 (0.234)	0	−0.013	0.174 (0.175)	0	−0.009	0.467 (0.480)	0	−0.017	0.359 (0.373)	0	−0.01 1	0.372 (0.373)
α2	1	0.997	0.231 (0.234)	1	0.986	0.174 (0.175)	1	0.991	0.467 (0.481)	1	0.982	0.360 (0.373)	1	0.990	0.372 (0.373)
α3	2	2.000	0.231 (0.234)	2	1.987	0.174 (0.176)	2	1.991	0.468 (0.481)	2	1.982	0.360 (0.374)	2	1.988	0.372 (0.374)
α4	3	2.998	0.231 (0.233)	3	2.988	0.175 (0.177)	3	2.990	0.468 (0.481)	3	2.982	0.360 (0.373)	3	2.988	0.373 (0.373)
ρ	0.143	0.147	0.018 (0.019)	0.714	0.710	0.023 (0.023)	0.192	0.198	0.026 (0.026)	0.769	0.761	0.027 (0.026)	0.476	0.481	0.039 (0.039)
var(ρ)	0.0003	0.0004		0.0005	0.0005		0.0006	0.0007		0.0007	0.0007		0.0015	0.0016
κm	0.035	0.036	0.005 (0.005)	0.264	0.262	0.015 (0.016)	0.048	0.049	0.007 (0.007)	0.306	0.300	0.020 (0.021)	0.141	0.144	0.015 (0.016)
var(κm)	0.00002	0.00002 (0.00003)		0.0002	0.0002 (0.0002)		0.00005	0.00005 (0.00005)		0.0004	0.0004 (0.0005)		0.0002	0.0002 (0.0003)
κma	0.091	0.094	0.012 (0.012)	0.506	0.503	0.021 (0.021)	0.123	0.127	0.017(0.017)	0.559	0.551	0.026 (0.026)	0.316	0.320	0.028 (0.029)
var(κma)	0.0001	0.0001 (0.0002)		0.0004	0.0004 (0.0004)		0.0003	0.0003 (0.0003)		0.0007	0.0007 (0.0007)		0.0008	0.0008 (0.0008)

Results demonstrate that variance components ${\sigma }_u^2$and ${\sigma }_v^2$ were estimated with little or no bias at small values $\left({\sigma }_u^2\text{and}{\sigma }_v^2=1\text{or}5\right)$ for small and large sample sizes (I, J) and for both normally and non-normally distributed random effects. Low to moderate levels of bias in the estimation of ${\sigma }_u^2$ and ${\sigma }_v^2$ was observed for larger values of the rater variance component $\left({\sigma }_v^2=10\text{or}20\right)$, especially for smaller sample sizes (I = 100, J = 10) and for non-normal random effects. For larger sample sizes (I = 250, J = 100) only minimal bias in the estimates of ${\sigma }_u^2$ and ${\sigma }_v^2$ was observed when the random effects were normally distributed; however, low to moderate bias remained in the estimates of ${\sigma }_u^2$ and ${\sigma }_v^2$ when non-normally distributed random effects were included.

Thresholds ${\alpha }_1,\dots ,{\alpha }_{C-1}\left({\alpha }_0=-\infty ,{\alpha }_C=+\infty \right)$ were generally estimated with no or minimal bias. When the variability between raters’ classifications was large $\left({\sigma }_v^2=10\text{or}20\right)$, some bias was noted. Some slight bias was observed in the estimates of α₁,…, α_C−1 for the simulation studies with non-normal random effects at smaller sample sizes, which receded at the larger sample size.

Coefficient ρ was estimated with slight bias at smaller sample sizes with the bias was more evident when the rater variability was large $\left({\sigma }_v^2=10\text{or}20\right)$. This is likely due to ρ being a function of ${\sigma }_u^2$ and ${\sigma }_v^2$ which also exhibited moderate bias for large rater variability. This bias receded at larger sample sizes for normally distributed random effects.

In summary, the simulation results suggest the parameters of the ordinal GLMM and the proposed measure of association are estimated with very little or no bias using the ordinal package in R especially when the rater random effect variance are moderately low $\left({\sigma }_v^2=1\text{or}5\right)$, which is common in real-life inter-rater agreement studies. Even at the smaller sample size (I = 100, J = 10), observed biases in parameter estimates were generally small, though some bias was observed in large and small sample sizes for non-normally distributed random effects.

Figures 2(a) and (b) displays the effects of varying disease prevalence on the different summary measures of association, κ_ma, ICC[2,1] and Cohen’s weighted κ_GLMM,a with linear weights as described in section 3.1 for an ordinal classification scale with five categories (C = 5). Cohen’s weighted κ_GLMM,a with quadratic weights generated very similar estimates to the ICC[2,1] coefficient and is not presented separately here. Table 5 presents the percent of classifications in each of the five categories for the various disease prevalences used in Figure 2(a) and (b). True parameter values were used in the plots with the exception of Shrout and Fleiss’ ICC[2,1] statistic, which was averaged over sets of 200 simulated datasets for each value of ρ. In Figure 2(a) and (b), it is seen that as ρ increases from 0 (minimum) to 1 (maximum), each measure of association increases in value and at a more extreme rate as ρ approaches 1. As shown in Figure 2(a), as disease prevalence varies from extremely high or low to being equally distributed over the five categories, κ_ma remains unchanged and is thus robust to changes in disease prevalence, while the ICC[2,1] statistic fluctuates in value with varying disease prevalence, and increases especially when disease prevalence is extreme. Figure 2(b) demonstrates that Cohen’s linear-weighted population-based GLMM measure κ_GLMM,a is also sensitive to changes in prevalence.

Figure 2.

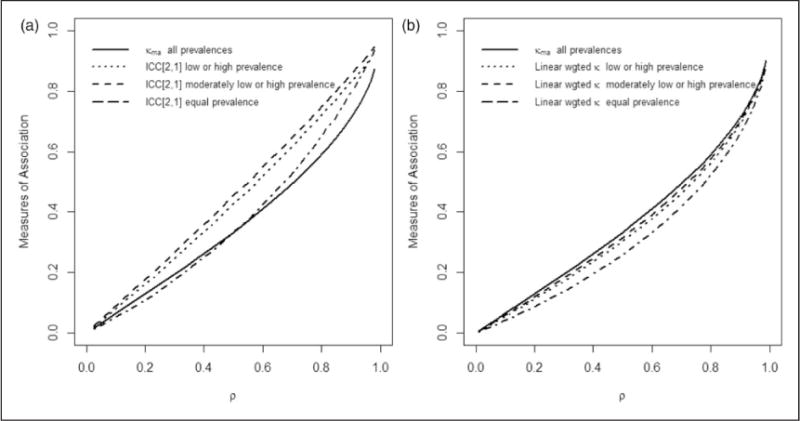
Plots of measures of association versus ρ at different prevalences (a) Shrout and Fleiss’ ICC[2,1] and κ_ma; (b) κ_ma and Cohen’s GLMM-based weighted kappa with linear weights κ_GLMM,a. The prevalence is varied (extreme low or high; moderately high or low; equal in each category) with the percent of observations falling into each of the C = 5 categories for each prevalence case given in Table 5.

Table 5.

Varying disease prevalence examined in Figure 2(a) and (b) based upon an ordinal classification scale with C=5 categories.

	Percentage (%) of classifications in each category
Disease prevalence	Category 1	Category 2	Category 3	Category 4	Category 5	Total
Very low	80	10	3.4	3.3	3.3	100
Moderately low	50	26	16	6	2	100
Equal	20	20	20	20	20	100
Moderately high	2	6	16	26	50	100
Very high	3.3	3.3	3.4	10	80	100

5 Applications to real-life studies

5.1 Breast cancer screening example

Beam et al.⁹ recently conducted a large-scale study to investigate factors that potentially may influence accuracy in radiologists’ interpretation of screening mammograms. A random sample of 104 radiologists independently classified screening mammograms of 148 women randomly selected via stratified sampling using a modified ordinal BI-RADS scale with five categories ranging from normal to probably malignant. Forty-three percent of the 148 sets of mammograms were from women with breast cancer. We examine levels of association and agreement between the radiologists in this dataset using our proposed methods and compare these with existing measures of association and agreement. Our population-based approach allows conclusions to be drawn regarding association between typical radiologists who interpet screening mammograms since the radiologists and patients were randomly selected from their respective populations. Table 6 presents a sample of the classifications made by individual radiologists.

Table 6.

Table of classifications by individual raters for the beam mammogram study.⁹ Based upon an ordinal classification scale with C=5 categories; I=148 mammograms; J=104 radiologists.

	Classifications by individual radiologists (J=104)
	Rater
Subject	1	2	3	4	…	100	101	102	103	104
1	1	1	1	1		4	4	3	2	3
2	1	4	3	4	…	3	2	1	4	2
3	4	4	4	4		4	3	4	5	4
4	5	4	5	4		4	2	3	5	3
5	2	4	3	2	…	4	5	5	2	2
⋮			⋮				⋮			⋮
144	1	4	3	1		1	1	1	1	2
145	4	1	4	4		1	4	5	5	3
146	4	3	4	2	…	5	5	3	5	3
147	5	4	5	5		4	5	5	5	4
148	5	4	4	4		5	3	3	5	4

The ordinal GLMM in equation (1) was fitted to the dataset consisting of n = 15,392 (IJ = 104 × 148) classifications using the clmm function in the ordinal package in R. The procedure took less than 2 min to run. Parameter estimates are presented in Table 7. Based upon the dataset, estimated model-based probabilities of being classified into each of the five ordered categories were 35% (normal), 15% (benign), 17% (probably benign), 22% (possibly malignant), and 11% (probably malignant).

Table 7.

Results for the beam mammogram study⁹ where 104 radiologists (J =104) classified mammograms of 148 patients (I = 148) using an ordered BIRADS scale with C = 5 categories (1 = normal; 2=benign; 3=probably benign; 4=possibly malignant; 5 = probably malignant).

Parameter	Symbol	Estimate	S.E.	Z-value
Ordinal GLMM:
Thresholds: (α0 = −∞, α5 = +∞)
Between categories 1 and 2	α1	−0.897	0.135	−6.643
Between categories 2 and 3	α2	−0.197	0.135	−1.460
Between categories 3 and 4	α3	0.761	0.135	5.630
Between categories 4 and 5	α4	2.539	0.137	18.574
Subject random effect variance	${\sigma }_u^2$	2.442	0.427
Rater random effect variance	${\sigma }_v^2$	0.158	0.073
Rho	ρ	0.678	0.026
GLMM-based observed agreement	p0	0.430
GLMM-based observed association (quadratic weights)	p0a	0.907
Measures of agreement:
Model-based (unweighted) kappa  (Nelson and Edwards41)	κm	0.241	0.015
Fleiss’ kappa (Fleiss47)	κF	0.297	0.001
Light and Conger’s kappa  (Light,48 Conger49)	κLC	0.298
Measures of association:  (with quadratic weights)
Model-based weighted kappa	κma	0.475	0.022
Shrout and Fleiss’ ICC[2,1]  (Shrout and Fleiss28)		0.652	95% c.i. = (0.601, 0.706)
Cohen’s GLMM-based weighted kappa	κGLMM,a	0.611

Estimates of the various measures of association for the Beam mammogram study are presented in Table 6 including the proposed measure of association κ_ma, Shrout and Fleiss’ ICC[2,1] statistic, and Cohen’s GLMM-based weighted kappa with quadratic weights, κ_GLMM,a (section 3.3). Quadratic weights were also used for κ_ma. Commonly used measures of (exact) agreement are also presented, including Fleiss’ kappa κ_F and Light and Conger’s kappa κ_LC, both adaptations of Cohen’s original kappa statistic, and an ordinal GLMM model-based agreement measure κ_m.^42,47–49 Model-based observed agreement is estimated as ${\widehat{p}}_0=0.430$, indicating low to moderate observed agreement between typical pairs of radiologists in this setting. In contrast, observed association is very strong at ${\widehat{p}}_{0a}=0.907$, suggesting that while pairs of radiologists may not often provide identical classifications to the same patient’s mammogram, raters’ classifications may typically disagree by only one category on the five-category ordered categorical scale, rather than by several categories.

The proposed measure of association was estimated as ${\widehat{\kappa }}_{ma}=0.475(se=0.022)$ indicating moderate chance-corrected association between radiologists who typically interpret screening mammograms, based upon the table in Landis and Koch.⁵⁰ Our proposed approach provides a chance-corrected measure of association for the study that is not affected by disease prevalence. The Shrout and Fleiss’ ICC[2,1] coefficient was estimated at 0.652 (95% c.i. = (0.601, 0.706)) suggesting moderately strong heterogeneity between subjects’ mammograms relative to the variability between raters’ classifications. Cohen’s GLMM-based weighted kappa with quadratic weights was estimated at ${\widehat{\kappa }}_{\mathit{\text{GLMM}},a}=0.611$, also a higher value than ${\widehat{\kappa }}_{ma}$ likely due to a prevalence effect as depicted in Figure 2(a).

Each of the estimated measures of (exact) agreement indicated only low levels of chance-corrected agreement between raters, including the model-based measure of (exact) agreement ${\widehat{\kappa }}_m=0.241(se=0.015)$ Fleiss’ kappa ${\widehat{\kappa }}_F=0.297$, Conger’s and Light’s kappa ${\widehat{\kappa }}_{LC}=0.298$, and Cohen’s GLMM-based (unweighted) kappa $\widehat{\kappa }=0.257$.

Overall, there appears to be substantial discrepancies between raters’ ordinal classifications for grading screening mammograms in this population, reflected in the low and moderate levels of chance-corrected agreement and association.

5.2 Gleason grading study for prostate cancer

Allsbrook et al.⁵¹ reported on a study conducted to examine agreement and association between 41 general pathologists each classifying the same sample of 38 biopsy slides for the severity of prostate cancer. They utilized a modified earlier version of the Gleason grading scale consisting of four categories defined as: category (i) Gleason scores 2–4 (mild disease); category (ii) Gleason scores 5–6; category (iii) Gleason score 7; category (iv) Gleason scores 8–9 (severe disease). However, there were two missing observations, and since the proposed approach accommodates missing data, this did not lead to any further issues. A sample of this dataset is presented in the supplemental material online.

To assess the association in a unified approach between the ordinal classifications of the 41 raters, the ordinal GLMM with a crossed random effects structure in equation (1) was fit to the dataset using the clmm function in the ordinal package in R. The resulting parameter estimates and summary measures are presented in Table 7.

Based upon this sample of 38 slides, the probabilities of being classified into the four categories (from mild to severe disease) according to the GLMM model were 17%, 30%, 21%, and 32% respectively. Observed association between the raters was estimated to be very strong at ${\widehat{p}}_{0a}=0.917$. The chance-corrected measure of association κ_ma with quadratic weights was estimated as ${\widehat{\kappa }}_{ma}=0.554(s.e.=0.043)$ indicating moderate levels of chance-corrected association between the 41 general pathologists, where a value of 1 indicates perfect association. In comparison, Shrout and Fleiss’ ICC[2,1] statistic is estimated at 0.734 (95% confidence interval 0.642, 0.824) reflecting the stronger heterogeneity between patients’ biopsies slides $({\widehat{\sigma }}_u^2=4.805)$ relative to the variability observed between raters’ classifications $({\widehat{\sigma }}_v^2=0.480)$. Cohen’s GLMM-based weighted kappa with quadratic weights was also estimated at a high value as ${\widehat{\kappa }}_{\mathit{\text{GLMM}},a}=0.687$. These large values of the ICC[2,1] coefficient and κ_GLMM,a compared to κ_ma in the Gleason grading study may be attributed to the tendency of these two measures to be influenced by the prevalence of disease (high or low), and to take higher values when ρ is large, as in the Gleason Grading study, where $\widehat{p}=0.765$ as demonstrated in Figure 2(a). The agreement measures κ_m, κ_F, and κ_LC all suggested low (exact) agreement.

Overall, these results indicate that chance-corrected (exact) agreement between the general pathologists is low, but chance-corrected association is moderate, where the proposed measure κ_ma does not over-estimate the strength of association between the pathologists as the other measures do due to a high value of ρ. The proposed methods used here allow classifications of all 41 pathologists to be analyzed and interpreted in one unified approach. This approach leads to easily interpretable results, in comparison to studying agreement and association between each pair of pathologists, which leads to many statistics that can be difficult to interpret. Characteristics of each pathologist and the subjects’ test slides included in the study can be examined through their estimated random effect terms ${\widehat{v}}_j$ if required, which is described for this Gleason grading study in the next section.

6 Estimation of individual rater and subject traits

The primary focus of population-based agreement studies is usually to draw conclusions about the strength of agreement and association between raters who typically classify patients’ test results in the underlying population. It can also be informative to examine unique characteristics of individual raters and subjects included in the study for rater awareness and training purposes which is discussed below.

Unique characteristics of each rater’s classifications are adjusted for in the ordinal GLMM in (1) via their random effect term v_j, (j = 1,…, J). In the ordinal package clmm, predictions of the rater estimated effects ${\widehat{v}}_j,(j=1,\dots ,J)$ are generated as part of the modeling process as conditional modes, i.e. the modes of the distributions for the random effects given the observed data and estimated model parameters (also known as posterior Bayesian modes) using a Newton–Raphson algorithm.³⁶ A corresponding measure of uncertainty for each estimated effect, the conditional variance computed from the second order derivatives of the conditional distribution of the random effects, is also generated in the model-fitting process. Figure 3(a) and (b) presents plots of the rater estimated effects (J = 41) and subject estimated effects (I = 38) respectively with 95% confidence intervals using the conditional variance for the Gleason grading agreement study (section 5.2). For example, pathologist 21 has a large negative estimated effect ${\widehat{v}}_{21}=-4.02$ indicating a rater who tends to consistently assign milder disease status to patient biopsy slides relative to the other raters. Rater 34 has a large positive estimated effect ${\widehat{v}}_{34}=4.12$ signaling a rater who assigns more severe disease categories to patients’ slides relative to other raters.

Figure 3.

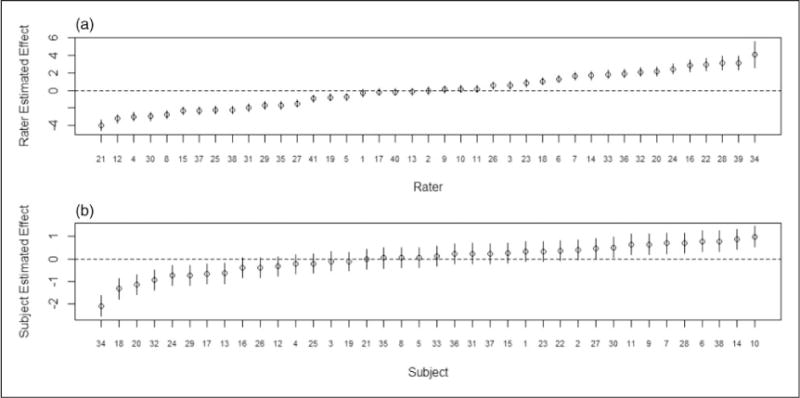
(a) Rater and (b) subject effects estimated as conditional modes for the Gleason grading study.⁵¹ Figure 3(a) shows J = 41 rater estimated effects and Figure 3(b) shows I = 38 subject estimated effects respectively, with 95% confidence intervals based upon the conditional variance.

A similar approach can be used to obtain predictions of the subject estimated effects, ${\widehat{u}}_i,i=1,\dots ,I$. These estimates reflect the heterogeneity observed between the patients’ test results. For the Gleason grading study, subject estimated effects ranged from −2.1 to 0.98. Large positive (negative) subject effects indicate test results that clearly show disease (no disease), while values close to 0 suggest a test result whose disease status is less obvious.

7 Discussion

The use of ordered classification scales is widespread in medical tests and diagnostic procedures to grade a patient’s disease or health status.^8–11 However, while strong reliability between raters is an important attribute of an accurate diagnostic procedure, poor agreement and association between raters have been reported in many of these settings.^1,4,9–12 Furthermore, in agreement studies with multiple raters using an ordinal classification scale to classify patients’ test results, it is challenging to assess levels of association and agreement in a unified approach since few statistical approaches are available or easy to implement.

In this paper, we have described a model-based approach to assess association between any number of raters (at least three) classifying subjects’ test results according to an ordered categorical scale. Missing data can be accommodated where some raters may not classify every subject in the sample. Many agreement studies report inter-rater reliability between two raters at a time which usually leads to several summary statistics with complexities in interpretation.^52,53 The proposed model-based approach describes association between the group of raters in a unified and comprehensive approach with a single summary measure, lending itself to increasing power and efficiency and simpler interpretation. An important advantage is that the chance-corrected measure of association is not affected by the underlying disease prevalence, in contrast to other existing measures including Shrout’s and Fleiss’ ICC[2,1] statistic. Results can be generalized to the raters and subjects who typically undertake these procedures and tests when the study participants and raters are randomly sampled from their respective populations. The proposed approach can be fit efficiently to an agreement dataset using author-written functions in the freely available R software package, making it a viable and attractive approach to implement in practice.

Simulation studies demonstrated that estimation of the proposed measure of association appears fairly robust to varying sample sizes of raters and subjects, large and small variance components which measure the variability between the groups of raters and subjects, and non-normally distributed random effect distributions of the raters and subjects under a varying range of situations encountered in real-life studies. Some bias was noted in the estimation of κ_ma when there was extreme variability between raters. Further work is required to fully explore the impact of non-normal random effects on the estimation of the measure of association, and to assess the effects of rater and subject characteristics on agreement by incorporating covariates into the ordinal GLMM model.

Measures of association are often preferred over measures of agreement when assessing strength of relationship between ordinal classifications since they incorporate information about the extent of disagreement in addition to exact agreement. For parametric approaches such as Cohen’s weighted kappa and our proposed measure of association, less “credit” is assigned in the kappa statistic to pairs of raters’ classifications that disagree more and are further apart on the categorical scale by use of a weighting scheme.¹⁶ While the choice of weights is left up to the researcher, quadratic and linear weights are common options, and use of these schemes makes for easier comparability between studies. The ICC has been shown to be equivalent to Cohen’s weighted kappa statistic for pairs of raters’ ordinal classifications.^46,54 Our simulation studies indicated that a modified version of Cohen’s weighted kappa with quadratic weights using population measures of chance and observed association yielded similar values to Shrout and Fleiss’ ICC[2,1] statistic, and was sensitive to the disease prevalence in a similar manner to Cohen’s original kappa.³¹

Liu and Agresti³⁸ note that when the ordinal classifications are assumed to be based upon an underlying unobserved latent variable, such as disease status, the effects are invariant to the number of categories and thresholds of the categorical scale used, and that different studies employing different scales should lead to similar conclusions.

Table 8.

Parameter estimates for the Gleason grading study⁵¹ with J = 41 general pathologists classifying the severity of prostate cancer of I = 38 patients from biopsy slides using a modified version of the Gleason grading scale with C = 4 categories: Category (i) Gleason scores 2–4 (mild disease); Category (ii) Gleason scores 5–6; Category (iii) Gleason score 7; Category (iv) Gleason scores 8–9 (severe disease).

Parameter	Symbol	Estimate	S.E.	Z-value
Ordinal GLMM:
Thresholds: (α0 = −∞, α4 = +∞)
Between categories 1 and 2	α1	−2.416	0.382	−6.326
Between categories 2 and 3	α2	−0.218	0.377	−0.578
Between categories 3 and 4	α3	1.168	0.378	3.094
Subject random effect variance	${\sigma }_u^2$	4.805	0.382
Rater random effect variance	${\sigma }_v^2$	0.480	0.368
Rho	ρ	0.765	0.043
GLMM-based observed agreement	p0	0.531
GLMM-based observed association (quadratic weights)	p0a	0.917
Measures of agreement:
Model-based (unweighted) kappa  (Nelson and Edwards41)	κm	0.357	0.036
Fleiss’ kappa (Fleiss47)	κF	0.404
Light and Conger’s kappa  (Light,48 Conger49)	κLC	0.405
Measures of association: (with quadratic weights)
Model-based weighted kappa	κma	0.554	0.043
Shrout and Fleiss’ ICC[2,1]  (Shrout and Fleiss28)		0.734	95% c.i. = (0.642, 0.824)
Cohen’s GLMM-based weighted kappa	κGLMM,a	0.687

Appendix 1 Derivation of observed association

$$\begin{array}{l}{p}_{0a}={\displaystyle \sum _{r=1}^C{\displaystyle \sum _{s=1}^C{w}_{rs}[\mathrm{Pr}(Y_{ij}=r\cap Y_{i{j}^{\prime }}=s)]}}\text{in the general population – based setting}\\ ={\displaystyle {\int }_{-\infty }^{+\infty }{\displaystyle \sum _{r=1}^C{\displaystyle \sum _{s=1}^C{w}_{rs}[\mathrm{Pr}(Q\le {\alpha }_r-u_i-v_j)-\mathrm{Pr}(Q\le {\alpha }_{r-1}-u_i-v_j)]}\times [\mathrm{Pr}(Q^{\prime }\le {\alpha }_s-u_i-v_{j^{\prime }})-\mathrm{Pr}(Q^{\prime }\le {\alpha }_{s-1}-u_i-v_{j^{\prime }})]f(u_i)\mathrm{d}u}}\\ ={\displaystyle {\int }_{-\infty }^{+\infty }{\displaystyle \sum _{r=1}^C{\displaystyle \sum _{s=1}^C{w}_{rs}[\mathrm{Pr}(Q+v_j\le {\alpha }_r-u_i)-\mathrm{Pr}(Q+v_j\le {\alpha }_{r-1}-u_i)]}\times [\mathrm{Pr}(Q^{\prime }+v_{j^{\prime }}\le {\alpha }_s-u_i)-\mathrm{Pr}(Q^{\prime }+v_{j^{\prime }}\le {\alpha }_{s-1}-u_i)]\varphi \left(\frac{u_i}{{\sigma }_u}\right)\frac{1}{{\sigma }_u}\mathrm{d}{u}_i}}\\ ={\displaystyle {\int }_{-\infty }^{+\infty }{\displaystyle \sum _{r=1}^C{\displaystyle \sum _{s=1}^C{w}_{rs}\left[\mathrm{Pr}\left(\frac{Q+v_j}{{\sigma }_u}\le \frac{{\alpha }_r}{{\sigma }_u}-z\right)-\mathrm{Pr}\left(\frac{Q+v_j}{{\sigma }_u}\le \frac{{\alpha }_{r-1}}{{\sigma }_u}-z\right)\right]}\times \left[\mathrm{Pr}\left(\frac{Q^{\prime }+v_{j^{\prime }}}{{\sigma }_u}\le \frac{{\alpha }_s}{{\sigma }_u}-z\right)-\mathrm{Pr}\left(\frac{Q^{\prime }+v_{j^{\prime }}}{{\sigma }_u}\le \frac{{\alpha }_{s-1}}{{\sigma }_u}-z\right)\right]}\varphi \left(z\right)\mathrm{d}z}\\ ={\displaystyle {\int }_{-\infty }^{+\infty }{\displaystyle \sum _{r=1}^C{\displaystyle \sum _{s=1}^C{w}_{rs}\left[\mathrm{\Phi }\left(\frac{\frac{{\alpha }_r}{{\sigma }_u}-z}{\sqrt{\frac{1+{\sigma }_v^2}{{\sigma }_u^2}}}\right)-\mathrm{\Phi }\left(\frac{\frac{{\alpha }_{r-1}}{{\sigma }_u}-z}{\sqrt{\frac{1+{\sigma }_v^2}{{\sigma }_u^2}}}\right)\right]\times \left[\mathrm{\Phi }\left(\frac{\frac{{\alpha }_s}{{\sigma }_u}-z}{\sqrt{\frac{1+{\sigma }_v^2}{{\sigma }_u^2}}}\right)-\mathrm{\Phi }\left(\frac{\frac{{\alpha }_{s-1}}{{\sigma }_u}-z}{\sqrt{\frac{1+{\sigma }_v^2}{{\sigma }_u^2}}}\right)\right]\varphi \left(z\right)\mathrm{d}z,}}}\\ ={\displaystyle {\int }_{-\infty }^{+\infty }{\displaystyle \sum _{r=1}^C{\displaystyle \sum _{s=1}^C{w}_{rs}\left[\mathrm{\Phi }\left(\frac{{\alpha }_r^{\ast }-z\sqrt{\rho }}{\sqrt{1-\rho }}\right)-\mathrm{\Phi }\left(\frac{{\alpha }_{r-1}^{\ast }-z\sqrt{\rho }}{\sqrt{1-\rho }}\right)\right]}}}\times \left[\mathrm{\Phi }\left(\frac{{\alpha }_s^{\ast }-z\sqrt{\rho }}{\sqrt{1-\rho }}\right)-\mathrm{\Phi }\left(\frac{{\alpha }_{s-1}^{\ast }-z\sqrt{\rho }}{\sqrt{1-\rho }}\right)\right]\varphi \left(z\right)\mathrm{d}z\end{array}$$

where, $\frac{Q+v_j}{{\sigma }_u}~N\left(0,\frac{1+{\sigma }_v^2}{{\sigma }_u}\right)$ and raters j and j′ (j≠ j′) are interchangeable since from the same large population of raters and z~N(0,1).

Appendix 2 Derivation of chance association

$$\begin{array}{l}{p}_{ca}={\displaystyle \sum _{r=1}^C{\displaystyle \sum _{s=1}^C{w}_{rs}[\mathrm{Pr}(Y_{ij}=r)\times \mathrm{Pr}(Y_{i^{\prime }{j}^{\prime }}=s)]}}\\ ={\displaystyle \sum _{r=1}^C{\displaystyle \sum _{s=1}^C{w}_{rs}[\mathrm{Pr}(Q\le {\alpha }_r-(u_i+v_j))-\mathrm{Pr}(Q\le {\alpha }_{r-1}-(u_i+v_j))]}\times [\mathrm{Pr}(Q\le {\alpha }_s-(u_{i^{\prime }}+v_{j^{\prime }}))-\mathrm{Pr}(Q\le {\alpha }_{s-1}-(u_{i^{\prime }}+v_{j^{\prime }}))]}\\ ={\displaystyle \sum _{r=1}^C{\displaystyle \sum _{s=1}^C{w}_{rs}[\mathrm{Pr}(Q+u_i+v_j\le {\alpha }_r)-\mathrm{Pr}(Q+u_i+v_j\le {\alpha }_{r-1})]\times [\mathrm{Pr}(Q+u_{i^{\prime }}+v_{j^{\prime }}\le {\alpha }_s)-\mathrm{Pr}(Q+u_{i^{\prime }}+v_{j^{\prime }}\le {\alpha }_{s-1})]}}\\ ={\displaystyle \sum _{r=1}^C{\displaystyle \sum _{s=1}^C{w}_{rs}\left[\mathrm{Pr}\right(\frac{Q+u_i+v_j}{\sqrt{1+{\sigma }_u^2+{\sigma }_v^2}}\le \frac{{\alpha }_r}{\sqrt{1+{\sigma }_u^2+{\sigma }_v^2}})-\mathrm{Pr}(\frac{Q+u_i+v_j}{\sqrt{1+{\sigma }_u^2+{\sigma }_v^2}}\le \frac{{\alpha }_{r-1}}{\sqrt{1+{\sigma }_u^2+{\sigma }_v^2}}\left)\right]}\times \left[\mathrm{Pr}\right(\frac{Q^{\prime }+u_{i^{\prime }}+v_{j^{\prime }}}{\sqrt{1+{\sigma }_u^2+{\sigma }_v^2}}\le \frac{{\alpha }_s}{\sqrt{1+{\sigma }_u^2+{\sigma }_v^2}})-\mathrm{Pr}(\frac{Q^{\prime }+u_{i^{\prime }}+v_{j^{\prime }}}{\sqrt{1+{\sigma }_u^2+{\sigma }_v^2}}\le \frac{{\alpha }_{s-1}}{\sqrt{1+{\sigma }_u^2+{\sigma }_v^2}}\left)\right]}\\ ={\displaystyle \sum _{r=1}^C{\displaystyle \sum _{s=1}^C{w}_{rs}[\mathrm{\Phi }({\alpha }_r^{\ast })-\mathrm{\Phi }({\alpha }_{r-1}^{\ast })]}\ast [\mathrm{\Phi }({\alpha }_s^{\ast })-\mathrm{\Phi }({\alpha }_{s-1}^{\ast })]},0.5\le p_{ca}\le 1.\end{array}$$

Appendix 3

Theorem

It can be shown in the population-based setting over many raters with ordinal classifications that p_0a≥p_ca≥0.5.

We begin with a proposition as follows:

Proposition

Under the model in equation (1), observed association is always greater or equal to chance association, i.e. p_0a≥p_ca.

Proof

Choose two raters at random, and let their ordinal ratings for randomly selected items i and i′ be denoted Y_i1, Y_i′2. We allow i = i′ to discuss the case where they look at the same randomly selected item. Let D=|Y_i1 − Y_i′2|. Let f and F be the mass function and cumulative distribution function of D, respectively.

We first show that p_0a can be written as a weighted average of F(d) values, d = 0, 1, 2,…, C−1

$$p_{0a}={\displaystyle \sum _{r=1}^C{\displaystyle \sum _{s=1}^C{w}_{rs}{p}_{rs}}}$$

Group terms by diagonals of the weight matrix corresponding to D = 0, D = 1, etc., and let w₀=1≥w₁≥w₂≥…w_C−1≥0 be the weights as determined by their off-diagonal locations.

$$\begin{array}{l}{p}_{0a}={\displaystyle \sum _{d=0}^{C-1}{w}_{d}f\left(d\right)}\\ =F\left(0\right)+{\displaystyle \sum _{d=1}^{C-1}{w}_d\left[F\left(d\right)-F\left(d-1\right)\right]}\\ =F\left(0\right)+{\displaystyle \sum _{d=1}^{C-1}{w}_{d}F\left(d\right)-}{\displaystyle \sum _{d=1}^{C-1}{w}_{d}F\left(d-1\right)}\\ =\left(1-w_1\right)F\left(0\right)+\left(w_1-w_2\right)F\left(1\right)+\left(w_2-w_3\right)F\left(2\right)+\dots \left(w_{C-2}-w_{C-1}\right)F\left(C-2\right)+w_{C-1}F\left(C-1\right).\end{array}$$

And since w₀ = 1 w₁≥w₂≥…w_C−1≥0, all coefficients of F(d) terms above are nonnegative. Now, if we can show that D is stochastically smaller when i=i′ than when i≠i′, it will follow that p_0a, the above expression with p_rs=Pr{(Y_i1=r) ∩ (Y_i2=s)} is greater than p_ca, the same expression with p_rs=Pr{(Y_i1=r)∩(Y_i′2=s)}

Suppress the asterisks on −∞= α₀^*, α₁^*, α₂^*,…, α_C^*=∞. Figure 4 shows the region {D≤1} in terms of the underlying variables W_i1,W_i2 and an irregular choice of α’s (when the threshold values α_c are unequally spaced) when C=5. Regions where D=0 are squares on the diagonal line W_i1=W_i2. Regions where D=1 are rectangles, some of which are infinite in extent. Note that the region {D≤1}, and more generally {D≤d}, is symmetric about the line W_i1=Wi₂.

Figure 4.

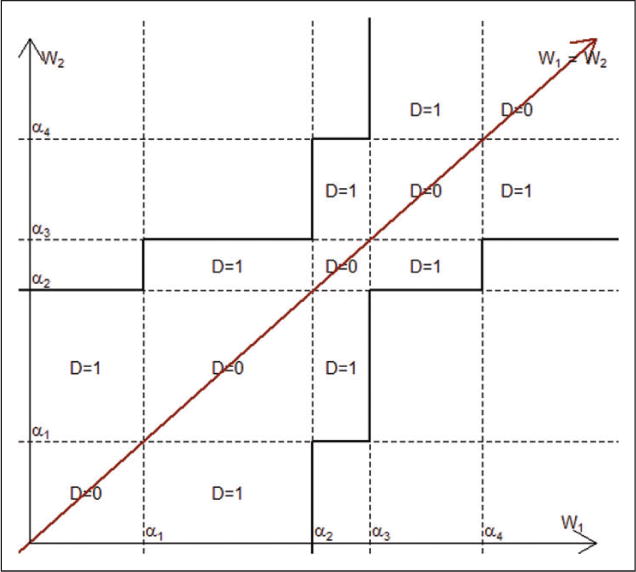
The region {D≤1} in terms of the underlying variables W_i1, W_i2 and an irregular choice of α’s (when the threshold values α_c are unequally spaced) when C=5.

Let R be any region symmetric about the line W_i1=W_i2. Define T_ii′=W_i1+W_i′2 and S_ii′=W_i1−W_i′2)=(u_i−u_i′)+(v₁−v₂) under our model W_ij=α_c−(u_i+v_j). Note that T_ii′, S_ii′ are independent. Let G_T denote the cdf of T_ii′ and given T_ii′=t, let the symmetric region R be defined by–b(t)≤S_ii′≤b(t).

$$\begin{array}{l}\stackrel{i{i}^{\prime }}{\mathrm{Pr}}\{R\}={\displaystyle {\int }_{t=-\infty }^{\infty }\mathrm{Pr}\{-b(t)\le S_{i{i}^{\prime }}\le b(t)|T_{i{i}^{\prime }}=t\}}\partial G_T(t)\\ ={\displaystyle {\int }_{t=-\infty }^{\infty }\mathrm{Pr}\{|S_{i{i}^{\prime }}|\le b(t)\}\partial G_T(t)}\\ ={\displaystyle {\int }_{t=-\infty }^{\infty }\mathrm{Pr}\{|(u_i-u_{i^{\prime }})+(v_1-v_2)|\le b(t)\}}\partial G_T(t)\\ \le {\displaystyle {\int }_{t=-\infty }^{\infty }\mathrm{Pr}\{|(v_1-v_2)|\le b(t)\}\partial G_T(t)}\\ =\stackrel{ii}{\mathrm{Pr}}\{R\}\end{array}$$

The inequality follows from the fact that | (u_i−u_i′) + (v₁−v₂) | is stochastically larger than | (v₁−v₂) |, they are the absolute values of normal variables with different variances. Since the probability of any region symmetric about the line W_i1=W_i2 is larger when i=i′, the random variable D is stochastically smaller when i=i′, and the result follows.

We can then demonstrate that p_ca≥0.5 using the following proof by induction: in equation (3), chance association p_ca is written as (for the ith item and jth rater)

$$\begin{array}{l}{p}_{ca}={\displaystyle \sum _{r=1}^C{\displaystyle \sum _{s=1}^C{w}_{rs}[\mathrm{Pr}(Y_{ij}=r)\times \mathrm{Pr}(Y_{i^{\prime }{j}^{\prime }}=s)]}}\\ ={\displaystyle \sum _{r=1}^C{\displaystyle \sum _{s=1}^C{w}_{rs}[\mathrm{\Phi }({\alpha }_r^{\ast })-\mathrm{\Phi }({\alpha }_{r-1}^{\ast })]}\times [\mathrm{\Phi }({\alpha }_s^{\ast })-\mathrm{\Phi }({\alpha }_{s-1}^{\ast })]}.\end{array}$$

Simplest case

For an ordinal scale with C = 2 categories, where thresholds α₀=−∞ and α_C=2=+∞. To find the value of ${\alpha }_1^{\ast }$ which minimizes chance association p_ca, we set the first derivative to 0:

$\frac{d{p}_{ca}}{\mathrm{d}{\alpha }_1^{\ast }}=4\mathrm{\Phi }\left({\alpha }_1^{\ast }\right)\phi \left({\alpha }_1^{\ast }\right)-2\varphi \left({\alpha }_1^{\ast }\right)=0\Rightarrow {\alpha }_1^{\ast }=0$ minimizes the expression for p_ca (with the second derivative > 0) and leads to the minimum value of p_ca=0.5 for linear and quadratic weights.

For an ordinal scale with C=3 categories, where α₀=−∞ and α_C=3=+∞.

To find the values of ${\alpha }_1^{\ast }$ and ${\alpha }_2^{\ast }$ which minimizes chance association p_ca, we can set each of the first derivatives to 0 and jointly solve:

$\frac{d{p}_{ca}}{\mathrm{d}{\alpha }_1^{\ast }}=0$ and $\frac{d{p}_{ca}}{\mathrm{d}{\alpha }_2^{\ast }}=0\Rightarrow {\alpha }_1^{\ast },{\alpha }_2^{\ast }=0$ minimizes the expression for p_ca (with the second derivatives > 0) and leads to the minimum value of p_ca=0.5. Since the ordinal GLMM model for association requires monotonically increasing thresholds, we set the thresholds to be ${\alpha }_0^{\ast }<{\alpha }_1^{\ast }<{\alpha }_2^{\ast }<{\alpha }_3^{\ast }$, or −∞ < 0.00001 < 0.00002 < +∞. Including these threshold values into the expression for chance association, p_ca leads to a minimum value of p_ca=0.5.

More generally, for any number of categories C, where C > 2, where α₀=−∞ and α_C=+∞.

To find the values that minimize chance association p_ca, we can set each of the first derivatives to 0 and jointly solve $\Rightarrow {\alpha }_1^{\ast },{\alpha }_2^{\ast },\dots ,,{\alpha }_{C-1}^{\ast }=0$ which minimizes the expression for p_ca (with the second derivatives > 0) and leads to the minimum value of p_ca=0.5. Since the ordinal GLMM model for association requires monotonically increasing thresholds, we set the thresholds to be ${\alpha }_0^{\ast }<{\alpha }_1^{\ast }<\dots <{\alpha }_{C-1}^{\ast }<{\alpha }_c^{\ast }$ or $\left({\alpha }_{min,1}^{\ast }=0.00001,{\alpha }_{min,2}^{\ast }=0.00002,\dots \right)$ with ${\alpha }_0^{\ast }=-\infty$ and ${\alpha }_C^{\ast }=+\infty$. By setting all the intermediate thresholds to be close to zero, this effectively turns the minimization into a two-category situation, which then leads to the minimum value of p_ca=0.5 as demonstrated above.

Thus, we have shown through proof by induction that the minimum value of p_ca is 0.5, and that this occurs when the monotonically increasing thresholds ${\alpha }_1^{\ast },{\alpha }_2^{\ast },\dots ,,{\alpha }_{C-1}^{\ast }$ take values −∞<0.00001<0.00002< … < +∞. Since we have demonstrated earlier that p_0a≥p_ca, we can state that 1≥p_0a≥p_ca≥0.5. These results hold for linear and quadratic weights.