A New Sensor for Measurement of Dynamic Contact Stress in the Hip

Abstract

Various techniques exist for quantifying articular contact stress distributions, an important class of measurements in the field of orthopaedic biomechanics. In situations where the need for dynamic recording has been paramount, the approach of preference has involved thin-sheet multiplexed grid-array transducers. To date, these sensors have been used to study contact stresses in the knee, shoulder, ankle, wrist, and spinal facet joints. Until now, however, no such sensor had been available for the human hip joint due to difficulties posed by the deep, bi-curvilinear geometry of the acetabulum. We report here the design and development of a novel sensor capable of measuring dynamic contact stress in human cadaveric hip joints (maximum contact stress of 20 MPa and maximum sampling rate 100 readings/s). Particular emphasis is placed on issues concerning calibration, and on the effect of joint curvature on the sensor's performance. The active pressure-sensing regions of the sensors have the shape of a segment of an annulus with a 150-deg circumferential span, and employ a polar/circumferential “ring-and-spoke” sensel grid layout. There are two sensor sizes, having outside radii of 44 and 48 mm, respectively. The new design was evaluated in human cadaver hip joints using two methods. The stress magnitudes and spatial distribution measured by the sensor were compared to contact stresses measured by pressure sensitive film during static loading conditions that simulated heel strike during walking and stair climbing. Additionally, the forces obtained by spatial integration of the sensor contact stresses were compared to the forces measured by load cells during the static simulations and for loading applied by a dynamic hip simulator. Stress magnitudes and spatial distribution patterns obtained from the sensor versus from pressure sensitive film exhibited good agreement. The joint forces obtained during both static and dynamic loading were within ±10% and ±26%, respectively, of the forces measured by the load cells. These results provide confidence in the measurements obtained by the sensor. The new sensor's real-time output and dynamic measurement capabilities hold significant advantages over static measurements from pressure sensitive film.

1. Introduction

Progress in reducing the incidence and severity of human articular joint pathologies depends in part on avoiding deleteriously elevated contact stress levels, such as those accompanying residual incongruity due to intra-articular fracture. A particular challenge is to ascertain whether a given fracture reduction is sufficiently precise to avoid harmful cartilage stress throughout physiologic loading. Methods to experimentally quantify these stresses therefore are desirable [1]. Thin-sheet multiplexed grid-array transducers are increasingly used for this purpose [2,3]. In the widely utilized form manufactured by Tekscan (Boston, MA), such sensors can be as thin as 0.1 mm, and consist of a matrix of electrically conductive strips, typically arranged in orthogonal rows and columns, printed on separate layers of Mylar film. Lines of piezoresistive ink are applied over each conductive strip in the sensing area, leaving visibly ink-free spaces between the sensing areas. Two such Mylar layers are adhered together around the edges, so that the piezoresistive ink-coated conductors face each other perpendicularly. The sensing (active) area of the sensor can be viewed as divided into squares centered on the intersections between conductors, each such square being referred to as a sensel—the sum total of individual sensel areas is equal to the sensing area. If the sensor is squeezed between opposing surfaces, each sensel acts as a variable resistor, whose resistance decreases monotonically with the instantaneous local compression at that location. The sensor is electrically connected to a host computer, which scans all sensels and encodes their resistance values as 8-bit integers (0–255). Given a user-conducted calibration, these integers are converted to stress at each sensel, for assembly of an instantaneous spatial map (frame) of contact stress between the surfaces. The digital nature of the sensel information facilitates additional post-processing, e.g., band-pass filtering or artifact removal. Serial frames can be dynamically sampled at rates as high as 100 frames per second [4,5].

A lithography/photoetching process is used to create a wide range of sensel layouts [6]. Among the parameters needing to be determined are sensing area size and shape, sensor thickness, spatial resolution, pressure range, pathway(s) of electrical lead-wire egress, and inclusion of anchor tabs with which to tether the sensor to the articular surface [7]. Design of a new sensor involves compromise between an ideal layout versus one that can be physically fabricated. A consequence of the custom nature of the design process is that development time is extended and sensors can be costly.

The aim of this study was to design, produce, and evaluate a new thin-sheet multiplexed grid-array transducer capable of measuring dynamic contact stress in human cadaveric hip joints. A description of this sensor, and suggestions for its calibration and use, are presented. Illustrative dynamic hip contact stress results are shown, and compared to static stress measurements made with pressure-sensitive film.

2. Design Criteria

2.1. Physical Dimensions.

Choosing the hip sensor physical dimensions involved striking an optimal balance between four objectives: maximum joint surface coverage, maximum spatial resolution of pressure, minimum wrinkling when the sensor was interposed between curved articular surfaces, and electrical lead routing that minimized disruption of and by other structures, especially the hip joint capsule. Dimensions were chosen through empirical testing of multiple sizes and shapes. Sensor surrogates for that purpose were designed using SolidWorks computeraidedengineering (CAE) software, and cut from Mylar sheets of appropriate thickness and stiffness. Preliminary screening of the surrogates was carried out in Sawbones^® hip joint models, with the most promising shapes then further evaluated in cadaver joints.

The sensor configuration adopted is shown in Fig. 1. The leftmost end of electrical contacts mates to a computer interface (“handle”) that electrically connects all sensels to the host computer. The active pressure-sensing region, at right, takes the shape of a segment of an annulus with a 150-deg circumferential span. The sensors were designed in two sizes, differing only in the principal dimensions of their active regions (Table 1). For sensor selection, our recommendation is to choose the sensor whose active region outer radius most closely matches the femoral head diameter of the cadaver joint. A polar/circumferential “ring-and-spoke” sensel grid layout is utilized. Experimentation with the surrogates showed that this particular shape and grid maximized sensel spatial density and minimized wrinkling. The parallel electrical leads for the spokes are located on the front (“UP”) surface of the sensor, and on reaching the active region, they diverge and re-group into four separate tracts to increase flexibility. The ring electrical leads are located on the back, and everywhere except in the active region, are electrically insulated from the spoke leads by a layer of Mylar. In the active region the ring and spoke leads are separated by piezoresistive ink, to form the sensels. Eight 1-mm diameter holes near the outer perimeter of the active region permit suturing of the sensor to the acetabular labrum.

Fig. 1.

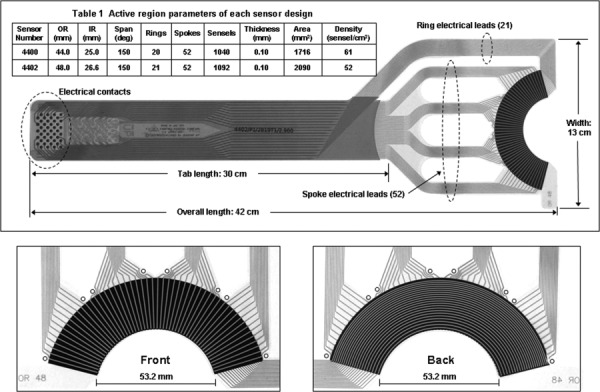
A hip joint contact stress sensor showing the ring-and-spoke configuration. The spoke leads, on the front (“UP”) of the sensor, and the ring leads, on the back, converge at the active region, where they are separated by an intervening layer of piezoresistive ink to form a grid of stress-sensing sensels. Eight 1-mm diameter holes on the periphery provide for suture tie-down to the acetabular labrum.

Table 1.

Active region parameters of each sensor design

Sensor number	OR (mm)	IR (mm)	Span (deg)	Rings	Spokes	Sensels	Thickness (mm)	Area (mm2)	Density (sensel/cm2)
4400	44.0	25.0	150	20	52	1040	0.10	1716	61
4402	48.0	26.6	150	21	52	1092	0.10	2090	52

Figure 2 illustrates sensor placement within a cadaver hip joint. The outer perimeter of the active region rests at approximately the equator, transverse to the femoral neck. When the femur is positioned in the acetabulum, the entire region of habitual joint contact during normal physiological movement is fully covered by the sensor. (The fovea and peri-foveal region, which normally experience little or no contact stress, are not covered.) The electrical leads for the spokes and rings exit the sensing area distant from the zone of predominant contact engagement, minimizing their potential to be damaged.

Fig. 2.

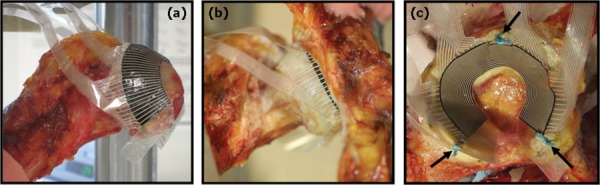
Hip contact stress sensor placement within a cadaver hip joint. (a) An oblique view of the femur showing the sensor positioned on the femoral head. The outer perimeter of the sensor active region rests approximately at the equator of the head. (b) An anterior view, showing the femoral head within the acetabulum. The periphery of the active region is still visible at the edge of the labrum. (c) A mediolateral view of the acetabulum only; arrows indicate where the sensor has been sutured to the labrum.

2.2. Contact Sensing Range.

The sensor is intended for measurement of stress both in normal native hips and those with various pathologies or injuries. Contact stress determinations from validated finite element models and experimental measurements using pressure sensitive film [8–11] led to a consensus judgment that the maximum stress level to be measured would be 20.0 MPa. The stress response of the sensor depends primarily upon its piezoresistive ink composition, formulated such that the sensor produces full electrical output at the desired peak pressure. To that end, multiple ink preparations were evaluated empirically using sensor prototypes loaded between rigid flat platens. Rigid platens are typically used for this purpose since they can be straightforwardly and consistently standardized. However, when sensing between less rigid surfaces such as cartilage-covered regions of an articular joint, some portion of the load will transfer across the intervening areas between sensels, so that sensor output is correspondingly reduced [12].

Experience with a previously custom-designed grid-array contact stress sensor for use in the human ankle joint had demonstrated that in situ output for cartilage-on-cartilage contact is approximately one-fourth of that obtained from metal-on-metal (aluminum) flat-platen loading [13–17]. Therefore, to ensure that the new hip sensor would have 20.0-MPa maximum pressure capability in situ, the ink composition was chosen so as to achieve maximum output for 5.0 MPa of rigid-flat-platen contact.

2.3. Calibration.

Sections 2.3.1 and 2.3.2 describe two sensor calibration techniques, developed for two primary purposes: to show that the sensor achieved maximum output at 20.0 MPa, and to confirm that sensor performance was not compromised under in situ joint curvature. These descriptions are not intended to constitute detailed calibration instructions, since the degree of appropriate calibration rigor of course will vary, depending on the results required by the user, the physical environment of the test, and the available resources.

2.3.1. Flat-Platen Calibration.

Although batch-specific calibration is performed during manufacture, end-user calibration of each individual sensor is usually desirable. An experimental setup for a flat-platen calibration is shown in Fig. 3(a). A broad lower platen supported the entire active region of the sensor, while a second, smaller, annular sector-shaped platen was placed on top, with its edges carefully aligned with rings and spokes to ensure that it was symmetrically located above a subsector of the full active area. Upper and lower surfaces of the sensor were lubricated with a thin coat of petroleum jelly, which reduces friction and eliminates any need to precondition the sensor. The upper platen shown spanned 36 deg circumferentially, covering 12 of the 52 spokes and all 21 rings of the sensor. Both upper and lower platens were machined from aluminum. The upper platen's contact face was lined with 1.0-mm thick 90A polyurethane (PU) rubber, a material layer that produced an approximate four-to-one attenuation of sensor output compared to the rigid platen case; thus simulating in situ cartilage behavior.

Fig. 3.

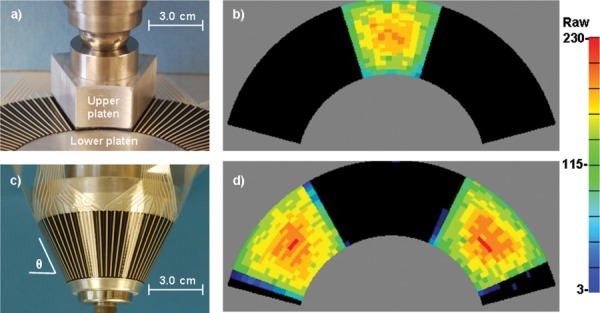
The hip sensor flat- and conical-calibration devices and representative contact patches. In (a), the flat upper platen spanned 12 spokes and 21 rings (not visible) of the sensor; (b) graphically indicates sensor raw output at an applied contact stress of approximately 10 MPa. Four repositionings of the platen were sufficient to calibrate the full surface of the sensor. (c) Conical upper platen with a sensor in place; raw output at 10 MPa is shown in (d). Two further rotations of the cone are sufficient to calibrate the entire sensor.

After the upper platen was positioned, a closed-loop servohydraulic test machine (MTS Corp., Eden Prairie, MN) drove the upper platen downward under programmed load control, which compressed the sensor between the platens. A ball joint between the actuator and the upper platen eliminated any rotational moment, so that the sensor experienced only axial compression. After the programmed peak load was reached, the load was reduced to zero to allow platen repositioning to an adjacent sector, after which the load was reapplied. The area of the upper platen was slightly greater than one-fifth of the total area of the sensor, so that four additional reposition/reload cycles were sufficient to calibrate 100% of the active region. Figure 3(b) shows the raw output of the sensor at a peak contact stress of approximately 10 MPa.

2.3.2. Conical-Platen Calibration.

Because of the sensor's intended usage on curved surfaces in situ, it was necessary to determine any effects of substrate curvature. A cone–cup calibration fixture was designed for that purpose. The cone was lathe-turned from aluminum, and was sized so that the sensor would wrap around its surface without wrinkling (Fig. 3(c)). The cone was subsequently used as a pattern against which to cast a matching cup of polymethyl-methacrylate (PMMA). Two 70-deg annular sector-shaped segments of 1.0-mm thick 90A PU were glued inside the cup, symmetrically opposite one another. The hip sensor was placed around the cone, and the cone/sensor was then inserted into the cup, effectively making the cone and cup analogous to the upper and lower platens of the flat-platen calibration. Both surfaces of the sensor were lubricated with petroleum jelly. An MTS machine was used to apply axial force to the cone. Because the 90A PU annular segments were symmetrically opposite one another, and because the cone was unconstrained transversely, the cup was self-centering in the cone, creating two similar contact stress patches. The area of the two conical platens was such that two additional cone rotation/reload cycles were sufficient to calibrate 100% of the active region. Figure 3(d) shows the raw output of the sensor at a peak contact stress of approximately 10 MPa.

2.4. Static Recording Methods.

Contact stress in a cadaveric hip (from a 33 year old male, femoral head diameter = 52 mm, acetabular opening diameter = 57 mm) was measured using both the new hip sensor and pressure-sensitive film (Fuji Prescale, Sensor Products Inc., Madison, NJ) during loading conditions that simulated two heel strikes, one during normal walking and one while ascending stairs, using an established protocol [9]. Direct comparison with pressure-sensitive film, currently the standard for measuring static in situ contact stress in the human hip [2], was chosen to illustrate the new sensor's ability to measure contact stress. A thorough description of the experimental loading protocol can be found in [9], and so is only briefly outlined here.

All soft tissue with the exception of articular cartilage was removed from the hip. This included dissection of most of the acetabular labrum, except for a small section left for attachment of the sensor. Experimental loading was based on published data for in vivo hip loads [18] obtained using instrumented femoral prostheses. The data for heel strike during walking and stair climbing were used for the current study. A custom loading apparatus was developed to apply the kinematics that corresponded to these loading conditions [9]. Peak loads for each activity were simulated by displacing the femur into the acetabulum at a constant rate. For each activity, the rate of actuator displacement was adjusted until peak loads were achieved within 0.33 s, representative of the uploading times for average subjects [18]. The specimen was allowed to recover between trials for periods over 100 times the interval that was needed to reach peak load. Identical trials were completed with either pressure-sensitive film (low range, 1.7–10.0 MPa), or the new sensor, in the joint space. The joint space was kept moist with saline. Various film sizes were cut into a rosette pattern, to facilitate covering the spherical femoral head with the flat film [9]. The film size was chosen to maximize contact area and minimize overlap. Similarly, the hip sensor that maximized contact area on the acetabulum and minimized wrinkling was chosen. The location of the sensor during testing was documented using CT scans and a stylus digitizer. The stresses from the sensor were mapped onto the acetabular cartilage in the experimental position and then were integrated over the known areas and orientations to determine force recovery. Details can be found in [9]. Additionally, the pressure patterns of the pressure-sensitive film and the new sensor were compared qualitatively.

2.5. Dynamic Recording Methods.

A multiaxial servohydraulic joint motion simulator (Fig. 4), actuated by an MTS Bionix test machine, was used to apply dynamic physiological loads to a human cadaveric hip joint (from a 67 year old female, femoral head diameter = 49 mm, acetabular opening diameter = 52 mm) through an operator-programmed, 3D loading profile. The simulator incorporated two heavy-duty aluminum yokes, mounted in series with the axial/rotary actuator of the MTS. The inner and outer yokes applied flexion/extension and abduction/adduction, respectively, to the cadaver hemi-pelvis. The rotary channel of the MTS imparted endorotation/exorotation, and its axial channel delivered joint contact loading. The hemi-pelvis specimen was rigidly affixed to a 6 degree-of-freedom (DOF) load cell mounted within the inner yoke of the simulator [19].

Fig. 4.

A hip motion simulator was used to drive a human cadaver hemi-pelvis through a user-programmed three-dimensional motion/force protocol. A PMMA-potted femur (a) is supported on a 2-DOF translational stage (b) (at 45 deg flexion in the case shown); the hemi-pelvis (c) is mounted to the inner yoke (d), which applies flexion/extension. The outer yoke (e) applies abduction/adduction while the Bionix axial-rotary actuator (f) delivers endorotation/exorotation and axial force. Hip joint forces and moments are transduced via a 6-DOF load cell (g).

As a test of its dynamic response, a lubricated sensor was placed in the joint space (Fig. 2), and a 5-segment protocol, beginning at 0 N load and 0 deg flexion was applied to the specimen. The segments were (i) a 5-s linear ramp from 0 to 600 N (nominal body weight), followed by (ii) a 1-s dwell at 600 N and 0 deg, followed by (iii) a 4-s flexion sequence: 0 → 30 → 0 deg at 15 deg/s, followed by (iv) a 1-s dwell at 600 N and 0 deg, followed by (v) a 5-s linear ramp from 600 to 0 N, for a total duration of 16 s. Sensor raw output was recorded at 5 frames per second, for a total of 80 frames. The sensor conical calibration curve (Sec. 2.3.2, above) was used to convert raw output to stress, which in turn was spatially integrated to return joint load for each frame; these loads were compared to the joint loads reported by the simulator's load cell.

3. Results

3.1. Calibration

3.1.1. Flat-Platen Calibration.

Figure 5 includes two representative calibration curves obtained using the flat-platen device and sensor as shown in Fig. 3(a), for the upper platen both without (rigid) and with a 90A PU lining. The lined condition simulated in situ cartilage behavior. Average stresses were calculated from the MTS-applied load divided by the area of the contact patch (Fig. 3(b)). For the rigid condition, the load was increased from 0 to 1400 N at a rate of 140 N/s, so that stress reached 2.9 MPa. For the PU-lined condition, the load was increased from 0 to 5000 N at a rate of 500 N/s, so that stress reached 10.4 MPa. To generate the curves shown, stresses (calculated at 70-N load increments for the rigid condition and 250-N increments for the lined condition) were plotted against average raw values and fitted to second-order polynomials (R ²> 0.98, both curves).

Fig. 5.

Sensor calibration curves obtained with three different platen configurations. Comparison of the flat-platen curves, rigid versus 90A polyurethane (PU), indicated that the PU lining attenuated sensor output by approximately a factor of 4, to simulate in situ cartilage response. The flat- and conical-platen results, when both platens were lined with PU, were virtually identical, which indicated that sensor behavior was unaffected by substrate curvature.

3.1.2. Conical-Platen Calibration.

Figure 5 also includes a calibration curve generated using the 90A PU conical platen shown in Fig. 3(c). MTS-applied load was again increased linearly from 0 to 5000 N at a rate of 500 N/s. However, in this case, vertical force equilibrium required that the average contact stress experienced by the sensor be equal to the load divided by the area of the contact patch (Fig. 3(d)), divided again by the cosine of the cone angle θ. The area and angle were 1154 mm² and 64.8 deg, respectively, so that average stress reached approximately 10.2 MPa. To generate the curve, stresses (calculated at 250 -N load increments) were plotted against average raw values and fitted to a second-order polynomial (R ²> 0.98). The 90A PU flat and conical calibration curves were virtually identical, which indicated that sensor behavior was essentially unaffected by a surface with a single noninfinite radius of curvature.

In generating calibration curves, the maximum loads were determined a priori to be those at which any sensel within the contact patch reached 90% (230) of the maximum raw output of 255. Individual sensel outputs of 255 are theoretically possible, but as a practical matter are to be avoided, as they would indicate full saturation of the electrical signal. To preclude this, a sensor was considered to meet its maximum stress specification if that stress produced an average sensel output (within the contact patch) of between 70% and 90% of 255 (i.e., 180 to 230). The curves in Fig. 5 were extrapolated to predict the 70% and 90% stresses, which are tabulated in Table 2. For the rigid flat-platen calibration, the target value of 5.0 MPa fell within the 70% to 90% limits (3.9–6.0 MPa), indicating that the sensor achieved the desired sensitivity level. For the 90A PU platens, both flat and conical, 20.0 MPa fell within the extrapolated values: the sensor therefore met the desired sensitivity for use in the hip joint.

Table 2.

Stress extrapolations to 70% and 90% of full output

Loading platens	Stress (MPa)
shape, material	70% (180)	90% (230)
Flat, rigid	3.9	6.0
Flat, 90A PU	14.3	22.8
Conical, 90A PU	14.1	22.5

3.2. Static Recording Results.

Joint contact stress results obtained from both the sensor and from pressure-sensitive film are shown in Fig. 6. As described in Sec. 2.4, the activities simulated were heel strike during walking and heel strike during stair climbing. Stress magnitudes and spatial distribution patterns exhibited good agreement. For the new sensor, the joint forces calculated by sensor calibrations and spatial integration of the contact stresses were within ±10% of the force as measured by the load cell. Numerical results are summarized in Table 3.

Fig. 6.

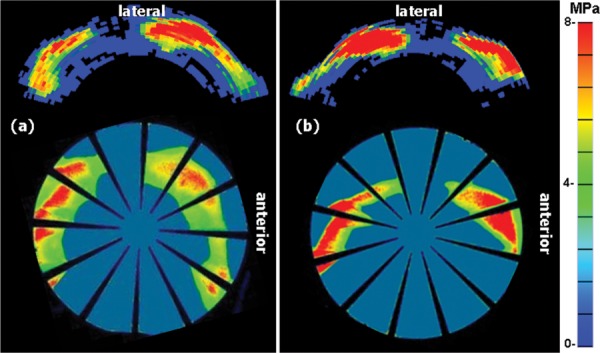
A comparison of hip sensor measured contact stress (top) versus pressure-sensitive film measured stress (bottom) for a statically loaded cadaver hip joint. Stress patterns exhibited good qualitative agreement. (a) and (b) Heel strike during walking and heel strike during stair climbing, respectively. Applied loads and the percentage of applied load recovered by the sensor are listed in Table 3.

Table 3.

Percentage of applied hip joint load recovered by the hip sensor for static and dynamic loading tests

Static tests
Activity	Applied load	Figure	% Load recovered by sensor
Walking heel strike	1966 N	6(a)	91
Ascending heel strike	2126 N	6(b)	110
Dynamic tests
	Applied load, Position	Figure	% Load recovered by sensor
Segment 1: Ramp 0 N to 600 N @ 120 N/s	200 N, 0 deg	7(a)	108
	400 N, 0 deg	7(b)	98
600 N, 0 deg	7(c)	81
Segments 2;3: Hold @ 600 N; 0 deg to 30 deg to 0 deg flexion @ 15 deg/s	600 N, 15 deg	7(d)	74
	600 N, 30 deg	7(e)	81
600 N, 15 deg	7(f)	89
Segments 4;5: Hold @ 600 N; 600 N to 0 N @ −120 N/s	600 N, 0 deg	7(g)	82
	400 N, 0 deg	7(h)	90
200 N, 0 deg	7(i)	86

3.3. Dynamic Recording Results.

Representative contact stress results for a dynamically loaded sensor are shown in Fig. 7. As described in Sec. 2.5, the hip joint loading consisted of load uptake, followed by joint flexion, followed by load removal. Throughout the complete protocol, stresses were recorded at 5 frames per second. Figure 7 shows three representative frames, spaced approximately evenly in time, for each of the load phases. Applied load and the percentage of that load recovered by the sensor for each frame are listed in Table 3.

Fig. 7.

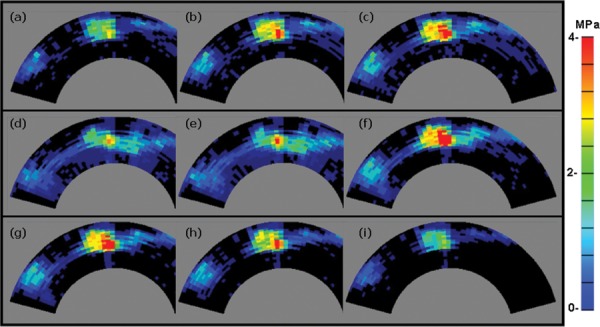
Contact stress dynamic results: Nine representative (of 80 total) frames recorded at 5 frames per second during a hip-simulator applied loading protocol. (a)–(c) were recorded during the load uptake phase; (d)–(f) were recorded during the joint flexion phase; and (g)–(i) were recorded during the load removal phase. Applied loads for each frame and the percentage of that load recovered by the sensor are listed in Table 3.

4. Discussion

In situations where the need for dynamic recording of intraarticular joint contact stress in cadavers has been paramount, the approach of preference has involved thin-sheet multiplexed grid-array transducers. Until now, however, no such sensor had been available for the human hip joint, despite the great need for scientific study of important hip disorders such as idiopathic osteoarthritis, developmental hip dysplasia, femoro-acetabular dysplasia, osteonecrosis, Legg–Perthes disease, and acetabular fractures.

Design decisions necessarily entail performance tradeoffs. For example, reducing sensor thickness to increase flexibility would have compromised durability, an important practical consideration. Several factors specific to the hip joint posed particular challenge, including the variation in joint size and shape, the tendency for wrinkling due to deep spherical joint curvature, and restricted access to the articular surface due to the presence of a very robust joint capsule. And, because the articular surfaces of the hip undergo large relative motion, the sensor needed to be tethered to one side of the joint, for purposes of preserving spatial registration and of reducing the potential for shear-induced damage.

The new sensors are produced in two configurations, 4400 and 4402, which differ primarily in the outer radii of their active regions (44.0 and 48.0 mm, respectively). Trial fittings showed that these sizes sufficed for most human cadaver hips. We suggest that a user choose the sensor whose active region outer radius most closely matches the femoral head diameter of the hip joint in which the sensor is to be used, which will generally insure that the region of habitual joint contact during normal physiologic movement is fully covered by the sensor, as shown in Fig. 2. This is not a rigid guideline, and trial-and-error may be required to ascertain which size produces the desired results. For example, if the user is primarily interested in measuring acetabular rim stresses, he/she may choose to always utilize the larger of the two sizes. However, if the larger size is used in a very small joint, the ends of the sensor may overlap, rendering its output invalid.

The maximum number of rings and spokes was limited by manufacturing tolerances for smallest possible electrical lead separation distance. Both sensors' active-region grids incorporated a unique layout: nonuniform ring spacing, where the ring-to-ring separation distance decreased gradually (inversely with radius) in the outward radial direction. (This ring spacing can be appreciated in Fig. 1.) Decreasing ring spacing, coupled with increasing spoke-to-spoke distance radially, achieved parity of sensel area over the entire active region. In addition to resulting in more uniform stress response across the active area, this feature also simplified spatial integration to return the applied joint load.

Calibration of the hip sensor presented other special challenges. The sensor's in situ behavior differed appreciably from that predicted by standard rigid-platen assessment. However, in most cases, an in situ calibration—i.e., the application of a series of known forces to the cadaver joint with the sensor in place—is not feasible. Because of irregular or discontinuous joint surfaces, even in a controlled experimental environment the actual load experienced by the sensor may be indeterminable. To prevent wrinkling of the sensor, it may not be possible to cover the entire region of load transfer. And, indeed, determination of an unknown joint load (via spatial integration of contact stress) is often itself the basis for the use of a stress sensor. For these reasons, it is normally necessary to perform an external calibration, under benchtop conditions chosen to best replicate in situ conditions.

Extensive calibration experience with this type of sensor had shown that, in order to achieve consistent response at the periphery of a contact patch, the loading platen needed to extend slightly beyond the edges of that patch. For example, the flat platen shown in Fig. 3(a) was sized to span 12 of the 52 spokes and all 21 rings of the sensor. Its inner and outer radii were 26.0 and 48.5 mm, respectively, and it subtended 36 deg of arc, to give a platen surface area of 527 mm². However, the corresponding dimensions of its contact patch (Fig. 3(b)) were 26.6 and 48.0 mm, with 34.6 deg of arc, for an area of 482 mm². Because the platen area was larger, some fraction of the applied load could be transmitted across the sensor without transduction by a sensel, particularly in the regions adjacent to the inner- and outermost rings. The average applied stresses plotted in Fig. 5 were calculated using the smaller area (482 mm², rather than 527 mm²), and; therefore, could be overestimated by as much as 9%. Similarly for the conical platens, the ratio of platen area to contact patch area was 1.11.

To track moving contact within a joint for an extensive range of joint motion, a stress sensor must be significantly larger in active area than the joint contact patch at any given instant within the range. The sensor size becomes such that external calibration of its entire surface at once would involve impracticably high force magnitudes. For example, to load the full sensing region of the larger hip sensor to its rated stress of 20.0 MPa would require a force greater than 40 kN, well beyond the experimental capabilities of loading equipment in most biomechanics research labs. Therefore, in practice, only a subsection of the sensor can be calibrated at once: calibration of the entire surface requires possibly tedious and time-consuming repetition. And indeed, calibration of the full surface is generally required—although the sensor response is initially uniform across its full surface, experience has shown that localized wear-and-tear during use often alters the response of individual or subgroups of sensels, rendering any earlier calibration suspect.

We consider the need for recalibration to be driven by sensor degradation—specifically, whether degradation is occurring, and to what degree, and, if so, whether it will affect critical results. The overall condition of the sensor can be monitored via its reported load (average sensel stress multiplied by total area of all active sensels); a decrease in this load relative to the known applied load indicates a decrease in sensitivity. A decision to recalibrate is based on operator judgment: in some situations, it may be desirable to expeditiously conduct multiple recalibrations of at least a significant portion of the entire sensor surface. Use of the conical platen method described herein both significantly reduces the required force magnitudes and streamlines calibration of the entire sensor surface. Along these lines, Kang et al. [20] have developed a pneumatically actuated wringerlike calibration device that subjects a tibio-talar (ankle) joint contact pressure sensor to traveling fiducial loads propagating across its full surface. Going forward, it might be possible to apply a similar concept to calibration of the hip sensor.

Life span of a contact stress sensor before it is irreparably damaged is highly application specific. For example, if one proposed to use hip sensors for measuring step-off contact pressures in displaced acetabular fractures, the sensor is likely to have a very limited life span. In several experimental studies employing the ankle sensor, we have found there to be a significant learning curve in reducing the need for recalibration and extending the life of the sensor. It is critical to carefully position the sensor so as to protect the electrical leads before load is applied across the joint. Condition of the cadaver joint surface is also important—abraded cartilage or exposed bone is more likely to quickly degrade the sensor. Finally, effective lubrication of the sensor is necessary.

Going forward, conceptually similar annular-segment sensor layouts are potentially applicable to other spherical surface contact stress measurements of orthopaedic interest, particularly the native glenohumeral joint, and implants for hip joint and shoulder joint replacement. Specific parameters of course would differ from those of the present sensors, and would need to again be determined empirically.

5. Conclusions

A new thin-sheet multiplexed grid-array transducer capable of measuring dynamic contact stress in human cadaveric hip joints has been designed and produced, and has now become commercially available for use by the orthopaedic research community. Real-time output and dynamic measurement capabilities give the new sensor significant advantages over stress measurements made using static recording techniques such as Fujifilm Prescale^®. The new sensor is sized to cover the critical contact region of the native hip, and to accommodate the curvature inherent to the joint. Two sizes are available, and guidelines are given for a potential user to choose the appropriate size. External benchtop calibration of the sensor–for example, using an MTS machine to apply known loads–is recommended, and an efficient means to do so is described. Although the sensor will experience curvature in situ, calibration using rigid flat platens can be employed. In such cases, it is recommended that the platens be lined with 1-mm thick 90A polyurethane rubber as an acceptable analog for articular cartilage. Sensor response (applied stress versus output) is best modeled by a second-order polynomial. In situ, it is critical to lubricate both sides with petroleum jelly to minimize shear-induced degradation, and to protect the electrical leads from pinching. If cadaver testing involves hip motion, the sensor must be tethered to either the femur or pelvis. Sensor degradation (reduction in output at a given stress) should be monitored and used to determine the need for recalibration.