Time-Course Statistical Evaluation of Intercellular Adhesion Maturation by Femtosecond Laser Impulse

Abstract

The maturation of intercellular adhesion is an essential process for establishing the signal transduction network in living cells. Although the maturation is naturally considered to enhance the signal transduction, the relationship between the signal transduction and the maturation process has not been revealed in detail using time-course data. Here, using a coculture of mast cells and neurites, differences in maturation between individual cells were estimated as a function of the adhesion strength by our original single-cell measurement method utilizing a laser-induced impulsive force. When an intense femtosecond laser is focused into a culture medium under a microscope, shock and stress waves are generated at the laser focal point that exert an impulsive force on individual cells. In our method, this impulse is used to break the adhesion between a mast cell and a neurite. The magnitude of the impulse is then quantified by a local force-measurement system utilizing an atomic force microscope, and the adhesion strength is estimated from the threshold of the impulse required to break the adhesion. The measurement is conducted within 1 min/cell, and thus, data on the individual differences of the adhesion strength can be obtained within only a few hours. Coculturing of neurites and mast cells for 4 h resulted in a specific adhesion that was stronger than the nonspecific adhesions between the substrate and mast cells. In the time-course investigation, we identified two distinct temporal patterns of adhesion: 1) the strength at 24 h was the same as the initial strength; and 2) the strength increased threefold from baseline and became saturated within 24 h. Based on these results, the distribution of CADM1 adhesion molecules in the neurites was suggested to be inhomogeneous, and the relationship between adhesion maturation and the signal-transduction process was considered.

Introduction

Maturation of intercellular adhesion is an important process for the functionalization of cells. For example, the signal transduction network of neurons is constructed based on the contact between their neurites and other cells. Although the time evolution of intercellular adhesion strength is essential information for understanding the maturation, there have been no reports quantifying this data. The main difficulty in determining the time evolution is that it differs widely among individual cells. This issue could be solved if we could obtain a large number of the individual strengths in a short time, e.g., with a frequency of >100 cells/h. However, the conventional methods for measuring the adhesion strength of individual cells are too slow to obtain such data. For example, single-cell force spectroscopy is a novel and widely used method for measuring the strength of individual cells (1, 2, 3).This technique allows us to precisely estimate the strength as the time required to break a single protein-protein binding, but it is difficult to make such estimations at a frequency >100 cells/h.

Recently, we developed, to our knowledge, an original measurement method to estimate the strength of individual cells utilizing a femtosecond laser. When a near-infrared femtosecond laser is tightly focused in an aqueous solution under a microscope, shock and stress waves are generated at the laser focal point (4, 5, 6). These waves localize in a micrometer-sized space around the laser focal point (4) and they act as an impulsive force on a micrometer-sized object, such as a single cell, which is located near the laser focal point (7, 8, 9, 10). We previously succeeded in quantifying the magnitude of the micrometer-sized impulsive force using atomic force microscopy (AFM) (11, 12). The quantified impulsive force has been applied as an external force to break the intercellular adhesion, and the adhesion strength has been estimated as a breaking force (13). Since the breaking could be induced in a short time, e.g., <10 μs, we can obtain a large number of the intracellular adhesions within only a few hours.

As a model system to study the adhesion maturation, a coculture system of nerve and mast cells was selected. Mast cells distribute in various systemic organs and tissues, e.g., the respiratory mucosa, skin dermis, or dura mater (14, 15, 16, 17, 18, 19). In such tissues, they tend to exist near or in contact with neurites of nerve cells (20); electron microscopic observation has revealed that the intercellular distance is generally <20 nm (21, 22). Many mast cells adhere to neurites when neurogenic inflammation occurs (23), and Furuno et al. reported that mast cells and nerve cells bidirectionally transduce signal molecules in an adhesion-dependent manner (24, 25). From these reports, the coculture system is generally regarded as a reproductive model of the anatomical and functional relationship between them. The adhesion is considered to be formed by specific bonds between cell adhesion molecules known as cell adhesion molecule-1s (CADM1s) (24, 26, 27, 28), which are membrane-spanning glycoproteins belonging to the immunoglobulin (Ig) superfamily (29, 30, 31, 32) and function by forming a dimer on the cell membrane (33, 34, 35).

In a previous study, our group evaluated the adhesion behavior between neuroblastoma cells (neuro2a) and mast cells, in which several isoforms of CADM1 were expressed exogenously (36). The results indicated that the spatial distribution of CADM1s on the neurite differed among the isoforms, resulting in different adhesion strengths. Cell pairs with CADM1 isoforms conferring higher adhesion strength tended to more effectively transduce the signal than pairs with isoforms conferring lower adhesion strength. Furthermore, it seemed that at least 14 h of coculturing was needed to observe the signal transduction in all isoforms, whereas the adhesions were formed within ∼3 h. This finding indicated the importance of investigating the maturation process to better understand the signal transduction mechanism.

In this study, we estimated the time course of the adhesion strength between a neurite and a mast cell as the femtosecond-laser-induced impulsive force required to break the adhesion at the single-cell level without apparent damage to both of the cells. The magnitude of the impulsive force required to break the adhesion was estimated by AFM. We were able to measure the breaking force for 200 cells within 90 min at maximum, and these data were obtained at 4, 8, 18.5, 21.5, and 24.5 h after coculturing. On the basis of these results, the difference in adhesion maturation among individual cells was discussed. Conclusively, our results suggest that the maturation of adhesion progresses via specific bonds between CADM1s.

Materials and Methods

Mice, cells, and establishment of neurite culture and coculture with mast cells

C57BL/6 and ICR mice were purchased from Japan SLC (Hamamatsu, Japan). Bone-marrow-derived cultured mast cells (BMMCs) from C57BL/6 were established as described elsewhere (37). Neuro2a cells were from the American Type Culture Collection (Rockville, MD).

Neuro2a cells were plated at a density of 4.8 × 10⁴ cells/dish onto glass-bottom culture dishes of 35-mm diameter (μ-Dish, Ibidi, Munich, Germany) coated with matrigel (BD Biosciences, San Jose, CA). They were cultured in glial conditioned medium (MB-X9501, Sumitomo, Tokyo, Japan) containing 40 ng/mL brain-derived neurotrophic factor (R&D Systems, Minneapolis, MN) and 2 μg/mL all-trans retinoic acid (Wako, Tokyo, Japan). After 2 days of culture, when neuro2a cells had extended their neurites enough, the resulting neuron cultures were overlaid with MEM-α medium containing 1.0 × 10⁴ cells/dish BMMCs. After 4–24.5 h of coculture in the presence of 3 ng/mL interleukin 3 (R&D Systems), the dishes were washed twice with Dulbecco’s modified Eagle’s medium to remove nonadherent BMMCs and the remaining cells were then subjected to measurements.

Experimental setup

Microscopic femtosecond laser irradiation system

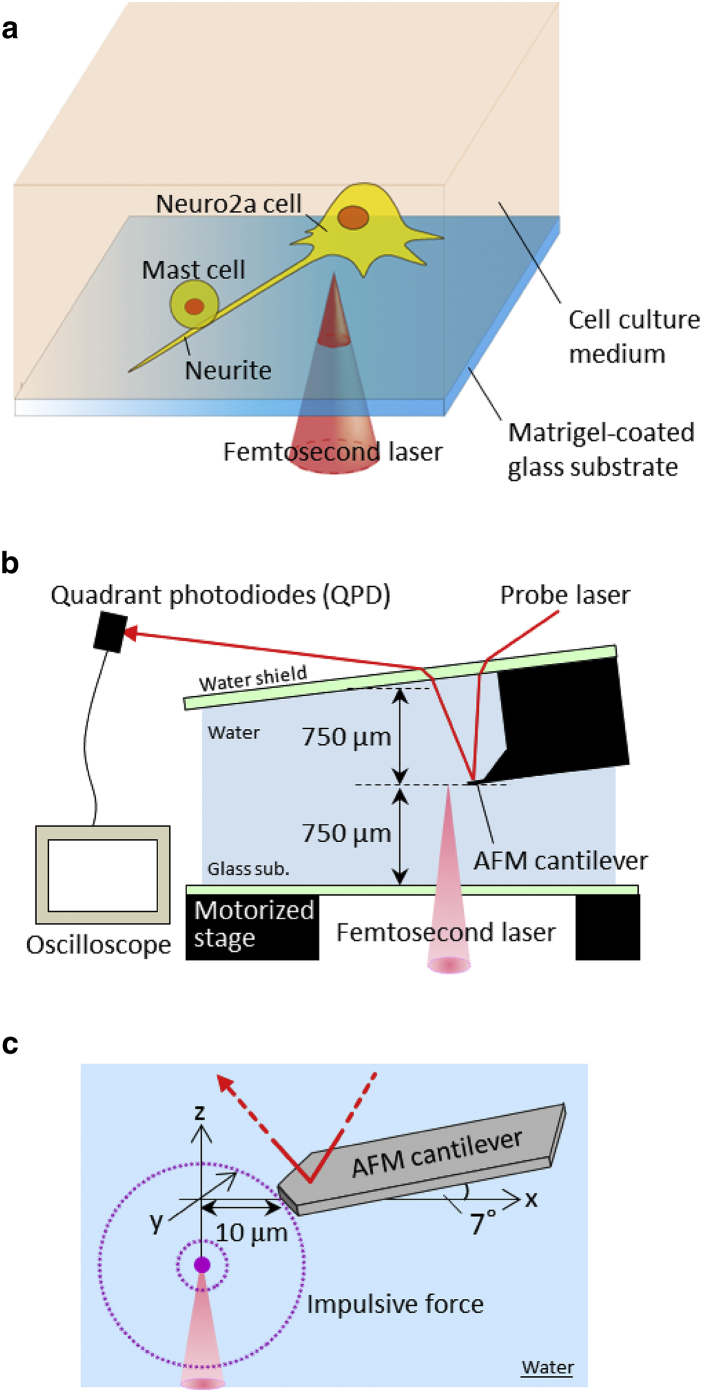
A fundamental pulse (wavelength, 780 nm; pulse duration, 250 fs; pulse repetition, 20 Hz) from a regeneratively amplified Ti:sapphire femtosecond laser system (IFRIT SP-01, Cyber Laser, Tokyo, Japan) was introduced to an inverted microscope (IX-72, Olympus, Tokyo, Japan) on which a coculture system of neurites and mast cells was set as shown in Fig. 1 a. A single pulse was extracted from the pulse train using a mechanical shutter with a gate time of 50 ms. After the pulse energy was tuned by a half-wave plate, polarizers, and a gradational neutral density filter, a single pulse was focused near the targeted cell through a 10× objective lens (NA 0.25; PlanN, Olympus) (Fig. 1 a). The diameter of the focused laser was estimated to be ∼5 μm. To avoid laser ablation of the substrate, the laser focal position in the Z-direction was adjusted to be 30 μm above the image plane by collimator lenses, which were placed before the microscope.

Figure 1.

Experimental setup for estimating the adhesion strength between mast cells and neurites. (a) Schematic spatial relation between a femtosecond laser and a targeted mast cell adhering to a neurite. A matrigel-coated glass substrate was set on the microscope stage. (b) Schematic of the local force measurement system using an AFM. (c) Coordinates in the impulsive-force quantification using the local-force-measurement system. To see this figure in color, go online.

Local-force-measurement system using an AFM

Quantification of the impulsive force was conducted separately from quantification of the adhesion break by setting an AFM head onto the stage of the microscope instead of the coculture system. In this method, the magnitude of the impulsive force is measured from the amplitudes of the oscillation of the cantilever induced by the impulsive force (11).

A tipless AFM cantilever (thickness, 3.80 μm; width, 27 μm; length, 123 μm; spring constant, 35 N/m; resonance frequency, 325 kHz in air) (TL-NCH-10, Nano World, Neuchatel, Switzerland) was magnetically attached to an AFM head (Nano-R2, Pacific Nanotechnology, Santa Clara, CA) and the head was mounted on the stage. By mounting the head, the cantilever was soaked in a water droplet which was put on the glass substrate in advance, as depicted in Fig. 1 b. After the soaking, the top of the cantilever was aligned with the image plane of the microscope by mechanically shifting the cantilever height, and this position was set as Z = 0. The top of the cantilever was then moved to a position 10 μm from the laser focal point by moving the stage (Fig. 1 c).

Transient oscillation of the cantilever, induced by the laser irradiation, was directly detected and monitored by an oscilloscope (DP4104, Tektronix, Beaverton, OR) as the voltage differences between the top- and bottom-side photodiodes of a quadrant photodiode. The signal was converted to the cantilever’s shift with a linear coefficient of 6.5 mV/nm. This coefficient was determined to push the cantilever onto the glass substrate using a piezoelectric motor.

Results

Estimation of the maximum distance to break the adhesion

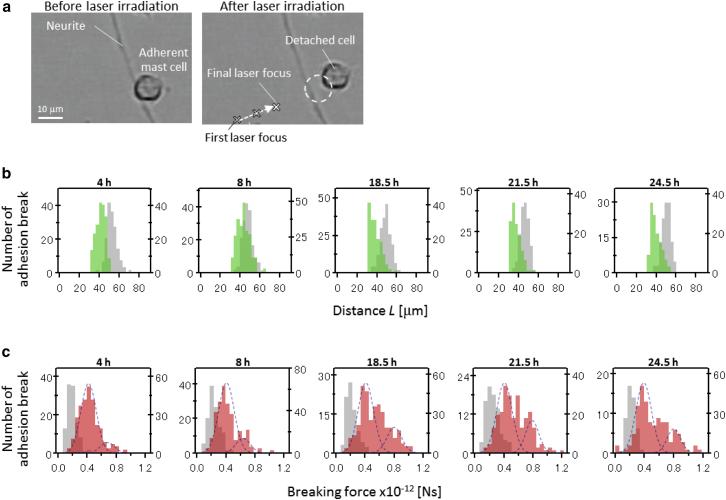
We quantified the adhesion strength as the threshold of the breaking force of the adhesion. The breaking force was first estimated as the distance between the mast cell and the laser focal point when the adhesion was broken. The breaking process was confirmed by real-time CCD images. The threshold of the distances was measured as follows: a laser with an energy of 700 nJ/pulse was initially focused at a position 100 μm from a targeted mast cell. After the first laser shot, the electrical stage was used to move the laser focal point closer to the target in steps of 5 μm until the adhesion was broken, and the distance between the mast cell and the final laser focal position in the XY plane was measured. A representative example is shown in Fig. 2 a. In this case, the adhesion was broken when the distance in the XY plane was 15 μm. Since the laser focal position in the Z-direction was 30 μm above the image plane of the objective lens, the three-dimensional distance was estimated to be 33 μm. This three-dimensional distance was defined as the threshold distance of the breaking, L^th_M-N.

Figure 2.

Statistical evaluation of the adhesion-breaking force between a mast cell and a neurite. (a) Representative result of breaking of the adhesion between a mast cell and neurite. The laser focal point was sequentially moved closer to the mast cell, as indicated by the X marks on the dashed arrow in the photograph at right. (b) Histograms of the threshold distance between the laser focal point and the mast cell to break the adhesion. Green and gray bars indicate individual differences in L^th_N-M and L^th_M-S, respectively. The time on the top of the graph is the coculturing time. (c) Histograms of the adhesion breaking force. Red and gray bars indicate individual differences in F^break_N-M and F^break_M-S, respectively. The threshold distances in (b) were converted to adhesion-breaking forces by Eq. 2, with the same coculturing times as in (b). To see this figure in color, go online.

In the experiment, the individual L^th_M-N values of 100–200 cells were sequentially estimated within 90 min and the data were acquired at 4, 8, 18.5, 21.5, and 24.5 h after the coculturing. The histograms of L^th_M-N are summarized in Fig. 2 b (green bars). Although most of the L^th_M-N values were distributed in the range between 30 and 50 μm throughout the measurements, the peak of the distribution shifted to shorter distance with increasing coculturing time. The decrease in the L^th_M-N values means that the cell adhesion was enhanced with time.

The distance between the laser focal point and the mast cell with nonspecific adhesion on the substrate, L^th_M-S, was also estimated by preparing a culture system in which only BMMCs were cultured on a dish for 4–24.5 h. The results are summarized by the gray bars in the histogram in Fig. 2 b. The L^th_M-S values were distributed between 40 and 60 μm. These values were longer than those for the L^th_M-N (30–50 μm). In addition, the peak of the distribution of L^th_M-S values did not change with time. This means that the breaking force of the nonspecific adhesion was smaller than that of the adhesion between the mast cells and neurites and did not maturate.

Quantification of the impulsive force and force required to break the adhesion

To estimate the breaking force as a mechanical parameter, the impulsive force required to break the adhesion was quantified. The quantification was conducted using AFM (11). In this method, first, the total impulsive force generated at the laser focal point, F₀, was quantified. Next, the impulsive force required to break the adhesion, which propagated from the laser focal point, was calculated from the L^th_M-N (L^th_M-S). The calculated impulsive force was treated as the breaking force between a mast cell and neurite, F^break_M-N (between the mast cell and substrate F^break_M-S).

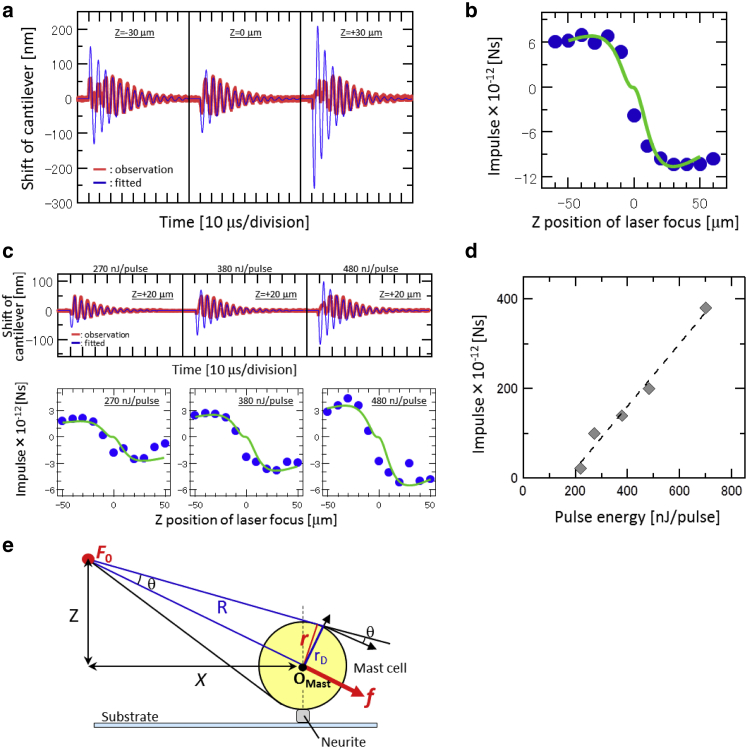
The transient oscillation of the AFM cantilever upon the impulsive force is shown in Fig. 3 a with red lines. As can be seen, the cantilever was oscillated immediately after the laser irradiation in every case. When the pulse was irradiated below (above) the cantilever, it first moved in an upward (downward) direction as shown in the left (right) graph of Fig. 3 a. This means that the cantilever was pushed by the impulsive force immediately after the laser irradiation.

Figure 3.

Quantification of the impulsive force required to break the adhesion. (a) Representative oscillations of the AFM cantilever upon the impulsive force. Red and blue solid lines are observation and fitting results, respectively, calculated by Eq. 1. (b) Z-position dependence of F_AFM. Blue solid circles are estimated from the fitting of the cantilever oscillation by Eq. 1. The green solid line is calculated from the geometrical model between the AFM cantilever and the laser focal point (see (13)), from which the total impulsive force at the laser focal point F₀ was estimated. (c) Representative oscillations of the AFM cantilever (top graphs) and Z-position dependence of F_AFM (bottom graphs) in the conditions with pulse energies of 270, 380, and 480 nJ/pulse. (d) Pulse-energy dependence of the quantified impulse F₀. (e) Geometrical model used to estimate the adhesion-breaking force between mast cell and neurite. On the basis of this model and F₀ in (b), the impulsive force required to break the adhesion was quantified as shown in Eq. 2. To see this figure in color, go online.

Assuming the force loaded on the cantilever could be approximated as an impulse (F × δ(t)), the oscillation was expressed by

$$Y\left(t\right)=\frac{{\omega }^2+{\alpha }^2}{\omega }\frac{F_{\text{AFM}}}{k}{e}^{-\alpha \times t}\times \text{sin}\left(\omega \times t\right),$$ (1)

where F_AFM is the impulse loaded on the cantilever (the integral of the force with respect to time (Ns)) and ω, a, and k are the angular velocity, damping constant, and spring constant of the cantilever, respectively. Although a simple damping oscillation is predicted in the equation, an irregular vibration was observed at the early stage of the experimental data collection. The irregularity can be interpreted as follows: 1) the time evolution of the impulsive force was not a simple impulse; 2) the bending modes of the cantilever, except for the fundamental mode with frequency ω, were simultaneously excited and interfered with each other; or 3) the amplitude of the oscillation was out of the detection range of the quadrant photodiode. As an approximation assuming that the influence of these phenomena is minimized by extrapolating the former vibration by the latter oscillation, least-squares fitting by Eq. 1 was performed for the experimental data. The fitted results are shown by the blue lines in Fig. 3 a. In every case, oscillations later than 30 μs were well-fitted. The damping constant and the oscillation frequency were hardly dependent on the laser focal point in the Z-direction, though only F_AFM was considerably changed with the Z-position.

Fig. 3 b shows the Z-position dependence of F_AFM. The Z-position dependence of F_AFM was calculated based on a spatial relationship between the cantilever and the laser focal point and fitted to the experimental data (Fig. 3 b, green line). The detailed procedure has been described in a previous study (13); we followed this procedure with F_0, which was proportional to the amplitude of the curve, being the only variable parameter in the fitting. The shape of the curve was determined by spatial constants with the relationship between the cantilever and the laser focal point. The fitting results were as accurate as those in our previous work (13). The estimated F₀ with a pulse energy of 700 nJ/pulse was 3.80 × 10⁻¹⁰ (Ns).

The pulse energy in this work significantly differed from that in previous research (12, 13). A threefold-higher pulse energy was needed to break the adhesion between the neurite and the mast cell. Furthermore, in this work, we selected an objective lens differing from that in previous work on the basis of measurement condition optimization results. Although a good fitting result was obtained, as indicated in Fig. 3 b, the reliability of our estimation in this study was further checked from the pulse-energy dependence of the impulsive force. As shown in the top graphs in Fig. 3 c, irregular vibration of the AFM cantilever was enhanced with an increase in pulse energy. The analysis by Eq. 1, in which the irregularity was neglected, indicated that the amplitude of the oscillations (F_AFM) increased with the pulse energy, as indicated by the blue lines in Fig. 3 c. From the Z-position dependence of F_AFM (Fig. 3 c, bottom graphs), F₀ for each pulse energy was estimated and plotted against the pulse energy (Fig. 3 d). From Fig. 3 i, we confirmed that F₀ increased proportionally with the pulse energy between 220 and 700 nJ/pulse. This linearly increasing dependency is quite similar to that previously reported (12).

In addition to the quantification, the breaking force of the adhesion between mast cells and neurites was estimated based on F₀. The spatial relationship between the mast cell and the laser focal point is indicated in Fig. 3 e. From this model, L^th_M-N in Fig. 2 b is converted to a force threshold to detach the mast cell from the neurite (F^break_M-N) by

$$F_{\text{M}\text{-}\text{N}}^{\text{break}}=F_0\times \frac{r^2}{4\pi {\left(L_{\text{M}\text{-}\text{N}}^{\text{th}}\right)}^2},$$ (2)

where r is the radius of the mast cell, with an average of 4.5 μm. In the calculation, each L^th_N-M constructing histograms in Fig. 2 b was individually converted to F^break_M-N, where r is not the average radius but the individual radius measured from captured images. The converted F^break_M-N was sorted and summarized as new histograms (Fig. 2 c, red bars). Thus, the shape of the histograms in Fig. 2 c does not simply correspond to those in Fig. 2 b. The L^th_M-S in Fig. 2 b was also converted to the force threshold to detach the mast cell from the substrate (F^break_M-S) in the same manner and summarized as histograms (Fig. 2 c, gray bars). The F^break_M-N and F^break_M-S would reflect the adhesion strength between the mast cell and the neurite and that between the mast cell and the substrate, respectively. The histograms were analyzed using a Gaussian approximation, because we considered that the specific and nonspecific adhesions could be in a continuous independent probability distribution.

Discussion

Reliability of the estimation of the breaking force

In this investigation, the pulse energy was a critical parameter in obtaining a reliable L^th_M-N. When the pulse energy was low, meaning the impulsive force was weak, some of the adhesions were not broken, even though the laser focal point contacted the edge of the targeted cells. Conversely, when we used high pulse energy, generating an intense impulsive force, many of the adhesions were broken by the first shot, even though the laser focal point was far enough from the targeted cell. In this case, it is difficult to determine L^th_M-N. We therefore explored the pulse energy that would best allow us to clearly estimate the distance.

We found that the most suitable pulse energy was in the range 650–700 nJ/pulse. In this range, throughout the measurement period, almost all of the adhesions were not broken by the first laser shot but were broken in the distances to be reliably estimated. In all the other ranges examined, the L^th_M-N was difficult to determine for the reasons mentioned above. In particular, when a laser shot with a pulse energy >700 nJ/pulse was used, the neurites were often destroyed. In the reliable range, the use of a more intense pulse energy could shorten the time required for breaking, since fewer loadings of the impulsive force were needed before the break. Therefore, the pulse energy was tuned to 700 nJ/pulse and this value was maintained throughout the measurements.

Since the pulse energy of 700 nJ/pulse was over three times higher than that used in previous studies, obvious irregular vibration of the AFM cantilever was induced, as shown in Fig. 3 b. As a result of the analysis by extrapolation using the latter regular vibration, the linearly increasing dependency of the impulsive force was confirmed in the pulse energy ranging from 220 to 700 nJ/pulse (Fig. 3 d). The dependency is quite similar to that previously reported (12). It is known that a pulse with extremely high energy leads the nonlinear absorption to the saturation point because of the absence of ground-state molecules at the laser focal point, and the excited molecules, which are excited by single-photon absorption, dominate the absorption (38, 39). Considering this phenomenon, the linearly increasing dependency in Fig. 3 d is reasonable, suggesting that the analysis using simple extrapolation is reliable in this study.

Maturation process between the neurites and mast cells

The adhesion between the neurites and mast cells was considered to be formed by specific bonds between CADM1 molecules (24, 26, 27, 28), which exist on the cell membrane of both neurites and mast cells. In addition, because the nonspecific adhesion due to electrostatic interaction would not be negligible, the contribution of the nonspecific bonds was also evaluated as F^break_M-S. The distribution of F^break_M-S values could be approximated by a single Gaussian profile with a peak at 0.2 × 10⁻¹² Ns, and it was almost constant throughout the measurement period (Fig. 2 c). On the other hand, the distribution of F^break_M-N values was dynamically changed with the coculturing time. An increase of F^break_M-N represented an enhancement of the adhesion strength between the mast cell and neurite. The distribution of F^break_M-N values at 4 h is nearly indicated as a single Gaussian profile with a peak at 0.4 × 10⁻¹² Ns, which is about two times larger than that of F^break_M-S (0.2 × 10⁻¹² Ns). After 8 h, although the peak at 0.4× 10⁻¹² Ns remained, a distribution with a peak at 0.8 × 10⁻¹² Ns seemed to increase relatively with time. The bimodal distribution with peaks at 0.4 × 10⁻¹² Ns and 0.8 × 10⁻¹² Ns was almost the same after 18.5 h. From these analyses, we found that 1) the adhesion maturation does not occur in all of the mast cells adhering on the neurite; and 2) the adhesion has two stable states before and after the adhesion maturation.

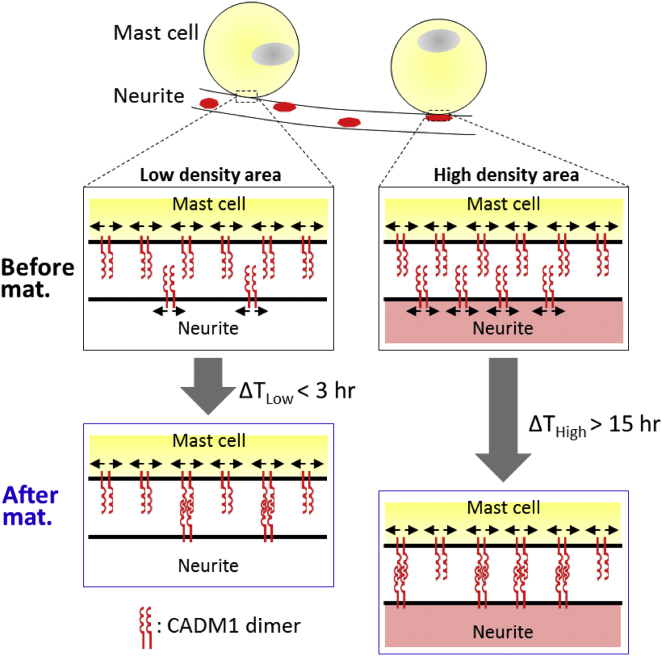
This fact indicates that the density of CADM1s on the neurite may be inhomogeneous, as shown in Fig. 4. After the mast cell contacts the neurite, the connection between CADM1s on the mast cell and neurite would be made during migration of CADM1s on their membranes due to fluidity of the membrane. When the density of CADM1s on the neurite is sufficiently lower than that on the mast cell (Fig. 4, left), the CADM1 on the neurite would be able to find easily the counter-CADM1 on the mast cell. In this case, the adhesion is matured immediately after contact. In contrast, with increasing density of the CADM1s on the neurite (Fig. 4, right), it would take a long time to complete the formation of binding pairs of CADM1s between the neurite and the mast cell, because the probability of CADM1s on the neurite meeting those on the mast cell in the two-dimensional area of the interface of the cellular membranes would decrease with the decreasing residual number of CADM1s without binding in the maturation process. The bimodal distribution of the adhesion strength can be explained by the presence of two different areas on the neurite, one with high and one with low density of CADM1s. The existence of inhomogeneity of the distribution of CADM1s has been suggested by Hagiyama et al. (36).

Figure 4.

Schematic presentation of the adhesion maturation process of mast cells on neurites with an inhomogeneous distribution of CADM1s. To see this figure in color, go online.

It is known that adhesion by CADM1s plays a role in the signal transduction between nerve and mast cells. Hagiyama et al. reported that the frequency of signal-transduction detection was ∼40% in their study (36). This percentage was similar to that of the cells indicating the higher breaking force (0.8 × 10⁻¹² Ns), which is estimated to be 30–40% (Fig. 2 c). In addition, the authors reported that the signal transduction was observed after overnight coculturing (∼14 h), although it was not observed immediately after coculturing (<3 h). This time evolution was also quite similar to that of enhancement of the adhesion strength. These facts suggest that the signal transduction occurs only in the cell pairs with maturation, which leads to the enhancement of interaction between the cell membranes.

Conclusion

Our results presented in this study indicate that a femtosecond-laser-induced impulsive force can be used to estimate the adhesion strength between a targeted single mast cell and a neurite of a neuro2a cell with a high frequency of >100 cells/h. Using this method, we first evaluate the adhesion strength as a statistical time-course datum. The statistical view indicates the adhesion maturation process and inhomogeneous distribution of CADM1s. In addition, these results suggest that maturation enhances the interaction between the membranes and the signal transduction between the neurite and the mast cell. Although we focused on the maturation process between the mast cell and the neurite in this work, this method would be available for several kinds of statistical analysis of adhesion between small biological objects that could be viewed under a microscope. For example, we have applied the method to evaluate the adhesion strength between chloroplasts and peroxisomes within plant cells and its light dependence (40). Wide application of this method is thus anticipated in both animal and plant cells.

Author Contributions

T.I. and Y.H. designed the research. T.F. and A.I. supervised the research and contributed to preparation of the cell. T.I. and M.H. performed the experiments. T.I. and Y.H. analyzed data. All authors contributed data interpretation. T.I and Y.H. wrote the article.

Editor: Elsa Yan.