Antagonistic Behaviors of NMY-1 and NMY-2 Maintain Ring Channels in the C. elegans Gonad

Abstract

Contractile rings play critical roles in a number of biological processes, including oogenesis, wound healing, and cytokinesis. In many cases, the activity of motor proteins such as nonmuscle myosins is required for appropriate constriction of these contractile rings. In the gonad of the nematode worm Caenorhabditis elegans, ring channels are a specialized form of contractile ring that are maintained at a constant diameter before oogenesis. We propose a model of ring channel maintenance that explicitly incorporates force generation by motor proteins that can act normally or tangentially to the ring channel opening. We find that both modes of force generation are needed to maintain the ring channels. We demonstrate experimentally that the type II myosins NMY-1 and NMY-2 antagonize each other in the ring channels by producing force in perpendicular directions: the experimental depletion of NMY-1/theoretical decrease in orthogonal force allows premature ring constriction and cellularization, whereas the experimental depletion of NMY-2/theoretical decrease in tangential force opens the ring channels and prevents cellularization. Together, our experimental and theoretical results show that both forces, mediated by NMY-1 and NMY-2, are crucial for maintaining the appropriate ring channel diameter and dynamics throughout the gonad.

Introduction

Cells use many types of channels to communicate between intra- and extracellular environments, and each has a specific function. These channels might transport particular molecules or serve as a conduit for bulk cytoplasm to be shared between cells. Cell-cell communication, which can be mediated by these channels, plays a critical role during development in many organisms. In this study, we focus on the mechanism of ring channel dynamics in the reproductive system of the nematode worm Caenorhabditis elegans because of its highly predictable development pattern (1, 2, 3). Ring channels, which allow for passage of material into developing oocytes, are formed through incomplete cellularization during oogenesis. The ring channel opening is maintained by the activity of motor proteins, which hydrolyze ATP to move along a substrate (e.g., actin filaments) to generate mechanical force.

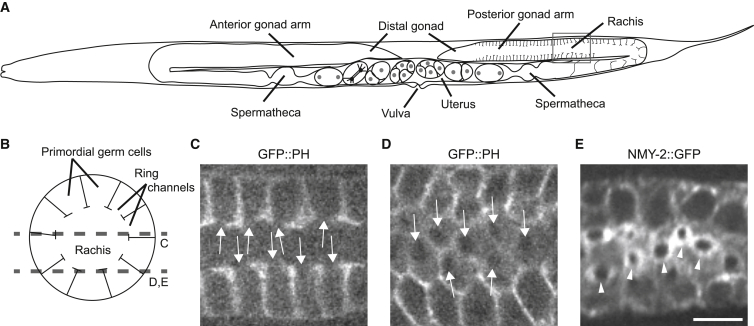
C. elegans hermaphrodites self-fertilize via two U-shaped gonad arms that produce sperm and oocytes (3, 4, 5) (Fig. 1 A). The hermaphrodite gonad makes sperm during the fourth larval stage and stores them in the spermatheca, where they will later fertilize the mature oocytes. From early adulthood, the gonad produces oocytes in a sequential manner as nuclei move from distal to proximal through the gonad arm toward the spermatheca (4). At the distal tip, mitosis generates nuclei that migrate to the periphery of the tube-shaped gonad, where lateral membrane growth separates the nuclei from each other as they enter meiosis. These separated nuclei, called germ cells, do not completely cellularize, and instead share a common cytoplasm through the ring channels where they are connected to the central core, or rachis (Fig. 1, A–C). The cells enlarge as they proceed around the bend in the gonad arm in preparation for oogenesis. The ring channels close as the oocytes mature at the proximal end of the gonad arm, severing the connection to the rachis.

Figure 1.

C. elegans adult hermaphrodite reproductive system. (A) Schematic representation of the adult worm’s reproductive organs, with cellular membranes drawn only in the posterior gonad arm. The gray box shows the region of the gonad in (B)–(E). (B) Schematic drawing of a cross section through the gonad, showing the approximate locations of the single imaging planes in the micrographs from live worms (C–E). (C) The view through the middle of the gonad of the membrane marker GFP::PH shows the ring channels as openings (arrows). (D and E) Direct view of ring channel openings of the membrane marker GFP::PH (D, arrows) and NMY-2::GFP rings (E, arrowheads). Scale bar, 5 μm (applies to all three micrographs).

In many organisms, connections between developing germ cells and extracellular environments enable the production of large, nutrient- and protein-rich oocytes in a relatively short amount of time (6, 7, 8). For instance, in the fruit fly, Drosophila melanogaster, nurse cells contribute to the developing oocyte via stable cytoplasmic bridges called ring canals. The canals are initially formed by incomplete cytokinesis, which leaves a hole ∼0.5 μm in diameter. Later structural components, such as septins, replace contractile-ring components and stabilize the canals with a diameter of ∼10 μm (6, 9). As mentioned above, cells in the C. elegans gonad are connected to the rachis by ring channels. These channels are also formed by a cytokinesis-like mechanism, utilizing contractile-ring proteins such as actin (10), formin CYK-1 (11, 12), anillin ANI-2 (13), and nonmuscle myosin NMY-2 (14). Unlike the ring canals in Drosophila, the ring channels in C. elegans, once formed, maintain a constant diameter throughout most of the distal gonad. During the process of oocyte maturation, the cells will either undergo cell death or reach the region where the ring channels will close. Because C. elegans ring channels close in the proximal gonad to form oocytes, the mechanism of maintenance must be reversible. To reversibly maintain a constant diameter, the ring channels may generate active forces that prevent closure until the appropriate time.

C. elegans expresses two nonmuscle type II myosins, NMY-1 and NMY-2, and they share a single regulatory light chain, MLC-4. All three proteins are required for the viability of developing C. elegans embryos (15, 16, 17). NMY-2 not only participates in cytokinesis (17, 18) but also affects germline development (14). Sterility and severe disruption of gonad morphology result from knocking down nmy-2 expression by RNA-mediated genetic interference (RNAi) (14, 19, 20, 21, 22). NMY-2 localizes to the growing lateral membranes that separate the nuclei in the distal gonad (14) and to ring channels (Fig. 1 E). Both NMY-1 and NMY-2 function in embryo elongation, regulated by Rho-binding kinase LET-502, myosin phosphatase MEL-11, and MLC-4 (17, 23). Although NMY-1 is not involved in cytokinesis (18), little is known about its role or localization in adult worms. Thus, we investigated whether NMY-1 could contribute force for ring channel maintenance in the adult gonad.

Ring channels and other contractile-ring structures share qualitatively similar features, and a number of theoretical models have been proposed to study wound healing, cytokinesis, and related multicellular processes. Experimental investigations of wound healing have mainly focused on the role of myosin-II and cytoskeletal polymers such as actin filaments and microtubules (24, 25), and their regulation by biochemical factors such as the small G proteins (26). Theoretical models of wound healing have mainly focused on biochemical regulation without explicitly incorporating the mechanical aspects of myosin contraction (26). Cytokinesis has been extensively explored in both the experimental and theoretical literature. Previous models of cytokinesis have explicitly taken into account the contractile activity of myosin-II (27, 28, 29, 30, 31). However, these models focused exclusively on the tangential motor activity of myosin-II without considering other motor proteins that could be acting in addition to the contractile force generated by myosin-II. In this study, we investigate the effect of motor proteins that may produce orthogonally directed forces, and how the balance of these motor proteins might regulate the rate of closure of ring channel openings, potentially yielding insights into the mechanical properties of similar structures such as contractile rings in wound healing and cytokinesis.

To investigate the role of motor proteins in ring channel maintenance, we develop a two-dimensional (2D) partial differential equation model that takes into account force directed tangentially and normally to the ring channel opening. By exploiting the circular geometry of the ring channel, we are able to reduce the model to a one-dimensional (1D) ordinary differential equation that is analytically tractable under certain assumptions. We use this model to demonstrate the need for both types of forces to maintain the ring channel opening, and we predict the phenotypes that will result in vivo if the force-generating proteins are partially depleted. To test the model predictions, we use RNAi against nmy-1 and nmy-2, to investigate the mechanism of ring channel maintenance in the C. elegans gonad. We identify NMY-1 as the active force that prevents premature ring channel closure in the distal gonad. This combined experimental and theoretical approach allows us to dissect the different force-generating capacities of NMY-1 and NMY-2, and demonstrate, to our knowledge, a novel function for NMY-1 in ring channel maintenance during oogenesis.

Mathematical model

Model derivation

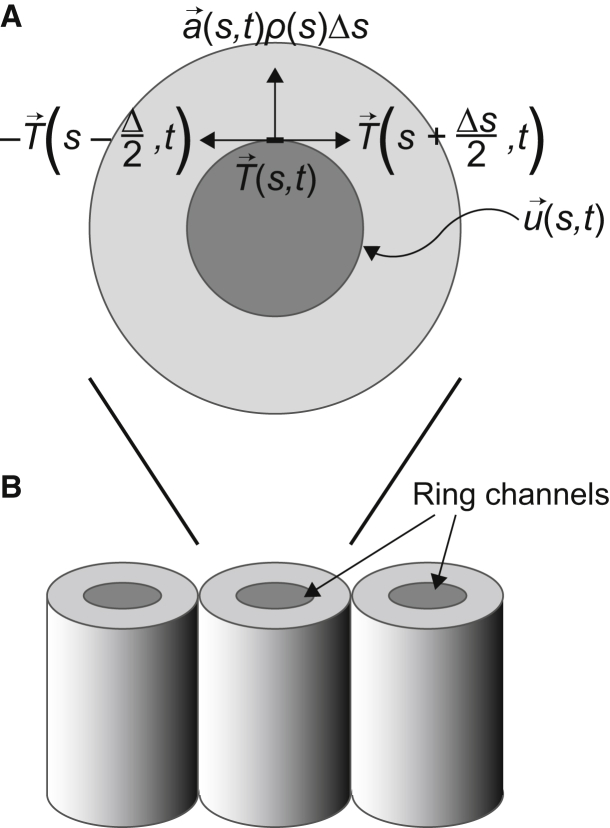
To study ring channel dynamics, we propose the following general model of force acting on a circular opening (see (32, 33, 34) for a similar approach). In brief, the curve representing the ring channel opening is parameterized according to its central angle, s, and we use the variable $\overrightarrow{u}$, which varies with respect to angle s and time t, to describe the evolution of the ring channel opening (Fig. 2 A). Taking advantage of the radial symmetry of the ring channel opening, the (x, y) coordinates of the ring channel opening are

$$\overrightarrow{u}\left(s,t\right)=\left[\begin{array}{c}r\left(t\right)\text{cos}\left(s\right)\\ r\left(t\right)\text{sin}\left(s\right)\end{array}\right],0\le s<2\pi .$$ (1)

Table 1 lists all of the parameters used for analysis and simulations in this work. We assume the ring channel is embedded in an infinite domain and thus we can ignore any potential boundary effects from the cell edge.

Figure 2.

Free body diagram of forces acting on the ring channel opening. (A) Top view of the forces acting on the ring channel. (B) Side view of primordial germ cells on one side of the gonad, represented as cylinders with circular openings at the top.

Table 1.

Model Parameters: Eq. 5

Parameter	Definition	Range	Value Used	Source
ρ	line density of material at the ring channel opening	1–2 pg/μm3	1–2 pg/μm3	(45)
r0	initial ring channel radius	1–2 μm	1 μm	this study
η	viscous resistance of actin meshwork	1–100 kPa·s = 1–100 × 1012 pg/μm·s	1 × 1012 pg/μm·s	(46, 47)
kc	force generator spring constant	1–100 × 109 pg/s2 = 1–100 pN/μm	5 × 109 pg/s2	(48, 49, 50, 51)
mc	line density of tangential force generators	200–300/μm	250/μm	(30, 42, 43)
fn	force generated per molecule	1–10 × 109 pg·μm/s2 = 1–10 pN	5 × 109 pg·μm/s2	(49, 52, 53)
mn	line density of normal force generators	200–300/μm	250/μm	(30, 42, 43)
ai, i = n, c	time of half max of protein reduction due to RNAi	30,000–50,000 s	40,000 s	(57), this study

To model the evolution of the ring channel, consider a small segment corresponding to the angle Δs (Fig. 2). The line density of material at the opening is denoted by ρ(s), which, for simplicity in the model, we assume to be constant (ρ(s) = ρ). We model two types of forces that act orthogonally to each other: contact forces and body forces. Contact forces, denoted by $\overrightarrow{T}\left(s,t\right)$, take into account active contraction forces acting on the ring channel and always act tangentially to the curve of interest. In contrast, body forces, denoted by $\overrightarrow{a}\left(s,t\right)$, act normal to the curve and thus normal to the contact forces. For simplicity, we assume the body of the cell is not generating any independent forces. We apply Newton’s second law to write the force-balance equation for this segment of the curve and pass to the limit as $\Delta s\to 0$ to arrive at the following second-order partial differential equation:

$$\rho {\overrightarrow{u}}_{tt}=\frac{\partial }{\partial s}\left(\overrightarrow{T}\left(s,t\right)\right)+\overrightarrow{a}\left(s,t\right),$$ (2)

which describes the evolution of the ring channel opening with respect to angle and time.

Focusing strictly on the activity of motor proteins interacting with the actin meshwork, we can write the contact forces, which act tangentially to the curve, as $\overrightarrow{T}\left(s,t\right)=T\left(s,t\right)\left({\overrightarrow{u}}_s/\Vert {\overrightarrow{u}}_s\Vert \right)$. We assume the ring channel has contractile and viscous properties, and we write the tension force as $T\left(s,t\right)=C\left(t\right)\Vert {\overrightarrow{u}}_s\Vert +\eta \left(d\Vert {\overrightarrow{u}}_s\Vert /dt\right)$, where C(t) represents active contractility (this parameter may depend on local concentrations of force generators and may vary with time, but remains consistent around the opening; Fig. 1 E). η, the magnitude of viscous resistance, is assumed to be independent of force generators and reflects the resistance of the actin meshwork to stretching and shrinking. We assume the normal body force is homogeneous around the ring channel opening so that it applies the same force everywhere, and we write the body force term as $a\left(s,t\right)\hat{n}\left(s,t\right)=a\left(t\right)\hat{n}\left(s,t\right)$. We also assume the body forces are due only to motor protein activity in the actin meshwork, since membrane resistance to stretching and shrinking is low compared with the actin meshwork (35, 36, 37, 38).

The contact and body-force terms are analogous to the line and surface tensions used to describe the radius of curvature of contractile cells (39). In (39), the radius of curvature was expressed as $R=\lambda /\sigma$, where λ is the effective line tension that is directly affected by contractility, and σ is the bulk surface tension. Although our terms are defined similarly, this previous investigation required the contractile cells to be pinned at specific points, allowing the contractile cell to exert force against the fixed points. Our approach does not require fixed points, and tracks stretching and shrinking events around the ring channel. Our model also incorporates the possible effect of motor proteins on the normally directed body-force term. We further assume that tension due to active contraction is constant since the contraction force is proportional to the number of myosin motors (40, 41), and in other circular contractile structures, such as cytokinetic rings, there is little variance in myosin concentration over time (30, 42, 43).

Under these assumptions, we can now write Eq. 2 as

$$\rho {\overrightarrow{u}}_{tt}={\left(C\left(t\right)\Vert {\overrightarrow{u}}_s\Vert +\eta \frac{d\Vert {\overrightarrow{u}}_s\Vert }{dt}\right)}_s\frac{{\overrightarrow{u}}_s}{\Vert {\overrightarrow{u}}_s\Vert }+a\left(t\right)\hat{n}\left(s,t\right).$$ (3)

For the initial conditions, we assume the ring channel has an initial radius of r₀ and the opening is not given any initial impulses:

$$\overrightarrow{u}\left(s,0\right)=\left[\begin{array}{c}{r}_0\text{cos}\left(s\right)\\ r_0\text{sin}\left(s\right)\end{array}\right],{\overrightarrow{u}}_t\left(s,0\right)=0.$$ (4)

We impose periodic boundary conditions to reflect the circular shape of the opening: $\overrightarrow{u}\left(0,t\right)=\overrightarrow{u}\left(2\pi ,t\right)$.

Writing Eq. 3 using Eq. 1 and noting the linear independence of sin and cos, we can express the evolution in time of the ring channel opening with the following ordinary differential equation:

$$\rho r^{″}\left(t\right)=-C\left(t\right)r\left(t\right)-\eta r^{\prime }\left(t\right)+a\left(t\right),$$ (5)

with the initial conditions

$$r\left(0\right)=r_0,r^{\prime }\left(0\right)=0.$$ (6)

The parameter ρ is small compared with the other parameters used in this investigation (Table 1). If we consider the case $\rho \to 0$, this results in a singular perturbation problem (44) that can be solved by construction of fast- and slow-timescale solutions. For the sake of generality, we include ρ in our calculations.

To incorporate the activity of motor proteins into the ring channel dynamics, we assume that active contraction $C\left(t\right)$ can be modeled as the product of the spring constant associated with the force generators, k_c, and the number of tangential force-generating proteins around the circumference of the ring channel, $m_c\left(t\right)$, so that $C\left(t\right)=k_c{m}_c\left(t\right)$. For the body force, we assume this can be modeled as the product of the force generated by a motor protein, $f_n$, and the number of normal force-generating proteins around the circumference of the ring channel, $m_n\left(t\right)$, so that $a\left(t\right)=f_n{m}_n\left(t\right)$.

Equation 5 is an inhomogeneous, damped, simple harmonic oscillator. For biological realism, we do not allow oscillatory solutions and require the model to be critically damped or overdamped. In other words, the model coefficients must satisfy $\left({\eta }^2/{\rho }^2\right)-4\left(C\left(t\right)/\rho \right)=\left({\eta }^2/{\rho }^2\right)-4\left(k_c{m}_c\left(t\right)/\rho \right)>0$. For the parameters given in Table 1, this condition is satisfied.

For a linear stability analysis and simulations with time-dependent motor protein densities, we transform the second-order ODE into a system of coupled first-order ODEs:

$$\{\begin{array}{l}{r}^{\prime }\left(t\right)=q\left(t\right)\\ q^{\prime }\left(t\right)=-\frac{1}{\rho }{k}_c{m}_c\left(t\right)r\left(t\right)-\frac{\eta }{\rho }q\left(t\right)+\frac{f_n{m}_n\left(t\right)}{\rho }\end{array}.$$ (7)

Numerical simulations of Eq. 7 were performed with the software package XPPAUT (http://www.math.pitt.edu/∼bard/xpp/xpp.html) using the Backward Euler solver.

Model parameters

The model contains a number of parameters, some of which can be estimated from the literature. The parameters and their definitions and ranges of values are given in Table 1. At a minimum, all parameters are assumed to be positive constants. For simplicity, and in the absence of more specific information, we assume the linear density of material at the ring channel opening, ρ, is similar to that reported at the level of a single cell (45), where we consider the ring channel to extend 1 μm into the cell. The initial radius of the ring channel is measured in this study (see Fig. 7). The viscous resistance of the actin meshwork, η, has been reported elsewhere for other systems and we assume the same values are relevant here (46, 47, 48). Ranges for the spring constant, $k_c$, and force generated per myosin molecule, $f_n$, have been previously reported ($k_c$ (48, 49, 50, 51), $f_n$ (49, 52, 53)). Since NMY-1 and NMY-2 are both type II myosins, we assume the properties of spring constants and force generation are identical for these two motor proteins. To determine the line density of tangential and normal directed force-generating proteins, we assume the number of motor proteins per micron around the circumference of the ring channel is similar to that observed in other contractile structures (30, 42, 43). We assume this line density is similar for both the tangential and normal force-generating proteins. The model is robust against parameter variation: changes in the order of magnitude of all parameters do not qualitatively change the behavior of the model provided we remain in the overdamped regime of Eq. 5.

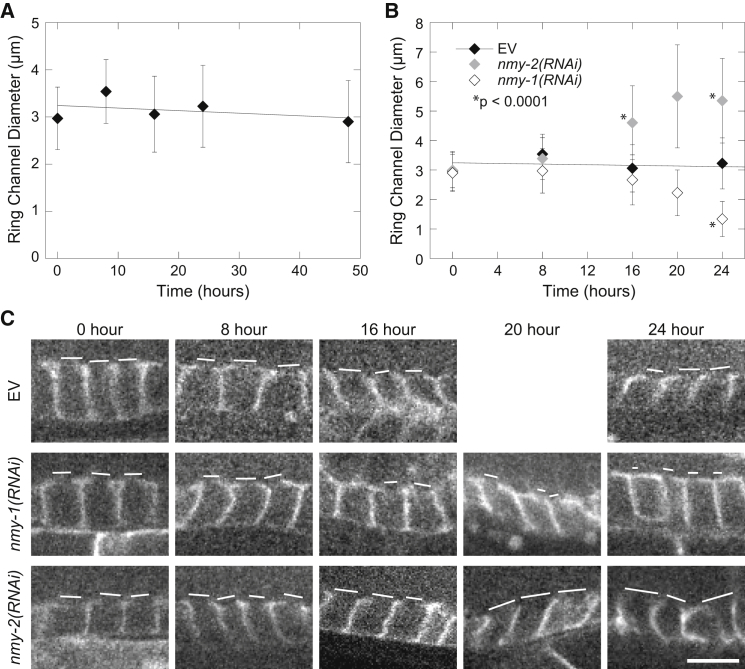
Figure 7.

Partial depletion of NMY-1 and NMY-2 results in phenotypes similar to model predictions. (A) Ring channel diameters do not change during an empty vector RNAi treatment time course. The graph of ring channel opening diameters (mean ± SD) shows that the size is maintained as the worms age (0–24 h) and is similar to that observed in asynchronous worms (48 h; n > 10 ring channels from at least two worms for each time point). (B) Graph of ring channel diameters (mean ± SD) during gradual depletion of type-II myosins NMY-1 (white diamonds) and NMY-2 (gray diamonds) by RNAi treatment for the times indicated. EV is the empty vector control, which results in no depletion of protein (black diamonds, line). EV data were repeated for 0–24 h from (A); n > 50 ring channels from at least seven worms for 8–24 h myosin RNAi; 0 h data are from independent experiments (n > 40 ring channels from at least four worms). (C) Fluorescent micrographs of representative sections of gonad for each treatment and time point. GFP::PH marks the membranes of primordial germ cells. All images are oriented with the rachis at the top, showing a single focal plane at the maximum diameter of the opening for the cells in view. The measured ring channel openings are indicated for clarity (white bars). The scale bar at bottom right applies to all of the images and is 5 μm in length.

Materials and Methods

Nematode strains and genetic methods

OD58 (ltIs38[pAA1; pie-1::GFP::PH(PLC1delta1) + unc-119(+)]) and JJ1473 (unc-119(ed3) III; zuIs45 [nmy-2::NMY-2::GFP + unc-119(+)] V) strains were provided by the Caenorhabditis Genetics Center, which is funded by the Office of Research Infrastructure Programs, National Institutes of Health (P40 OD010440), and were maintained on nematode growth media agar plates seeded with OP50 Escherichia coli as a food source. Strain stocks were maintained at 20°C by chunking or picking worms as needed, and also stored at −80°C according to standard practices (54, 55).

RNAi was performed by feeding as described previously (16). Briefly, the worms were fed an HT115 E. coli strain expressing small RNA sequences from the gene to be knocked down. Sequences were verified by sequencing the expression plasmids and performing a BLAST search to ensure that they were specific to the gene of interest. Standard RNAi treatments of 48 h were used to assess the effect on gonads lacking the genes that were knocked down (Fig. 3). For 48 h RNAi treatments, worms were chunked from a 3-day-old plate with no OP50 E. coli remaining. Partial knockdown was achieved by shorter incubation of worms on HT115 E. coli (see Fig. 7). For shorter RNAi time-course experiments, fertile OD58 hermaphrodite adults were bleached to release eggs and the plates were kept at 20°C for 3 days. After 3 days, late L4 (the final larval stage before adult) worms were transferred to bacteria-free plates, allowed to crawl around to rid themselves of OP50 E. coli, and then transferred to plates containing RNAi bacteria for the indicated time frames. Thus, 0–24 h RNAi time courses had similarly aged worms for each treatment. The empty vector control showed that the ring channel diameters in the area we measured did not change as the worms aged (see Fig. 7 A). Although we did not directly measure protein abundance after RNAi treatment, the partial RNAi phenotypes were consistent with the 48 h knockdowns after 16–24 h, indicating that the treatment had taken effect.

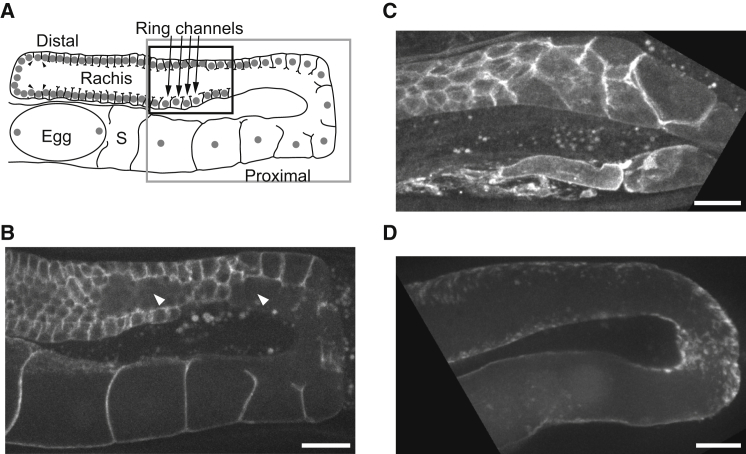
Figure 3.

NMY-1 and NMY-2 affect cellularization in the C. elegans hermaphrodite gonad. (A) Schematic of a cross section of one side of a wild-type hermaphrodite gonad, showing the U-shape with distal and proximal ends, nuclei (gray dots), lateral membrane growth (arrowheads), the central shared cytoplasm (rachis), the spermatheca (S), and a fertilized egg. Sperm, located in the spermatheca, are omitted for clarity. The region near the bend (gray box) is shown in subsequent micrographs. The region at the rachis opening (black box) was used for ring channel (arrows) measurements throughout this work. (B–D) Fluorescent micrographs of GFP::PH, a membrane marker, expressed in wild-type gonads treated with RNAi for 48 h. (B) Empty vector RNAi control treatment: maximum projection of three Z-sections spaced at 1.5 μm. The well-formed rachis is visible in two locations (arrowheads; n = 8). (C) nmy-1(RNAi) treatment: maximum projection of three Z-sections spaced at 1.5 μm, showing premature cellularization and lack of a rachis (n = 9). (D) nmy-2(RNAi) treatment: maximum projection of 10 Z-sections spaced at 1.5 μm, showing a complete lack of membranous structures and loss of cellularization (n = 11). Scale bars, 10 μm.

Indirect immunofluorescence

Indirect immunofluorescence of C. elegans gonads was performed using an adapted tissue-extrusion method based on that described by Crittenden et al. (56). Briefly, 10–15 young adult hermaphrodites of the strain expressing NMY-2::GFP were placed on a poly-L-lysine-coated coverslip in 5 μL of 0.25 mM levamisole (in M9 medium) to immobilize the worms. The heads or tails of the worms were sliced off using a 25 gauge syringe needle, which caused the gonads and intestines to extrude from the body cavities. After extrusion, excess liquid was removed with a drawn-out Pasteur pipette and specimens were fixed for 10–15 min in 1% formaldehyde (16% solution, methanol-free; 28906; Thermo Scientific, Waltham, MA) diluted in phosphate-buffered saline (137 mM NaCl; 2.7 mM KCl; 10 mM Na₂HPO₄; 1.8 mM KH₂PO₄). After fixation, the specimens were incubated for 5 min in TBSB (0.5% (w/v) bovine serum albumin in Tris-buffered saline: 50 mM Tris-Cl; 150 mM NaCl; pH 7.6) supplemented with 0.1% Triton X-100 to permeabilize the gonads. The samples were washed twice with TBSB and then incubated in TBSB for 30 min.

Rabbit anti-NMY-1 primary antibody (a gift from Dr. Alisa Piekny, Concordia University) (23) was diluted 1:200 in blocking buffer (3% bovine serum albumin; 0.1% Triton X-100 in phosphate-buffered saline). Fixed worms were incubated with primary antibodies at room temperature for 2 h 40 min and then washed three times for 15 min each in TBSB. Goat anti-rabbit IgG ATTO 594-conjugated (611-155-122; Rockland, Limerick, PA) secondary antibody was diluted 1:5000 in blocking buffer. Samples were incubated with secondary antibodies at room temperature for 2 h and then washed three times for 15 min each in TBSB. After the last wash, excess liquid was removed with a drawn-out Pasteur pipette, and 8 μL of SlowFade Gold antifade reagent with DAPI (S36938; Life Technologies, Waltham, MA) was added. Coverslips with mounting medium were inverted onto a slide and sealed with nail polish. Imaging was carried out within 3 days after the slides were made.

Microscopy and image analysis

Microscopy images were taken using a 60×/1.4 NA Plan-Apo objective lens (Nikon, Melville, NY) on a spinning-disk confocal microscope (UltraVIEW Vox CSUX1 system; PerkinElmer, Waltham, MA) with 405-, 440-, 488-, 515-, and 561-nm solid-state lasers and a back-thinned EMCCD camera (Hamamatsu Photonics, Bridgewater, NJ) on a Ti-E inverted microscope (Nikon) without binning. Live RNAi-treated worms were immobilized on a 5% agar pad (in egg salts buffer: 118 mM NaCl; 48 mM KCl; 2 mM MgCl₂; 2 mM CaCl₂; 0.025 mM HEPES, pH 7.4) and a coverslip was added and sealed with petrolatum (S80117; Fisher, Waltham, MA). Z-stacks were taken with 0.5–1.5 μm spacing, spanning 40 μm centered on the mid-plane of the gonad. Generally, one gonad arm was imaged per worm, as the intestine usually blocked the other side. For indirect immunofluorescence imaging, Z-stacks were taken with 0.5 μm spacing spanning 30 μm centered on the mid-plane of the extruded gonads.

Images were analyzed using ImageJ (National Institutes of Health, Bethesda, MD) and MATLAB (The MathWorks, Natick, MA) software. The maximum-intensity projections shown in the figures were made in ImageJ. Measurements of ring channel openings were done in the single best-focus plane for each cell expressing GFP::PH. Multiple in-focus cells in the region at the rachis opening (black box, Fig. 3) were measured in each image. Because we had no control over the orientation of the gonad with respect to the imaging planes, only those cells that appeared to be in focus were included in the measurements. As a result, the measured diameters should be very close to the actual diameters of the ring channels, with a slight possibility for the data to be biased in the smaller direction. This slight bias would affect all experimental conditions similarly, and would show up as variation well within the standard deviations of our measurements. A line-scan measurement across each ring channel opening recorded the position and intensity of each pixel. The line scans were analyzed using custom MATLAB code to find the largest gap in membrane-GFP (GFP::PH) intensity. A pixel was considered part of the gap if its intensity was <55% of the difference between the minimum and maximum for each line scan.

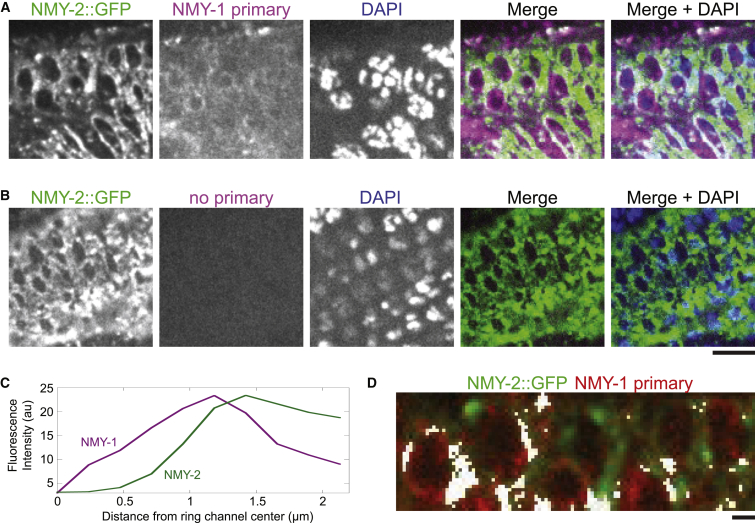
Analysis of the NMY-1 and NMY-2 localization in the immunofluorescence images was performed using a segmented line (10 pixels wide) drawn around each ring channel. The line was straightened and a plot profile was obtained for the entire region from the center of the ring channel toward the outside for each fluorescence channel. The average of nine ring channels is shown in Fig. 4 C, and each is consistent with the relationship seen in the average. To determine the level of colocalization, a region of interest with preserved ring channel morphology was selected by hand, and the fluorescence levels were normalized in both channels so that the values ranged from 0 to 255. Colocalization analysis in the scaled images was performed using the ImageJ plugin Colocalization Threshold (http://wwwfacilities.uhnresearch.ca/wcif/software/Plugins/colocalisation_threshold.html).

Figure 4.

NMY-1 localizes near NMY-2::GFP ring channels. (A) NMY-2::GFP gonads were extruded and stained with an antibody to NMY-1. DAPI stains DNA. The localization of NMY-1 was consistent in multiple gonads (n = 8). (B) A control gonad to which only the secondary antibody was added reveals that no gonad structures are labeled in the absence of NMY-1 antibody (n = 6). Scale bar, 5 μm. The view shown here is similar to the NMY-2::GFP live imaging (Fig. 1E), although the ring channels appear a bit stretched as a result of the gonad extrusion method. (C) Plot profile of NMY-1 and NMY-2 signal intensities in ring channels as measured from the center of the opening outward. (D) Colocalization threshold image, showing an overlap (white) between NMY-1 and NMY-2 in a cropped and rotated region of the image shown in (A). Scale bar, 1 μm. To see this figure in color, go online.

Results

Experimental evidence of NMY-1 and NMY-2 activity and localization in the gonad

To characterize the ring channel morphology under different conditions, we used RNAi against NMY-1 and NMY-2. When wild-type worms are fed bacteria expressing RNA sequences from a gene of interest, RNAi silences the gene within 48 h (21). A control treatment using an empty RNA expression vector yielded wild-type gonad membrane structures (Fig. 3 B). After complete knockdown of the type II myosin motor protein, NMY-2 (48 h of RNAi), the hermaphrodite gonad lost all cellularization, similar to what was reported in a previous study (14) (Fig. 3 D). In contrast, RNAi to knock down a different type II myosin motor protein, NMY-1, caused premature cellularization in the distal gonad (Fig. 3 C). These data suggest that NMY-1 and NMY-2 have antagonistic activities within the gonad, specifically with respect to cellularization.

NMY-2::GFP localized to ring channel openings as a ring (Fig. 1 E). Using a fixation method that would preserve GFP expression, we stained NMY-2::GFP-expressing gonads with antibodies to NMY-1 (Fig. 4). The gonad structure was stained by a primary antibody against NMY-1, which revealed that NMY-1 localized to a region just inside the NMY-2::GFP ring (Fig. 4, A and C). The Manders thresholded coefficients are ∼0.3 for both channels, indicating that for pixels above the threshold, 30% of the pixels corresponding to NMY-1 overlap with NMY-2, and vice versa. In terms of image volume, ∼8% of the pixels in the image are overlapping (Fig. 4 D, overlapping pixels shown in white). The NMY-2::GFP rings in the fixed gonads are similar to those in live worms (compare Fig. 1 E and Fig. 4 A). In a control experiment without the primary antibody, the secondary antibody did not label any structures in the gonad (Fig. 4 B). Thus, the localization of NMY-1 to a ring just inside the NMY-2 ring is not an artifact of secondary antibody staining alone.

The mathematical model shows that a balance of tangential and normal forces is needed to maintain the ring channel opening

We first consider the case of constant densities of motor proteins around the ring channel opening. That is, we assume the proteins that are responsible for generating the tangential and normal forces to the ring channel opening are constant in time: $m_c\left(t\right)=m_c,m_n\left(t\right)=m_n$. With this assumption of constant motor proteins, we can explicitly solve Eq. 5 with initial conditions given by Eq. 6:

$$r\left(t\right)=-\frac{\left(f_n{m}_n-k_c{m}_c{r}_0\right)}{2k_c{m}_c\left({\eta }^2-4k_c{m}_c\rho \right)}\left(e^{\frac{\left(-\eta +\sqrt{{\eta }^2-4k_c{m}_c\rho }\right)t}{2\rho }}\left({\eta }^2-4k_c{m}_c\rho +\eta \sqrt{{\eta }^2-4k_c{m}_c\rho }\right)+e^{\frac{\left(-\eta -\sqrt{{\eta }^2-4k_c{m}_c\rho }\right)t}{2\rho }}\left({\eta }^2-4k_c{m}_c\rho -\eta \sqrt{{\eta }^2-4k_c{m}_c\rho }\right)\right)+\frac{f_n{m}_n}{k_c{m}_c}.$$ (8)

For physically reasonable solutions, we require r(t) to be real valued, so we impose the constraint ${\eta }^2-4k_c{m}_c\rho >0$. Note that this inequality is identical to the condition for the model to be in the overdamped regime, and is satisfied by the parameters in Table 1.

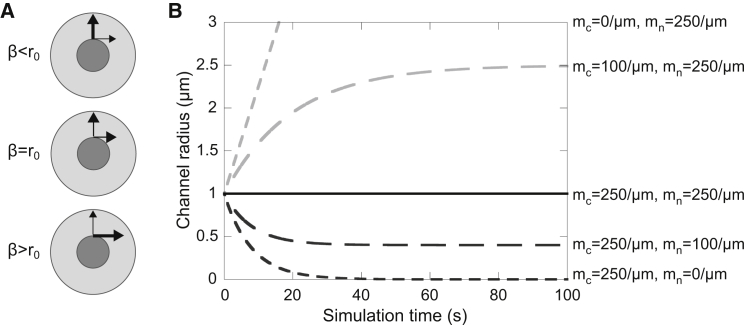
As discussed above, NMY-2 is believed to exert force in a tangential direction to the opening of a wound or a cytokinetic ring. If we assume that NMY-1 acts in a similar manner, then we only have force acting tangentially to the ring channel opening with no body forces: $m_c\ne 0,m_n=0$. Using the general solution (Eq. 8), we find that $r\left(t\right)\to 0$ as $t\to \infty$ under these conditions, meaning that the radius of the ring channel is strictly decreasing as t increases (Fig. 5 B). This suggests that when NMY-1 and NMY-2 act tangentially, the ring channel opening cannot be maintained and will continue to constrict until closure occurs, similar to the case with a cytokinetic ring.

Figure 5.

(A and B) Schematic of forces (A) and a plot of the ring channel radius (B) when the motor protein density is assumed to be constant over time. The ring channel radius r(t) tends to $\beta =\left(f_n{m}_n/k_c{m}_c\right)$ as $t\to \infty$ when $m_c\ne 0$; r₀ refers to the ring channel radius in its reference configuration (Table 1). Greater force exerted normal to the opening results in expansion of the ring channel (light gray dotted and dashed lines), whereas greater force exerted tangential to the opening results in constriction of the ring channel (dark gray dotted and dashed lines). The ring channel can be maintained at a nonzero radius provided there is a balance between tangential and normal forces. The time course plotted here was obtained using Eq. 8 with the parameter values given in Table 1.

We next considered the case in which there are only normal forces, with no forces acting tangential to the opening: $m_c=0,m_n\ne 0$. Since Eq. 8 is undefined in this case, we solve Eq. 5 with $m_c=0$ to find

$$r\left(t\right)=\frac{1}{\eta }\left(\frac{\rho f_n{m}_n}{\eta }\left(e^{-\eta t/\rho }-1\right)+f_n{m}_{n}t+r_0\eta \right)\Rightarrow r^{\prime }\left(t\right)=\frac{f_n{m}_n}{\eta }\left(1-e^{-\eta t/\rho }\right).$$ (9)

Since $r^{\prime }\left(t\right)>0$ for $t>0$, then $r\left(t\right)\to \infty$ as $t\to \infty$, and the radius of the ring channel grows without bound (Fig. 5 B). Note that since the ring channel is embedded in an infinite domain, there is no maximum radius the ring channel can assume.

These results suggest that to maintain the ring channel opening at a constant radius, we must have a balance of tangential and normal forces: $m_c\ne 0,m_n\ne 0$. Using Eq. 8 and as illustrated in Fig. 5, we find that the ring channel radius tends to β as $t\to \infty$, where $\beta =\left(f_n{m}_n/k_c{m}_c\right)$. Increasing the density of normal-acting motor proteins $\left(m_n\right)$ or decreasing the density of tangential motor proteins $\left(m_c\right)$ results in an increase in the ring channel radius, whereas decreasing the density of normal motor proteins $\left(m_n\right)$ or increasing the density of tangential motor proteins $\left(m_c\right)$ results in a decrease in the ring channel radius (Fig. 5).

A steady-state analysis of Eq. 7 when $m_c\ne 0,m_n\ne 0$ confirms that this equilibrium is a stable node: the system has strictly real valued, negative eigenvalues. This suggests that under normal developmental conditions, the balance of motor protein activity must be tightly regulated to ensure that the ring channels maintain an appropriate radius. In particular, there must be motor proteins acting both tangentially and normally to the ring channel opening to allow for constriction while preventing premature closure.

The mathematical model indicates that a gradual depletion of force generators yields opposite phenotypes

Since 48 h experimental depletion of the motor proteins NMY-1 and NMY-2, which localize to the ring channel, yielded opposite phenotypes, we next wished to simulate the effect of a gradual depletion of normal and tangential force-generating proteins, similar to the gradual protein depletion associated with RNAi experiments (57). We assume the time courses of $m_n\left(t\right)$ and $m_c\left(t\right)$ are monotonically decreasing, positive-valued functions of time. For the purposes of simulation, we multiply the density of motor proteins by the following function:

$${\delta }_j\left(t\right)=\frac{a_j}{a_j+t},\text{where}j=n,c.$$ (10)

Based on protein quantification during RNAi (57), we choose a_j = 40,000 s.

When we numerically deplete one force generator at a time while keeping the other constant, we see opposite phenotypes. The three cases (Fig. 6) are as follows:

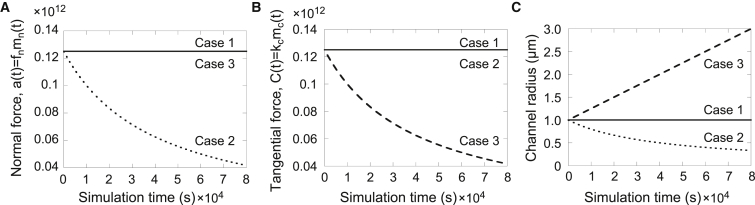
• Case 1: $m_n\left(t\right)=m_n,m_c\left(t\right)=m_c$; control, no depletion.

• Case 2: $m_n\left(t\right)=m_n{a}_n/\left(a_n+t\right),m_c\left(t\right)=m_c$; gradual depletion of the normal force generator.

• Case 3: $m_n\left(t\right)=m_n,m_c\left(t\right)=m_c{a}_c/\left(a_c+t\right)$; gradual depletion of the tangential force generator.

Figure 6.

Gradual depletion of tangential or normal force-generating proteins in the mathematical model shows opposite phenotypes. (A) Graphical representation of the level of normal force generator over time in each of three cases. (B) Graphical representation of the level of tangential force generator over time in each of three cases. (C) Changes in channel radius over time (case 1: control, no depletion of either protein; case 2: depletion of normal force generator; case 3: depletion of tangential force generator). Depletion of normal force-generating proteins results in constriction of the ring channel opening, whereas depletion of tangential force-generating proteins results in expansion of the ring channel, consistent with earlier results (Fig. 5). Numerical solutions were calculated using Eq. 7. Parameters are listed in Table 1. The normal force a(t) has units pg·μm/s², and the tangential force C(t) has units pg/s².

The values of m_n, m_c, a_n, and a_c are reported in Table 1.

With time-dependent motor protein densities, we no longer have a closed-form analytic solution, so to determine the time course for changes in the ring channel opening, we simulate Eq. 7. As shown in Fig. 6, a gradual depletion of the normal force generator (case 2) results in a decrease in the ring channel radius, whereas a gradual depletion of the tangential force generator (case 3) results in an increase in the ring channel radius. These time-dependent results are consistent with our investigation regarding the constant density of normal and tangential force-generating motor proteins (Fig. 5).

Although we assume a Michaelis-Menten-type form for the function in cases 2 and 3, the results are unchanged by using other decreasing, nonnegative functions. Varying the parameters a_n and a_c does not qualitatively change the behavior of the solutions.

Taken together, these results suggest the following testable hypothesis: if depletion of a target protein by RNAi results in an increase in the ring channel radius, that protein is likely exerting force tangential to the ring channel opening, whereas if the RNAi treatment results in a decrease in the ring channel opening, the target protein is likely exerting force normal to the opening.

Experimental partial depletion of NMY-1 and NMY-2 is consistent with model predictions of normally and tangentially directed force-generating proteins

To determine whether NMY-1 and NMY-2 antagonistically regulate ring channel maintenance, we gradually depleted each one in RNAi time-course experiments (58). To ensure that changes in the gonad during aging did not account for changes in the ring channels, we controlled for age in our experiments (see Materials and Methods; Fig. 7 A). By 16 h, treatment against NMY-2 resulted in significantly larger ring channel diameters compared with the empty vector control, in which no protein was depleted (Fig. 7, B and C). By 24 h, treatment against NMY-1 resulted in significantly smaller ring channel diameters compared with the empty vector control (Fig. 7, B and C), consistent with the premature cellularization phenotype at 48 h (Fig. 3 C). A 20-h time point for NMY-1 and NMY-2 depletion was added to refine the shape of the curve. Although we did not directly observe protein levels in these worms, the results are consistent with gradual depletion of tangential (NMY-2) and normal (NMY-1) force generators in our model. Together with our model, these data indicate that NMY-2 might generate force tangential to the ring channel opening, similarly to its role in contractile ring constriction during cytokinesis (27, 28, 29, 30), whereas NMY-1 might generate force normal to the opening.

Discussion

The assumed tangential activity of type-II myosins in cytokinesis is based on electron microscopy data from numerous organisms showing that the orientation of actin filaments in the contractile ring is predominantly tangential (59, 60, 61, 62, 63, 64). Because myosin motors move directionally on actin filaments, the orientation of actin filaments dictates the orientation of the force produced by myosin. We find, to our knowledge, a novel direction of force generation in C. elegans ring channels produced by NMY-1 that maintains the ring channel openings in the region of the distal gonad surrounding the rachis. Thus, actin filaments in the primordial germ cells must orient circumferentially in the ring, but might also radiate outward like spokes. In fission yeast and animal cells, actin filaments that are assembled outside of contractile rings are drawn in toward the ring in a perpendicular orientation and can incorporate into the ring in a parallel orientation (65, 66, 67, 68, 69, 70, 71). The perpendicular filaments might be stabilized in some contractile networks (71), as our data suggest for ring channels.

In contrast to the ring channel opening, contractile rings typically close all the way either with consistent dynamics (72, 73) or in two phases (31, 42, 72, 74). The rate of closure has not been specifically attributed to the amount of force available from myosin-II. For example, in Schizosaccharomyces pombe the concentration of myosin increases during ring constriction (43), but the rate of constriction remains constant (73). The rate of actin filament polymerization or depolymerization might also play a significant role in the rate of closure (42, 73, 75). In some cell types, perpendicular actin/myosin could regulate the timing of ring constriction, perhaps to coordinate with formation of the extracellular matrix or other events. S. pombe has two type-II myosins involved in contractile ring constriction: Myo2 is important for ring assembly and constriction, whereas Myp2 is recruited later, before ring constriction (76, 77, 78). However, these two myosins work cooperatively to constrict the ring instead of antagonizing each other (79). It is possible that septum formation during fission yeast cytokinesis, which is lacking in C. elegans gonads, could provide some force counteracting ring closure to regulate the timing.

The experimental and theoretical results presented here apply specifically to the stage of ring channel maintenance and do not apply to ring channel formation or closure. By considering only ring channel maintenance, we can exploit the geometry of the ring channel to reduce our model to a second-order ODE. The activity of both type-II myosins must be regulated to coordinate these ring channel events along the gonad. NMY-2, together with the UNC-45 myosin chaperone, is critical for lateral membrane assembly and ring channel closure (14), but the role of NMY-1 at these stages is unknown. It is unclear what affect an orthogonal force might have on lateral membrane assembly, but according to our model, the activity of NMY-1 could prevent ring closure in the proximal gonad. Thus, due to the connectedness of the gonad structure, a mechanism might exist to localize or activate NMY-1 exclusively in the region where the ring channels remain open. Alternatively, closure might occur by increasing the activity of NMY-2 relative to NMY-1 so that the ring channels can close (Fig. 5). Investigation of the localization dynamics of NMY-1 and NMY-2 in the ring channels throughout the gonad will allow us to distinguish between these possibilities.

Although the in vivo behavior of NMY-1 and NMY-2 depletion is consistent with the tangentially and normally directed forces predicted by the model, the evidence for these particular roles is indirect. It is possible that other motor proteins not considered here contribute to either the tangential or normal forces involved in ring channel maintenance in vivo. We rely on the radial symmetry of material in the ring channel, although small variations in motor protein density could cause an asymmetric contraction of the ring channel, and might be a factor in the asymmetric contraction seen during C. elegans embryonic cytokinesis (80). We have also neglected any potential roles of the cell geometry of the developing oocytes, and any dynamics that might be mediated by cytoplasmic flow in the rachis. Future theoretical and experimental investigations will address these deficiencies.

The distinct but overlapping localization of NMY-1 and NMY-2 in the ring channels (Fig. 4) suggests that these two myosins might exclude one another from certain areas of the actin meshwork at the ring. It is unknown how they might accomplish this exclusion, but it is consistent with their unique functions: NMY-1 must localize to and pull on perpendicular filaments, whereas NMY-2 must localize to and pull on parallel filaments. The actin filaments must be part of the same network, connected by actin cross-linking proteins to exert force in both directions on the ring. Future work will focus on the mechanism of this exclusive behavior within a single actin filament network.

In this investigation, we experimentally tested the response of the ring channel to depletion of nonmuscle myosins and found that the activity of NMY-1 is consistent with a normally directed force, which, to our knowledge, is a previously unreported functional role. The generality of the theoretical approach makes it a suitable modeling framework for investigating the activity of motor proteins in other biological contexts.

Author Contributions

V.C.C. designed and performed experiments, analyzed data and model results, and wrote the manuscript. T.M.K. designed and performed preliminary experiments. D.B.P. designed experiments and edited the manuscript. A.T.D. designed and implemented the mathematical model, analyzed model results, designed experiments, and wrote the manuscript.

Editor: David Odde.