Resolving Non‐Specific and Specific Adhesive Interactions of Catechols at Solid/Liquid Interfaces at the Molecular Scale

Abstract

The adhesive system of mussels evolved into a powerful and adaptive system with affinity to a wide range of surfaces. It is widely known that thereby 3,4‐dihydroxyphenylalanine (Dopa) plays a central role. However underlying binding energies remain unknown at the single molecular scale. Here, we use single‐molecule force spectroscopy to estimate binding energies of single catechols with a large range of opposing chemical functionalities. Our data demonstrate significant interactions of Dopa with all functionalities, yet most interactions fall within the medium–strong range of 10–20 k _B T. Only bidentate binding to TiO₂ surfaces exhibits a higher binding energy of 29 k _B T. Our data also demonstrate at the single‐molecule level that oxidized Dopa and amines exhibit interaction energies in the range of covalent bonds, confirming the important role of Dopa for cross‐linking in the bulk mussel adhesive. We anticipate that our approach and data will further advance the understanding of biologic and technologic adhesives.

Marine mussels spend their lifetime in the tidal, nutrient‐rich seawater where they can attach to any available surface while withstanding strong currents in high salt concentration and wet environment. Therefore mussels developed a complex adhesive system providing adhesion to rocks or biofilm‐covered surfaces with remarkable efficiency.1 The mussel feet consist of a variety of proteins fulfilling different functions but share one important attribute: Abundance on the modified amino acid 3,4‐dihydroxyphenylalanine (Dopa).2 In particular the proteins located at the foot/substrate interface contain a significant amount of Dopa and mediate strong adhesion.2b

Both surface forces apparatus (SFA)2b, 3 and single‐molecule force spectroscopy (SM‐AFM)4 experiments indicated that Dopa adheres well to metal‐oxide surfaces by bidentate H‐bonding and metal coordination.3a, 5 In particular, Lee et al.4a immobilized single, Dopa‐terminated molecules on AFM tips and quantified their adhesion forces and interaction kinetics with titania surfaces. Using Bell–Evans theory,6 an approximate binding energy of 37 k _B T per Dopa was estimated. Moreover Yu et al.3a demonstrated that natural surfaces are usually covered with organic films, which will alter the interaction type and energy of Dopa binding to those surfaces.

Here, we uniquely quantify at the single molecular scale how Dopa molecules bind to both, inorganic and organic functionalities, which is essential to further understand and technologically use molecular principles of mussel adhesives. In particular, recent advances allow to directly measure energy landscapes of single‐molecule unbinding at interfaces using SM‐AFM. In particular, Raman et al.7 used Jarzynski's equality8 (JE) to unravel the equilibrated binding energy of single molecules sticking to an AFM tip through acid–base interactions. In the present study we aim to quantify the binding energy between a single, Dopa‐terminated molecule and various differently functionalized AFM tips.

Figure 1 shows the experimental model for studying interactions of single Dopa units with various surfaces. We immobilize Dopa on a polymer chain with a contour length L _C≈6.7 nm. The basis for anchoring Dopa is a thiol‐based, mixed self‐assembled monolayer (SAM) consisting of COOH‐ and OH‐terminated thiols in a 1/500 ratio. Further modification is carried out by functionalization of the free COOH group (see the Supporting Information). The 1/500 dilution of carboxylic acid groups and consequently of immobilized Dopa, is essential to probe single Dopa interactions, rather than interactions involving multiple molecules. This surface is facing functionalized/modified AFM tips providing various interaction partners for Dopa. Using SAMs as well the AFM tip is modified with OH, NH₂, COOH or alkyl‐based surface functionalities, respectively. In addition, unmodified gold and titania‐coated AFM tips are used (the preparation can be found in the Supporting Information).

Figure 1.

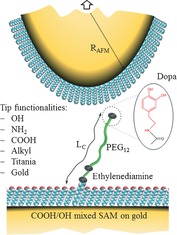
Experimental model system to study the interaction of Dopa with different surfaces on a single molecular level (cf. text for details).

Figure 2 A depicts a measured force trajectory showing a single molecular event. The example shows Dopa interacting with an NH₂‐modified AFM tip at pH 4.2, where Dopa is reduced to the 1,2‐hydroquinone. All other measured interactions of Dopa are shown in the Supporting Information (Figures S3–S5). The red curve represents the force signal while the AFM tip approaches the surface. An attractive force is visible which can be fit using DLVO‐theory (solid black line; see the Supporting Information). Upon retraction of the tip (green curve) a primary adhesive minimum at around 1 nm distance is visible. This minimum is due to the integral interaction of the AFM tip with the modified surface representing background adhesion. Also, a second pronounced adhesive minimum can be seen in Figure 2 A. This minimum is attributed to stretching of a polymer chain linking AFM tip and extended surface because of specific bond formation. Once this bond breaks at the breaking force F _B, the force drops to zero. Force–distance curves exhibiting this characteristic single‐molecular feature are collected for analysis, if the following conditions are fulfilled: (1) A single rupture event is visible at D<L _C≈6.7 nm, and (2) the force–distance characteristics obey the wormlike chain (WLC) model describing the stretching of a single polymer molecule with the expected contour and persistence length9 (WLC fit, see the Supporting Information). These criteria are satisfied for about 2–5 % of the recorded force curves.

Figure 2.

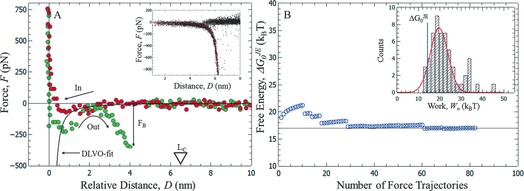
A) Force–distance curve showing a single molecular rupture event of Dopa interacting with an NH₂‐functionalized AFM tip at pH 4.2. The inset shows all detected single molecular rupture events aligned to the WLC model (red solid line). B) Convergence of the calculated interaction free energy using JE [Eq. (1)] for a particular loading rate. Inset: Distribution of measured work values.

All collected single‐molecular events are aligned to a WLC model (solid red line in inset of Figure 2 A) giving a physically meaningful dataset where the pulling starts at zero distance and time7 (inset of Figure 2 A). In order to estimate the free energy for the observed single molecular unbinding we use a recently established approach7, 10 which is based on Jarzynski's non‐equilibrium work theorem (JE) given in Equation (1):8

$$\mathrm{e}\mathrm{x}\mathrm{p}\left(-\frac{{\Delta G}_0^{\mathrm{J}\mathrm{E}}}{kT}\right)={⟨\mathrm{e}\mathrm{x}\mathrm{p}\left(-\frac{W_n}{kT}\right)⟩}_n$$ (1)

JE relates the work done in any non‐equilibrium process W_n to the underlying equilibrated free energy $\Delta G_0^{\mathrm{J}\mathrm{E}}$ . Therefore, W_n is exponentially averaged over the number of work trajectories n. For n→∞ this exponential average converges to the exponent of$\Delta G_0^{\mathrm{J}\mathrm{E}}$ . JE has proven useful for unraveling energy landscapes of single molecular unfolding8b, 11 or single‐molecule adhesion at interfaces.7, 10

Here we use JE to estimate binding energies for Dopa adhesion to various surfaces. In our case W_n can be extracted by integration of the characteristic part of each single molecular rupture event (Figure 2 A). Integration of 60–150 characteristic force trajectories results in a work histogram (Inset of Figure 2 B) and application of JE to the measured work distribution provides an estimate for $\Delta G_0^{\mathrm{J}\mathrm{E}}$ . The convergence behavior of $\Delta G_0^{\mathrm{J}\mathrm{E}}$ with the number of averaged work values is shown in Figure 2 B. Typically averaging of around 60–80 force curves yields well‐converged binding energies. For example, in Figure 2 B averaging of approximately 80 work values leads to a converged $\Delta G_0^{\mathrm{J}\mathrm{E}}$ of 17 k _B T for the interaction of Dopa with an amine‐terminated SAM at pH 4.2. Table 1 summarizes all measured binding energies of Dopa with titania‐coated AFM‐tips, gold‐coated AFM‐tips, and tips functionalized with thiol‐based self‐assembled monolayers providing NH₂, COOH, OH, and alkyl headgroups (see Figure S3).

Table 1.

Interaction free energies of Dopa with various surfaces at pH 4.

Surface interacting with Dopa	Interaction free energy [k B T]
titania	29±2
OH‐SAM	16±2
NH2‐SAM	17±1
COOH‐SAM	13±1
alkyl‐SAM	9±1
gold	9±1

All shown binding energies are measured in 5 mm NaCl solution with an adjusted pH of 4.2, which is the local pH during mussel‐foot attachment, and where Dopa is present in a reduced state. Table 1 demonstrates the highly diverse and adaptive interactions of Dopa with chemically very different surfaces. The strongest binding energy of 29 k _B T is measured for the interaction between Dopa and a titania‐coated tip. This is not unexpected since it has been pointed out previously that bidentate H‐bonding and metal coordination leads to strong adhesion between catechols and metal‐oxide surfaces.3a, 5 While our approach only provides equilibrated interaction free energies, insight into the exact binding mechanism is not possible. Interestingly, the value of 29 k _B T is also in good agreement with recent theoretical work, which suggests a bidentate binding mechanism that gives rise to similar Dopa/silica interaction energies of 24 k _B T–38 k _B T.12

Second, SAMs that are able to form hydrogen bonds (OH, NH₂, and COOH‐terminated) with Dopa show comparable binding energies ranging from 13 to 17 k _B T, which is approximately 50 % of the interaction energy of Dopa with titania (Table 1). Remarkably this result shows that Dopa can similarly act as H‐donor and H‐acceptor in a hydrogen bond and also the SAMs surface charge does not seem to influence H‐bond formation. Moreover, it is interesting that the interaction energy of Dopa with SAMs via H‐bonding is half the interaction energy of Dopa interacting with titania. Recently, Yu et al.3a measured similar effects in SFA using proteins containing Dopa that bridge mica and an OH‐SAM coated surface. They argue that bidentate H‐bonding is sterically hindered. Consequently, Dopa possibly interacts with SAM surfaces through a single phenolic H‐bond, the interaction energy of which was calculated to be approximately 14 k _B T.13 This value agrees well with our data. However, other reasons for the observed decrease in Dopa/OH‐SAM binding energy compared to Dopa/titania are possible, such as the lack of metal coordination or increased spacing between neighbor thiols at a highly curved AFM tip compared to flat surfaces.

Third, we measure interaction energies of 9 k _B T for the interaction of Dopa with both, bare gold as well as with alkyl modified gold. In a previous study Weinhold et al.14 pointed out that Dopa interacts with gold surfaces through its phenylene ring. Thereby the attractive interaction may arise from charge transfer or the polarizability of the π‐electron system.14 On the other hand, the interaction between Dopa and an alkyl SAM may arise from hydrophobic interactions as pointed out by Yu et al.3a

These data indicate that a single catechol molecule is able to interact with various surfaces, yet via very different interaction mechanisms involving bidentate H‐bonding and metal coordination (for metal oxides), monodentate H‐bonding (for SAMs providing H‐bonding partners), the electronic properties of the phenylene ring (gold surfaces) and hydrophobic interactions (alkyl SAMs).

It is generally important to note that application of JE can lead to strongly biased interaction energies,15 in particular because of inappropriate sampling of low work events. To estimate biasing we perform a series of control experiments shown in Figures S4 and S5. First, we carry out the described analysis as a function of the bond‐loading rate. Since $\Delta G_0^{\mathrm{J}\mathrm{E}}$ is an equilibrium quantity it should be independent from the probed loading rate while the measured work distribution is expected to broaden. Indeed, we find no pronounced influence of loading rate on $\Delta G_0^{\mathrm{J}\mathrm{E}}$ . Second, the calculated $\Delta G_0^{\mathrm{J}\mathrm{E}}$ exceeds the lowest measured work value by 3–5 k _B T indicating low sensibility to single low work values. Third, as pointed out by Hummer and Szabo16 and Friddle17 the mechanical work stored in the pulling apparatus must be taken into account to extract a correct estimate for ΔG. Here, integrating the mechanical work from the point where pulling starts (F=0) until post‐bond rupture (F=0 again) provides an excellent estimate,7 which is due to the fact that the molecule is not loaded once the integration starts and ends.

While JE provides access to equilibrated interaction energies of single molecular unbinding, SM‐AFM allows probing unbinding pathways and energy barriers using Bell–Evans theory [Eq. (2)].6

$$F_{\mathrm{B}}=\frac{k_{\mathrm{B}}T}{x_{\mathrm{B}}}\log \left(\frac{x_{\mathrm{B}}}{k_{\mathrm{o}\mathrm{f}\mathrm{f}}{k}_{\mathrm{B}}T}\right)+\frac{k_{\mathrm{B}}T}{x_{\mathrm{B}}}\mathrm{l}\mathrm{o}\mathrm{g}\left(L_{\mathrm{R}}\right)$$ (2)

In this theoretical framework the most probable rupture force (F _B) is evaluated as a function of the bond loading rate (L _R) and a logarithmic relation is anticipated and well‐studied.6b The kinetic off‐rate (k _off) characterizes the lifetime of a molecular bond and x _B the transition state distance. As such k _off and x _B represent the energy barrier between a bound and unbound state. The relation between F _B and L _R for the Dopa unbinding from bare gold surfaces and CH₃‐terminted SAMs are shown in Figure 3 A/B3.

Figure 3.

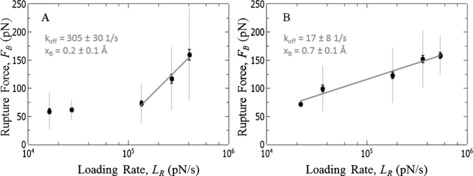
A) Loading rate dependence of the Dopa/gold interaction. B) Loading rate dependence of the interaction between Dopa and a hydrophobic surface (Alkyl‐SAM).

It is now interesting to compare the unbinding kinetics of the Dopa/gold and the Dopa/alkyl‐SAM interaction. Both surfaces exhibited the same interaction energy although the physical nature of the involved interactions may be fundamentally different. In particular, it was argued that bare gold surfaces attract small amounts of organic contaminants easily, leading to measurable hydrophobic properties of gold surfaces.18 In order to exclude that the Dopa/gold interaction is also of hydrophobic nature we can compare their unbinding kinetics.

Figure 3 A reveals the loading rate dependence of the Dopa/gold interaction. Two distinct regimes are visible. At low loading rates we do not observe pronounced loading rate dependence. This is usually attributed to the fact that the molecular bond is probed in a regime close to equilibrium where rebinding is still possible.19 At loading rates of about 10⁵ pN s⁻¹ a second dynamic regime appears where we observe the anticipated logarithmic relation between F _B and L _R indicating an unbinding rate of k _off=305±30 s⁻¹ and a transition state distance of x _B=0.2±0.1 Å. Figure 3 B depicts the loading rate dependence of the Dopa/alkyl‐SAM interaction. In contrast, a single dynamic regime following Bell–Evans model is visible over the entire range of loading rates. For this interaction we find k _off=17±8 s⁻¹ and x _B=0.7±0.1 Å.

Combining the Bell‐Evans analysis and binding energies extracted from JE we can hence unravel mechanistic details. Specifically, the interactions of Dopa with gold or alkyl‐SAMs have comparable binding energies of 9 k _B T but the energy barrier between the two states is fundamentally different. In particular, k _off is almost 18 times smaller for Dopa/alkyl compared to Dopa/gold interactions indicating a higher transition state barrier and hence more stable bond under applied load of the former. Hence two different interaction mechanisms are at work: hydrophobic interactions on CH₃ SAMs, and Pi‐interactions of the Dopa phenylene ring on gold. A Bell–Evans analysis of Dopa interacting with the other surfaces is shown in Figure S6.

The catechol oxidizes in alkaline pH to a quinone.2b The catechol/quinone transformation significantly alters the adhesive properties of Dopa.20 For example, Lee et al.4a speculated that at high pH Dopa and primary amines possibly crosslink to form strong covalent bonds, as assumed by Burzio and Waite21 earlier.

Figure 4 shows the influence of pH on the measured single‐molecule interaction between Dopa and an amine terminated SAM. At pH≈4 we estimate a binding energy of 17 k _B T (see Table 1). If the solution's pH is changed to alkaline values with pH 9, the measured work distribution shifts to significantly higher values of more than 100 k _B T. The inset of Figure 4 B shows all measured rupture events in alkaline pH, which are again aligned to a WLC model. Application of JE leads to a binding energy of 102 k _B T (Figure 4 B). This suggests that Dopa oxidation leads to a condensation with primary amines. The calculated binding energy of 102 k _B T is in the range of a covalent bond, demonstrating that oxidized Dopa—despite its importance for interfacial adhesion—does also play an important role in crosslinking bulk mussel foots. We would like to point out that at pH 9 also the amine is more likely to be neutral compared to pH 4, which is possibly a necessary requirement to initiate a condensation reaction. Here, the estimated $\Delta G_0^{\mathrm{J}\mathrm{E}}$ should be interpreted as an upper bound for the underlying binding energy. Adequate sampling of low‐work events is challenging for very strong interactions, which are probed very far from equilibrium. Moreover, every covalent link within the polymer chain is a candidate for bond rupture leading to additional difficulties assigning the measured interaction free energy to a particular bond. In particular the sulfur–gold bonds that link the SAMs to the substrates seem to be a likely candidate for bond rupture (calculated and measured binding energies range from 62 to 93 k _B T).22 In any case, the results shown in Figure 4 clearly demonstrate that catechol/quinone transformation strongly increases the interaction energy of Dopa with primary amines.

Figure 4.

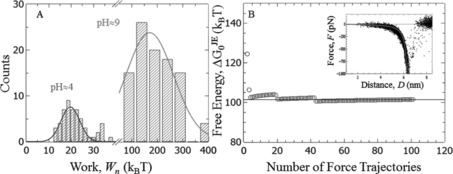
Interaction of Dopa with an amine SAM at different pH. A) Work histograms, B) calculated interaction energy at pH 9. Inset: Force trajectories at pH 9 aligned to the worm‐like‐chain model (solid line).

In summary, we report a unique set of binding energies of a single Dopa interacting with various surfaces. Dopa is able to interact with surfaces exposing different functionalities via different types of interactions ranging from bidentate H‐bonding plus metal coordination (titania), monodentate H‐bonding (SAMs exposing H‐donor or H‐acceptor headgroups), the hydrophobic interaction (alkyl SAM) or interactions involving the π‐electron system of the catechol ring of Dopa (gold).

Our data confirm at the single molecular scale that Dopa adhesion is adaptive allowing mussels to adhere to many different types of substrates (Table 1). We show that bond stability and hence lifetime can vary greatly for interactions exhibiting comparable interaction energies. In particular, the comparison of gold and hydrophobic surfaces demonstrates that the lifetime varies greatly although the binding energy is similar. Hence for interfacial adhesion it is important to take into account kinetic data (unbinding rates) describing the energy barrier between a bound and unbound state.

Also, experimental confirmation of the long‐suspected covalent character of interfacial amine/Dopa bonds suggests new strategies for utilizing Dopa/amine‐based systems for biomedical and adhesive bonding. We also anticipate that our approach and data will further advance the understanding of biologic adhesives as well as technologic adhesive systems. Finally, these data may serve as benchmark for experimental and theoretical work in the field of mussel adhesion.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supplementary

T. Utzig, P. Stock, M. Valtiner, Angew. Chem. Int. Ed. 2016, 55, 9524.