Skip to main content
PMC home page
Wiley Open Access Collection logoLink to Wiley Open Access Collection
. 2016 Sep 17;88(2):328–342. doi: 10.1111/tpj.13290

The impact of mechanical compression on cortical microtubules in Arabidopsis: a quantitative pipeline

Marion Louveaux 1,2, Sébastien Rochette 3, Léna Beauzamy 1,2, Arezki Boudaoud 1,2, Olivier Hamant 1,2,✉
PMCID: PMC5113706  PMID: 27482848

Summary

Exogenous mechanical perturbations on living tissues are commonly used to investigate whether cell effectors can respond to mechanical cues. However, in most of these experiments, the applied mechanical stress and/or the biological response are described only qualitatively. We developed a quantitative pipeline based on microindentation and image analysis to investigate the impact of a controlled and prolonged compression on microtubule behaviour in the Arabidopsis shoot apical meristem, using microtubule fluorescent marker lines. We found that a compressive stress, in the order of magnitude of turgor pressure, induced apparent microtubule bundling. Importantly, that response could be reversed several hours after the release of compression. Next, we tested the contribution of microtubule severing to compression‐induced bundling: microtubule bundling seemed less pronounced in the katanin mutant, in which microtubule severing is dramatically reduced. Conversely, some microtubule bundles could still be observed 16 h after the release of compression in the spiral2 mutant, in which severing rate is instead increased. To quantify the impact of mechanical stress on anisotropy and orientation of microtubule arrays, we used the nematic tensor based FibrilTool ImageJ/Fiji plugin. To assess the degree of apparent bundling of the network, we developed several methods, some of which were borrowed from geostatistics. The final microtubule bundling response could notably be related to tissue growth velocity that was recorded by the indenter during compression. Because both input and output are quantified, this pipeline is an initial step towards correlating more precisely the cytoskeleton response to mechanical stress in living tissues.

Keywords: mechanical stress, indenter, microtubules, compression, bundling, Arabidopsis thaliana, technical advance

Significance Statement

Mechanical stress is known to affect diverse cellular processes, from gene expression to mitosis, but experiments are frequently qualitative and the effects of growth not considered. Here we developed a pipeline, based on microindentation and image analysis, to quantitatively investigate the impact of a precisely controlled compression on a growing plant tissue. This pipeline should help to precisely correlate the response of the cytoskeleton to mechanical stresses in living tissues.

Introduction

There is increasing evidence that mechanical stress can have an instructive role in cell biology, from the modulation of gene expression and cytoskeleton behaviour to cell fate, polarity, or division. Several micromechanical set‐ups have been designed to analyze these responses at different scales, from isolated cells to whole organs, and to different types of mechanical stress (compression, shearing … ). For instance, mechanical impulses on metaphasic HeLa cells showed that anaphase progression can be accelerated or delayed depending on the angle between the direction of maximal compression and the spindle axis (Itabashi et al., 2012). Compression of a Drosophila embryo for a few minutes with a coverslip induced the expression of the patterning gene Twist (Farge, 2003). In Poplar, stem bending was correlated with gene expression levels, revealing that the expression of the mechanosensitive transcription factor gene PtaZFP2 displays a linear relation to strain (Coutand et al., 2009). Finally calcium peak and pH change were shown to appear within seconds after mechanical perturbation (Monshausen et al., 2009) and the transcriptional induction of the TOUCH gene to occur within minutes (Lee et al., 2004).

Because cortical microtubules largely contribute to the oriented deposition of cellulose in cell walls, their response to mechanical stress has been studied extensively (Green and King, 1966; Williamson, 1990). Microtubules are able to reorganize into arrays parallel to maximal tensile stress directions in response to an ablation or a lateral compression at the shoot apical meristem (Hamant et al., 2008). Compression also enhances the supracellular coalignment of microtubules in leaves and cotyledons (Jacques et al., 2013; Sampathkumar et al., 2014). A millimetric needle attached to a micromanipulator, and indenting the surface of cotyledons to mimick the force exerted by a penetrating pathogen, in contrast leads to localized microtubule depolymerization within minutes (Hardham et al., 2008). Reorganization of microtubules arrays is generally mediated by self‐organization processes, which involve severing, (de)polymerization and zippering (Dixit and Cyr, 2004; Ehrhardt and Shaw, 2006; Wasteneys and Ambrose, 2009; Sampathkumar et al., 2014). The protein katanin was shown to be involved in microtubule severing. Interestingly, when the microtubule severing protein katanin is overexpressed, microtubules first form apparent bundles within 48 h and ultimately become completely depolymerized if increased severing activity is maintained (Stoppin‐Mellet et al., 2006). Katanin‐dependent microtubule severing also regulates the timing of the microtubule response to mechanical stress: the re‐alignment of cortical microtubules according to the new tensile stress pattern after ablation takes longer in a katanin mutant, both in the shoot apical meristem (Uyttewaal et al., 2012) and in cotyledons (Sampathkumar et al., 2014).

So far, the analysis of the microtubule response to mechanical perturbations has involved qualitative or semi‐quantitative protocols only. In that case, the applied load was estimated at the beginning of the experiment. Lateral compressions with a microvice on the meristem can reach 0.1 N and induce anisotropic tensile stresses at the meristem tip, leading to microtubule bundling and reorientation within a few hours (Hamant et al., 2008; Uyttewaal et al., 2012). On the contrary stretching sunflower epidermal hypocotyl peels with an 8 g load can lead to significant strain rates, but no visible effect on microtubules (Burian and Hejnowicz, 2010). Most of the devices do not allow a precise control of the applied load over time because, for instance, the distribution of forces can vary due to sample growth. Furthermore, the effects of mechanical perturbation on microtubule arrays have rarely been quantified extensively. In the cases where such measurements were conducted, the focus was on microtubule arrays’ orientation (Burian and Hejnowicz, 2010), and anisotropy (Uyttewaal et al., 2012; Boudaoud et al., 2014).

Here we used microindentation to apply quantified loads on living and growing shoot apical meristems and designed tools to quantify the cytoskeleton response to mechanical perturbations. This pipeline could also be applied to other cell effectors, such as actin.

Results

A microindenter‐based set‐up to apply prolonged and controlled compression on the growing shoot apical meristem

Indenters are commonly used in the industry to check mechanical properties of materials. While atomic force microscopy is adapted for nanoscale deformations, microindenters allow to probe larger domains of the tissue from a few micrometres to a hundred micrometres, depending on the choice of the tip (Figure 1a, b). As previously described in Beauzamy et al. (2015), we adapted this technology to the indentation of a living material: the shoot apical meristem of Arabidopsis thaliana. Shoot apices were cut from the plant, and young floral buds were dissected out to give access to the shoot apical meristem at the centre of the apex. These apices were kept alive in agarose medium supplemented with sugar and vitamins (see Experimental Procedures). Meristems were immersed in pure water during the whole experiment to avoid dehydration. Note that this protocol has been used successfully in the past to visualize microtubules and provided comparable results to naked meristems from NPA‐treated seedlings, i.e. without dissection (Uyttewaal et al., 2012; Hamant et al., 2014). To indent, a flat tip of ca. 97 μm in diameter was used, as in Beauzamy et al. (2015). In the following, the tip of the indenter was always centred on and in contact with the meristem (but not the primordia), thanks to a dry ×10 magnification objective. The diameter of the meristem was between 100 and 121 μm.

Figure 1.

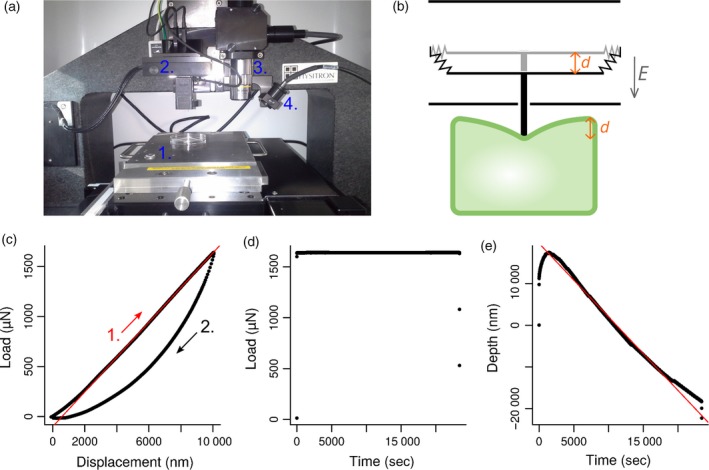
Figure 1

Open in a new tab

Indentation protocol.

(a) The indenter. 1. Motorized stage. 2. Tip and transducer. 3. ×10 (dry) objective. 4. Bright light.

(b) Drawing of the transducer (black) indenting a biological object (green). Transducer is a three‐plate capacitor. The central plate is attached to springs and can move between the two other fixed plates. When a voltage difference is applied between the plates, an electrostatic field E is created, forcing the middle plate to move over a distance d. A feedback loop is implemented in the system to compensate for growth or shrinkage of the tissue over time.

(c–e) Applied load and tip displacement are recorded precisely during the whole experiment. (c) Load versus displacement curve. A first indentation at an imposed displacement (here d = 10 μm) is performed on the sample over a few seconds. The fitted part of the curve (red line) corresponds to the tip approach (1.) and is linear. The slope is the apparent stiffness of the sample. The second part of the curve (2.) corresponds to the retraction of the tip. The differences between approach and retract curves highlight the visco‐plastic behaviour of the sample. (d) Load versus time curve. A constant load is maintained on the sample over 6 h 30 min (23 400 sec). The load value is chosen according to the maximum load reached in (c). (e) Depth versus time curve. The position of the stage along z‐axis changes over time to maintain a constant load at the tip. A linear fit (red line) was applied between 4000 and 20 000 sec to compute speed displacement of the stage, which is more likely to be due to growth of the apex than to any indenter drift. We found a stage speed displacement in the range of 1–4 nm sec−1 (mean 2.4 nm sec−1 ± 1, all genotypes taken into account).

As meristems may vary in shape and stiffness, they were indented first using a displacement‐controlled ramp with a maximum indentation depth that we imposed (Figure 1c). In other words, the motorized stage was lifted up in order to gradually decrease the distance between the indenter tip and the meristem surface until the tip was in contact with the meristem surface. From this initial contact point, the stage was lifted up by the imposed maximum indentation depth, and the load needed to obtain such indentation was recorded. Compression was then applied continuously for 6 h 30 min (Figure 1d), which roughly corresponds to the duration needed to observe full microtubule response in the shoot apical meristem (Hamant et al., 2008).

A major technical difficulty arises from the continuous growth of living plant tissues. If the tip is static, the growing meristem presses on the tip and the total compressive force exerted on the tissue increases progressively. Growth can also deviate from the vertical axis. In such cases, the apex escapes compression by growing preferentially on one side of the device and is thus exposed to a smaller load. Here we took advantage of the indenter's feedback loop between the motorized stage and the tip to maintain a constant load on the sample, by adjusting the position of the stage in function of the force measured at the tip. At any time during compression, applied load and tip position were precisely known, and the load remained close to the chosen value, as set from the first indentation ramp (Figure 1d, e).

The mechanical stress pattern of the indented region of the meristem before indentation is predicted to be isotropic at the top and anisotropic circumferentially on the flanks (Boudaoud, 2010). The indentation is expected to lower stress intensity at the centre of the indented region and to increase stress intensity at the periphery. Indeed, when a thin pressurized shell is flattened by a plane, turgor pressure is locally balanced by this plane, so that stress distribution can be deduced from the flattening of a non‐pressurized shell (Audoly and Pomeau, 2010). Thus the mechanical stress pattern of the compressed meristem is still isotropic at the centre and becomes gradually more anisotropic and circumferential toward the periphery. This pattern (isotropy at the centre and anisotropy on the flanks) is not qualitatively different from the non‐indented situation.

Controlled compressive loads on the shoot apical meristem impacts microtubule behaviour

To visualize the microtubule response to mechanical compression, we acquired confocal images of the meristems before (Figure 2a, e, i, l) and 15 min after (Figure 2b, d, f, h, j, m) compression in two microtubule marker lines: GFP–MBD and GFP–TUA6 under the control of the p35S promoter. The fluorescent reporter construct GFP–MBD encodes a microtubule binding domain from MAP4 fused to the green fluorescent protein (GFP), and thus decorates microtubules, whereas GFP–TUA6 encodes a tubulin subunit fused to GFP and is incorporated into the lattice. The 15 min lag corresponds to the time it takes to move the sample from the indenter to the confocal microscope and perform the scan. In past work, mechanical perturbations on shoot apical meristems led to detectable microtubule array alterations after 2 h, but not before (Hamant et al., 2008; Uyttewaal et al., 2012). We thus suspect that this 15 min time window is short enough to preserve the overall microtubule organization.

Figure 2.

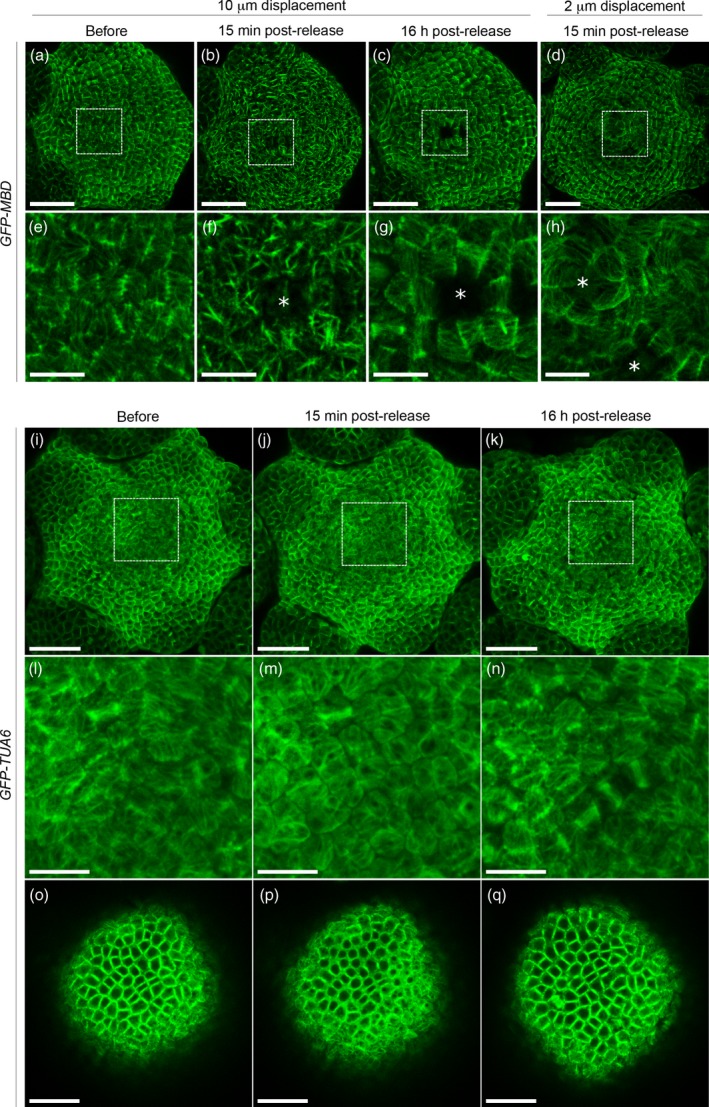
Figure 2

Open in a new tab

Microtubule response to compression in the GFP–MBD and GFP–TUA6 lines.

(a–h) Confocal images of GFP–MBD meristems projected in 2D. (a–c) Load value imposed during the 6 h 30 min compression corresponds to an initial displacement of 10 μm. (a) Before compression. (b) 15 min after release of compression. (c) 16 h after release of compression. (d) Load value imposed during the 6 h 30 min compression corresponds to an initial displacement of 2 μm. Image is taken 15 min after release of compression. (e–h) Close‐ups of (a–d) (white rectangle). White asterisks point at ablation sites. Scale bar = 30 μm in (a–d), and 10 μm in (e–h).

(i–n) Confocal images of GFP–TUA6 meristems projected in 2D. Load value imposed during the 6 h 30 min compression corresponds to an initial displacement of 10 μm. (i) before, (j) 15 min after and (k) 16 h after release of compression. (l–n) Close‐ups of (i–k) (white rectangles).

(o–q) One slice through the epidermis from (i–k), (o) before, (p) 15 min after and (q) 16 h after release of compression. Scale bar = 30 μm in (i–k), 10 μm in (l–n) and 20 μm in (o–q).

We tested different indentation depths. Indentations at 10 μm, followed by continuous compression at the corresponding load, had a visible effect on cortical microtubules (see below, and Figure 2a–c, e–g), whereas indentations at 2 μm had no major impact (see Figure 2d, h). These tests guided our choice of indentation depth. In the following experiments, we fixed the indentation depth at 10 μm. For that depth, the corresponding force was in the range of 1.2–3.0 mN (mean 2.1 ± 0.5 mN), depending on the meristem and on the genotype. Considering that, at that depth, the tip was in full contact with the meristem, this force was applied on a disk of a ca. 7400 μm2 and was on the order of magnitude of turgor pressure found in the meristem (see Beauzamy et al., 2015 for an experimental estimation of turgor pressure at the shoot apical meristem).

A 6 h 30 min long compression on p35S::GFP–MBD (WS‐4) lines induced microtubule aggregation into thick bundles (Figure 2b, f). This response was also reversible: the microtubule network 16 h after the release of compression looked very similar to the microtubule network before compression (Figure 2c, g). The degree of apparent bundling varied among meristems from very aligned network to very thick bundles (as the ones shown in Figure 2b, f, and Figure 5a), and among cells of the same meristem (see Figures 6c and S1a–e). Our results confirmed previous observations of microtubule hyperalignment to bundling in epidermal cells of leaves and cotyledons expressing the GFP–MBD marker, after compression with a coverslip (Jacques et al., 2013; Sampathkumar et al., 2014).

Figure 5.

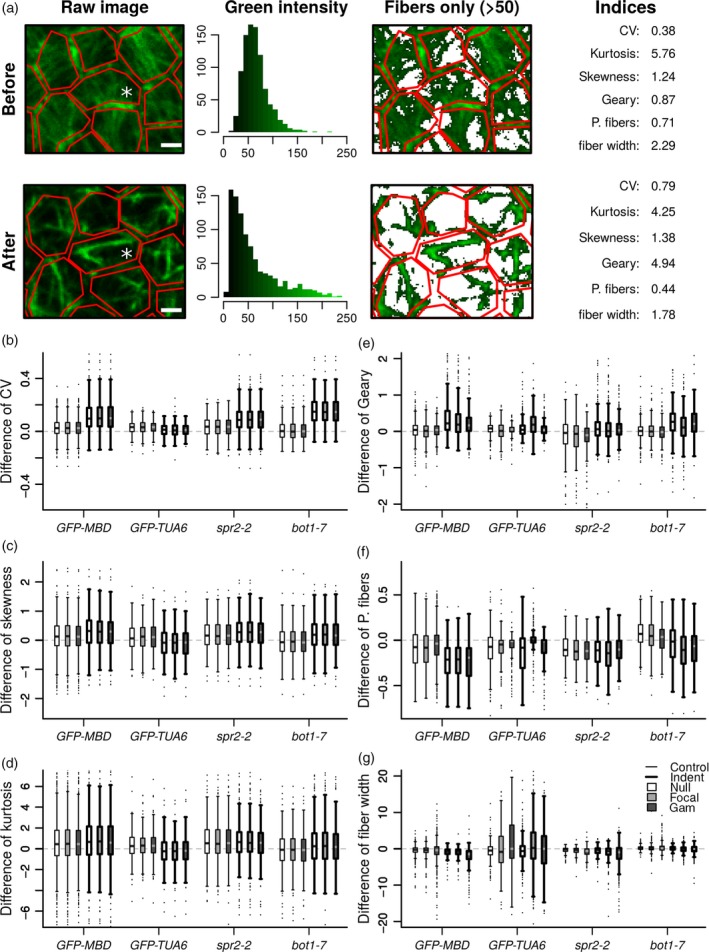
Figure 5

Open in a new tab

Quantitative analysis of microtubule networks in cells.

(a) Example of analyses performed on a GFP–MBD compressed cell (white asterisk). Several data sets were extracted from the green channel of confocal images (‘raw image’) before and after indentation: distribution of fluorescence intensity in each cell (delineated with the red polygons) and its characteristic parameters (coefficient of variation i.e. standard deviation over mean, skewness, a measure of the symmetry of the distribution, and kurtosis, a measure of the presence of outliers). Spatial autocorrelation between fluorescent pixels was computed with the Geary index. The percentage of microtubule fibers per cell (‘P. fibers’) and width of bundles (‘fiber width’) were computed on the binarized image. A threshold was applied on the distribution of fluorescence intensity to binarize the image. Pixels above 50 were considered as belonging to microtubule fibers, whereas pixels under 50 were considered as belonging to the background. Scale bar = 2 μm.

(b–g) Distribution of cell indices difference between time 6 h 45 min and time zero for all control meristems (thin lines boxplots) and indented meristems (thick lines boxplots). Indices were computed on raw images (‘null’) and on images corrected for fluorescence intensity with the ‘focal and ‘gam’ methods (see Experimental Procedures).

Figure 6.

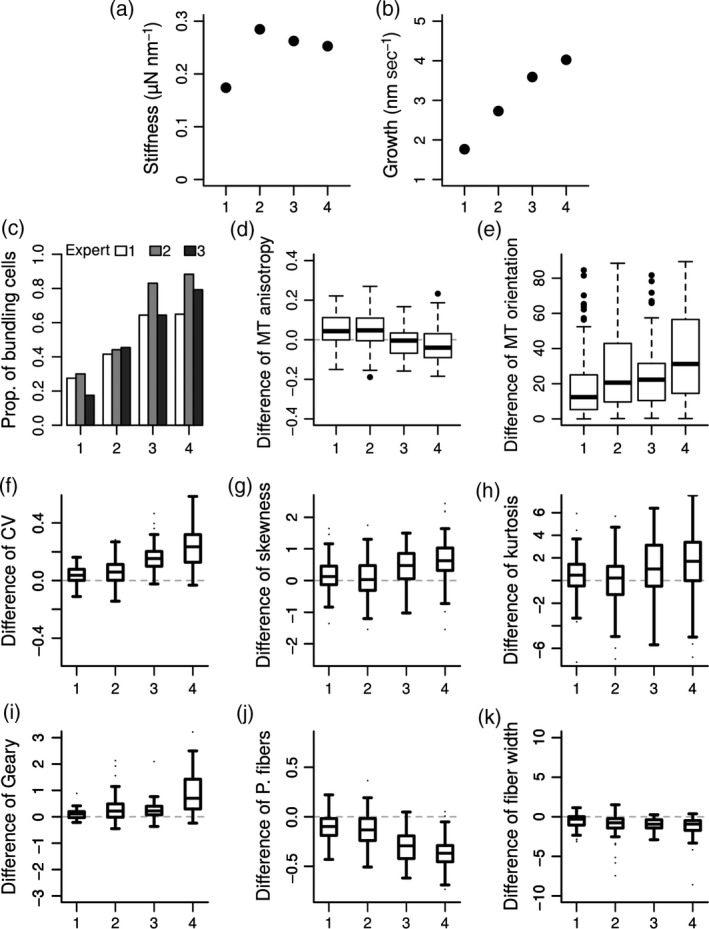
Figure 6

Open in a new tab

Relations between tissue growth and variable microtubule responses to compression in the GFP–MBD line.

(a, b) The four indented meristems are ordered by increasing apparent growth. Apparent stiffness (a) and apparent growth (b) were deduced resp. from the slope of the approach curve of the indentation ramp (Figure 1c) and from the displacement of the stage during the 6 h 30 min compression (Figure 1e).

(c) Proportion of cells showing apparent bundling deduced from three visual analyses.

(d–k) Same indices as in Figures 4 and 5.

Compression‐induced ablation of one or a few cells in several cases, for both 10 and 2 μm indentation depths (Figure 2f–h). In those cases, microtubules reoriented circumferentially within the first row of cells neighbouring the ablation in the hours following compression. This local circumferential pattern could still be observed 16 h after the end of compression, whereas, in other part of the meristem, microtubules had recovered from compression (Figure 2c, g). The pattern of ablated cells differed significantly between samples, suggesting that ablations occurred randomly and were not due to putative bumps on the tip surface, which could locally increase load on a few cells.

Because the GFP–MBD construct was previously reported to induce artifactual bundling in various mutants and growth conditions (Celler et al., 2016), we tested our protocol in a line expressing a GFP–tubulin (GFP–TUA6) fusion under the control of the p35S promoter. Some bundling events could be detected in that line 15 min after release of compression, but we also observed an increased cytosolic GFP background, consistent with microtubule depolymerization (Figure 2i, j, l, m, o, p) as previously reported in Hardham et al. (2008). The effect of compression on microtubules was also reversible in the GFP–TUA6 line: 16 h after release of compression, the microtubule networks looked very similar to the microtubule networks before compression (Figure 2k, n, q). While the impact of compression on microtubule bundling may be slightly underestimated when using the GFP–TUA6 line (e.g. Thitamadee et al., 2002; Abe and Hashimoto, 2005; Ishida et al., 2007), the strong apparent microtubule bundling under mechanical compression may be artificially promoted by the stabilizing effect of the MBD sequence (see e.g. Olson et al., 1995; Granger and Cyr, 2001; Van Damme et al., 2004).

Compression‐induced apparent microtubule bundling is modulated by katanin activity

The microtubule response to mechanical stress depends on katanin‐dependent microtubule severing protein (Uyttewaal et al., 2012; Sampathkumar et al., 2014). Katanin‐mediated severing activity was also shown to transiently promote the formation of thick bundles before leading to complete microtubule depolymerization, using a p35S::GFP–MBD microtubule marker and an inducible over expressor of katanin (Stoppin‐Mellet et al., 2006). To check whether compressions with a microindenter could also reveal the role of katanin in the microtubule response to stress, we next performed 6 h 30 min long compressions on the bot1‐7 katanin mutant allele, in which microtubule severing is largely impaired. As SPIRAL2 [also called TORTIFOLIA (Buschmann et al., 2004)], was shown to act antagonistically on KATANIN (Wightman et al., 2013; Hervieux et al., 2016), we also included the spr2‐2 mutant in the analysis. Because the GFP background signal in the GFP–TUA6 line is high and because the meristematic cells are small, the image quality of microtubule array in this line is low in the shoot apical meristem (Figure 2i–q). The GFP–MBD microtubule marker was thus introgressed into the bot1‐7 and spr2‐2 mutants.

We observed a response to compression in both mutants but to a different extent. At the scale of the entire meristem, spr2‐2 GFP–MBD displayed microtubule bundles (Figure 3b, e and Figure S1f–h) qualitatively similar to those observed in the GFP–MBD line (Figure 3a, d). In contrast, although some bundling was also observed in bot1‐7 GFP–MBD after compression, the microtubule arrays appeared mostly less intermingled (i.e. more parallel) and a higher proportion of cells displayed changes in microtubule network organization, when compared to the GFP–MBD line (Figure 3c, f and Figure S1i–l). In both lines, as in GFP–MBD, microtubule reorganization in response to compressive stress was variable between meristems and among cells of the same meristem (Figure S1). Interestingly, 16 h after the release of the compression, apparent bundling could still be observed in some cells of two spr2‐2 meristems, suggesting that the reversion might be slower in that line (Figure S2).

Figure 3.

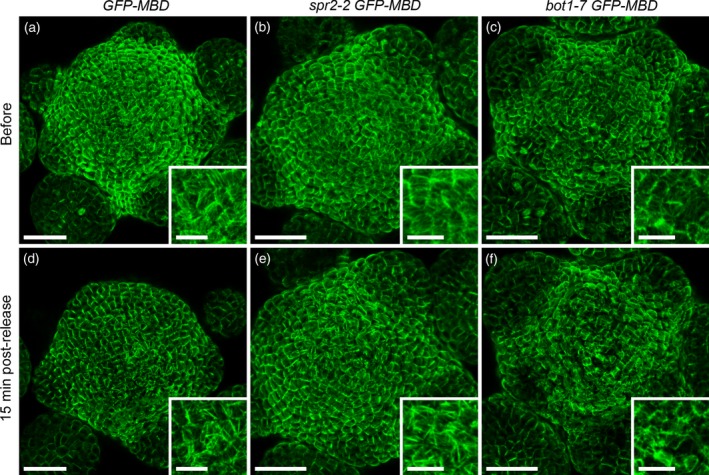
Figure 3

Open in a new tab

Microtubule response to compression in spr2‐2 GFP–MBD and bot1‐7 GFP–MBD.

(a–f) Load value imposed during the 6 h 30 min compression corresponds to an initial displacement of 10 μm. Confocal images of dissected meristems projected in 2D from top and corresponding close‐ups taken (a–c) before compression and (d–f) 15 min after release of compression. (a, d) GFP–MBD microtubule marker line (control). (b, e) spr2‐2 GFP–MBD line. (c, f) bot1‐7 GFP–MBD line. Scale bar = 30 μm, and 10 μm in the close‐ups.

Altogether, this result shows that this microindenter set‐up can reveal different microtubule responses to mechanical compression in mutants. Overall, our results are rather consistent with a requirement for katanin activity in the promotion of microtubule self‐organization in response to mechanical perturbations.

Quantifying the microtubule response to mechanical perturbations

As shown above, responses appeared somewhat variable, depending on genotype, marker line or even individual sample. To go beyond the qualitative assessment of the microtubule response to compression, we analyzed the variations of anisotropy and orientation of the microtubule arrays and quantified the variations in the degree of apparent bundling between time 6 h 45 min (i.e. 15 min after the release of compression) and time zero (before compression). The approach was partially automated with the prospect to ease statistical analysis of bigger data sets. Here, we analyzed thirteen GFP–MBD meristems (four indented and nine controls), six GFP–TUA6 meristems (three indented and three controls), seven spr2‐2 GFP–MBD meristems (four indented and three controls) and six bot1‐7 GFP–MBD meristems (three indented and three controls). On each meristem, on the snapshots taken at time zero and at time 6 h 45 min, 80 cells were segmented manually using the Fiji Polygon tool (Schindelin et al., 2012). The Fiji plugin FibrilTool (Boudaoud et al., 2014) was used to compute microtubule array anisotropy and mean orientation per cell. Polygon segmentation was then imported in the R software with the R ImageJ Region of Interest (ROI) package (R Core Team, 2015; Sterratt and Vihtakari, 2015) to quantify the degree of apparent bundling.

Compression from the top is known to induce a better alignment of microtubule arrays per cell in cotyledons and leaves, i.e. an increase in the anisotropy of microtubule arrays (Jacques et al., 2013; Sampathkumar et al., 2014). Lateral compression of the shoot apical meristem is known to induce the formation of supracellular microtubule alignments in the direction of maximal tensile stress (Hamant et al., 2008). The difference of anisotropy between the two snapshots (time 6 h 45 min and time zero) was computed separately for the control and the indented meristems of each line. Results showed no significant variation in array anisotropy or orientation between the two snapshots in all lines (Figure 4). This finding seems consistent with the prediction that the mechanical stress pattern at the meristem (isotropic at the centre and anisotropic at the periphery) is conserved during compression. Nevertheless, as highlighted by our qualitative observations, the degree of apparent bundling among meristems and among cells of the same meristem varied from very aligned network to very thick bundles in GFP–MBD, spr2‐2 GFP–MBD and bot1‐7 GFP–MBD. We thus cannot exclude the possibility that cell‐to‐cell variability hinders the detection of global trends in microtubule anisotropy and reorientation in these lines, as explored below for the GFP–MBD line (see Figure 6).

Figure 4.

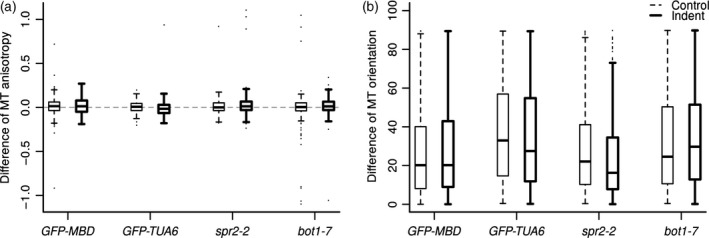
Figure 4

Open in a new tab

Differences of anisotropy and orientation of microtubule arrays between time 6 h 45 min and time zero in two microtubule marker lines (GFP–MBD and GFP–TUA6) and in two mutants (spr2‐2 and bot1‐7).

(a) Differences of microtubule array anisotropy, as measured with the FibrilTool plugin.

(b) Differences of microtubule array orientation, as measured with the FibrilTool plugin. A mean direction of microtubules with the x‐axis is computed at time 6 h 45 min and compared to those of the snapshot at time zero. Differences are computed in degrees modulo 90. Dashed thin lines: control, i.e. non‐indented meristem. Continous thick lines: indented meristems.

Next, we quantified the degree of apparent bundling in each segmented cells (see above and Experimental Procedures) of the non‐indented (control) and indented meristems. When GFP–MBD decorated microtubules form bundles, the fluorescent signal aggregates, leading to a new spatial fluorescence intensity distribution with an increase of the number of pixels with fluorescence intensity maximum (green) and minimum (dark), and a reduction in the number of pixels with intermediate intensity. To assess these changes quantitatively, we tested different indices commonly used to describe the shape of distributions (Figure 5a and Figure S4, see below).

Because differences can be subtle, Wilcoxon rank sum tests were used to detect whether differences of (not necessarily Gaussian) indices between indented meristems and controls are truly significant. For each cell, changes of indices were calculated as the difference of values between time 6 h 45 min and time zero. The one‐sided alternative of the Wilcoxon test allowed examining if the distribution of cell changes for indented meristems was greater (or lower, depending on indices) than the distribution of cell changes for controls (see below and Table S1). In parallel, we normalized fluorescence intensity in two different ways (‘focal’ and ‘gam’), because its distribution could be biased by image acquisition protocol (see Experimental Procedures and Figure S3). Indeed, gain and laser intensity were not exactly the same between the two snapshots taken before and just after the experiment, and between meristems. Nevertheless, microtubules close to anticlinal cell walls were deliberately overexposed but not microtubules close to periclinal cell walls. Both normalization methods aimed at ensuring that each part of the meristem would have the same basal level of fluorescence, relative to nearby cell walls. Comparison between normalized and raw data revealed marginal differences in our indices, showing that distribution of fluorescence intensity was unbiased by our image acquisition protocol (Figure 5b–g). In the following, we consider that an index for the indented meristem is significantly different from the index for the control meristems if Wilcoxon tests P‐values of the two normalization methods (‘focal’ and ‘gam’) are consistent with those of the non‐normalized method (‘null’):

  1. The coefficient of variation (CV, ratio of standard deviation over mean) is a measure of dispersion of a given distribution: CV increases when the distribution spreads out. In our case, when microtubules are gathered into bundles, there are more dark and bright pixels; CV should thus increase. For all genotypes, with the notable exception of GFP–TUA6, we could indeed detect an increase of CV in the indented cells, when compared to the controls (P‐value < 4.5 × 10−14, Table S1 and Figure 5b). This confirmed the visual impression that fluorescence was more contrasted after indentation.

  2. The skewness is a measure of the symmetry of a distribution. Skewness of fluorescence level was previously used to characterize actin bundling (Higaki et al., 2010). When GFP–MBD decorated microtubules form bundles, distribution of fluorescence is expected to extend more toward high fluorescence levels than toward low levels, thus increasing asymmetry (and skewness) of distribution. As for CV, the change of skewness was significantly greater in all genotypes, except for GFP–TUA6 (Figure 5c; P‐value < 0.02, Table S1). This was consistent with the longer tail of distributions toward high fluorescent values observed after indentation.

  3. The kurtosis is a measure of the presence of outliers (i.e. infrequent extreme values). Kurtosis increases when there are more and more extreme outliers. We do not expect isolated outliers to appear when microtubules form bundles. As expected, changes in kurtosis were low (Figure 5d) and only significantly greater for bot1‐7 GFP–MBD (P‐value < 0.02, Table S1).

  4. To assess the spatial aggregation of fluorescence, we used a coefficient of spatial autocorrelation, the Geary index. The Geary index compares the fluorescence of each pixel to the fluorescence of its neighbours. An increase in Geary index reflects a decrease in complexity of the network, i.e. the network is less intermingled and more aggregated (see example on Figure 5a). All genotypes, except GFP–TUA6, displayed a change in the Geary index, which was significantly greater for the indented than for the control meristems (Figure 5e; P‐value < 1.9 × 10−04, Table S1),

  5. Two last indices, (v) the percentage of microtubule fibers, and (vi) the width of microtubule network, were computed on binarized images. The word ‘fiber’ is here used to designate and distinguish aggregated microtubules from isolated microtubules. In each cell, microtubules were separated from the background by applying a threshold on grayscale intensities of images. Some preliminary tests on our 2D projected confocal images showed that a threshold equal to 50 over 255 (grayscale values in the green channel for 8 bits RGB images) gave the best compromise between a good filtering of microtubules and a large spreading of resulting indices, amenable to discriminate the different cell configurations (see example on Figure 5a). (v) The percentage of microtubule fibers was computed as the ratio of the number of pixels above threshold (intensity = 50/255) over total number of pixels in each cell between the two snapshots (at time 6 h 45 min and at time zero) for indented and control meristems. In our case, it amounts to the percentage of microtubule array per cell, independent of the thickness of the bundles; therefore this index is predicted to decrease after compression. Note that this index is not identical to the density index used in Higaki et al. (2010), as here the binarized image was not skeletonized after thresholding. We observed a significant decrease in the percentage of microtubule fibers in indented meristems for GFP–MBD and bot1‐7 × GFP–MBD when compared to the controls (Figure 5f; P‐value < 3.4 × 10−08, Table S1), but not for GFP–TUA6 and spr2‐2 GFP–MBD.

  6. Width of microtubule network is complementary to the Geary index (iv) in characterizing the complexity of a microtubular network. This index corresponds to the distance of a microtubule pixel to the nearest non‐microtubule pixel. We could expect an increased width when bundling occurs. However, in our case, because of the image resolution, large width indicates that the network is intermingled and small width indicates that microtubules are isolated i.e. aggregated into bundles (see example on Figure 5a). Decrease in the width of the network was significantly more important after indentation for GFP–MBD only (Figure 5g; P‐value < 4.8 × 10−11, Table S1). The response was not as clear for other lines for which tests were not significant for all normalizations (Table S1).

Interestingly, in the control (i.e. not indented) bot1‐7 GFP–MBD meristems, the different indices (except for Geary and fiber width) showed opposite results compared to the other, non‐indented, lines. CV, skewness and kurtosis were centred on zero indicating a balanced evolution of the three parameters across the duration of the compression experiments (Figure 5b–d). The percentage of microtubule fibers increased in bot1‐7 GFP–MBD controls between time zero and time 6 h 45 min while it decreased for the other lines (Figure 5f). These opposite results could reflect the difference of microtubule architecture (more intermingled) observed in the bot1‐7 GFP–MBD line before compression. However, as revealed by the different indices computed on compressed meristems, the response of indented bot1‐7 GFP–MBD was similar to that of GFP–MBD and spr2‐2 GFP–MBD lines. These quantitative results are consistent with the qualitative impression that bot1‐7 GFP–MBD does respond to compression, albeit more slowly, as also seen after ablation (see Uyttewaal et al. 2012).

Towards correlating the stress‐induced microtubule response to tissue growth and stiffness

Last, we explored whether the observed variability between individual meristems could be related to the stiffness or to the growth of our samples. The indenter not only allows us to compress the meristem with a known load, it also provides the apparent stiffness and apparent growth velocity of the shoot apex. Here we present only the results for the GFP–MBD microtubule marker line. The apparent stiffness was calculated as the slope of the approach curve during the first indentation ramp (Figure 6a, see also Figure 1c). The apparent growth velocity was deduced from the continuous displacement of the stage to maintain the load constant during the 6 h 30 min compression (Figure 6b, see Figure 1e). We compared these measurements to all the indices computed above (see Figures 4 and 5) and to our cell‐by‐cell visual expertise (see Experimental Procedures). Interestingly, the results of these three expertise were consistent with one another, overall (Figure 6c). They revealed that strong bundling is only visible in a fraction of the 80 analyzed cells of each meristem, varying roughly between 20% and 80%, depending on the meristem (Figure 6c). More interestingly, the fraction of cells showing a clear bundling increased when growth velocity of the apex was higher. Similarly, the difference of orientation, the CV, the skewness, the kurtosis and the Geary indices increased when growth was higher (Figure 6e–i), whereas difference of microtubule anisotropy, percentage of fibers and mean fiber width showed a decreasing relation with growth (Figure 6d, j, k). This suggests that apparent bundling after compression is related to growth. This seems consistent with the idea that high turgor pressure is required for both high growth rate and high tension in cell walls.

Altogether this pipeline illustrates how quantitative analyses can help better explain observations (and the associated variability), and provide a way to relate cell mechanics to cytoskeleton behaviour, two very complex and integrated variables.

Discussion

‘Complex self‐organizing phenomena can only be fully understood with quantitative mathematical frameworks that allow specific hypotheses to be formulated and tested’ (Oates et al., 2009). The microtubule response to mechanical perturbations is a perfect illustration of a complex self‐organization phenomena and, in the present article, we provided several tools to obtain quantitative data on microtubule behaviour in response to quantified loads. We used a microindenter to apply a quantified and constant mechanical compression on growing shoot apical meristems, we performed correlative microscopy, with confocal imaging, before and after compression, and we analyzed the orientation, anisotropy and apparent bundling of microtubules in the confocal images.

The proposed indenting protocol and its coupling with confocal live‐imaging offers interesting perspectives to test quantitatively the response of cytoskeleton and gene expression to a quantified and constant mechanical compression. However, the biological response cannot be monitored during application of compressive stress, and switching from indenter to confocal microscope directly imposes a minimum of 15 min between the end of compression and the observation under the confocal microscope. Furthermore, current limitations of the indenter software limit the duration of compression to a few hours (~7 h). The use of a commercial microindenter may also limit the range of available tips.

Our qualitative observations, using two microtubule marker lines, confirmed the previously observed microtubule bundling response to mechanical stress and the stabilizing effect of MBD. As bundling can be promoted by the katanin protein, we include spr2‐2 (exhibiting higher severing frequency) and bot1‐7 (exhibiting reduced severing frequency) in our study. In spr2‐2 GFP–MBD, the bundling response seemed qualitatively similar to those of GFP–MBD, but some bundles could still be observed 16 h after release of the compression, suggesting a possibly slower reorganization of microtubules. A response of microtubules after compression could also be observed in bot1‐7 GFP–MBD, but microtubule networks were less intermingled and more parallel rather than being organized into thick bundles, when compared to the GFP–MBD control line.

To go beyond the qualitative assessment of microtubule behaviours in these lines and assays, we used several quantitative tools to analyse the microtubule response to mechanical loads, in the prospect to use the microtubule response as an internal quantitative sensor of tensile stress intensity and anisotropy. Microtubules were shown to reorganize along the maximal tensile stress direction when the mechanical stress pattern is perturbed (Hamant et al., 2008) and to align in parallel arrays in response to compressive stress in cotyledons and leaves (Jacques et al., 2013; Sampathkumar et al., 2014). Anisotropy and orientation of microtubule arrays over time, measured with an ImageJ/Fiji macro called FibrilTool (Boudaoud et al., 2014), did not seem to be affected by the compression. Note that bundling in the GFP–MBD line was much more pronounced in our conditions than in previous reports, hindering a comparative analysis with previous quantifications with FibrilTool (Uyttewaal et al., 2012; Sampathkumar et al., 2014). Furthermore, the variability of the microtubule response to compressive stress between meristems and among cells of the same meristem could also mask changes in microtubule anisotropy and orientation, as suggested by our in‐depth study of the GFP–MBD indented meristems. However, here, the number of individual meristems is too low to conclude with confidence.

To analyze apparent bundling, we calculated six different indices; the first three characterize the fluorescence intensity distribution within the cells (CV, skewness and kurtosis), the three others were specifically designed to be sensitive to modifications of the microtubules network like the spatial autocorrelation of the network (Geary index), the percentage of microtubules per cell, and the width of the microtubule network. On the control meristems, the three‐first indices and the percentage of microtubules per cell, but not the Geary index and the width, separated bot1‐7 GFP–MBD from the others lines. This result is consistent with previous description of microtubular network of the mutant, which displays a more web‐like architecture (Bichet et al., 2001; Burk and Ye, 2002) and slower dynamics than the WT. Interestingly, reorganization of the microtubule network in response to mechanical perturbations could be detected in the bot1‐7 mutant with these indices, further demonstrating that the perception of mechanical cues has not been impaired in this mutant, but instead, the response to mechanical cues is slower.

Because the indenter also provides an indirect measurement of growth, the microtubule response to compression could be related to the status of the tissue. This revealed that the apparent variability in the response to compression that is observed in the GFP–MBD line can be explained by differences in tissue growth. Variability is a typical biological feature and as the resolution of imaging tools improves, a role of such variability in biological processes is unraveled (Laslo et al., 2006; Wernet et al., 2006; Martin et al., 2009; Singh et al., 2010; Gupta et al., 2011; Uyttewaal et al., 2012).

The quantification of variable behaviour at the cell level will need to be assessed and compared to the status of the tissue, notably to differentiate between true variability (white noise) to more patterned or synchronized behaviours (coloured noise). As suggested by the results of the manual expertise, visual analysis may not be sufficient. Our correlative imaging pipeline using an indenter, which measures growth and stiffness at the tissue scale, and a confocal microscope combined with the development of quantitative tools, which allows the monitoring of cell effectors, provides a way to address that question quantitatively and more objectively. Altogether, the pipeline described in this paper may be used to calibrate the microtubule response to mechanical perturbations in plant tissues. Microtubule behaviour may then be monitored to deduce stress patterns, quantitatively.

Experimental Procedures

Plants material and growth conditions

The microtubule binding domain marker line GFP–MBD (WS‐4) was previously described in Marc et al. (1998). The GFP–TUA6 tubulin marker line was previously described in Ueda et al. (1999). The bot1‐7 GFP–MBD line was previously described in Uyttewaal et al., 2012. The spr2‐2 mutant (in Col‐0), first described in Buschmann et al. (2004) and Shoji et al. (2004) was obtained from NASC (NASC ID: N6549) and crossed with GFP–MBD (WS‐4). Seeds were sown on soil, kept at 4°C during 48 h, then grown in short day conditions (8 h light at 19°C; 16 h night at 17°C) during 4 weeks and at last transferred 2–3 weeks in long days conditions (16 h day at 21°C; 8 h night at 19°C) prior to dissection.

Meristems were cut from the stem, dissected the day before indentation and stuck in ‘Arabidopsis apex culture medium’ (ACM) (2.2 g L−1 Duchefa Biochemie – MS basal salt mixture without vitamins, 1% sucrose; adjust pH to 5.8 with KOH and add 1.6% agarose) supplemented with vitamins and 6‐benzylaminopurine (BAP). If necessary, meristems were stabilized by extra drops of ACM without vitamins and BAP. Dissected meristems were kept overnight in a phytotron in long days conditions (Sanyo, 16 h day at 21°C; 8 h night at 19°C, synchronized with growth culture chambers) prior to indentation.

Imaging

Plants were imaged prior to indentation (9 a.m. on day 1), and 15 min (5 p.m. on day 1) and 16 h (9 a.m. on day 2) after indentation. 1024 × 1024 pixels images with slices every 1 μm were acquired on a LSM 700 upright confocal microscope (Zeiss), with a water‐dipping ×40 magnification lens (NA = 1). At each indentation experiment, a minimum of three plants (one indented and minimum two controls) were dissected and put in ACM medium.

Indentation

As in Beauzamy et al. (2015), indentation experiments were performed with a TI 950 TriboIndenter and its associated extended stage from Hysitron (Figure 1a), using a truncated cone tip with a disk‐shaped flat end of 96.96 μm diameter. A 30 × 10 mm Petri dish containing the dissected meristem stuck in ACM was placed on the stage and fixed at its periphery with adhesive gum to prevent any sliding (see Figure 1a, and Figure 1a in Beauzamy et al., 2015). A quick approach of the tip in the air was performed for the indenter to roughly assess the position of the meristem surface. Then, the meristem was immersed in pure water. The force (in μN) needed to indent the meristem at 10 μm depth was deduced from a first indentation ramp (5 sec approach from 0 to 10 μm; 5 sec retraction from 10 μm to 0, see Figure 1c). This force value was used as the setpoint of the long‐lasting indentation ramp (5 sec approach from 0 to maximum force set point; 6 h 30 min constant load at the set point; 15 sec retraction from set point to 0, see Figure 1d). We used the ‘Extended stage’ feature of the indenter to allow the system to compensate for tissue growth or shrinkage by moving the stage up or down (Figure 1e). All indenter curves were exported as text files and analyzed in the R software (R Core Team, 2015).

Image analysis

All confocal stacks were projected in 2D with the MerryProj software (Barbier de Reuille et al., 2005). On each stack, starting from the top of the stack, 80 cells were manually delineated as ROI with ImageJ Polygon tool (Schindelin et al., 2012). The total area of these 80 cells had a diameter between 53.3 and 75.0 μm, smaller than the diameter of the indenter tip (96.96 μm). FibrilTool macro (Boudaoud et al., 2014) was used to compute direction and quality of orientation of microtubules on 2D projection within each ROI. Reorientation of microtubules during the two snapshots, prior to and 15 min after indentation, was computed as the difference of angle with the x‐axis, which was checked to not rotate between snapshots with the ImageJ plugin Align3_TP (Parker, 2010). Polygon segmentation was then imported in the R software thanks to the RImageJROI package (R Core Team, 2015; Sterratt and Vihtakari, 2015). Although a great attention was taken to ensure similar fluorescence exposure conditions among snapshots, differences could remain, possibly intensified by the 2D projection. Two different ways of normalization were thus tested, allowing comparison of results with the ‘null’ normalization, which is simply the raw image. Both methods assumed that fluorescence intensity near anticlinal walls should be maximal, following the idea that contrast should normally have been fixed so that all anticlinal walls should be overexposed in each slice. Hence, for each pixel, if no nearby cell wall reaches maximum intensity (green = 255), then it is probably under‐exposed and its green intensity should be increased:

  1. The method named ‘focal’ is a local normalization (Figure S3a). For each pixel, the value of green intensity in the surrounding pixels in a radius of 70 pixels (big enough to include around two cells on average) is computed. If the maximum (255) is not reached in the search of radius, the pixel intensity is multiplied by 255 over the maximum intensity of the neighbours. This ensured an intensity still included in the 0–255 interval for each pixel.

  2. The method named ‘gam’ is a global smoothed normalization based on cell walls (Figure S3b). Note that this method could be applied here as signal near anticlinal cell walls was generally overexposed when compared to microtubule signal below the outer wall. The aim is to fit a smoothed statistical model linking green intensity to the coordinates of pixels: intensity = f(x, y). As for ‘focal’, this model predicts, for each pixel, the maximum intensity of surrounding pixels but is smoothed over the entire meristem, thus avoiding local effects, in contrast to ‘focal’. 2D projected confocal stacks of meristems can be seen as altimetric maps, where altitude is the green intensity. In spatial data science, the topographic position index (tpi) allows to detect hollows and bumps on altimetric maps. We used a modified tpi to detect major bumps of green intensities (characterizing mainly anticlinal walls) with an appropriately chosen radius (here, 3 pixels, which is the half of the average of the distance between the contours of two polygonal ROI). A bump is defined as a pixel for which intensity ≥ 1.2 multiplied by the average of three‐radius neighbours. The model then applied is a Generalized Additive Model (GAM) defined with a tensor having a low smoothing parameter corresponding to the 3D shape of the meristems: intensity = tensor(x, y, k = 5). As for ‘focal,’ the predictions of the model for each pixel were rescaled from 0 to 255 to estimate the smoothed local maximum for each pixel of the meristem. If the maximum (255) is not reached in the prediction, the pixel intensity is multiplied by 255 over the prediction of the model. The GAM was fitted with library ‘mgcv’ in the R software (Wood, 2011; R Core Team, 2015).

The distribution of fluorescent intensity of pixels and the microtubule network found in each cell of a meristem were described with different indices computed with the R software (R Core Team, 2015). Skewness and kurtosis of distributions were computed with the R package moments (Komsta and Novomestky, 2015). The Geary spatial autocorrelation index and the width index (i.e. distance to the nearest non‐microtubule pixel) were computed with the R package raster (Hijmans, 2015). Geary index was computed on an equally weighted 3 × 3 neighbourhood (default R library raster settings) and averaged on the cell.

Visual analysis

Cells images were extracted individually from meristem images with the R software and presented in a random order through a specific R‐shiny web application (Chang et al., 2016). Three of the five authors looked at 500 cells before and after putative compression without knowing whether the meristem had been indented and without seeing neighbouring cells (as in Figure S1). All cells from the indented GFP–MBD marker line were analyzed, in addition to a random set of cells from the control GFP–MBD meristems, and from the other lines, for a non‐biased expertise. Each cell (before/after) was rated as ‘showing more microtubules bundles in the second time point compared to the first time point’ or ‘not showing more microtubules bundles.’ The Shiny web application used for visual analysis is displayed on http://statnmap.com/rshiny-expert-image-comparison-app/.

Conflict of Interest

The authors declare no conflicts of interest.

Supporting information

Figure S1. Examples of cells pairs from indented meristems extracted from snapshots taken at time zero, i.e. before compression (left cell), and at time 6 h 45, i.e. 15 min after release of compression (right cell).

Click here for additional data file. (6.7MB, tiff)

Figure S2. Microtubule bundling persistence 16 h after release of compression in two spr2‐2 GFP–MBD meristems.

Click here for additional data file. (7.3MB, tif)

Figure S3. Methods used to rescale green intensities values, when exposure was too low, illustrated with GFP–MBD images (see also Experimental Procedures).

Click here for additional data file. (15MB, tiff)

Figure S4. Examples of analyses performed on compressed meristems in (a) spr2‐2 GFP–MBD; and (b) bot1‐7 GFP–MBD.

Click here for additional data file. (15MB, tiff)

Table S1. Wilcoxon rank sum tests P‐values.

Click here for additional data file. (16.6KB, docx)

 

Click here for additional data file. (15KB, docx)

Acknowledgements

We are grateful to Nelly Dubrulle for additional tests and help while preparing this manuscript. We also thank Platim (UMS 3444 Biosciences Gerland‐Lyon Sud) for providing support on imaging. This work was supported by a PhD grant from Région Rhône‐Alpes and by the European Research Council (ERC grant 307387 « PhyMorph » and ERC grant 615739 ‘MechanoDevo’).

References

  1. Abe, T. and Hashimoto, T. (2005) Altered microtubule dynamics by expression of modified α‐tubulin protein causes right‐handed helical growth in transgenic Arabidopsis plants: right‐handed helical growth in transgenic Arabidopsis plants. Plant J. 43, 191–204. [DOI] [PubMed] [Google Scholar]
  2. Audoly, B. and Pomeau, Y. (2010) Elasticity and Geometry: From Hair Curls to The Non‐Linear Response of Shells. UK: Oxford University Press. [Google Scholar]
  3. Barbier de Reuille, P. , Bohn‐Courseau, I. , Godin, C. and Traas, J. (2005) A protocol to analyse cellular dynamics during plant development. Plant J. 44, 1045–1053. [DOI] [PubMed] [Google Scholar]
  4. Beauzamy, L. , Louveaux, M. , Hamant, O. and Boudaoud, A. (2015) Mechanically, the shoot apical meristem of arabidopsis behaves like a shell inflated by a pressure of about 1 MPa. Front. Plant Sci. 6, p 1038. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Bichet, A. , Desnos, T. , Turner, S. , Grandjean, O. and Höfte, H. (2001) BOTERO1 is required for normal orientation of cortical microtubules and anisotropic cell expansion in Arabidopsis. Plant J. 25, 137–148. [DOI] [PubMed] [Google Scholar]
  6. Boudaoud, A. (2010) An introduction to the mechanics of morphogenesis for plant biologists. Trends Plant Sci. 15, 353–360. [DOI] [PubMed] [Google Scholar]
  7. Boudaoud, A. , Burian, A. , Borowska‐Wykręt, D. , Uyttewaal, M. , Wrzalik, R. , Kwiatkowska, D. and Hamant, O. (2014) FibrilTool, an ImageJ plug‐in to quantify fibrillar structures in raw microscopy images. Nat. Protoc. 9, 457–463. [DOI] [PubMed] [Google Scholar]
  8. Burian, A. and Hejnowicz, Z. (2010) Strain rate does not affect cortical microtubule orientation in the isolated epidermis of sunflower hypocotyls. Plant Biol. 12, 459–468. [DOI] [PubMed] [Google Scholar]
  9. Burk, D.H. and Ye, Z.‐H. (2002) Alteration of oriented deposition of cellulose microfibrils by mutation of a katanin‐like microtubule‐severing protein. Plant Cell, 14, 2145–2160. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Buschmann, H. , Fabri, C.O. , Hauptmann, M. , Hutzler, P. , Laux, T. , Lloyd, C.W. and Schäffner, A.R. (2004) Helical growth of the Arabidopsis mutant tortifolia1 reveals a plant‐specific microtubule‐associated protein. Curr. Biol. 14, 1515–1521. [DOI] [PubMed] [Google Scholar]
  11. Celler, K. , Fujita, M. , Kawamura, E. , Ambrose, C. , Herburger, K. , Holzinger, A. and Wasteneys, G.O. (2016) Microtubules in plant cells: strategies and methods for immunofluorescence, transmission electron microscopy, and live cell imaging. Methods Mol. Biol. 1365, 155–184. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Chang, W. , Cheng, J. , Allaire, J.J. , Xie, Y. and McPherson, J. (2016) shiny: Web Application Framework for R, Available at: https://CRAN.R-project.org/package=shiny.
  13. Coutand, C. , Martin, L. , Leblanc‐Fournier, N. , Decourteix, M. , Julien, J.L. and Moulia, B. (2009) Strain mechanosensing quantitatively controls diameter growth and PtaZFP2 gene expression in poplar. Plant Physiol. 151, 223–232. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Dixit, R. and Cyr, R. (2004) The cortical microtubule array: from dynamics to organization. Plant Cell, 16, 2546–2552. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Ehrhardt, D.W. and Shaw, S.L. (2006) Microtubule dynamics and organization in the plant cortical array. Annu. Rev. Plant Biol. 57, 859–875. [DOI] [PubMed] [Google Scholar]
  16. Farge, E. (2003) Mechanical induction of twist in the drosophila foregut/stomodeal primordium. Curr. Biol. 13, 1365–1377. [DOI] [PubMed] [Google Scholar]
  17. Granger, C.L. and Cyr, R.J. (2001) Spatiotemporal relationships between growth and microtubule orientation as revealed in living root cells of Arabidopsis thaliana transformed with green‐fluorescent‐protein gene construct GFP–MBD. Protoplasma, 216, 201–214. [DOI] [PubMed] [Google Scholar]
  18. Green, P.B. and King, A. (1966) A mechanism for the origin of specifically oriented textures in development with special reference to Nitella wall texture. Aust. J. Biol. Sci. 19, 421–438. [Google Scholar]
  19. Gupta, P.B. , Fillmore, C.M. , Jiang, G. , Shapira, S.D. , Tao, K. , Kuperwasser, C. and Lander, E.S. (2011) Stochastic state transitions give rise to phenotypic equilibrium in populations of cancer cells. Cell, 146, 633–644. [DOI] [PubMed] [Google Scholar]
  20. Hamant, O. , Heisler, M.G. , Jönsson, H. et al. (2008) Developmental patterning by mechanical signals in arabidopsis. Science, 322, 1650–1655. [DOI] [PubMed] [Google Scholar]
  21. Hamant, O. , Das, P. and Burian, A. (2014) Time‐lapse imaging of developing meristems using confocal laser scanning microscope In Plant Cell Morphogenesis (Žárský V. and Cvrčková F., eds). Totowa, NJ: Humana Press, pp. 111–119. Available at: http://link.springer.com/10.1007/978-1-62703-643-6_9. [DOI] [PubMed] [Google Scholar]
  22. Hardham, A.R. , Takemoto, D. and White, R.G. (2008) Rapid and dynamic subcellular reorganization following mechanical stimulation of Arabidopsis epidermal cells mimics responses to fungal and oomycete attack. BMC Plant Biol. 8, 63. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Hervieux, N. , Dumond, M. , Sapala, A. , Routier‐Kierzkowska, A.L. , Kierzkowski, D. , Roeder, A.H. , Smith, R.S. , Boudaoud, A. and Hamant, O. (2016) A mechanical feedback restricts sepal growth and shape in arabidopsis. Curr. Biol. 26, 1019–1028. [DOI] [PubMed] [Google Scholar]
  24. Higaki, T. , Kutsuna, N. , Sano, T. , Kondo, N. and Hasezawa, S. (2010) Quantification and cluster analysis of actin cytoskeletal structures in plant cells: role of actin bundling in stomatal movement during diurnal cycles in Arabidopsis guard cells. Plant J. 61, 156–165. [DOI] [PubMed] [Google Scholar]
  25. Hijmans, R.J. (2015) raster: Geographic Data Analysis and Modeling, Available at: http://CRAN.R-project.org/package=raster.
  26. Ishida, T. , Kaneko, Y. , Iwano, M. and Hashimoto, T. (2007) Helical microtubule arrays in a collection of twisting tubulin mutants of Arabidopsis thaliana. Proc. Natl Acad. Sci. USA, 104, 8544–8549. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Itabashi, T. , Terada, Y. , Kuwana, K. , Kan, T. , Shimoyama, I. and Ishiwata, S. (2012) Mechanical impulses can control metaphase progression in a mammalian cell. PNAS, 109, 7320–7325. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Jacques, E. , Verbelen, J.‐P. and Vissenberg, K. (2013) Mechanical stress in Arabidopsis leaves orients microtubules in a ‘continuous’ supracellular pattern. BMC Plant Biol. 13, 163. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Komsta, L. and Novomestky, F. (2015) moments: Moments, cumulants, skewness, kurtosis and related tests, Available at: http://CRAN.R-project.org/package=moments.
  30. Laslo, P. , Spooner, C.J. , Warmflash, A. , Lancki, D.W. , Lee, H.‐J. , Sciammas, R. , Gantner, B.N. , Dinner, A.R. and Singh, H. (2006) Multilineage transcriptional priming and determination of alternate hematopoietic cell fates. Cell, 126, 755–766. [DOI] [PubMed] [Google Scholar]
  31. Lee, D. , Polisensky, D.H. and Braam, J. (2004) Genome‐wide identification of touch‐ and darkness‐regulated Arabidopsis genes: a focus on calmodulin‐like and XTH genes. New Phytol. 165, 429–444. [DOI] [PubMed] [Google Scholar]
  32. Marc, J. , Granger, C.L. , Brincat, J. , Fisher, D.D. , Kao, T. , McCubbin, A.G. and Cyr, R.J. (1998) A GFP–MAP4 reporter gene for visualizing cortical microtubule rearrangements in living epidermal cells. Plant Cell, 10, 1927–1939. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Martin, A.C. , Kaschube, M. and Wieschaus, E.F. (2009) Pulsed contractions of an actin–myosin network drive apical constriction. Nature, 457, 495–499. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Monshausen, G.B. , Bibikova, T.N. , Weisenseel, M.H. and Gilroy, S. (2009) Ca2 +  regulates reactive oxygen species production and pH during mechanosensing in Arabidopsis roots. Plant Cell, 21, 2341–2356. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Oates, A.C. , Gorfinkiel, N. , González‐Gaitán, M. and Heisenberg, C.‐P. (2009) Quantitative approaches in developmental biology. Nat. Rev. Genet. 10, 517–530. [DOI] [PubMed] [Google Scholar]
  36. Olson, K.R. , McIntosh, J.R. and Olmsted, J.B. (1995) Analysis of MAP 4 function in living cells using green fluorescent protein (GFP) chimeras. J. Cell Biol. 130, 639–650. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Parker, J.A. (2010) Align3_TP: stack alignment plug‐in for ImageJ, Available at: http://www.med.harvard.edu/JPNM/ij/plugins/Align3TP.html.
  38. R Core Team . (2015) R: A Language and Environment for Statistical Computing, Vienna, Austria: R Foundation for Statistical Computing; Available at: http://www.R-project.org/. [Google Scholar]
  39. Sampathkumar, A. , Krupinski, P. , Wightman, R. , Milani, P. , Berquand, A. , Boudaoud, A. , Hamant, O. , Jönsson, H. and Meyerowitz, E.M. (2014) Subcellular and supracellular mechanical stress prescribes cytoskeleton behavior in Arabidopsis cotyledon pavement cells. Elife, 3, e01967. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Schindelin, J. , Arganda‐Carreras, I. , Frise, E. et al. (2012) Fiji: an open‐source platform for biological‐image analysis. Nat. Methods, 9, 676–682. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Shoji, T. , Narita, N. , Hayashi, K. , Asada, J. , Hamada, T. , Sonobe, S. , Nakajima, K. and Hashimoto, T. (2004) Plant‐specific microtubule‐associated protein SPIRAL2 is required for anisotropic growth in arabidopsis. Plant Physiol. 136, 3933–3944. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Singh, D.K. , Ku, C.‐J. , Wichaidit, C. , Steininger, R.J. , Wu, L.F. and Altschuler, S.J. (2010) Patterns of basal signaling heterogeneity can distinguish cellular populations with different drug sensitivities. Mol. Syst. Biol. 6, p 369. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Sterratt, D.C. and Vihtakari, M. (2015) RImageJROI: Read ‘ImageJ’ Region of Interest (ROI) Files, Available at: https://github.com/davidcsterratt/RImageJROI.
  44. Stoppin‐Mellet, V. , Gaillard, J. and Vantard, M. (2006) Katanin's severing activity favors bundling of cortical microtubules in plants. Plant J. 46, 1009–1017. [DOI] [PubMed] [Google Scholar]
  45. Thitamadee, S. , Tuchihara, K. and Hashimoto, T. (2002) Microtubule basis for left‐handed helical growth in Arabidopsis. Nature, 417, 193–196. [DOI] [PubMed] [Google Scholar]
  46. Ueda, K. , Matsuyama, T. and Hashimoto, T. (1999) Visualization of microtubules in living cells of transgenic Arabidopsis thaliana. Protoplasma, 206, 201–206. [Google Scholar]
  47. Uyttewaal, M. , Burian, A. , Alim, K. et al. (2012) Mechanical stress acts via katanin to amplify differences in growth rate between adjacent cells in arabidopsis. Cell, 149, 439–451. [DOI] [PubMed] [Google Scholar]
  48. Van Damme, D. , Van Poucke, K. , Boutant, E. , Ritzenthaler, C. , Inzé, D. and Geelen, D. (2004) In vivo dynamics and differential microtubule‐binding activities of MAP65 proteins. Plant Physiol. 136, 3956–3967. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Wasteneys, G.O. and Ambrose, J.C. (2009) Spatial organization of plant cortical microtubules: close encounters of the 2D kind. Trends Cell Biol. 19, 62–71. [DOI] [PubMed] [Google Scholar]
  50. Wernet, M.F. , Mazzoni, E.O. , Çelik, A. , Duncan, D.M. , Duncan, I. and Desplan, C. (2006) Stochastic spineless expression creates the retinal mosaic for colour vision. Nature, 440, 174–180. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Wightman, R. , Chomicki, G. , Kumar, M. , Carr, P. and Turner, S.R. (2013) SPIRAL2 determines plant microtubule organization by modulating microtubule severing. Curr. Biol. 23, 1902–1907. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Williamson, R.E. (1990) Alignment of cortical microtubules by anisotropic wall stresses. Aust. J. Plant Physiol. 17, 601–613. [Google Scholar]
  53. Wood, S.N. (2011) Fast stable restricted maximum likelihood and marginal likelihood estimation of semiparametric generalized linear models. J. R. Stat. Soc. 73, 3–36. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Figure S1. Examples of cells pairs from indented meristems extracted from snapshots taken at time zero, i.e. before compression (left cell), and at time 6 h 45, i.e. 15 min after release of compression (right cell).

Click here for additional data file. (6.7MB, tiff)

Figure S2. Microtubule bundling persistence 16 h after release of compression in two spr2‐2 GFP–MBD meristems.

Click here for additional data file. (7.3MB, tif)

Figure S3. Methods used to rescale green intensities values, when exposure was too low, illustrated with GFP–MBD images (see also Experimental Procedures).

Click here for additional data file. (15MB, tiff)

Figure S4. Examples of analyses performed on compressed meristems in (a) spr2‐2 GFP–MBD; and (b) bot1‐7 GFP–MBD.

Click here for additional data file. (15MB, tiff)

Table S1. Wilcoxon rank sum tests P‐values.

Click here for additional data file. (16.6KB, docx)

 

Click here for additional data file. (15KB, docx)

Articles from The Plant Journal are provided here courtesy of Wiley

RESOURCES