Interepidemic and between season persistence of Rift Valley fever: vertical transmission or cryptic cycling?

Summary

Rift Valley fever (RVF) is an emerging zoonotic mosquito-borne infectious disease that has been identified as a risk for spread to other continents and can cause mass livestock mortality. In equatorial Africa, outbreaks of RVF are associated with high rainfall, when vector populations are at their highest. It is, however, unclear how RVF virus persists during the interepidemic periods and between seasons. Understanding interepidemic persistence as well as the role of vectors and hostsis paramount to creating effective management programs for RVF control. We created a mathematical model for the spread of RVF and used the model to explore different scenarios of persistence including vertical transmission and alternate wildlife hosts, with a case study on buffalo in Kruger National Park, South Africa. Our results suggest that RVF persistence is a delicate balance between numerous species of susceptible hosts, mosquito species, vertical transmission, and environmental stochasticity. Further investigations should not focus on a single species, but should instead consider a myriad of susceptible host species when seeking to understand disease dynamics.

Introduction

Rift Valley fever (RVF) is an emerging infectious disease that has been identified as a risk for international spread by the Office of International Epizootics (OIE), Center for Disease Control (CDC) and World Health Organization (WHO). Large epizootics have occurred through sub-Saharan Africa and have a significant impact on livestock production, inducing up to 90% mortality of juvenile small livestock (sheep and goats) and episodes of abortion in cattle, sheep and goats (Swanepoel & Coetzer, 2004). Rift Valley Fever virus (RVFV) is a mosquito-borne, zoonotic pathogen (Phlebovirus Family: Bunyaviridae) that infects numerous mammalian species (Swanepoel & Coetzer, 2004) including domestic and wild ruminants. Since its discovery in the 1930’s (Daubney & Hudson, 1931) RVF was confined to Sub-Saharan Africa and Madagascar until 2000, when it was detected on the Arabian Peninsula (confirmed in by the CDC in a MMWR report, 2000; reviewed in Balkhy & Memish, 2003).

In Southern Africa, focal or large-scale epidemics occur in a variable temporal cycle of between 7 and 11 years. Generally these outbreaks occur in the mid-to late summer months with above average rainfall, when vector abundance has peaked (Swanepoel & Coetzer, 2004). It is unclear how RVF virus persists during the interepidemic periods. Furthermore, in Kruger National Park, distinct wet and dry seasons result in peaking mosquito populations during the wet season, but during the dry season mosquito density is close to zero. This suggests that transmission of RVF likely does not occur during the average dry season. Since there are no known long-term mammalian carriers of RVF, persistence from wet season to wet season is also a mystery. One possible mode of between season and between epidemic persistence is vertical transmission with desiccation resistant mosquito eggs that are viable for several years (Chevalier, 2010; Chevalier et al, 2004). As many as 23 mosquito genera have been found to be capable of RVF virus transmission worldwide, however, mosquitoes in the genera Aedesmay be particularly important for virus maintenance in the interepidemic period (Pepin, 2010; Turell et al, 2008). Aedine mosquitoes are able to transmit RVF transovarially and RVF outbreaks are associated with increased activity of these mosquitoes during years with elevated rainfall when many Aedine mosquitoes emerge (Linthicum et al, 1991;Balkhy & Memish, 2003; Martin et al, 2008). Aedine mosquitoes lay their eggs on the soil or vegetation on the verges of low-lying depressions and pans filled with water (Becker, 1989). These eggs must undergo a period of dehydration followed by wetting before hatching (Gargan, 1998) and can lie dormant for many years, hatching when seasonal pools refill with water during heavy rainfall (Gargan, 1998). During periods of high rainfall, infected Aedes eggs, laid as many as 8 years prior, can hatch and transmit RVF virus to susceptible hosts (Gargan, 1998; Linthicum et al 1983). For these reasons, mosquitoes in the genus Aedesare widely believed to be important as an endemic maintenance vector of RVF between seasons and during inter-epidemic periods, however whether they are sufficient as a maintenance mechanism for RVF during inter-epidemic periods is unclear.

It has also been suggested that wildlife may play a role in interepidemic maintenance of RVF. Studies in Kenya (Rostal et al, 2010) and in South Africa (Labeaud et al, 2010) have found that wildlife species convert from seronegative to seropositive outside of any known outbreak and antibodies to RVFV have been found in many wildlife species, including, but not limited to, impala, white rhinoceroses, bushbuck and waterbuck (Davies, 1975; Anderson and Rowe, 1998; Fischer-Tenhagen et al, 2000; Paweska et al, 2005; Evans et al, 2008; Paweska et al, 2008).One species of significant concern is African buffaloes (Syncerus caffer) (Swanepoel & Coetzer, 2004; Labeaud et al, 2010), which are water dependent social bovids. As with most ruminants, viremic buffalo may transmit the disease, via a mosquito vector, to livestock, to other wild ruminants and to humans(Woods et al, 2002; Flick & Bouloy, 2005). Due to the large populations of buffalo in game parks, their propensity to mingle with livestock and humans on the borders and their known competence as RVF hosts, there has been special interest in whether they could serve as an interepidemic host for RVF.

Mathematical models can compare different mechanisms for persistence of RVF. Gaff et al, 2007 and Gaff et al, 2012 modeled RVF without seasonality in order to explore methods of control once an outbreak is occurring. The Xue et al, 2011 model of RVF in South Africa focused on livestock and human cases, while Anyamba et al, 2006 worked on predicting risk of RVF outbreaks in East Africa based on weather data. Although wildlife is considered to play a part in RVF persistence between epidemics, it is has been largely ignored or included implicitly in previous models. We explicitly include wildlife in our model, including African buffalo and other potential reservoir species. Unlike previous authors, in this paper we focus on the inter-epidemic persistence of RVF by adapting the Chitnis et al, 2013 model for RVF to include marked seasonality and to store infected eggs during the dry season.

We used this adapted mathematical model of the spread of RVF to study different scenarios of persistence, starting with an emphasis on African buffalo as a possible wildlife reservoir host. We use Kruger National Park (KNP) as a model system, but the conclusions are generalizable to other savannah ecosystems in sub-Saharan Africa and offer insights to the spread of RVF into previously uninfected areas. We first tested if vertical transmission alone can result in interepidemic persistence of RVF in a herd of buffalo in KNP. We then included an alternate “cryptic” host in the model to test if the presence of multiple hosts could account for the inter-epidemic persistence of RVF. We propose that rather than one or the other, the combination of vertical transmission and cryptic cycling in other hosts is the most likely mechanism for persistence of RVF during interepidemic periods. Lastly we considered how host immunity affected persistence.

Methods

The underlying transmission model

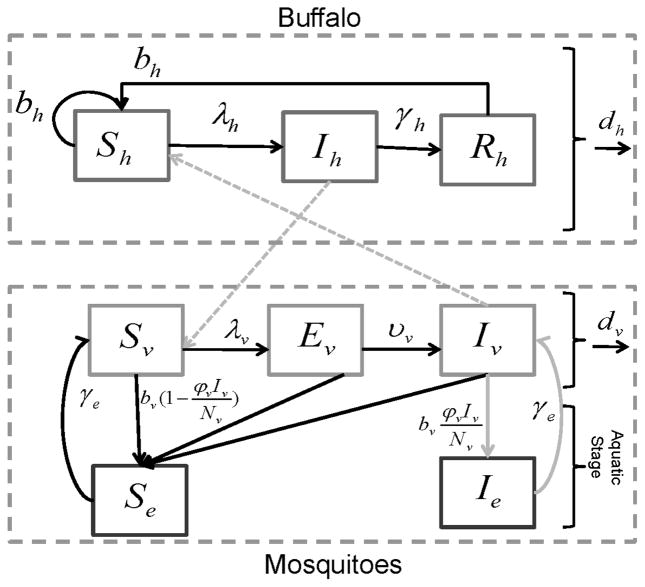
Our model adapted from Chitnis et al, 2013 divides African buffalo into three distinct compartments: susceptible S_h, infectious I_h, and recovered R_h. The total buffalo population is then N_h=S_h+I_h+R_h. Buffalo enter the susceptible class through a per-capita birth rate, b_h, and leave all compartments through a natural per-capita death rate, d_h where 1/d_h is the average lifespan of a buffalo, about 15 years. To simplify the model, we assume that the buffalo herd is at a stable carrying capacity, H₀. We considered a geographically restricted area with the “herd” consisting of a reasonable number of buffalo likely to come into contact with mosquitoes at a given water hole. A susceptible buffalo can be infected by the bite of an infected mosquito with probability γ_h and is subsequently moved into the infectious compartment, I_h. The incubation period in buffalo is ignored here since it is relatively short (1-3 days). The buffalo recover and are moved into the recovered compartment R_h at a rate γ_h where 1/γ_h is the average time spent infectious. We assume buffalo remain immune for life once recovered. Infected buffalo, mostly the young, die from infection at a low rate, δ_h (Swanepoel & Coetzer, 2004). Although some horizontal transmission may take place due to contact with aborted fetuses, it is not likely to play a role in inter-epidemic persistence, so is ignored here. See Table 1 for a list of all parameters, variables, and their units.

Table 1.

The parameters and variables for the RVF model and their dimensions

Symbol	Description	Dimensions
bh/dh	Buffalo per-capita birth/death rates	Day−1
bv/dv	Mosquito per-capita birth/death rates	Day−1
Ho	Stable buffalo population in absence of disease	Animals
Vo	Stable adult female mosquito population	Animals
γe	Mosquito hatch and emergence rate	Day−1
λv	Contact/transmission rate for mosquitoes	Day−1
λh	Contact/transmission rate for buffalo	Day−1
γh	Rate buffalo move from infectious to recovered	Day−1
δh	Rate at which buffalo die from RVF	Day−1
νv	Rate mosquitoes move from incubating to infectious	Day−1
φv	Proportion of infectious mosquitoes that lay infectious eggs	Dimensionless
Sh	Susceptible buffalo	Animals
Ih	Infectious buffalo	Animals
Rh	Recovered and immune buffalo	Animals
Se	Susceptible eggs/larvae	Animals
Ie	Infectious eggs/larvae	Animals
Sv	Susceptible adult female mosquitoes	Animals
Ev	Incubating, or exposed, adult female mosquitoes	Animals
Iv	Infectious adult female mosquitoes	Animals

Adult female mosquitoes are divided into three compartments: susceptible, S_v, those in the extrinsic incubation period, E_v, and infectious, I_v. The total adult female mosquito population is then N_v. For the purpose of understanding long term persistence via vertical transmission, we include only Aedes mosquitoes in our model since they are the only mosquito genera known to exhibit vertical transmission between infected adults and eggs for Rift Valley fever (Pepin, 2010). Adult female mosquitoes enter the susceptible compartment through the hatching and emergence of susceptible eggs/larvae/pupae. Mosquito eggs and larvae are divided into two compartments: susceptible aquatic mosquitoes S_e, and infectious aquatic mosquitoes I_e. Mosquitoes enter the susceptible aquatic mosquito compartment through a per-capita natural birth rate b_v. The birth term for mosquitoes accounts for the egg-laying rate of mosquitoes, the survival and hatching rate of eggs, and the survival and emergence rate of larvae. Mosquitoes hatch at a per-capita rate γ_e where 1/γ is the average time it takes to move from egg to emerging adult mosquito. The total number of aquatic stage mosquitoes is N_e. Adult mosquitoes leave all compartments via a constant per-capita death rate d_v where 1/d_v is the average lifespan of an adult female mosquito. To simplify, we assume thatduring the wet season the mosquito population quickly reaches a stable size, V₀ since once eggs are submerged, adult mosquitoes emerge within days. Since adult female mosquito populations drive transmission, there are enough eggs available for the mosquitoes to reach carrying capacity every wet season. These assumptions ignore some of the more complex aspects of mosquito ecology, such as predation and competition in larvae in favor of simplicity and better known parameters.

An adult female mosquito is infected by biting an infectious buffalo with probability λ_v and move into the incubating compartment E_v. Although many epidemic models assume that the contact rate, and thus transmission, is either frequency dependent or density dependent (Wonham et al, 2006), we use a contact rate that falls between the two and depends on both the density of mosquitoes and available hosts as outlined in the Chitnis et al, 2013 model (Appendix 1). Incubating mosquitoes enter the infectious compartment I_v at rate ν_v where 1/ν_v is the average time spent in the extrinsic incubation period. Once a mosquito is infectious, it remains so for the rest of its life. An adult female mosquito can also be born infected. Since infectious Aedes mosquitoes can transmit RVF virus transovarially, we assume that a proportion of infectious mosquitoe ϕ_v (referred to here as the ‘vertical transmission rate’), will produce at least one infectious egg that survives to adulthood and emerges as an infectious female. See Appendix 1 for a full description of the model and associated differential equations.

Seasonality

Since Kruger National Park, and the majority of sub-Saharan Africa, has distinct wet and dry seasons that significantly affect the mosquito populations, we include seasonality in our model by alternating wet season and dry season parameters. See Table 2 for the parameter values used in the wet and dry seasons. Figure 2 shows a typical mosquito population in our model. The general shape remains the same regardless of mosquito carrying capacity and disease status. We make the assumption that the wet and dry season parameters do not vary from year to year so the same amount of rain falls every wet season. This is a simplifying assumption but allows us to consider the ‘best case scenario’ from the perspective of RVF and to consistently compare different scenarios. Additionally, directly correlating absolute mosquito population size with weather data is not straightforward. During the wet season, some of the eggs that Aedes mosquitoes lay do not hatch until the subsequent wet season. To include this in our model, we computed the number of infectious mosquitoes for the last 30 days of the peak of the wet season, let a proportion (ϕ_v) of them lay at least one infectious egg that will survive the dry season and result in an emerging infectious adult female mosquito during the next wet season. If the total number of infectious eggs that survive the dry season and emerge is below 1, then we say RVF has died out. During the dry season, we assume there are no mosquitoes. This assumption could also be easily relaxed for areas that do not have as distinct wet and dry seasons.

Table 2.

Parameter values for wet and dry seasons (see Chitnis et al, 2013 for references)

Parameter	Wet Season	Dry Season
1/dh	15 Years	15 Years
1/dv	20 Days	14 Days
1/γe	10 Days	1000 Days
σV	0.33 Day−1	0.25 Day−1
σh	19 Day−1	19 Day−1
βhv	0.12	0.12
βvh	0.38	0.38
1/γh	4 Days	4 Days
δh	0.01 Day−1	0.01 Day−1
1/νv	14 Days	14 Days

Figure 2.

A typical time series of mosquito populations over 5 years. Half of the year is a wet season, characterized by many mosquitoes and half of the year is the dry season with very few or no mosquitoes present. We assume eggs are available all year long so if a flooding even occurs, some mosquitoes will hatch.

Although eggs have been known to remain viable and infected with RVF for up to 7 years after being laid, very little data exists on the rate at which eggs die or how long they live, so for simplicity we assume for most runs that eggs do not hatch more than one year after being laid. We explored the impact of this assumption by allowing eggs to survive for up to three years for several scenarios and found that multiple year egg survival only had an impact for the lowest vertical transmission and vector-to-host ratios and for introduction of RVF into a naïve herd. As more data is made available about mosquito dynamics this assumption can be reevaluated.

Simulation scenarios

To test the first hypothesis that vertical transmission alone can allow for long-term persistence of RVF in buffalo, we ran the model for values of ϕ_v ranging from 0-10%. We also varied the vector-to-host ratio and the transmission rates to determine how sensitive our results are to those values. We chose to vary these parameters based on sensitivity analysis of a similar model in Chitnis et al, 2013, indicating that the basic reproduction number is sensitive to transmission probability from mosquito to host, vector to host ratio, the mosquito biting rate, and mosquito lifespan. Female Aedes mosquitoes typically do not disperse more than 500 meters from their natal habitat to find a host, so we assumed mosquito migration is negligible and that most female mosquitoes will encounter only the animals that water near where they hatched. A herd of buffalo will typically return to the same watering holes in their home range, so it is also unlikely that a female Aedes mosquito will encounter buffalo from another herd. Thus we assume the mosquitoes will only be exposed to the buffalo herd that frequents the natal watering hole. Since herds of buffalo in Kruger average about 1000 individuals, we use 1000 buffalo as our baseline value for H₀ but also run the simulations for 500 and 1500 individuals . We considered the minimum vector to host ratio (MVH) necessary to maintain persistence under various vertical transmission rates. Remember that here ‘vector’ means female Aedes mosquitoes.

To test the second hypothesis that the primary means of persistence is through circulating in an alternate host in addition to buffalo, we simulate the system with an alternate host. Since we do not know what that host may be, we simply assumed that there are some additional susceptible hosts every year that can acquire and transmit RVF to the resident mosquitoes. We assumed that the alternate host has an equal or shorter lifespan, or herd turnover, to buffalo since buffalo are among the most long-lived ungulates in the park that are susceptible to RVF. Since buffalo live for 15 years on average, we vary the alternate host lifespan from 3–15 years. We vary the force of infection from alternate host to mosquito, λ_r to determine what level of infection in the alternate host is necessary to maintain RVF in the system, and in particular buffalo, over long periods of time (see Appendix 1 for description of λr).

Finally, we combined both vertical transmission and an alternate host. We ran the model for varying levels of infection in the reservoir species, varying values of vertical transmission and various host-to-vector ratios and transmission rates. We did not consider any scenarios in which no vertical transmission occurs, and transmission is dependent on mammalian hosts alone. In order for RVF to survive the dry season without any vertical transmission, there must be transmission during the dry season. Since there are very few mosquitoes during the dry season, RVF does not persist through the dry season even with an alternate host in our simulations. Between-season persistence depends entirely on vertical transmission (or, alternatively, on consistent introduction of the virus from outside the system, which we are notconsidering here).

Results

Buffalo as the main mammalian interepidemic host

We started by considering the case where buffalo are the only host in order to determine if RVF can persist locally in a buffalo herd with reasonable vertical transmission rates for mosquitoes. Currently, most buffalo herds in Kruger have some level of immunity from previous outbreaks (Beechler et al, accepted pending revision). We therefore considered scenarios where 15% of the buffalo herd is immune to RVF from previous exposure (Figure 3a). RVF can persist at 1% vertical transmission rates in the larger herd sizes and with very large minimum vector to host ratios (MVHs), while persistence does not occur for the smaller herd of 500 buffalo. We found that 6–10% vertical transmission allows for persistence in the widest range of scenarios. Still, an MVH of at least 8:1 is required every rainy season even for high vertical transmission rates.

Figure 3.

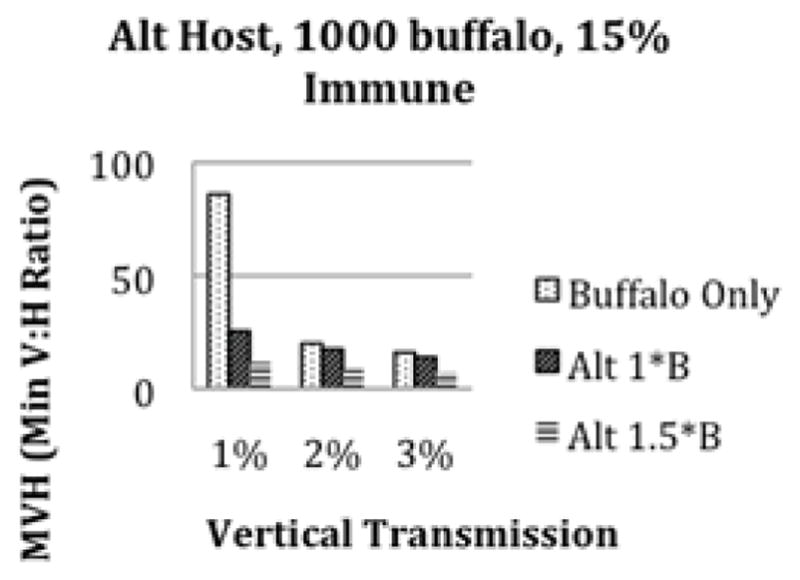
The minimum vector to host (MVH) ratio needed for long term persistence of RVF with 15% initial immunity. Plot (a) is for 500, 1000, or 1500 buffalo without an alternate host present. Persistence is not possible at 1% vertical transmission with only 500 buffalo present. Plot (b) is the MVH needed for persistence with 1000 buffalo and 1000 alternate hosts. The alternate hosts have either the same transmission rates as buffalo (1B) or 1.5 times the transmission rates of buffalo (1.5B). Plot (c) is the MVH needed for persistence with 500 buffalo and 500 alternate hosts with the same transmission rate as buffalo and with 1.5 times the transmission rate of buffalo. Adding hosts that are as good or better transmitters than buffalo decreases the MVH needed for persistence.

Since Aedes mosquito eggs are desiccation resistant and can potentially survive for several years, we let the eggs last for up to 3 years in the scenario with 1000 buffalo with 15% initial immunity. Letting the eggs survive longer only had a large impact on the MVH needed for 1% vertical transmission, reducing it from 86:1 to 34:1.It appears that with steady yearly rainfall assumed in this model, multiple year survival for eggs does not have a big impact on the results so we assume for the rest of the scenarios that eggs survive only one year. This assumption would need to be revisited for varying rainfall or when new data becomes available about egg survival across seasons.

Other mammalian interepidemic hosts?

After considering buffalo alone as the primary hosts of RVF, we added a local alternate host (waterbuck, impala, etc.)that is also susceptible to RVF. This alternate host adds an additional transmission term to the model, representing the force of infection to mosquitoes from the alternate host(s) and to the alternate hosts from the mosquitoes. We ran the simulations for varying levels of vertical transmission and alternate host scenarios. Figures 3b and 3c show the alternate host transmission rates, vertical transmission, and minimum vector to host ratios (MVHs) needed for RVF to persist long term. We found with both an alternate host and vertical transmission, RVF can persist long term at 1–3% vertical transmission rates when the host transmits RVF relatively well. We found that the smaller the lifespan of the alternate host, the better the chance of persistence, since susceptibles become available sooner (Figure 4). We let the alternate host transmission rates (both to and from the vectors) vary from half that of buffalo (.5B) to 1.5 times that of buffalo (1.5B). When the alternate host is half as good at transmitting RVF (.5B), they have a dilution effect and RVF is less likely to persist in our simulations. For this case, RVF does not persist for 1–2% vertical transmission, but can persist at high MVHs for 3% vertical transmission with 1000–1500 buffalo and 1000–1500 alternate hosts. When the alternate host transmits as well as buffalo (1B), RVF is more likely to persist than with buffalo alone due to availability of more susceptible hosts and the shorter lifespan of the alternate hosts (Figure 3b). Finally, when the alternate host transmits better than buffalo (1.5B), RVF becomes much more likely to persist under a wide range of scenarios for low vertical transmission (Figure 3c).

Figure 4.

The effect of alternate host lifespan and transmission competency on the minimum V:H ratio (MVH) needed for persistence in a herd of 750 buffalo/750 alternate hosts . Although lifespan does have an effect, the transmission competency and not lifespan (herd turnover) is most important as seen in Figure 3.

Scenarios considering both MVH and number of infected eggs surviving

In addition to evaluating minimum vector to host ratio we also evaluated the model output to determine the number of eggs persisting in each scenario. Due to environmental stochasticity, scenarios where persistence is dependent on to 1 or 2 infected eggs for multiple seasonsis very unlikely. At the MVH needed for persistence, the average number of eggs surviving every year is quite low (usually less than 5) so we computed the average number of infected eggs surviving the dry season for various V:H ratios and vertical transmission rates (Figure 5). For 1000 buffalo alone (no alternate host) and for 2% vertical transmission, there needs to be 2 times the MVH in order for the average number of infected eggs surviving the dry season to be above 10 per year. For 3% vertical transmission, there has to be at least 1.5 times the MVH to have average infected eggs surviving the dry season above 10 eggs per year. In scenarios where alternate hosts are present and where the alternate hosts are the same or superior transmitters, the MVH ratio needed for at least 10 eggs surviving per year is reduced. So, the presence of alternate hosts decreases the vector to host ratio needed for a more reasonable level of egg survival (Figure 5 and Figure A2).

Figure 5.

The average number of infected eggs surviving the dry season for 2% vertical transmission rates with various V:H ratios. Both 1000 buffalo alone and 1000 buffalo with 1000 alternate hosts are considered. Alternate hosts either have the same transmission as buffalo (1B) or 1.5 times the transmission rates of buffalo (1.5B). The first bar is the average number of infected eggs surviving each dry season at the MVH (denoted 1VH). The second bar is the average number of infected eggs surviving for 1.25 times the MVH (1.25VH), the third for 1.5 times the MVH (1.5VH), and the fourth for 2 times the MVH (2VH). Figure A2 in Appendix 1 shows the 1% and 3% scenarios.

Outbreaks without host immunity

Last we considered an RVF outbreak in a completely susceptible herd of buffalo. These results are applicable to invasion of RVF in geographical areas where it was not previously present. In this case, RVF does not persist long term for any scenario with a 3% vertical transmission or less (see Figure 6). For 4% vertical transmission, RVF will persist in larger herds (1000–1500) with very high vector to host ratios, while for smaller herds (500 animals), RVF still does not persist. The initial outbreak in a susceptible herd is large, thus herd immunity is high, and since buffalo are quite long-lived, RVF must survive in eggs and with very low level transmission for 10–20 years. If the V:H ratio is too large, then RVF no longer persists either, as it spreads too quickly initially, leaving too few susceptible buffalo for subsequent outbreaks. This results in a fairly narrow range across which RVF will persist for 4% vertical transmission. When the vertical transmission reaches 6%, RVF can persist for all three herd sizes. The MVH remains high for 500 and 1000 individuals, but is lower for 1500 individuals (about 10:1). For 8–10% vertical transmission, persistence is much more likely for all scenarios. Figure 6 shows MVHs needed for persistence with a fully susceptible herd.

Figure 6.

Minimum vector to host ratio (MVH) needed for persistence when RVF is introduced to a fully susceptible or naïve buffalo herd. No persistence occurs below 4% vertical transmission. It seems that either high vertical transmission rates or reintroduction of RVF from an outside source is necessary for persistence in a naïve herd.

Discussion

Buffalo as the main interepidemic mammalian hosts

If RVF is already established in a buffalo population and herd immunity is about 15% then RVF can persist at 1–3% vertical transmission, but requires consistent and high minimum V:H ratios (MVHs) and the number of eggs persisting from season to season is low (1–5 eggs). Although there is no consensus on what typical vector to host ratios are in KNP, evidence so far suggests that a 2:1–20:1 ratio of female mosquitoes to available hosts is reasonable. Our model output suggests that dropping the minimum VH ratio below 20:1 require at least 3% consistent vertical transmission and at least 1000 buffalo present. Here, 3% vertical transmission means that 3% of the infected female mosquitoes living in the last month of the wet season will lay at least one infected egg that will survive the dry season, hatch, and emerge as an infected adult female the next wet season. For this scenario, the average number of infected eggs surviving and continuing transmission are 1–3 eggs per dry season.

Models considering both MVH and number of infected eggs surviving

In addition to the V:H ratio we also considered surviving eggs as an important variable. We show that although the minimum V:H ratio (MVH) results in persistence, it is often with only 1–5 infected eggs surviving each dry season. Environmental stochasticity minimizes the likelihood that a small number of eggs will consistently survive the dry season and re-infect the hosts. In order for the number of surviving infected eggs to have a minimum of 5 per dry season while keeping the V:H ratio at 20:1, a vertical transmission rate of 12% with a population of 1000 buffalo is required. This vertical transmission rate is unreasonably high, and even at a herd size of 1500 buffalo the vertical transmission rate required to maintain infection and a reasonable number of infected eggs (a minimum of 5 each year) at a 20:1 V:H ratio is 10%. We believe these rates of vertical transmission are ecologically unrealistic, with reasonable vertical transmission rates in Aedes mosquitoes for other infections (ex. Lutomiah et al, 2007; Diallo et al, 2007; Baqar et al, 1993) ranging between 1–6% with 5–6% being high but within the realm of possibility. Therefore, given the uncertainty of environmental stochasticity and the high vertical transmission rates or high host population required, it is unlikely that RVF can persist in buffalo alone as the predominant mammalian host.

As more data is made available, these conclusions may be modified. Since the results of our model are sensitive to vector to host ratios, vertical transmission rates, and egg survival over dry seasons, it is important that more be learned about these aspects of mosquito biology. Considering the impact of environmental stochasticity on egg survival for more than 1 year may also play an important role in RVF virus maintenance emphasizing the importance of data elucidating the probability of long term survival of eggs. If the vertical transmission rates our model suggests are necessary for persistence are not viable, then focus can be shifted to the importance of unknown additional hosts. When we incorporate these cryptic hosts, the vertical transmission rate necessary and the minimum V:H ratio (MVH) are decreased to more reasonable levels. A 20:1 V:H ratio required only a 2.5% percent vertical transmission rate for 1000 buffalo and 1000 alternate hosts with average lifespan of 7 years. This 2.5% vertical transmission rate results in a minimum of 5 infected eggs and average of greater than 10 eggs surviving each dry season. With more infected eggs surviving, the virus is more likely to persist through stochastic events.

Other mammalian interepidemic hosts

In general, more infected eggs survive with higher V:H ratios and with more available hosts in our simulations. This suggests that the most likely mode of persistence apart from consistent re-introduction is a combination of buffalo and alternate competent hosts with high vector to host ratios in the wet season. When we explored how transmission efficiency and lifespan (herd turnover) of the cryptic alternate host affect the likelihood of persistence, we found that transmission efficiency plays a much larger role. Possible host species are numerous, as many ungulates have been shown to be susceptible to RVF. Antibodies to RVFV have been found in many wildlife species, including, but not limited to, impala, white rhinoceroses, bushbuck and waterbuck (Davies, 1975; Anderson & Rowe, 1998; Fischer-Tenhagen et al, 2000; Paweska et al, 2005; Evans et al, 2008; Paweska et al, 2008), but very little data exists on transmission efficiency for these species. Further studies are required to determine which species are most likely to be efficient transmitters of RVF in the inter-epidemic period.

Outbreaks without host immunity

We also used this model to briefly explore how considering a naïve population of mammalian hosts would affect the maintenance of the virus in the interepidemic period. We set initial herd immunity to 0, so the entire population of buffalo is susceptible to infection. We found that the initial outbreak in a naïve herd leads to so many infected animals that there are no susceptibles for future generations of RVF. In this case, persistence without re-introduction of either an infected host or more susceptibles, depends on high (6–10%) vertical transmission rates. This affects the invasion potential of the disease and the need for susceptible hosts with high turnover rates for it to successfully invade into and persist new areas as is feared in Europe (Chevalier et al, 2010) and North America (Kasari et al, 2008).

Possible model extensions and model refinement

Missing data about parameters such as the vertical transmission rates, how many Aedes(and Culex) mosquitoes are present in the wet season on average, reasonable vector to host ratios, the variation in number of mosquitoes present as weather varies, and transmission rates from alternate hosts increase the level of uncertainty in models such as ours. Acquisition and analysis of such data would not only greatly increase our understanding of Rift Valley fever, but would give us important insight into various other zoonotic mosquito born infectious diseases such as chikungunya, West Nile virus, and dengue among many others. With more and better data, researchers together with veterinarians, doctors, and public health colleagues, can better predict risk, good surveillance methods, total consequence, and optimal methods of control and prevention. This lack of data about mosquito biology and ecology as well as transmission rates for various species extends across most mosquito-borne diseases and will become more important with climate change and increased globalization.

In addition to benefiting from more data about mosquitoes and alternate host species, a reasonable next step is to include environmental stochasticity in the model via varying rainfall and mosquito carrying capacities, mosquito and egg survival, and vertical transmission rates. As we learn more about species that are competent hosts for RVF, we can include specific species information in the model instead of a general ‘alternate host’. How immunity plays a role is also important and the effect of waning immunity over time or maternal immunity should be considered. Our current model gives qualitative insights into the system, showing that a combination of mammalian hosts and vertical transmission are necessary to maintain the disease in the interepidemic period. But as we learn more about RVF and acquire better data, we can move toward developing models that can provide more accurate risk of outbreaks over time.

Appendix 1: Description of the Model

Let σ_v be the number of times a mosquito would bite a buffalo per unit time given the opportunity, σ_h be the maximum number of bites a buffalo sustains per unit time, and β_hv be the probability that when an infectious mosquito bites a buffalo it successfully transmits RVF to the buffalo. The value of σ_v depends on the mosquito’s gonotrophic cycle and preference, if any, for biting buffalo (see Chitnis et al, 2006 and Chitnis et al, 2013 for a complete description of the contact rate and its properties). The value of σ_h depends upon the size of buffalo, time spent near the mosquitoes, and evasive techniques such as switching the tail. When mosquito populations are very high, the contact rate is limited by availability of hosts; at lower to medium-high mosquito populations, the contact rate is dominated by the density of mosquitoes. The force of infection from mosquitoes to buffalo is ${\lambda }_h=\frac{{\sigma }_v{N}_v{\sigma }_h}{{\sigma }_v{N}_v+{\sigma }_h{N}_h}·\frac{I_v}{N_v}·{\beta }_{hv}$

or, in words, the product of (number of bites that one buffalo receives per unit time)*(probability that the biting mosquito is infectious)*(probability of transmission given an infected bite). Similarly, if we let σ_vh be the probability that if a susceptible mosquito bites an infectious buffalo it will be infected, then the force of infection from buffalo to mosquitoes is ${\lambda }_v=\frac{{\sigma }_v{\sigma }_h{N}_h}{{\sigma }_v{N}_v+{\sigma }_h{N}_h}·\frac{I_h}{N_h}·{\beta }_{vh}$.

Under these assumptions, the differential equations that model the system are:

$$\begin{array}{lll}\hfill \mathbf{Buffalo}\hfill & \hfill \mathbf{Mosquitoes}\hfill & \hfill \\ \frac{{dS}_h}{dt}=b_h{H}_0-d_h{S}_h-{\lambda }_h{S}_h,\hfill & \frac{{dS}_e}{dt}=b_v{V}_0\left(1-\frac{{\phi }_v{I}_v}{N_v}\right)-{\gamma }_e{S}_e\hfill & \frac{{dS}_v}{dt}={\gamma }_e{S}_e-d_v{S}_v-{\lambda }_v{S}_v\hfill \\ \frac{{dI}_h}{dt}={\lambda }_h{S}_h-d_h{I}_h-{\gamma }_h{I}_h-{\delta }_h{I}_h\hfill & \frac{{dI}_e}{dt}=b_v{V}_0\left(\frac{{\phi }_v{I}_v}{N_v}\right)-{\gamma }_e{I}_e\hfill & \frac{{dE}_v}{dt}={\lambda }_v{S}_v-d_v{E}_v-{\nu }_v{E}_v\hfill \\ \frac{{dR}_h}{dt}={\gamma }_h{I}_h-d_h{R}_h\hfill & \hfill & \frac{{dI}_v}{dt}={\nu }_v{E}_v-d_v{I}_v\hfill \end{array}$$

See Figure 1 for a transfer diagram of the model. If seasonality and disease are ignored and if it is assumed both mosquitoes and buffalo are at carrying capacity, then the disease free equilibrium is N_v =V₀, N_e =b_vV₀/γ_e , and N_h=H₀.

Figure 1.

Diagram for the disease transmission model. Arrows represent flow in or out of a compartment and letters above the arrows represent the rate of flow. The light grey arrows highlight where vertical transmission in mosquitoes occurs and mosquito-buffalo contact (i.e. a successful bite).

Seasons are implemented by adjusting V₀, the carrying capacity of mosquitoes, and other mosquito-related parameters through time. The number of infected eggs stored during the dry season is determined by multiplying ϕ_v times the number of infectious mosquitoes in the last month of the wet season.

The alternate reservoir host changes the susceptible and incubating mosquitoes equations to:

$$\begin{array}{l}\frac{{dS}_v}{dt}={\gamma }_e{S}_e-d_v{S}_v-({\lambda }_v+{\lambda }_r)S_v\\ \frac{{dE}_v}{dt}=({\lambda }_v+{\lambda }_r)S_v-{\nu }_v{E}_v-d_v{E}_v\end{array}$$

where λ_r is the force of infection from some reservoir host species to the mosquitoes, following the same format as σ_h distributing mosquito bites evenly between the alternate hosts and the buffalo.

Figure A1.

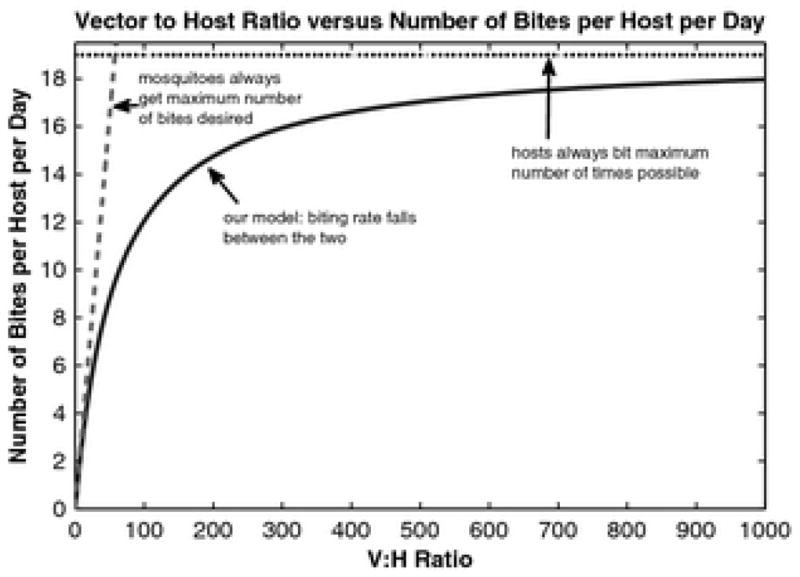
Plot of the number of bites per host per day as a function of the vector to host ratio.

Figure A2.

As in Figure 5, the average number of infected eggs surviving each dry season for (a) 1% and (b) 3% vertical transmission with varying host composition and varying vector to host ratios.