A model for the evolution in water chemistry of an arsenic contaminated aquifer over the last 6000 years, Red River floodplain, Vietnam

Abstract

Aquifers on the Red River flood plain with burial ages ranging from 500 to 6000 years show, with increasing age, the following changes in solute concentrations; a decrease in arsenic, increase in Fe(II) and decreases in both pH, Ca and bicarbonate. These changes were interpreted in terms of a reaction network comprising the kinetics of organic carbon degradation, the reduction kinetics of As containing Fe-oxides, the sorption of arsenic, the kinetics of siderite precipitation and dissolution, as well as of the dissolution of CaCO₃. The arsenic released from the Fe-oxide is preferentially partitioned into the water phase, and partially sorbed, while the released Fe(II) is precipitated as siderite. The reaction network involved in arsenic mobilization was analyzed by 1-D reactive transport modeling. The results reveal complex interactions between the kinetics of organic matter degradation and the kinetics and thermodynamic energy released by Fe-oxide reduction. The energy released by Fe-oxide reduction is strongly pH dependent and both methanogenesis and carbonate precipitation and dissolution have important influences on the pH. Overall it is the rate of organic carbon degradation that determines the total electron flow. However, the kinetics of Fe-oxide reduction determines the distribution of this flow of electrons between methanogenesis, which is by far the main pathway, and Fe-oxide reduction. Modeling the groundwater arsenic content over a 6000 year period in a 20 m thick aquifer shows an increase in As during the first 1200 years where it reaches a maximum of about 600 μg/L. During this initial period the release of arsenic from Fe-oxides actually decreases but the adsorption of arsenic onto the sediment delays the build-up in the groundwater arsenic concentration. After 1200 years the groundwater arsenic content slowly decreases controlled both by desorption and continued further, but diminishing, release from Fe-oxide being reduced. After 6000 years the arsenic content has decreased to 33 μg/L. The modeling enables a quantitative description of how the aquifer properties, the reactivity of organic carbon and Fe-oxides, the number of sorption sites and the buffering mechanisms change over a 6000 year period and how the combined effect of these interacting processes controls the groundwater arsenic content.

1. Introduction

The high geogenic arsenic concentrations in the groundwater of the great floodplains of SE and S Asia are a health threat to over 100 million people (Ravenscroft et al., 2009). The source of arsenic in the groundwater is generally believed to be arsenic contained in iron oxides that are deposited in association with the sediments on the floodplain by the rivers. Once the As-containing iron oxides enter the groundwater zone, arsenic is mobilized through reductive dissolution of the iron oxide with organic matter being the electron donor (McArthur et al., 2001; Dowling et al., 2002; Harvey et al., 2002; Swartz et al., 2004; Fendorf et al., 2010; Postma et al., 2007, 2010, 2012). A major unresolved problem concerning the arsenic contamination of groundwater in the floodplains of SE Asia, concerns the high spatial variability of the arsenic content (BGS/DPHE, 2001; van Geen et al., 2003; Winkel et al., 2011). Wells with a high arsenic content in the groundwater may be located within a few hundreds of meters from wells containing very little arsenic without any apparent explanation. Several explanations for the variability in groundwater arsenic have been put forward. Winkel et al. (2011) used a geostatistical approach in particular linking the occurrence of high arsenic groundwater to variation in geology and soil properties. Changes in the groundwater arsenic content have also been related to sedimentological variations at a small scale. Thus Weinman et al. (2008), Papacostas et al. (2008) and Sahu and Saha (2015) showed that high arsenic groundwater typically occurs in recently abandoned river channel deposits. Others have found that topography, small scale hydrogeology and the water levels have a decisive influence on arsenic mobilization (Polizzotto et al., 2008; Stuckey et al., 2015a). Also anthropogenic activities such as drawdown of reactive DOC by pumping (Harvey et al., 2002; Winkel et al., 2011; Lawson et al., 2013) or focused infiltration of high DOC at the margins of rice paddies (Neumann et al., 2010) have been proposed.

A more general feature is that the geochemical properties of the aquifer sediments are expected to change over time. Most arsenic contaminated groundwater on the great floodplains of SE Asia is found in the Holocene aquifers and the depositional age of these aquifer sediments ranges from a few decades to 11,700 years. The aquifer sediment initially consists of young, immature and therefore highly reactive material. Thus recent sediments may during unamended incubation become anoxic and release arsenic to water in a matter of days (Postma et al., 2010; Stuckey et al., 2015a). After deposition on the floodplain, the geochemical properties of the aquifer sediment will change over time in a fashion similar to that occurring during early diagenesis of anoxic marine sediment where such changes have been studied extensively (Berner, 1980; Boudreau, 1997; Burdige, 2006).

First of all, during early diagenesis of marine sediment there is a strong decrease in the reactivity of sedimentary organic carbon caused by the preferential microbial consumption of the most reactive carbon (Middelburg, 1989; Boudreau and Ruddick, 1991; Boudreau, 1997; Arndt et al., 2013). The sedimentary organic matter will successively react in terminal electron accepting processes (TEAP) following the energy yield related to each electron acceptor. In this fashion marine anoxic sediment will pass through a range of diagenetic changes that last for thousands of years and have been well studied. Aquifer sediment resembles marine anoxic sediments but with two major differences. First of all the transport mechanisms in marine sediments are predominantly diffusion and bioturbation, while advective transport characterizes aquifers. Secondly, in contrast to marine sediments, the sulfate content of water entering fresh aquifers is generally low and therefore Fe-oxide reduction and methanogensis become the predominant TEAP’s. Here we present a first attempt to comprehensively quantify the early diagenesis of the Holocene sediments in an arsenic contaminated aquifer and elucidate how early diagenesis affects the groundwater arsenic content.

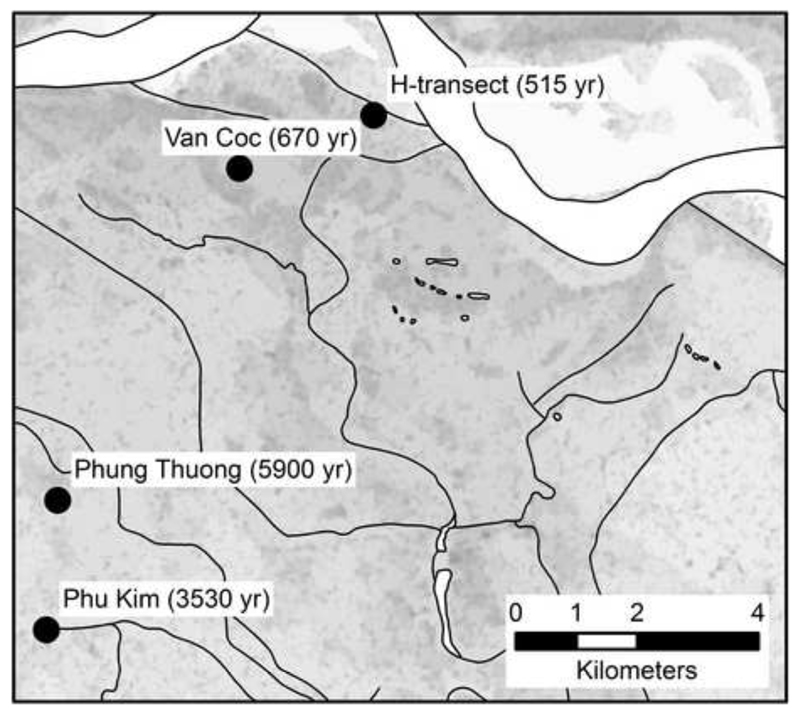
Towards this objective we have used and extended the datasets of a field site (Fig. 1) on the Red River floodplain (Postma et al., 2007, 2010, 2012; Larsen et al., 2008; Jessen et al., 2012). At this field site aquifer sediments of different burial ages, ranging from 500 to 6000 years, have been identified and extensive data is available on groundwater and sediment chemistry as well as on groundwater dating. Here we use this dataset to analyze how the geochemical processes change as a function of time and incorporate this new knowledge into a reactive transport model that is able to quantify and predict how the bulk groundwater chemistry, including the arsenic concentration, changes in the course of 6000 years of burial of the aquifer sediment.

Fig. 1.

The location of investigation sites on the Red River floodplain about 30 km NW of Hanoi. Years indicate the burial age of the aquifer sediment as measured by optical stimulated luminescence (Postma et al., 2012).

2. Materials and Methods

2.1. Geology and hydrogeology of the field area

The geology of the field area consists of unconsolidated Quaternary deposits overlying consolidated pre-Quaternary deposits. The Holocene deposits are dominated by sandy channel deposits and fine grained deposits of silt and clay. An up to six meter thick layer of fractured overbank clay and silt is overlying most of the Holocene aquifer. Pleistocene deposits, predominantly gravel deposits but also containing sand and clay layers, are underlying the Holocene deposits.

At Phu Kim (Fig. 1), only Holocene sandy aquifer deposits are present with a thickness of 12 m. At Phung Thuong the Holocene aquifer is 10 m thick, and overlying an 18 m thick silt and clay layer, which is situated on top of a lower aquifer, probably of Pleistocene age. At Van Coc, a 17 m thick upper Holocene aquifer is found on top of a 16 m thick sequence of silt and clay, which separates the Holocene and Pleistocene aquifers. At the H-transect, the Holocene aquifer has about the same thickness and is in direct hydraulic contact with the underlying Pleistocene aquifer. The sediment burial age of the upper aquifers was determined, on sediments from 8-15 m depth, by optical stimulated luminescence (Postma et al., 2012). The sediments for dating were taken with a piston corer in stainless steel coreliners to prevent any daylight exposure. The obtained ages are shown in Fig. 1.

The hydrogeology of the field area was described by Larsen et al. (2008). The overall groundwater flow in the shallow Holocene sandy aquifer is directed towards the Red River in the northeast. The flow is, however, locally controlled by the presence of low-permeable layers and the interaction with the many bodies of surface water yielding a groundwater flow regime consisting of a series of local shallow flow systems. Groundwater flow in the cross-section has been simulated numerically in a 2D model using the code MODFLOW (Postma et al., 2012). Tritium-Helium dating of the groundwater showed a vertical groundwater flow rate of 0.5 m/yr at Phu Kim, Phung Thuong and the H-transect while at Van Coc a rate of 0.25 m/yr was found (Postma et al., 2012).

The groundwater chemistry for the H-transect was first presented by Postma et al. (2007). For the other localities, selected parameters were shown by Postma et al. (2012) while the bulk chemistry is presented here for the first time. The methods for sampling and analysis are similar to those described by Postma et al. (2007). Speciation and saturation states for various minerals were calculated using PHREEQC-3 (Parkhurst and Appelo, 2013) employing the WATEQ4F.DAT database but using the compilation of Langmuir et al. (2006) for arsenic speciation.

Sediment chemistry was partly presented by Postma et al. (2012) but is here extended with new data together with revised and corrected data. Secondary precipitates were extracted by sediment leaching at pH 3 under anoxic condition. The pH was controlled at 3 by using an automatic titrator loaded with HCl. The sediment content of crystalline Fe-oxides was extracted using 0.2 M ammonium oxalate and 0.1 M ascorbic acid adjusted at pH 3 (Wenzel et al., 2001). Naturally this also extracts secondary precipitates and the Fe-oxide bound Fe and As contents were determined by subtraction of the Fe and As released in HCl at pH 3, carried out in parallel extractions.

2.2. Methodology for reactive transport modeling

One-dimensional reactive transport modeling was done using PHREEQC-3 (Parkhurst and Appelo, 2013), again employing the WATEQ4F.DAT database with the compilation of Langmuir et al. (2006) for arsenic speciation. Briefly a modeling column of 40 cells, each of 0.5 m length, was used with a time step of one year yielding a transport rate of 0.5 m/yr in agreement with groundwater dating. A period of 6000 years was modeled covering the time space indicated by dating the sediment burial age. Dispersion was not considered. As input solution into the column, water with a chemical composition similar to the Red River was used (Postma et al., 2007). The oxidation of organic carbon, the reduction of iron oxide, the precipitation and dissolution of siderite and the dissolution of calcite are all controlled by kinetic rate equations. The formulations of the rate equations and their parameters are presented in Section 3. The ordinary differential equation solver (CVODE) for stiff systems was used for the kinetic calculations which stabilized the calculations a lot. All kinetic processes are uniformly distributed over cells 2-40, with the exception of calcite dissolution which is constrained to cell 1 together with a constant partial pressure of CO₂ of 10^-1.1 in order to simulate unsaturated zone open system calcite dissolution.

The composition of the iron oxide was redefined to contain a trace of As(V). Upon reduction of the iron oxide, arsenic is released to the aqueous phase, reduced to As(III) which may subsequently adsorb onto the surface of the remaining iron oxide. As(III) adsorption is described using the Langmuir equation and the number of sorption sites available for As(III) is linked to the amount of iron oxide present. As the iron oxide becomes reduced, the As(III) sorption sites disappear. The input file is given in the Electronic Annex and is also available upon request, together with the used database, from the first author.

3. Results

3.1. Groundwater chemistry and process understanding

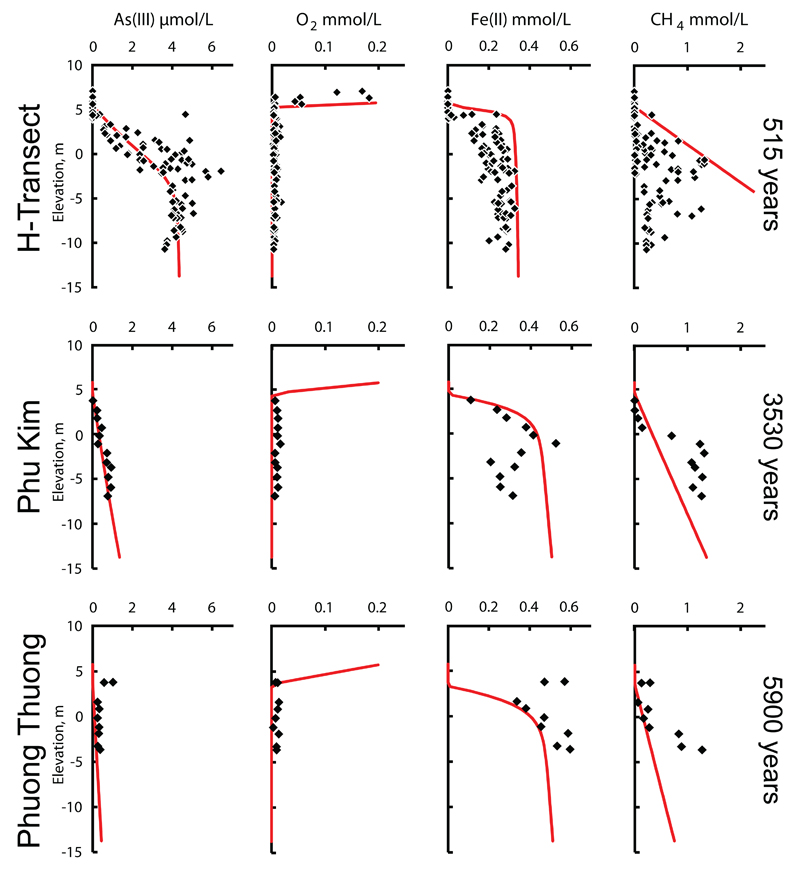
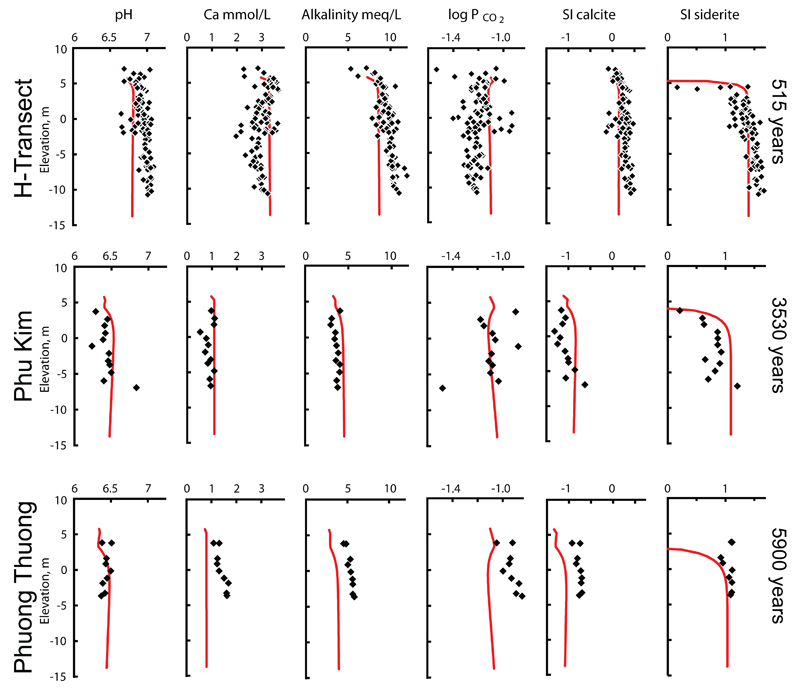
Figures 2 and 3 show the groundwater chemistry respectively after a sediment burial age of 515, 3530 and 5900 years. The most eye-catching change is the decrease in the groundwater arsenic content over time; from up to 7 μmol/L at 515 years in the H-transect, via up to 1.5 μ mol/L at Phu Kim after 3530 years and to up to 1 μmol/L at Phuong Thuong after 5900 years of burial. Groundwater data from the locality Van Coc (Fig. 1) is not shown in Figs. 2-3 for space reasons, also because the burial age at Van Coc of 670 years is close to the H-transect with 515 years and the water chemistry resembles that of the H-transect. Additional significant changes in water chemistry that are observed as a function of burial age comprise an increase in the groundwater Fe(II) concentration from 0.3 mmol/L in the H-transect at 515 years, to close to 0.6 mmol/L at Phuong Thuong at 5900 years (Fig. 2), as well as decreases in pH from close to 7 to 6.5, Ca declining from 3.5 mmol/L to less than 1 mmol/L and alkalinity dropping from 10 meq/L to about 4 meq/L (Fig. 3). Associated major changes are found in the saturation indices (SI) of calcite and siderite which decrease from slightly above zero to -1 for calcite and from 1.4 to around 1 for siderite (Fig. 3).

Fig. 2.

The groundwater chemistry at three sites (Fig. 1) with the burial age, as measured by optical stimulated luminescence (Postma et al., 2012), indicated at the right margin. The solid lines reflect model predictions.

Fig. 3.

The groundwater chemistry at three sites (Fig. 1) with the burial age, as measured by optical stimulated luminescence (Postma et al., 2012), indicated at the right margin. The solid lines reflect model predictions.

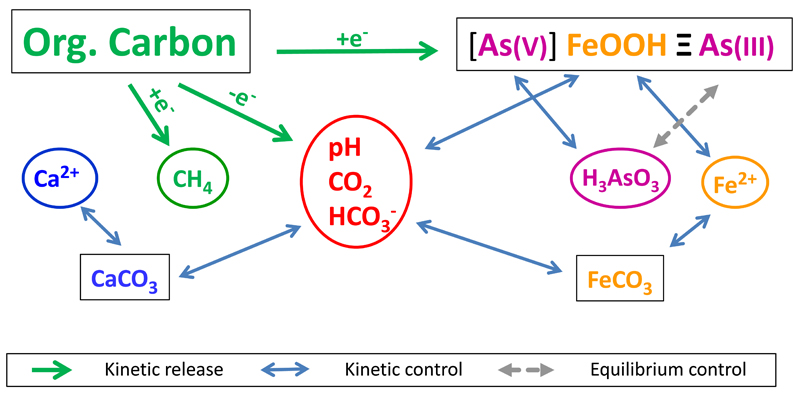
These changes in the groundwater chemistry are the combined result of the geochemical processes summarized in Fig. 4. The key reaction is the oxidation of sedimentary organic carbon. Coupled to the reduction of iron oxide the process proceeds according to reaction:

$$\text{C}{\text{H}}_2\text{O}+4\text{FeOOH}+7{\text{H}}^{+}\to 4\text{F}{\text{e}}^{2+}+\text{HC}{\text{O}}_3^{-}+6{\text{H}}_2\text{O}$$ (1)

This reaction increases the Fe(II) and alkalinity as well as the pH in the groundwater (Fig. 2-3). The main competing redox reaction is methanogenesis following the overall reaction:

$$2\text{C}{\text{H}}_2\text{O}\to \text{C}{\text{H}}_4+\text{C}{\text{O}}_2$$ (2)

The importance of this reaction is reflected by the elevated methane concentration of the groundwater (Fig. 2). Overall it is the reactivity of the organic carbon source that limits the extent of organic matter degradation (McArthur et al., 2001; Postma et al., 2007; Rowland et al., 2007; Fendorf et al., 2010; Stuckey et al., 2015a). The relative importance of organic matter degradation through methanogenesis and Fe-oxide reduction primarily depends on the reaction kinetics of reductive dissolution of Fe-oxide. The influence of other terminal electron acceptors is small because their abundance is low. Oxygen (Fig. 2) and nitrate (not shown) only appear in the uppermost samples and sulfate concentrations are generally very low (Postma et al., 2007).

Fig. 4.

Geochemical processes controlling the groundwater composition and their interactions.

The source of arsenic in the groundwater is believed to be arsenic contained in Fe-oxide (McArthur et al., 2001; Akai et al., 2004; Islam et al., 2004; Postma et al., 2007, 2010; Fendorf et al., 2010; Stuckey et al., 2015b). Figure 5a shows the arsenic content of the Fe-oxide phase in our sediments to be close to an As/Fe ratio of 1.2 mmol/mol and to be quite constant from site to site. This value is much higher than the As/Fe ratio of 0.2 mmol/mol reported by Kocar and Fendorf (2009) and Kocar et al. (2014). The compilation of Fendorf et al. (2010) for sediments from Bangladesh, Cambodia and Vietnam yielded an As/Fe ratio of around 0.3 mmol/mol but with a great deal of scatter. However, as already noted by Postma et al. (2007) the Red River floodplain sediments are apparently richer in arsenic than those in Bangladesh. Comparison with the As/Fe ratio in the groundwater (Fig. 5b) shows that in the course of reductive dissolution of Fe-oxide, arsenic is partitioned stronger into the aqueous phase than iron, as reflected by the data distribution relative to the line indicating the As/Fe ratio of 1.2 mmol/mol in both panels of Fig. 5. This partitioning reflects that most of the released Fe(II) must be reprecipitated as secondary phases while more of the released As remains in solution. To illustrate the extent of Fe(II) precipitation a line has been added to Fig. 5b delineating 90% reprecipitation of Fe as compared to As. Experiments where aquifer sediment was leached at pH 3 show the accumulation of Fe(II) which is highest in the youngest sediments at Van Coc and the H-transect while these secondary precipitates contained very little arsenic (Postma et al., 2012). Siderite has been identified in the sediment and probably constitutes the major part of the sedimentary Fe(II).

Fig. 5.

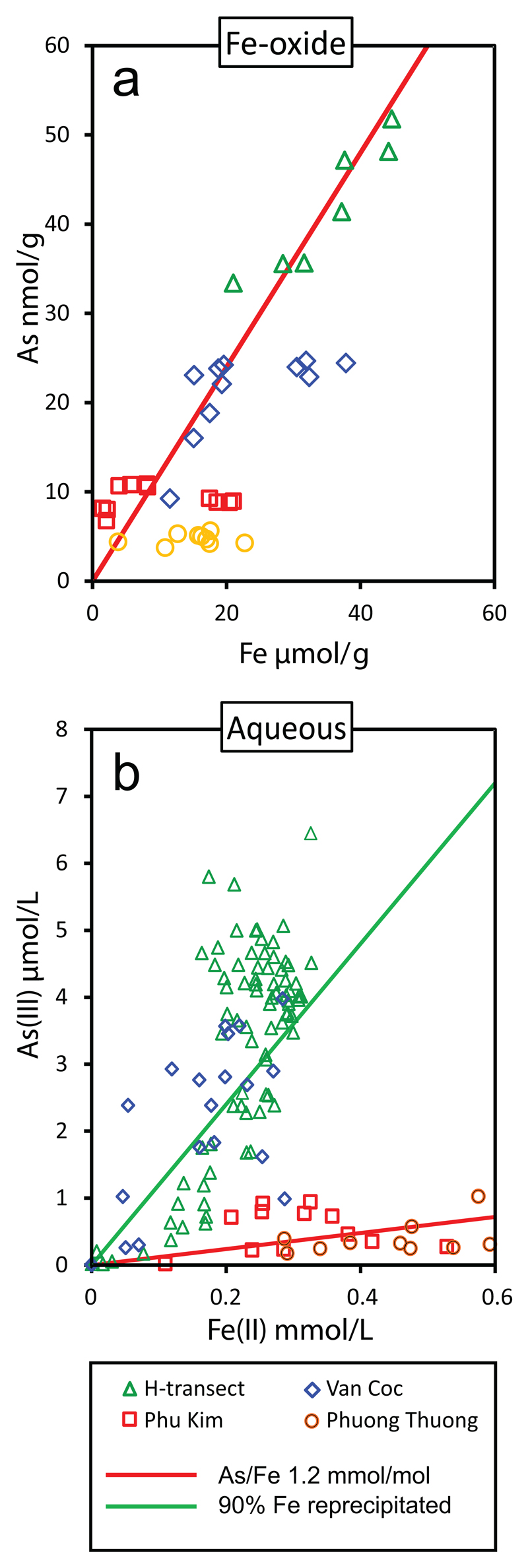
The partitioning of arsenic and iron between solid and aqueous phases: a) the As/Fe ratio in the iron oxides of the sediments at the four sampling sites (Fig. 1), b) the As/Fe ratio in the groundwater at the same sites. The red line indicates the same As/Fe ratio in both panels. The green line in the right panel reflects 90% reprecipitation of the Fe released from the Fe-oxide phase.

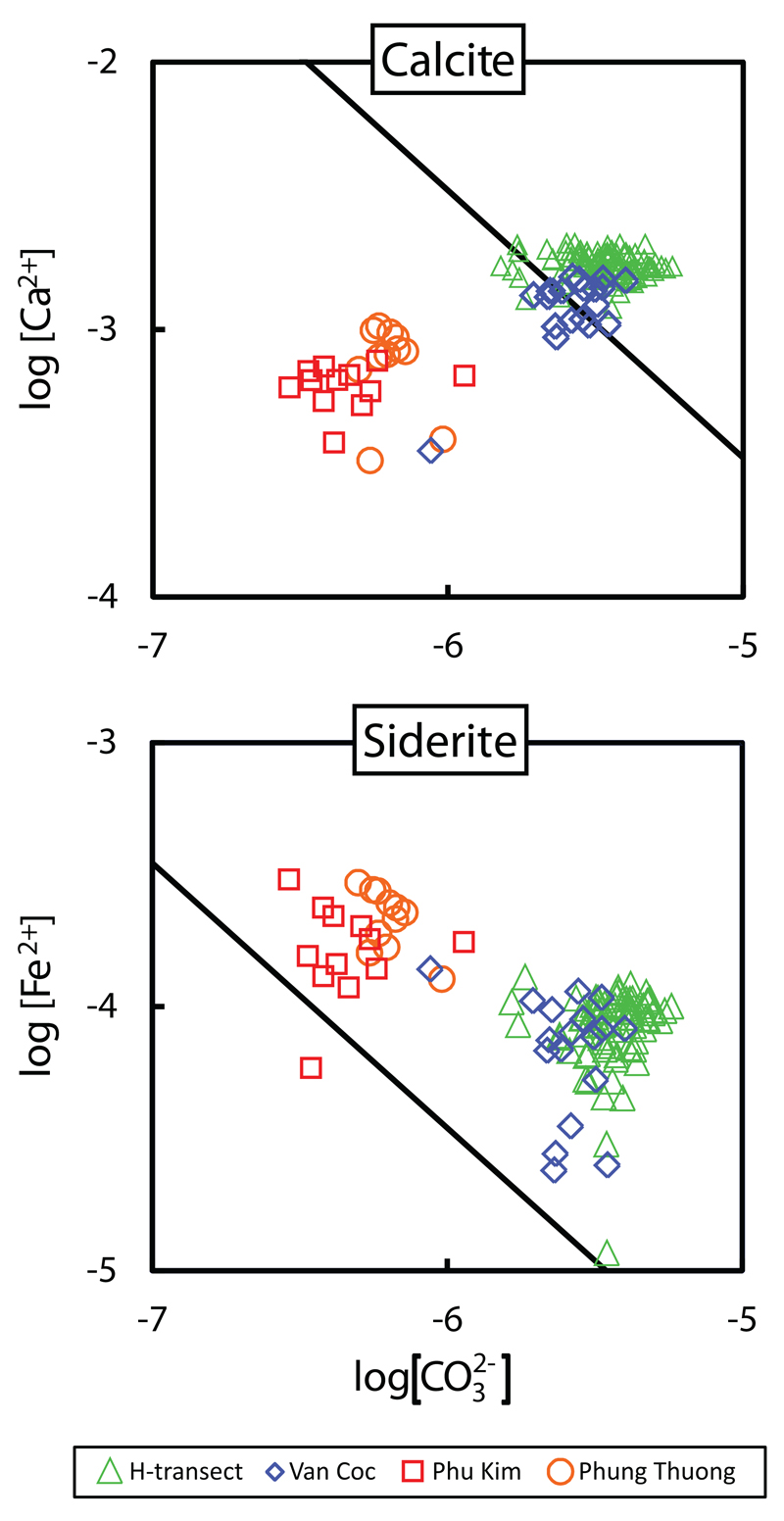
At all sites, the P_CO2 is very high (Fig. 3) and near constant at 10^-1.1 from the top of the profile downward, indicating that most of the CO₂ production takes place in the soil or unsaturated zone. The Ca concentration in the groundwater is at each site also nearly constant from the top of the saturated zone and downward (Fig. 3). Together, these observations indicate that most calcite dissolution proceeds in the soil or unsaturated zone under open system conditions with respect to CO₂ (Appelo and Postma, 2005). Over time the CaCO₃ available for dissolution apparently becomes less reactive as is reflected by the increasing degree of subsaturation for calcite (Fig. 3). Figure 6 shows the groundwater ion activity distribution for the ions in siderite and calcite. For calcite, the youngest sites, H-transect and Van Coc, are close to saturation or slightly supersaturated while the older sites, Phu Kim and Phuong Thuong, move away from the saturation line and become distinctly subsaturated and suggests simple dissolution of CaCO₃. For siderite the data distribution is roughly parallel with the siderite line, as if FeCO₃ equilibrium is controlling the distribution of the aqueous activities of Fe²⁺ and CO₃^2-. However, the data is displaced towards supersaturation, most in the young sites and somewhat less in the older sites. Supersaturation for siderite in sediments where siderite is precipitating has been observed previously (Postma, 1982; Swartz et al., 2004; Kocar and Fendorf, 2009).

Fig. 6.

The activities of Fe²⁺, Ca²⁺, CO₃^2- in groundwater as compared to the solubility products of siderite and calcite. For siderite, the line indicates the solubility product, pK = 10.45, for calcite the solubility product pK = 8.48.

Once released to the groundwater, the mobility of arsenic is confined by adsorption to the sediment particles. In the field data the adsorption of As(III) to the sediment is reflected in the delayed downward appearance of As(III) as compared to Fe(II) (Fig. 2). Jessen et al. (2012) showed in a forced gradient experiment at our field site that the As(III) concentration quickly responded to changes in the water composition, indicating reversible sorption of As(III) to the sediment, in agreement with the results of Radloff et al. (2015). At a field locality 50 km to the SE of the present locality on the Red River flood plain we investigated the adsorption of As(III) onto aquifer sediment (Nguyen et al., 2014) and found that As(III) adsorption was fully reversibly and showed almost linear adsorption with few indications of competitive adsorption.

3.2. The reactive transport model

3.2.1. Model development and formulation

The challenge in building a reactive transport model describing the change in the arsenic concentration of the groundwater over time is that all processes displayed in Fig. 4 interact. Most of these interactions proceed through the strong pH dependency of the Fe-oxide reduction reaction that is displayed in Eqn. (1). Reductive dissolution of Fe-oxides by itself has a strong pH increasing effect (Eqn. 1), disfavoring Fe-oxide reduction. However, the precipitation of siderite, written in terms of predominant species in Eqn. 3:

$$\text{F}{\text{e}}^{2+}+\text{HC}{\text{O}}_3^{-}\leftrightarrow \text{FeC}{\text{O}}_3+{\text{H}}^{+}$$ (3)

favors Fe-oxide reduction by lowering the pH and removing dissolved Fe(II). Any other process that lowers pH will also favor Fe-oxide reduction and vice versa. For example methanogenesis produces carbon dioxide (Eqn. 2) which forms carbonic acid and lowers the pH and thereby increases the extent of Fe-oxide reduction. Finally, the P_CO2, pH and alkalinity of the infiltrating water will influence the processes listed above. Accordingly, a reactive transport model that is able to predict the groundwater arsenic concentration over time must include all major geochemical processes affecting the bulk water composition.

The present model is an extension of the model published by Postma et al. (2007). Again the flow system is modeled as a 1D flow tube by only modeling the vertical flow component of the groundwater. This is justified by groundwater dating, using the Tritium–Helium method, which showed that the H-transect, Phu Kim and Phuong Thuong sites all had the same vertical infiltration rate of 0.5 m/yr (Postma et al., 2012). The implicit assumption is that the present day flow rate is also valid backward in time. The model of Postma et al. (2007) only covered the passage of one pore volume over 40 years employing a constant rate of organic carbon degradation and equilibrium controls for all other reactions, including the stability for Fe-oxides. The Postma et al. (2007) model is clearly inadequate for modeling changes in water chemistry over 6000 years.

The degradation of organic carbon is the overall engine driving the reduction of As-containing Fe-oxides (Postma et al., 2007; Kocar et al., 2014; Stuckey et al., 2015a) and the degradation rate will decrease as time goes by. Boudreau and Ruddick (1991) and Boudreau (1997) developed a concept to describe the reactivity of natural organic carbon as a reactive continuum of pools of organic carbon, each with a different rate, whose distribution is described by a gamma distribution function. This model has since been used to model the degradation of organic matter in marine sediments over time (Contreras et al., 2013; Meister et al., 2013; Stolpovski et al., 2015). Postma (1993) demonstrated that the rate equation for the reactive continuum of Boudreau and Ruddick (1991) is equivalent to the formulation of the rate law shown in Eqn. (4) which we have used to describe the degradation of organic carbon over time.

$$-\text{d}{\text{C}}_{\text{C}}\text{/dt}={\text{m}}_{\text{O}}\cdot 9.3\cdot {10}^{-12}\cdot {({\text{m}}_{\text{t}}\text{/}{\text{m}}_{\text{O}})}^{2.5}(\text{mol/sec})$$ (4)

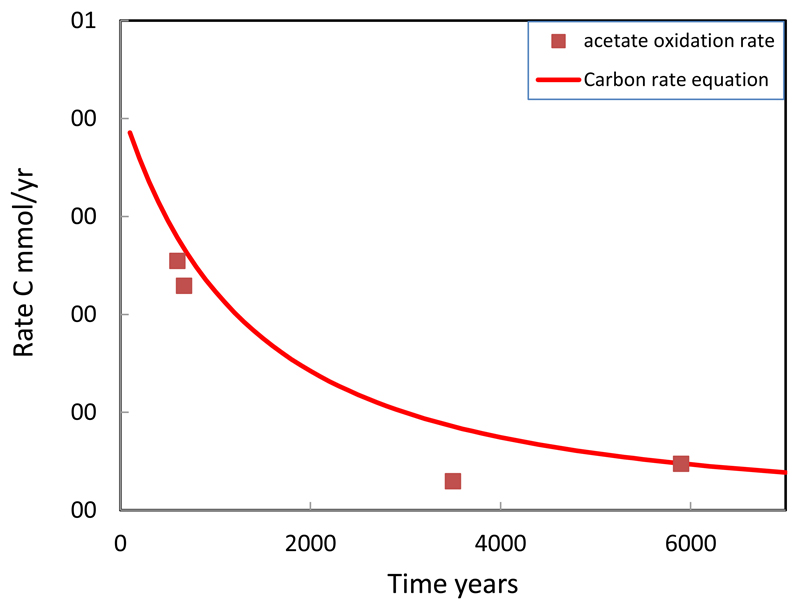
Here m_o = 1.36 mol/L is the initial mass of organic matter based on the analytical concentration 0.27 % C in the H-transect, recalculated to the concentration per liter of contacting groundwater, m_t, the mass of organic carbon at time t and 9.3·10^-12 sec^-1 the rate constant. The exponent to (m_t/m_o) reflects the heterogeneity of the organic carbon reactivity. For a first order rate dependency the exponent would be one; the exponent value of 2.5 reflects a larger difference between the most and least reactive organic carbon. The values of the rate constant and the exponent were derived by trial and error fitting of the equation to the field data. The change in the rate of carbon degradation predicted by Eqn. 4 is shown in Fig. 7.

Fig. 7.

The rate of organic carbon degradation as a function of time. Symbols represent radiotracer acetate oxidation rate measurements on sediments whose burial age was dated by optical stimulated luminescence (Postma et al., 2012). The solid line is given by rate Eqn. (4) as incorporated in the model.

In the model the rate expression for organic carbon controls the sum of the rates of methanogenesis and Fe-oxide reduction by using the partial equilibrium concept of Postma and Jakobsen (1996). Postma et al. (2012) measured the in situ rates of methanogenesis by CO₂ reduction and acetate reduction by radiotracer methods in order to derive the in situ rate of organic matter oxidation. The measured rates of methanogenesis by CO₂ reduction were two to three orders of magnitude higher than those by acetate reduction (Postma et al., 2012). Also acetate oxidation rates were measured and in the absence of other TEAP’s, such as O₂, NO₃, SO₄ or MnO₂, acetate oxidation rates must reflect the rate of Fe-oxide reduction. The acetate oxidation rate decreases over time as displayed in Fig. 7 and is shown to concord reasonably with the rate equation (Eqn. 4) fitted to the groundwater chemistry data. It might be noticed that measured rates of methanogenesis by CO₂ reduction (Postma et al., 2012) were about an order of magnitude higher than rates of acetate oxidation. The introduction of carbon degradation rates corresponding to measured rates of methanogenesis by CO₂ reduction into the model resulted in far too high methane concentrations. A partial explanation could be that strong degassing of methane from the aquifer occurs (Postma et al., 2012). Another explanation could be a spatial discretization in the availability of H₂ and acetate for the various TEAP’s, e.g. most of the H₂ produced from organic carbon is used by methanogens before it reaches Fe-oxide containing domains of the sediments. It is also possible that the partial equilibrium approach is too simple to represents the microbial pathways of methanogenesis and Fe-oxide reduction. In any case we may conclude that organic carbon degradation rates given by acetate oxidation are consistent with the bulk water chemistry.

The reduction rate of Fe-oxides in the sediments is controlled by their mineralogy, which controls the thermodynamic stability, and by their reactivity through factors like reactive surface area, crystal surface properties, bacterial reduction kinetics etc. Clearly the more stable iron oxides like hematite and goethite yield less energy during reduction than the least stable iron oxides such as ferrihydrite. Also the less stable iron oxides, like ferrihydrite, are generally more reactive than the more stable ones (Larsen and Postma, 2001; Bonneville et al., 2009). In addition catalytic transformations can occur in the presence of aqueous Fe(II) transforming ferrihydrite into more stable iron oxides (Pedersen et al., 2005). In our sediment, hematite and goethite are the only Fe-oxides that have been identified (Postma et al. 2010). In aquifer sediments an assembly of Fe-oxides with varying mineralogy and different kinetic properties will be present which can be described as a reactive continuum similar to the approach used for organic matter (Postma, 1993). We have constructed a rate equation to describe the reduction of Fe-oxides in the aquifer sediment that both contains the thermodynamic and the kinetic contributions.

$$-\text{d}{\text{C}}_{\text{FeOOH}}\text{/dt}=m_{\text{O}}\cdot 2.54\cdot {10}^{-11}\cdot {(m_t\text{/}{m}_{\text{O}})}^{1.5}\cdot (1-{\text{SR}}_{\text{FeOOH}})(\text{mol/s})$$ (5)

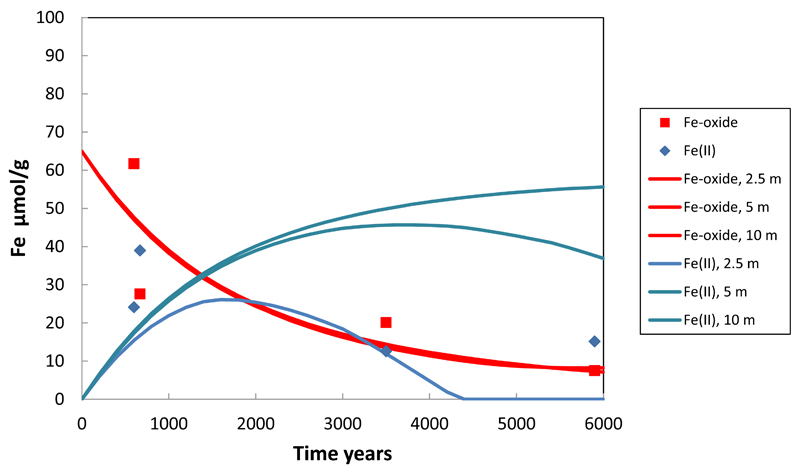
Here m_o is 0.394 mol/L corresponding 65 μmol FeOOH/g obtained by extrapolation from the field data. SR_FeOOH is the Saturation Ratio (IAP/K). In the model, the solubility of Fe-oxide (for the reaction FeOOH + 3H⁺ → Fe³⁺ + 2H₂O) has a value of logK = 0.391, much closer to goethite (logK = -1.0) than to ferrihydrite (logK = 4.891). In addition the composition of the Fe-oxide was changed to contain 1.2 mmol As(V) per mol of Fe (Fig. 5a). The approach of introducing arsenic into the system as constituent of the Fe-oxide is similar to that used by Postma et al. (2007). The parameters in the rate equation were again obtained by trial and error on reproducing the groundwater chemistry. In Fig. 8 the decrease in Fe-oxide content in the sediment calculated by the model is compared with the measured Fe-oxide content and even though the measured data shows a great deal of scatter, there is a reasonable agreement.

Fig. 8.

Symbols indicate concentrations of Fe-oxide and Fe(II) measured in sediments whose burial age was dated by optical stimulated luminescence (Postma et al., 2012). The solid lines give the Fe-oxide and Fe(II) sediment concentration at different depths as calculated by the model.

The precipitation of siderite in natural sediments generally appears to take place at about one order of magnitude of supersaturation (Postma, 1982; Swartz et al., 2004; Kocar and Fendorf, 2009). In our data the Saturation Index (SI = logSR) ranges from about 1.6 in the young sediments to < 0 in the older sediments; i.e. from precipitation at strong supersaturation to dissolution at SI < 0. In the model this behavior is described using the following rate equation:

$$-\text{d}{\text{C}}_{\text{FeC}{\text{O}}_3}\text{/dt}=3.17\cdot {10}^{-12}\cdot (1-\text{S}{\text{R}}_{\text{FeC}{\text{O}}_3})(\text{mol/s})$$ (6)

Where the Saturation Ratio is SR _FeCO3 = IAP/K and K _FeCO3 = 10^-9.89 which corresponds to ten times supersaturation relative to the solubility product of siderite. Fig. 8 compares the model calculated siderite content with the amount of Fe(II) extracted from the sediment with HCl at pH 3, which should comprise siderite. Particularly at later times the agreement is not very good. However, only one measured data point per profile is available while the model predicts a major depth variation in siderite content.

The depth profiles for Ca and P_CO2 are at all sites constant from the top of the saturated zone to the base of the profile (Figs. 3). In addition the P_CO2 is very high, near 10^-1.1 (Fig. 3), indicating that most of the CO₂ production and CaCO₃ dissolution takes place already in the soil and unsaturated zone. Therefore a constant P_CO2 of 10^-1.1 was imposed only to the uppermost cell in the model and this is also the only place where CaCO₃ dissolution is allowed to take place. At Phu Kim and Phuong Thuong the SI for CaCO₃ as well as the Ca concentration are lower (Fig. 3) indicating that progressively less reactive CaCO₃ is available for dissolution. The rate law for dissolution of CaCO₃ is:

$$-\text{d}{\text{C}}_{\text{CaC}{\text{o}}_3}\text{/dt}=m_{\text{O}}\cdot 2.38\cdot {10}^{-11}\cdot {(m_t\text{/}{m}_{\text{O}})}^{3.0}\cdot (1-\text{SRCaC}{\text{O}}_3)(\text{mol/s})$$ (7)

In this equation SR _CaCO3 contains a K _Calcite that is increased by log 0.25 to be consistent with the measurements in the groundwater of the youngest sediments (Figs. 3, 6). This could reflect the presence of slightly more soluble aragonite from shells fragments in the sediment.

For sorption of arsenic we only consider adsorption of As(III) and use the Langmuir adsorption model of Nguyen et al. (2014). The Langmuir equation states:

$$[S_{H_{3}As{O}_3}]=\frac{[s_{tot}]K[H_{3}As{o}_3]}{1+K[H_{3}As{o}_3]}$$ (8)

Here [S_H3Aso3] reflect sorbed As(III), [S_tot] the total number of available sites and the adsorption constant K = 10^3.176 as determined by Nguyen et al. (2014). Work in progress has since shown that [S_tot] is related to the Fe-oxide content of the sediment. In the model the number of adsorption sites is therefore coupled to the amount of Fe-oxide present with a site density of 0.07 moles adsorption sites per mole of Fe-oxide. Accordingly the number of adsorption sites decreases as more Fe-oxide becomes reduced.

3.2.2. Model results and comparison with field data

The model results for different times are presented as full lines together with the field data in Figs. 2-3. Most conspicuous is the decrease in the groundwater arsenic content over time which is well captured by the model (Fig. 2). The decrease of arsenic in the groundwater is fundamentally a result of a decrease in the rate of Fe-oxide reduction, which contains As(V), caused by declining rates of organic carbon degradation and Fe-oxide reactivity over time. The decline in the reactivity of organic carbon is also reflected in the decrease of the modeled methane content (Fig. 2). Over time the rate of Fe-oxide reduction declines faster than the rate of organic carbon degradation; at 200 years the rate of Fe-oxide reduction constitutes 54-58% of the rate of organic carbon degradation while at 6000 years the percentage has fallen to 21-23%. Translating these numbers in terms of electron flow; because each oxidized carbon releases four electrons, the rate of Fe-oxide reduction should be divided by four and only constitutes between about 14% (200 yr) and 5.5% (6000 yr) of the electron flow from organic C degradation. Because the rate of methanogenesis is half that of organic carbon degradation (Eqn. 2) the rate of Fe-oxide reduction is between 28% (200 yr.) and 11%, (6000 yr.) of the rate of methanogenesis. Clearly, most of the modeled electron flow from organic C degradation proceeds through the methanogenesis pathway.

While arsenic decreases over time, Fe(II) in groundwater increases over time (Fig. 2). As shown in Fig. 5, arsenic is strongly partitioned into particularly the young groundwater, but delayed by sorption, while the bulk of the produced Fe(II) is precipitated as siderite. It confirms previous writings on the decoupling of the processes controlling the arsenic and iron concentrations in groundwater (Horneman et al., 2004; van Geen et al., 2006). The increase in Fe(II) concentration is the result of the decrease in groundwater pH (Fig. 3) which is again caused by less dissolution of CaCO₃ in the soil and unsaturated zone in the older sediments lowering the Ca and alkalinity concentrations (Fig. 3) as well as SI_calcite (Fig. 3). The lower pH and alkalinity allow more Fe(II) to remain in solution in equilibrium with siderite.

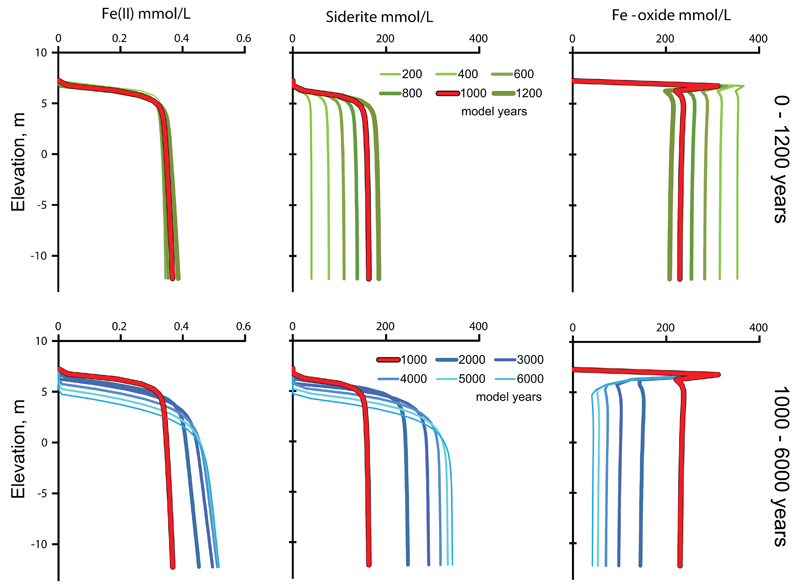
Figure 9 shows arsenic cycling between the different model pools in the course of time in more detail. The concentration of arsenic in the solid phase is expressed per liter of contacting groundwater to enable direct comparison of the pool sizes of arsenic. In the upper left panel the groundwater arsenic content is shown in time steps of 200 years and it increases until a maximum of about 8μmol/L or 600 μg/L is reached at the base of the profile at 1200 years. The source of As is the release from Fe-oxide being reduced and the rate of this process decreases over time. In principle this should cause a continuous decreasing As concentration in the groundwater. However during the first 1200 years most of the As(V) released from the Fe-oxides becomes adsorbed as As(III) to the remaining Fe-oxide. Therefore the As increase in the groundwater during the first 1200 years reflects the progression of arsenic adsorption (Fig. 9). The lower left panel shows in time steps of 1000 years how the arsenic concentration subsequently declines with the decreasing rate of Fe-oxides reduction but now delayed by the desorption of arsenic from the Fe-oxide. Even after 6000 years the groundwater arsenic concentration is still up to 0.44 μmol/L or 33 μg/L As, more than three times the WHO limit.

Fig. 9.

The turnover of arsenic between aqueous and sedimentary models pools. Upper row 200-1200 years in 200 yr steps, lower row 1000-6000 years in 1000 yr steps. The bold red line, indicating 1000 years, is the same in upper and lower panels. Solid phase concentrations have been recalculated to concentration per liter of contacting groundwater to enable comparison.

The largest pool of arsenic in the system is at all times As(V) contained in the Fe-oxide which contains 1.2 mmol As(V)/mol Fe-oxide. This pool decreases from an initial 425 μmol/L to about 52 μmol/L at 6000 years (Fig. 9). A layer enriched in Fe-oxide bounded arsenic develops uppermost in the profile. This arises because the presence of oxygen in the incoming solution inhibits Fe-oxide reduction. The second largest pool is As(III) adsorbed on Fe-oxides. Initially it is small but builds up together with the aqueous concentration to a maximum at about 1200 years and then decreases as arsenic is leached from the column and also the amount of adsorbent Fe-oxide declines. While the pool of adsorbed As(III) mirrors the aqueous As(III) concentration, adsorbed As(III) is, calculated per liter of contacting groundwater, about twenty times higher than aqueous As(III). Thus by comparison, the aqueous pool of arsenic is always much smaller than the sedimentary pools and therefore remains very sensitive towards changes in these.

During the first 1200 years, the Fe(II) concentration of the groundwater (Fig. 10) is near constant, being buffered by precipitation of siderite. The amount of Fe-oxide reduced is almost quantitatively (initially 90 to 99 %) replaced by siderite. This causes the gradual increase in the amount of siderite, mirroring the decrease in the Fe-oxide content during the first 1200 years (Fig. 10). In terms of dominant species the reaction becomes close to:

$$\text{C}{\text{H}}_2\text{O}+4\text{FeOOH}+3\text{C}{\text{O}}_2\to 4\text{FeC}{\text{O}}_3+3{\text{H}}_2\text{O}$$ (9)

This reaction should cause a decrease in the P_CO2. Reversely methanogenesis (Eqn. 2) causes an increase in the P_CO2. The observation that the P_CO2 calculated from field pH and alkalinity does not change, neither over depth nor from sites with a high organic C degradation rate to those with a low organic C degradation rate (Fig. 3) indicates that the two processes affecting the P_CO2 must more or less balance. The reaction stoichiometry (Eqn. 9 and Eqn. 2) predicts that the rate of carbon oxidation for methanogenesis should be 6 times the rate of carbon oxidation for Fe-oxide to exactly balance the CO₂ production and consumption. In our model it varies between 9 at 200 years and 3.6 at 6000 years indicating that a large part of the CO₂ production of methanogenesis is consumed by siderite precipitation. If the two reactions balance exactly then the net reaction becomes:

$$7\text{C}{\text{H}}_2\text{O}+4\text{FeOOH}\to 4\text{FeC}{\text{O}}_3+3\text{C}{\text{H}}_4+3{\text{H}}_2\text{O}$$ (10)

Thermodynamically a low pH strongly favors Fe-oxide reduction (Postma and Jakobsen 1996). On the other hand a low pH influences the rate of methanogenis negatively (Ye et al., 2012). These authors also found that at lower pH, Fe-oxide reduction became more important even though methanogenesis remained the dominant process. In that case there could be a dynamic balance established between methanogenesis and Fe-oxide reduction each pushing the pH in opposite direction while maintaining a near constant P_CO2 (Jakobsen and Cold, 2007).

Fig. 10.

The turnover of iron between aqueous and sedimentary models pools. Upper row 200-1200 years in 200 yr steps, lower row 1000-6000 years in 1000 yr steps. The bold red line indicating 1000 years is the same in upper and lower panels. Solid phase concentrations have been recalculated to concentration per liter of contacting groundwater to enable comparison.

During times greater than 1000 years the Fe(II) concentration starts to increase due to a lower pH and alkalinity which is caused by declining CaCO₃ dissolution and less Fe-oxide reduction. Siderite continues to be produced but now the dissolution of siderite starts to dominate in the top of the profile. The Fe-oxide content continues to decline while the peak in the Fe-oxide content develops uppermost due to oxygen in the incoming water. Similar to dissolved arsenic, dissolved Fe(II) is only a minor fraction of the iron that is turned over in the model.

4. Discussion

4.1. Modeling arsenic mobility and spatial variation

Most model studies that analyze the spatial variations of the arsenic concentration in aquifers in terms of geochemical processes have focused on the adsorption of arsenic to the sediment. Some investigators have explored the competitive adsorption between dissolved arsenic and anions like bicarbonate, phosphate or silicate using surface complexation models (SCM) developed for synthetic iron oxides, either by employing the original databases (Charlet et al., 2007; BGS and DPHE, 2001; Swartz et al., 2004), or by using adapted databases (Stollenwerk et al., 2007; Biswas et al., 2014). However, as noted by Jessen et al. (2012) the application of different SCM’s produces very different results, which weakens our confidence in their predictive value. Nguyen et al. (2014) investigated whether the competitive effects predicted by SCM’s for synthetic Fe-oxides also can be found in experiments with aquifer sediments and noted that only phosphate at a high concentration seem to have a competitive effect on arsenic adsorption while aquifer relevant concentration ranges for bicarbonate, Fe(II) or silicate had little or no effect.

Other sorption studies apply the more simple distribution coefficient approach, using either K_d values determined in the laboratory in sediment batch experiments (Nath et al., 2009; Itai et al., 2010; Radloff et al., 2011; Nguyen et al., 2014) or by using the groundwater arsenic concentration in combination with adsorbed arsenic extracted by phosphate from the contacting sediment (BGS and DPHE, 2001; Swartz et al., 2004; Radloff et al., 2007; van Geen et al., 2008; Nath et al., 2009; Itai et al., 2010). Finally there are some studies that derive the adsorption properties by determining the in situ retardation (Harvey et al., 2002; Radloff et al., 2011; van Geen et al., 2013).

Stute et al. (2007) interpreted a relation between groundwater residence time and arsenic content in terms of the flushing history. Radloff et al. (2015) extended this approach by combining a single component arsenic adsorption model with a flushing model. In this model the sediment sorption sites have an initial loading of arsenic while arsenic mobilization through Fe-oxide reduction within the aquifer, which we find important in our study, is neglected. As flushing proceeds, arsenic is removed from the sorption sites and the depth where there is a steep increase in the groundwater As concentration indicates the extent of flushing. The model was used on various data sets from Bangladesh and was also applied on data from our field site. While the model provides insight into the dynamics of sorption and groundwater flushing and their combined effect on the arsenic concentration of groundwater, it fails to contain the complexity of the arsenic behavior in the aquifer induced by the occurrence of various processes at the same time. To consider an initial state with a homogeneous distribution of As sorbed within the aquifer as starting point for flushing modeling is probably too simplistic. As shown in Fig. 9, it takes considerable time to build-up the adsorption of arsenic in the aquifer after the onset of reducing conditions and the adsorption process also runs in tandem with the mobilization of arsenic by the reduction of Fe-oxide. The result is a gradual increase of As over depth during the first 1200 years. Only then does desorption become predominant but in combination with continued, although decreased, release of arsenic from Fe-oxide reduction. In addition the reduction of Fe-oxide causes the removal of sorption sites on the surface of Fe-oxides. The fact that high methane concentrations are present together with high rates of methanogenesis and acetate oxidation indicates that reactive carbon degradation is taking place in the aquifer and consequently that Fe-oxide is being reduced while releasing arsenic. Therefore capturing the behavior of arsenic in aquifers by only considering flushing and sorption is inadequate and a more comprehensive approach is needed, one that includes all major processes affecting the groundwater chemistry.

4.2. Model controls on redox processes

There are only a few studies attempting reactive transport modeling of the complete set of processes controlling the bulk groundwater chemistry, including the release of arsenic. Postma et al. (2007) modeled the water chemistry at the H-transect using a model based on the partial equilibrium approach of Postma and Jakobsen (1996). In this model the degradation of organic C is the only kinetically described reaction and the overall rate determining process. The rate of organic C degradation was assigned a constant value which was found by trial and error. The distribution of the electron flow between the TEAP’s, mainly Fe-oxide reduction and methanogensis depended on equilibrium constraints where particularly the stability of the As-containing Fe-oxide was crucial. If the Fe-oxide being reduced was ferrihydrite then the equilibrium model showed the electron flow to proceed exclusively through Fe(III)-reduction which is also what has been observed in experimental studies (Roden and Wetzel, 1996; Qu et al., 2004; Hori et al., 2010). At our field site goethite and hematite are the dominant Fe-oxides present in the sediment (Postma et al., 2010) and as the result more of the electron flow proceeded through methanogenesis. It is of interest to note that hematite through its conductive properties can catalyze methanogenesis (Zhou et al., 2014; Zhuang et al., 2015).

The partial equilibrium approach used by Postma et al. (2007) is fundamentally different from the purely kinetic approach where the different TEAP’s each have their own separate Monod type kinetic equation that include terms inhibiting competing TEAP’s (Mayer et al,, 2002). Kocar et al. (2014) used a hybrid model of the partial equilibrium model and the Monod type of model. Here particulate organic carbon is assigned a solubility and a rate term, generating DOC, while the different TEAP’s compete for DOC using Monod type of equations. In areas with active arsenic mobilization the DOC rate term is set to a high value so that DOC becomes abundant and the Monod equations control the rate of the TEAP reactions. In spite of the different approaches, the results of Postma et al. (2007) and Kocar et al. (2014) resemble each other well.

In our present model the degradation of organic C is controlled by a rate equation with rates decreasing strongly over time (Fig. 7 and Eqn. 4). The reduction of Fe-oxides is also controlled by a rate equation which partially depends on the thermodynamic energy release (Eqn. 5). The distribution of the electron flow between the two main TEAP’s, Fe-oxide reduction and methanogenesis, is basically regulated by the rate equation for Fe-oxide reduction. Over time, the relative rates for organic C degradation and Fe-oxide reduction change and lead to a different distribution of the electron flow between the TEAP’s.

A major difference between the model of Kocar et al. (2014) and the present model is that our model includes methanogenesis while Kocar et al. (2014) does not. We find in our model, as well as in field rate measurements (Postma et al., 2012), that most of the electron flow from organic matter degradation passes through methanogenesis. In our model the CO₂ production of methanogenesis influences the pH which, together with carbonate dissolution and precipitation, has an important feedback on the energy released by Fe-oxide reduction and thereby on the rate of Fe-oxide reduction (Eqn. 5). In the model of Kocar et al. (2014) this matter is resolved by fixing the pH at a neutral value, corresponding to the average value observed in the field, while the rate of Fe-oxide reduction is independent of the energy release of the reaction. The model of Kocar et al. (2014) also includes sulfate reduction. In our system the sulfate input is very low and sulfur seems to be recycled in the uppermost part of the saturated zone were some iron sulfide formation may occur in the wet season for being reoxidized in the subsequent dry season where the water table decreases 2-3 m (Larsen et al., 2008). In any case we cannot detect any Fe-sulfide accumulation in the sediment. The final difference between the three studies is the duration of the modeled time. While Postma et al. (2007) modeled the processes over 40 years, equivalent to one pore-volume, Kocar et al. (2014) modelled the processes until steady state was attained, usually after 500-1000 years. Our present model is apparently the only one that explicitly addresses the evolution in groundwater chemistry over a six thousand year period.

4.3. Time trends and organic matter reactivity

Acharyya et al. (2000) were probably the first to relate the age of the aquifer sediment to the arsenic content of the groundwater. They found that arsenic contaminated aquifers in Bangladesh and West Bengal were particularly abundant in aquifers of middle age Holocene (7000-10000 yr B.P.), while early Holocene and Pleistocene aquifers mostly were low in arsenic. Kocar et al. (2008) found for the Mekong floodplain in Cambodia that 7000-8400 years old sediments did not mobilize arsenic to the groundwater while younger sediments (1800-1900 years) still mobilized arsenic. At our field site we find young sediments (500-700 years) to actively release arsenic while older aquifer sediments (6000 years) almost have stopped releasing arsenic. Thus at each site older aquifer sediments appear to release less arsenic than younger sediments but apparently this occurs on different time scales.

Because the degradation rate of organic C constrains the rate of reductive dissolution of Fe-oxide, and thereby the release of arsenic, it seems obvious to relate the burial age of the aquifer deposits to the reactivity of the organic carbon. For long timescales such a decrease in organic matter reactivity has already been documented for aquifers (Jakobsen and Postma 1994; Appelo and Postma, 2005). By analogy, in marine sediments the effect of time on the reactivity of organic matter is well established and extensively studied (Middelburg, 1989; Boudreau and Ruddick, 1991; Boudreau 1997; Arndt et al., 2013). Middelburg (1989) found for a wide range of marine sediments that the reactivity of organic matter reactivity decreased as a power function of time. Katsev and Crowe (2015) found almost the same relation for freshwater lake sediments. In fact the power law of Middelburg (1989) and of Katsev and Crowe (2015) predicts that the reactivity of organic matter is approximately related to the inverse of time. Inspecting Fig. 7 it may be observed that the decrease in organic matter reactivity found for our aquifer sediments is also close to the inverse of time. However, while the decrease in reactivity was a power function of time, Middelburg (1989) found the “initial rates”, the starting point rate so to say, to vary widely among environments depending on biological production, burial rate and various other factors. For aquifer sediments the variation in “initial rates” implies that a common relation covering the change in organic matter reactivity over time cannot be expected for all arsenic contaminated aquifers in S and SE Asia as was illustrated by the examples in the start of this section. Between Bangladesh, West Bengal, Cambodia and the Red River flood plain there will be sedimentological parameters that differ from site to site. The Ganges-Brahmaputra delta has for example had a much larger subsidence rate than the Red River delta which likely improves preservation of reactive carbon.

The reactivity of sedimentary organic carbon is of course only of interest when it constitutes the carbon source for the reduction of Fe-oxides leading to the mobilization of arsenic. The relation between organic carbon reactivity and burial age in our aquifers strongly suggests that sedimentary organic carbon provides the electrons for the reduction of Fe-oxides. The observation that the aquifer burial age controls the rate of organic carbon degradation contradicts infiltrating DOC being the carbon source because then the rate of organic carbon degradation should be independent of the aquifer burial age. Also Kocar et al. (2014) found that particulate organic matter was the most important carbon source. However, in other situations downward transported DOC, for example induced by pumping or lateral variations in infiltration rate (Harvey et al., 2002; Winkel et al., 2011; Neumann 2010; Lawson et al., 2013) may be the carbon source for arsenic mobilization, although Mailloux et al. (2013) showed that downward migrating DOC is strongly retarded by adsorption onto the sediment.

5. Conclusions

Early diagenesis of the aquifer sediments on the Red River flood plain over a 6000 year period, results in a strong decrease in the groundwater arsenic concentration over time. Comparison with other localities suggests a similar decrease in groundwater arsenic content with increasing burial age of the aquifer sediment.

Using the Red River flood plain data we have established a reactive transport model quantifying the changes in groundwater chemistry as a function of burial age. The key processes are the kinetics of organic matter degradation and of Fe-oxide reduction. The rate of organic carbon degradation determines the total electron flow. However, the kinetics of Fe-oxide reduction distributes the electron flow between methanogenesis and Fe-oxide reduction. There are important feedbacks on the kinetics of Fe-oxide reduction through methanogenesis, carbonate precipitation and dissolution and their combined effect on the pH, which in turn influences the energy release from Fe-oxide reduction.

In our model arsenic is released to the groundwater by reductive dissolution of Fe-oxides containing As(V). Over time the rate of As release decreases because of the diminishing reactivities of organic carbon and Fe-oxides. The model predicts the groundwater arsenic content to pass through a maximum at a burial age of about 1200 years. Initially most arsenic released from the Fe-oxides becomes adsorbed to the sediment, but after 1200 years the decreasing release of arsenic from Fe-oxide reduction, together with desorption of As(III) from the sediment controls the groundwater arsenic content. Our model results suggest that the sedimentary history of the flood plains is the key to understanding the spatial variation in the arsenic content of the groundwater, because the groundwater chemistry is a function of the age of the aquifer.