Abstract
The selectivity of ion channels is fundamental for their roles in electrical and chemical signaling, and ion homeostasis. Although most ion channels exhibit stable ion selectivity, the prevailing view for purinergic P2X receptor channels, transient receptor potential V1 (TRPV1) channels and acid sensing ion channels (ASICs) is that their ion conduction pores dilate upon prolonged activation. We investigated this mechanism in P2X receptors and found that the hallmark shift in equilibrium potential observed with prolonged channel activation does not result from pore dilation, but from time-dependent alterations in the concentration of intracellular ions. We derived a physical model to calculate ion concentration changes during patch-clamp recordings, which validates our experimental findings and provides a quantitative guideline for effectively controlling ion concentration. Our results have fundamental implications for understanding ion permeation and gating in P2X receptor channels, and more broadly for using patch-clamp techniques to study ion channels and neuronal excitability.
The permeability of an ion channel protein to its namesake ion is a defining and typically stable property of this diverse class of membrane proteins1. Voltage-activated potassium (Kv), sodium (Nav) and calcium (Cav) channels, for example, contain ion selectivity filters (containing ion binding sites) at the extracellular end of their pores 2, 3 that impart exquisite ion selectivity and enable them to play key roles in the generation and propagation of action potentials, or in excitation-secretion and excitation-contraction coupling1. However, a large number of studies on P2X receptor channels 4-16, TRPV1 channels 17, 18 and ASICs19, 20 have reported that ion selectivity can change dynamically in response to agonist activation. In the case of P2X receptors, the prevailing view is that the pore initially opens rapidly to a conducting state that is relatively selective for small cations (such as Na+, K+ and Ca2+), but then gradually dilates over time to become more permeable to large organic cations such as N-methyl-D-glucamine (NMDG+), as well as to fluorophores as large as 14Å 4-16. For TRPV1 channels, pore dilation has been reported to alter Ca2+ permeability and proposed to modulate the role of TRPV1 in nociceptive signaling 17. In the case of ASIC channels, the concept of dynamic ion selectivity has guided interpretation of X-ray structures as representing open states with differing ion selectivity 21, 22. Thus, for all of these ion channel proteins, the mechanisms of ion permeation and pore dilation has profound implications for understanding operational and structural mechanisms, as well as their physiological functions and therapeutic applications.
Results
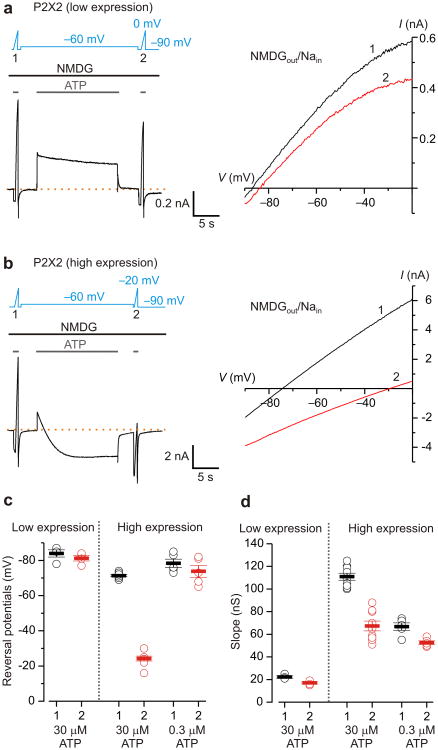
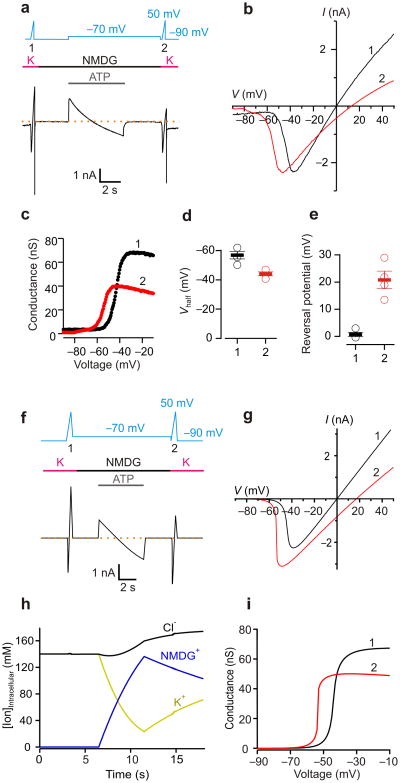
The principal experimental findings supporting the pore dilation model for P2X receptor channels have been obtained from electrophysiological recordings using bi-ionic solutions with NMDG+ present outside the cell and Na+ inside (NMDG+out/Na+in). Under such conditions, brief activation of P2X receptors by extracellular ATP opens a pore that is initially more permeable to Na+ than NMDG+, and the voltage at which there is no net flow of ions (Vrev, reversal potential or equilibrium potential) is correspondingly quite negative (e.g. -70 to -85 mV). However, during prolonged activation of the channel by ATP, Vrev shifts towards significantly less negative values, consistent with a dramatic increase in the permeability to NMDG+4, 5. We began our study by confirming that the hallmark shift in Vrev requires high channel density 11. We transfected human embryonic kidney (HEK-293) cells with the rat P2X2 (rP2X2) receptor channel cloned into vectors that consistently give rise to relatively low (pcDNA1) or high (pRK5-IRES-EGFP; abbreviated pIE) expression of functional channels on the cell surface measured using the whole-cell configuration of the patch-clamp technique23. We then devised a protocol to independently characterize potential changes in ion selectivity and intracellular ion concentrations by applying rapid linear changes in voltage (voltage ramps; 120-180 mV s-1) to measure Vrev during brief applications of extracellular ATP before and after a 15-s prolonged ATP application at -60 mV in bi-ionic NMDG+out/Na+in solutions (Fig. 1a, b). At low channel density, a net outward Na+ current was observed throughout the prolonged activation by a saturating concentration of ATP (30 μM; Fig. 1a), and the initial Vrev was only modestly more negative when compared to that measured at the end of the protocol (Fig. 1a), suggesting that the permeability to NMDG+ relative to that of Na+, or PNa+:PNMDG+, is largely unchanged. Similar results were obtained at high channel density when the channel was activated with a relatively low concentration of ATP 24 (0.3 μM; Fig. 1c). In contrast, as previously reported 4, 5, 11, when activating the channel with saturating concentrations of ATP at high channel density, we initially observed a net outward Na+ current at -60 mV that diminished over time during prolonged activation, crossing zero current and stabilizing as a net inward NMDG+ current, a phenomenon that we term current-reversal (Fig. 1b). On average, prolonged activation of the channel by a saturating concentration of ATP resulted in a 48 ± 2 mV shift in Vrev to less negative voltages (n=9 cells, Fig. 1b, c). Interestingly, the shift in Vrev was accompanied by a decrease in the slope of the current-voltage (I-V) relationship (Fig. 1d), a result that is unexpected if the pore dilates in response to prolonged application of ATP. Because current-reversal and shifts in Vrev, were only observed at high channel density, all subsequent experiments were performed using the high-expression vector.
Figure 1. Shifts in equilibrium potentials after prolonged activation of P2X2 receptors in bi-ionic NMDGout/Nain solutions.
a) Left, macroscopic currents recorded from a HEK cell transfected with P2X2 in pcDNA1. Dashed line is the zero current level. The voltage protocol and the extracellular ATP application are presented above the current trace. Voltage ramps were applied in the presence of 30 μM ATP to estimate the reversal potential before (1) and after (2) a prolonged (15-s) activation of the channel by ATP at -60 mV in NMDGout/Nain solutions. Raccess for this recording was 6 MΩ, and the cell capacitance was 14 pF. Right, current (I)-voltage (V) relations measured before (black, 1) and after (red, 2) the prolonged activation of the channel by ATP. Same cell as shown on the left. b) Macroscopic currents recorded from a HEK cell transfected with P2X2 in pIE. Raccess for this recording was 7 MΩ, and the cell capacitance was 8 pF. Right, I-V relations measured before (black, 1) and after (red, 2) prolonged activation of the channel by ATP. Same cell as shown on the left. c,d) Summary of the reversal potentials and slopes of I-V relations (conductance, calculated between -90 to -60 mV) before (black, 1), and after (red, 2) the 15-s ATP activation. Open circles are individual cells, solid bars are mean values and error bars are S.E.M. Data were collected from 4 cells (low expression, 30 μM ATP), 9 cells (high expression, 30 μM ATP) and 5 cells (high expression, 0.3 μM ATP).
P2X receptor channels are permeable to organic cations
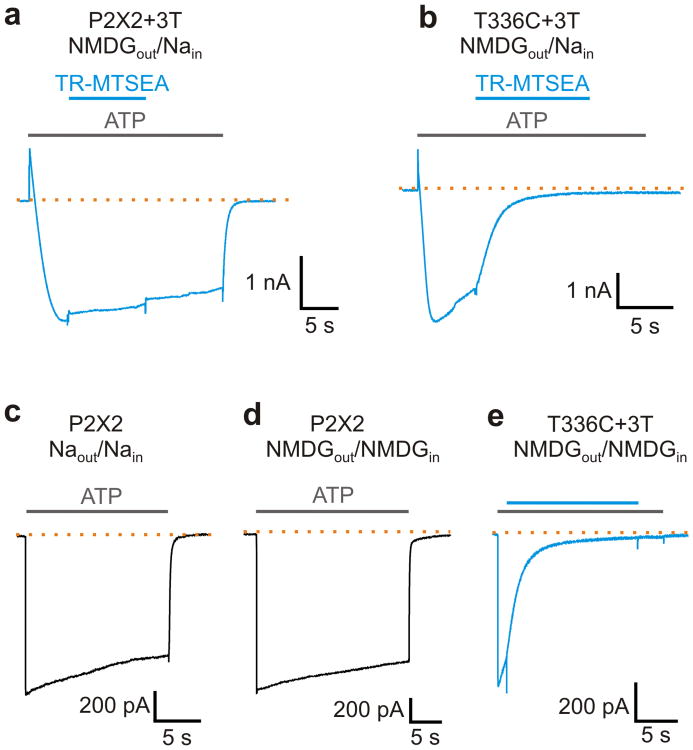
To determine whether the pore of P2X2 receptor channels is the permeation pathway for NMDG+ 8, 9, 25, we tested whether a Cys-reactive methanethiosulfonate (MTS) compound could inhibit NMDG+ currents following prolonged ATP application when a Cys residue was inserted at position T336 in transmembrane helix 2 within the gate region of the channel 26-28. In previous studies, this position within the pore of P2X2 receptor channels was only accessible to MTS compounds when the channel was first opened with ATP, and the MTS reaction inhibited the channel 26, 28. In control experiments, prolonged activation of the background P2X2+3T construct (in which Cys9, Cys348 and Cys430 are mutated to threonine) with saturating concentrations of ATP gave rise to current-reversal when using bi-ionic NMDG+out/Na+in solutions, and the steady-state NMDG+ current was not sensitive to the relatively large Texas Red 2-sulfonamidoethyl methanethiosulfonate (TR-MTSEA) (Fig. 2a). In contrast, for the rP2X2 T336C+3T mutant26, TR-MTSEA produced robust inhibition of the net inward NMDG+ current following current-reversal with prolonged activation of the channel with ATP (Fig. 2b), suggesting that the pore of P2X2 receptors is the permeation pathway for NMDG+.
Figure 2. Rapid activation of NMDG+ currents in P2X2 receptor channels.
a) Currents activated by 30 μM ATP from a cell expressing the P2X2+3T receptor channel recorded in NMDGout/Nain solutions at -60 mV. Current-reversal is observed in response to prolonged activation by ATP as with the wt receptor (Fig. 1b). 100 μM Texas-Red MTSEA (TR-MTSEA) applied to the external solution does not significantly affect the inward NMDG+ current. Extracellular ATP (grey bars) and TR-MTSEA (blue bar) applications are presented above the current trace. Similar results were obtained from 3 cells. b) 100 μM TR-MTSEA rapidly inhibits NMDG+ currents carried through T336C+3T receptors (n=4). c) Macroscopic P2X2 receptor channel current recorded in symmetric Na+ solutions at -10 mV. d) Macroscopic P2X2 receptor channel current recorded in symmetric NMDG+ solutions at -40 mV. The 10-90% rise time for activation of Na+ currents was 4.9±0.8 ms (n=7), and that for NMDG+ currents was 10±0.3 ms (n=6). e) ATP application to T336C+3T channels activates NMDG+ currents in milliseconds and subsequent external application of TR-MTSEA rapidly inhibits the current. Voltage was -40 mV (n=3).
Rapid activation of organic cation permeability
In the pore dilation model for P2X receptors, the shifts in Vrev observed in bi-ionic NMDG+out/Na+in solutions reflect an increase in the permeability of NMDG+ that results from a slow dilation of the pore. To look for time-dependent increases in the macroscopic conductance of the channel for NMDG+, we examined the kinetics of channel activation in either symmetric NMDG+ or symmetric Na+ solutions. In both cases (Fig. 2c, d), we observed rapid activation of the channel (10-90% rise-time of 4.9-10 ms), indicating the conductance of the channel for large cations activates almost as rapidly as for small cations. NMDG+ currents measured in symmetric NMDG+ solutions were also inhibited by TR-MTSEA in the rP2X2 336C-3T channel, suggesting that these rapidly activating NMDG+ currents arise from permeation of the organic cation through the pore of the P2X2 receptor channel (Fig. 2e). Taken together, the results thus far demonstrate that Vrev measured in bi-ionic NMDG+out/Na+in solutions shifts in response to prolonged activation of the channel by ATP at high channel density, and that the channel has a very significant permeability to NMDG+. However, the permeability of the channel to NMDG+ activates on the ms timescale, with no increase in NMDG+ current upon prolonged activation, raising the possibility that the shift in Vrev developing over several seconds does not reflect an increased permeability of the channel to NMDG+.
Shifts in Vrev are dependent on permeant ions
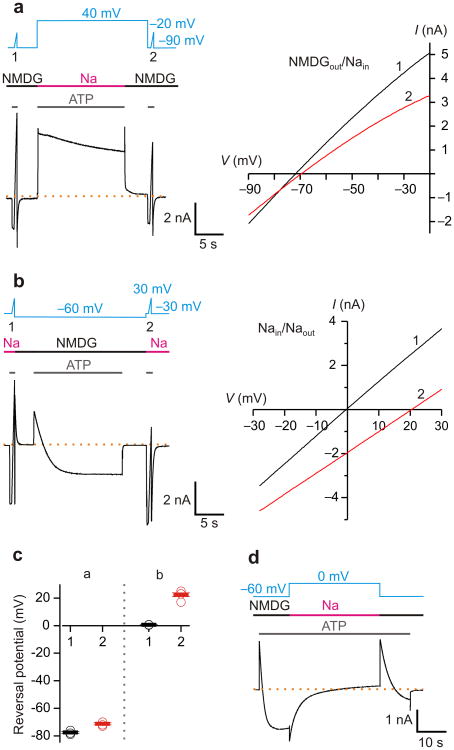
The observed shifts in Vrev in bi-ionic solutions must reflect either a change in the ion selectivity of P2X receptor channels, or a change in the concentrations of ions on the two sides of the membrane 29-33. To explore the second possibility, we began by measuring the extent to which the concentration of intracellular Na+ changes when recording at high channel density in symmetrical solutions. When the solutions in the external recording chamber and patch pipette are identical, a non-zero Vrev can only occur if the concentration of intracellular ions at the membrane is different from the pipette. (Although external ion concentrations in an unstirred layer could also contribute, for small compact cells these effects are much smaller30 and were not considered here.) When recording in symmetrical Na+ solutions with a protocol similar to Fig. 1, the initial Vrev measured before prolonged activation by ATP was consistently near 0 mV (Supplementary Fig. 1a,b), confirming that the internal and external concentrations of Na+ are the same. After prolonged activation at negative voltages (where the driving force for Na+ is inward) or positive voltages (where the driving force for Na+ is outward), we observed only relatively small negative or positive shifts of Vrev (Supplementary Fig. 1a,b), indicating that these protocols produce only small changes in the intracellular concentration of Na+. Since the intracellular concentration of Na+ changes very little when using symmetric solutions, we maintained symmetric Na+ solutions during the prolonged activation by ATP and tested whether Vrev shifts by rapidly applying an external solution containing NMDG+ only during the initial and final voltage ramps (Fig. 3a). Remarkably, however, Vrev did not change appreciably despite prolonged activation of the channel by ATP (Fig. 3a), indicating that the ion selectivity of the channel remains unaltered under these conditions. This result is consistent with a previous report for the P2X7 receptor, where pore dilation was not observed in the presence of external Na+ 34.
Figure 3. Prolonged P2X2 receptor channel activation in bi-ionic NMDGout/Nain solutions changes intracellular ion concentrations.
a) Left, macroscopic currents recorded from a HEK cell transfected with P2X2 in pIE. Voltage ramps were applied in the presence of 30 μM ATP to estimate the reversal potential in bi-ionic NMDG+out/Na+in solutions, before and after 15-s channel activation at -60 mV in symmetric Na+ solutions. I-V relations obtained from the voltage ramps are plotted on the right. Raccess was 9 MΩ, and the cell capacitance was 7 pF. b) Macroscopic currents recorded using a similar protocol as in a, but the voltage ramps were applied in symmetric Na+ solutions to estimate changes in the intracellular Na+ concentration, and the long ATP activation was in NMDG+out/Na+in solutions. I-V relations obtained from the voltage ramps are plotted on the right. Raccess was 5 MΩ, and the cell capacitance was 12 pF. c) Summary of reversal potential from recordings like those shown in a (n=4) and b (n=5). Open circles are individual cells, solid bars are mean values and error bars are S.E.M. d) Macroscopic P2X2 receptor channel current recorded in NMDGout/Nain solutions at -60 mV in response to prolonged ATP application followed by switching to symmetric Na+ solutions at 0 mV, as indicated above the current trace. Similar results have been obtained from 3 cells. The dashed lines in a, b, and d represent the zero current level.
Testing for changes in permeant ion concentration
Having demonstrated that Vrev does not shift dramatically following prolonged activation in symmetric Na+ solutions (Fig. 3a), conditions where we do not observe appreciable ion depletion or accumulation (Supplementary Fig. 1), we next directly tested whether the bi-ionic solutions required for observing shifts in Vrev might alter the concentration of intracellular ions (Supplementary Fig. 2). To this end, we modified our protocol to have symmetrical Na+ solutions present when measuring Vrev and NMDG+out/Na+in solutions present only during the prolonged activation (Fig. 3b, c). The Vrev measured before the prolonged activation was again near 0 mV, verifying that the internal and external concentrations of Na+ are equal at the beginning of the experiment. However, we found that Vrev shifted positive by more than 20 mV following prolonged ATP activation, demonstrating that the concentration of ions inside the cell must have changed during the experiment. Considering the permeability of the channel to NMDG+ (PNa+:PNMDG+ = 30 at low expression where Vrev = -84 mV; Fig 1c, Fig. 2d) and the voltage during the prolonged activation (-60 mV), the observed shift in Vrev with symmetrical Na+ solutions would reflect both a depletion of internal Na+ and an accumulation of NMDG+ internally (Supplementary Fig. 2).
If ion depletion and accumulation are responsible for the current-reversal observed during the prolonged activation by ATP in bi-ionic solutions, it should be possible to reverse this process by replenishing internal Na+ and removing internal NMDG+. To examine this possibility, we first activated the P2X2 receptor for sufficient time for current-reversal to occur at -60 mV, and then immediately exchanged external NMDG+ for Na+ while simultaneously stepping the voltage to 0 mV (Fig. 3d). Under these conditions, no current should flow if the intracellular solution contained no NMDG+ and the concentration of Na+ remained fixed. However, upon exchanging to external Na+ and stepping to 0 mV, we initially observed a large inward current, confirming that there had been dramatic depletion of internal Na+ and accumulation of NMDG+ (Fig. 3d). This large inward current slowly decayed over several seconds (Fig. 3d), suggesting that the cell was refilling with Na+ while NMDG+ diffused out. Upon subsequent replacement of external Na+ with NMDG+ and stepping back to -60 mV, we again observed current-reversal, although the process of depleting Na+ and accumulating NMDG+ inside the cell was slower, suggesting that the cell had not fully recovered to its initial state.
A reservoir model for whole-cell recordings
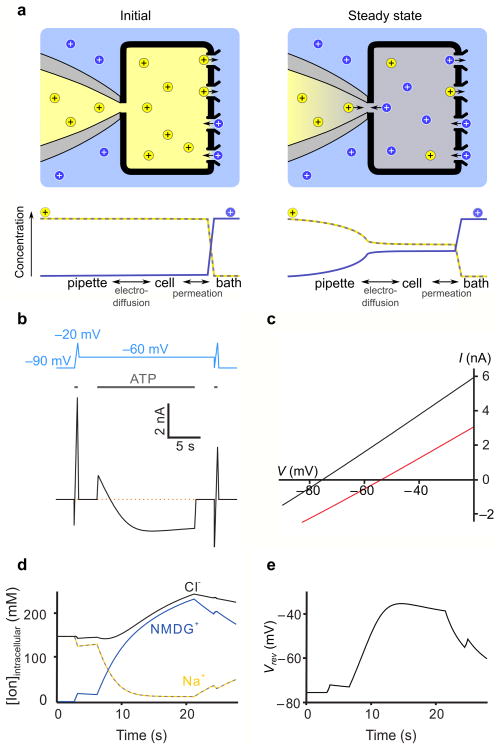
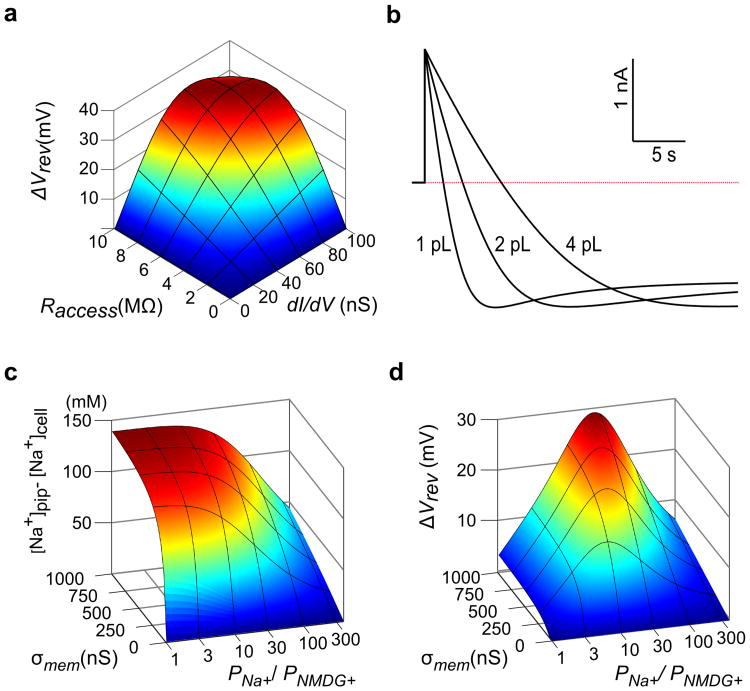
To put our results on a quantitative foundation and provide an analytical tool for designing and interpreting electrophysiological experiments, we constructed a reservoir model of a whole-cell patch clamp recording of mammalian cells in which ion concentrations in the cell change due to the flow of ions across the membrane or between the pipette and cytoplasm (Fig. 4a; Supplementary Fig. 3). Building on earlier work 30, 33, this new model explicitly accounts for concentration, voltage, and pressure gradients between the cell and pipette electrode to provide a physically consistent description of ion accumulation and depletion under bi-ionic conditions. The key parameters of the model are the access resistance between the cell and pipette electrode (Raccess), the volume of the cell and the conductance of the membrane for Na+ and NMDG+(see Online Methods; Supplementary Figs. 3-5). The model predicts that for a typical value of Raccess (5 MΩ) and high channel density (100 nS, with a relative permeability of Na+ to NMDG+, or PNa+:PNMDG+, of 20:1), prolonged application of ATP would cause current-reversal at -60 mV and produce a 22 mV shift of Vrev (Fig. 4b,c). Although the model predicts that the largest steady-state shifts in Vrev (ΔVrev) would be 33 mV (Fig. 5a), this limit results from the assumption that the cell membrane is completely impermeable to water and anions. Water influx increases the intracellular depletion of Na+ and decreases the intracellular accumulation of NMDG+, leading to larger steady-state shifts (Supplementary Fig. 4), and including water permeation and a very small relative permeability of the cell membrane to Cl- enables Vrev to shift by as much as 70 mV. Importantly, the time course of the transition from an outward Na+ to an inward NMDG+ current observed experimentally is faithfully reproduced in the model (compare Fig. 1b and Fig. 5b), and corresponds to measured timescales of exchange between patch pipettes and cells 29, becoming slower as the cell volume increases. For a realistic range of cell volumes, a 15 s long ATP application approaches steady-state, at which point intracellular Na+ decreases from 140 mM to around 20 mM and NMDG+ accumulates to over 200 mM (assuming no water influx; Fig. 4d). At low channel expression (∼20 nS as in Fig. 1a), ΔVrev will remain less than 10 mV if Raccess is less than 7 MΩ, as is evident from the relationship between ΔVrev, Raccess and membrane conductance at Vrev (dI/dV) (Fig. 5a), consistent with our experimental results obtained under comparable conditions (Fig. 1c). Although the model predicts that the extent to which ion concentrations change will be highly variable from cell to cell because small changes in channel density, Raccess and cell volume will have large effects on ΔVrev, it reproduces our key experimental findings.
Figure 4. A reservoir model of intracellular ion concentrations during patch-clamp recordings.
a) Schematic of a whole-cell patch clamp reservoir model with Na+ ions depicted as yellow spheres and NMDG+ ions as blue spheres. The initial condition (left) depicts a point in time after the pipette and cell have equilibrated and immediately after opening P2X receptor channels. The concentration of ions in the cell change as Na+ leaves and NMDG+ enters, until at steady state (right) the flow of ions between the pipette and cell balances the flow of ions between the cell and bath. Ion concentrations are graphed below the illustrations. b) Calculated current as a function of time using the reservoir model with an identical voltage protocol to Fig. 1b. The initial reversal potential (-75mV) and slope (105nA/V) were used to set the relative (PNa+:PNMDG+ = 20:1) and absolute permeability. respectively. Raccess was 5 MΩ and the cell volume was 1.5pL. The pipette contains 150 mM NaCl at the start of the simulation and perfusion is assumed to clamp the external solution surrounding the cell at a concentration of 150 mM NMDG-Cl. For these calculations, the membrane was assumed to be impermeable to Cl- and water. c) Simulated initial and final I-V plots. d) Calculated intracellular ion concentrations as a function of time, aligned with the time course shown in b. e) Calculated Vrev as a function of time using the reservoir model, based on the voltage and ATP application protocol shown in b.
Figure 5. Predicted influence of experimental parameters on shifts in equilibrium potentials and intracellular ion concentrations.
a) Dependence of shift in reversal potential (ΔVrev) on Raccess and initial conductance at the reversal potential (dI/dV) for a constant relative permeability of PNa+:PNMDG+ = 20:1. ΔVrev was evaluated after holding at -60mV (∼ 15mV above the initial reversal potential) until the current reached steady-state. b) Effect of cell volume on the time course of current reversal for otherwise identical simulation parameters to Fig. 4b. Assuming a spherical cell with 50% cytosol by volume, the 1pL, 2pL and 4pL cytosol volumes correspond to cell diameters of 16 μm, 20 μm and 25 μm. c,d) Influence of ion channel selectivity (PNa+ : PNMDG+) and ion channel density (membrane conductance, σmem) on depletion of intracellular Na+ ([Na+]pip-[Na+]cell; c) and reversal potential shift (ΔVrev; d). The channel density was parameterized by the membrane conductance in symmetric 150 mM NaCl at 0 mV, and steady state conditions were evaluated for a holding voltage 15 mV above the initial reversal potential [i.e. Vhold = -(RT/F) * ln(PNa+/PNMDG+) + 15 mV]with bi-ionic conditions (Bath : 150mM NMDG-Cl; Pipette : 150mM NaCl) and Raccess = 5 MΩ.
Using a Kv channel to detect changes in ion concentration
To independently measure changes in the intracellular concentration of ions and further test the physical model, we co-expressed the Shaker Kv channel (along with P2X receptors) and used it to estimate the extent to which the intracellular concentrations of ion changes with prolonged activation of P2X receptors. The Shaker Kv channel is exquisitely selective for K+ 35, and thus can be used to estimate internal K+ concentration, and should not interfere with ionic fluxes during long ATP applications as it is effectively closed at negative membrane voltages. The relative permeability of rP2X2 receptor channels to Na+ and K+ are similar 36, 37, suggesting that it should be possible to replace internal Na+ with K+ and still observe current reversal and shifts in Vrev with prolonged ATP application.
To explore the feasibility of using the Shaker Kv channel to estimate internal ion concentrations, we undertook experiments with rP2X2 receptors where internal Na+ was replaced with K+ (NMDG+out/K+in). With these ionic conditions, we measured initial Vrev values of -73.3±2.1 mV, and observed that prolonged activation by ATP cause Vrev to shift to -40.2±2.6 mV (Supplementary Fig. 5), indicating that ion depletion and accumulation can also be observed with NMDG+out/K+in solutions. We then undertook control experiments with the Shaker Kv channel studied in inside-out patches to establish how varying the concentrations of internal K+ and NMDG+ influenced the measured Vrev and the midpoint of the conductance-voltage (G-V) relationship (Vhalf). As internal K+ was gradually replaced with internal NMDG+, we observed progressive shifts of Vrev to more positive voltages (Supplementary Fig. 6), as expected given the very low permeability of Shaker to NMDG+. In contrast, the G-V relations for Shaker shifted to more negative voltages as K+ was replaced with NMDG+ (Supplementary Fig. 6), likely the result of internal NMDG+ stabilizing the open state of Shaker 38, as well as a junction potential between the NMDG+ containing solution at the intracellular face of the membrane and the ground chamber in the bath containing KCl. These results with the Shaker Kv channel provide the basis for using this channel to measure how the internal concentration of K+ and NMDG+ change following prolonged activation of P2X receptors.
Next, we co-expressed the Shaker Kv channel along with the rP2X2 receptor channel and used a protocol consisting of voltage ramps elicited in external K+ solution, before and after a prolonged ATP application in the presence of external NMDG+ (Fig. 6a-e). In this instance, the external solution contained K+ and no ATP during each of the voltage ramps because the ramps are used to activate the Shaker Kv channel and measure internal ion concentration. In order to separate Shaker and P2X receptor channel activation, ATP was applied for only 5s at -70 mV because our conventional protocol (15 s prolonged ATP activation at -60 mV) caused appreciable activation and subsequent inactivation of the Shaker Kv channel. During the initial ramp we observed depolarization activated K+ currents with a Vrev near 0 mV (Fig. 6a and b), confirming the concentration of K+ in the internal and external solutions was equal at the start of the experiment. After ATP application in the presence of external NMDG+, Vrev shifted to +13.5 mV in the example shown (Fig. 6b, +20.8±3.2 mV on average), which is similar to that produced in inside-out patches with internal solutions containing 50 mM K+ plus 90 mM NMDG+ (Supplementary Fig. 6). To simulate these experiments, the reservoir model was extended to include a permeability of P2X receptors to K+ relative to NMDG+ as 25:1, as well as a voltage-dependent K+ permeability of the Shaker Kv channel. The model predicts a shift in Vrev of +17 mV for a 5-s activation of P2X receptors (Fig. 6f-i), corresponding to a depletion of internal K+ from 140 mM to 50 mM, values that are very close to our experimental results. Even though the model for K+ permeability does not include a specific stabilization of the open state by NMDG+, it predicts a modest shift in G-V for the Shaker owing to a liquid junction potential between the pipette and cell generated by intracellular NMDG+ accumulation to 120 mM. Indeed, in the co-expression experiments, prolonged activation of P2X receptors produced shifts in the G-V for Shaker (Fig. 6b-d), similar to that predicted by our model and observed in inside-out patches with internal solutions containing NMDG+ (compare Fig. 6b-d and Supplementary Fig. 6). These experiments and simulations with the Shaker Kv channel are in agreement with each other, further demonstrating that prolonged activation of P2X receptors leads to profound depletion of intracellular alkali metal cations and accumulation of NMDG+.
Figure 6. Using the Shaker Kv channel to measure depletion of intracellular K+ and accumulation of NMDG+.
a) Macroscopic currents recorded from a HEK cell co-transfected with Shaker Kv channels and P2X2 in pIE. Voltage ramps from -90 mV to 50 mV (500 ms duration) were applied in the absence of ATP in symmetric K+ solutions to activate Shaker Kv channels, before (1) and after (2) 5s application of ATP to activate P2X2 receptor channels at -70 mV in NMDGout/Kin solutions. Raccess for this recording was 5 MΩ, and the cell capacitance was 9 pF. b) I-V relations for Shaker Kv channels measured before (black, 1) and after (red, 2) prolonged activation of the P2X2 receptor. Same cell as in a. c) G-V relations for Shaker Kv channels measured before (1) and after (2) activation of the P2X2 receptor. d) Midpoint of G-V relations for Shaker Kv channels before (1) and after (2) activation of P2X2 receptor channels (n=4). e) Vrev for Shaker channels before (1) and after (2) P2X receptor activation (n=4). f) Calculated current as a function of time using the reservoir model. g) Simulated initial and final I-V relations using the reservoir model. h) Calculated intracellular ion concentrations as a function of time using the reservoir model. i) G-V relationships from the initial and final simulated voltage ramps. (Simulation parameters – Shaker PK+/PNMDG+ = 1:0; P2X (PK+/PNMDG+ = 25:1); Raccess = 5 MΩ; Cell volume =1.5pL; Pipette : 140mM KCl;Bath : 140mM NMDG-Cl or KCl).
Discussion
Taken together, our results on P2X receptor channels have important implications for studying the permeation properties of ion channel proteins. Our results overturn the prevailing model of dynamic ion selectivity in P2X receptors, which posits that the sustained activation of P2X receptors causes the protein to undergo a slow conformational change in which the pore dilates. Our results show 1) that P2X receptors rapidly activate and lack a slow phase of activation when studied in symmetrical ionic conditions, 2) that changes in Vrev require the presence of NMDG+ in the external solution during sustained activation and 3) that prolonged activation in bi-ionic solutions leads to the depletion of internal Na+ and accumulation of NMDG+. Indeed, the fundamental principles of physics employed in our reservoir model dictate that ion concentrations must change in whole-cell patch-clamp recording with the bi-ionic conditions, channel densities and Raccess we and others have used to observed changes in Vrev following prolonged activation of P2X receptor channels. We also employed the Shaker Kv channel to measure the internal concentrations of K+ and NMDG+, and these results confirm that prolonged activation of P2X receptor channels with ATP causes profound ion depletion and accumulation, in quantitative agreement with the reservoir model.
The permeation properties of P2X receptors are, however, unique in that these channels exhibit a very significant permeability to relatively large cations like NMDG+, and that the macroscopic current-voltage relationship remains relatively linear through Vrev in bi-ionic solutions (Fig. 1a,b). Even in the absence of pore-dilation, these unusual permeation properties of P2X receptors would allow them to serve as conduits for relatively large molecules to enter or exit cells, as suggested by the ability of these channels to support dye uptake 4, 5, 8, 34 or to permeabilize mast cells 39. Because the detection of dyes within cells is exquisitely sensitive, an inherent low dye permeability is likely all that is required to observe gradual increases in cell fluorescence during prolonged ATP application, although our results do not exclude the involvement of another permeation pathway 8, 9, 25. Similarly, TRPV1 channels can serve as a permeation pathway for dyes 17, 40 and local anesthetics41, allowing the selective delivery of anesthetics to TRPV1 expressing nociceptors under experimental conditions where pore dilation is not observed 42. It will be fascinating to further investigate the structural basis of ion permeation in P2X receptor channels 27, 43, 44 and TRPV1 channels 45, 46, to understand the mechanistic basis of organic cation and dye permeation.
The changes in ion concentration that we uncover during experiments with P2X receptors highlight a fundamental and underappreciated problem inherent to voltage-clamp recordings, where the flow of ionic currents across the membrane can alter the concentration of intracellular ions 30, 33. Under symmetrical ionic conditions, the measured current will always be greater than or equal to the flux of any individual ionic species (Supplementary Fig. 2a), and thus ion concentrations can be controlled by working under conditions where current amplitudes are modest. In contrast, in asymmetric ionic conditions, even when the cell is clamped at Vrev so the net current is zero, large changes in the intracellular concentration of ions are possible when channel density is high because there will be large (and balanced) outward and inward currents of different ionic species (Supplementary Fig. 2a,b). As a result, to adequately control the concentrations of ions when recording under bi-ionic conditions, the membrane conductance (σmem) must be sufficiently small (σmem × Raccess ≪ 1; see Methods). The present results with P2X receptors, together with our reservoir model, provide sufficient motivation to reexamine the phenomenon of dynamic ion selectivity reported for TRPV1 channels 17, 18, TRPA1 channels 47, 48, ASICs 19, 20, and TMEM16A calcium-activated Cl- channels 49, 50. Dynamic ion selectivity for TRPV1 channels requires high agonist concentrations and high channel density 17, and these channels have an appreciable permeability to NMDG+ 17 and dyes 17, 40, raising the possibility that ion depletion and accumulation may be responsible for the reported changes in ion selectivity of these channels. One of the general implications emerging from the reservoir model is that the ion selectivity of a channel can make it more or less prone to causing ion depletion and accumulation and subsequent shifts in Vrev in bi-ionic experimental conditions. The most non-selective channels will cause the greatest changes in ion concentration, but Vrev will remain unaffected because of the lack of selectivity. Small changes in Vrev would also be predicted for the most highly selective channels because they will cause the smallest changes in ion concentration (Fig. 5c,d). In contrast, ion depletion and accumulation will be particularly prominent and cause large shifts in Vrev for channels such as P2X receptors and TRPV1 channels that have PNa+:PNMDG+ of around 20:1 (Fig. 5c,d), explaining why shifts in Vrev have been so frequently reported in the case of these ion channels 4-18. Our model provides a tool for determining when both membrane voltage and ion concentrations are effectively clamped in a whole-cell recording, which is essential for studying the functional properties of any ion channel protein or the influence they have on the electrical properties of excitable cells.
Online Methods
Channel constructs
rP2X2 36 in pcDNA1 was generously provided by D. Julius (UCSF). The bicistronic pRK5-IRES-EGFP vector was a gift from M. Mayer (NICHD). Cysteine mutations were introduced into a rP2X2 receptor channel construct where Cys9, Cys348 and Cys430 were mutated to Thr (P2X2-3T) 26. The Shaker Kv channel 51 in GW1 was obtained from G. Yellen (Harvard Medical School), and contains a deletion of residues 6-46 to remove fast inactivation 52, 53.
Cell culture and transfection
Human embryonic kidney (HEK-293) cells were cultured in Dulbecco's Modified Eagle's Medium (DMEM) supplemented with 10% fetal bovine serum and 10 mg/L gentamicin. HEK-293 cells were purchased from ATCC (CRL-1573) without further authentication and were not tested for Mycoplasma contamination. All cell culture reagents were obtained from GIBCO. Trypsin treated HEK-293 cells were seeded onto glass coverslips in 6-well plates before transfection and placed in a 37°C incubator with 95% air and 5% CO2. Transfections were performed using FuGENE6 Transfection Reagent (Promega). P2X2 in either pCDNA1 or pRK5-IRES-EGFP were co-transfected with a green fluorescent protein (GFP) cDNA construct in pGreen-Lantern (Invitrogen) at a ratio of 1:2. Cells were used for whole-cell recording 18-24 hours after transfection.
Electrophysiology
Standard whole-cell patch clamp recording was used to record P2X receptor channel currents from transiently transfected HEK-293 cells. Membrane currents were recorded under voltage-clamp using an Axopatch 200B patch clamp amplifier (Axon Instruments, Inc.) and digitized on-line using a Digidata 1322A interface board and pCLAMP 9.2 software (Axon Instruments, Inc.). Currents were filtered at 2 kHz using a 8-pole Bessel filter, and digitized at 5 or 10 kHz. Cell capacitance was between 5 to 15 pF, and access (series) resistance was between 3 to 10 MΩ. Series resistance compensation was not used because the critical parameter being determined (Vrev) will not be influenced by series resistance errors and it would complicate modeling our results. I-V relations obtained using voltage ramps in the presence of external ATP were corrected for leak currents and small capacitive currents by subtracting I-V relations obtained with the same protocol in the absence of ATP. The pipette solutions contained (mM): 140 NaCl (or NMDG free salt), 10 HEPES and 10 EDTA, adjusted to pH 7.0 with NaOH (or HCl). The extracellular solution contained (mM): 140 NaCl (or NMDG free salt) and 10 HEPES, adjusted to pH 7.3 with NaOH (or HCl). For experiments with the Shaker Kv channel, KCl was used in place of NaCl and KOH was used to adjust pH. Stock solutions of the MTS reagent was prepared daily and diluted to the desired concentration in extracellular solution immediately before each experiment (after obtaining the whole-cell configuration). Solution exchange (∼50 ms) was achieved using the Rapid Solution Changer RSC-200 (BioLogic), which has the capacity of switching between nine solutions. All current-voltage relations shown in the figures have been leak subtracted by measuring leak currents with the same protocol in the absence of ATP. The Goldman-Hodgkin-Katz voltage equation 54, 55
| (1) |
where R is the gas constant, T is the temperature and F is Faraday's constant (9.65 × 104 C mol-1) was used to estimate the relative permeability of Na+:NMDG+.
Whole-cell reservoir model
Simple reservoir models have previously been used to characterize the limitations of the whole-cell patch clamp geometry to clamp intracellular concentrations30, 33. This model extends on this earlier work by explicitly accounting for the effects of both concentration and voltage gradients between the cell and pipette electrode, as well as water flow.
For compact, relatively small cell types such as HEK-293, the voltage and concentration of ionic species within the cytosol are fairly uniform. The cell can then be thought of as a reservoir which can be characterized by the cell volume, Λcell(t) and the average concentration of each ionic species “j” in the cytosol, ρj,cell(t). As shown in Fig. 4a and Supplementary Fig. 3, in the whole-cell patch-clamp configuration, water and ions can enter or leave the cell via the membrane or pipette, which will in turn change the volume, ion concentrations and voltage in the cell. For each species, the concentration in the cell will change according to the conservation equation,
| (2) |
where Ij,pip(t) is the current flowing from the pipette into the cell carried by species j, Ij,mem(t) is the current flowing from the cell across the membrane carried by species j, zj is the unit charge per ion of species j (e.g. +1 of Na+ and -1 for Cl-), and F is Faraday's constant (F = 9.65 × 104 C mol-1). It is important to note that the concentration of individual species can change even if the net electric current is zero. For instance, in the example shown in Supplementary Fig. 3a, the net current flowing across the membrane and the net current flowing between the cell and pipette are identically zero. However, the concentration of blue cations inside the cell will increase because the influx of blue cations across the membrane is greater than the efflux into the pipette, while the concentration of yellow cations inside the cell will decrease because the efflux across the membrane is greater than the influx from the pipette. The cell volume will also change in response to the flow of water according to the equation,
| (3) |
where fpip(t) is the rate at which water flows from the pipette into the cell, and fmem(t) is the rate at which water flows from the cell into the bath. To use Equations 2 and 3 to calculate the time-dependent evolution of ρj,cell(t), and Λcell(t), it is then necessary to determine how the currents carried by each ionic species (Ij,pip(t), Ij,mem(t)), and water flow (fpip(t), fmem(t)) depend upon the conditions in the cell, pipette and bath.
Membrane currents
Perfusion will limit the concentration gradients in the extracellular media, so the concentrations of ions at the extracellular side of the membrane can be approximated by the bath concentration, ρj,bath(t). The current flowing across the cell membrane then depends on the membrane permeability, concentration in the cell (ρj,cell) and bath (ρj,bath), and voltage across the cell membrane (Vcell). One simple and widely used model for membrane permeation is the Goldman-Hodgkin-Katz flux equation,
| (4) |
where Pj(t) is the permeability of the membrane for species “j”, Acell is the membrane area, R is the gas constant and T is the temperature. For a voltage-gated channel like Shaker, the voltage-dependence of the permeability can be described by a simple, two-state Boltzmann distribution,
| (5) |
where PK+,max is maximum permeability for K+, V1/2 is the voltage with 50% maximum permeability, and Vw describes the width of the Boltzmann distribution.
Pipette currents
Because the volume of the pipette is much greater than the volume of the cell, and the electrode is located relatively far from the cell, the concentration of each ionic species near the pipette electrode, ρj,pip (e.g. j = Na+, NMDG+, Cl-, etc.), remains essentially constant during the experiment. In addition, the voltage-clamp amplifier holds the pipette electrode at the desired voltage, Vpip(t), relative to the bath, so the pipette acts as a reservoir with both defined voltage and ionic concentrations. As illustrated in Supplementary Fig. 3b, ions moving between the pipette electrode and tip should follow quasi-1D trajectories that converge towards the tip. Using the diffusion-drift equation, at a distance, x, from the tip the electric current due to ionic species “j”, can be approximated by,
| (6) |
where A(x) is the pipette cross-sectional area, Dj is the diffusion coefficient, ρj(x,t) is the concentration of the j-th ionic species at position x, V(x,t) is the voltage at position x, and fpip(t) is the rate at which solution flows from the pipette into the cell. The first term characterizes the flux due to ions diffusing down concentration gradients, the second describes the collective drifting of ions due to the local electric field (i.e. voltage gradient), while the third term describes the advection due to solvent flow.
For a given current, the concentration and voltage changes are inversely proportional to the cross-sectional area, and so the largest changes in ion concentration and voltage occur within the narrow tip of the pipette. In a whole-cell patch-clamp experiment, the size and volume of this region is typically much smaller than the cell, and so the voltage and ion concentrations in the tip region respond rapidly in comparison to the rate of change of ionic concentrations in the cell. As a result, for the timescales over which ion concentrations change in the cell, the current flowing from the pipette into the cell can be well-approximated by its steady-state value. At steady-state, the same ionic current,
| (7) |
must enter and exit every segment, independent of position, x. If the currents and flow are not too large, the voltage and ion concentrations in the pipette and cell will not differ too greatly, and one can make the simplifying approximation that,
| (8) |
Substituting these constraints into Equation 6 yields,
| (9) |
To express the current in terms of the ion concentrations and voltages at the ends of the pipette, it is convenient to define the pipette solution conductivity,
| (10) |
and access resistance,
| (11) |
Integrating both sides of Equation 9 with respect to dx/A(x) from the tip to the electrode then gives the approximate pipette current,
| (12) |
The first term is the diffusion current, which is proportional to the concentration difference and inversely proportional to the access resistance. The second term is the drift current which is proportional to the voltage difference and concentration in the pipette, and is inversely proportional to the access resistance. Finally, the third term is the advection current which depends only upon the flow rate, and concentration in the pipette.
When the currents and/or flow are larger, the ion concentrations in the cell and pipette may be quite different, Equation 8 is no longer a reasonable approximation, and the ionic concentrations, ρj(x,t) and voltage, V(x,t), must be determined at each point. While the voltage can be determined exactly using Gauss' Law, the charge densities associated with physiologically relevant voltages (e.g. ∼100mV) are many orders of magnitude smaller than the total density of ions (∼100mM) in physiological solutions. Even considering surface charges, the sum of positive electric charges and sum of negative charges are approximately equal, which may be expressed mathematically by the electro-neutrality (Planck) approximation,
| (13) |
Applying the electro-neutrality approximation to Equation 6 gives,
| (14) |
where the index, k, is summed over all species. The voltage gradient is then,
| (15) |
where,
| (16) |
Substituting the voltage gradient back into Equation 6 then gives the concentration gradients,
| (17) |
as a simple function of the individual ionic currents. Finally, Equations 15 and 17 can be integrated from the pipette electrode towards the tip, to give
| (18) |
and,
| (19) |
Equations 18 and 19 give the ionic concentration and voltage at each point in the pipette as a function of the individual ionic currents. To obtain the steady-state pipette currents as a function of the ion concentration and voltage in the cell (ρj,cell(t), Vcell(t)) and near the pipette electrode (ρj,pip(t), Vpip(t)), and the flow of solution from the pipette into the cell, fpip(t), Equations 18 and 19 can be inverted numerically using an iterative Singular Value Decomposition (SVD) to satisfy the boundary conditions,
| (20) |
Membrane water flow
For this simplified model of the cell, the flow of water across the membrane can be described by,
| (21) |
where Pf is the osmotic water permeability (Pf∼ 5×10-5 m.s-1 for HEK-293 cells 56, ΛH20= 1.8×10-5 m3/mol is the molar volume of water, pcell(t) is the hydrostatic pressure in the cell, pbath(t) is the hydrostatic pressure in the bath, and σj is the membrane reflection coefficient for species j. It is helpful to define a flow rate coefficient,
| (22) |
From literature values for HEK-293 cells56, χmem∼ 4 ×10-22 m3. s-1.Pa-1 so if the osmolarity inside the cell is ∼ 100mOsm greater than in the bath (Posm ∼ 2.4×105 Pa), then water will flow into the cell at a rate fmem ∼ 10-16 m3, which is approximately 1 cell volume every 20 seconds.
Pipette water flow
To a first approximation, the flow rate should be given by,
| (23) |
where ppip(t) is the hydrostatic pressure of the pipette, and χpip is the pipette flow rate coefficient which characterizes how readily fluid can flow through the pipette. The value of χpip will depend strongly on the solution properties at the tip of the pipette. If the pipette tip contains electrode solution, then the water movement can be approximated by laminar pipe flow using Poiseuille's equation,
| (24) |
where μ is the solution viscosity (μ ∼ 10-3 Pa.s for water). For a conical pipette profile with cone angle, θ, and tip diameter, dtip, integration from the electrode to the tip gives,
| (25) |
Assuming a cone angle of θ ∼ 20°, the tip radius and pipette resistance are related by,
| (26) |
so for a pipette resistance of Raccess< 10MΩ (in a solution with σpip ∼ 2 S/m), the tip radius should be greater than dtip ∼ 0.2μm. Substituting these values into Equation 25 gives a flow coefficient of χpip ∼ 10-19 m3.s-1.Pa-1, which is 2 orders of magnitude larger than χmem. Thus, if the solution in the pipette tip flowed as a liquid then almost all the resistance to flow would come from the membrane. However, in the whole-cell configuration the pipette tip can easily become filled with cytoplasm which will slow the flow of water. The movement of water within the cytoplasm is often modelled using Darcy's law,
| (27) |
where k(x) is the hydraulic permeability of the solution a distance x from the tip (kcell ∼ 10-14 m2.Pa-1.s-1 for cytoplasm57. The hydraulic permeability depends sensitively on the water content of the cytoplasm, but if one assumes a constant hydraulic permeability (k(x) = kcell), the pipette flow rate coefficient would then be,
| (28) |
For an access resistance of Raccess ∼ 10 MΩ and solution conductance of σpip ∼ 2 S.m-1, the pipette flow rate coefficient would then be χpip ∼ 5 ×10-22 m3.s-1.Pa-1, which is comparable to the membrane coefficient.
Cell voltage
The currents flowing from the pipette into the cell, and from the cell into the bath both depend upon the cell voltage, Vcell(t). If the total electric current flowing from the pipette into the cell,
| (29) |
does not balance the total electric current flowing form the cell into the bath,
| (30) |
then the net electric charge inside the cell will change, and the cell voltage will change according to,
| (31) |
where Ccell(t) is the cell capacitance. The change in voltage will then alter the movement of all ionic species so as to bring the net current flowing in from the pipette and net current flowing out through the membrane into balance. For example, if the total electric current flowing out of the cell through the membrane is greater than the total electric current flowing in to the cell through the pipette (e.g. Imem(t) > Ipip(t)), the cell voltage will decrease which will reduce the membrane current and increase the pipette current. The time-scale needed for the cell voltage to balance the pipette and membrane currents is,
| (32) |
In a typical whole-cell experiment (e.g. Ccell ∼ 10pF, Raccess< 10 MΩ), τcell ∼ 0.1ms, which is very rapid compared to the time needed for significant ion accumulation/depletion to occur (e.g. seconds). Thus, on timescales relevant to ion accumulation, Vcell(t) will assume a value such that,
| (33) |
Cell hydrostatic pressure
The hydrostatic pressure in the cytoplasm is actively regulated and depends on many factors, including the activity of the cytoskeleton. Although there is not currently a simple, accurate model, two useful limiting cases can be considered. Firstly, if the cell is very soft (i.e. provides little resistance to changes in volume), then the hydrostatic pressure of the cell will remain constant, and the flow of water from the pipette into the cell, and from the cell into the bath will be uncoupled. Alternatively, if the cell is relatively stiff (i.e. cannot change volume easily), then the cell pressure will rapidly adjust so that the flow rate from the pipette to cell is equal to the flow rate from the cell into the bath,
| (34) |
Importantly, Equation 34 must also be true at steady state, and substituting Equations 21 and 23, then gives
| (35) |
Thus, for a very stiff cell, or a cell at steady-state, the flow of water through the pipette and membrane in series is essentially equivalent to the flow of water through a membrane with an effective permeability of,
| (36) |
Simulation details
Calculations were performed using scripts written in GNU Octave (http://www.octave.org). For simplicity, the immobile anions in the cell were neglected and the pipette, cell and bath were assumed to contain only Na+, NMDG+ and Cl-, with the following diffusion coefficients: DNa+/DK+ = 0.682 58, DNMDG+/DK+ = 0.33 59, DCl-/DK+ = 1.0388 60, DK+ = 1.957 m2.s-1 (at 25°C 60).
The pipette was assumed to have a conical profile with a tip angle of, θ = 20°, and a tip diameter, dtip = 0.2 μm to 2 μm, selected to give the appropriate access resistance (1 MOhms to 10 MOhms). However, both θ and dtip were varied to confirm that steady-state ion depletion depended primarily on access resistance, and not the specific geometry of the pipette tip.
While cell volume clearly varies between cells, HEK-293 cells in culture have a typical diameter of ∼20 μm 61 corresponding to a total cell volume of ∼ 4pL. As at least half of the cell volume is occupied by the nucleus and other membrane-bound organelles, the effective cytosolic volume was then taken to be Λcell ∼ 1 to 3 pL, and cell area of Acell = 103 μm2. For simplicity, all calculations were performed assuming the cell membrane is impermeable to water (Pf = 0 m.s-1), with the exception of Supplementary Fig. 4.
P2X channels were assumed to be impermeable to ions in the absence of ATP. For the simulation shown in Fig. 4, the initial reversal potential of Vrev ∼ -75mV in Fig. 1b was used to establish the relative permeabilities of PNa+:PNMDG+= 20:1, and the absolute permeabilities were then scaled to match the slope of the initial I-V scan (110 nA/V). Shaker channels were assumed to be permeable only to K+, and PK+,max, V1/2 and Vw were adjusted to match the initial current voltage ramp shown in Fig. 6b.
For each time point during simulations, the cell membrane voltage, Vcell(t) was adjusted until the membrane ionic currents, Ij,mem(t), and pipette ionic currents, Ij,pip(t), satisfied Equation 33. Cellular ionic concentrations were then evolved by applying a simple, first-order forward Euler algorithm to Equation 2.
For the steady-state ion concentration calculations shown in Fig. 5 and Supplementary Fig. 4, the holding potential was set to 15mV above the initial reversal potential (that is, Vhold = -(RT/F)× ln(PNa+/PNMDG+) + 15 mV), and the cell voltage and ionic concentrations were then adjusted to satisfy the steady state condition,
| (37) |
for all ionic species. The steady-state reversal potential shifts shown in Fig. 4e, Fig. 5, and Supplementary Fig 4d were then determined by finding the pipette voltage at which the net current was zero.
The full simulation parameters for Fig. 4b-e were PNa+ = 2.8 × 10-6 m/s, PNMDG+ = 1.4 × 10−7 m/s, Pf= 0 m/s, Raccess =5 MΩ, Λcell =1.5pL, Acell = 103 μm2, with 150mM NaCl in the pipette and 150mM NMDG-Cl in the bath. For Fig. 5b, all parameters were the same as in Fig. 4b-e except for the volume. For Fig. 5b, PNa+:PNMDG+ was held fixed at 20:1 and the holding voltage was kept constant at −60mV (∼15mV above the initial reversal potential). For Fig. 5c,d, the access resistance was held constant at Raccess =5 MΩ and for each ratio of PNa+:PNMDG+, the holding voltage was set to 15mV above the initial reversal potential. Similarly, for Supplementary Figure 4, the access resistance was held constant at Raccess =5 MΩ, PNa+ : PNMDG+ was held fixed at 20:1 and the holding voltage was -60mV. For Fig. 6f-i, the pipette contained 140mM KCl and a resistance of Raccess =5 MΩ, while the bath was switched between 140mM KCl and 140mM NMDG-Cl. The parameters for the Shaker current were PK+ = 2.0×10-7 m/s, V1/2= -33.8mV, and Vw = 5mV while for the P2X current were PK+ = 3.3×10-6 m/s, and PNMDG+ = 1.3×10-7 m/s.
Code availability
GNU Octave scripts are available upon request.
Approximation of ion concentration changes
Consider an experiment performed under bi-ionic conditions in which the pipette contains a single permeant monovalent cation of type A (e.g. Na+), while the bath contains a single permeant monovalent cation of type B (e.g. NMDG+), both at the same concentration ρ0 (e.g. ρ0 = 150mM). For simplicity, the pipette solution contains just a single impermeant monovalent anion of type C (e.g. Cl-) again at concentration ρ0.
If the channels in the membrane can be described by the GHK flux equation (Eq. 4), the membrane currents for species A and B will be given by,
| (38) |
and,
| (39) |
Before activation of the channels, the concentration in the pipette and cell are identical, and so the initial reversal potential is just,
| (40) |
At the reversal potential, the current carried by the two cationic species are,
| (41) |
where σmem is the membrane conductance. For example, if the initial membrane conductance is σmem = 40nS, then at the reversal potential there will be an outward current IA,mem = 1nA, and an inward current IB,mem = -1nA.
The outward flow of A will lower the intra-cellular concentration of A, while the inward current of B will increase the intracellular concentration of B. As the difference in concentration between the pipette and cell increases, there will be an exchange of ions between the pipette and cell until at steady-state the currents flowing between the pipette and cell match those flowing between the cell and bath. If osmotic effects are neglected, then pipette currents can be approximated using Equation 12 as,
| (42) |
Noting that the membrane is impermeable to anions (IC,mem = 0), that the concentration of the cations and anions must balance,
| (43) |
and that the pipette solution conductance is just,
| (44) |
the steady-state voltage difference between the pipette and cell is then,
| (45) |
while the steady-state intracellular concentration of A and B are,
| (46) |
Thus, the difference between initial and steady-state ion concentrations can be estimated from the access resistance, membrane conductance, and diffusion coefficients of the ions. For example, for an access resistance Raccess = 5 MΩ and membrane conductance of σmem = 40nS, with 150mM NaCl in the pipette and 150 mM NMDG-Cl in the bath (diffusion coefficients in previous section), Equation 46 gives ρNa+ = 86mM (vs 99mM for numeric solution) and ρNMDG+ = 76mM (vs 68mM for numeric solution). The linear approximation works fairly well when the concentration changes are < 50%, but is inadequate for larger membrane conductances. As a result, the approximate expressions are most useful estimating if there is an ion accumulation problem, rather than attempting to correct for cellular ion concentrations.
If the diffusion coefficients of the different ionic species are comparable, the concentration changes are,
| (47) |
and so to limit steady-state concentration errors, it is then necessary to limit the membrane conductance to,
| (48) |
For example, for an access resistance of 5 MΩ, steady-state concentration errors of 10% or less require that the membrane conductance be less than 10 nS.
The concentration changes then influence the steady-state reversal potential of the cell. Using the same linear approximation,
| (49) |
Combining this with the steady-state voltage difference between the pipette and cell, the measured reversal potential shift will then be,
| (50) |
For the example considered above (150mM NaCl in pipette, 150mM NMDG-Cl in bath, Raccess = 5 MΩ; σmem = 40nS; PNa+/PNMDG+ = 20) the approximation gives a reversal potential shift of 8.1mV, which is fairly similar to the numerical solution result of 7.8mV. However, the linear approximation cannot be relied upon for larger changes in reversal potential (i.e > 10mV).
Supplementary Material
Acknowledgments
We thank M. Mayer, J. Mindell, A. Jara-Oseguera and members of the Swartz lab for helpful discussions. This work was supported by the Intramural Research Program of the NINDS, NIH (to K.J.S.) and by a K99 pathway to independence award NS070954 (M.L.).
Footnotes
Author contributions: M.L. performed experiments and G.E.S.T. performed modeling. All authors contributed to the study design and to writing the manuscript.
Competing Financial Interests: The authors declare no competing financial interest.
References
- 1.Hille B. Ion channels of excitable membranes. Sinauer; Sunderland, Mass.: 2001. [Google Scholar]
- 2.Doyle DA, et al. The structure of the potassium channel: molecular basis of K+ conduction and selectivity. Science. 1998;280:69–77. doi: 10.1126/science.280.5360.69. [DOI] [PubMed] [Google Scholar]
- 3.Tang L, et al. Structural basis for Ca2+ selectivity of a voltage-gated calcium channel. Nature. 2014;505:56–61. doi: 10.1038/nature12775. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Virginio C, MacKenzie A, Rassendren FA, North RA, Surprenant A. Pore dilation of neuronal P2X receptor channels. Nat Neurosci. 1999;2:315–321. doi: 10.1038/7225. [DOI] [PubMed] [Google Scholar]
- 5.Khakh BS, Bao XR, Labarca C, Lester HA. Neuronal P2X transmitter-gated cation channels change their ion selectivity in seconds. Nat Neurosci. 1999;2:322–330. doi: 10.1038/7233. [DOI] [PubMed] [Google Scholar]
- 6.Khakh BS, Egan TM. Contribution of transmembrane regions to ATP-gated P2X2 channel permeability dynamics. J Biol Chem. 2005;280:6118–6129. doi: 10.1074/jbc.M411324200. [DOI] [PubMed] [Google Scholar]
- 7.Eickhorst AN, Berson A, Cockayne D, Lester HA, Khakh BS. Control of P2X(2) channel permeability by the cytosolic domain. J Gen Physiol. 2002;120:119–131. doi: 10.1085/jgp.20028535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Browne LE, Compan V, Bragg L, North RA. P2X7 receptor channels allow direct permeation of nanometer-sized dyes. J Neurosci. 2013;33:3557–3566. doi: 10.1523/JNEUROSCI.2235-12.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Chaumont S, Khakh BS. Patch-clamp coordinated spectroscopy shows P2X2 receptor permeability dynamics require cytosolic domain rearrangements but not Panx-1 channels. Proc Natl Acad Sci U S A. 2008;105:12063–12068. doi: 10.1073/pnas.0803008105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Yan Z, Li S, Liang Z, Tomic M, Stojilkovic SS. The P2X7 receptor channel pore dilates under physiological ion conditions. J Gen Physiol. 2008;132:563–573. doi: 10.1085/jgp.200810059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Fujiwara Y, Kubo Y. Density-dependent changes of the pore properties of the P2X2 receptor channel. J Physiol. 2004;558:31–43. doi: 10.1113/jphysiol.2004.064568. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Zemkova H, et al. Allosteric regulation of the P2X4 receptor channel pore dilation. Pflugers Arch. 2015;467:713–726. doi: 10.1007/s00424-014-1546-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Khadra A, et al. Gating properties of the P2X2a and P2X2b receptor channels: experiments and mathematical modeling. J Gen Physiol. 2012;139:333–348. doi: 10.1085/jgp.201110716. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Rokic MB, Stojilkovic SS. Two open states of P2X receptor channels. Frontiers in cellular neuroscience. 2013;7:215. doi: 10.3389/fncel.2013.00215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Fisher JA, Girdler G, Khakh BS. Time-resolved measurement of state-specific P2X2 ion channel cytosolic gating motions. J Neurosci. 2004;24:10475–10487. doi: 10.1523/JNEUROSCI.3250-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Bernier LP, Ase AR, Boue-Grabot E, Seguela P. P2X4 receptor channels form large noncytolytic pores in resting and activated microglia. Glia. 2012;60:728–737. doi: 10.1002/glia.22301. [DOI] [PubMed] [Google Scholar]
- 17.Chung MK, Guler AD, Caterina MJ. TRPV1 shows dynamic ionic selectivity during agonist stimulation. Nat Neurosci. 2008;11:555–564. doi: 10.1038/nn.2102. [DOI] [PubMed] [Google Scholar]
- 18.Munns CH, Chung MK, Sanchez YE, Amzel LM, Caterina MJ. Role of the outer pore domain in transient receptor potential vanilloid 1 dynamic permeability to large cations. J Biol Chem. 2015;290:5707–5724. doi: 10.1074/jbc.M114.597435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Lingueglia E, et al. A modulatory subunit of acid sensing ion channels in brain and dorsal root ganglion cells. J Biol Chem. 1997;272:29778–29783. doi: 10.1074/jbc.272.47.29778. [DOI] [PubMed] [Google Scholar]
- 20.de Weille JR, Bassilana F, Lazdunski M, Waldmann R. Identification, functional expression and chromosomal localisation of a sustained human proton-gated cation channel. FEBS Lett. 1998;433:257–260. doi: 10.1016/s0014-5793(98)00916-8. [DOI] [PubMed] [Google Scholar]
- 21.Baconguis I, Bohlen CJ, Goehring A, Julius D, Gouaux E. X-ray structure of acid-sensing ion channel 1-snake toxin complex reveals open state of a Na(+)-selective channel. Cell. 2014;156:717–729. doi: 10.1016/j.cell.2014.01.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Baconguis I, Gouaux E. Structural plasticity and dynamic selectivity of acid-sensing ion channel-spider toxin complexes. Nature. 2012;489:400–405. doi: 10.1038/nature11375. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Hamill OP, Marty A, Neher E, Sakmann B, Sigworth FJ. Improved patch-clamp techniques for high-resolution current recording from cells and cell-free membrane patches. Pflugers Arch. 1981;391:85–100. doi: 10.1007/BF00656997. [DOI] [PubMed] [Google Scholar]
- 24.Li M, Silberberg SD, Swartz KJ. Subtype-specific control of P2X receptor channel signaling by ATP and Mg2+ Proc Natl Acad Sci U S A. 2013;110:E3455–3463. doi: 10.1073/pnas.1308088110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Pelegrin P, Surprenant A. Pannexin-1 mediates large pore formation and interleukin-1beta release by the ATP-gated P2X7 receptor. Embo J. 2006;25:5071–5082. doi: 10.1038/sj.emboj.7601378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Li M, Chang TH, Silberberg SD, Swartz KJ. Gating the pore of P2X receptor channels. Nat Neurosci. 2008;11:883–887. doi: 10.1038/nn.2151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Kawate T, Michel JC, Birdsong WT, Gouaux E. Crystal structure of the ATP-gated P2X(4) ion channel in the closed state. Nature. 2009;460:592–598. doi: 10.1038/nature08198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Li M, Kawate T, Silberberg SD, Swartz KJ. Pore-opening mechanism in trimeric P2X receptor channels. Nat Commun. 2010;1:44. doi: 10.1038/ncomms1048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Pusch M, Neher E. Rates of diffusional exchange between small cells and a measuring patch pipette. Pflugers Arch. 1988;411:204–211. doi: 10.1007/BF00582316. [DOI] [PubMed] [Google Scholar]
- 30.Mathias RT, Cohen IS, Oliva C. Limitations of the whole cell patch clamp technique in the control of intracellular concentrations. Biophys J. 1990;58:759–770. doi: 10.1016/S0006-3495(90)82418-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Frankenhaeuser B, Hodgkin AL. The after-effects of impulses in the giant nerve fibres of Loligo. J Physiol. 1956;131:341–376. doi: 10.1113/jphysiol.1956.sp005467. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Zimmerman AL, Karpen JW, Baylor DA. Hindered diffusion in excised membrane patches from retinal rod outer segments. Biophys J. 1988;54:351–355. doi: 10.1016/S0006-3495(88)82966-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Frazier CJ, George EG, Jones SW. Apparent change in ion selectivity caused by changes in intracellular K(+) during whole-cell recording. Biophys J. 2000;78:1872–1880. doi: 10.1016/S0006-3495(00)76736-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Jiang LH, et al. N-methyl-D-glucamine and propidium dyes utilize different permeation pathways at rat P2X(7) receptors. Am J Physiol Cell Physiol. 2005;289:C1295–1302. doi: 10.1152/ajpcell.00253.2005. [DOI] [PubMed] [Google Scholar]
- 35.Heginbotham L, Lu Z, Abramson T, MacKinnon R. Mutations in the K+ channel signature sequence. Biophys J. 1994;66:1061–1067. doi: 10.1016/S0006-3495(94)80887-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Brake AJ, Wagenbach MJ, Julius D. New structural motif for ligand-gated ion channels defined by an ionotropic ATP receptor. Nature. 1994;371:519–523. doi: 10.1038/371519a0. [DOI] [PubMed] [Google Scholar]
- 37.Ding S, Sachs F. Single channel properties of P2X2 purinoceptors. J Gen Physiol. 1999;113:695–720. doi: 10.1085/jgp.113.5.695. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Melishchuk A, Armstrong CM. Mechanism underlying slow kinetics of the OFF gating current in Shaker potassium channel. Biophys J. 2001;80:2167–2175. doi: 10.1016/S0006-3495(01)76189-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Tatham PE, Cusack NJ, Gomperts BD. Characterisation of the ATP4- receptor that mediates permeabilisation of rat mast cells. Eur J Pharmacol. 1988;147:13–21. doi: 10.1016/0014-2999(88)90628-0. [DOI] [PubMed] [Google Scholar]
- 40.Meyers JR, et al. Lighting up the senses: FM1-43 loading of sensory cells through nonselective ion channels. J Neurosci. 2003;23:4054–4065. doi: 10.1523/JNEUROSCI.23-10-04054.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Binshtok AM, Bean BP, Woolf CJ. Inhibition of nociceptors by TRPV1-mediated entry of impermeant sodium channel blockers. Nature. 2007;449:607–610. doi: 10.1038/nature06191. [DOI] [PubMed] [Google Scholar]
- 42.Puopolo M, et al. Permeation and block of TRPV1 channels by the cationic lidocaine derivative QX-314. J Neurophysiol. 2013;109:1704–1712. doi: 10.1152/jn.00012.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Hattori M, Gouaux E. Molecular mechanism of ATP binding and ion channel activation in P2X receptors. Nature. 2012;485:207–212. doi: 10.1038/nature11010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Heymann G, et al. Inter- and intrasubunit interactions between transmembrane helices in the open state of P2X receptor channels. Proc Natl Acad Sci U S A. 2013;110:E4045–4054. doi: 10.1073/pnas.1311071110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Liao M, Cao E, Julius D, Cheng Y. Structure of the TRPV1 ion channel determined by electron cryo-microscopy. Nature. 2013;504:107–112. doi: 10.1038/nature12822. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Cao E, Liao M, Cheng Y, Julius D. TRPV1 structures in distinct conformations reveal activation mechanisms. Nature. 2013;504:113–118. doi: 10.1038/nature12823. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Banke TG, Chaplan SR, Wickenden AD. Dynamic changes in the TRPA1 selectivity filter lead to progressive but reversible pore dilation. Am J Physiol Cell Physiol. 2010;298:C1457–1468. doi: 10.1152/ajpcell.00489.2009. [DOI] [PubMed] [Google Scholar]
- 48.Chen J, et al. Pore dilation occurs in TRPA1 but not in TRPM8 channels. Molecular pain. 2009;5:3. doi: 10.1186/1744-8069-5-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Jung J, et al. Dynamic modulation of ANO1/TMEM16A HCO3(-) permeability by Ca2+/calmodulin. Proc Natl Acad Sci U S A. 2013;110:360–365. doi: 10.1073/pnas.1211594110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Yu Y, Kuan AS, Chen TY. Calcium-calmodulin does not alter the anion permeability of the mouse TMEM16A calcium-activated chloride channel. J Gen Physiol. 2014;144:115–124. doi: 10.1085/jgp.201411179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Kamb A, et al. Multiple products of the Drosophila Shaker gene may contribute to potassium channel diversity. Neuron. 1988;1:421–430. doi: 10.1016/0896-6273(88)90192-4. [DOI] [PubMed] [Google Scholar]
- 52.Zagotta WN, Hoshi T, Aldrich RW. Restoration of inactivation in mutants of Shaker potassium channels by a peptide derived from ShB. Science. 1990;250:568–571. doi: 10.1126/science.2122520. [DOI] [PubMed] [Google Scholar]
- 53.Hoshi T, Zagotta WN, Aldrich RW. Biophysical and molecular mechanisms of Shaker potassium channel inactivation. Science. 1990;250:533–538. doi: 10.1126/science.2122519. [DOI] [PubMed] [Google Scholar]
- 54.Goldman DE. Potential, Impedance, and Rectification in Membranes. J Gen Physiol. 1943;27:37–60. doi: 10.1085/jgp.27.1.37. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Hodgkin AL, Katz B. The effect of sodium ions on the electrical activity of giant axon of the squid. J Physiol. 1949;108:37–77. doi: 10.1113/jphysiol.1949.sp004310. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Tsunoda SP, Wiesner B, Lorenz D, Rosenthal W, Pohl P. Aquaporin-1, nothing but a water channel. J Biol Chem. 2004;279:11364–11367. doi: 10.1074/jbc.M310881200. [DOI] [PubMed] [Google Scholar]
- 57.Charras GT, Coughlin M, Mitchison TJ, Mahadevan L. Life and times of a cellular bleb. Biophys J. 2008;94:1836–1853. doi: 10.1529/biophysj.107.113605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Barry PH, Lynch JW. Liquid junction potentials and small cell effects in patch-clamp analysis. J Membr Biol. 1991;121:101–117. doi: 10.1007/BF01870526. [DOI] [PubMed] [Google Scholar]
- 59.Ng B, Barry PH. The measurement of ionic conductivities and mobilities of certain less common organic ions needed for junction potential corrections in electrophysiology. Journal of neuroscience methods. 1995;56:37–41. doi: 10.1016/0165-0270(94)00087-w. [DOI] [PubMed] [Google Scholar]
- 60.Vanýsek P, et al. Electrochemical science and technology of copper : proceedings of the international symposium. Electrochemical Society; Pennington, N.J.: 2002. [Google Scholar]
- 61.Gentet LJ, Stuart GJ, Clements JD. Direct measurement of specific membrane capacitance in neurons. Biophys J. 2000;79:314–320. doi: 10.1016/S0006-3495(00)76293-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.