Skip to main content
PMC home page
The ISME Journal logoLink to The ISME Journal
. 2016 Apr 8;10(11):2715–2724. doi: 10.1038/ismej.2016.50

Interactions between growth-dependent changes in cell size, nutrient supply and cellular elemental stoichiometry of marine Synechococcus

Nathan S Garcia 1, Juan A Bonachela 2, Adam C Martiny 1,3,*
PMCID: PMC5113841  PMID: 27058506

Abstract

The factors that control elemental ratios within phytoplankton, like carbon:nitrogen:phosphorus (C:N:P), are key to biogeochemical cycles. Previous studies have identified relationships between nutrient-limited growth and elemental ratios in large eukaryotes, but little is known about these interactions in small marine phytoplankton like the globally important Cyanobacteria. To improve our understanding of these interactions in picophytoplankton, we asked how cellular elemental stoichiometry varies as a function of steady-state, N- and P-limited growth in laboratory chemostat cultures of Synechococcus WH8102. By combining empirical data and theoretical modeling, we identified a previously unrecognized factor (growth-dependent variability in cell size) that controls the relationship between nutrient-limited growth and cellular elemental stoichiometry. To predict the cellular elemental stoichiometry of phytoplankton, previous theoretical models rely on the traditional Droop model, which purports that the acquisition of a single limiting nutrient suffices to explain the relationship between a cellular nutrient quota and growth rate. Our study, however, indicates that growth-dependent changes in cell size have an important role in regulating cell nutrient quotas. This key ingredient, along with nutrient-uptake protein regulation, enables our model to predict the cellular elemental stoichiometry of Synechococcus across a range of nutrient-limited conditions. Our analysis also adds to the growth rate hypothesis, suggesting that P-rich biomolecules other than nucleic acids are important drivers of stoichiometric variability in Synechococcus. Lastly, by comparing our data with field observations, our study has important ecological relevance as it provides a framework for understanding and predicting elemental ratios in ocean regions where small phytoplankton like Synechococcus dominates.

Introduction

A clear understanding of biogeochemical cycles is key to predicting long-term global change associated with rising atmospheric carbon dioxide (CO2). The elemental composition of marine phytoplankton is central to ocean biogeochemistry as it links the global carbon (C) cycle with the cycling of other elements, such as nitrogen (N) and phosphorus (P) (Sterner and Elser, 2002; Galbraith and Martiny, 2015). The ratio of elements within organisms is known to vary with energy and nutrient flow through ecosystems (Sterner et al., 1997; Sterner and Elser, 2002; Urabe et al., 2002) and is linked to growth rates and nutritional status. The elemental stoichiometry of biological organisms propagates through the food web to shape community structure and function (Elser et al., 2000) and in turn, marine biota provides a flexible interface, linking global biogeochemical cycles together and can thereby have large effects on climate systems (Finkel et al., 2010; Galbraith and Martiny, 2015). Thus, understanding the factors that influence the elemental stoichiometry of marine organisms is necessary to refine models that forecast how the earth system will change in the future.

Models of biogeochemical cycles traditionally use a fixed ratio of C:N:P for major lineages of marine phytoplankton, although C:N:P of phytoplankton can vary substantially. Countless studies indicate that cellular elemental stoichiometry is highly variable within isolates (Goldman et al., 1979; Geider et al., 1998; Geider and La Roche, 2002) and recent research indicates that C:N:P is also highly variable among ocean regions (Martiny et al., 2013; DeVries and Deutsch, 2014; Teng et al., 2014). Basic knowledge of the underlying physiological mechanisms that control this variability can provide a framework to understand and predict how marine biota interacts with biogeochemical cycles both now and in the future.

Cell models and laboratory studies have examined how multiple factors, such as growth rate and nutrient limitation interact to influence cellular elemental stoichiometry of phytoplankton. Basic physiological mechanisms link growth rates with chemical components within cells, which determine the cellular stoichiometry of elements. For example, the growth rate hypothesis (Sterner and Elser, 2002) predicts that ribosomes are needed in high concentrations when cells are growing fast, and the high P-content (~9%) in ribosomal RNA can cause changes in C:P and N:P with growth (Elser et al., 2000). Variability in other cell components, such as proteins (Rhee, 1978; Lourenço et al., 1998), pigments, phospholipids (Van Mooy et al., 2006) and polyphosphates (Rao et al., 2009; Martin et al., 2014), which are rich in specific elements like N or P, also contribute to variation in cellular elemental stoichiometry and may also co-vary with growth (Rhee 1973). Thus, variable nutrient supply ratios (for example, N:P) are known to influence cellular biochemical content, which can affect growth and elemental stoichiometry of organisms (Rhee, 1978; Goldman et al., 1979; Geider and La Roche, 2002; Klausmeier et al., 2008).

Related to the growth rate hypothesis, empirical data have shown that C:P and N:P of phytoplankton varies when nutrients limit growth (Rhee, 1978; Goldman et al., 1979). This relationship has motivated the use of the classic Droop model to predict C:N:P as a function of growth in single- or multiple-nutrient theoretical models (Droop, 1968; Morel, 1987; Legović and Cruzado, 1997; Klausmeier et al., 2004a, b; Pahlow and Oschlies, 2009). In the Droop model, the growth rate of an organism increases hyperbolically as the cellular elemental quota of a single, growth-limiting element (for example, P) increases. Klausmeier et al. (2004a) used empirical data to build a Droop-based model in which growth rates decline because of decreasing concentrations of a limiting nutrient (for example, NO3-), whereas other nutrients that are abundant (for example, PO43-) are acquired to store a given element in excess. In other models, phytoplankton elemental stoichiometry results from resource allocation strategies and regulation of nutrient-uptake proteins (Pahlow and Oschlies, 2009; Bonachela et al., 2013), which are known to comprise high portions (up to 50%) of cellular N in microbial organisms (Geider and La Roche, 2002). Thus, imbalanced nutrient supplies interact with growth rates to influence the cellular elemental composition through ribosomal RNA, elemental storage and nutrient acquisition mechanisms.

Nearly all of the systematic approaches to studying growth-dependent changes in cellular elemental stoichiometry have focused on large eukaryotic lineages, which are rare or absent from the large oligotrophic gyres throughout the world's oceans. Although some studies have focused on small freshwater phytoplankton including Cyanobacteria (Healey, 1985; Claquin et al., 2002; Verspagen et al., 2014), less is known about these mechanistic relationships within marine Cyanobacteria, which are known to dominate vast nutrient-poor gyres (Flombaum et al., 2013). Recent estimates suggest that they contribute 25% of global marine net primary production and are found in most ocean regions in high abundance (Flombaum et al., 2013). Despite their large influence on global biogeochemical cycles, only a few studies have examined the cellular elemental stoichiometry of marine Cyanobacteria (Bertilsson et al., 2003; Heldal et al., 2003; Ho et al., 2003; Finkel et al., 2010) and even fewer have focused on physiological mechanisms that may control cellular C:N:P of lineages within Cyanobacteria (Fu et al., 2007; Kretz et al., 2015; Mouginot et al., 2015). Furthermore, none of these studies have examined the well-known interactive influence of growth physiology and nutrient supply on its cellular elemental stoichiometry. These relationships could be different in small phytoplankton in comparison with large phytoplankton, as cell size can reflect important differences in cellular physiology, such as the ability to store nutrients. Knowledge of basic mechanisms that regulate the C:N:P of Cyanobacteria is essential to understand how this globally ubiquitous functional group of primary producers influences ocean biogeochemical cycles and how this influence may change in the future.

Here, we asked how cellular elemental stoichiometry of an isolate of one of the most numerically abundant phytoplankton genera in the global ocean (Flombaum et al., 2013), Synechococcus (WH8102), varies across a range of N- and P-limited steady-state growth rates in laboratory chemostat cultures. We also evaluated how nucleic acids contribute to cellular elemental stoichiometry by determining how cellular P is biochemically apportioned. Finally, because we documented changes in cell size as a function of growth rate in our chemostat cultures, we used a theoretical model to ask how growth-dependent changes in cell size contributes to relationships between nutrient-limited growth, elemental quotas and cellular elemental stoichiometry. Our results provide a basic understanding of how one of the most abundant marine phytoplankton lineages regulates its elemental composition in the oceans.

Materials and methods

Experiments

Using a modified method from Mouginot et al. (2015), cultures of Synechococcus (strain WH8102) were grown with a continuous dilution method in 8 l-polycarbonate bottles at 24 °C in an artificial seawater medium at ~195 μmol quanta m-2 s-1 on a 14:10 light:dark cycle. Light was supplied with cool white fluorescent lamps. We prepared artificial seawater modified from Waterbury and Willey (1988) (Supplementary Table 1), in 50 l batches before autoclaving 7 l volumes, to which, after cooling, we added 0.2-μm-filter-sterilized carbonates, trace metals, nitrate (NO3-) and phosphate (PO43-) (Supplementary Table 1). Transfer of media and cultures to the chemostat system were done using a hood and open flame to minimize contamination. The culturing system was enclosed with 0.2 μm-filtered air pumped into the chamber with a 0.2 μm filter attached to an air outlet. We controlled the culture dilution rate and hence the growth rate, by controlling the medium supply rate and the culture volume. The liquid volume in the reservoirs ranged from 2.3 to 5.25 l, thereby yielding a range in dilution rates and steady-state growth rates with equivalent medium input rates. The accumulation of cellular biomass was limited by NO3- (added as NaNO3), where measured nutrient concentrations in the medium were 15.9 μM NO3- and 9.2 μM PO43- (added as K2HPO4) yielding a N:Pinput supply ratio of 1.7, or by PO43- with measured concentrations in the medium of 38 μM NO3- and 0.56 μM PO43-, yielding an N:Pinput supply ratio of 68. PO43- and NO3- were measured with a colorimetric assay as described in the Bermuda Atlantic Time-series Methods (Michaels et al, 1997a, b) with a spectrophotometer (Genesis 10vis Thermo Scientific, Madison, WI, USA) at 885 and 543 nm, respectively.

Samples from chemostat cultures were collected on pre-combusted 450 °C GF/F filters (Whatman, GE Healthcare, Little Chalfont, Buckinghamshire, UK) for the analysis of particulate organic C and N (200 ml), particulate organic P (50 ml), and DNA and RNA (200 ml). Samples for the analysis of particulate organic C and particulate organic N were dried at 50–80 °C (48+ h), pelletized and analyzed on a Flash EA 1112 NC Soil Analyzer (Thermo Scientific). Samples for the analysis of particulate organic P were rinsed with 0.17 M NaSO4, dried at 60–80 °C with 2 ml of 0.017 M MgSO4, and combusted at 450 °C for 2 h before adding 5 ml 0.2 M HCl and baking at 80–90 °C. The resulting orthophosphate concentrations were measured as described above.

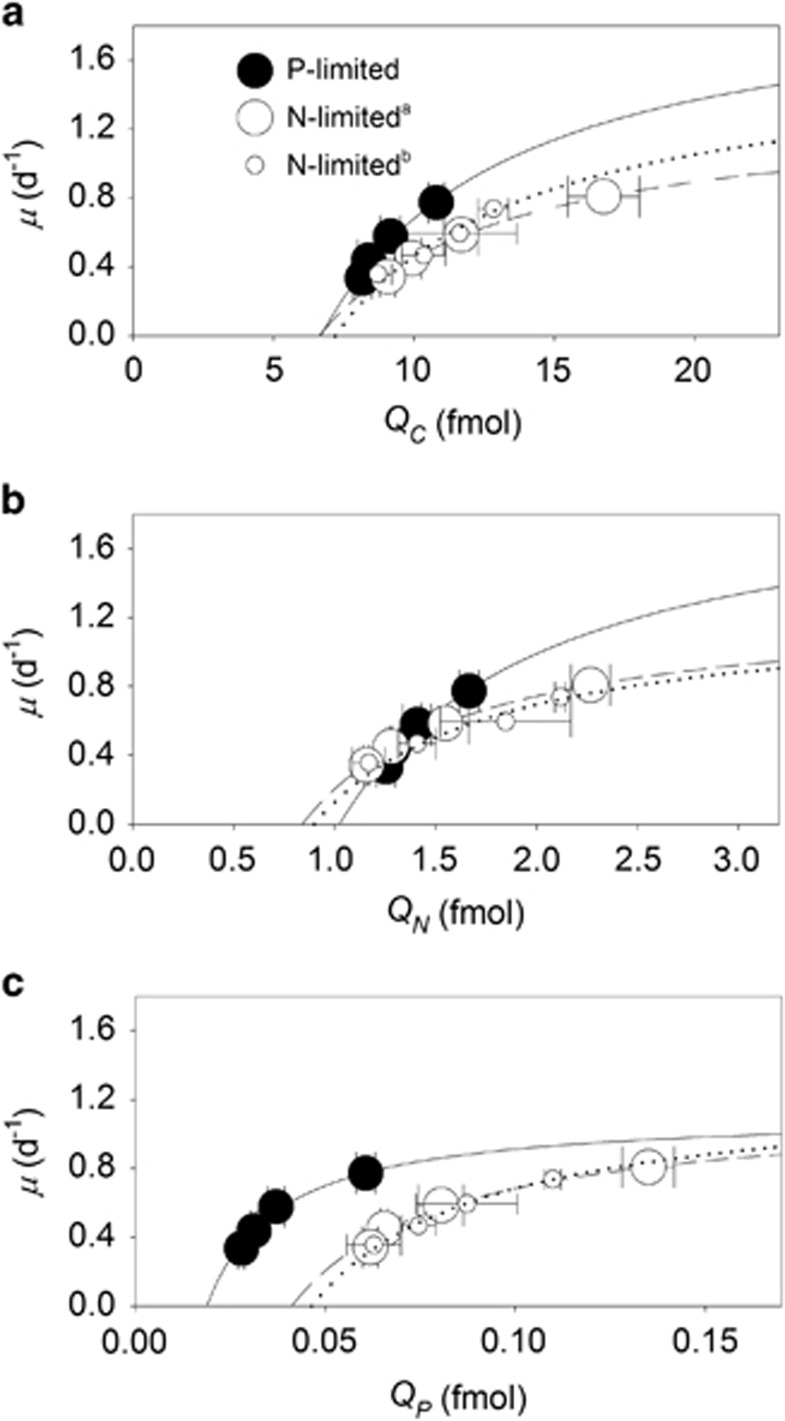
Nucleic acid samples were stored in liquid N until analysis. Cells were lysed with a bead-beater containing 1 ml of a mixed solution containing one part RNA preservation solution (20 mM ethylenediaminetetraacetic acid; 25 mM sodium citrate; and saturated with ammonium sulfate) and four parts 5 mM Tris buffer. Nucleic acids were measured in the supernatant with the Qubit dsDNA HS Assay Kit and the Qubit HS RNA Assay Kit (Invitrogen, Eugene, OR, USA) according to the method described by Zimmerman et al. (2014). This technique provides a linear signal in response to the amount of cell material analyzed and is able to recover nearly 100% of material from standards (from Qubit HS Assay Kit) that were spiked into the samples. Cells were counted with an Accuri C6 Flow Cytometer (Ann Arbor, MI, USA) by identifying particles with forward scatter (the proxy flow cytometry estimate for cell size, FSCH) and Chl a fluorescence. Fluorescence of phycoerythrin was also determined with the flow cytometer. We estimated cell diameter with a cell–carbon/cell–volume conversion factor calculated with data acquired from a related Synechococcus strain (WH8103) growing in artificial seawater (Heldal et al., 2003). To summarize trends in steady-state responses to N- and P-limited growth rates, we report the mean and standard deviations on measurements from samples collected on the final three time points of the experimental trials. We fit the Droop model to the growth rate and elemental quota data in Figure 1 using a simple nonlinear least squares method with R statistical software (www.r-project.org) with the form Q=a/(b–μ), where a=μ∞· Q′min, b=μ∞, Q is elemental quota, and μ is growth rate.

Figure 1.

Figure 1

Open in a new tab

Interactive influence of growth rate and nutrient supply on cellular elemental quotas of Synechococcus. Cellular C (QC, a), N (QN, b) and P (QP, c) quotas of Synechococcus as a function of steady-state growth (μ) in chemostat cultures limited by nitrate (open symbols) or phosphate (closed symbols). Data were fitted to the Droop model (μ=μ∞ · [1–Q′min/Q]) for P-limited (solid lines), and N-limited (dasheda and dottedb lines) cells, where μ is the growth rate, μ∞ is the conditional maximum growth rate, Q′min is the conditional minimum elemental quota and Q is the elemental quota. Largea and smallb open symbols represent data from independent, N-limited culture trials. Standard deviations are plotted on means of triplicate measurements from the last three sampling time points during a trial.

Model

We used the empirical data from the chemostat cultures to expand on an existing model where cellular elemental stoichiometry emerges as a function of the nutrient-limited growth rate (see also Supplementary Information). This model uses physiological foundations similar to other models of cell stoichiometry (Lehman et al., 1975; Bonachela et al., 2013) and includes quota-regulated dynamics that encode changes in the number of nutrient-uptake proteins (Bonachela et al., 2013). These dynamics depend on the quota of the nutrient that is taken up through the so-called expression function, F, and the P quota (as a proxy for the availability of protein-synthesizing ribosomes) through the repression function, G. The former encodes protein regulation strategies based on nutrient availability (upregulation for low nutrient, downregulation for high nutrient) (Dyhrman and Palenik, 2001). The latter encodes the feasibility of those strategies based on ribosome availability (for example, low levels of RNA prevent synthesis from happening). For the number of proteins that take up N in the population, nN, for example, these dynamics are given by the equation:

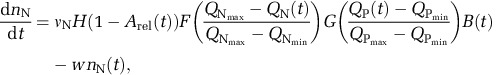graphic file with name ismej201650e1.jpg

where B represents population size, w is the dilution rate of the chemostat, νN is the maximum protein synthesis rate per cell and unit time and H is a Heaviside function that depends on the ratio absorbing-to-total area (Arel; that is, a switch that stops protein synthesis when the absorbing area reaches the total area). As explained in the Supplementary Information, nN is positively correlated with the maximum uptake rate for N; in turn, nP is positively correlated with the maximum uptake rate for P.

Unlike previous models, however, the maximum and minimum value for the quotas in our model (that is, physiological ranges) are positively correlated with cell size (see Supplementary Information, Equations (18–21)). These expression levels are deduced from our laboratory data. Differently from previous models, we also de-couple the dynamics of population C and population number. Although the dynamics of population C are somewhat controlled by the regulation of photosynthetic proteins (see Supplementary Information, Equation (15)) and other metabolic expenses, the equation for the population number purely depends on cellular quota availability:

graphic file with name ismej201650e2.jpg

where f is a multiplicative function that depends on the three cellular elements. Thus, our expanded model implements variable cellular C quotas. Using different forms for the functional dependence between the C, N and P quotas and the population dynamics of the chemostat cultures, f, allowed us to study how the emergent growth rates depend on the shape of this functional dependence (for example, linear or Droop-like hyperbola).

All these components act as a feedback loop. From our chemostat cultures, we were able to deduce that the cellular growth rate influences the maximum C quota and that the cellular C quota influences the maximum and minimum N and P quotas. These extreme quotas are key to the regulation of the nutrient-uptake and photosynthetic proteins, which, in turn, strongly influence nutrients and growth. As the cellular C quota is tightly correlated with cell size, the model ultimately links cell size and growth rate, which influence quota dynamics and elemental stoichiometry. See Supplementary Information for further details.

Results

To understand the interaction between nutrient limitation, growth physiology and cellular elemental stoichiometry, we analyzed steady-state chemostat cultures of Synechococcus WH8102 across four growth rates and two different nutrient supply regimes (N:Pinput=1.7 and N:Pinput=68). First, we monitored the culture cell density, cell size and particulate organic matter in cultures to ensure they were growing at steady state (Supplementary Figure 1). Both residual dissolved PO43- in P-limited cultures and residual dissolved NO3- in N-limited cultures were below the detection limit of the spectrophotometric methods used. This indicated that the biomass in cultures, and hence the physiology of cells, were strongly P limited or N limited, respectively (Supplementary Figure 2). In addition, the sum of the residual dissolved PO43- and NO3- with particulate organic P and particulate organic N concentrations, respectively, were close to measured input concentrations of PO43- and NO3-. This indicated that cells were able to drawdown nearly all of the PO43- or NO3- supplied to P-limited or N-limited chemostat cultures, respectively (Supplementary Figure 2). Hence, estimates of culture cell densities, cellular elemental stoichiometry (C:Pcell and N:Pcell) and residual nutrient concentrations suggested that cells had reached a steady state by the end of each chemostat trial (Supplementary Figures 1–3).

Growth rate and culture cell density varied in a negative relationship, with a stronger relationship in P-limited vs N-limited cultures (Supplementary Figures 1A–C). In contrast, the proxy FSCH was positively correlated with the growth rate in steady-state chemostats under both N- and P limitation (Supplementary Figures 1D–F). Throughout each trial, particulate organic C decreased as a function of the P-limited growth rate but was relatively invariable under N-limited growth (Supplementary Figures 1G–I).

The steady-state cellular elemental quotas of C, N and P (QC, QN and QP) all increased as a function of growth following a hyperbolic curve resembling the Droop model equation (r2≥0.94, Figure 1 and Table 1). To quantify physiological limits on growth rates and elemental quotas, we defined μ∞ and Q′min as the conditional maximum growth rate and the conditional minimum elemental quota, respectively, given the ambient light and temperature levels in our experiments. Although the conditional minimum C and N quotas (Q′C,min, Q′N,min) did not vary between P-limited and N-limited cells (Student's t-test, P>0.05, Figure 1a,Table 1), the conditional minimum P quota (Q′P,min), significantly increased by 118–146% under N-limited conditions in comparison with P-limited conditions (Figure 1c, Table 1). Also, in P-limited cultures, μ∞ was significantly higher (Student's t-test, P<0.05) when calculated from the QC or QN data in comparison with that calculated from the QP data (Table 1). Collectively, these differences reflect strong differences in the cell quotas as a function of growth and nutrient conditions (Figures 1a–c).

Table 1. Parameters of the Droop model (μ=μ∞ (1–Q′min/Q) fit to the data in Figure 1 for N-limited and P-limited cultures of Synechococcus.

Parameter P limited N limiteda
Conditional maximum growth rate (day-1)
 μ∞C 2.1±0.1 1.3±0.0, 1.6±0.2
 μ∞N 2.0±0.1 1.3±0.0, 1.3±0.1
 μ∞P 1.1±0.0 1.2±0.0, 1.3±0.0
     
Conditional minimum quota (fmol cell-1)
 Q′C,min 6.7±0.7 6.6±0.2, 7.2±1.5
 Q′N,min 1.0±0.1 0.8±0.02, 0.9±0.2
 Q′P,min 0.02±0.00 0.04±.00, 0.05±0.00
     
Model fit to quotas
 r2C 0.98 0.99, 0.95
 r2N 0.98 0.99, 0.94
 r2P 0.99 0.99, 0.99
Open in a new tab

Abbreviations: C, carbon; N, nitrogen; P, phosphorus.

Variation is reported as the standard error.

a

Duplicate means represent data from independent N-limited culture trials.

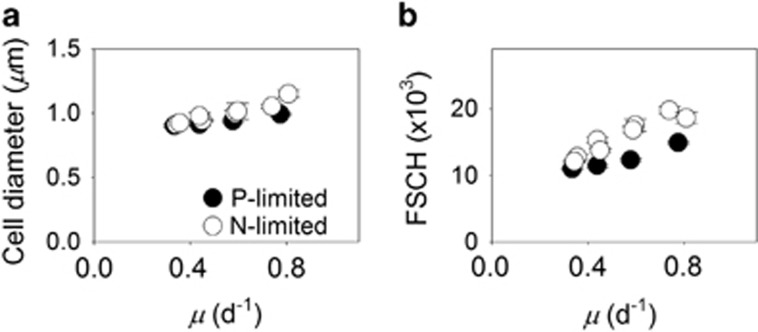
The observed increase in cell quotas with growth rate could lead to changes in overall cell size (Figure 2a). To further examine this, we compared FSCH with growth rates. Growth physiology had a significant effect on FSCH (analysis of covariance test, F1, 32=239, P<0.001; Figure 2b). In addition, growth rate and limitation type (N or P) had a significant interactive effect on FSCH (analysis of covariance test, F1, 32=13, P=0.001). Thus, N-limited cells were larger than P-limited cells when the growth rate was high (analysis of covariance test, F1, 32=122, P<0.001), but the effect of limitation type on FSCH was reduced in slower-growing cells (Figure 2b). We also compared FSCH with other cellular measurements. Cellular nucleic acids (DNAcell and RNAcell, Supplementary Figures 5A and B), pigment fluorescence (fluorescence of Chl a and phycoerythrin; Supplementary Figures 4C and D) and cell quotas (Supplementary Figure 4) all varied in a positive linear relationship with FSCH (t-test, P<0.05) regardless of limitation type (Supplementary Figure 1). Thus, the effect of growth on cell size was linked to a general increase in cellular mass. Furthermore, the fluorescence of cellular pigments (Chl a and phycoerythrin) was elevated under P limitation in comparison with N limitation (analysis of covariance, F1, 32>9; P<0.05; Supplementary Figures 4C and D), suggesting an additional effect of limitation type.

Figure 2.

Figure 2

Open in a new tab

Growth-dependent changes in cell size of Synechococcus. Cell size (estimated with a cell C to cell volume relationship) (a) and forward scatter (FSCH, a proxy for cell diameter; b) of Synechococcus cells as a function of steady-state growth (μ) in chemostat cultures limited by nitrate (open symbols) or phosphate (closed symbols). Open circles represent data from two independent, N-limited culture trials. Standard deviations are plotted on means of triplicate measurements from the last three sampling time points during a trial.

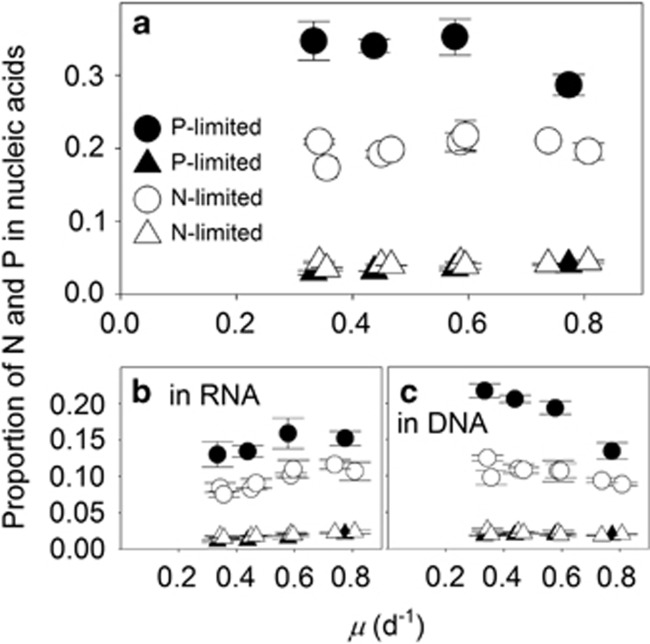
We next identified the role of nucleic acids in setting QP, as P in RNA has previously been shown to be an important driver of elemental stoichiometry (Sterner and Elser, 2002). First, we observed that the proportion of QN in nucleic acids increased as a function of growth under both N- and P limitation, reflecting the general positive relationship between growth and cellular nucleic acid concentrations (Figure 3a, triangles). Despite this positive relationship, the proportion of QP devoted to nucleic acids (Figures 3b and c) declined as a function of increasing growth in P-limited cultures (P<0.05; Figure 3a, closed circles). This declining contribution suggested that P-containing cellular resources other than nucleic acids also varied in a positive relationship with P-limited growth. This effect was not observed under N limitation, however, suggesting a tradeoff between non-nucleic acid, P-containing cellular resources or function under N-limited growth (for example, between storage and physiologically active P-containing resources; Figure 3a).

Figure 3.

Figure 3

Open in a new tab

Proportion of cellular N and P quotas devoted to nucleic acids. Cellular N (triangles) and P (circles) in total cellular nucleic acids (a), cellular RNA (b) and cellular DNA (c) as a proportion of total cellular N and P, respectively, as a function of steady-state growth (μ) in chemostat cultures of Synechococcus limited by nitrate (open symbols) or phosphate (closed symbols). Open symbols represent data from two independent, N-limited culture trials. Standard deviations are plotted on means of triplicate measurements from the last three sampling time points during a trial.

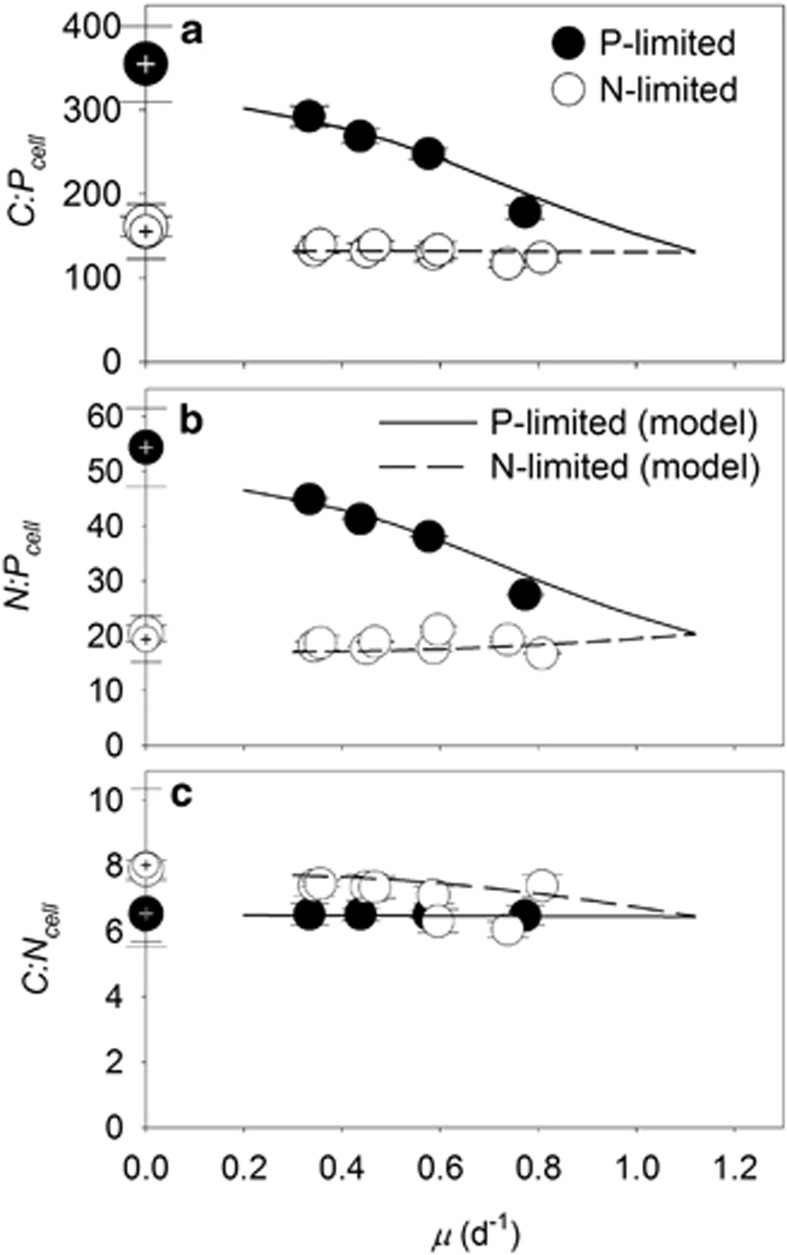
We then identified trends in cellular elemental stoichiometry of Synechococcus. C:Pcell and N:Pcell of Synechococcus declined as a linear function with increasing growth (t-test, P<0.05; Figures 4a and b) under P limitation. In contrast to the negative linear relationship between N:Pcell and P-limited growth, N:Pcell was stable under N-limited growth (t-test, P>0.05). C:Pcell only decreased marginally with N-limited growth (t-test, P<0.05, Figure 4b). C:Ncell was generally elevated in slow-growing N-limited cultures in comparison with slow-growing P-limited cultures, but was more variable at higher growth rates (Figure 4c). As a result of the strong contrast between our observations, some previous findings, and models of phytoplankton stoichiometry under N limitation, we repeated our N-limited trials with Synechococcus and ensured our results could be replicated (Figure 4).

Figure 4.

Figure 4

Open in a new tab

Interactive influence of growth rate and nutrient limitation on cellular stoichiometry of Synechococcus. Cellular elemental ratios of C:P (C:Pcell, a), N:P (N:Pcell, b) and C:N (C:Ncell, c) as a function of steady-state growth (μ) in chemostat cultures of Synechococcus limited by nitrate (open circles) or phosphate (closed circles). Open circles represent data from two independent, N-limited culture trials. Hashed symbols where μ= 0 represent calculated ratios from conditional minimum elemental quotas (Q′min) from Droop models in Figure 1. Standard deviations are plotted on means of triplicate measurements from the last three sampling time points during a trial. Model output data are also included (see further details in Supplementary Information).

Although the observed behavior of QP and QN initially mimicked Droop model curves, we were not able to replicate empirical trends in cellular elemental ratios by using existing Droop-based variable quota models nor by using more mechanistic quota-based models with fixed minimum and maximum elemental quota values (Legović and Cruzado, 1997; Klausmeier et al., 2004a). We tested whether the absence of a link between growth-dependent changes in all three elemental quotas and cell size (common to all existing models) is the reason for this failure to replicate our data. Thus, we modified an existing physiological model (Bonachela et al., 2013) to include growth-dependent changes in cell size that influence cellular elemental quotas as well as their maximum and minimum values, which in turn are key in the regulation of nutrient-uptake proteins (see Supplementary Information). Our expanded model captures the observed relationship between cellular elemental stoichiometry and growth (Figure 4) including the ‘Droop-like' behavior for all cellular elemental quotas. Only the inclusion of growth-dependent cell size and quota-dependent protein regulation enabled the replication of the observed behavior. Importantly, these two key underlying mechanisms are fundamentally different than those in the Droop model, and confirm the strong influence of cell size on the resulting cellular elemental quotas and ratios.

Discussion

Using controlled chemostat cultures of an isolate representing one of the most abundant marine phytoplankton lineages, we observed strong inconsistencies between our data and some fundamental conceptual mechanisms that have commonly been invoked to understand the elemental composition of phytoplankton. First, although RNAcell and DNAcell increased with increasing growth rate, thereby supporting a key aspect of the growth rate hypothesis (Sterner and Elser, 2002), the proportion of QP devoted to nucleic acids did not increase with increasing growth, suggesting that P in nucleic acids is not the central driver of the cellular elemental stoichiometry of Synechococcus within this growth rate range. Our estimates of this proportion agree with previous estimates indicating that RNAcell is low in Synechococcus (Mouginot et al., 2015) and imply that P-rich biomolecules other than nucleic acids also co-vary with growth (Figure 3). Nucleic acids may have a more dominant influence when growth rates are very close to μmax, however, and in absence of μmax data for WH8102, our high growth rate cultures represent ~67–73% of μmax of a related isolate of Synechococcus (Moore et al., 1995). Nucleic acids may also have a stronger influence on stoichiometric differences across lineages where maximum growth rates are vastly different (Elser et al., 2000), rather than within a single isolate.

A second departure from the accepted conceptual models of cellular elemental stoichiometry is the observed role of cell size and associated quotas as a function of growth. Although none of the previous theoretical models include growth-dependent variability in cell size, our data indicate that cell size and all of the cell components that we measured (QC, QN, QP, DNAcell, RNAcell and cellular pigment fluorescence) were positively related to the cellular growth rate (Figure 2, Supplementary Figures 4 and 5). Cell size is a critical ingredient in our expanded model of cellular elemental stoichiometry because it allows QC, QN and QP to change as a function of growth, however, disproportionately. In support of this, some previous data acknowledge growth-dependent changes in cell size of phytoplankton (Cook, 1963). The positive relationship between cell size and growth rate is a common observation within specific isolates of microbes and has been termed the growth rate law (Schaechter et al., 1958; Vadia and Levin, 2015). However, QC or cell size has typically been held constant under variable growth rates in previous theoretical models (for example,, Shuter, 1979; Klausmeier et al., 2008; Bonachela et al., 2013). Instead, theoretical models typically rely on the Droop model equation to describe growth-dependent relationships in the ratios of cellular elements.

Although the Droop model equation fits our QN and QP data well, the model's underlying mechanism is fundamentally different than the cell size–growth rate relationship. The traditional Droop model focuses on growth-dependent changes in a single growth-limiting elemental quota (such as QN or QP), whereas our data demonstrate that the cell size–growth relationship contributes to growth-dependent changes in all three of the cellular elemental quotas that we measured. For example, the Droop model fits our QC data very well, but this fit did not result from C limitation, as the Droop model would predict. Instead, changes in QC were directly related to growth-dependent changes in cell size, and the Droop model coincidentally fit these changes in cell size. This is also evident from our QN data, which follow the Droop model relationship in contrasting P-limited chemostats. Under P-limited growth, nitrate was in high abundance but QN fit the Droop model in nearly the same way as N-limited cells (Figure 1b). Therefore, the Droop model fits to QN and QP do not result directly from N or P acquisition, but instead, as our model confirms, result from the cell size–growth rate relationship. Thus, by decoupling the equations for the population C and number of cells, we achieved a dynamic regulation of QC (and hence a cell size–growth rate link), which together with the dynamics of QN and QP and their effect on protein regulation, was necessary to predict our observed trends in cellular elemental stoichiometry of Synechococcus.

In contrast with Droop-based models of phytoplankton stoichiometry, where C:Pcell and N:Pcell change sharply as a function of P-limited growth (Klausmeier et al., 2004b; Bonachela et al., 2013), our model and data indicate that C:Pcell and N:Pcell of Synechococcus decrease almost linearly as a function of P-limited growth (Figures 4a and b). We also obtained marginal changes in C:Pcell and no change in N:Pcell as a function of N-limited growth, and collectively, these trends have been observed previously in other phytoplankton (Goldman et al., 1979). The invariable N:Pcell under N-limited growth is remarkable for the globally abundant Synechococcus because N:Pcell is consistently close to the Redfield ratio (16) even under severe N limitation, a common state among field populations (Moore et al., 2013). Understanding environmental controls on cellular elemental stoichiometry in the small but dominant prokaryotic phytoplankton lineages under N limitation may be key to understanding the primary drivers of Redfield stoichiometry in the oceans. But the mechanisms that contribute to variability in cellular elemental stoichiometry may be different for different lineages because this invariable trend does not appear to be consistent across lineages of phytoplankton (Goldman et al., 1979).

We also observed moderate decreases in C:Ncell under severely P-limited growth in comparison with severely N-limited growth, which seem to be related to cell size and pigment fluorescence (Figure 4). N-limited cells were larger than P-limited cells, evident from differences in FSCH (Figure 2) and QC (Figure 1a) between these two treatments. Despite differences in cell size, QN was relatively invariable between N- and P-limited cells (Figure 1b). This generally resulted in elevated C:Ncell in slow-growing N-limited cells in comparison with other treatments (Figure 4c), which, based on our pigment fluorescence data, seems to be caused by higher cellular concentrations of N-rich pigments in P-limited cells (Supplementary Figures 5C and D). As phycoerythrin, a dominant pigment in Synechococcus (Scanlan et al., 2009), is composed of protein, and proteins comprise a large portion of QN (Rhee, 1978; Lourenço et al., 1998), the rigidity in QN between P- and N-limited cells may be caused by differences in phycoerythrin, which is known to have a dual role in photosynthesis and N storage (Wyman et al., 1985; Yeh et al., 1986). Thus, the decline in C:Ncell in severely P-limited cells seems to result from the combined effect of smaller cells and higher pigment fluorescence in comparison with severely N-limited cells.

In general, small phytoplankton are thought to lack major nutrient storage reservoirs. Aside from small differences in cellular pigment fluorescence, we did not observe signs of abundant N or P storage in Synechococcus. Some theoretical models rely on cellular storage components to predict cellular stoichiometry (Daines et al., 2014), but our observed changes in QN with growth were mainly dependent on changes in cell size, regardless of limitation type. This observation is consistent with the general lack of the major N storage compound—cyanophycin—in Synechococcus isolates (Wingard et al., 2002). In models, QN or QP increases as a function of decreasing growth in environments, where N or P is abundant, respectively (that is, where P or N is limiting growth, respectively) (Klausmeier et al., 2004b, 2008). Although pigments probably contributed to minor N storage under slow P-limited growth, the large increases in N:Pcell (Figure 4b) in our experiments did not result from abundant increases in cellular N storage, as QN was roughly linked to cell volume (Supplementary Figure 6A, closed symbols). Instead, the strong variation in N:Pcell as a function of P-limited growth (Figure 4b) resulted from stronger changes in QP (Figure 1c) relative to moderate changes in cell size (that is, QC) (Figure 1a) and relative to small changes in QN under N limitation. Even under slow N-limited growth, cells did not store P in high excess either; changes in QP in P-replete environments were also tightly linked to changes in cell volume (Supplementary Figure 6B, open symbols). Thus, the major variation in C:Pcell and N:Pcell within Synechococcus (Figures 4a and b) seems to be driven by a larger percent change in QP relative to percent changes in cell size (QC) and QN under P-limited growth, in comparison with small percent changes in QN relative to changes in cell size (QC) and QP under N-limited growth. But we did not observe drastic increases in QP or QN under different N- or P-limited environments as modeled previously (Klausmeier et al., 2004a), indicating that N and P were not stored in high abundance in N- or P-replete environments, respectively.

In consideration of how C:Pcell and N:Pcell varies relative to cell size (QC) and QN in P- and N-limited environments, we postulate that variable cell concentrations of P-rich biomolecules must be major drivers of stoichiometric variation in Synechococcus. Cellular phospholipid concentrations are known to decline under P limitation (Van Mooy et al., 2006) but in general do not represent a large proportion of cellular P (Mouginot et al., 2015). Although much less is known about polyphosphates in Cyanobacteria, they may also co-vary with growth in Synechococcus, as documented in another species of phytoplankton (Rhee, 1973). Although some data suggest that the adenylate pool increased with increasing growth rate in heterotrophic bacteria (Marriot et al., 1981), adenosine triphosphate in Synechococcus WH8102 was highly correlated with FSCH regardless of the chemostat dilution rate and represented <1% of QP in another experiment (unpublished data). The general lack of major storage reservoirs in small Cyanobacteria may be key to distinguishing trends in cellular elemental stoichiometry from those in larger phytoplankton, as previous data with diatoms suggest that QC increases with decreasing P-limited growth (Laws and Bannister, 1980), contrasting the diminishing QC with decreasing growth of Synechococcus (Figure 1a).

Ecological implications

Our results may be applied to broadly understand the physiological status of unicellular Cyanobacteria in the ocean. If we compare our results with stoichiometric data compiled by Martiny et al. (2013) and inversely estimated by Teng et al. (2014), the high C:P ratios observed in the P-limited North Atlantic Subtropical Gyre (Moore et al., 2009; Lomas et al., 2010) are congruent with C:Pcell of Synechococcus when growth rates are strongly P limited. In contrast, the moderate C:P ratios (but above Redfield proportions) observed in the presumed N-limited Southern Atlantic Subtropical Gyre (Teng et al., 2014) are similar to the C:P ratios that we observed in slower-growing N-limited cultures. The low C:P estimates in the eastern equatorial Atlantic upwelling region (where nutrients are abundant) are consistent with a high frequency of fast-growing Synechococcus cells. Thus, our data and model seem to corroborate the physiological status of biota in major ocean basins and our observations suggest that the growth-dependent variability in cell size and the lack of elemental storage capacity both influence the cellular elemental stoichiometry of small marine phytoplankton within field populations. In comparison with data collected from other species of phytoplankton, our findings further suggest that fundamentally different biochemical mechanisms may control the cellular elemental stoichiometry of small vs large phytoplankton, such as Cyanobacteria vs eukaryotes. Such biochemical mechanisms can contribute to understanding broad scale patterns in ocean biogeochemistry and regional differences in C:N:P. As studies of environmental controls on cellular elemental stoichiometry emerge among broader lineages of phytoplankton, we may begin to forecast how ocean biogeochemical cycles will respond to global change.

Acknowledgments

Support for this research was provided by the UCI Chancellor's ADVANCE Postdoctoral Program and the National Science Foundation Dimensions of Biodiversity (OCE-1046297) and Major Research Instrumentation programs (OCE-1126749). JAB acknowledges support of the MASTS pooling initiative (The Marine Alliance for Science and Technology for Scotland). MASTS is funded by the Scottish Funding Council (grant reference HR09011) and contributing institutions.

The authors declare no conflict of interest.

Footnotes

Supplementary Information accompanies this paper on The ISME Journal website (http://www.nature.com/ismej)

Supplementary Material

Supplementary Information
Click here for additional data file. (1.4MB, doc)
Supplementary Table S1
Click here for additional data file. (11.1KB, pdf)
Supplementary Figure 1
Click here for additional data file. (1.7MB, tif)
Supplementary Figure 2
Click here for additional data file. (1.1MB, tif)
Supplementary Figure 3
Click here for additional data file. (1.3MB, tif)
Supplementary Figure 4
Click here for additional data file. (472.1KB, tif)
Supplementary Figure 5
Click here for additional data file. (732.3KB, tif)
Supplementary Figure 6
Click here for additional data file. (761.4KB, tif)

References

  1. Bertilsson S, Berglund O, Karl DM, Chisholm SW. (2003). Elemental composition of marine Prochlorococcus and Synechococcus: Implications for the ecological stoichiometry of the sea. Limnol Oceanogr 48: 1721–1731. [Google Scholar]
  2. Bonachela JA, Allison SD, Martiny AC, Levin SA. (2013). A model for variable phytoplankton stoichiometry based on cell protein regulation. Biogeosciences 10: 4341–4356. [Google Scholar]
  3. Claquin P, Martin-jézéquel V, Kromkamp JC, Veldhuis MJW, Kraay GW. (2002). Uncoupling of silicon compared with carbon and nitrogen metabolisms and the rol of the cell cycle in continuous cultures of Thalassiosira pseudonana (Bacillariophyceae) under light, nitrogen, and phosphorus control. J Phycol 38: 922–930. [Google Scholar]
  4. Cook JR. (1963). Adaptations in growth and division in euglena effected by energy supply. J Protozool 10: 436–444. [DOI] [PubMed] [Google Scholar]
  5. Daines SJ, Clark JR, Lenton TM. (2014). Multiple environmental controls on phytoplankton growth strategies determine adaptive responses of the N: P ratio. Ecol Lett 17: 414–425. [DOI] [PubMed] [Google Scholar]
  6. DeVries T, Deutsch C. (2014). Large-scale variations in the stoichiometry of marine organic matter respiration. Nat Geosci 7: 890–894. [Google Scholar]
  7. Droop MR. (1968). Vitamin B12 and marine ecology. IV. The kinetics of uptake, growth and inhibtition in Monochrysis lutheri. J Mar Biol Ass UK 48: 689–733. [Google Scholar]
  8. Dyhrman ST, Palenik B. (2001). A single-cell immunoassay for phosphate stress in the dinoflagellate Prorocentrum minimum (Dinophyceae). J Phycol 37: 400–410. [Google Scholar]
  9. Elser JJ, O'Brien WJ, Dobberfuhl DR, Dowling TE. (2000). The evolution of ecosystem processes: growth rate and elemental stoichiometry of a key herbivore in temperate and arctic habitats. J Evol Biol 13: 845–853. [Google Scholar]
  10. Elser JJ, Sterner RW, Gorokhova E, Fagan WF, Markow TA, Cotner JB et al. (2000). Biological stoichiometry from genes to ecosystems. Ecol Lett 3: 540–550. [Google Scholar]
  11. Finkel ZV, Beardall J, Flynn KJ, Quigg A, Rees TAV, Raven JA. (2010). Phytoplankton in a changing world: cell size and elemental stoichiometry. J Plankton Res 32: 119–137. [Google Scholar]
  12. Flombaum P, Gallegos JL, Gordillo RA, Rincón J, Zabala LL, Jiao N et al. (2013). Present and future global distributions of the marine Cyanobacteria Prochlorococcus and Synechococcus. Proc Natl Acad Sci USA 110: 9824–9829. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Fu FX, Warner ME, Zhang Y, Feng Y, Hutchins DA. (2007). Effects of increased temperature and CO2 on photosynthesis, growth, and elemental ratios in marine Synechococcus and Prochlorococcus (Cyanobacteria). J Phycol 43: 485–496. [Google Scholar]
  14. Galbraith ED, Martiny AC. (2015). A simple nutrient-dependence mechanism for predicting the stoichiometry of marine ecosystems. Proc Natl Acad Sci USA 112: 201423917. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Geider R, La Roche J. (2002). Redfield revisited: variability of C:N:P in marine microalgae and its biochemical basis. Eur J Phycol 37: 1–17. [Google Scholar]
  16. Geider RJ, MacIntyre HL, Kana TM. (1998). A dynamic regulatory model of phytoplanktonic acclimation to light, nutrients, and temperature. Limnol Oceanogr 43: 679–694. [Google Scholar]
  17. Goldman JC, McCarthy JJ, Peavey DG. (1979). Growth rate influence on the chemical composition of phytoplankton in oceanic waters. Nature 279: 210–215. [Google Scholar]
  18. Healey F. (1985). Interacting effects of light and nutrient limitation on the growth rate of Synechococcus linearis (Cyanophyceae). J Phycol 21: 134–146. [Google Scholar]
  19. Heldal M, Scanlan DJ, Norland S, Thingstad F, Mann NH. (2003). Elemental composition of single cells of various strains of marine Prochlorococcus and Synechococcus using X-ray microanalysis. Limnol Oceanogr 48: 1732–1743. [Google Scholar]
  20. Ho T-Y, Quigg A, Finkel ZV, Milligan AJ, Wyman K, Falkowski PG et al. (2003). The elemental composition of some marine phytoplankton. J Phycol 39: 1145–1159. [Google Scholar]
  21. Klausmeier CA, Litchman E, Daufresne T, Levin SA. (2004. a). Optimal nitrogen-to-phosphorus stoichiometry of phytoplankton. Nature 429: 171–174. [DOI] [PubMed] [Google Scholar]
  22. Klausmeier CA, Litchman E, Daufresne T, Levin SA. (2008). Phytoplankton stoichiometry. Ecol Res 23: 479–485. [Google Scholar]
  23. Klausmeier CA, Litchman E, Levin SA. (2004. b). Phytoplankton growth and stoichiometry under multiple nutrient limitation. Limnol Oceanogr 49: 1463–1470. [Google Scholar]
  24. Kretz CB, Bell DW, Lomas DA, Lomas MW, Martiny AC. (2015). Influence of growth rate on the physiological response of marine Synechococcus to phosphate limitation. Front Microbiol 6: 6–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Laws EA, Bannister TT. (1980). Nutrient- and light-limited growth of Thalassiosira fluviatilis in continuous culture, with implications for phytoplankton growth in the ocean. Limnol Oceanogr 25: 457–473. [Google Scholar]
  26. Legović T, Cruzado A. (1997). A model of phytoplankton growth on multiple nutrients based on the Michaelis-Menten-Monod uptake, Droop's growth and Liebig's law. Ecol Modell 99: 19–31. [Google Scholar]
  27. Lehman JT, Botkin DB, Likens GE. (1975). The assumptions and rationales of a computer model of phytoplankton dynamics. Limnol Oceanogr 20: 343–364. [Google Scholar]
  28. Lomas MW, Burke AL, Lomas DA, Bell DW, Shen C, Dyhrman ST et al. (2010). Sargasso Sea phosphorus biogeochemistry: an important role for dissolved organic phosphorus (DOP). Biogeosciences 7: 695–710. [Google Scholar]
  29. Lourenço SO, Barbarino E, Marquez UML, Aidar E. (1998). Distribution of intracellular nitrogen in marine microalgae: Basis for the calculation of specific nitrogen-to-protein conversion factors. J Phycol 34: 798–811. [Google Scholar]
  30. Marriot ID, Edwin AD, Rowley BI. (1981). Effect of growth rate and nutrient limitation on the adenine nucleotide content, energy charge and enzymes of adenylate metabolism in Azotobacter beijerinckii. J Gen Microbiol 125: 375–382. [Google Scholar]
  31. Martin P, Dyhrman ST, Lomas MW, Poulton NJ, Van Mooy BAS. (2014). Accumulation and enhanced cycling of polyphosphate by Sargasso Sea plankton in response to low phosphorus. Proc Natl Acad Sci USA 111: 8089–8094. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Martiny AC, Pham CTA, Primeau FW, Vrugt JA, Moore JK, Levin SA et al. (2013). Strong latitudinal patterns in the elemental ratios of marine plankton and organic matter. Nat Geosci 6: 279–283. [Google Scholar]
  33. Michaels A, Dow R, Elardo K. (1997. a). The determination of phosphorus in seawater. In: Bermuda Atlantic Time-Series Study Methods. JGOFS Planning Office: Woods Hole, MA, USA, pp 71–74. [Google Scholar]
  34. Michaels A, Dow R, Howse F. (1997. b). The determination of nitrate in seawater. In: Bermuda Atlantic Time-series Study Methods. JGOFS Planning Office: Woods Hole, MA, USA, pp 61–66. [Google Scholar]
  35. Moore CM, Mills MM, Achterberg EP, Geider RJ, LaRoche J, Lucas MI et al. (2009). Large-scale distribution of Atlantic nitrogen fixation controlled by iron availability. Nat Geosci 2: 867–871. [Google Scholar]
  36. Moore CM, Mills MM, Arrigo KR, Berman-Frank I, Bopp L, Boyd PW et al. (2013). Processes and patterns of oceanic nutrient limitation. Nat Geosci 6: 701–710. [Google Scholar]
  37. Moore LR, Goericke R, Chisholm S. (1995). Comparative physiology of Synechococcus and Prochlorococcus: influence of light and temperature on the growth, pigments, fluorescence and absorptive properties. Mar Ecol Prog Ser 116: 259–275. [Google Scholar]
  38. Morel FMM. (1987). Kinetics of nutrient uptake and growth in phytoplankton. J Phycol 23: 137–150. [Google Scholar]
  39. Mouginot C, Zimmerman AE, Bonachela JA, Fredricks H, Allison SD, Van Mooy BAS et al. (2015). Resource allocation by the marine cyanobacterium Synechococcus WH8102 in response to different nutrient supply ratios. Limnol Oceanogr 60: 1634–1641. [Google Scholar]
  40. Pahlow M, Oschlies A. (2009). Chain model of phytoplankton P, N and light colimitation. Mar Ecol Prog Ser 376: 69–83. [Google Scholar]
  41. Rao NN, Gómez-García MR, Kornberg A. (2009). Inorganic polyphosphate: essential for growth and survival. Annu Rev Biochem 78: 605–647. [DOI] [PubMed] [Google Scholar]
  42. Rhee GY. (1978). Effects of N:P atomic ratios nitrate limitation on algal growth, cell composition, nitrate uptake. Limnol Oceanogr 23: 10–25. [Google Scholar]
  43. Rhee G-Y. (1973). A continuous culture study of phosphate uptake, growth rate, and polyphosphate in Scenedesmus sp. J Phycol 9: 495–506. [Google Scholar]
  44. Scanlan DJ, Ostrowski M, Mazard S, Dufresne A, Garczarek L, Hess WR et al. (2009). Ecological genomics of marine picocyanobacteria. Microbiol Mol Biol Rev 73: 249–299. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Schaechter M, MaalOe O, Kjeldgaard NO. (1958). Dependency on medium and temperature of cell size and chemical composition during balanced growth of Salmonella typhimurium. J Gen Microbiol 19: 592–606. [DOI] [PubMed] [Google Scholar]
  46. Shuter B. (1979). A model of physiological adaptation in unicellular algae. J Theor Biol 78: 519–552. [DOI] [PubMed] [Google Scholar]
  47. Sterner RW, Elser JJ. (2002) Ecological Stoichiometry: The Biology of Elements from Molecules to the Biosphere. Princeton University Press: Princeton, NJ, USA. [Google Scholar]
  48. Sterner RW, Elser JJ, Fee EJ, Guildford SJ, Chrzanowski TH. (1997). The light: nutrient ratio in lakes: the balance of energy and materials affects ecosystem structure and process. Am Nat 150: 663–684. [DOI] [PubMed] [Google Scholar]
  49. Teng Y-C, Primeau FW, Moore JK, Lomas MW, Martiny AC. (2014). Global-scale variations of the ratios of carbon to phosphorus in exported marine organic matter. Nat Geosci 7: 895–898. [Google Scholar]
  50. Urabe J, Kyle M, Makino W, Yoshida T, Andersen T, Elser JJ. (2002). Reduced light increases herbivore production due to stoichiometric effects of light/nutrient balance. Ecology 83: 619–627. [Google Scholar]
  51. Vadia S, Levin PA. (2015). Growth rate and cell size: a re-examination of the growth law. Curr Opin Microbiol 24: 96–103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Van Mooy BAS, Rocap G, Fredricks HF, Evans CT, Devol AH. (2006). Sulfolipids dramatically decrease phosphorus demand by picocyanobacteria in oligotrophic marine environments. Proc Natl Acad Sci USA 103: 8607–8612. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Verspagen JMH, Van de Waal DB, Finke JF, Visser PM, Huisman J. (2014). Contrasting effects of rising CO2 on primary production and ecological stoichiometry at different nutrient levels. Ecol Lett 17: 951–960. [DOI] [PubMed] [Google Scholar]
  54. Waterbury J, Willey JM. (1988). Isolation and growth of marine planktonic Cyanobacteria. Methods Enzymol 167: 100–105. [Google Scholar]
  55. Wingard LL, Miller SR, Sellker JML, Stenn E, Allen MM, Wood A M. (2002). Cyanophycin production in a phycoerythrin-containing marine Synechococcus strain of unusual phylogenetic affinity. Appl Environ Microbiol 68: 1772–1777. [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. Wyman M, Gregory RP, Carr NG. (1985). Novel role for phycoerythrin in a marine cyanobacterium, Synechococcus strain DC2. Science 230: 818–820. [DOI] [PubMed] [Google Scholar]
  57. Yeh SW, Ong LJ, Glazer AN. (1986). Role of phycoerythrin in marine picoplankton Synechococcus spp. Science 234: 1422–1423. [DOI] [PubMed] [Google Scholar]
  58. Zimmerman AE, Allison SD, Martiny AC. (2014). Phylogenetic constraints on elemental stoichiometry and resource allocation in heterotrophic marine bacteria. Environ Microbiol 16: 1398–1410. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information
Click here for additional data file. (1.4MB, doc)
Supplementary Table S1
Click here for additional data file. (11.1KB, pdf)
Supplementary Figure 1
Click here for additional data file. (1.7MB, tif)
Supplementary Figure 2
Click here for additional data file. (1.1MB, tif)
Supplementary Figure 3
Click here for additional data file. (1.3MB, tif)
Supplementary Figure 4
Click here for additional data file. (472.1KB, tif)
Supplementary Figure 5
Click here for additional data file. (732.3KB, tif)
Supplementary Figure 6
Click here for additional data file. (761.4KB, tif)

Articles from The ISME Journal are provided here courtesy of Oxford University Press

RESOURCES