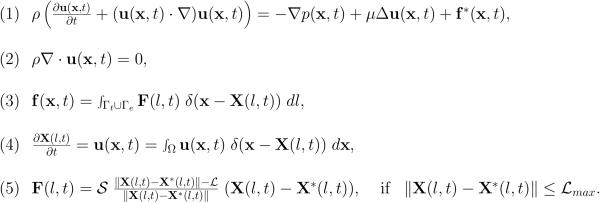Abstract
Solid tumor dissemination from the primary site to the sites of metastasis involves tumor cell transport through the blood or lymph circulation systems. Once the tumor cells enter the bloodstream, they encounter a new hostile microenvironment. The cells must withstand hemodynamic forces and overcome the effects of fluid shear. The cells are exposed to immunological signaling insults from leukocytes, to collisions with erythrocytes, and to interactions with platelets or macrophages. Finally, the cells need to attach to the blood vessel walls and extravasate to the surrounding stroma to form tumor metastases. Although only a small fraction of invasive cells is able to complete the metastatic process, most cancer-related deaths are the result of tumor metastasis. Thus, investigating the intracellular properties of circulating tumor cells and the extracellular conditions that allow the tumor cells to survive and thrive in this microenvironment is of vital interest. In this chapter, we discuss the intravascular microenvironment that the circulating tumor cells must endure. We summarize the current experimental and computational literature on tumor cells in the circulation system. We also illustrate various aspects of the intravascular transport of circulating tumor cells using a mathematical model based on immersed boundary principles.
Keywords: circulating tumor cells, metastatic cascade, tumor microemboli, cell deformation, computational modeling, immersed boundary method
1. Introduction
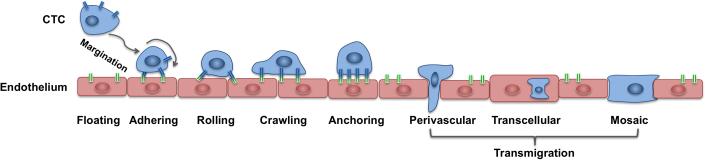
Metastasis to distant organs is the major cause of mortality for patients with many types of cancer. Metastasis accounts for nearly 90% of cancer-related deaths, although no more than 0.01% of circulating tumor cells (CTCs) is able to successfully form secondary lesions [67]. In order to metastasize, the cancer cells must detach from the primary tumor mass, migrate through the stromal tissue surrounding the primary tumor, enter the blood or lymph circulation system, travel with the blood flow, and, finally, extravasate into the new site, invade the local matrix, and colonize the target organ [39,43,71]. The process of CTC intravenous transport and the physical properties that allow CTCs to survive under the physiological blood flow is still poorly understood. One of the hypotheses is called the “adhesion cascade” (Figure 1) and was formulated and observed in the context of circulating leukocytes (reviewed in [44]). During this process, a single tumor cell is expected to switch among various locomotion strategies, from floating with the bloodstream to rolling on the endothelial wall, to tumor cell arrest and crawling, and finally, to tumor cell transmigration through the endothelial layer [44,71].
Figure 1. Schematics of the CTC adhesive cascade.
A cell floating with the blood flow need to reach an endothelial wall via margination process; once near the endothelial wall, it needs to adhere to the endothelium, undergo the transitions from rolling to crawling migration before anchoring to the endothelium and transmigrate the endothelial wall using one of the following ways: perivascular migration, transcellular migration or a mosaic process.
Tumor cell dissemination from primary to metastatic sites has not only a biological meaning but also important clinical implications. With the detection of metastasis in a patient, the clinical strategy for therapy changes from localized to systemic. However, how chemotherapeutic drugs directed at primary tumors affect the distant metastases is not known. Neither is it known how intravenously administered drugs affect CTCs. Therefore, investigating methods for how to prevent CTCs from metastatic spread is of vital interest to cancer biology. A deeper understanding of what factors allow CTCs to survive in the circulation system could be used to design novel therapeutic treatments. Moreover, understanding and characterizing CTCs is the first step toward utilizing them as biopsy material and directly as a biomarker of disease progression or as a measure of patient response to an anti-cancer treatment.
Although CTCs can be found in the blood of patients with various types of cancers, these cells are quite rare—one in a million in comparison with leukocytes [31] or one in a billion in comparison with blood cells [74]. In recent years, several approaches were undertaken to design highly specialized technical devices capable of capturing and isolating CTCs from patients’ peripheral blood [2,9,10,18,28]. These methods allowed the cancer biology community to gain enormous knowledge about the biological and physical properties of CTCs and to correlate the presence of CTCs with patients’ clinical outcomes [17,45,61,69].
One such method, a high-definition CTC assay (HD-CTC), was developed by Kuhn and colleagues to capture CTCs from patients’ blood without using surface protein-based enrichment. This method allows not only for identification of significant numbers of CTCs in patients with different types of cancers but also for imaging of the captured cells. Significant heterogeneity has been observed between tumor cells of various origins, as well as within cells of the same type of cancer [30,32,33]. The patients’ CTCs varied in size, shape, expression of specific proteins, and the cytoplasm to nucleus ratio. For example, the prostate cancer cell diameter ranged from 8 to 16 microns, and the breast cancer cells reached 9-19 microns in diameter [51,30]. Several blood samples contained also CTCs’ clusters (emboli) of various sizes and shapes [7,32,34]. These cell aggregates were found in blood from patients with breast, lung, pancreatic, and prostate cancers which indicates that the emboli may not be a sporadic case and that cell aggregates may present certain advantages for CTC survival in blood flow.
Recent advances in real-time fluorescent microscopy imaging allow for a visual account of CTCs in the circulation system in animal models (Figure 2). Experiments conducted by the Hoffman group showed both individual cells and multicellular emboli in the blood and lymph circulation systems in mouse skin [15,16,72,73]. In particular, the researchers showed that injected human fibrosarcoma cells acquire different shapes depending on the size of the vessel. The CTCs in microvessels were relatively circular and nondeformed, with the minor and major axes equal to 19.3 and 23.3 microns on average, respectively (Figure 2A). However, in capillaries (typically 3-8 microns in diameter), the cells were elongated reaching four times their normal size (7.8×92.6 microns on average), and the length of the nuclei increased 1.6 times reaching 7.8×27.6 microns on average. These cells occupied the full diameter of the vessel (Figure 2B). The same group also observed occasional small masses of tumor cells and larger multicellular emboli traveling through the large venules [15,16].
Figure 2. Circulating tumor cells in the vessel in the mouse skin.
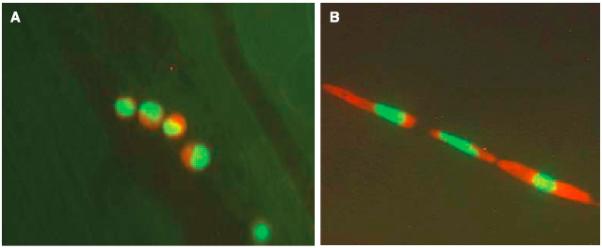
An image of tumor HT-1080 sarcoma cells: A. nondeformed cells within a microvessel; B. deformed cells occupying the full diameter of the vessel. Cells are labeled with green fluorescent protein in the nucleus, and red fluorescent protein in the cytoplasm. Image acquired using the Olympus OV100 system at x100 magnification. Reproduced from Yamauchi et al. Cancer Research 2005 Fig.3, with permission. [73]
Once in the circulation system, CTCs are exposed to various microenvironmental factors that are novel for cells arising from a solid tumor mass. In order to survive, the cells must withstand hemodynamic forces and overcome the effects of fluid shear [51,71,41]. Blood flow velocities in the circulation system can range from 0.03 to 40 cm/s depending on the vessel size [36], and the hemodynamic shear forces in the bloodstream can reach 0.5-4.0 dyn/s2 in the venous circulation and 4.0-30.0 dyn/s2 in the arterial circulation [68,41]. The pattern of the blood flow and its shear stress, as well as the movement of other cells in the circulation system can affect CTC trajectory. Moreover, CTCs may also be exposed to collisions with red blood cells or adhesion to leukocytes, platelets, and microphages [42,51,66]. How individual CTCs and CTC emboli can withstand these intercellular interactions and persist in the fluid flow is not yet fully understood, and many questions are still unanswered. Mathematical modeling based on physical principles and available experimental and clinical data can provide an invaluable tool for reconstructing the intravascular microenvironment and for testing what properties of CTCs allow them to survive in the circulation system.
In this chapter, we present a mathematical model of circulating tumor cells in the microvessel that utilizes fluid-structure interaction principles. We also discuss CTCs’ biophysical properties, including cell deformability and dynamical changes in cell structure (both locally and globally) that are necessary for cell survival in the blood flow, and switches in cell locomotion strategies. This will allow us to identify combinations of parameters that can be manipulated experimentally in order to disrupt some steps of the CTC adhesive cascade.
2. The IBCell mathematical model of circulating tumor cells
To model interactions between the bodies of circulating tumor cells and the surrounding blood plasma flow, fluid-structure-interactions methods are a natural modeling choice. One such modeling framework is the Immersed Boundary Method developed by Charles Peskin to model blood flow in the heart [47-50]. We adapted this computational framework to design a model of a deformable eukaryotic cell, IBCell (an Immersed Boundary model of a Cell [55,56]). This model includes various cellular processes that the cells can experience, such as cell growth, division, death, adhesion, and migration. Subsequently, we applied the IBCell framework to model circulating tumor cells in the blood flow [57].
We present here the details of this two-dimensional (2D) model of deformable circulating tumor cells traveling through a microvessel. Note, that a 3D version of this model can be based on the same principles, as described in [57]. Here, we consider a microvessel large enough that the cells are able to preserve a circular shape as shown in Figure 1A. During the simulations, cell deformation is a result of the blood flow, not the occlusion within the vessel. The cells are exposed to both hemodynamic forces exerted by the blood plasma flow and adhesive-repulsive forces between either other tumor cells or the tumor cell attaching to or migrating along the endothelial cells of the microvessel. All components of this model are described below and are presented in Figure 3.
Blood plasma flow—this model takes into account the fluid phase of the blood (the plasma) only. No other cells, such as red blood cells, leukocytes or platelets, are included. The blood plasma is modeled as a viscous incompressible Newtonian fluid governed by Navier-Stokes equations. The fluid flow inside the vessel is laminar of a parabolic profile with zero velocity at the microvessel walls and a maximum velocity of 0.6 mm/s in the center of the microvessel. However, in the presence of obstacles, such as deformable tumor cells, the plasma flow profile may be distorted. In these simulations, we use a small 30-micron-wide and 75-micron-long vessel.
Endothelium structure—the endothelium is modeled as a mesh of short and relatively stiff linear springs that form a uniform rigid wall. For simplicity, no individual endothelial cells are included in the model. While we are aware that the blood flow can alter the biophysical state of the endothelium (for example, some membrane receptors can be expressed differently under the flow), for simplicity, we neglect any changes that the plasma flow may have on the endothelium.
Circulating tumor cell structure—in this model, we consider a circular cell with a diameter of 10 microns, a 4-micron-wide nucleus, and a 2-micron-wide cortex band. No other cell cytoskeleton elements and intracellular organelles are included in the model, but the whole cell structure is interpenetrated by viscous incompressible cytoplasm. Cell shape and stiffness are modulated by the cell actin cortex and the cell nuclear envelope. Both are modeled as dense networks of linear Hookean springs. The model allows modifications in spring stiffness globally (i.e., for all springs forming the structure) and locally (i.e., for an individual spring in the structure), and separately for the cell nucleus and the cortex. This enables testing the relative role of the nucleus and the cortex in preserving the overall cell shape under the blood flow.
Circulating tumor cells-endothelium interactions—all interactions between circulating tumor cells and the endothelium are modeled via the pseudo-receptors located on the tumor and the endothelial cell membranes. The adhesive links emerge when these receptors are in close proximity. They adhesive links, which are modeled as short linear Hookean springs, can be dynamically assembled and disassembled based on the distance between the receptors, as well as the adhesive spring stiffness. For simplicity, we assume that the receptor-ligand binding is always effective when the distance between the receptors is small enough.
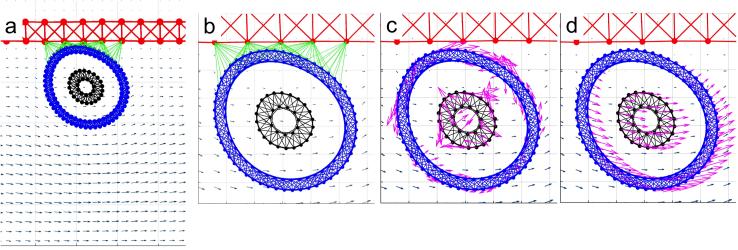
Figure 3. Schematics of the CTC and endothelium structure.
A schematic representation of the 2D model of the tumor cell in circulation. (a) The blood vessel (red top wall) is interpenetrated by a blood flow (grey arrows representing a velocity field); the CTC nucleus (black) is surrounded by the cell cortex (blue) both composed from cross-linked Hookean springs. (b) The cell near the endothelial wall develops adhesive connections (green links). (c) As a result of cell deformation, the springs are stretched and exert restoring forces (magenta arrows). (d) The cell boundary points are moved on a local fluid velocity (magenta arrows). This mathematical model utilizes the computational frameworks of the Immersed Boundary method.
The mathematical framework of the immersed boundary method is given in Figure 4. In this method, Equation 1 is the Navier–Stokes equation of a viscous incompressible fluid defined on the Cartesian grid x=(x1,x2), where p is the fluid pressure, μ is the fluid viscosity, ρ is the fluid density, u is the fluid velocity, and f is the external force density. Equation 2 is the law of mass balance. Interactions between the fluid and the material points X(l,t) on the tumor cell membrane and the endothelial wall boundaries (l is an index along either the boundaries of the tumor cells Γt or the boundaries of the endothelial walls Γe) are defined in Equations 3–4. Here, the force density F(l,t) acting on the cell and wall boundaries is applied to the fluid using the 2D Dirac delta function δ, while all material boundary points X(l,t) are carried along with the fluid. The boundary forces F(l,t) arise from the elastic properties of the tumor cell membranes, from the rigid properties of the endothelial walls and from tumor cell-endothelial cell adhesion and are all represented by the short linear Hookean springs in Equation 5, where S is the spring stiffness, L is the spring resting length and X*(l,t) is the adjacent, opposite, or neighboring point for the elastic, rigid, or adhesive forces, respectively. These equations are solved using the finite difference methods with a discrete approximation of the Dirac delta function and are described in detail in [55,58].
Figure 4. IBCell model equations.
Equations Eq.1–Eq.5 define the mathematical frameworks of the Immersed Boundary method.
The equations of the immersed boundary method are solved in the following steps:
Define the structure of the endothelium and the circulating tumor cells.
Define the forces that determine the cells and the endothelium structure; define the adhesive forces between the cells and between the cells and the endothelium.
Spread the forces to the underlying fluid grid.
Solve the Navier-Stokes equations on the Cartesian fluid grid for the fluid velocities.
Interpolate the fluid velocities to the boundary points of the cells and the endothelium.
Move the immersed boundary points based on the computed velocities.
Repeat steps 2-6.
In the following sections, we discuss several stages of the intravascular transport and, whenever possible, illustrate them with simulations from the IBCell model. In particular, we discuss the relative stiffness of the CTC cortex versus the stiffness of the CTC nuclear envelope that controls cell deformation under blood flow (section 3), collisions with other cells (section 4), how CTC cytoskeletal properties need to be modified in order to attach and roll on the endothelium (section 5), how CTC cytoskeleton reorganization and cell membrane receptor redistribution enable CTC anchorage and migration on the endothelium (section 6), and CTC transmigration through the endothelium (section 7). Finally, we discuss how the formation of cell emboli changes the dynamics of the cells in the circulation system (section 8).
3. Circulating tumor cell survival in the blood flow
Laboratory experiments with CTCs in the mouse circulation system showed that the cells are able to undergo high levels of deformability (Figure 2 and [16,73]). The overall cell shape and the shape of the cell nucleus were able to adjust to the size of the small capillaries. Similar deformability was also observed in human tumor cells transplanted into the vasculature of a transparent zebrafish [59,60] and in modeled nucleus-free red blood cells [54] and neutrophils [22].
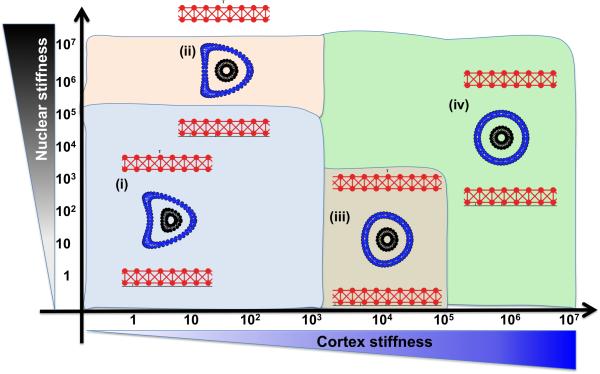
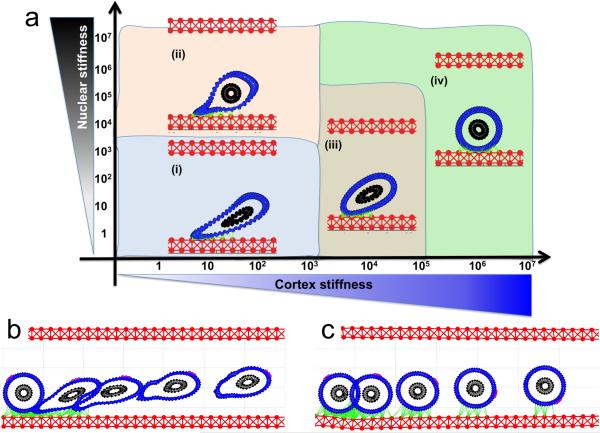
We previously used the IBCell model to investigate how changes in the stiffness of the cell cortex and the cell nucleus influence the survival of the whole cell when it is exposed to the same pattern of blood flow [57]. The results are summarized in Figure 5 in the form of a parameter space graph. We varied the stiffness constant of the individual fibers forming the cell cortex and, independently, the stiffness constant of the fibers forming the cell nuclear envelope. Following the values reported in the literature, the range was 1-106 g/cm·s2 for each fiber [58,46,29,35]. The final cell shapes were recorded after the cell reached two thirds of the length of a straight vessel (i.e., at 50 microns).
Figure 5. Deformation of a CTC under a steady blood flow.
A parameter space of final cellular morphologies when the stiffness of the cell cortex (blue) and the cell nuclear envelope (black) is varied by 7 orders of magnitude. Insets (i-iv)—the representative deformable (i-ii) and non-deformable (iii-iv) cell morphologies are shown within each parameter range.
All simulations started with a cell with a perfectly circular cortex and nucleus. The cell was initially located in the middle of the vessel. The cases in which both the cortex and the nucleus were very stiff resulted in no significant deformation during the whole simulation, and the cells retained their initial circular shapes (Figure 5(iv)). However, when both the cell cortex and the cell nucleus were very soft, the cells did not survive the flow and underwent clasmatosis—cytoplasmic fragmentation. For the relatively soft cortex (fiber stiffness of 10-100 g/cm·s2) the cells acquired a concave shape with the central inward deformation (a parachute-like shape) at the location of the highest blood flow (Figure 5(i)). For the same cortex stiffness, these invaginations became smaller when the nuclear envelope became stiffer (Figure 5(ii)). Interestingly, a stiff nucleus with a softer (but not too soft) cortex prevented significant cell deformations (Figure 5(iii)). Thus, actin cortex stiffness is crucial for cell survival during passive transport of the cell by the blood flow, and the combination of a soft cortex and a soft nuclear envelope may lead to cell damage by the bloodstream.
4. Circulating tumor cell collision dynamics
An interesting question is, how do CTCs approach the endothelial vessel walls? Is the CTCs’ movement a result of collisions with other cells? Or do the CTCs need to be pushed by the flow created by other cells? The phenomenon of the cells’ translocation to the periphery of the vessel wall is known as margination. This process has been computationally modeled for large colonies of red blood cells [75], for interactions between red blood cells and platelets [8,12], and for interactions between red and white blood cells [11,63]. These results indicated that red blood cell-induced drift effectively leads to margination of leukocytes and platelets in both small and large vessel channels. The duration of the margination process depends on the vessel size, but once margination is achieved, the process is sustained for a long time. Moreover, the size of the cell-free layer depends on the cell deformability and the aggregation strength. Recently published mathematical models [27,64] were drawn on previous studies of leukocyte-red blood cell interactions and tested whether margination processes can be also observed for CTCs. In particular, a mathematical model discussed in [27] showed that when three different CTC membrane elasticities were considered the cells with rigid bodies were directed toward the vessel walls the quickest. The softest CTCs showed only small fluctuations along the initial trajectory. How such properties of the CTCs in the circulation system can be used for therapeutic purposes should be investigated in a quantitative and predictive way.
5. Circulating tumor cell adhesion and rolling on the endothelium
In the adhesive cascade process (Figure 1), which has been proposed as a mechanism for extravasation for both the leukocytes and CTCs, adhesion to the endothelium is a prerequisite of cell transmigration through the endothelial wall. Various receptor-ligand bond formations (via a family of selectin adhesion molecules) and hydrodynamic interactions have previously been modeled for leukocytes-endothelium adhesion [26,65,19,23]. Recent experiments in microfluidic devices have also reported either selectin-mediated [40] or platelet-enhanced [37] adhesive capture of tumor cells. Moreover, cell rolling along the endothelium that was observed in in vitro experiments and modeled in silico in the case of leukocytes [3,19,25,38] has also been postulated to work in the case of circulating tumor cells [37,67].
The model we used in [57] does not include detailed receptor-ligand kinetics. The adhesion process between CTCs and the endothelium was simplified to have high affinity and to assemble easily if both the receptor and the ligand were in close proximity to one another. Instead, we focused again on the cortex and nucleus structures and their deformation when the CTCs adhere to the endothelium under the blood flow. Using the same range of stiffness values as in section 3, IBCell produced the parameter space shown in Figure 6. We, again, started with a perfectly circular cell (the cell cortex and the cell nucleus), but this time, the cell was located near the bottom wall of the vessel. This allowed the cell to adhere to the endothelium. Moreover, this location also resulted in the cell being exposed to nonsymmetrical blood shear stress with increasing blood velocity far from the endothelium.
Figure 6. CTC attachment to endothelium under a steady blood flow.
(a) A parameter space of final cellular morphologies when the stiffness of the cell cortex (blue) and the cell nuclear envelope (black) is varied by 7 orders of magnitude. Insets (i-iv)—the representative cell morphologies for each category; the adhesive links between CTC and the endothelium shown in green. The time course image (b and c) shows the same cell at five different time point overimposed on the same image: (b) shows cell detachment from the endothelium, and (c) cell rolling on the endothelium. A fixed small part of the cell cortex is stained in magenta to illustrate the rolling effect.
The simulated cases revealed that cells with a soft cortex underwent quite significant deformation due to the flow pushing on one side of the cells while the opposite side was attached to the vessel wall (Figure 6a(i)). In these cases, the area of CTC-endothelium adhesion was quite large, but the cells were more likely to detach from the endothelium and be carried out with the blood flow. However, with the increasing stiffness of the nucleus, the cell's overall shape became less elongated, but these cells were also not able to firmly adhere to the endothelium (Figure 6a(ii)). Interestingly, the cells with a moderately soft cortex but a stiffer nucleus remained less deformed and adhered quite strongly to the endothelial cells (Figure 6a(iii)). Similar dynamics was also observed in the cases of a stiff cortex (Figure 6a(iv)). The simulations showed that although the deformable cells with a softer cortex had a larger area of adhesion to the endothelium, they were also more responsive to blood shear stress, as their area of contact with higher-velocity flow could increase with time due to their deformability. The stiffer cells had a smaller area of adhesion to the endothelium, but as the cells’ shape was not deforming, they were able to maintain this area of adhesion over time, and were less likely to detach.
We stained a fixed part of the cell cortex in each cell to show its translocation along the cell perimeter (Figure 6b,c). When both the cortex and the nucleus were relatively stiff, the cells showed a rolling motion. These simulations indicated that the transition in the CTC transport phase from floating with the blood flow to attaching and rolling on the endothelial wall requires stiffening of the whole CTC cortex.
6. Circulating tumor cell crawling dynamics
One of the steps of the leukocyte adhesive cascade is cell crawling—a slow migration along the endothelium before the cells can completely stop and start the extravasation process [44,70]. Such intraluminal cell crawling has been observed in time-lapse video-microscopy within the postcapillary venules [53]. It has also been shown that leukocyte crawling can trigger specific signaling between white blood cells and endothelial cells that can induce the transient weakening of endothelial cell junctions that may play an important role in enabling cell transmigration [44].
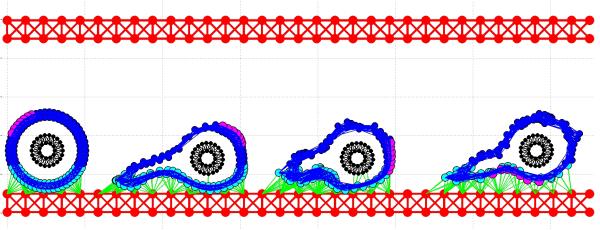
We used the IBCell model to reproduce the cell crawling movement under the blood flow and to test the mechanical properties of the migrating cell. Based on the results described in section 5, we chosen a cell configuration for which the cell was able to attach to the endothelium and withstand the hemodynamic forces of the flowing blood (Figure 6c). In the case we considered here, the cell had a relatively stiff nucleus but a softer cortex. Therefore, we tested whether further softening of the cell cortex around the cell's focal adhesions would result in better cell migration. The softer and stiffer parts of the cell cortex were stained differently, as shown in Figure 7. Following the example in Figure 6, we also stained a small part of the cortex opposite the cell-endothelium adhesions, to indicate their translocation along the cell perimeter. These simulations revealed that in order for the circulating tumor cell to progress from rolling to anchoring and to crawling, the stiffness of the cell's cytoskeleton has to be dynamically altered between the part in adhesion to the endothelium and the opposite side (Figure 7). Cell rolling required a quite stiff actin cortex that could be pushed by the blood flow without extensive deformation. Upon transition to anchoring, the CTC cytoskeleton must become more flexible along the contact surface. Cell crawling required that the cortex fibers were softened around the cell focal adhesions with the endothelium, and the cortex fibers became stiffer immediately after the focal adhesions were broken. This local softening of the cell cytoskeleton along the contact area with the endothelium may be potentially modulated by signals from the endothelial cells in contact.
Figure 7. CTC migrating on the endothelium.
A time course shows the same cell at different time point overimposed on the same image. To illustrate cell crawling a fixed small part of the cell cortex is stained in magenta. Cell cortex is stained differently depending on its local stiffness: soft (cyan) close to cell focal adhesion with the endothelium, and stiff (blue) far from the adhesive contacts (green).
7. Circulating tumor cell anchorage to the endothelium and transmigration
The final step in the adhesive cascade is cell transmigration through the endothelium and extravasation to the surrounding stromal tissue. This is an area of very active research with in in vitro microfluidic devices and in vivo animal models [5,6,20,24]. It has been shown experimentally using the laminar flow chamber that cancer cells can utilize three distinct mechanisms of tumor cell-endothelial cell interactions in order to initialize the transmigration process [67]. Tumor cells can use paracellular transmigration that takes place at the junction of three adjacent endothelial cells. The second mechanism allowed the tumor cell to form a mosaic with endothelial cells in which the tumor cell became inserted within the endothelial layer, sometimes for as long as 24 hours. The third observed transmigration mechanism was penetration through the endothelial cell. This transcellular migration process did not occur on the endothelial cell junctions, but the tumor cell was engulfed in a large vacuole and transported through the endothelial cell [67]. The complex process of CTC transmigration through the endothelium has not yet been explored with mathematical modeling.
8. The dynamics of circulating tumor cell microemboli
Although tumor emboli have been observed clinically in the blood of patients with different tumors [1,4,7], how such emboli can arise is not yet well understood, especially given how rare CTCs in the circulation system are. The observed CTC clusters numbered from two to several cells in clinical samples [4,7] and even up to 50 cells in animal experiments [15,16]. It has also been observed that CTC emboli can contain other cells, such as platelets, that may guard the tumor cells from immune elimination and promote their arrest at the endothelium [14,42].
With the IBCell model, we considered microemboli that consisted only of CTCs. The simulations showed that such CTC clusters were able to survive the fluid flow shear stress longer than individual CTCs (Figure 8). Their collective ability to adhere to the endothelium was also superior to the adhesion capabilities of individual CTCs. However, further, more systematic investigations are needed to determine the trade-offs between the size of the CTC cluster, the probability of surviving intravenous transport, and the chances of creating vessel occlusion because of the embolus size. The latter was investigated in [52] by reconstructing the size and shape of emboli observed in patients’ blood. This work showed that small CTC clusters tumbled during the flow and were able to reach the vessel walls, even in the absence of other cells. However, large CTC clusters were capable of vascular occlusion, slowing the blood's velocity and increasing the levels of local generation of coagulation factors.
Figure 8. CTC microemboli in the blood circulation system.
A time course (a-c) shows the same CTC cluster at different time points with cellular adhesions and adhesion to the endothelium indicated as green links. The cluster structure allows individual cells to withstand the blood shear stress and survive in the blood flow (showed as grey vector field).
9. Summary
The fluid environment of the blood to which circulating tumor cells are exposed presents a formidable challenge to cells of epithelial origin. Although experimental studies showed that dysplastic and metastatic cells exhibit a different degree of mechanical stiffness and cell deformability [62,13,21], the precise mechanisms and the extent of such deformations in circulating tumor cells in the blood flow are not known. Most of the currently used methods for capturing CTCs require cell attachment or anchorage to the substrate. This may result in changes in the cytoskeletal properties of the cell in a way that subsequent measurements will not reflect the cell properties in the circulation system. Numerous in vivo studies showed that metastatic tumor cells are quite deformable, and the cell cytoplasm and the cell nucleus can undergo strong compression and shape deformation in small capillaries [16,59,60,72,73].
Computational simulations can help determine which properties of CTCs must be altered so that they can successfully travel through the blood or lymph circulation systems. This knowledge can lead to designing the next generation of therapeutic interventions that will prevent CTCs from completing the adhesive cascade or from forming multicellular emboli that can result in vessel occlusions. However, such models need to be based on physical principles and need to be able to formulate and test various hypotheses of CTC biomechanics and mechanotransduction. Quantitative integration of physics-based computational models with in vitro experimentation and ex vivo CTC analysis will lead to advancements from the biomechanical and therapeutic perspectives.
Acknowledgment
This work was initiated through a Moffitt-PSOC Pilot Project from the Physical Sciences-Oncology Program Phase I at the National Institute of Health U54-CA-143970.
References
- 1.Aceto N, Bardia A, Miyamoto DT, Donaldson MC, Wittner BS, Spencer JA, Yu M, Pely A, Engstrom A, Zhu H, Brannigan BW, Kapur R, Stott SL, Shioda T, Ramaswamy S, Ting DT, Lin CP, Toner M, Haber DA, Maheswaran S. Circulating tumor cell clusters are oligoclonal precursors of breast cancer metastasis. Cell. 2014;158(5):1110–1122. doi: 10.1016/j.cell.2014.07.013. doi:10.1016/j.cell.2014.07.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Alunni-Fabbroni M, Sandri MT. Circulating tumour cells in clinical practice: Methods of detection and possible characterization. Methods. 2010;50(4):289–297. doi: 10.1016/j.ymeth.2010.01.027. doi:10.1016/j.ymeth.2010.01.027. [DOI] [PubMed] [Google Scholar]
- 3.Bose S, Das SK, Karp JM, Karnik R. A semianalytical model to study the effect of cortical tension on cell rolling. Biophys J. 2010;99(12):3870–3879. doi: 10.1016/j.bpj.2010.10.038. doi:10.1016/j.bpj.2010.10.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Carlsson A, Nair VS, Luttgen MS, Keu KV, Horng G, Vasanawala M, Kolatkar A, Jamali M, Iagaru AH, Kuschner W, Loo BW, Jr., Shrager JB, Bethel K, Hoh CK, Bazhenova L, Nieva J, Kuhn P, Gambhir SS. Circulating tumor microemboli diagnostics for patients with non-small-cell lung cancer. J Thorac Oncol. 2014;9(8):1111–1119. doi: 10.1097/JTO.0000000000000235. doi:10.1097/JTO.0000000000000235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Chen MB, Lamar JM, Li R, Hynes RO, Kamm RD. Elucidation of the roles of tumor integrin ss1 in the extravasation stage of the metastasis cascade. Cancer Res. 2016 doi: 10.1158/0008-5472.CAN-15-1325. doi:10.1158/0008-5472.CAN-15-1325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Chen MB, Whisler JA, Jeon JS, Kamm RD. Mechanisms of tumor cell extravasation in an in vitro microvascular network platform. Integr Biol (Camb) 2013;5(10):1262–1271. doi: 10.1039/c3ib40149a. doi:10.1039/c3ib40149a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Cho EH, Wendel M, Luttgen M, Yoshioka C, Marrinucci D, Lazar D, Schram E, Nieva J, Bazhenova L, Morgan A, Ko AH, Korn WM, Kolatkar A, Bethel K, Kuhn P. Characterization of circulating tumor cell aggregates identified in patients with epithelial tumors. Phys Biol. 2012;9(1):016001. doi: 10.1088/1478-3975/9/1/016001. doi:10.1088/1478-3975/9/1/016001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Crowl L, Fogelson AL. Analysis of Mechanisms for Platelet Near-Wall Excess under Arterial Blood Flow Conditions. Journal of Fluid Mechanics. 2011;676:348–375. [Google Scholar]
- 9.Diamond E, Lee GY, Akhtar NH, Kirby BJ, Giannakakou P, Tagawa ST, Nanus DM. Isolation and characterization of circulating tumor cells in prostate cancer. Front Oncol. 2012;2:131. doi: 10.3389/fonc.2012.00131. doi:10.3389/fonc.2012.00131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Farace F, Massard C, Vimond N, Drusch F, Jacques N, Billiot F, Laplanche A, Chauchereau A, Lacroix L, Planchard D, Le Moulec S, Andre F, Fizazi K, Soria JC, Vielh P. A direct comparison of CellSearch and ISET for circulating tumour-cell detection in patients with metastatic carcinomas. Br J Cancer. 2011;105(6):847–853. doi: 10.1038/bjc.2011.294. doi:10.1038/bjc.2011.294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Fedosov DA, Gompper G. White blood cell margination in microcirculation. Soft Matter. 2014;10(17):2961–2970. doi: 10.1039/c3sm52860j. doi:10.1039/c3sm52860j. [DOI] [PubMed] [Google Scholar]
- 12.Fitzgibbon S, Spann AP, Qi QM, Shaqfeh ES. In vitro measurement of particle margination in the microchannel flow: effect of varying hematocrit. Biophys J. 2015;108(10):2601–2608. doi: 10.1016/j.bpj.2015.04.013. doi:10.1016/j.bpj.2015.04.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Fuhrmann A, Staunton JR, Nandakumar V, Banyai N, Davies PC, Ros R. AFM stiffness nanotomography of normal, metaplastic and dysplastic human esophageal cells. Phys Biol. 2011;8(1):015007. doi: 10.1088/1478-3975/8/1/015007. doi:10.1088/1478-3975/8/1/015007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Gay LJ, Felding-Habermann B. Contribution of platelets to tumour metastasis. Nat Rev Cancer. 2011;11(2):123–134. doi: 10.1038/nrc3004. doi:10.1038/nrc3004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Hayashi K, Jiang P, Yamauchi K, Yamamoto N, Tsuchiya H, Tomita K, Moossa AR, Bouvet M, Hoffman RM. Real-time imaging of tumor-cell shedding and trafficking in lymphatic channels. Cancer Res. 2007;67(17):8223–8228. doi: 10.1158/0008-5472.CAN-07-1237. doi:10.1158/0008-5472.CAN-07-1237. [DOI] [PubMed] [Google Scholar]
- 16.Hoffman RM. Imaging in mice with fluorescent proteins: from macro to subcellular. Sensors. 2008;8:1157–1173. doi: 10.3390/s8021157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Hou JM, Krebs M, Ward T, Morris K, Sloane R, Blackhall F, Dive C. Circulating tumor cells, enumeration and beyond. Cancers (Basel) 2010;2(2):1236–1250. doi: 10.3390/cancers2021236. doi:10.3390/cancers2021236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Hsieh HB, Marrinucci D, Bethel K, Curry DN, Humphrey M, Krivacic RT, Kroener J, Kroener L, Ladanyi A, Lazarus N, Kuhn P, Bruce RH, Nieva J. High speed detection of circulating tumor cells. Biosens Bioelectron. 2006;21(10):1893–1899. doi: 10.1016/j.bios.2005.12.024. doi:10.1016/j.bios.2005.12.024. [DOI] [PubMed] [Google Scholar]
- 19.Jadhav S, Eggleton CD, Konstantopoulos K. A 3-D computational model predicts that cell deformation affects selectin-mediated leukocyte rolling. Biophys J. 2005;88(1):96–104. doi: 10.1529/biophysj.104.051029. doi:10.1529/biophysj.104.051029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Kelley LC, Lohmer LL, Hagedorn EJ, Sherwood DR. Traversing the basement membrane in vivo: a diversity of strategies. J Cell Biol. 2014;204(3):291–302. doi: 10.1083/jcb.201311112. doi:10.1083/jcb.201311112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Ketene AN, Schmelz EM, Roberts PC, Agah M. The effects of cancer progression on the viscoelasticity of ovarian cell cytoskeleton structures. Nanomedicine. 2012;8(1):93–102. doi: 10.1016/j.nano.2011.05.012. doi:10.1016/j.nano.2011.05.012. [DOI] [PubMed] [Google Scholar]
- 22.Khismatullin DB, Truskey GA. Three-dimensional numerical simualtion of receptor-mediated leukocyte adhesion to surfaces: effects of cell deformability and viscoelasticity. Physics of Fluids. 2005;17:031505. [Google Scholar]
- 23.Khismatullin DB, Truskey GA. Leukocyte rolling on P-selectin: a three-dimensional numerical study of the effect of cytoplasmic viscosity. Biophys J. 2012;102(8):1757–1766. doi: 10.1016/j.bpj.2012.03.018. doi:10.1016/j.bpj.2012.03.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Kim Y, Williams KC, Gavin CT, Jardine E, Chambers AF, Leong HS. Quantification of cancer cell extravasation in vivo. Nat Protoc. 2016;11(5):937–948. doi: 10.1038/nprot.2016.050. doi:10.1038/nprot.2016.050. [DOI] [PubMed] [Google Scholar]
- 25.King MR, Hammer DA. Multiparticle adhesive dynamics: hydrodynamic recruitment of rolling leukocytes. Proc Natl Acad Sci U S A. 2001;98(26):14919–14924. doi: 10.1073/pnas.261272498. doi:10.1073/pnas.261272498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.King MR, Hammer DA. Multiparticle adhesive dynamics. Interactions between stably rolling cells. Biophys J. 2001;81(2):799–813. doi: 10.1016/S0006-3495(01)75742-6. doi:10.1016/S0006-3495(01)75742-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.King MR, Phillips KG, Mitrugno A, Lee TR, de Guillebon AM, Chandrasekaran S, McGuire MJ, Carr RT, Baker-Groberg SM, Rigg RA, Kolatkar A, Luttgen M, Bethel K, Kuhn P, Decuzzi P, McCarty OJ. A physical sciences network characterization of circulating tumor cell aggregate transport. Am J Physiol Cell Physiol. 2015;308(10):C792–802. doi: 10.1152/ajpcell.00346.2014. doi:10.1152/ajpcell.00346.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Kirby BJ, Jodari M, Loftus MS, Gakhar G, Pratt ED, Chanel-Vos C, Gleghorn JP, Santana SM, Liu H, Smith JP, Navarro VN, Tagawa ST, Bander NH, Nanus DM, Giannakakou P. Functional characterization of circulating tumor cells with a prostate-cancer-specific microfluidic device. PLoS One. 2012;7(4):e35976. doi: 10.1371/journal.pone.0035976. doi:10.1371/journal.pone.0035976. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Laurent VM, Planus E, Fodil R, Isabey D. Mechanical assessment by magnetocytometry of the cytosolic and cortical cytoskeletal compartments in adherent epithelial cells. Biorheology. 2003;40(1-3):235–240. [PubMed] [Google Scholar]
- 30.Lazar DC, Cho EH, Luttgen MS, Metzner TJ, Uson ML, Torrey M, Gross ME, Kuhn P. Cytometric comparisons between circulating tumor cells from prostate cancer patients and the prostate-tumor-derived LNCaP cell line. Phys Biol. 2012;9(1):016002. doi: 10.1088/1478-3975/9/1/016002. doi:10.1088/1478-3975/9/1/016002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Maheswaran S, Haber DA. Circulating tumor cells: a window into cancer biology and metastasis. Curr Opin Genet Dev. 2010;20(1):96–99. doi: 10.1016/j.gde.2009.12.002. doi:10.1016/j.gde.2009.12.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Marrinucci D, Bethel K, Kolatkar A, Luttgen MS, Malchiodi M, Baehring F, Voigt K, Lazar D, Nieva J, Bazhenova L, Ko AH, Korn WM, Schram E, Coward M, Yang X, Metzner T, Lamy R, Honnatti M, Yoshioka C, Kunken J, Petrova Y, Sok D, Nelson D, Kuhn P. Fluid biopsy in patients with metastatic prostate, pancreatic and breast cancers. Phys Biol. 2012;9(1):016003. doi: 10.1088/1478-3975/9/1/016003. doi:10.1088/1478-3975/9/1/016003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Marrinucci D, Bethel K, Lazar D, Fisher J, Huynh E, Clark P, Bruce R, Nieva J, Kuhn P. Cytomorphology of circulating colorectal tumor cells:a small case series. J Oncol. 2010;2010:861341. doi: 10.1155/2010/861341. doi:10.1155/2010/861341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Marrinucci D, Bethel K, Luttgen M, Bruce RH, Nieva J, Kuhn P. Circulating tumor cells from well-differentiated lung adenocarcinoma retain cytomorphologic features of primary tumor type. Arch Pathol Lab Med. 2009;133(9):1468–1471. doi: 10.1043/1543-2165-133.9.1468. doi:10.1043/1543-2165-133.9.1468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Mathur AB, Truskey GA, Reichert WM. Atomic force and total internal reflection fluorescence microscopy for the study of force transmission in endothelial cells. Biophys J. 2000;78(4):1725–1735. doi: 10.1016/s0006-3495(00)76724-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.McCarty OJ, Ku D, Sugimoto M, King MR, Cosemans JM, Neeves KB, Subcommittee on B. Dimensional analysis and scaling relevant to flow models of thrombus formation: communication from the SSC of the ISTH. J Thromb Haemost. 2016;14(3):619–622. doi: 10.1111/jth.13241. doi:10.1111/jth.13241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.McCarty OJ, Mousa SA, Bray PF, Konstantopoulos K. Immobilized platelets support human colon carcinoma cell tethering, rolling, and firm adhesion under dynamic flow conditions. Blood. 2000;96(5):1789–1797. [PubMed] [Google Scholar]
- 38.Migliorini C, Qian Y, Chen H, Brown EB, Jain RK, Munn LL. Red blood cells augment leukocyte rolling in a virtual blood vessel. Biophys J. 2002;83(4):1834–1841. doi: 10.1016/S0006-3495(02)73948-9. doi:10.1016/S0006-3495(02)73948-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Mina LA, Sledge GW., Jr. Rethinking the metastatic cascade as a therapeutic target. Nat Rev Clin Oncol. 2011;8(6):325–332. doi: 10.1038/nrclinonc.2011.59. doi:10.1038/nrclinonc.2011.59. [DOI] [PubMed] [Google Scholar]
- 40.Mitchell MJ, Castellanos CA, King MR. Immobilized surfactant-nanotube complexes support selectin-mediated capture of viable circulating tumor cells in the absence of capture antibodies. J Biomed Mater Res A. 2015;103(10):3407–3418. doi: 10.1002/jbm.a.35445. doi:10.1002/jbm.a.35445. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Mitchell MJ, King MR. Computational and experimental models of cancer cell response to fluid shear stress. Front Oncol. 2013;3:44. doi: 10.3389/fonc.2013.00044. doi:10.3389/fonc.2013.00044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Mitrugno A, Tormoen GW, Kuhn P, McCarty OJ. The prothrombotic activity of cancer cells in the circulation. Blood Rev. 2016;30(1):11–19. doi: 10.1016/j.blre.2015.07.001. doi:10.1016/j.blre.2015.07.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Nguyen DX, Bos PD, Massague J. Metastasis: from dissemination to organ-specific colonization. Nat Rev Cancer. 2009;9(4):274–284. doi: 10.1038/nrc2622. doi:10.1038/nrc2622. [DOI] [PubMed] [Google Scholar]
- 44.Nourshargh S, Hordijk PL, Sixt M. Breaching multiple barriers: leukocyte motility through venular walls and the interstitium. Nat Rev Mol Cell Biol. 2010;11(5):366–378. doi: 10.1038/nrm2889. doi:10.1038/nrm2889. [DOI] [PubMed] [Google Scholar]
- 45.Oakman C, Pestrin M, Bessi S, Galardi F, Di Leo A. Significance of micrometastases: circulating tumor cells and disseminated tumor cells in early breast cancer. Cancers (Basel) 2010;2(2):1221–1235. doi: 10.3390/cancers2021221. doi:10.3390/cancers2021221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Park S, Koch D, Cardenas R, Kas J, Shih CK. Cell motility and local viscoelasticity of fibroblasts. Biophys J. 2005;89(6):4330–4342. doi: 10.1529/biophysj.104.053462. doi:10.1529/biophysj.104.053462. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Peskin CS. Flow patterns around heart valves: a numerical method. J ComputPhys. 1972;10:252–271. [Google Scholar]
- 48.Peskin CS. Numerical analysis of blood flow in the heart. J Comput Phys. 1977;25:220–252. [Google Scholar]
- 49.Peskin CS. The Immersed Boundary Method. Acta Numerica. 2002;11:479–517. [Google Scholar]
- 50.Peskin CS, McQueen DM. A general method for the computer simulation of biological systems interacting with fluids. Symp Soc Exp Biol. 1995;49:265–276. [PubMed] [Google Scholar]
- 51.Phillips KG, Kuhn P, McCarty OJ. Physical biology in cancer. 2. The physical biology of circulating tumor cells. Am J Physiol Cell Physiol. 2014;306(2):C80–88. doi: 10.1152/ajpcell.00294.2013. doi:10.1152/ajpcell.00294.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Phillips KG, Lee AM, Tormoen GW, Rigg RA, Kolatkar A, Luttgen M, Bethel K, Bazhenova L, Kuhn P, Newton P, McCarty OJ. The thrombotic potential of circulating tumor microemboli: computational modeling of circulating tumor cell-induced coagulation. Am J Physiol Cell Physiol. 2015;308(3):C229–236. doi: 10.1152/ajpcell.00315.2014. doi:10.1152/ajpcell.00315.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Phillipson M, Heit B, Colarusso P, Liu L, Ballantyne CM, Kubes P. Intraluminal crawling of neutrophils to emigration sites: a molecularly distinct process from adhesion in the recruitment cascade. J Exp Med. 2006;203(12):2569–2575. doi: 10.1084/jem.20060925. doi:10.1084/jem.20060925. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Pozrikidis C. Numerical simulation of cell motion in tube flow. Ann Biomed Eng. 2005;33(2):165–178. doi: 10.1007/s10439-005-8975-6. [DOI] [PubMed] [Google Scholar]
- 55.Rejniak KA. An immersed boundary framework for modelling the growth of individual cells: an application to the early tumour development. J Theor Biol. 2007;247(1):186–204. doi: 10.1016/j.jtbi.2007.02.019. doi:10.1016/j.jtbi.2007.02.019. [DOI] [PubMed] [Google Scholar]
- 56.Rejniak KA. Modelling the development of complex tissues using individual viscoelastic cells. In: Anderson MC A, Rejniak KA, editors. Single-Cell-Based Models in Biology and Medicine. Birkhauser-Verlag; 2007. [Google Scholar]
- 57.Rejniak KA. Investigating dynamical deformations of tumor cells in circulation: predictions from a theoretical model. Front Oncol. 2012;2:111. doi: 10.3389/fonc.2012.00111. doi:10.3389/fonc.2012.00111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Rejniak KA, Dillon RH. A Single Cell Based Model of the Ductal Tumor Microarchitecture. Computational and Mathematical Methods in Medicine. 2007;8(51-69) [Google Scholar]
- 59.Stoletov K, Kato H, Zardouzian E, Kelber J, Yang J, Shattil S, Klemke R. Visualizing extravasation dynamics of metastatic tumor cells. J Cell Sci. 2010;123(Pt 13):2332–2341. doi: 10.1242/jcs.069443. doi:10.1242/jcs.069443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Stoletov K, Montel V, Lester RD, Gonias SL, Klemke R. High-resolution imaging of the dynamic tumor cell vascular interface in transparent zebrafish. Proc Natl Acad Sci U S A. 2007;104(44):17406–17411. doi: 10.1073/pnas.0703446104. doi:10.1073/pnas.0703446104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Swaby RF, Cristofanilli M. Circulating tumor cells in breast cancer: a tool whose time has come of age. BMC Med. 2011;9:43. doi: 10.1186/1741-7015-9-43. doi:10.1186/1741-7015-9-43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Swaminathan V, Mythreye K, O'Brien ET, Berchuck A, Blobe GC, Superfine R. Mechanical stiffness grades metastatic potential in patient tumor cells and in cancer cell lines. Cancer Res. 2011;71(15):5075–5080. doi: 10.1158/0008-5472.CAN-11-0247. doi:10.1158/0008-5472.CAN-11-0247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Takeishi N, Imai Y, Nakaaki K, Yamaguchi T, Ishikawa T. Leukocyte margination at arteriole shear rate. Physiol Rep. 2014;2(6) doi: 10.14814/phy2.12037. doi:10.14814/phy2.12037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Takeishi N, Imai Y, Yamaguchi T, Ishikawa T. Flow of a circulating tumor cell and red blood cells in microvessels. Phys Rev E Stat Nonlin Soft Matter Phys. 2015;92(6-1):063011. doi: 10.1103/PhysRevE.92.063011. doi:10.1103/PhysRevE.92.063011. [DOI] [PubMed] [Google Scholar]
- 65.Tang J, Hunt CA. Identifying the rules of engagement enabling leukocyte rolling, activation, and adhesion. PLoS Comput Biol. 2010;6(2):e1000681. doi: 10.1371/journal.pcbi.1000681. doi:10.1371/journal.pcbi.1000681. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Tormoen GW, Haley KM, Levine RL, McCarty OJ. Do circulating tumor cells play a role in coagulation and thrombosis? Front Oncol. 2012;2:115. doi: 10.3389/fonc.2012.00115. doi:10.3389/fonc.2012.00115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Tremblay PL, Huot J, Auger FA. Mechanisms by which E-selectin regulates diapedesis of colon cancer cells under flow conditions. Cancer Res. 2008;68(13):5167–5176. doi: 10.1158/0008-5472.CAN-08-1229. doi:10.1158/0008-5472.CAN-08-1229. [DOI] [PubMed] [Google Scholar]
- 68.Turitto VT. Blood viscosity, mass transport, and thrombogenesis. Prog Hemost Thromb. 1982;6:139–177. [PubMed] [Google Scholar]
- 69.Wendel M, Bazhenova L, Boshuizen R, Kolatkar A, Honnatti M, Cho EH, Marrinucci D, Sandhu A, Perricone A, Thistlethwaite P, Bethel K, Nieva J, Heuvel M, Kuhn P. Fluid biopsy for circulating tumor cell identification in patients with early-and late-stage non-small cell lung cancer: a glimpse into lung cancer biology. Phys Biol. 2012;9(1):016005. doi: 10.1088/1478-3967/9/1/016005. doi:10.1088/1478-3967/9/1/016005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Weninger W, Biro M, Jain R. Leukocyte migration in the interstitial space of non-lymphoid organs. Nat Rev Immunol. 2014;14(4):232–246. doi: 10.1038/nri3641. doi:10.1038/nri3641. [DOI] [PubMed] [Google Scholar]
- 71.Wirtz D, Konstantopoulos K, Searson PC. The physics of cancer: the role of physical interactions and mechanical forces in metastasis. Nat Rev Cancer. 2011;11(7):512–522. doi: 10.1038/nrc3080. doi:10.1038/nrc3080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Yamauchi K, Yang M, Jiang P, Xu M, Yamamoto N, Tsuchiya H, Tomita K, Moossa AR, Bouvet M, Hoffman RM. Development of real-time subcellular dynamic multicolor imaging of cancer-cell trafficking in live mice with a variable-magnification whole-mouse imaging system. Cancer Res. 2006;66(8):4208–4214. doi: 10.1158/0008-5472.CAN-05-3927. doi:10.1158/0008-5472.CAN-05-3927. [DOI] [PubMed] [Google Scholar]
- 73.Yamauchi K, Yang M, Jiang P, Yamamoto N, Xu M, Amoh Y, Tsuji K, Bouvet M, Tsuchiya H, Tomita K, Moossa AR, Hoffman RM. Real-time in vivo dual-color imaging of intracapillary cancer cell and nucleus deformation and migration. Cancer Res. 2005;65(10):4246–4252. doi: 10.1158/0008-5472.CAN-05-0069. doi:10.1158/0008-5472.CAN-05-0069. [DOI] [PubMed] [Google Scholar]
- 74.Yu M, Stott S, Toner M, Maheswaran S, Haber DA. Circulating tumor cells: approaches to isolation and characterization. J Cell Biol. 2011;192(3):373–382. doi: 10.1083/jcb.201010021. doi:10.1083/jcb.201010021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Zhang J, Johnson PC, Popel AS. Effects of erythrocyte deformability and aggregation on the cell free layer and apparent viscosity of microscopic blood flows. Microvasc Res. 2009;77(3):265–272. doi: 10.1016/j.mvr.2009.01.010. doi:10.1016/j.mvr.2009.01.010. [DOI] [PMC free article] [PubMed] [Google Scholar]