Skip to main content
PMC home page
Nature Communications logoLink to Nature Communications
. 2016 Nov 11;7:13485. doi: 10.1038/ncomms13485

Spin injection and inverse Edelstein effect in the surface states of topological Kondo insulator SmB6

Qi Song 1,2, Jian Mi 1,2, Dan Zhao 3,4, Tang Su 1,2, Wei Yuan 1,2, Wenyu Xing 1,2, Yangyang Chen 1,2, Tianyu Wang 1,2, Tao Wu 3,4,5, Xian Hui Chen 3,4,5,6, X C Xie 1,2, Chi Zhang 1,2,a, Jing Shi 7,b, Wei Han 1,2,c
PMCID: PMC5114616  PMID: 27834378

Abstract

There has been considerable interest in exploiting the spin degrees of freedom of electrons for potential information storage and computing technologies. Topological insulators (TIs), a class of quantum materials, have special gapless edge/surface states, where the spin polarization of the Dirac fermions is locked to the momentum direction. This spin–momentum locking property gives rise to very interesting spin-dependent physical phenomena such as the Edelstein and inverse Edelstein effects. However, the spin injection in pure surface states of TI is very challenging because of the coexistence of the highly conducting bulk states. Here, we experimentally demonstrate the spin injection and observe the inverse Edelstein effect in the surface states of a topological Kondo insulator, SmB6. At low temperatures when only surface carriers are present, a clear spin signal is observed. Furthermore, the magnetic field angle dependence of the spin signal is consistent with spin–momentum locking property of surface states of SmB6.

Inline graphicSpin injection in pure topological surface states of topological insulators is challenging due to the coexistence of highly conducting bulk states. Here, Song et al. report spin injection and inverse Edelstein effect in the spin–momentum locked surface states of topological Kondo insulator SmB6.

Spintronics aims to use the spin degrees of freedom for information technologies1,2,3. The injection of spin-polarized carriers into two-dimensional quantum materials, including graphene and the surface states of topological insulators (TIs), is particularly interesting4,5. Different from graphene showing weak spin–orbit coupling and long spin lifetimes6,7,8,9, the surface states of TI exhibit very large spin–orbit coupling10,11,12,13. Even more interestingly, the spin and the momentum directions are strongly coupled to each other in the surface states of TI4,10,11,12,13,14. Since the observation of the spin–momentum locking properties with scanning tunneling microscopy and spin-angle-resolved photoemission spectroscopy (spin-ARPES)15,16, a great deal of effort has been made to demonstrate various unique effects associated with this property, such as large spin polarization currents and large spin–orbit torque in the Bi2Se3-based three-dimensional TI17,18,19,20,21,22,23,24,25. However, a major obstacle to the clean demonstration of the Edelstein/inverse Edelstein effects for the spin–momentum locked surface states is the presence of unavoidable bulk carriers which dominate the conduction in these Bi2Se3-based three-dimensional TI19,26. Recently, SmB6, a Kondo insulator, has been found to be a new type of TI based on transport measurements and ARPES27,28,29,30,31,32,33,34,35. At temperatures below ∼3 K, the bulk states are insulating, and only surface carriers contribute to the conduction, as demonstrated by the previous surface Hall measurements30,31.

Here, we report the spin injection into the surface states using the spin pumping and the observation of the inverse Edelstein effect in this topological Kondo insulator (TKI). The temperature and magnetic field angle dependences of the spin voltage are consistent with the spin–momentum locking properties of the surface states, which have been shown to be topological in previous studies29.

Results

Spin injection into the surface states of SmB6

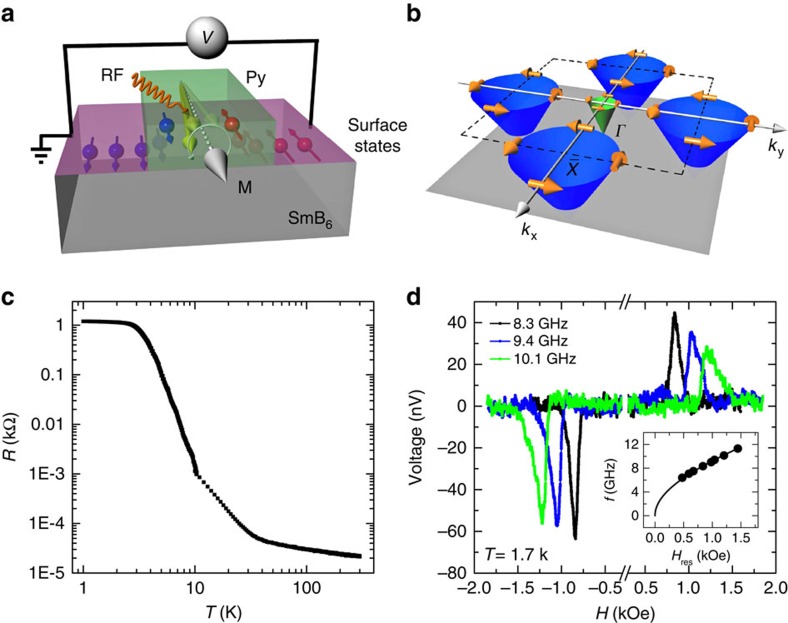
The spin injection experiment is performed using Ni80Fe20 (Py) as the spin injector, which is deposited onto the (001) surface of the SmB6 single crystals, as shown in Fig. 1a (see the ‘Methods' for details). When the ferromagnetic resonance condition for Py is fulfilled under certain magnetic fields and microwave frequencies, the precessing magnetization launches a spin current, which enters the adjacent nonmagnetic SmB6 layer. This technique is called spin pumping, which has been widely used to measure the spin to charge conversion in various materials, including metals, semiconductors and graphene and so on36,37,38,39,40,41,42,43. In our measurements, we use a radio frequency (RF) signal generator to provide the microwave power and standard lock-in technique for better sensitivity and signal-to-noise ratio (see the ‘Methods' for details). Figure 1b shows the schematic drawing of energy dispersion relationship of the surface states at the Fermi level for both Inline graphic and Г points. The resistance of the SmB6 device is measured from 300 to ∼0.8 K, as shown in Fig. 1c. Clearly, the resistance saturates blow ∼3 K, which indicates that the surface states are dominant and the bulk states do not contribute to conduction. As the temperature increases, the resistance decreases quite rapidly, owing to a large number of the activated bulk carriers as the temperature increases.

Figure 1. Spin injection into the surface states of SmB6.

Figure 1

Open in a new tab

(a) Schematic drawing of device structure and the spin injection and inverse Edelstein effect measurements. (b) Schematic drawing of the spin–momentum locking properties of the topological surface states at the 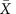Inline graphic and Г points based on previous photoemission spectroscopy measurements and DFT calculations34,44. (c) The resistance of the SmB6 as a function of the temperature. (d) Typical magnetic field dependence of the voltage with various GHz microwave frequencies. The power of the microwave is 100 mW and the temperature is 1.7 K. Inset: the resonance frequency (f) as a function of the resonance magnetic field (Hres). The solid line is a fitted curve based on the Kittel formula, equation (2) in the main text.

Figure 1d shows the typical magnetic field dependence of the spin voltage measured at 1.7 K with three representative microwave frequencies of 8.3, 9.4 and 10.1 GHz, respectively. We first confirm that the magnetic fields, at which we observe the voltage signals, are the same as the resonance magnetic fields (Hres) of the Py under the same microwave frequencies (Supplementary Fig. 1 and Supplementary Note 1). It is noticed that there are mainly three contributions to the voltages, namely the voltage due to the spin pumping and inverse Edelstein effect (VSP), the voltage due to the Seebeck effect from the microwave heating (VSE) and the anomalous Hall effect (VAHE) of the Py. Due to their different symmetries as a function of the magnetic field, we can obtain the voltage amplitudes of all these three contributions by fitting the magnetic field dependence of the voltage with the following equation (Supplementary Fig. 2 and Supplementary Note 2).

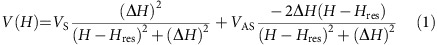graphic file with name ncomms13485-m2.jpg

where VS and VAS are the voltage amplitudes for the symmetric and antisymmetric Lorentzian shapes, respectively, and ΔH is the half-line width. The VSP exhibits a positive sign for positive magnetic fields and the positive sign of the spin-to-charge conversion in the surface states of the SmB6 is theoretically expected from the counter-clockwise spin textures for the electron band of the topological surface states18,42. The counter-clockwise spin textures have been shown by both spin-ARPES measurements and DFT calculations34,44. After the determination of Hres and ΔH for all applied microwave frequencies, we obtain the effective magnetization (Meff) and the Gilbert damping constant for the Py layer. Our results show that Meff is 781±16 e.m.u.  cm−3, which is obtained using the Kittel formula shown below45:

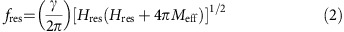graphic file with name ncomms13485-m3.jpg

where γ is the geomagnetic ratio. From the slope of the linearly fitted curve of the half-line width versus microwave frequency at 1.7 K, we calculate the Gilbert damping constant of the Py on SmB6 to be 0.0166±0.0006 (Supplementary Fig. 3).

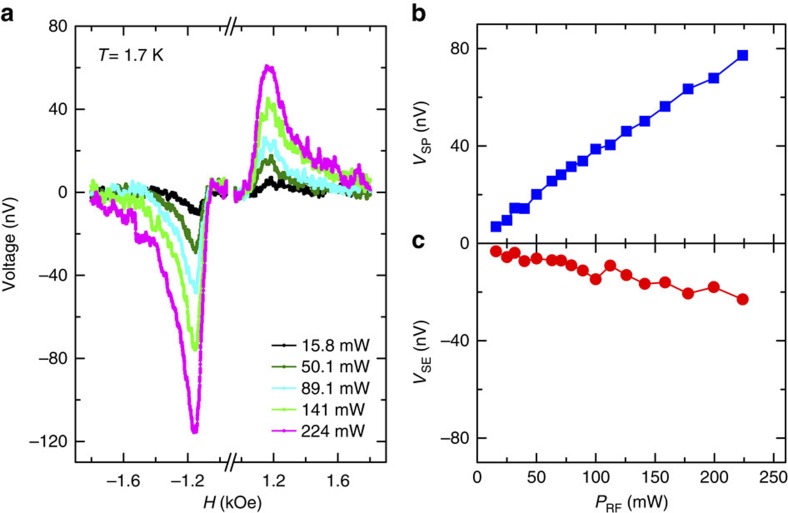
The microwave power dependence of the spin voltage is shown in Fig. 2a measured at 1.7 K and with the microwave frequency of 10.1 GHz. The measured resonance peak increases as the microwave power increases. Following the same fitting procedure (Supplementary Note 2), we obtain the power dependence of VSP and VSE. Both VSP and VSE show a linear relationship with the microwave power, as shown in Fig. 2b,c.

Figure 2. Microwave power dependence of the spin injection into the surface states of SmB6.

Figure 2

Open in a new tab

(a) Magnetic field dependence of the voltage measured at the temperature of 1.7 K and with the microwave frequency of 10.1 GHz and power of 15.8, 50.1, 89.1, 141 and 224 mW, respectively. (b,c) Microwave power dependence of the measured voltage due to spin pumping and inverse Edelstein effect (VSP in b) and the voltage that is related to the Seebeck effect (VSE in c).

Temperature dependence of the spin voltage

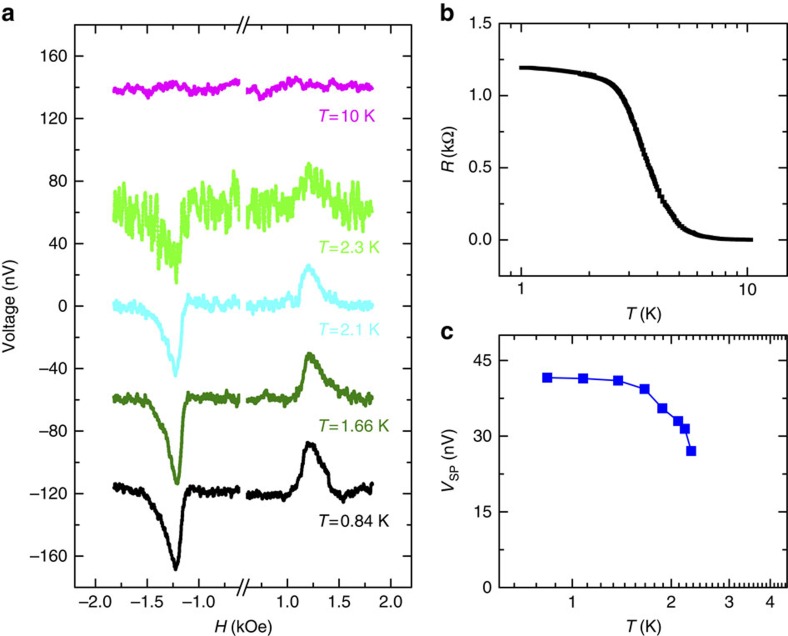
As mentioned earlier, the surface states of SmB6 dominate the transport as the bulk carriers freeze out below ∼3 K; above ∼3 K, the contribution from the bulk states is thermally activated. When a spin current enters the spin–momentum locked surface states, an electric field is resulted due to the inverse Edelstein effect, which is measured as a spin voltage. To investigate how the spin voltage evolves as the surface states emerge and become dominant, we perform the measurements from ∼0.8 to 10 K. Below ∼0.8 K, it is difficult to stabilize the temperature due to the microwave heating. Figure 3a shows the typical measurements of the voltage as a function of the magnetic field with the microwave power of 100 mW and frequency of 10.1 GHz at 0.84, 1.66, 2.1, 2.3 and 10 K, respectively. At 0.8 K, when only spin–momentum locked surface states exist, the spin signal is ∼42 nV. This value is relatively small compared with previous studies on Bi1.5Sb0.5Te1.7Se1.3 and α-Sn (refs 18, 42), which could be related to the spin pumping efficiency and/or the spin-to-charge conversion efficiency and needs further studies (Supplementary Note 3). The spin voltage steadily decreases as the temperature increases, and when the temperature reaches 10 K, no voltage can be detected. The resistance of the SmB6 from 10 to ~0.8 K is shown in Fig. 3b, indicating that the bulk states start to contribute to the total conductance between 2 and 3 K. From 3 to 5 K, the conduction due to the bulk carriers quickly increases, resulting in a 100-fold decrease in the total resistance. This feature is consistent with the previous surface conductance and Hall measurements, indicating the nearly pure surface states contributing to the conduction30,31. The temperature dependence of the VSP is summarized in Fig. 3c. VSP shows little temperature dependence below ∼2.2 K. At temperatures above ∼2.2 K, VSP steadily decreases as the temperature increases. The temperature dependences of both VSP and the resistance strongly support that the spin signal originates from the spin–momentum locked surface states. When the spin polarization is generated in the surface states, an in-plane electrical voltage is produced in the direction perpendicular to the spin directions, due to the inverse Edelstein effect. As the temperature further increases, more bulk carriers are activated and the spin voltage is greatly suppressed. This is very interesting, for the bulk states should have strong spin–orbit coupling as well and therefore ordinary inverse spin Hall effect from bulk states could give rise to a finite voltage. However, we do not observe any voltage signal at high temperatures.

Figure 3. Temperature dependence of the spin injection into the surface states of SmB6.

Figure 3

Open in a new tab

(a) Magnetic field dependence of the voltage measured for the temperatures of 0.84, 1.66, 2.1, 2.3 and 10 K, respectively. The measurement is performed with a microwave power 100 mW and frequency of 10.1 GHz. (b) The resistance of the SmB6 as a function of the temperature from 10 to ∼0.8 K. (c) Temperature dependence of VSP.

Magnetic field angle dependence of the spin voltage

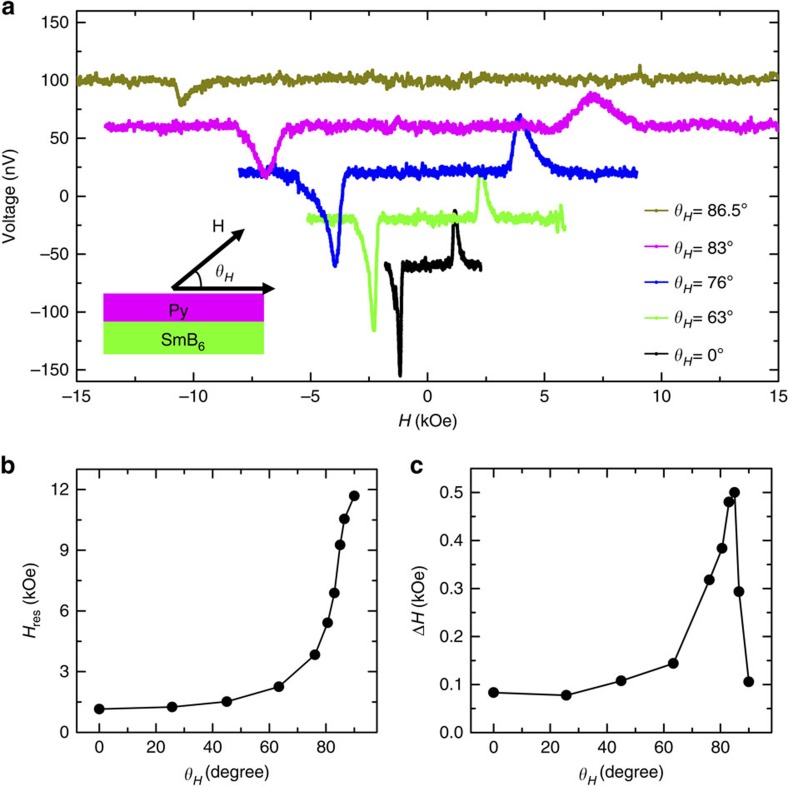
To further confirm the spin injection and detection in the surface states of the TKI, SmB6, we study the in-plane and out-of-plane spin polarization injection by changing the magnetic field direction. Figure 4a shows the typical results of the magnetic field-dependent voltages at 1.7 K with a microwave power of 200 mW and frequency of 10.1 GHz for the angles between the magnetic field and the Py electrode (shown in the inset figure), θH, equal to 0°, 63°, 76°, 83° and 86.5°. As θH increases, the resonance magnetic field increases accordingly, and in the meantime, the spin signal shows a decrease. At 86.5°, the spin-dependent voltage becomes vanishingly small. The Hres and ΔH as a function of θH are shown in Fig. 4b,c, which are consistent with the previous measurement of the ferromagnetic resonance of Py under different magnetic field directions37,46. This further confirms that the measured spin voltage indeed arises from the precession of the Py magnetization.

Figure 4. The measured voltage as a function of the magnetic field angle.

Figure 4

Open in a new tab

(a) Magnetic field dependence of the voltage measured at 1.7 K for θH=0°, 63°, 76°, 83° and 86.5°, respectively. Inset: the schematic illustration of the coordinate system for magnetic field angle. (b,c) The resonance magnetic field and half-line width as a function of θH.

Discussion

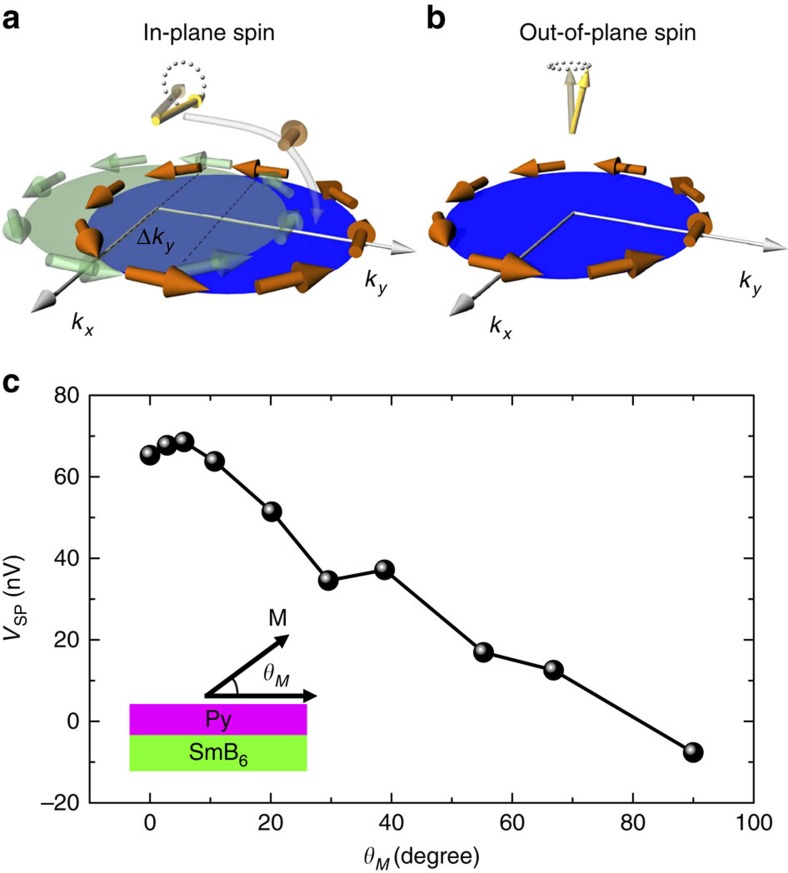
It is particularly interesting that only in-plane spin polarization injection generates an electric field, whereas the out-of-plane spin polarization injection does not show this effect. This observation could be attributed to the spin–momentum locking properties of the surface states of the TKI, as illustrated in Fig. 5a,b. For the in-plane spin polarization injection along the x direction, the Fermi surface shifts along the y direction, and Δky indicates the total shift due to the spin injection and the inverse Edelstein effect, as shown in Fig. 5a. On the other hand, for the out-of-plane spin polarization injection, there is no net effect of spin injection as the spins of the surface states lie in-plane and are locked perpendicular to the momentum directions, as shown in Fig. 5b. Finally, we calculate the Py magnetization angle, θM, from the θH dependence of the resonance magnetic field (Supplementary Fig. 4) based on the 0 and 90 degrees data and the following equation37.

Figure 5. Magnetization angle dependence of the voltage due to spin pumping and inverse Edelstein effect.

Figure 5

Open in a new tab

(a,b) Schematic drawings for the in-plane (a) and out-of-plane (b) spin polarization injection into the surface states of SmB6. The in-plane spin polarization injection leads to the generation of the in-plane electric field due to inverse Edelstein effect, while the out-of-plane spin injection is forbidden due to the spin–momentum locking properties of the surface states of SmB6, which have been shown to be topological in previous studies. (c) VSP as a function of θM. Inset: the schematic illustration of the coordinate system for θM.

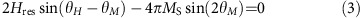graphic file with name ncomms13485-m4.jpg

where MS is the saturated magnetization. It is clearly seen that VSP almost vanishes as θM approaches 90 degrees (Fig. 5c), which is also consistent with the spin–momentum locking properties of the surface states of the TKI, as discussed above and illustrated in Fig. 5a,b. The complete understanding of the VSP as a function of the θM needs future theoretical studies to quantitatively calculate how much the Fermi surface shift as a result of the inverse Edelstein effect of the spin polarization injection (Supplementary Fig. 5 and Note 4).

Our experimental results strongly support the demonstration of spin injection and the observation of the inverse Edelstein effect in the surface states of SmB6. The temperature and magnetization angle dependences, as well as the sign of the spin-to-charge conversion are well consistent with spin–momentum locking properties of the surface states, which have been shown to be topological with the counter-clockwise spin textures for the electron bands in previous studies29,34,44. Since the detailed spin textures of the Rashba surface states have not been reported yet, it is premature to exclude any contribution from the Rashba-split surface states at the current stage. To fully understand this, further studies, including the detailed spin textures from spin-ARPES measurements of the Rashba surface states and the quantitative theoretical calculations of the contributions from topological and Rashba surface states, are needed. Our observation could lead to future studies of the role of strong correlation in TKIs for spintronics and highly efficient spin current generation in the surface states of TIs via the materials design and engineering.

Methods

Materials growth

High-quality single crystalline SmB6 samples are grown using the conventional Al-flux method. A mixture consisting of a Sm chunk (purity: 99.9%), Boron (purity: 99.99%) and Al powders (purity: 99.99%) with a ratio of 1:6:400 is heated at high temperatures in the circumstance with continuously flowing Ar gas to form SmB6 single crystals. Then the SmB6 samples are put into diluted HNO3 acid to remove the residual aluminum flux.

We choose the samples with large rectangular crystals of millimeters size and large (001) facet for spin injection experiment. A 20 nm thick Py electrode is deposited on the (001) surface of the SmB6 single crystal by radio frequency magnetron sputtering with a growth rate of 0.02 Å s−1. To prevent the oxidation of Py, a capping layer of 3 nm Al is deposited in situ before taking the samples out.

Device fabrication

A shadow mask technique (size: ∼0.9 × 3 mm2) is used to define the shape and position of the ferromagnetic electrode (Py/Al) on the (001) surface of the SmB6 crystal (size: ∼1 × 5 mm2, thickness: ∼0.5 mm). Al wires are used to contact the two ends of SmB6 sample for the electrical voltage measurement.

Device measurement

The spin injection is performed using the spin pumping method and the spins are detected via the inverse Edelstein effect of the surface states of SmB6. The microwave power is supplied by a signal generator (Anritsu LTD. MG3690C) modulated with a digital lock-in amplifier (NF Co. LI5640) with the frequency of 373 Hz to enhance the sensitivity and signal-to-noise ratio. The spin pumping measurement is performed by precessing the Py magnetization around its resonance conditions with a coplanar waveguide from 10 to ∼0.8 K in a Janis He-3 system. The resistance of the SmB6 single crystal is measured using Keithley K2400 and K2002 in Quantum Design Physical Properties Measurement System (PPMS) from 300 to 10 K and in a Janis He-3 system from 10 to ∼0.8 K.

Data availability

The authors declare that the data supporting the findings of this study are available within the paper and its Supplementary Information files.

Additional information

How to cite this article: Song, Q. et al. Spin injection and inverse Edelstein effect in the surface states of topological Kondo insulator SmB6. Nat. Commun. 7, 13485 doi: 10.1038/ncomms13485 (2016).

Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary Material

Supplementary Information

Supplementary Figures 1-5, Supplementary Notes 1-4 and Supplementary References

ncomms13485-s1.pdf (2.3MB, pdf)
Peer Review File
ncomms13485-s2.pdf (386.8KB, pdf)

Acknowledgments

We acknowledge the fruitful discussions with Professor Fa Wang and the financial support from National Basic Research Programs of China (973 program Grant Nos. 2014CB920902, 2015CB921104 and 2013CB921903) and National Natural Science Foundation of China (NSFC Grant Nos. 11574006 and 11374020). D.Z., T.W. and X.H.C. acknowledge the financial support from the Strategic Priority Research Program of the Chinese Academy of Sciences (Grant No. XDB04040100). T.W. acknowledges Recruitment Program of Global Experts and CAS Hundred Talent Program. J.S. acknowledges the support by the DOE BES Award No. DEFG02-07ER46351. W.H. acknowledges the support by the 1000 Talents Program for Young Scientists of China.

Footnotes

Author contributions W.H. proposed and designed the experiment. Q.S. did the Py growth and fabricated the devices. Q.S. and J.M. performed the electrical measurements. J.M. and C.Z. developed the microwave techniques in the He3 refrigerator used for the measurements below 10 K in Professor Zhang's group. Q.S. and W.H. analysed the data. D.Z., T.W. and X.H.C. provided the single crystalline SmB6 sample. W.H. wrote the manuscript. All the authors commented on the manuscript and contributed to its final version.

References

  1. Wolf S. A. et al. Spintronics: a spin-based electronics vision for the future. Science 294, 1488–1495 (2001). [DOI] [PubMed] [Google Scholar]
  2. Zutic I., Fabian J. & Das Sarma S. Spintronics: fundamentals and applications. Rev. Mod. Phys. 76, 323–410 (2004). [Google Scholar]
  3. Bader S. D. & Parkin S. S. P. Spintronics. Annu. Rev. Cond. Mat 1, 71–88 (2010). [Google Scholar]
  4. Pesin D. & MacDonald A. H. Spintronics and pseudospintronics in graphene and topological insulators. Nat. Mater. 11, 409–416 (2012). [DOI] [PubMed] [Google Scholar]
  5. Han W. Perspectives for spintronics in 2D materials. APL Mater. 4, 032401 (2016). [Google Scholar]
  6. Tombros N., Jozsa C., Popinciuc M., Jonkman H. T. & van Wees B. J. Electronic spin transport and spin precession in single graphene layers at room temperature. Nature 448, 571–574 (2007). [DOI] [PubMed] [Google Scholar]
  7. Han W., Kawakami R. K., Gmitra M. & Fabian J. Graphene spintronics. Nat. Nanotechnol 9, 794–807 (2014). [DOI] [PubMed] [Google Scholar]
  8. Stephan R. et al. Graphene spintronics: the European Flagship perspective. 2D Materials 2, 030202 (2015). [Google Scholar]
  9. Dlubak B. et al. Highly efficient spin transport in epitaxial graphene on SiC. Nat. Phys. 8, 557–561 (2012). [Google Scholar]
  10. Qi X.-L. & Zhang S.-C. Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057–1110 (2011). [Google Scholar]
  11. Hasan M. Z. & Kane C. L. Colloquium: topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010). [Google Scholar]
  12. Moore J. E. The birth of topological insulators. Nature 464, 194–198 (2010). [DOI] [PubMed] [Google Scholar]
  13. Ando Y. Topological insulator materials. J. Phys. Soc. Jpn. 82, 102001 (2013). [Google Scholar]
  14. Yazyev O. V., Moore J. E. & Louie S. G. Spin polarization and transport of surface states in the topological insulators Bi2Se3 and Bi2Te3 from first principles. Phys. Rev. Lett. 105, 266806 (2010). [DOI] [PubMed] [Google Scholar]
  15. Hsieh D. et al. A tunable topological insulator in the spin helical Dirac transport regime. Nature 460, 1101–1105 (2009). [DOI] [PubMed] [Google Scholar]
  16. Roushan P. et al. Topological surface states protected from backscattering by chiral spin texture. Nature 460, 1106–1109 (2009). [DOI] [PubMed] [Google Scholar]
  17. Li C. H. et al. Electrical detection of charge-current-induced spin polarization due to spin-momentum locking in Bi2Se3. Nat. Nanotechnol 9, 218–224 (2014). [DOI] [PubMed] [Google Scholar]
  18. Shiomi Y. et al. Spin-electricity conversion induced by spin injection into topological insulators. Phys. Rev. Lett. 113, 196601 (2014). [DOI] [PubMed] [Google Scholar]
  19. Mellnik A. R. et al. Spin-transfer torque generated by a topological insulator. Nature 511, 449–451 (2014). [DOI] [PubMed] [Google Scholar]
  20. Fan Y. et al. Magnetization switching through giant spin–orbit torque in a magnetically doped topological insulator heterostructure. Nat. Mater. 13, 699–704 (2014). [DOI] [PubMed] [Google Scholar]
  21. Tang J. et al. Electrical detection of spin-polarized surface states conduction in (Bi0.53Sb0.47)2Te3 topological insulator. Nano Lett. 14, 5423–5429 (2014). [DOI] [PubMed] [Google Scholar]
  22. Ando Y. et al. Electrical detection of the spin polarization due to charge flow in the surface state of the topological insulator Bi1.5Sb0.5Te1.7Se1.3. Nano Lett. 14, 6226–6230 (2014). [DOI] [PubMed] [Google Scholar]
  23. Liu L. et al. Spin-polarized tunneling study of spin-momentum locking in topological insulators. Phys. Rev. B 91, 235437 (2015). [Google Scholar]
  24. Wang Y. et al. Topological surface states originated spin-orbit torques in Bi2Se3. Phys. Rev. Lett. 114, 257202 (2015). [DOI] [PubMed] [Google Scholar]
  25. Lee J. S., Richardella A., Hickey D. R., Mkhoyan K. A. & Samarth N. Mapping the chemical potential dependence of current-induced spin polarization in a topological insulator. Phys. Rev. B 92, 155312 (2015). [Google Scholar]
  26. Jiang Z. et al. Enhanced spin Seebeck effect signal due to spin-momentum locked topological surface states. Nat. Commun 7, 11458 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Dzero M., Sun K., Galitski V. & Coleman P. Topological Kondo insulators. Phys. Rev. Lett. 104, 106408 (2010). [DOI] [PubMed] [Google Scholar]
  28. Lu F., Zhao J., Weng H., Fang Z. & Dai X. Correlated topological insulators with mixed valence. Phys. Rev. Lett. 110, 096401 (2013). [DOI] [PubMed] [Google Scholar]
  29. Dzero M., Xia J., Galitski V. & Coleman P. Topological Kondo insulators. Annu. Rev. Condens. Matter Phys. 7, 249–280 (2016). [Google Scholar]
  30. Kim D. J., Xia J. & Fisk Z. Topological surface state in the Kondo insulator samarium hexaboride. Nat. Mater. 13, 466–470 (2014). [DOI] [PubMed] [Google Scholar]
  31. Kim D. J. et al. Surface Hall effect and nonlocal transport in SmB6: evidence for surface conduction. Sci. Rep. 3, 3150 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Li G. et al. Two-dimensional Fermi surfaces in Kondo insulator SmB6. Science 346, 1208–1212 (2014). [DOI] [PubMed] [Google Scholar]
  33. Jiang J. et al. Observation of possible topological in-gap surface states in the Kondo insulator SmB6 by photoemission. Nat. Commun 4, 3010 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Xu N. et al. Direct observation of the spin texture in SmB6 as evidence of the topological Kondo insulator. Nat. Commun. 5, 4566 (2014). [DOI] [PubMed] [Google Scholar]
  35. Syers P., Kim D., Fuhrer M. S. & Paglione J. Tuning bulk and surface conduction in the proposed topological Kondo insulator SmB6. Phys. Rev. Lett. 114, 096601 (2015). [DOI] [PubMed] [Google Scholar]
  36. Mosendz O. et al. Quantifying spin Hall angles from spin pumping: experiments and theory. Phys. Rev. Lett. 104, 046601 (2010). [DOI] [PubMed] [Google Scholar]
  37. Ando K. et al. Inverse spin-Hall effect induced by spin pumping in metallic system. J. Appl. Phys. 109, 103913 (2011). [Google Scholar]
  38. Ando K. et al. Electrically tunable spin injector free from the impedance mismatch problem. Nat. Mater. 10, 655–659 (2011). [DOI] [PubMed] [Google Scholar]
  39. Czeschka F. D. et al. Scaling behavior of the spin pumping effect in ferromagnet-platinum bilayers. Phys. Rev. Lett. 107, 046601 (2011). [DOI] [PubMed] [Google Scholar]
  40. Ando K. & Saitoh E. Observation of the inverse spin Hall effect in silicon. Nat. Commun. 3, 629 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Zhang W. et al. Spin Hall effects in metallic antiferromagnets. Phys. Rev. Lett. 113, 196602 (2014). [DOI] [PubMed] [Google Scholar]
  42. Rojas-Sánchez J. C. et al. Spin to charge conversion at room temperature by spin pumping into a new type of topological insulator: α-Sn films. Phys. Rev. Lett. 116, 096602 (2016). [DOI] [PubMed] [Google Scholar]
  43. Dushenko S. et al. Gate-tunable spin-charge conversion and the role of spin-orbit interaction in graphene. Phys. Rev. Lett. 116, 166102 (2016). [DOI] [PubMed] [Google Scholar]
  44. Yu R., Weng H., Fang Z. & Dai X. Pseudo-spin, real-spin and spin polarization of photo-emitted electrons. 94, 085123 (2016).
  45. Kittel C. On the theory of ferromagnetic resonance absorption. Phys. Rev 73, 155–161 (1948). [Google Scholar]
  46. Luo C. et al. Enhancement of magnetization damping coefficient of permalloy thin films with dilute Nd dopants. Phys. Rev. B 89, 184412 (2014). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary Figures 1-5, Supplementary Notes 1-4 and Supplementary References

ncomms13485-s1.pdf (2.3MB, pdf)
Peer Review File
ncomms13485-s2.pdf (386.8KB, pdf)

Data Availability Statement

The authors declare that the data supporting the findings of this study are available within the paper and its Supplementary Information files.

Articles from Nature Communications are provided here courtesy of Nature Publishing Group

RESOURCES