MIDA boronates are hydrolysed fast and slow by two different mechanisms

Abstract

MIDA boronates (N-methylimidodiacetic boronic acid esters) serve as an increasingly general platform for building-block-based small molecule construction, largely due to the dramatic and general rate differences with which they are hydrolysed under various basic conditions. Yet the mechanistic underpinnings of these rate differences have remained unclear, hindering efforts to address current limitations of this chemistry. Here we show that there are two distinct mechanisms for this hydrolysis: one is base-mediated and the other neutral. The former can proceed more than three orders of magnitude faster, and involves rate-limiting attack at a MIDA carbonyl carbon by hydroxide. The alternative ‘neutral’ hydrolysis does not require an exogenous acid/base and involves rate-limiting B-N bond cleavage by a small water cluster, (H₂O)_n. The two mechanisms can operate in parallel, and their relative rates are readily quantified by ¹⁸O incorporation. Whether hydrolysis is ‘fast’ or ‘slow’ is dictated by the pH, the water activity (a_w), and mass-transfer rates between phases. These findings stand to rationally enable even more effective and widespread utilisation of MIDA boronates in synthesis.

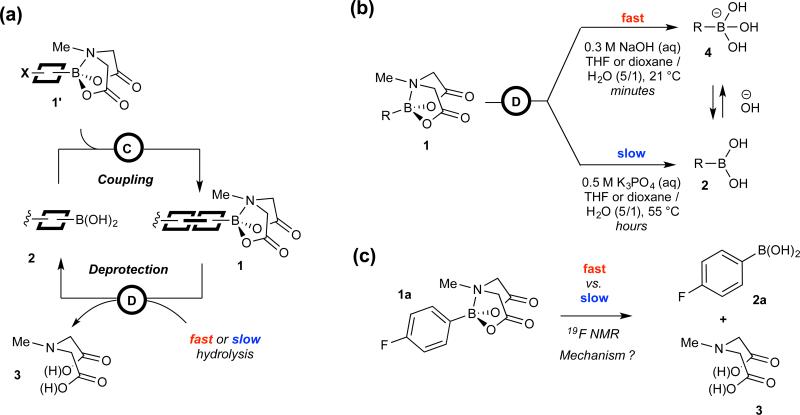
N-Methylimidodiacetic acid esters (1) of boronic acids (2) (“MIDA boronates”) have emerged as an increasingly general and automated platform for building-block-based small molecule synthesis,¹ Figure 1a. One of the most important and yet poorly understood features that enable such utility is distinct rates of hydrolysis for MIDA boronates under various basic conditions.^2,3 When ethereal solutions of MIDA boronates are treated with aqueous NaOH, they are hydrolysed within minutes at room temperature,² whereas with aqueous K₃PO₄, slow hydrolysis takes several hours at elevated temperatures,³ Figure 1b. When performing cross-couplings of boronic acids (2) in the presence of anhydrous K₃PO₄, MIDA boronates (1) undergo little or no hydrolysis, even though small amounts of water are presumably formed via boronic acid oligomerisation.²

Figure 1. Hydrolytic Deprotection and Coupling of MIDA boronates.

(a) Iterative coupling platform for small molecule synthesis from MIDA boronate (1) building blocks. Current limitations include suboptimal generality and/or fine tuning of hydrolysis rates during deprotections, and undesired hydrolysis during building block syntheses and selective cross-coupling; these all stand to benefit from better understanding of the mechanism(s) of MIDA boronate hydrolysis; (b) Deprotection of MIDA boronates 1 under ‘fast’ and ‘slow’ conditions, k_REL ≥ 3 × 10³ at 21 °C in homogeneous THF / H₂O; (c) Fluorinated substrate (1a) selected for mechanistic investigation, including kinetics, pH profile, homo/heterogeneity, Hammet ρ, ΔS^‡, site of cleavage (¹⁸O), water activity, ²H, ¹¹B, ¹³C, and ¹⁵N KIES, and DFT (M06-2X/6-31G* & M06L/6-311++G**)

In contrast to other boronates,⁴ MIDA hydrolysis rates are remarkably insensitive to the structure of the organic fragment,^2,3 and this generality has enabled these dramatic rate differences to be harnessed to great effect. The lack of hydrolysis under conditions that promote cross-coupling, combined with fast hydrolysis by NaOH, collectively enable iterative synthesis of small molecules from a wide range of halo-MIDA boronate building blocks in a manner analogous to iterative peptide coupling.^2,5 Harnessing this approach, many different types of natural products (including highly complex macrocyclic and polycyclic structures), biological probes, pharmaceuticals, and materials components have now been prepared using just one reaction iteratively.¹ A machine has also been created that can execute such building-block-based small molecule construction in a fully automated fashion.⁶ With suitably active catalysts, slow hydrolysis of MIDA boronates can release boronic acids at a rate that avoids their accumulation during cross-coupling. Using this approach, substantial improvements in yields have been achieved using MIDA boronates as stable surrogates for unstable boronic acids,³ including the notoriously unstable but very important 2-pyridyl systems.⁷ Careful modulation of the extent of base hydration can also be used to control hydrolysis and thus speciation in mixtures of boron reagents, allowing selective cross-coupling followed by MIDA redistribution.⁸ Collectively, these findings have provided substantial momentum towards a general and automated approach for small molecule synthesis.

Understanding the mechanism(s) by which these distinct rates of hydrolysis occur is critical, however, for addressing three areas of current limitations of this platform (Figure 1a) and thereby maximising its generality and impact. First, MIDA boronates can undergo undesired hydrolysis during selective cross-couplings. For example, iterative cross-couplings with more challenging Csp² centers that are performed at higher temperatures and/or longer reaction times can be accompanied by undesired MIDA hydrolysis and thus suboptimal yields. Generalised iterative couplings with sp³ hybridised carbon and heteroatoms would be highly enabling,^9,10 but such reactions can require even more forcing conditions, causing extensive MIDA hydrolysis. Transitioning this iterative cross-coupling platform to a flow chemistry format would open up many additional opportunities, and boronates that are unreactive under aqueous basic cross-coupling conditions would substantially facilitate this transition. Second, MIDA boronates can undergo undesired hydrolysis during building block synthesis. For example, executing iterative cross-coupling-based syntheses requires access to complex boron-containing building blocks, and doing so from simpler MIDA boronate starting materials plays an important role in this process.¹¹ However, such transformations can be hindered by competitive hydrolysis during various reactions, work-ups, and/or purifications. MIDA boronate hydrolysis under various mixed-phase HPLC conditions can also hinder analysis. Third, MIDA boronates sometimes demonstrate suboptimal generality and/or capacity for fine-tuning of their hydrolysis rates during deprotections. For example, we have noted that when performing deprotections using aqueous-ethereal NaOH some MIDA boronates initially hydrolyse rapidly and then relatively slowly, requiring extended reaction times for complete hydrolysis. Eliminating such effects would substantially enable efforts towards faster and more generalised automation. There are also cases where finely tuned increases or decreases in boronate hydrolysis rates would enable the slow-release cross-coupling strategy to be more effective and/or boron-selective deprotections of polyboronated inermediates to be achieved. For all of these reasons, we set out to understand the mechanism(s) by which MIDA boronates hydrolyse, both fast and slow.

Results

Distinction of limiting mechanisms for ‘fast’ and ‘slow’ release

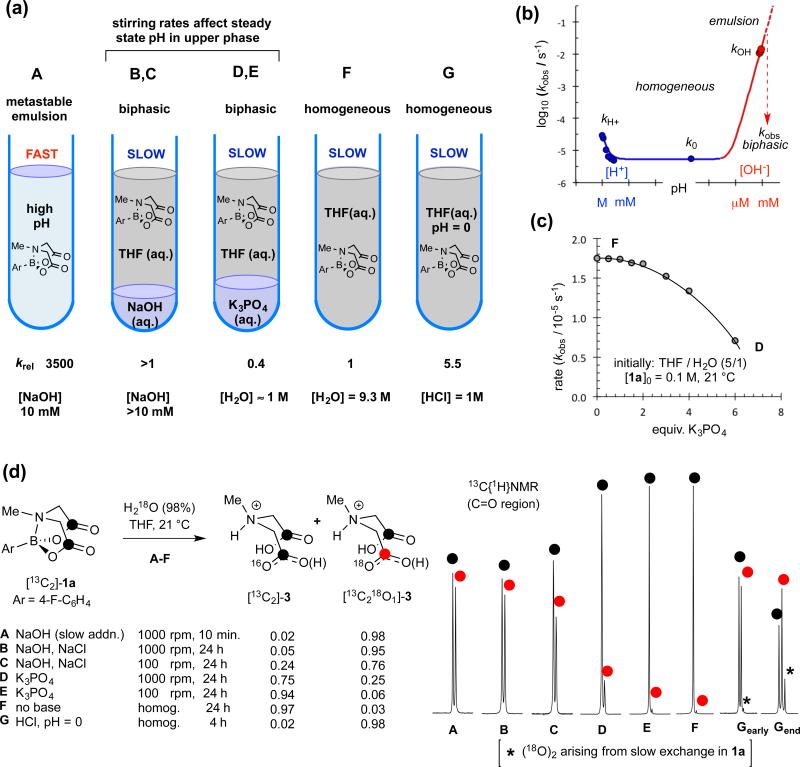
After preliminary tests with alkyl and aryl MIDA boronates, we focussed on 1a (Figure 1c) using in situ ¹⁹F NMR (Nuclear Magnetic Resonance) to analyse a range of conditions (A to G, Figure 2a). We began by study of ‘fast release’² (conditions A), where a key aspect is the heterogeneity of the medium: addition of aq. NaOH to a vigorously agitated solution of 1a in THF (tetrahydrofuran) generates a metastable emulsion. If addition rates are too fast, phase-separation begins to occur. Full phase-separation leads to precipitous reductions in hydrolysis rates (~10⁻³; conditions B, C).

Figure 2. Distinction of limiting pathways for basic (fast, A), neutral (slow, F) and acidic (G) hydrolysis of 1a.

(a) Schematic representation of conditions A-G; (b) pH rate profile; arbitrary pH scale (autoprotolysis constant of 0.5 mol-fraction aq. THF estimated as pK_app = 20).¹² Hydrolysis of water-soluble Me-B(MIDA) in aqueous buffer (pH 1-11) confirms k_obs = k_H+[H⁺] + k₀ + k_OH[OH⁻]. (c) Impact of K₃PO₄ on hydrolysis rate under heterogeneous conditions. Line through data is an aid to the eye. (d) ¹³C{¹H}NMR Sub-spectra (178.70-178.85 ppm; Δδ_C¹⁸O/¹⁶O = 30 ppb) of MIDA ligand (3) from hydrolysis of [¹³C₂]-1a in THF/¹⁸OH₂ under conditions A to G; see Supplementary Figures 4 and 5 confirming slow ¹⁸O exchange in 1a but not in 3 under acidic conditions (G_early:25% conversion, G_end:>98 % conversion) and no exchange in 1a, and very slow ¹⁸O exchange in 3 (≤1.4%, 48 h) under neutral conditions.

The ‘slow release’ conditions,³ (aq. K₃PO₄, 7.5 equiv.) rapidly induce full phase-separation, with less than 3% hydrolysis of 1a occurring prior to this, irrespective of the stirring rate (conditions D, E). Hydrolysis of 1a proceeds in the absence of any exogenous base (conditions F) and does so faster than under ‘slow release’ conditions (D). This phenomenon arises from partial dehydration of the organic phase by the K₃PO₄ (Figure 2c).

We also tested strongly acidic conditions (pH = 0, conditions G). These induce only modest rate accelerations (about 5-fold, see Supplementary Figure 26). Three distinct hydrolytic regimes (Figure 1b) were thus identified: acid (k_H+), neutral (k₀) and basic (k_OH).

Further insight came from ¹³C{¹H} NMR analysis of the MIDA ligand liberated by hydrolysis of [¹³C₂]-1a in THF/H₂¹⁸O (9.1 M), Figure 2d. Two distinct reactivity patterns emerged: under basic or acidic homogeneous conditions (A and G), hydrolysis leads to mono ¹⁸O-incorporation, whereas under neutral conditions (F) there is no significant ¹⁸O-incorporation. For conditions B to E, intermediate between strongly basic and neutral, a quantifiable transition between the two outcomes is evident. Importantly, it can be seen that ‘slow-release’ with K₃PO₄ (conditions D, E) predominantly, but not exclusively, proceeds via neutral hydrolysis, with mixing efficiency dictating base transport rates into the upper organic phase, and in turn, the extent of ¹⁸O-incorporation (6%-25%).

In the context of MIDA boronate hydrolysis for cross-coupling,^2,3 there are thus two competing processes to consider: neutral (k₀) and basic (k_OH). Base-mediated hydrolysis is by far the fastest (>10³ fold), provided that an emulsive state is attained by vigorous agitation during dispersive slow-addition of the NaOH. These conditions result in C-O cleavage in just one of the two esters in 1a, as identified by single ¹⁸O incorporation in 3. Neutral hydrolysis solely cleaves [B-OC(O)] bonds, resulting in no ¹⁸O incorporation in 3 at all.

Rate laws for basic (k_OH) and neutral (k₀) hydrolysis

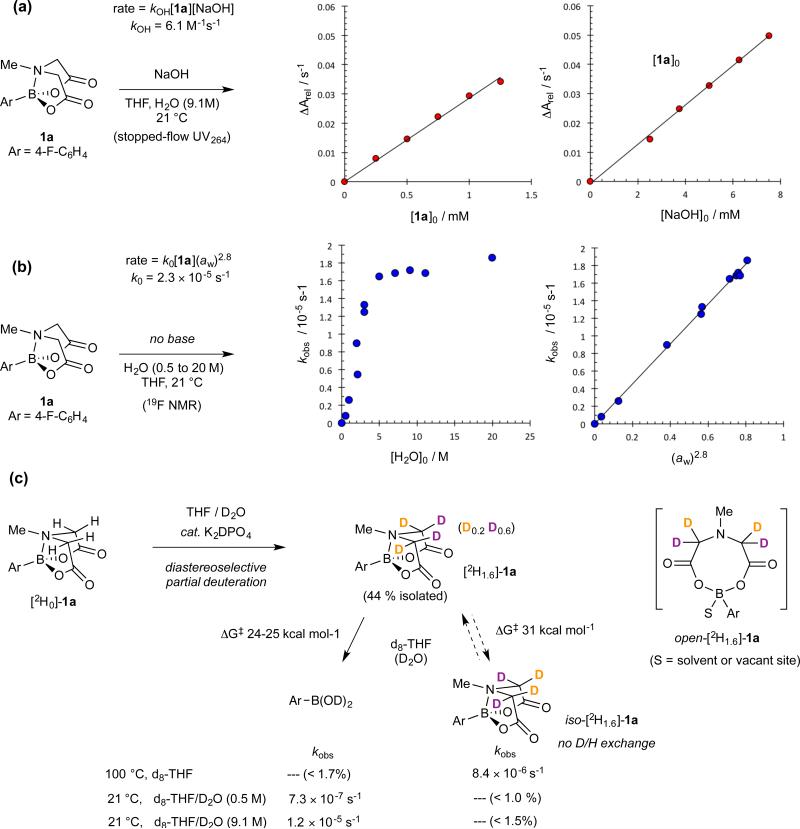
The kinetics of ‘fast-release’ (k_OH), were determined by UV at low reactant concentrations using stopped-flow techniques, Figure 3a. The data are indicative of rate-limiting attack by a single hydroxide (rate = k_OH[1a][NaOH]; k_OH = 6.1 M⁻¹ s⁻¹) with 1a being similarly reactive to a p-NO₂-benzoate ester.¹³ A linear free energy relationship for k_OH was established across a series of ArB(MIDA) substrates. In the context of attack by hydroxide, the relative insensitivity of the aromatic ring (log(k_X/k_H) = 0.5σ) weighs strongly against a pathway involving rate-limiting generation of a boronate anion. The acid catalysed pathway (Figure 2, G) is even less sensitive to aryl substitution, log(k_X/k_H) ≤ 0.01σ.

Figure 3. Kinetics of fast and slow hydrolysis of MIDA boronate 1a.

(a) Homogeneous basic conditions analysed by stopped-flow UV (ΔA₂₆₄ / s⁻¹). Oxidation¹⁶ of nascent 2a to the phenol (4-F-C₆H₄OH) is accounted for in the analysis. (b) Homogeneous neutral conditions, analysed by ¹⁹F NMR. Hydrolysis rates correlate with water activity, k₀ = k'(a_w)^2.8; k' = 2.3 × 10⁻⁵ s⁻¹, 21 °C. As hydrolysis proceeds, nascent zwitterion 3 either precipitates from solution ([H₂O] ≤ 3 M), or induces minor phase-separation. Control experiments confirmed these phenomena had negligible impact on rates. (c) Tests (negative) for “open 1a” under conditions of homogeneous neutral hydrolysis.

The kinetics of neutral hydrolysis (k₀) were measured across a wide range of water concentrations (0.5 to 20 M). Clean pseudo first-order decays in 1a (k_obs, s⁻¹) were observed in all cases, however, despite the hydrolysis being ‘slow’, determination of an overall rate law was not straightforward, Figure 3b.

Analysis of k_obs as a function of water concentration gave a profile in which there is a rate-plateau, suggestive of a change in rate-limiting step, as might occur if pre-dissociation of the B-N bond in 1a, to give a reactive “open-1a” intermediate was involved. However, this was not consistent with the entropy of activation (ΔS^‡ = −16 cal K⁻¹ mol⁻¹, 9.0 M H₂O) and tests for “open-1a”, using diastereoselectively deuterated [²H_1.6]-1a, were negative (Figure 3c). Indeed, [²H_1.6]-1a required heating to 100 °C before significant rates of interconversion with iso-[²H_1.6]-1a were detected (ΔG^‡ = 31 kcalmol⁻¹). Moreover, near-identical kinetic isotope effects, vide infra, were obtained for hydrolysis of 1a at 0.5 M and at 9.1 M H₂O, above and below the rate plateau, suggestive of mechanistic continuity. Aqueous THF forms non-ideal mixtures,¹⁴ and by inclusion of a higher-order term for the water activity (a_w)¹⁵ the kinetic dichotomy is resolved (Figure 2b). The resulting correlation (k₀ = k'a_w^2.8) suggests rate-limiting attack of 1a by water clusters (H₂O)_n, with average n = 2.8. The linear free energy relationship for neutral hydrolysis (log(k_X/k_H) = 0.8σ; 9.1 M H₂O) indicates moderate charge accumulation at the aromatic ring, as for example in a partially-developed boronate anion.

Kinetic Isotope Effects (KIEs)

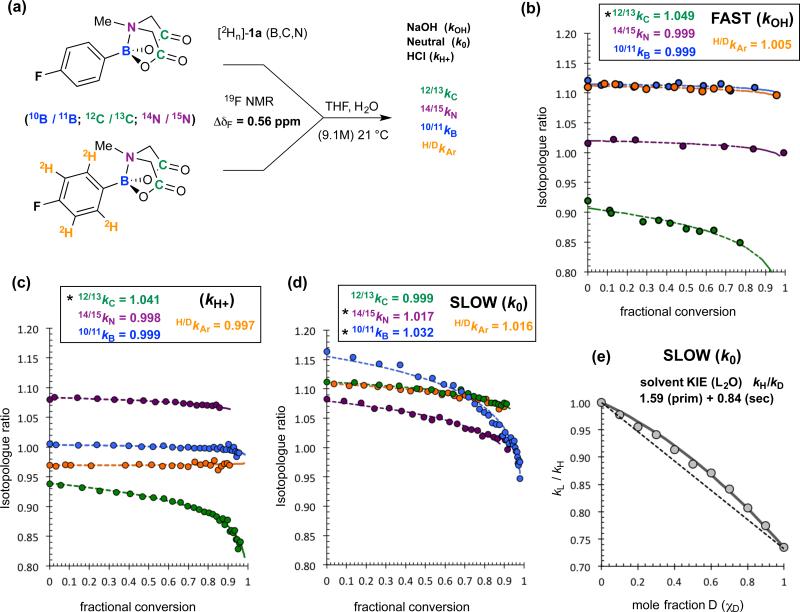
Further information on the sites of attack of 1a (at C versus at B) during the rate-limiting events (k_OH, k₀, k_H+) was deduced from KIEs. Heavy-atom KIEs were determined by double-labelling, analysing [¹H₄] / [²H₄] ratios in [aryl-²H_n(B,C,N)]-1a mixtures (Δδ_F = 0.56 ppm) as a function of fractional conversion. First-order competitive rates (k_rel) were extracted by non-linear regression, and corrected for independently-determined ²H-KIEs, to yield ^10/11k_B, ^12/13k_c and ^14/15k_N, under basic, neutral and acidic conditions, Figure 4a-d.

Figure 4. Kinetic isotope effects (KIEs) for Ar-B(MIDA) (1a) hydrolysis.

(a) outline of methodology allowing KIE values to be extracted by a standard pseudo first-order competition model; heavy atom KIEs shown are those after correction for aryl deuteration,^17,18 net-σ_D = −6.3(±0.15) × 10⁻³, and competing processes (k_H+ + k₀). (b) Fast hydrolysis: substoichiometric aq. NaOH added to vigorously stirred solutions of 1a (10 mM) to attain a suitable span of fractional conversions. Hydrolysis post phase-separation inhibited by addition of anhydrous MgSO₄. (c) Acidic hydrolysis (1M HCl) analysed in situ. (d) Neutral hydrolysis analysed in situ. Identical KIES (Δ≤ ±0.002) were obtained with 0.5 M H₂O. (e) Proton inventory conducted with 1a in THF/L₂O (9.1 M, L = H, D). The net solvent KIE (χ_D = 1) increases from 1.4 to 2.0 as [D₂O] is decreased from 9.1 to 0.5 M.

For basic hydrolysis (k_OH), syringe-pump addition of aq. NaOH, via a submerged narrow bore needle into a vigorously stirred solution of 1a (10 mM), ensured reactions proceeded in a basic aqueous-organic emulsion, prior to phase-separation. The KIE (^12/13k_C = 1.049; Figure 4b) together with the rate-law, indicates that a carbonyl group in 1a is attacked by hydroxide in the rate-determining step, without direct involvement of either B or N. The outcome for acid-catalysed hydrolysis was analogous (^12/13k_C = 1.041, Figure 4c), indicative of rate-limiting ester hydrolysis (k_H+), albeit much less efficient (k_H+ / k_OH = 1 × 10⁻⁵).

For neutral hydrolysis (k₀), the KIEs (^10/11k_B = 1.032, ^14/15k_N = 1.017; Figure 4d) are complementary to those for the acid/base mechanisms, with no KIE detected at carbon. Proton inventory¹⁹ (Figure 4e) for neutral hydrolysis (k₀) in H₂O/D₂O/THF identified simultaneous primary (k_H/D = 1.59) and secondary (k_H/D = 0.84) KIEs; the effect of deuteration on the water activity in the neutral reaction (k₀) is expected to be negligible.²⁰ The three normal primary KIEs (k_H, k_B, k_N) indicate that an O-H bond in the attacking water cluster, (H₂O)_n, is cleaved in the rate-determining event, and that the B-N bond, not the carbonyl unit, in 1a is involved in this process. The inverse secondary k_H/D arises from changes in solvation and H-bonding of the residual (non-transferred) water proton(s).²¹

Discussion

Pathways for hydrolysis

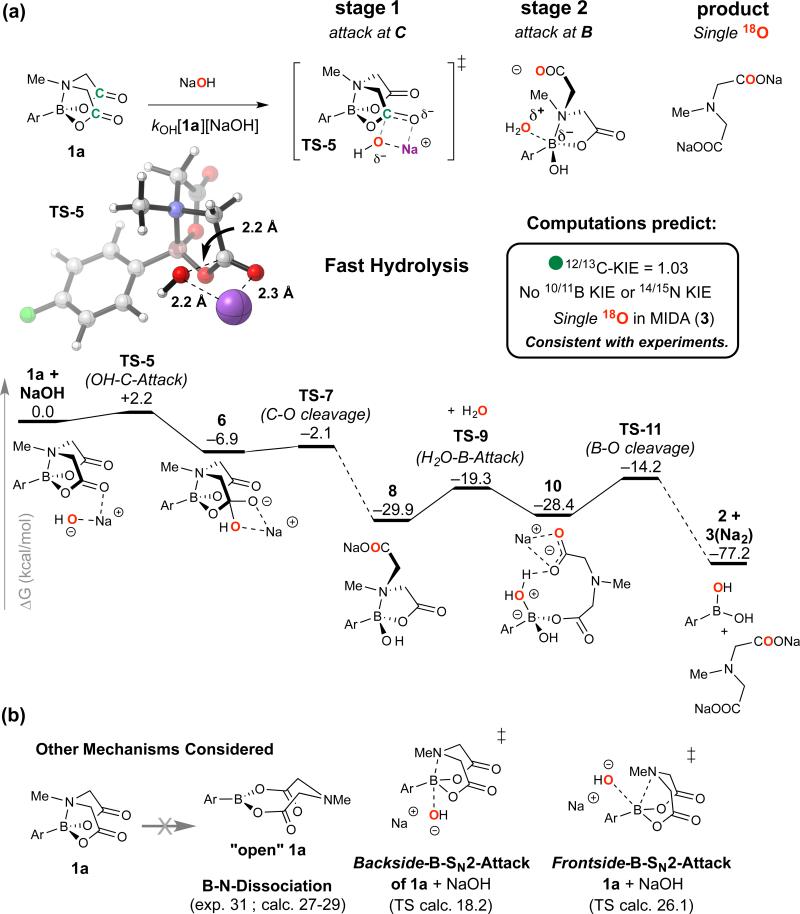
The data reported above allow a large number of mechanistic possibilities to be ruled out. The unassisted cleavage of B-N to generate “open-1a” (Figure 3c) is 6-12 kcal mol⁻¹ greater in energy than the experimentally determined hydrolysis rates (k_OH, k₀, and k_H+) thus eliminating S_N1-like pathways. Processes consistent with the rate-limiting events are attack of 1 at the carbonyl carbon by OH⁻ (k_OH) or H⁺/H₂O (k_H+), and at the B-N unit by water (k₀). The slow (k_H+) or undetected (k_OH; k₀), rates of ^16/18O-exchange in 1a are inconclusive as the oxygen atoms in the tetrahedral intermediates remain inequivalent, irrespective of proton exchange rates.²² Nonetheless, in none of the hydrolyses were intermediates detected by NMR (¹H, ¹⁹F, ¹¹B), or UV (isosbestic points) suggesting that after rate-limiting addition of (H⁺/H₂O), OH⁻, or (H₂O)_n, hydrolytic evolution to the boronic acid (2a) and MIDA ligand (3) is rapid. Substantial additional insight to the ‘fast-release’ (k_OH) and ‘slow-release’ (k₀) pathways relevant to coupling conditions^2,3 was gained by computations, using Gaussian 09²³ at the M06-2X²⁴/6-31G*²⁵/PCM²⁶(THF) level of theory. In Figures 5a and 6a we provide a summary of the key stages of the two pathways identified. Below both pathways we also outline some of the other processes considered. Full details of these pathways are provided in Supplementary Figures 33-64.

Figure 5. Fast-release Hydrolysis (k_OH).

(a) Summary key computational data for hydrolysis of 1a via C-O cleavage (TS-5). Computed minimum-energy pathway and experimental data are fully self-consistent. Nonetheless, these computed results do not resort to exhaustive, time-dependent sampling, and should thus be taken only as a model of the processes taking place in solution. (b) Other key processes considered, but eliminated on the basis of energy or kinetic isotope effects.

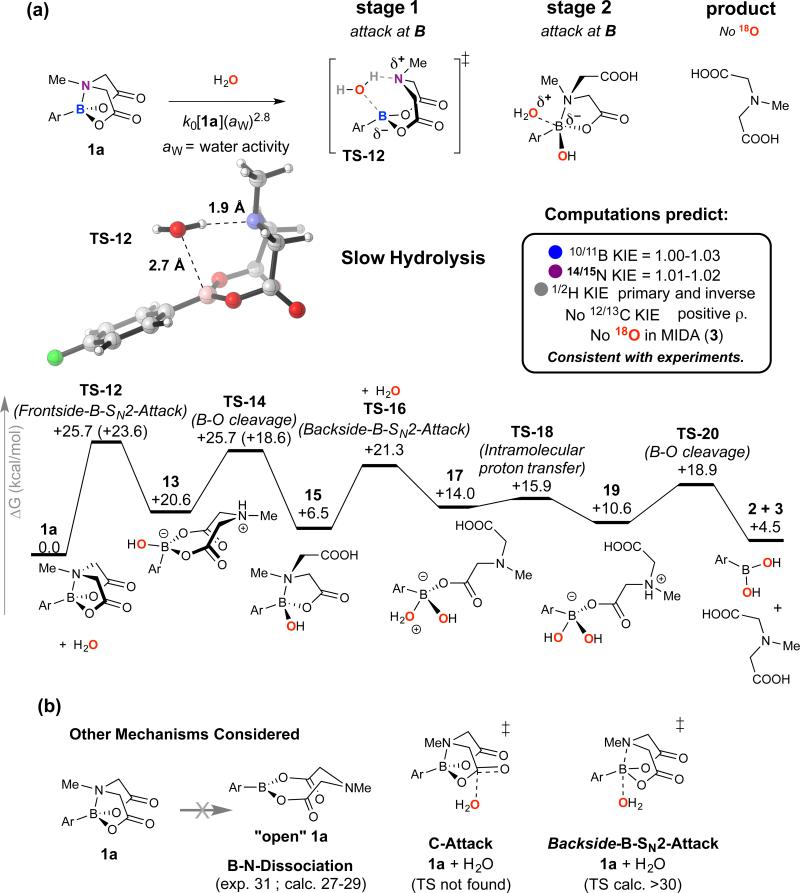
Figure 6. Slow-release Hydrolysis (k₀).

(a) Summary key computational data for hydrolysis of 1a via B-N bond cleavage (TS-12). Computed minimum-energy pathway and experimental data are fully self-consistent. Nonetheless, these computed results do not resort to exhaustive, time-dependent sampling, and should thus be taken only as a model of the processes taking place in solution. (b) Other key processes considered, but eliminated on the basis of energy or kinetic isotope effects.

In the fast-release (k_OH) pathway, the minimum energy pathway begins with the rate-limiting, irreversible, attack by hydroxide at one of the two ester carbonyls in 1a (C-Attack TS-5, ΔG^‡ = 2.2 kcal/mol, Figure 5a). Fast (ΔG^‡ ≤5 kcal/mol), highly exothermic, irreversible collapse of the now tetrahedral carbonyl carbon (TS-7) generates ring-opened intermediate 8 (ΔG = −29.9 kcal/mol).

Due to the presence of a pendent carboxylate and increased lability of the B-N bond, 8 is substantially more prone to hydrolysis than neutral 1a. Stage 2 hydrolysis proceeds via attack of 8 at the boron by water (TS-9, ΔG^‡ = 10.6 kcal/mol), leading to 10, and thus to final products (2 + 3) via B-O bond cleavage and ionization/salt formation. NaOH-mediated rate-limiting C=O attack is consistent with experiment (computed ^12/13k_C KIE 1.03), the low sensitivity to aryl substituents (ρ = 0.5), and the absence of experimentally observable ^14/15k_N or ^10/11k_B KIEs.

In the slow-release (k₀) pathway, the minimum energy pathway begins with the rate-limiting insertion of water into a stretching, but not cleaved, B-N bond (Frontside-B-S_N2-Attack,TS-12, +25.7 kcal/mol), Figure 6a. At higher water concentrations, B-N cleavage by (H₂O)_n, n = 1,2,3 has similar free energy barriers, and KIEs for these were computed with a range of levels of theory.²⁷ The best quantitative agreement was found in a late transition state using M06L/6-311++G**. As the B-O bond is formed to a great degree, with significant proton transfer to the nitrogen, there is negative charge accumulation at B (ρ 0.4 to 1.0). Stage 2 hydrolysis again involves a ring-opened intermediate (15), which via intramolecular deprotonation of boron-coordinated water (TS-18), rapidly leads to complete hydrolysis. Rate-limiting B-N cleavage by H₂O is consistent with experiment (computed KIEs ^14/15k_N 1.01, ^10/11k_B 1.03, ^1/2k_H 0.9 and 1.4) the sensitivity to aryl substituents (ρ = 0.8), and the absence of experimentally observable ^12/13k_C KIE.

We also extensively probed alternative mechanisms for fast and slow hydrolysis, at both the first- and second-stages. For stage one of fast hydrolysis (Figure 5b), B-N bond cleavage by backside-B-S_N2 or frontside-B-S_N2 attack of hydroxide is disfavoured over TS-5 by ≥16 kcal/mol. The barrier for attack of 8 by hydroxide in stage two, at carbon or at boron (the latter being slightly favoured ΔΔG^‡ 2.2 kcal mol⁻¹), is also prohibitively high. The kinetics, KIEs, and ¹⁸O incorporations, indicate that a similar overall pathway (attack of a C=OH⁺ intermediate by H₂O, then attack at B) operates under acid catalysis (k_H+). Slow hydrolysis (k₀) proceeds without exogenous acid or base, and no transition state for H₂O attack at carbon (C-Attack, Figure 6b) could be located. Nonetheless, simple esters do slowly hydrolyse in pure water (ΔG^‡ = 21-28 kcal/mol),²⁸ a process for which water chains,^28,29 and water autoionisation mechanisms (ΔG^‡ = 23.8 kcal/mol)³⁰ have been proposed. Thus, irrespective of whether hydrolytic cleavage (k₀) of B-N in 1a (ΔG^‡ = 23.6 kcal/mol) involves transient water autoionisation, or concerted transfer (as in TS-12), appropriate dynamic fluctuations of water chains³¹ will be required to facilitate it.

An alternative mechanism for stage one slow-hydrolysis involves Backside-B-S_N2-Attack (Figure 6b) leading to a weakly bound complex, from which water-deprotonation by carboxylate cleaves the B-O bond. This is computed to have a higher energy barrier than Fronstide-B-S_N2-Attack (TS-12) and to result in a large primary KIE (^1/2k_H ≈ 3.8), inconsistent with experiment (Figure 4e and Supplementary Table 26). Overall, the differing rates and sites of first stage attack (OH⁻ at C in TS-5, versus H₂O at B-N in TS-12) can be rationalised by: i) hydroxide being much more nucleophilic than water (k_OH[OH] >> k₀[H₂O]ⁿ); ii) the anionic charge from attacking hydroxide being delivered to an electrophilic site (C=O); and iii) that B-N in 1 can simultaneously function as a Bronsted base and Lewis acid to provide a ‘receptor’ for activating water. After the stage one rate-limiting processes (k_OH, k₀ and k_H+), all pathways converge at stage two, albeit with different net charges, with flexible ring-opened intermediates (e.g. 8 and 15) providing intramolecular assistance to hydrolysis at boron.

MIDA boronate hydrolysis under conditions of application

We have identified two general mechanisms (ester versus B-N cleavage) for hydrolysis of 1a operating under basic, neutral and acidic conditions. Of these, k_OH is by far the most efficient, becoming the major pathway when [NaOH] ≥ 3 μM. At concentrations used for synthesis, the conditions for ‘fast’ and ‘slow’ release, Figure 1, result in separation into aqueous and organic phases. Maintaining high rates of fast release (k_OH) is assisted by generation of a transient emulsion, usually attained by vigorous agitation during slow dispersive addition of aq. NaOH. In the fully phase-separated medium, boronate (1a) undergoes slow hydrolysis in the bulk organic-aqueous upper phase, the rate being mildly dependent on stirring and mass-transfer rates between phases, and the activity of the water (a_w) in the bulk organic phase. This detailed mechanistic understanding of the rate-limiting events for both hydrolysis pathways, and the physicochemical factors that govern their partitioning, enable rationalisation of many of the phenomenological observations previously recorded with the MIDA platform.

The more than three orders of magnitude difference in rate attainable for fast versus slow hydrolysis results from the distinct mechanisms underlying these processes. The remarkable insensitivity of these rates to the structure of the appended organic fragment is consistent with minimal charge build-up at the boron center during attack at the carbonyl during fast release and the presence of a common intramolecular base for facilitating insertion of water into the N-B bond during slow-release. The stability of MIDA boronates in anhydrous solvents in the presence of inorganic bases, essential for iterative coupling, is consistent with the requirement for substantial water in the organic phase in order to promote neutral hydrolysis. MIDA boronates bearing exceptionally lipophilic organic fragments induce accelerated phase-separation when treated with NaOH, resulting in resulting in more rapid switching to neutral hydrolysis and thus significantly extended reaction times for their complete hydrolysis. The slow-release cross-coupling of boronic acids proceeds via MIDA boronate hydrolysis in the upper aqueous-organic phase, while the inorganic base remains in the lower aqueous phase. The rates of hydrolysis under these slow-release conditions are highly reliable because the activity of water in THF,¹⁵ and in dioxane,³² is approximately constant (a_w ≈ 0.8–1.0) above concentrations of 3.0 M. The stability of MIDA boronates to many acidic conditions is consistent with their substantially slower rates of hydrolysis observed at low versus high pH.

This advanced mechanistic understanding also stands to practically enable more effective and widespread utilisation of MIDA boronates in synthesis. For example, simply increasing the dielectric constant of aqueous phases during reaction work-ups should help avoid undesired hydrolysis of MIDA boronates in organic phases and thereby enable more effective iterative cross-coupling as well as building block syntheses. Using more organic soluble hydroxide salts should help further generalize the rates of MIDA boronate deprotections via fast hydrolysis, even for highly lipophilic MIDA boronate intermediates. The rates of “slow-release” of unstable boronic acids from their MIDA boronate counterparts³ can now be rationally tuned by simply varying the conditions to increase or decrease the contribution of basic vs. neutral hydrolysis mechanisms. Using buffered HPLC (high performance liquid chromatography) eluents should maximise MIDA boronate stability during analysis and purifications. This same understanding forms the basis for rational design of new MIDA boronate analogues where both modes of hydrolysis are deliberately retarded or accelerated by modifications to the iminodiacetic acid backbone. Such ligands stand to broadly enable advanced applications of organoboron compounds in synthesis, including expanding the range of reaction conditions compatible with complex building block construction and iterative assembly, opening new opportunities for selective boron deprotections and even one-pot pre-programmed iterative synthesis, and faciltating a transition in automation platforms from batch to flow chemistry. Such efforts can also now be guided by quantitatively tracking the relative contributions of the mechanisms of hydrolysis (k_OH / k₀) simply by determining the ¹⁸O-incorporation in the cleaved ligands (3) when conducting reactions in labelled water. Collectively, these advances stand to powerfully assist in the development of a more general and automated approach for small molecule synthesis.

Methods

General

DFT calculations of full reaction profiles for MIDA boronate solvolysis in basic and neutral aqueous THF were conducted at the M06-2X/6-31G* level of theory with solvation using a polarized continuum model (PCM) for THF. The level of theory that provided best quantitative agreement between predicted and observed kinetic isotope effects for k₀ was M06L/6-311+G** with solvation in both THF and water computed as a single point using the default PCM settings in Gaussian09²³ combined with the same level of theory. The MIDA boronates were prepared from the corresponding labelled boronic acids (2a, ²H₄-2a, ¹⁰B-2a, ¹¹B-2a) and N-methyliminodiacetic acids (3, ¹⁵N-3, ¹³C₂-3) using standard procedures,² and purified via silica-gel column chromatography (Et₂O/MeCN 4:1) then recrystallisation (MeCN-Et₂O).

Kinetics of MIDA Boronate Solvolysis in Basic Organic Emulsion (Fast Release)

A stopped-flow system (TgK Scientific) was employed to deliver solutions of the isolated reactants (1a, 0.5 to 2.5 mM and NaOH, 2.5-7.5 mM) in aqueous THF ([H₂O] = 9.1 M) in 1 : 1 volume ratio, via thermostatted reagent lines, into a fused-silica UV-vis cuvette (pathlength 10 mm) with integral pre-mixer (dead-time < 8 msec). Spectra were collected at 10 msec intervals on an Ocean Optics USB4000 detector and data processed (Kinetic Studio; TgK Scientific) to afford the rate of change in absorbance (A) at 264 nm. To determine heavy atom KIEs, samples of [aryl-²H_n]-1a, as an approximately 1: 1 mixture of n = 0 and n = 4, with isotopically labelled MIDA boronate moieties (¹⁰B/¹¹B/¹³C₂/¹⁵N), in one or other sample, were dissolved in 50 mL THF to give a total concentration of 10 mM. 4,4'-bis-(CF₃)-biphenyl was added as an internal standard. Aliquots (5 mL) were then transferred to round-bottom flasks, and vigorously stirred (> 1000 rpm) as 1 mL of an aqueous solution of NaOH was added via syringe pump, through a narrow-bore needle, over 5 minutes. A series of NaOH concentrations (1-30 mM) were delivered to the sequence of aliquots to attain a suitable range of fractional conversions under metastable locally emulsified conditions. Immediately after addition of the requisite volume of NaOH solution, the reactions were chilled in ice, and sufficient anhydrous MgSO₄ added to inhibit further hydrolysis (both k_OH and k₀). The solutions were concentrated (40 °C, 150 mBar) to approximately 0.5 mL and the isotope ratio and conversion analysed by ¹⁹F NMR.

Kinetics of Solvolysis of MIDA Boronate 1a in the Absence of Exogenous Base (Slow Release)

Reactions were conducted in 5 mm NMR tubes kept at constant temperature (± 0.5 °C) in a thermostatted environment. A 0.6-x mL aliquot of a stock solution of MIDA boronate 1a in THF containing 4-CF₃-bromobenzene as internal standard, followed by x mL of aqueous THF, were added to the tube to establish final concentrations of 0.1 M 1a and 9.1 M H₂O. The sample was vigorously mixed, a sealed glass capillary containing DMSO-d₆ added, the NMR tube sealed (J-Young valve) and then inserted into the NMR spectrometer (Bruker Advance; 376.3 MHz ¹⁹F). After the spectrometer had been ²H-frequency-locked to the DMSO-d₆, a series of ¹⁹F NMR spectra were recorded. The spectra were processed, as a block, and the integration of the ¹⁹F NMR signals (inter-FID delays > 5 T₁) for the internal standard, 1a and 2a used to calculate concentrations. The pseudo-first order rate constant (k_obs) was obtained from plots of ln([1a]₀/[1a]_t) = k_obs·t; correlations were generally excellent (r² typically ≥ 0.99). Reactions were conducted across a wide range of other initial water concentrations (0.5 to 20.0 M), and with mixtures of H₂O/D₂O; [L₂O] = 9.1 M. The same procedure was employed to determine heavy atom KIEs, except that [aryl-²H_n]-1a, as an approximately 1: 1 mixture of n = 0 and n = 4; with isotopically labelled MIDA boronate moieties (¹⁰B/¹¹B/¹³C₂/¹⁵N), in one or other sample, were employed.