Abstract
Vision typically has better spatial accuracy and precision than audition, and as a result often captures auditory spatial perception when visual and auditory cues are presented together. One determinant of visual capture is the amount of spatial disparity between auditory and visual cues: when disparity is small visual capture is likely to occur, and when disparity is large visual capture is unlikely. Previous experiments have used two methods to probe how visual capture varies with spatial disparity. First, congruence judgment assesses perceived unity between cues by having subjects report whether or not auditory and visual targets came from the same location. Second, auditory localization assesses the graded influence of vision on auditory spatial perception by having subjects point to the remembered location of an auditory target presented with a visual target. Previous research has shown that when both tasks are performed concurrently they produce similar measures of visual capture, but this may not hold when tasks are performed independently. Here, subjects alternated between tasks independently across three sessions. A Bayesian inference model of visual capture was used to estimate perceptual parameters for each session, which were compared across tasks. Results demonstrated that the range of audio-visual disparities over which visual capture was likely to occur were narrower in auditory localization than in congruence judgment, which the model indicates was caused by subjects adjusting their prior expectation that targets originated from the same location in a task-dependent manner.
Keywords: Audio-Visual Integration, Visual Capture, Auditory Localization, Bayesian Inference
1 Introduction
Many real-world objects produce both auditory and visual cues, which we integrate to estimate object location. This integration can occur even when there is spatial disparity between auditory and visual cues, which leads to an auditory location bias generally referred to as the “ventriloquism effect” (Howard and Templeton, 1966; Jack and Thurlow, 1973; Thurlow and Jack, 1973). Movie theaters provide an everyday example of this phenomenon, because the screen and speakers are typically located in different locations, but the corresponding visual and auditory signals are both perceived as originating from the screen. This mislocalization of auditory signal location can be framed as vision capturing auditory perception, which arises because vision typically has much better spatial precision and accuracy than audition (however, when visual precision is degraded vision can be in turn influenced by audition, as in Alais and Burr (2004)). The probability of visual capture occurring depends on a number of factors, including spatial disparity, temporal disparity, and semantic congruence between auditory and visual targets (Jack and Thurlow, 1973; Slutsky and Recanzone, 2001; Thurlow and Jack, 1973; Warren et al., 1981). Here, we focus on how spatial disparities influence visual capture, with a specific interest in the decrease in visual capture that occurs with increasing disparity.
In the laboratory, the effect of spatial disparity on visual capture is typically probed by presenting concurrent auditory and visual targets over a range of spatial disparities (including no disparity, i.e. spatial congruence), and asking subjects to report perceived attributes of these targets. Previous experiments have focused on having subjects judge whether or not the targets were congruent (i.e. if they originated from a common source) (Godfrey et al., 2003; Lewald and Guski, 2003; Slutsky and Recanzone, 2001; Thurlow and Jack, 1973), localize the perceived location of the auditory and/or visual targets (Warren et al., 1981; Wozny et al., 2010), or both judge congruence and localize the auditory target sequentially (Bertelson and Radeau, 1981; Hairston et al., 2003; Wallace et al., 2004). In the congruence judgment task, visual capture manifests as explicit reports that auditory and visual targets originated from a common source despite a spatial disparity between targets (also known as “binding”). In the auditory localization task, visual capture produces a bias in perceived auditory target location toward the spatially disparate visual target (also known as “cross-modal bias”). Typically, reports that auditory and visual targets originated from a common source are accompanied by auditory bias toward the visual target when both tasks are performed sequentially (Wallace et al., 2004). However, auditory bias has been demonstrated to occur even when subjects report that targets did not originate from a common source (Bertelson and Radeau, 1981), which provides some evidence that these measures, while related, may be distinct phenomena. Previously, Hairston et al. (2003) compared responses when subjects simultaneously performed judgment and localization with responses when subjects performed either task alone, although no direct comparison was made between the tasks when performed independently and only a limited set of auditory target locations was used. Here, our goal is to explicitly compare judgment and pointing when performed independently, which we address by determining whether or not these tasks produce equivalent measures of visual capture as a function of spatial disparity.
To assess the relationship between judgment and pointing tasks, subjects performed each task independently across three separate sessions. For the first session, subjects were randomly assigned to perform either congruence judgment or auditory localization of audio-visual target pairs. For the second session subjects switched tasks, and for the third session they switched back to the same task as in the first session. This allowed us to dissociate any experience-dependent changes from differences in performance across tasks. A Bayesian inference model was fit to data from each session and fit parameters were compared across sessions for each subject, to quantify performance differences across tasks.
2 Materials and Methods
Subjects performed three sessions of audio-visual spatial perception tasks. Each session started with unimodal auditory and visual localization, followed by either congruence judgment or auditory localization of bimodal targets. Subjects performed either congruence judgment or auditory localization in sessions 1 and 3 (counterbalanced across subjects), and the other task in session 2. This allowed us to dissociate experience and task-dependent differences.
2.1 Subjects
Eight volunteers (5 female, 3 male; age 19-26) recruited from the Rochester community participated in this experiment. All subjects were screened with routine clinical examinations to ensure they had normal hearing and normal or corrected-to-normal vision.
Experiment protocols were approved by the Institutional Review Board at the University of Rochester and were performed in accordance with the 1964 Declaration of Helsinki. All subjects gave informed consent and were compensated at a rate of $10 per hour for their participation.
2.2 Apparatus
Experiments were conducted in a dark, sound-attenuated chamber designed for the presentation of auditory and visual targets from a range of locations in space (for additional detail, see Zwiers et al. (2003)). Subjects were seated 2 meters from a speaker on a mobile robotic arm, which was hidden from sight by an acoustically transparent speaker cloth. Visual targets were presented by projecting a laser onto the speaker cloth, and could be positioned by adjusting the orientation of an electronic mirror system.
Subjects were head-fixed via bite bar, which was oriented such that, for each subject, Reid's baseline was horizontal and the subject's cyclopean eye (midway between the eyes) was pointed at the origin of the room. Eye movements were monitored continuously via electrooculogram, in order to detect any breaks of fixation between trials and during target presentation.
Subjects manipulated a cylindrical joystick to perform congruence judgment and localization tasks, then pressed a button to enter their response. For congruence judgment, subjects pitched the joystick up or down to indicate response. For target localization, a LED pointer attached to the joystick was illuminated, and subjects pointed the LED to the perceived target location on the speaker cloth.
Continuous signals and event times were sampled at a rate of 1 kHz by a realtime Lab VIEW system (National Instruments, Austin, TX). Data analysis was performed in R (www.r-project.org) and Matlab (MathWorks Inc., Natick, MA).
2.3 Stimuli
Auditory targets were 50 ms broadband noise bursts (0.2-20 kHz, 65 dB SPL, 1 ms cos2 on/off ramps, equalized to have a flat spectrum). Between trials, noise (Gaussian white noise at 65dB SPL) was presented from two speakers outside of the range of targets used in the experiment (±75° horizontal, +20° vertical behind screen) in order to mask robotic arm movement sound. All auditory stimuli were generated by a TDT RX8 Multi I/O Processor (Tucker-Davis Technologies, Alachua, FL).
Visual targets were 50 ms green laser points projected onto the speaker cloth. Between trials, a red center fixation laser was projected at 0°, to provide a visual fixation reference point. Both the visual target and fixation laser had a diameter of 0.1°.
2.4 Experimental Procedure
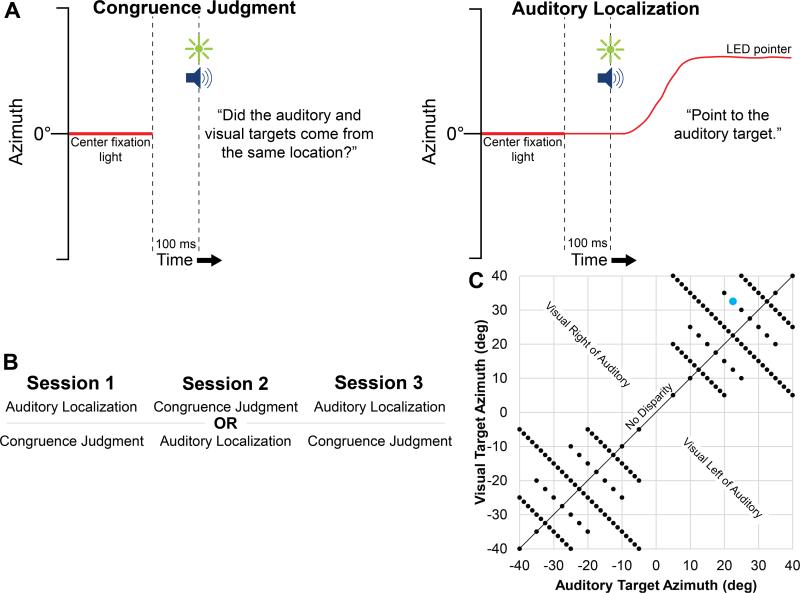
Each subject performed three experimental sessions. Each session started with 108 unimodal auditory and visual localization trials (54 in each modality), followed by 146 trials of either congruence judgment or auditory localization of bimodal targets (Figure 1 A), for a total of 254 trials per session. Subjects performed either congruence judgment or auditory localization in sessions 1 and 3 (counterbalanced across subjects), and the other task in session 2 (Figure 1B).
Fig. 1.
Experimental protocol. A, Trial timeline for both tasks. Between trials, subjects look at the center fixation light and maintain fixation until after target presentation. At the start of a trial, the center fixation light was extinguished, and 100 ms later an auditory and a visual target were presented from independent locations, in order to produce a disparity in azimuth between them. After target presentation, subjects were instructed to either indicate whether or not the targets came from the same location (Congruence Judgment) or point a LED pointer to the auditory target (Auditory Localization). B, Task sequence across experimental sessions. Subjects were randomly assigned to perform either the auditory localization or congruence judgment task in sessions 1 and 3, and the other task in session 2. C, Target array for both tasks. Auditory and visual target pairs were distributed in azimuth as shown, with each dot representing one pair of auditory and visual target locations. Location pairs were selected from the array in a pseudorandom order, and presented once each. Audio-visual disparity ranged from 0° (i.e. no disparity, black line) to 35° (visual target at ±5° and auditory target at ±40°, or vice versa) in azimuth. The highlighted point indicates the example target locations in panel A.
2.4.1 Unimodal Auditory and Visual Localization
In each unimodal localization trial, a single visual or auditory target was presented. Following target presentation, subjects were instructed to look at the remembered target location, orient the LED pointer to that location, and press the button. Targets ranged from −40° to −5° and 5° to 40° azimuth in 2° increments. Targets at ±10°, ±20°, ±30°, and ±40° were presented three times to provide more data for estimating accuracy and uncertainty as a function of target azimuth, while targets were presented once at all other azimuths. All targets were constrained to 0° elevation. Between trials, subjects fixated on a center light (0° azimuth, 0° elevation) and aimed the LED pointer at it. The center light was extinguished 100 ms before target presentation. Targets within ±5° of the center light were excluded from the target array, to minimize the possibility that responses would be biased by the remembered center light.
2.4.2 Congruence Judgment Task
In each congruence judgment trial, an auditory and a visual target were presented synchronously from the set of locations in Figure 1C. Following target presentation, subjects were instructed to indicate whether the auditory and visual targets came from the same location or two separate locations. Subjects were instructed to pitch the pointer (without the light on) up to indicate “same location” or down to indicate “two different locations”, then press the button. Note that the specific phrasing of the task requirements can alter performance (Lewald and Guski, 2003), so we might expect performance to differ if subjects were instead told to indicate if targets came from a “common source”. We chose to have our instructions focus specifically on the spatial aspects of this task because the auditory localization task also focuses solely on spatial location, and to facilitate comparison with previous studies which have used similar phrasing (Hairston et al., 2003; Wallace et al., 2004). Subjects were told that “sometimes the targets will originate from the same location, and sometimes they will not”. This wording was specifically chosen in order to discourage subjects from always giving one type of response without explicitly establishing an expectation of how often the targets would originate from the same location. Targets were distributed as shown in Figure 1C, with auditory and visual targets ranging between −40° to −5° and 5° to 40° azimuth. Targets were always constrained to the same hemifield in order to avoid any potential confounding influence of the recently extinguished center fixation light. Spatial audio-visual disparity varied across trials, from a minimum disparity of 0° (same location) and maximum disparity of 35°. Each pair of locations was presented once. Target sequence was fixed for each session and for all subjects regardless of task, but was random across sessions. Subjects fixated on the center light between trials.
2.4.3 Auditory Localization Task
As in the congruence judgment task, each auditory localization trial started with presentation of synchronous auditory and visual targets from the set of locations in Figure 1C. Following target presentation, subjects were instructed to look at and orient the LED pointer to the remembered auditory target location, then press the button. As in the congruence judgment task, subjects were told that sometimes the targets would originate from the same location, and sometimes they would not. Subjects fixated on and aimed the LED pointer at the center light between trials.
2.5 Bayesian Inference Modeling
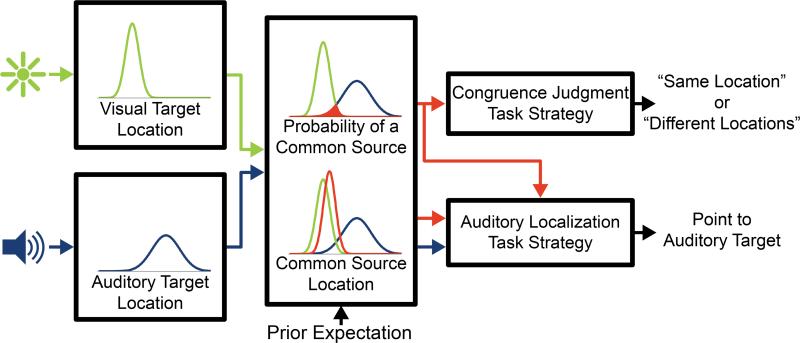
The different forms of response in the congruence judgment and auditory localization tasks preclude direct comparison of data across experiment sessions. However, if we assume that the processes that perform spatial perception remain the same regardless of task, we can make inferences about the percepts that lead to a given subject's responses. Specifically, we assume that the computations underlying auditory and visual cue encoding and common source estimation are constant, with only task strategy changing across tasks, as shown in Figure 2.
Fig. 2.
Audio-visual spatial integration model. Auditory and visual target locations are encoded by their respective sensory pathways, in accordance with each pathway's accuracy and precision. Encoded locations are combined with prior expectation to compute the common source location (weighted sum of encoded target locations), and the probability that the targets originated from a common source. At this point the model diverges based on task, with the auditory localization task dependent on common source location and probability, and the congruence judgment task dependent on common source probability alone. This model allows us to directly compare performance across tasks by estimating model parameters that are decoupled from task.
We used a Bayesian inference model of audio-visual spatial integration (Körding et al., 2007; Sato et al., 2007; Wozny and Shams, 2011; Wozny et al., 2010) to compare performance across congruence judgment and auditory localization tasks. The majority of the approach used here has been described previously (Körding et al., 2007; Wozny and Shams, 2011; Wozny et al., 2010), so we will summarize the model and highlight differences here. The full set of model equations are available in the appendix.
The model starts with the encoding of perceived location (auditory and visual target location in Figure 2), denoted XA and XV for auditory and visual percepts, of auditory and visual targets with physical locations SA and SV. Sensory encoding is inherently uncertain and subject to biases, so it is best represented as conditional probability distributions, p(XV|SV) and p(XA|SA) (Wozny and Shams, 2011). Previous research has demonstrated that perceived target locations tend to be normally distributed, although they are subject to idiosyncratic offsets, a tendency to overshoot auditory target azimuth, a tendancy to undershoot visual target azimuth, and reliability that decreases with distance from midline (Dobreva et al., 2011, 2012; Odegaard et al., 2015; Razavi et al., 2007). To model these aspects of perception, we assume normal distributions with means that are scaled and offset with respect to target location. The scaling parameters (i.e. spatial gain) are denoted GV and GA, which can model a pattern of overshooting (G > 1) or undershooting (G < 1) target azimuth. Constant offsets in target location are denoted μV and μA. Recent studies have modeled localization inaccuarcies by applying a corrective factor for each target location (Odegaard et al., 2015, 2016), although the relatively large number of target locations used here precludes a similar approach. Localization uncertainty (inverse reliability) is represented by σV and σA. This model also includes parameters that model increase in uncertainty as a function of distance from midline, given as GσV, and GσA. Note that linear scaling of uncertainty ignores the strong increase in visual precision at the fovea (Dobreva et al., 2012), but the target range is limited to avoid presenting targets near the fovea. Putting these terms together in a normal distribution gives the equations:
| (1) |
| (2) |
The next step in the model is to use the perceived target locations to calculate the probability that the targets originated from a common source (denoted p(C = 1|XV, XA)), as represented by the Probability of a Common Source block in Figure 2. This computation was identical to previous papers (Körding et al., 2007; Wozny and Shams, 2011), in which Bayes’ Rule is used to express p(C = 1|XV, XA) as a function of perceived target location, prior expectation of a common source (i.e. bias for or against integration, denoted pcommon) and prior expectation of target distribution (modeled as a normal distribution and denoted ). Prior expectation terms are typically stable over time and are independent of the trial-by-trial calculation of common source probability (Beierholm et al., 2009), but experimental conditions designed to heavily skew responses toward integration or segregation can cause changes in prior terms (Van Wanrooij et al., 2010). Because the target array used here was designed to equally elicit both integration and segregation responses, we assume that prior terms are invariant within an experimental session.
Additionally, the auditory localization task requires calculating the estimated auditory target location when the auditory and visual targets originated from a common source (denoted ŜA,C=1) or from two different sources (denoted ŜA,C=2), as represented by the Common Source Location block in Figure 2. Estimated auditory target location (ŜA) is the weighted sum of perceived auditory target location (XA), perceived visual target location (XV), and mean expected target location (μP) in the common source case (C = 1), and is the weighted sum of auditory target location (XA) and mean expected target location (μP) in the two difference sources case (C = 2) (Körding et al., 2007; Wozny and Shams, 2011).
The final step in the model is to use preceding calculations to predict responses to the task (Task Strategy blocks in Figure 2). In the congruence judgment task, the output is a binary decision of whether the auditory and visual target came from the same location or two different locations (denoted C = 1 and C = 2, respectively). In the auditory localization task, the output is a continuous estimate of auditory target location (denoted ŜA). Previous studies have indicated that task strategy for auditory localization can vary across individuals (Wozny et al., 2010), so we considered multiple strategies for both tasks. For the auditory localization task we consider three strategies: averaging, model selection, and probability matching (see Wozny et al. (2010) for more detail). The averaging model computes the average of ŜA,C=1 and ŜA,C=2, weighted by p(C = 1|XV, XA). The model selection strategy always chooses the most likely explanation for the perceived targets, i.e. respond ŜA = ŜA,C=1 if p(C = 1|XV, XA) > 0.5. The probability matching strategy randomly chooses between explanations at a rate commensurate with their probability, i.e. if p(C = 1|XV, XA) = 0.7 respond ŜA = ŜA,C=1 70% of the time. For the congruence judgment task we only consider model selection and probability matching, since responses are constrained to one of two outcomes.
The above approach can be used to estimate the probability distribution of responses for a given set of inputs, model parameters, and task strategy. Responses are simulated by sampling perceived target location, XV and XA, from equations 1 and 2 10,000 times. Each pair of samples is used to calculate the probability of a common source, p(C = 1|XV, XA). These values are then used to calculate a response to the task (C or ŜA, respectively). Additionally, it is possible that on some trials a subject may lose focus on the task, and simply guess. To model this, responses are replaced with a guess based solely on prior expectation (for congruence judgment, p(C = 1|XV, XA) = pcommon, and for auditory localization, ) at the model's inattention rate (denoted λ). 10,000 simulated responses are generated by this process, which can be used to estimate a histogram of responses. For congruence judgment, the histogram only had two values, C = {1, 2}, while for auditory localization responses were binned in 1 degree intervals. This histogram can be compared to subject data to estimate the likelihood of an observed subject response resulting from the given model parameters and task strategy.
The ultimate goal of this model is to compare perception across tasks, in order to identify task-related changes in how spatial disparity influences visual capture. If we assume that the model parameters described above are sufficient to describe visual capture, then this goal can be reframed as comparing the model parameters that best explain observed responses across tasks. To achieve this goal, we estimated a set of optimal parameter values by searching for the set of values that maximizes the likelihood of the observed data in each session for each subject, using an implementation of Pattern Search (Hooke and Jeeves, 1961) in Matlab. To obtain a distribution of optimal value estimates and reduce the potential for the search algorithm to get stuck in local minima, the search was run 120 times from random starting values. The search reaches a different set of optimal value estimates each time it is run due to the stochastic nature of likelihood estimation that arises from using simulated sampling to estimate response probability. As a result, the distribution of optimal value estimates demonstrates the sensitivity of the model fit to each parameter, with wide distributions indicating low sensitivity and narrow distributions indicating high sensitivity. The distribution of optimal value estimates for each parameter was compared across sessions for each subject to test for significant differences due to task and experience.
3 Results
3.1 Unimodal Localization
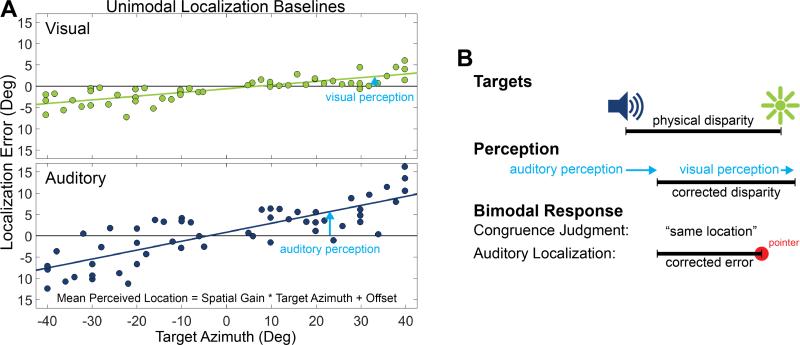
Figure 3 shows a representative example of unimodal localization from one session. Responses were similar to previous experiments (Dobreva et al., 2011, 2012; Razavi et al., 2007), with subjects demonstrating better accuracy and precision with vision than with audition. Simple linear regression was used to estimate auditory and visual spatial gain, offset, and uncertainty for each session, as summarized in Table 1. Offset (μ) and gain (G) were defined as the regression intercept and slope respectively, and uncertainty (σ) was defined as the standard deviation of the residual error. Spatial gains were consistently higher in audition than in vision, indicating that subjects are likely to be biased more toward the center when localizing visual targets and biased more toward the periphery when localizing auditory targets, in agreement with previous studies (Odegaard et al., 2015). Additionally, auditory localization showed a small bias to the left, which has also been previously observed (Odegaard et al., 2015). To our knowledge there is no analytic method of estimating changes in standard deviation as a function of a continuous variable (in this case, target position) without repeatedly sampling at several discrete locations, so the results in Table 1 assume uncertainty was constant across space (i.e. Gσ = 0).
Fig. 3.
Representative unimodal task data. A, In each session, subjects localized remembered auditory and visual targets presented in isolation. Both modalities were subject to idiosyncratic inaccuracies, with visual localization generally being more precise and accurate than auditory localization. Linear fits to localization error provided estimates of offset (intercept, uniform errors in azimuth) and spatial gain (slope, tendency to overestimate or underestimate target azimuth), which were used to correct target locations in the bimodal task. The labeled visual and auditory corrections were applied to the highlighted point in Figure 1 for this session's bimodal data analysis. B, Unimodal responses were used to estimate perceived target locations in bimodal tasks. Physical target locations were corrected for spatial gain and offset in each sense, and corrected values were used to estimate corrected audio-visual disparity. Corrected disparity was used as the basis for bimodal data analysis.
Table 1.
Medians and range of medians for each measured parameter in the unimodal task. Bold values indicate grand medians, with ranges in parentheses indicating the maximum and minimum medians across all sessions.
| Parameter | Medians | |
|---|---|---|
| Auditory Perception | ||
| Auditory Offset | μ A | −1.9° (−8.0° - 3.1°) |
| Auditory Spatial Gain | GA | 1.00 (0.88 - 1.55) |
| Auditory Uncertainty | σ A | 4.09° (3.4° - 9.6°) |
| Visual Perception | ||
| Visual Offset | μ V | −0.5° (−1.8° - 1.5°) |
| Visual Spatial Gain | GV | 0.92 (0.86 - 1.12) |
| Visual Uncertainty | σ V | 1.80° (1.10° - 2.83°) |
Regression results were used to calculate corrected audio-visual disparity, which was the physical disparity (auditory target location minus visual target location) corrected by auditory and visual localization fits for each subject at the respective target locations, as illustrated in Figure 3B. Corrected audio-visual disparity was used to analyze the congruence judgment and auditory localization data, as described below.
3.2 Congruence Judgment and Auditory Localization
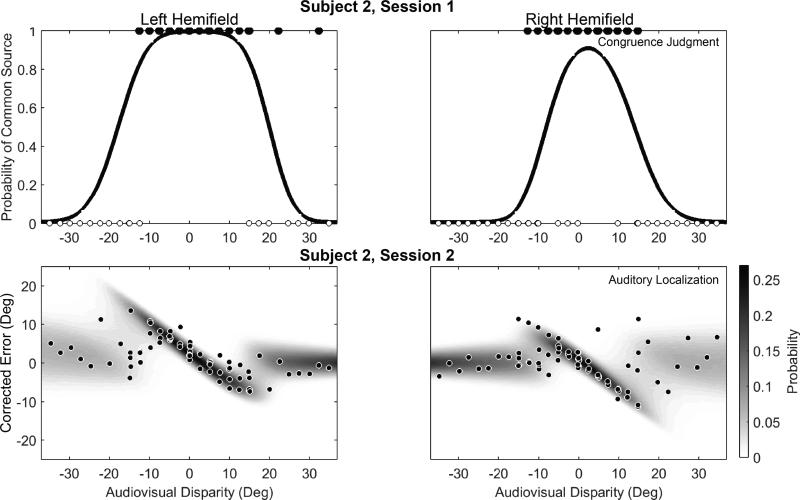
Figure 4 shows congruence judgment and auditory localization data from three representative subjects. Data collected when targets were in the left hemifield were mirrored through the origin after correction, so negative corrected audio-visual disparity corresponds to visual targets located farther from midline than auditory targets and positive values correspond to visual targets located closer to midline than auditory targets. For congruence judgment data, we estimated the Probability of Same Location by binning responses in 5° increments along corrected audio-visual disparity, and calculating the percentage of “same location” responses in each bin. For auditory localization data, we calculated corrected error as the distance between a localization response and the response location predicted by the unimodal auditory fit. Subjects 1 and 3 performed auditory localization for session 1, while subject 2 performed congruence judgment in session 1. Regardless of task, responses appeared to be similar between sessions 1 and 3.
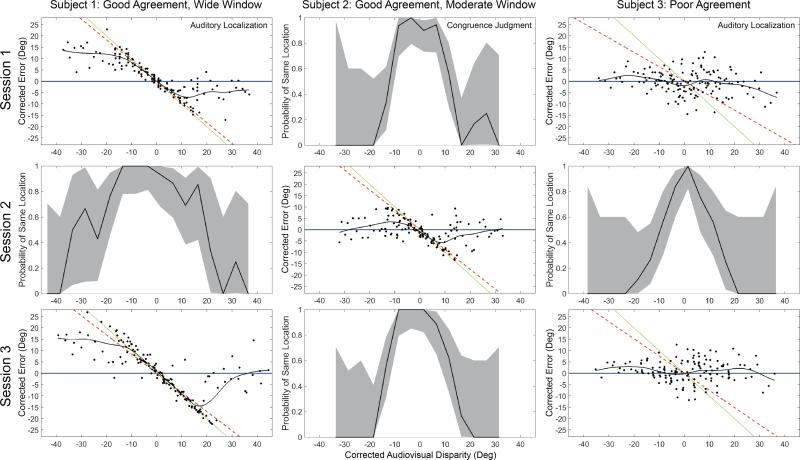
Fig. 4.
Representative data from congruence judgment and auditory localization tasks in three subjects. For congruence judgment sessions the probability of a same location response is given as a function of corrected audio-visual disparity. Targets in the left hemifield were mirrored through the origin after correction, so negative corrected audio-visual disparity corresponds to visual targets located farther from midline than auditory targets and positive values correspond to visual targets located closer to midline than auditory targets. For all subjects, “same location” responses are more likely when disparity is small, and become less likely as the disparity magnitude increases. Gray regions represent Clopper-Pearson 95% confidence intervals, and vary in size with the number of points in the histogram bin. In comparison, for auditory localization sessions, corrected localization error relave to each subject's unimodal localization responses (indicated by the horizontal line) was plotted as a function of corrected audio-visual disparity. In subjects 1 and 2, auditory localization shows a pronounced shift toward the common source location (broken line, slope is the ratio of visual to auditory weight), whereas in subject 3 no shift toward common source location is evident. For reference, the solid diagonal line indicates where responses would fall if they were based solely on the visual target.
In the congruence judgment task, audio-visual integration manifests as explicit report that targets came from the same location (i.e. binding). As shown, when corrected audio-visual disparity was near zero, the probability of subjects reporting that the two targets came from the same location was close to 1, and decreased quickly as corrected disparity magnitude increased.
In the auditory localization task, audio-visual integration manifests as an error in corrected auditory location toward the visual target (i.e. auditory bias). If localization responses were based solely on the auditory target location (denoted by blue flat lines), responses should have a distribution equal to the responses in the unimodal task, and corrected error should have zero mean. However, subjects 1 and 2 had pointing responses that showed a strong error toward the common source location (ŜA,C=1, denoted by broken red lines) when disparity was small, indicating that the visual target was biasing auditory perception. As corrected disparity magnitude increased, the distribution of responses returns toward zero, indicating that they were no longer influenced by the visual target. However, subject 3 showed little auditory bias toward the common source location in the auditory localization task, indicating that he was able to segregate corrected auditory and visual location even at small corrected audio-visual disparities. To guide visual estimation of the trend in corrected error, a cubic spline (black line) was fit to the data.
Theoretically, the audio-visual disparity at which this transition from integration to segregation occurs can be qualitatively compared across tasks to provide an estimate of their agreement. However, we were surprised that the range of capture for some subjects fell outside of the most sampled region of the target array, since the array was designed based on previous studies to most heavily sample the region in which the transition from integration to segregation occurs. As a result, any comparison of the raw data is limited by the amount of data available and response noise in the auditory localization task, so quantitative comparison requires a different approach, as described in the next section.
3.3 Model Fit With All Parameters Free
In order to test the model's ability to explain the data collected in this experiment, it was first fit with all model parameters free. For each session, 120 runs of a global optimization algorithm were run from random starting points to find the set of parameters that minimized the negative sum log-likelihood of the model predictions of subject response data. This approach fit the data well, with median generalized R2 values (Nagelkerke, 1991) of 0.98 for the auditory localization task and 0.51 for the congruence judgment task. We used a null model that simulated subjects always guessing as if no targets had been presented, i.e. λ = 1. The difference in generalized R2 values can be attributed to the difference in null model ability to guess correct responses by chance, because in congruence judgment the null has only two options to choose from, whereas in auditory localization the null model has many possible options (for purposes of comparison, the data and model were considered in agreement if responses fell within the same 1°bin). The negative sum log likelihoods for the fit and null models in the congruence judgment task ranged from 32.6 - 82.8 and 97.3 - 150.9, respectively, whereas the negative sum log likelihoods for the fit and null models in the auditory localization task ranged from 350.7 - 513.0 and 692.6 - 841.27 (smaller values indicate better fits). The difference between fit and null models is larger for auditory localization, which accounts for the difference in generalized R2 values, but the negative log likelihoods are much lager for both the fit and null models in auditory localization than in congruence judgment, indicating that the auditory localization data is overall harder to fit. Therefore, the smaller difference (and lower generalized R2) for congruence judgment reflects the fact that the congruence judgment data is easier to predict, not that the model is inappropriate for both tasks.
Example model fits are shown in Figure 5 for data from subject 2 in Figure 4. Examples were generated by stepping in half-degree increments through physical audio-visual disparities such that |SV + SA| = 45° (corresponding to the largest diagonal of target locations in Figure 1C), simulating 100,000 responses, and estimating the distribution of those simulated responses. Negative values of audio-visual disparity indicate when the visual target was to the right of the auditory target, and vice versa. Congruence judgment model predictions are represented as a single curve, corresponding to the probability of a “same location” response at a particular audio-visual disparity. As shown, the probability of a “same location” response is high when audio-visual disparity is small, and decreases sharply beyond about 10°. Note that the window in which “same location” responses are likely is dependent on several factors, and varies from subject to subject. Auditory localization model predictions are represented as a probability distribution at each audio-visual disparity, with higher probabilities corresponding to darker regions in the figure. At small audio-visual disparities, the probability distribution is narrow and has a roughly linear pattern of error, which corresponds to auditory bias toward the visual target. Additionally, the distribution gets wider with increasing auditory target distance from midline (negative audio-visual disparity in the left hemifield, positive audio-visual disparity in the right hemifield), since GσA causes auditory uncertainty to increase with distance from midline.
Fig. 5.
Example Bayesian inference model fits with all parameters free. For session 1 (congruence judgment task) the model simulates responses to estimate the probability of a “same location” response for all audio-visual disparities (black line). For comparison, data from this subject is plotted with filled circles indicating “same location” responses and hollow circles indicating “different location” responses. For session 2 (auditory localization task), the model predicts the probability of pointing errors for all audio-visual disparities (grayscale coloration, with darker shades indicating higher probabilities). The model successfully reproduces the auditory bias toward visual targets observed at small audio-visual disparities, which fits the subject's responses (black points) well. Model fits demonstrate an asymmetry across hemifields, which is due to interactions between offset and spatial gain.
Model sampling of target locations includes spatial gain and offset (fequations 1 and 2), so audio-visual disparity is not corrected for perception as it was in Figure 4. Corrected audio-visual disparity is a function of spatial gain and offset in each sense, so interactions between these terms can introduce asymmetries in corrected disparity across hemifields. This is evident when comparing across hemifields for the congruence jugment data, where higher corrected audio-visual disparities in the right hemifield (due to a leftward bias and a spatial gain greater than 1 in corrected auditory location) resulted in lower probabilties of “same location” responses than at the same physical audio-visual disparity in the left hemifield.
Probability matching was used to simulate session 1, and averaging was used to simulate session 2, which were the best (lowest negative sum log-likelihood) model strategies for each session in this subject. Switching task strategies produced characteristic changes in probability distributions as previously demonstrated by Wozny et al. (2010), but changes were generally minor and are therefore not shown here.
Our estimation method produced a distribution of optimal parameter estimates for each session performed by each subject, from which we computed the median and 95% range (out of 120 estimates, remove the 3 largest and 3 smallest values). Median values were reported for each parameter because the difference in log-likelihood of the best and second best fits for each session were often small (ranging from 0.012 to 3.24, median 0.367), indicating that different runs of the fitting algorithm could produce similarly good fits. Given that the objective function was stochastic, differences in log-likelihood of this magnitude could easily be due to noise, and so we opt to report the range and median of the fit results, rather than best fit values. Cross-subject heterogeneity of each parameter was observed by comparing median values, and model estimate sensitivity to each parameter could be observed in 95% ranges within each session. Generally, optimal model parameter estimates were similar to previously reported values, as shown in Table 2. Subjects tended to overshoot auditory spatial perception, undershoot visual spatial perception, and had small offsets. Uncertainties were similar to those previously reported by our lab (Dobreva et al., 2012), although it should be noted that auditory and visual uncertainty differ across labs (e.g. Alais and Burr (2004); Hairston et al. (2003); Recanzone et al. (1998); Wozny and Shams (2011)). The prior mean location and range reflected the wide range of potential target locations, and were similar to values previously reported in other labs (Wozny and Shams, 2011). Model fits demonstrated a wide range of values for prior expectation of common source, with a median in the middle of the parameter bounds. Inattention rate was low for all subjects, confirming that subjects rarely missed target presentation.
Table 2.
Medians and range of medians for each model parameter. Bold values indicate grand medians, with ranges in parentheses indicating the maximum and minimum medians across the subject population. Within-session ranges indicate the maximum and minimum values for the 95% range across all sessions.
| Parameter | Medians | Within-Session Ranges | |
|---|---|---|---|
| All Parameters Free | |||
| Auditory Perception | |||
| Auditory Offset | μ A | −1.8° (−6.2° - 2.4°) | 0.8° - 9.0° |
| Auditory Spatial Gain | GA | 1.04 (0.91 - 1.97) | 0.06 - 0.56 |
| Auditory Uncertainty | σ A | 3.01° (1.47° - 7.61°) | 1.68° - 6.99° |
| Auditory Uncertainty Gain | GσA | 0.109 (0.028 - 0.210) | 0.082 - 0.424 |
| Visual Perception | |||
| Visual Offset | μ V | −0.1° (−1.2° - 0.9°) | 0.6° - 2.0° |
| Visual Spatial Gain | GV | 0.93 (0.87 - 1.18) | 0.03 - 0.15 |
| Visual Uncertainty | σ V | 0.38° (0.14° - 0.75°) | 0.67° - 3.34° |
| Visual Uncertainty Gain | GσV | 0.0729 (0.042 - 0.176) | 0.051 - 0.205 |
| Prior | |||
| Prior Mean Location | μ P | 4.0° (−26.2° - 38.4°) | 5.4° - 76.0° |
| Prior Uncertainty | σ P | 23.79° (12.5° - 87.6°) | 4.1° - 81.4° |
| Prior Expectation of a Common Cause | pcommon | ||
| Congruence Judgment Task | 0.61 (0.20 - 0.98) | 0.03 - 0.26 | |
| Auditory Localization Task | 0.41 (0.01 - 0.98) | 0.01 - 0.95 | |
| Inattention Rate | λ | 0.008 (0.006 - 0.037) | 0.014 - 0.057 |
|
| |||
| Only pcommon Free | |||
| Prior Expectation of a Common Cause | pcommon | ||
| Congruence Judgment Task | 0.63 (0.26 - 0.99) | 0.01 - 0.08 | |
| Auditory Localization Task | 0.48 (0.01 - 0.98) | 0.02 - 0.95 | |
For each session, log-likelihoods were compared for each task strategy, to determine if one particular strategy best predicted subject responses. We classified a model as significantly better if the log-likelihood difference between the lowest and second lowest log-likelihoods was greater than three, as in Wozny et al. (2010). For the auditory localization task, 6 sessions were best explained by the averaging strategy, 2 by matching, 0 by selection, and 4 were indeterminate (no strategy had a log-likelihood at least 3 better than all other strategies). One subject switched best fits between session 1 and 3, from matching to averaging. For congruence judgment, 4 sessions were best explained by matching, 2 by selection, and 6 were indeterminate. This indicates that our subject population has a similar heterogeneity for task strategy as has been reported previously (Wozny et al., 2010), although due to a relatively small number of subjects we cannot compare population percentages across studies. Qualitatively, task strategies produced similar parameter estimates, although for congruence judgment fitting with the matching strategy consistently estimated pcommon to be higher than fitting with the selection strategy. To prevent this bias across task strategies from confounding analysis we only compared model parameters estimated with the same task strategy.
From the model fits, we calculated the spatial range over which visual capture occurred for each experimental session. Capture range was defined as the distance between the perceived auditory and visual locations at which the probability of integrating or segregating the auditory and visual targets was equal (p(C = 1|XV, XA) = 0.5, as calculated by equation 8 in the appendix). For this calculation, we fixed |XV| + |XA| = 45°, XV > XA, used only the matching task strategy to avoid bias across task strategies, and used the uncertainties associated with target locations in the middle of the array so that the uncertainty gains would have their mean influence. Note that, because uncertainty is dependent on target distance from the midline (equations 1 and 2), these calculated values will change depending on the distance of each target from the midline, and is not solely dependent on the distance between the targets as this calculation simplifies it. Despite this simplification, this calculation provides an approximation of the capture range that can be compared across tasks. Pairwise differences were calculated between each session (session 1 and 2, session 1 and 3, session 2 and 3, with sign corrected to be consistent across task type comparisons) for each parameter, and nonparametric rank comparison (Kruskal-Wallis H test) was used to test for significant changes in difference across session pairs. The capture range was significantly larger for congruence judgment than for auditory localization (df = 1, χ2 = 5.86, p = 0.016), as summarized in Table 3. Repetition of this analysis using the selection task strategy produced the same result (df = 1, χ2 = 5.01, p = 0.025), indicating that it is not specific to one task strategy, but represents a small but significant difference in capture range across tasks.
Table 3.
Median and range of capture range for each task, calculated from the probability matching task strategy model fits. Bold values indicate grand medians, with ranges in parentheses indicating the maximum and minimum medians across the subject population. Paired differences (judgment minus localization) indicate capture occurred over a wider range in judgment than in localization.
| Congruence Judgment | Auditory Localization | Paired Difference |
|---|---|---|
| 11.1° (8.7° - 22.3°) | 9.8° (0° - 19°) | 2.8° (−6.5° - 11.4°) |
Additionally, we compared the difference in each model parameter across sessions. Pairwise differences were calculated as for capture range and the same nonparametric rank comparison was used. The only significant difference observed was for pcommon (df = 1, χ2 = 9.4, p = 2.2 × 10−3). Post-hoc comparison demonstrated that pcommon was significantly lower in auditory localization than congruence judgment (difference between sessions 1 and 2 and sessions 2 and 3) when compared against repetitions of the same task (difference between sessions 1 and 3). However, this observation could be explained as an interaction between model terms that changes across tasks, so we re-ran the model fit with pcommon as the only free parameter to confirm this observation.
3.4 Model Fit With Only pcommon Free
To ensure that the difference in pcommon across tasks wasn't an artifact of model over-fitting, the model fit was re-run with only pcommon as a free parameter. Parameters that could be estimated from unimodal data were fixed to the estimated value from each session, and all other parameters except pcommon were set to a constant value across all subjects. This approach was used to eliminate the possibility that the difference in pcommon across tasks could be attributed to covariation with other free parameters in the model fit. For each session, GA, GV, μA, and μV were fixed to corresponding coefficients in the unimodal linear fits, and σA and σV were fixed at the standard deviation of the residual of the unimodal linear fit (from Table 1). GσA, and GσV were fixed at zero, since their values could not be estimated from the unimodal data and tended to be relatively small in the model fit with all parameters free. For all sessions, μP was set to 0° and σP was set to 40°, which corresponds to the physical range of targets. λ was set to 0.01, which is close to its average value across subjects in the model fit with all parameters free. Fit values did not substantially suffer as a result of this simplification, with median generalized R2 values of 0.95 for the auditory localization task and 0.51 for the congruence judgment task. These generalized R2 values were calculated with respect to a null model that used the same fixed parameters as the model with only pcommon free, which prevents direct comparison with the values from the fit with all parameters free. Instead, AIC values (Akaike, 1974) were calculated, and were significantly better for the model fit with all free parameters for most (43 out of 60) model fits, indicating that although the model with only pcommon free was still a good representation of subject responses, it missed some of the detail that the model fit with all free parameters could provide.
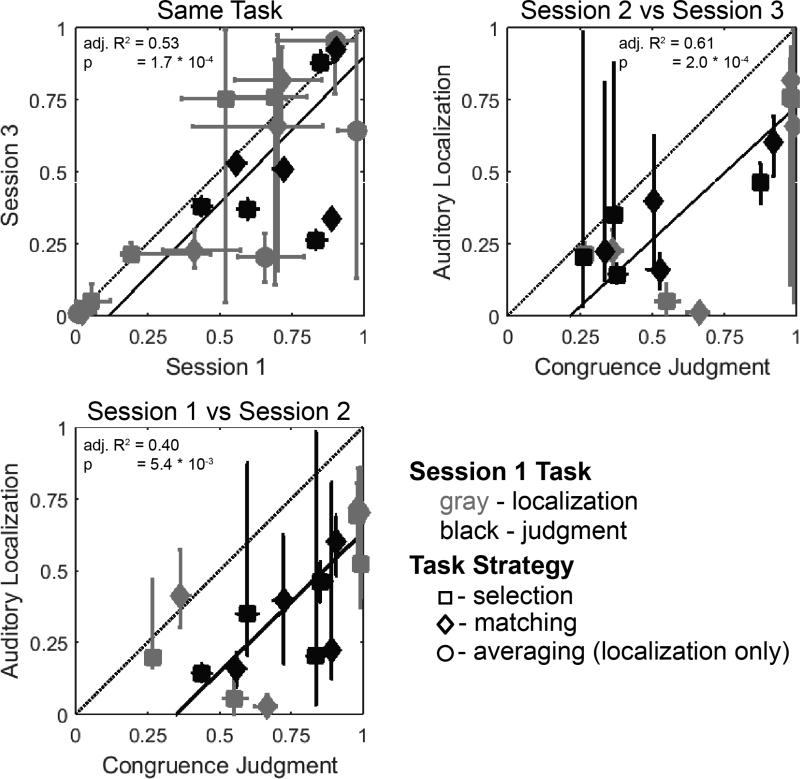
Figure 6 shows the correlation of pcommon across sessions in the model fit with only pcommon free. Simple linear regression for repetitions of the same task (top left panel) did not produce a significant intercept term (p = 0.75), indicating that pcommon values did not significantly change across repetitions of the same task. This is consistent with previous studies of audio-visual integration, which similarly showed that integration tended to be stable over repetitions of the same task (Odegaard and Shams, 2016). As was found in the model with all parameters free, pcommon was significantly lower in the auditory localization task than in the congruence judgment task (shown in the bottom left and top right panels) relative to the difference when the task was repeated (i.e. the intercept of the correlation is lower in the comparisons across tasks than when the same task is compared to its repetition, Kruskal-Wallis H test, df = 1 across groups, χ2 = 11.08, p = 8.7 × 10−4). Critically, restricting the model to one free parameter did not change the relationship between tasks, indicating that this finding reflects a true perceptual difference, not model overfitting. Additionally, pcommon was significantly correlated across repetitions of the same task (simple linear regression, p = 1.7 × 10−4, adjusted R2 = 0.53), and across tasks (session 1 and 2, p = 5.4 × 10−3, adjusted R2 = 0.40; session 2 and 3, p = 2.0 × 10−4, adjusted R2 = 0.61), indicating that results from these tasks are still related, but biased relative to one another.
Fig. 6.
Prior Expectation of a Common Source (pcommon) correlated across sessions. Each point represents a pair of median model fit values for pcommon from the same subject and task strategy, across two different sessions. Each pairwise correlation of parameters across sessions is represented by a separate subfigure. As shown, when the same task was repeated subjects generally demonstrated good agreement in fitted values, but across tasks pcommon was significantly lower in the auditory localization task than in the congruence judgment task (black trend line was significantly lower in cross-task comparisons, Session 1 vs Session 2 and Session 2 vs Session 3, than in the Same Task comparison). Multiple task strategies were considered as in Wozny et al. (2010), although parameter estimates were similar across task strategies and group trends were consistent regardless of task strategy. Error bars represent 95% parameter ranges, estimated from the 120 runs of the model fitting algorithm. Standard Major Axis Regression (Legendre, 2013) was used to fit trend lines.
4 Discussion
The objective of this work was to compare estimates of visual capture across congruence judgment and auditory localization tasks when performed independently. Results presented here demonstrate that the prior expectation that targets originate from a common source is larger in congruence judgment than in auditory localization. This difference in prior expectation produces capture over a larger range in congruence judgment than in auditory localization, indicating that these two methods do not produce equivalent measures of visual capture.
Both the congruence judgment and auditory localization results show qualitative agreement with previous findings. As has been demonstrated, when audio-visual disparity is small, there is a high probability subjects will report that the auditory and visual targets came from the same source in the congruence judgment task (Lewald and Guski, 2003; Slutsky and Recanzone, 2001), and a corresponding pattern of auditory bias toward the visual target in the auditory localization task (Hairston et al., 2003; Wallace et al., 2004). This shift is weighted in accordance to relative cue reliability, so that the more precise visual target captures perception of the less precise auditory target in a manner consistent with optimal estimation (Alais and Burr, 2004; Battaglia et al., 2003). As audio-visual disparity increases, visual capture becomes less likely to occur, and both reports that targets came from the same source and auditory bias drop off in the corresponding tasks. Additionally, previous experiments have found that visual capture in congruence judgment varies with auditory and visual target location (Godfrey et al., 2003), with visual capture being more likely when the visual target was farther from midline than the auditory target. This can be explained by our model as auditory and visual spatial gains altering perceived audio-visual disparity. In particular, visual spatial gains tended to be smaller than auditory spatial gains (see Table 1), so visual targets will be perceived as being closer to the auditory targets when the visual is farther from the midline than the auditory, and therefore visual capture is more likely to occur.
Caution is required when comparing the range of visual capture observed here to data obtained in other labs, since several perceptual factors (notably σA, σV, and pcommon) govern the limits of visual capture, and they may co-vary across labs. In particular, several labs have reported much larger auditory and visual uncertainties (σA ≈ 8° and σV ≈ 3.25°) (Alais and Burr, 2004; Hairston et al., 2003; Körding et al., 2007; Wozny and Shams, 2011) than those observed in our lab (Dobreva et al., 2011, 2012; Razavi et al., 2007; Zwiers et al., 2003), indicating that there are unidentified factors that influence perceptual uncertainty across experimental setups. These differences across labs may be explained by differences in the number of targets in and the total spatial span of the target array. Specifically, Hartmann et al. (1998) demonstrated that measures of auditory localization uncertainty (i.e. RMS pointing error) depends on an interaction between true localization uncertainty, the number of targets in the array, and the spatial span of the array, with small numbers of targets and narrow spans artifically increasing the measured uncertainty. The difference may also depend on whether or not subjects know the number and location of targets, because Odegaard et al. (2015) hid their target locations from subjects and measured uncertainty similar to our current results, despite using only a few targets over a narrow spatial span. Additionally, the amount of visual capture observed varies substantially across individuals (i.e. the broad range of values for pcommon), which further highlights the heterogeneity in the spatial range of visual capture. Finally, the range over which visual capture is likely to occur in both tasks was often much broader than auditory spatial uncertainty, which indicates that perceptual discrimination thresholds alone cannot predict the range of visual capture, in contrast to conclusions from some earlier studies (Slutsky and Recanzone, 2001).
Despite the ability of both tasks to measure visual capture, our evidence suggests that they do not produce equivalent estimates when performed independently. Specifically, model fits to each session show that pcommon is lower in auditory localization than it is in congruence judgment, indicating that prior expectation is sensitive to task requirements. Critically, no other model parameter showed a difference across tasks, indicating that the difference in task performance observed here is solely attributable to modulation of prior expectation, and not a change in sensory precision or accuracy. This difference in visual capture when tasks were performed independently does not occur when tasks are performed together (Wallace et al., 2004), indicating that responses to each task interact to bring them into agreement with one another. To fully address the influence of pcommon on visual capture in each task, future experiments should focus on systematically manipulating prior expectation, either by manipulating instructions given to subjects (as in Lewald and Guski (2003); Warren et al. (1981)), or by providing subjects with previous experience in which audio-visual congruence is highly likely or unlikely to occur (as in Van Wanrooij et al. (2010)). Additionally, the 95% ranges for pcommon were wide for some sessions (as shown by error bars in Figure 6), which may be due to insufficient data to precisely estimate pcommon. Although the relatively small number of trials in this experiment is offset by the dense target array used here (Figure 1C), future experiments would likely also benefit from more trials per session and more subjects.
The neural mechanisms that implement the computations described here are likely complex and distributed through the nervous system. Recent fMRI work by Rohe and Noppeney (2015) used auditory and visual localization to demonstrate that independent auditory and visual location (XA and XV) are best predicted by activity in the respective primary sensory areas, wheras fused audio-visual location (ŜA,C=1) is best predicted by activity in posterior intraparietal sulcus, and the final decision about target location (ŜA) is best precited by activity in anterior intraparietal sulcus. These results suggest that behavioral differences in pcommon observed here across tasks may also be reflected in neural activity in posterior intraparietal sulcus. Although the computational components of this model are reflected by activity in different neural regions, it is unlikely that the brain performs the exact calculations described here, because the nervous system is restricted to computations that can be performed with neural circuits. Wei and Stocker (2015) demonstrated that constraining causal inference models with efficient coding requirements causes the model to make predictions that deviate from those made by an optimal encoder, but agree with previously observed biases in visual perception. Similar mechanisms may also account for the inaccurate spatial perception (i.e. SG ≠ 1 and μ ≠ 0) observed here and in previous localization experiments, which highlights the need to further study the underlying neural mechanisms that could implement the calculations described in the current model.
In other forms of audio-visual integration, subjects can partially, but not completely, suppress cross-modal bias in a context-dependent manner (Bizley et al., 2012; Mishra et al., 2010; Soto-Faraco and Alsius, 2007; van Atteveldt et al., 2013). It is possible that a similar effect is responsible for the current findings. In congruence judgment, subjects are required to explicitly attend the relationship between auditory and visual targets, whereas in the auditory localization task subjects only need to attend the auditory target location. This modulation of attention across tasks could be responsible for the difference in visual capture demonstrated here. However, previous studies have shown that selectively attending only one stimulus modality versus attending both in auditory localization does not alter pcommon (Odegaard et al., 2016), indicating that this explanation may not be the case. Alternatively, the threshold for subjects to report visual capture in the congruence judgment task may simply be lower than in the auditory localization task, because subjects may decide that auditory and visual targets are “close enough” to judge them as coming from the same location, when the same percept might not produce a bias in perceived auditory location.
Acknowledgements
We thank Martin Gira and Robert Schor for their technical assistance, and we are immensely grateful we had the opportunity to receive David Knill's assistance in developing the computational model before his untimely passing. Research was supported by NIDCD Grants P30 DC-05409 and T32 DC-009974-04 (Center for Navigation and Communication Sciences), NEI Grants P30-EY01319 and T32 EY-007125-25 (Center for Visual Science), and an endowment by the Schmitt Foundation.
Appendix: Bayesian Inference Modeling of Auditory Localization and Congruence Judgment Tasks
This model simulates the perception of temporally synchronous but spatially disparate auditory and visual targets, and subsequent performance of two perceptual tasks (auditory localization and congruence judgment). The model described here is a modified version of previously published work (Körding et al., 2007; Wozny and Shams, 2011; Wozny et al., 2010).
Perception of Visual and Auditory Target Locations
Targets locations are constrained to a fixed elevation and a range of azimuths within the frontal field, denoted as SV and SA for visual and auditory targets, respectively. Previous research has demonstrated that spatial perception is inherently uncertain and subject to biases, so the first step of this model is to produce a probability distribution that represents the set of percepts that could be generated by a given target. The generated percepts for visual and auditory targets are denoted XV and XA, respectively, and the probabilities of a percept occurring given a particular target are denotedp p(XV|SV) and p(XA|SA). Previous research has demonstrated that perceived target locations tend to be normally distributed, although they are subject to idiosyncratic biases, a tendency to overestimate eccentricity for auditory targets, and reliability that decreases with eccentricity (Dobreva et al., 2012; Odegaard et al., 2015). To model these aspects of perception, we assume normal distributions with means that are scaled and offset with respect to target location, similar to Odegaard et al. (2015, 2016). The scaling parameters are denoted GV and GA, which can model a pattern of overestimating (SG > 1) or underestimating (SG < 1) target eccentricity. Constant biases in target location are denoted μV and μA. Localization uncertainty (inverse reliability) is represented by σV and σA. This model also includes parameters that model increase in uncertainty as a function of eccentricity, given as GσV and GσA. Putting these terms together in a normal distribution gives the equations:
| (3) |
| (4) |
Perception is simulated by sampling XV and XA from these distributions. For convenience in later equations, the standard deviation parameters are expressed as as σSV = σV + GσV |SV| and σSA = σA + GσA |SA|. In addition, we assume the existence of a prior bias in target locations, which limits target locations to the frontal field.
| (5) |
Estimating The Probability That Targets Originate From A Common Source
In order to combine auditory and visual information in a behaviorally advantageous manner, it is necessary to be able to estimate whether or not crossmodal signals originate from a common source. Note that this process does not necessitate conscious decision making, as it could be performed early in the crossmodal sensory pathway. A common method of representing the probability of a common source for two targets (denoted p(C = 1|XV, XA)) is given by Bayes’ Theorem:
| (6) |
pcommon is the prior expectation that targets originate from a common source (C = 1). We assume that the number of targets in the room is limited to either 1 or 2 (C = 1, C = 2). Therefore, the law of total probability states that p(XV, XA) can be expressed as:
| (7) |
Substituting into equation 6 gives:
| (8) |
In order to obtain the conditional probabilities for target location, we integrate over the latent variable Si.
| (9) |
| (10) |
The Analytic solutions to these integrals are (Körding et al., 2007):
| (11) |
| (12) |
Substituting these integrands into equation 8 enables the probability of common source (p(C = 1|XV, XA)) to be computed.
Performing the Congruence Judgment Task
The congruence judgment task is a two alternative forced choice paradigm in which the subject decides whether the visual and auditory targets came from the same location (C = 1) or two different locations (C = 2). This decision can be made directly from the probability of a common source, p(C = 1|XV, XA), in one of two ways: model selection and probability matching. These two models can be directly compared for a data set, to determine which decision model best explains the observed data.
Model Selection
One approach to selecting a response is to always choose the most likely response, i.e. if p(C = 1|XV, XA) > 0.5 choose C = 1 (Körding et al., 2007).
| (13) |
Probability Matching
A second possible approach is to choose each response in proportion to its probability, i.e. if p(C = 1|XV, XA) = 0.7 choose C = 1 70% of the time (Wozny et al., 2010).
| (14) |
Performing the Auditory Localization Task
In the auditory localization task, subjects use a laser to point to the estimated location of the auditory target, ŜA. Estimating the auditory target location requires integrating the percept from each sense, XA and XV, with the probability they originated from a common source, p(C = 1|XV, XA). ŜA is calculated for both C = 1 and C = 2 (equations 15 and 16 (Körding et al., 2007)), then combined in one of three ways: averaging, model selection, and probability matching (Wozny et al., 2010). As before, these models can be directly compared for a given data set.
| (15) |
| (16) |
Averaging
One approach to estimating auditory target location is to perform a weighted average of ŜA,C=1 and ŜA,C=2 based on their probability (Körding et al., 2007):
| (17) |
Model Selection
As in the congruence judgment task, subjects may simply choose the most likely explanation for the observed signals (either C = 1 or C = 2) and respond based solely on that explanation (Wozny et al., 2010).
| (18) |
Probability Matching
Also as in the congruence judgment task, subjects may choose explanations at a rate commensurate with their probability (Wozny et al., 2010).
| (19) |
Simulating Task Performance
The above equations can be used to estimate the probability distribution of responses for a given set of inputs, model parameters, and task strategy. Responses are simulated via repeated sampling perceived target locations, XV and XA, from equations 3 and 4 10,000 times. Each pair of perceived target locations is used to calculate the probability of a common cause, p(C = 1|XV, XA), from equation 8. XV, XA, and p(C = 1|XV, XA) for each sample are then used to compute a response from one congruence judgment or auditory localization task strategy (C or ŜA, respectively). Additionally, it is possible that on some trials a subject may lose focus on the task, and simply guess. To model this, responses are replaced with a guess based solely on prior expectation (for congruence judgment, p(C = 1|XV, XA) = pcommon, and for auditory localization, ŜA ~ (N)(μP, σP)) at a probability equal to the Inattention Rate parameter (λ). This produces a total of 10,000 simulated responses, which can be used to estimate the probability distribution of responses. This probability distribution can be compared to subject data to estimate the likelihood of an observed subject response occurring given a set of model parameters and task strategy. For congruence judgment, the histogram only had two values, C = 1, 2, while for auditory localization responses were binned in 1 degree intervals.
Comparing Common Underlying Processes Across Both Tasks
The ultimate goal of this model is to be able to compare perception across task types, in order to identify any differences in visual capture across task types. If we assume that the model parameters described above are sufficient to describe visual capture, than this goal can be reframed as comparing the model parameters that best explain observed responses across task types. Therefore, we need to find the model parameters and task strategy that best explain each data set.
Table 4 provides the limits for each parameter in this model. For each data set, we searched for a set of parameter values that maximizes the likelihood of the observed data in that set. Specifically, Matlab's Pattern Search algorithm was used to search for a set of parameters that minimized negative log likelihood. Negative log likelihood was computed by estimating the probability distribution of responses to each target pair via the simulation described above, then summing the negative log of the probability of the response given for each target pair. Essentially, this penalized a parameter set for predicting that a set of subject responses has a low probability of occurring. If the negative log likelihood was ever infinite (i.e. the probability of a response was zero), it was replaced by a large, non-infinite value (10,000) to prevent the search algorithm from failing. The search algorithm starts from a random point (independently drawn for each parameter from a uniform distribution between the limits in Table 4) in the parameter space, computes the negative log likelihood of a set of ordinal points (referred to as a mesh) centered on the current point, and selects the point with the smallest negative log likelihood as the new current point. If no point with a smaller negative log likelihood than the current point is found, the size of the mesh is reduced and the search is repeated with the same point (Hooke and Jeeves, 1961). The search algorithm stops when the change in mesh size, change in current point, or change in likelihood value drops below a set tolerance (1*10−4 for Mesh size, 1*10−4 for current point, and 1*10−2 for likelihood). Unimodal localization trials were included in optimization, with probability in unimodal localization trials computed analytically from equations 3 and 4.
Table 4.
Bounds for each model parameter.
| Parameter | Lower Bound | Upper Bound | |
|---|---|---|---|
| Auditory Offset | μ A | −20 | 20 |
| Auditory Spatial Gain | GA | 0 | 2 |
| Auditory Uncertainty | σ A | 0 | 30 |
| Auditory Uncertainty Gain | GσA | 0 | 2 |
| Visual Offset | μ V | −20 | 20 |
| Visual Spatial Gain | GV | 0 | 2 |
| Visual Uncertainty | σ V | 0 | 10 |
| Visual Uncertainty Gain | GσV | 0 | 2 |
| Prior Mean Location | μ P | −40 | 40 |
| Prior Uncertainty- | σ P | 0 | 100 |
| Prior Expectation of a Common Cause | pcommon | 0 | 1 |
| Inattention Rate | λ | 0 | 1 |
This approach is complicated by the fact that the objective function is stochastic, which may lead to different best model parameters each time the minimization algorithm is run. Pattern Search is an ideal algorithm for this condition, since it does not compute derivatives (Hooke and Jeeves, 1961) and is therefore robust for stochastic objective functions. However, it is still capable of finding different solutions or getting stuck in local minima each time it is run. To address this concern, the search was run 120 times from a random starting point each time. To ensure the parameter space was well conditioned, the space of parameter values was normalized relative to the upper and lower bounds for each parameter in the search algorithm, then un-normalized when computing likelihood. Medians, and 95% confidence intervals were computed for each parameter from the search results.
Contributor Information
Adam K. Bosen, Department of Biomedical Engineering, University of Rochester, Rochester, NY
Justin T. Fleming, Department of Neurobiology and Anatomy, University of Rochester, Rochester, NY
Sarah E. Brown, Department of Brain and Cognitive Sciences, University of Rochester, Rochester, NY
Paul D. Allen, Department of Neurobiology and Anatomy, University of Rochester, Rochester, NY
William E. O'Neill, Department of Neurobiology and Anatomy, University of Rochester, Rochester, NY
Gary D. Paige, Department of Neurobiology and Anatomy, University of Rochester, Rochester, NY
References
- Akaike H. A new look at the statistical model identification. IEEE Trans Autom Control. 1974;19(6):716–723. [Google Scholar]
- Alais D, Burr D. The ventriloquist effect results from near-optimal bimodal integration. Curr Biol. 2004;14(3):257–262. doi: 10.1016/j.cub.2004.01.029. [DOI] [PubMed] [Google Scholar]
- Battaglia PW, Jacobs RA, Aslin RN. Bayesian integration of visual and auditory signals for spatial localization. J Opt Soc Am A. 2003;20(7):1391–1397. doi: 10.1364/josaa.20.001391. [DOI] [PubMed] [Google Scholar]
- Beierholm UR, Quartz SR, Shams L. Bayesian priors are encoded independently from likelihoods in human multisensory perception. J Vision. 2009;9(5):23, 1–9. doi: 10.1167/9.5.23. [DOI] [PubMed] [Google Scholar]
- Bertelson P, Radeau M. Cross-modal bias and perceptual fusion with auditory-visual spatial discordance. Percept Psychophys. 1981;29(6):578–84. doi: 10.3758/bf03207374. [DOI] [PubMed] [Google Scholar]
- Bizley JK, Shinn-Cunningham BG, Lee AKC. Nothing is irrelevant in a noisy world: sensory illusions reveal obligatory within-and across-modality integration. J Neurosci. 2012;32(39):13402–10. doi: 10.1523/JNEUROSCI.2495-12.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dobreva MS, O'Neill WE, Paige GD. Influence of aging on human sound localization. J Neurophysiol. 2011;105(5):2471–86. doi: 10.1152/jn.00951.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dobreva MS, O'Neill WE, Paige GD. Influence of age, spatial memory, and ocular fixation on localization of auditory, visual, and bimodal targets by human subjects. Exp Brain Res. 2012;223(4):441–55. doi: 10.1007/s00221-012-3270-x. [DOI] [PubMed] [Google Scholar]
- Godfroy M, Roumes C, Dauchy P. Spatial variations of visual - auditory fusion areas. Perception. 2003;32(10):1233–1245. doi: 10.1068/p3344. [DOI] [PubMed] [Google Scholar]
- Hairston WD, Wallace MT, Vaughan JW, Stein BE, Norris JL, Schirillo JA. Visual localization ability influences cross-modal bias. J Cogn Neurosci. 2003;15(1):20–9. doi: 10.1162/089892903321107792. [DOI] [PubMed] [Google Scholar]
- Hartmann WM, Rakerd B, Gaalaas JB. On the source identification method. J Acoust Soc Am. 1998;104(6):3546–3557. doi: 10.1121/1.423936. [DOI] [PubMed] [Google Scholar]
- Hooke R, Jeeves TA. “Direct Search” Solution of Numerical and Statistical Problems. J ACM. 1961;8(2):212–229. [Google Scholar]
- Howard IP, Templeton WB. Human Spatial Orientation. Wiley; New York: 1966. [Google Scholar]
- Jack CE, Thurlow WR. Effects of degree of visual association and angle of displacement on the “ventriloquism” effect. Percept Mot Skills. 1973;37(3):967–79. doi: 10.1177/003151257303700360. [DOI] [PubMed] [Google Scholar]
- Körding KP, Beierholm U, Ma WJ, Quartz S, Tenenbaum JB, Shams L. Causal inference in multisensory perception. PloS One. 2007;2(9):e943. doi: 10.1371/journal.pone.0000943. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Legendre P. Model II regression user's guide. R edition R Vignette; 1998. [Google Scholar]
- Lewald J, Guski R. Cross-modal perceptual integration of spatially and temporally disparate auditory and visual stimuli. Brain Res Cog Brain Res. 2003;16(3):468–78. doi: 10.1016/s0926-6410(03)00074-0. [DOI] [PubMed] [Google Scholar]
- Mishra J, Martínez A, Hillyard SA. Effect of attention on early cortical processes associated with the soundinduced extra ash illusion. J Cogn Neurosci. 2010;22(8):1714–29. doi: 10.1162/jocn.2009.21295. [DOI] [PubMed] [Google Scholar]
- Nagelkerke NJD. A note on a general definition of the coefficient of determination. Biometrika. 1991;78(3):691–692. [Google Scholar]
- Odegaard B, Shams L. The Brain's Tendency to Bind Audiovisual Signals Is Stable but Not General. Psychological Science. 2016;27(4):583–91. doi: 10.1177/0956797616628860. [DOI] [PubMed] [Google Scholar]
- Odegaard B, Wozny DR, Shams L. Biases in Visual, Auditory, and Audiovisual Perception of Space. PLoS Computational Biology. 2015;11(12):1–23. doi: 10.1371/journal.pcbi.1004649. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Odegaard B, Wozny DR, Shams L. The effects of selective and divided attention on sensory precision and integration. Neuroscience Letters 12. 2016;614:24–28. doi: 10.1016/j.neulet.2015.12.039. [DOI] [PubMed] [Google Scholar]
- Razavi B, O'Neill WE, Paige GD. Auditory spatial perception dynamically realigns with changing eye position. J Neurosci. 2007;27(38):10249–58. doi: 10.1523/JNEUROSCI.0938-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Recanzone GH, Makhamra SD, Guard DC. Comparison of relative and absolute sound localization ability in humans. J Acoust Soc Am. 1998;103(2):1085–97. doi: 10.1121/1.421222. [DOI] [PubMed] [Google Scholar]
- Rohe T, Noppeney U. Cortical Hierarchies Perform Bayesian Causal Inference in Multisensory Perception. PLoS Biology. 2015;13(2):1–18. doi: 10.1371/journal.pbio.1002073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sato Y, Toyoizumi T, Aihara K. Bayesian inference explains perception of unity and ventriloquism aftereffect: identification of common sources of audiovisual stimuli. Neural Comput. 2007;19(12):3335–55. doi: 10.1162/neco.2007.19.12.3335. [DOI] [PubMed] [Google Scholar]
- Slutsky DA, Recanzone GH. Temporal and spatial dependency of the ventriloquism effect. Neuroreport. 2001;12(1):7–10. doi: 10.1097/00001756-200101220-00009. [DOI] [PubMed] [Google Scholar]
- Soto-Faraco S, Alsius A. Conscious access to the unisensory components of a cross-modal illusion. Neuroreport. 2007;18(4):347–50. doi: 10.1097/WNR.0b013e32801776f9. [DOI] [PubMed] [Google Scholar]
- Thurlow WR, Jack CE. Certain determinants of the “ventriloquism effect”. Percept Mot Skills. 1973;36(3):1171–84. doi: 10.2466/pms.1973.36.3c.1171. [DOI] [PubMed] [Google Scholar]
- van Atteveldt NM, Peterson BS, Schroeder CE. Contextual control of audiovisual integration in low-level sensory cortices. Hum Brain Mapp. 2013;35(5):2394–411. doi: 10.1002/hbm.22336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Wanrooij MM, Bremen P, Van Opstal AJ. Acquired prior knowledge modulates audiovisual integration. Eur J Neurosci. 2010;31(10):1763–71. doi: 10.1111/j.1460-9568.2010.07198.x. [DOI] [PubMed] [Google Scholar]
- Wallace MT, Roberson GE, Hairston WD, Stein BE, Vaughan JW, Schirillo JA. Unifying multisensory signals across time and space. Exp Brain Res. 2004;158(2):252–258. doi: 10.1007/s00221-004-1899-9. [DOI] [PubMed] [Google Scholar]
- Warren DH, Welch RB, McCarthy TJ. The role of visual-auditory “compellingness” in the ventriloquism effect: implications for transitivity among the spatial senses. Percept Psychophys. 1981;30(6):557–64. doi: 10.3758/bf03202010. [DOI] [PubMed] [Google Scholar]
- Wei XX, Stocker AA. A Bayesian observer model constrained by efficient coding can explain ‘anti-Bayesian’ percepts. Nature neuroscience. 2015;18(10):1509–17. doi: 10.1038/nn.4105. [DOI] [PubMed] [Google Scholar]
- Wozny DR, Shams L. Computational characterization of visually induced auditory spatial adaptation. Front Integr Neurosci. 2011 Nov;4(5):75. doi: 10.3389/fnint.2011.00075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wozny DR, Beierholm UR, Shams L. Probability matching as a computational strategy used in perception. PLoS Comput Biol. 2010 Aug;56(8) doi: 10.1371/journal.pcbi.1000871. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zwiers MP, Van Opstal AJ, Paige GD. Plasticity in human sound localization induced by compressed spatial vision. Nat Neurosci. 2003;6(2):175–81. doi: 10.1038/nn999. [DOI] [PubMed] [Google Scholar]