Susceptibility Weighted Imaging: Current Status and Future Directions

Abstract

Susceptibility weighted imaging (SWI) is a method that uses the intrinsic nature of local magnetic fields to enhance image contrast in order to improve the visibility of various susceptibility sources and to facilitate the diagnostic interpretation. It is also the precursor to the concept of using phase for quantitative susceptibility mapping (QSM). Nowadays, SWI has become a widely used clinical tool to image deoxyhemoglobin in veins, iron deposition in the brain, hemorrhages, microbleeds, and calcification. In this paper, we review the basics of SWI, including data acquisition, data reconstruction and post-processing. In particular, the source of cusp artifacts in phase images is investigated in detail and an improved multi-channel phase data combination algorithm is provided. In addition, we show a few clinical applications of SWI for imaging stroke, traumatic brain injury, carotid vessel wall, siderotic nodules in cirrhotic liver, prostate cancer, prostatic calcification, spinal cord injury and intervertebral disc degeneration. As the clinical applications of SWI continue to expand both in and outside the brain, improving SWI in conjunction with QSM is an important future direction of this technology.

1. Introduction

Susceptibility weighted imaging (SWI) is a method that uses the intrinsic nature of local magnetic fields to enhance image contrast to improve the visibility of various susceptibility sources and to facilitate the diagnostic interpretation (1–8). Historically, the idea for SWI came from the fact that bulk susceptibilities change the local frequency, similar to what happens with chemical shift in spectroscopy, but in this case as a function of the geometry of the object (1–8). It is also a precursor to the concept of using phase for quantitative susceptibility mapping (QSM) (8–11). Imaging deoxyhemoglobin lies at the root of imaging veins. SWI provided a means to enhance the contrast between veins and surrounding tissue, especially as the level of deoxyhemoglobin changes in diseases such as stroke. Unlike spectroscopic imaging of metabolites where the water signal needs to be suppressed, the macro-effects of local susceptibility are immediately apparent. Further, the signatures of spheres and cylinders are unique and the polarity of each as seen in the phase images can be used to distinguish calcium from iron (which is not the case in magnitude images) (12). The only thing that had basically prevented phase from being used earlier was the fact that there were macroscopic fields permeating the image masking out the interesting structural information. The early papers on SWI dealt with this by performing a homodyne high-pass filter that basically removed all the low spatial frequencies leaving visible the now well-known local susceptibility effects of veins, microbleeds, calcium and iron deposition in structures like the basal ganglia and midbrain (3–8). Now this phase information can be used by itself (1), or to generate a new mask to enhance the contrast in the magnitude image, creating what was called the SWI data or susceptibility weighted image (8). This form is currently available on several manufacturers’ systems and it has spurred the writing of papers that cite SWI more than 1000 times in the literature, most of which are clinical in nature. The predominant use of SWI is imaging venous oxygen saturation (2–4,13,14), iron deposition (15–17) and calcification (18,19) in the brain, but there are a few studies venturing to other parts of the body such as those studying the vessel wall in the leg (20), bleeding in the spine (21) and some abdominal applications looking for either bleeding or increased iron content (22–24). The main focus in the past has been on subtle changes in susceptibility in the brain, but recently it has become clear that the past sources of angst in phase imaging, the air/tissue, bone and calcium deposits may actually be important sources of information in and of themselves (25). With the susceptibility maps in hand, one can make the next big leap to improve SWI and that is using the susceptibility maps themselves to create masks allowing for true susceptibility weighted imaging (tSWI) where phase dependence on angle and shape is no longer a concern (26,27). This may open the door to the use of susceptibility mapping methods at not just long echoes but also at short echoes, since these susceptibility effects are large enough to be easily seen there.

Although SWI is a technically straight-forward process, care should be taken to reduce unwanted and confounding artifacts which arise from sources such as air/bone-tissue interface (28) and uncompensated blood flow (29). In this paper, we will review the details in data acquisition and post-processing of SWI, and introduce strategies which may further improve its quality and accuracy. Specifically, we will discuss: 1) theories and data processing steps in SWI (homodyne high-pass filtering, susceptibility weighting mask, orientation dependence and tSWI); 2) data acquisition for SWI (echo time, resolution, simultaneous MRA/SWI); 3) data reconstruction (multi-channel phase data combination and cusp artifacts); and 4) clinical applications of SWI (imaging stroke, cerebral microbleeds, carotid vessel wall, siderotic nodules in cirrhotic liver, prostate cancer and prostatic calcification, spinal cord injury, as well as intervertebral disc degeneration). With these things in mind, we now proceed to discuss the basics of SWI followed by current and future applications.

2. Basics of SWI

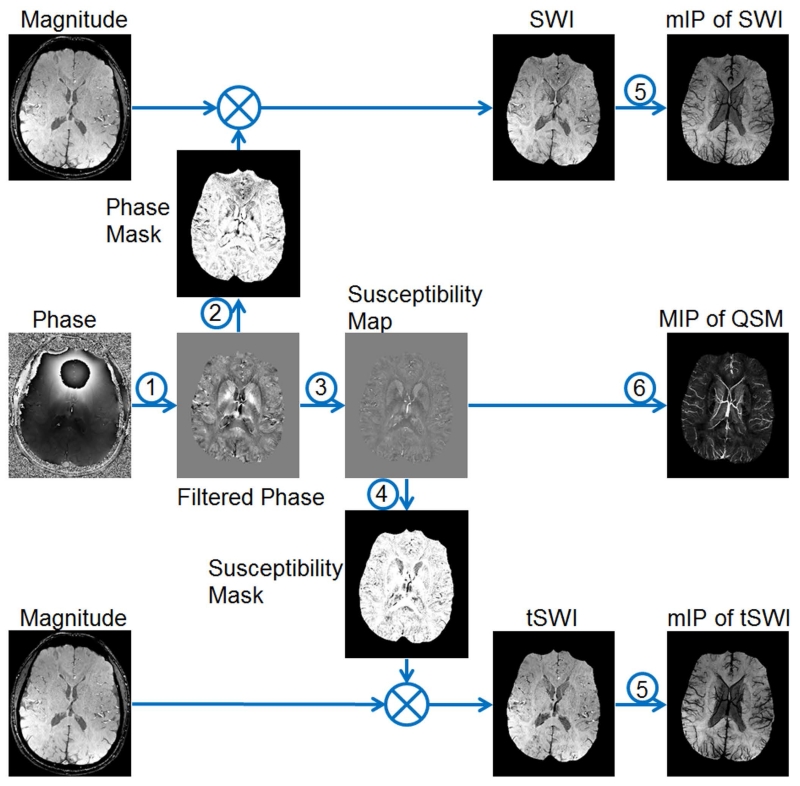
In SWI, the phase images are used to create weighting masks which will be multiplied to the magnitude images to enhance the susceptibility contrast (8,30). An overview of the data processing steps is given in Figure 1. In this section, detailed discussions on background phase removal and susceptibility weighting mask generation are provided.

Figure 1.

Overview of data processing steps in SWI. 1: background phase removal. 2: generating the weighting masks using filtered phase images for conventional SWI. 3: quantitative susceptibility mapping (QSM). 4: generating the weighting masks using susceptibility maps for tSWI. 5: minimum intensity projection (mIP). 6. maximum intensity projection (MIP).

2.1. Background phase removal

For a left-handed system, the phase of the signal acquired using a gradient-echo sequence is given as

$$\varphi \left(\mathit{r}\right)=\gamma \Delta B\left(\mathit{r}\right)\mathit{TE}+{\varphi }_0\left(\mathit{r}\right)$$ [1],

where ΔB(r) is the field variation, γ the gyromagnetic ratio, TE the echo time and ϕ₀(r) the TE-independent phase offset which is mainly related to coil-sensitivity and tissue conductivity (12,31,32). ΔB(r) contains both the components induced by the global sources such as air-tissue interface and local sources such as the susceptibility distribution of brain tissues (12). Various algorithms have been proposed to remove the former component (33–36). This background field removal step is critical to both SWI and QSM (9). In SWI, the background field is traditionally removed through the homodyne high-pass filtering (8). The sophistication of this algorithm is attributed to its simplicity in implementation and effectiveness in reducing the background field which has relatively lower spatial frequency than the local field variation. A particular advantage of homodyne high-pass filtering is that no phase unwrapping is required, since homodyne high-pass filtering is applied to the complex data directly as

$${\varphi }_{\mathit{hp}}\left(\mathit{r}\right)=\arg \{{\mathrm{e}}^{i{\varphi }_{\mathit{ori}}(r)}∕{\mathit{FT}}^{-1}[\mathit{FT}\left({\mathrm{e}}^{i{\varphi }_{\mathit{ori}}\left(\mathit{r}\right)}\right)\cdot H\left(\mathit{k}\right)\left]\right\}$$ [2],

where FT and FT⁻¹ represent the forward and inverse Fourier transform, while / and ∙ represent point-wise division and multiplication. H(k) is conventionally chosen to be the Hanning window (8,30). The size of the Hanning window applied in k-space is usually used to indicate the effects of high-pass filtering, with larger window size leads to more suppression of the low spatial frequencies (9). Typically, the window size is 64×64 for a 512×512 matrix (8). The homodyne high-pass filtering is commonly applied in 2D, i.e., in a slice-by-slice fashion. This makes it suitable for processing the data collected with not only a 3D sequence but also a 2D sequence which may cause shifts in the baseline of the phase in different slices. In addition, operating in 2D gives more flexibility in implementing the algorithm in a more time and memory efficient way. For example, one can choose to apply homodyne high-pass filtering in parallel to each slice acquired from each coil prior to the multi-channel data combination, without processing the whole 3D volumes which may require a memory size too big to be practical. This channel-by-channel high-pass filtering turns out to be advantageous for SWI in eliminating the phase singularities, known as cusp artifacts, as will be discussed in Section 4.

However, homodyne high-pass filtering may lead to a loss of phase information induced by the local susceptibility distribution (28,33,34). This will in turn lead to under-estimation of the susceptibilities in quantitative susceptibility mapping (9). One way to reduce this signal loss is to predict the field variation induced by the air-tissue interface, using a priori information about the geometries, and then remove this predicted field before applying homodyne high-pass filtering (25,28). This enables the use of a much smaller filter size and thus preserves the local phase information better, as demonstrated in Figure 2. In fact, a much milder filter can be used in the central part of the brain where the global geometry induced phase has lower spatial frequency, while a stronger filter can be used in regions close to the air-tissue interface (9). This is better than conventional homodyne high-pass filtering since more local phase information can be preserved, especially for basal ganglia structures which are usually the structures of interest for studies focused on in vivo iron deposition. For structures near the edge of the brain (e.g., the cerebral cortex), the accuracy in preserving the local phase will be much lower than in the central part. This is a common problem even for some newer algorithms (33–36). Most recently developed background phase removal algorithms are based on the spherical mean value property of harmonic functions to separate the background phase (harmonic) and the local phase (non-harmonic) (33,35,36). These algorithms have been demonstrated to be effective in preserving the local phase, much better than the conventional high-pass filtering. This is largely attributed to the deconvolution step in the end, in which the effects of spherical mean value filtering on the local phase are compensated by solving an inverse problem (33,35,36). Clearly, the accuracies of these algorithms will also be dependent on the deconvolution which requires regularization. In other background phase removal algorithms, the susceptibility distribution of the air/bone-tissue interface is estimated, in order to predict the induced field (25,34). This procedure can be performed either prior to or simultaneously with the mapping of susceptibilities of the structures inside the brain (34,37). Except for homodyne high-pass filtering, phase unwrapping is required for background phase removal (33–37). Consequently, homodyne high-pass filtering is still the most popular phase processing algorithm for SWI.

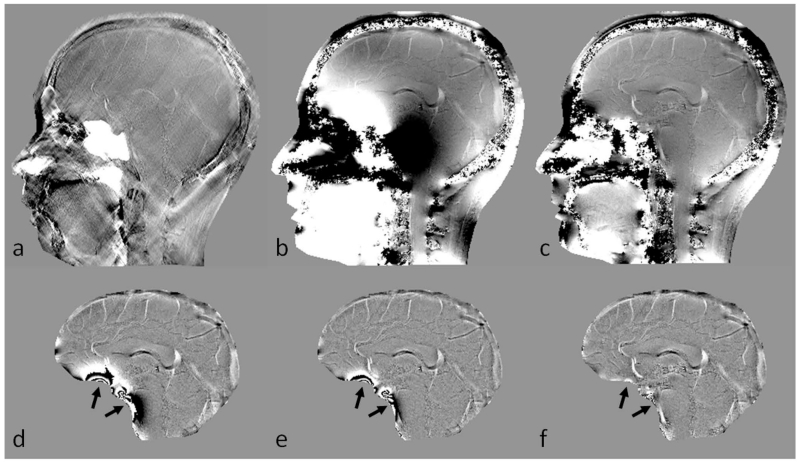
Figure 2.

Background phase removal using forward modeling. a. Susceptibility map b. Unwrapped phase image at TE = 7.5ms. c. Resultant phase after subtracting the predicted phase induced by sinuses and bones. d. Homodyne high-pass pass filtering (k-space window size = 32×32) result of b. e. Homodyne high-pass filtering (k-space window size = 64×64) result of b. f. Homodyne high-pass filtering (k-space window size = 32×32) result of c. There are still remnant background phase artifacts even after applying a 64×64 high-pass filter to the original phase image (e). Removal of the predicted phase due to sinuses and bones helped in suppressing most of this unwanted background phase, together with a milder high-pass filter (arrows in d, e and f).

2.2. Susceptibility weighting masks, orientation dependence and true-SWI

Susceptibility weighting masks are generated from the high-pass filtered phase images. Usually only the positive (negative) phase for a left- (right-) handed system will be used to enhance the contrast between iron content/veins and surrounding tissues, for images acquired in a transverse view, while the phase with the opposite sign will have a weighting factor of one:

$$W\left(\mathit{r}\right)=\{\begin{array}{cc}1-\frac{\varphi \left(\mathit{r}\right)}{\pi },\hfill & \text{for}\varphi \left(\mathit{r}\right)>0\hfill \\ 1,\hfill & \text{otherwise}\hfill \end{array}\phantom{\}}$$ [3].

In the above equation, it is assumed that |ϕ(r)| ≤ π, which is true when homodyne high-pass filtering is used. For the local phase obtained using other algorithms, W(r) is set to 0 when ϕ(r) > π.

This strategy, designed to enhance the paramagnetic content, is very effective for visualizing the veins, microbleeds etc., as has been proved in various clinical applications. One can also choose to enhance the diamagnetic content by reversing the sign of phase first and then create the weighting masks using the same procedures. However, the remnant background phase may also cause false enhancement, especially in regions close to the sinuses, which will lead to dark regions with reduced contrast on the SWI data. This can be solved by using more advanced background phase removal techniques (28,33,34,38) or using a stronger high-pass filter (39). Alternatively, regions affected by remnant background phase can be avoided in creating the susceptibility weighting masks. For example, a Fermi weighting function using the local field gradients was created to suppress the effects of remnant background phase on the weighting masks (40).

Finally, susceptibility weighted images are generated by multiplying the weighting masks into the original magnitude images:

$${\mathit{mag}}_{\mathit{SWI}}\left(\mathit{r}\right)=\mathit{mag}\left(\mathit{r}\right)\cdot W{\left(\mathit{r}\right)}^n$$ [4],

where the number of multiplications, n, is usually chosen to be 4 to maximize the CNR (8). For better visualization, a minimum intensity projection is commonly used in the end.

However, due to the orientation-dependence nature of phase information, there are also limitations in SWI related to faithfully delineating the actual geometries, especially for veins aligned at the magic angles in a high imaging resolution setting (26), as shown in Figure 3. This leads to the idea of using the susceptibility maps, instead of the phase images, to create susceptibility weighting masks (26,27). We named this method true susceptibility weighted imaging (tSWI), as the weighting is now directly associated with the susceptibility distribution, which is not dependent on orientation and imaging parameters (to a large extent). For example, tSWI has been shown to improve the delineation of the veins and microbleeds in TBI (9,26). Nonetheless, conventional SWI might be better in detecting small objects such as subvoxel microbleeds, for which the susceptibility quantification is subject to large uncertainty while the phase still clearly indicates the presence of those small objects (9).

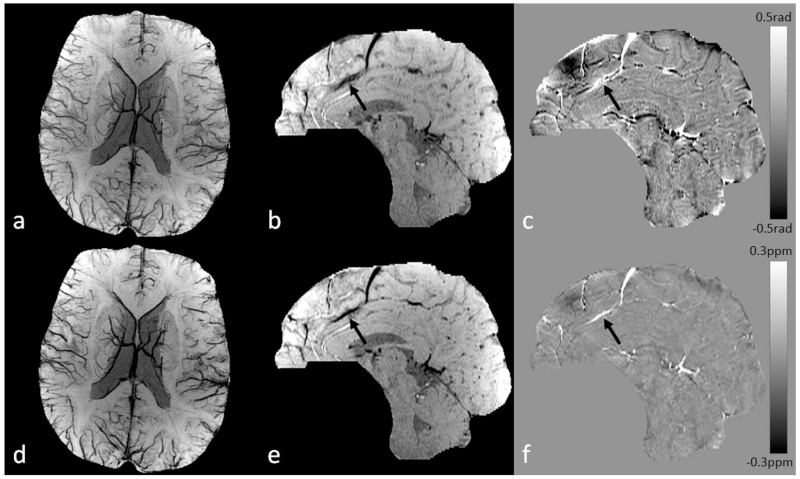
Figure 3.

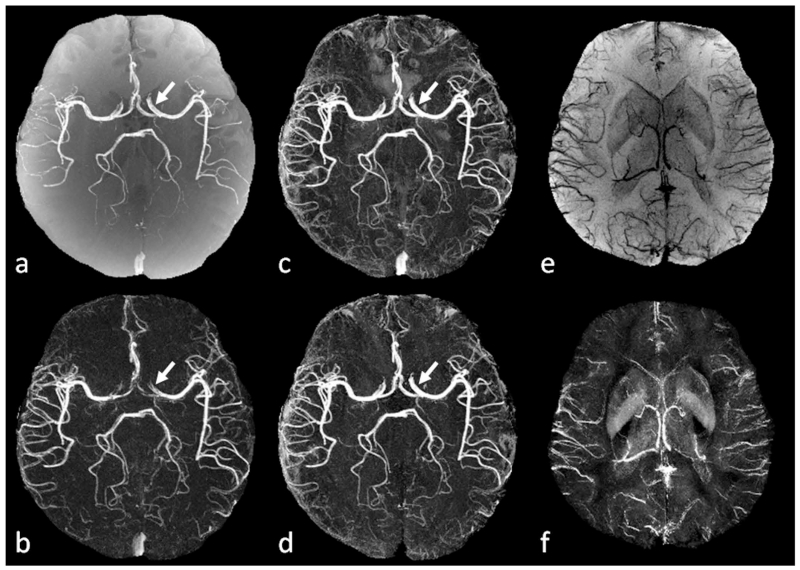
Conventional SWI vs. true SWI (tSWI). a. Minimum intensity projection (mIP) of conventional SWI. b. Single slice conventional SWI in sagittal view. c. High-pass filtered phase image. d. mIP of tSWI. e. Single slice tSWI in sagittal view. f. Susceptibility map generated from c using the geometry constrained iterative SWIM algorithm (65). The quality of conventional SWI is similar to that in tSWI for visualizing the veins in transverse view (a and d). The orientation dependent phase causes improper enhancement of the vein in sagittal view on conventional SWI (arrows in b and c). This orientation dependence is avoided in tSWI (arrows in e and f). Images in sagittal view (b, c, e, and f) are all at the same anatomical position, and were interpolated to isotropic resolution for better visualization.

3. Data acquisition

Data are conventionally acquired using gradient-echo sequences. The example imaging parameters for different SWI applications are listed in Table 1 (modified from the appendix in ref. (9)). For visualization of the veins, 3D full flow compensation (including compensation in slab select, phase and partition encoding, as well as readout directions) is preferred to avoid flow artifacts (although phase encoding and partition encoding flow compensation can be avoided but then there will be shift artifacts in fast flowing angled vessels) (12,41,29). The presence of background field gradients may cause failure in flow compensation, even with the ideal theoretically designed first order moment nulling gradients (29,42). The remnant flow induced phase components in the arteries are demonstrated in Figure 4. In addition, imaging parameters such as echo time (TE), resolution, flip angle (FA) and readout bandwidth need to be chosen properly. In order to maximize the SNR in magnitude images, a TE close to the T2* of the tissue of interest is usually used, e.g. TE=25ms for imaging veins at 3T. However, since phase is proportional to TE, longer TEs will also cause more severe phase aliasing. Depending on the susceptibility of the object of interest, a short TE might give better contrast than a longer TE, as demonstrated also in Figure 4, in which the vessel wall is better visualized at the shorter echo than at the longer echo. To reduce signal decay due to strong susceptibility effects, higher imaging resolution can be used. In that case, the recovery of the signal is attributed to the narrower phase dispersion across a voxel (12,43).

Table 1.

Examples of imaging parameters for SWI at different field strengths^a.

1.5 T	Single-echo SWI	4-echo SWI	5-echo SWI	11-echo SWI
TE (ms)	28 or 40b	10, 20, 32.5, 42.5c	7.5, 15, 22.5, 30, 40c	10 to 60, echo spacing=5ms
TR (ms)	40 (for TE=28ms) or 50 (for TE=40ms)	50	50	70
FA (degrees) d	20	20	20	20
Voxel size (mm3)	0.67×0.67×1.3	0.67×0.67×1.3	0.67×0.67×1.3	0.67×0.67×1.3
	0.5×0.5×2	0.5×0.5×2	0.5×0.5×2	0.5×0.5×2
3.0 T	Single-echo SWI	Double-echo SWI	5-echo SWI	11-echo SWI
TE (ms)	14 or 20b	7.5/17.5	5,7.5,10,12.5,16.25c; 2.5, 6.25,10, 14, 18c, e	6 to 36, echo spacing= 3ms
TR (ms)	24 (for TE=14ms), 30 (for TE=20ms)	24	24	41
FA (degrees) d	15	15	15	15
Voxel size (mm3)	0.67×0.67×1.3	0.67×0.67×1.3	0.5×0.5×2	0.67×0.67×1.3
			0.7×0.7×1.4	0.5×0.5×2
7.0 T	Single-echo SWI	Three-echo SWI	5-echo SWI	Interleaved SWI
TE (ms)	6 or 10b	3, 6, 10.5c	6, 9, 12, 16.5, 19.5c	8.25, 9, 9.75c
TR (ms)	15 (TE=6ms), 25 (TE=10ms)	15	25	45(effective)
FA (degrees) d	10	10	10	10
Voxel size (mm3)	0.5×0.5×0.5	0.5×0.5×0.5	0.5×0.5×0.5	0.5×0.5×0.5
	0.25×0.25×1.0	0.25×0.25×1.0	0.25×0.25×1.0	0.25×0.25×1.0

^aModified from the appendix in ref. (9). The other parameters such as FOV, matrix size, and BW can be chosen according to the requirements of the specific application. For applications related to imaging the veins, 3D full flow compensation for all the echoes is recommended; while for other applications, full flow compensation should be applied for the first echo if possible. A particular sequence should be chosen based on the purpose of the application. For example, multi-echo sequences provide more flexibility in selecting the TEs and can be used for imaging stroke, CMBs, spine and other structures with a wide range of susceptibilities. See Haacke et. al 2015 (9) for a more detailed version of example imaging parameters for SWI and QSM.

^bThe choice of the shorter TE for single-echo SWI sequence is to reduce phase aliasing, in order to improve the quality and accuracy of SWI. This is primarily for imaging structures with high susceptibilities such as veins or microbleeds with high iron content. Otherwise, the longer TE can be used (or increased to even longer) to further improve GM/WM contrast but at the expense of much worse aliasing and T2* signal loss in other parts of the brain.

^cThese TEs are chosen, so that one can get low effective TE for better phase unwrapping and separating water and fat.

^dThe FAs were chosen to accommodate a wide range of T1s in the brain, and can be changed according to the square root of TR.

^eThis sequence is for imaging sinuses, bones and teeth in the head and for imaging cervical spine.

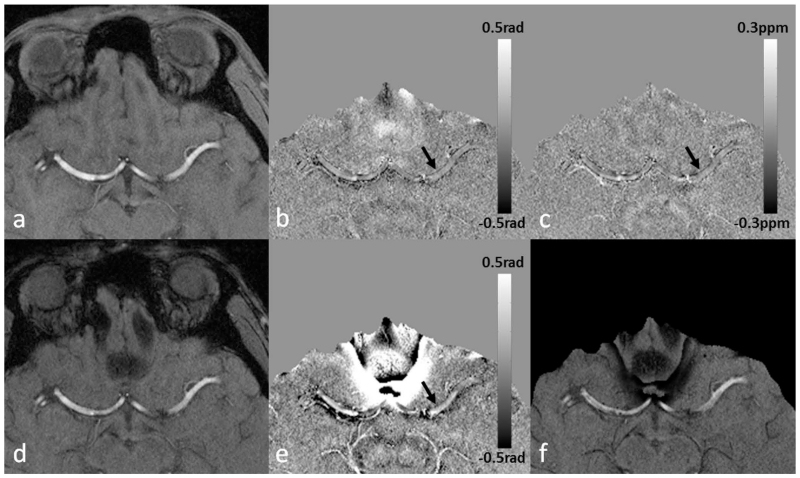
Figure 4.

The remnant flow induced phase and the visualization of the vessel wall of MCA on SWI and QSM. Data were collected using a fully flow-compensated double-echo sequence with TE1=7.5ms, TE2=17.5ms. a. Magnitude image at TE1. b. High-pass filtered phase image at TE1. c. Susceptibility map generated from b using a truncated k-space division algorithm with a k-space threshold 0.2 (64). d. Magnitude image at TE2. e. High-pass filtered phase image at TE2. f. SWI generated using e. On the filtered phase images, the vessel wall is better visualized at the shorter echo (b) than at the longer echo (e). The diamagnetic property of the vessel wall can be seen from both the filtered phase image and the susceptibility map (arrows). The remnant phase in the arteries indicates errors in flow compensation, mainly due to the presence of background field gradients.

SWI data can be acquired using either a single or multi- echo sequence, with the latter providing more flexibility in choosing echo times which will affect the image contrast due to susceptibility effects (39,44–46). When multi-echo data are available, it is possible to obtain MR Angiography (MRA) and SWI simultaneously, which are both necessary to depict the cerebral vascular system morphologically and functionally (47). We have developed a new interleaved double-echo sequence with arbitrary TEs to achieve simultaneous high resolution MRA and venography (48), through enhanced time of flight (TOF) angiography and SWI, allowing clear separation of arteries and veins in a single scan. One particular advantage of this sequence is that the interleaved images are precisely aligned to each other and, hence, image registration is not required. In this sequence, two consecutive TR blocks were executed with two echoes for each block (referred to as echo₁₁, echo₁₂, echo₂₁ and echo₂₂). Specifically, echo₁₁ echo₁₂, and echo₂₁ are flow rephased using first order moment nulling gradients. On the other hand, echo₂₂ is flow dephased using bipolar gradients with a low VENC value. A conventional TOF-MRA image can be generated as the average of echo₁₁ and echo₂₁. While echo₁₂ provides the SWI image, echo₂₂ provides the dark blood image. A direct subtraction between echo₁₂ and echo₂₂ removes the background tissues, leading to an enhanced MRA image (since the veins are dark in both images), as shown in Figure 5. Although the visualization of small vessels with slow blood flow is excellent, the longer echo times sometimes have difficulties portraying the larger arteries with fast flow near the sinuses, because of the presence of background field gradients that destroy the flow compensation (29). To overcome this problem, another enhanced MRA image can be obtained from a linear subtraction between the TOF-MRA (average of echo₁₁ and echo₂₁) and the flow dephased second echo (echo₂₂) as (echo₁₁+echo₂₁)/2−λecho₂₂, where λ was set to 1.3 to compensate for the T2* signal decay at the longer echo. Finally, utilizing the magnitude, phase and susceptibility maps, the veins can be suppressed and an improved MRA image can be obtained. Now there is no difficulty in visualizing the major arteries such as the internal carotid arteries and the middle cerebral arteries (Figure 5.d), because of the use of the shorter echo which leads to better flow compensation.

Figure 5.

Simultaneous MRA, SWI and QSM using the interleaved double-echo sequence. Data were collected on a Siemens 3T Verio system using a 32 channel head coil, with TE1/TE2/TR=6/19.2/24ms, FA=15° and voxel size 0.6×0.6×1.2mm³. a. TOF-MRA generated as the average of echo₁₁ and echo₂₁. b. Enhanced MRA by subtracting echo₂₂ from echo₁₂. c. Enhanced MRA by subtracting echo₂₂ from a (TOF-MRA). d. Enhanced MRA after venous structures were removed from c. e. Minimum intensity projection of SWI data generated from echo₁₂. f. Maximum intensity projection of susceptibility maps generated from echo₁₂, using the geometry constrained iterative SWIM algorithm (65). Small arteries are clearer on b and d than on a. Internal cerebral arteries, middle cerebral arteries and anterior cerebral arteries are better visualized on d than on b (arrows), due to the better flow compensation at the shorter echo. See the main text for the definition of different echoes.

4. Data reconstruction

Proper reconstruction of the phase images from a gradient echo sequence is critical for both SWI and QSM, since any noise or artifact in the phase images will be propagated into the final results during the phase unwrapping and/or background phase removal (41,49,50). While SWI and QSM may be largely affected when severe signal cancelation occurs due to improper combination, local cusp artifacts could also be mis-interpreted as microbleeds (9,51).

When GRAPPA is used for parallel imaging, magnitude and phase images will be reconstructed for each channel of the phased array coil and then combined to generate the final images (52–54). The optimal combination requires knowledge of the coil sensitivities which are usually not available (55–58). Using the conjugates of the complex data as an approximation of the coil sensitivity leads to the sum-of-squares combination which provides a near optimal combination of the multichannel data when SNR is sufficiently high (55). For phase images, however, a simple magnitude weighted averaging of the complex data may lead to phase singularities/cusp artifacts in the combined phase images, mainly attributed to the variation in the coil sensitivity induced phase components between different coils/channels (53,54,59–61). Based on Eq. 1, the phase from channel j in a left-handed system can be written as:

$${\varphi }_j\left(\mathit{r}\right)=\gamma \Delta B\left(\mathit{r}\right)\mathit{TE}+{\varphi }_{0,j}\left(\mathit{r}\right)$$ [5],

where ϕ_0,j(r) is the coil sensitivity dependent phase. A commonly used strategy is to model the ϕ_0,j(r) as a constant and the baseline of the phase images in each channel is registered to that of a selected reference channel, where the baseline is estimated using central voxels with sufficiently high SNR (53). This approach, referred to as the constant phase offset algorithm in this paper, eliminates cusp artifacts in the central part of the field of view. However, the quality of the combined phase images will be dependent on the selected region since ϕ_0,j(r) is not spatially uniform, as demonstrated in Figure 6. A more sophisticated approach is to use either a body coil or multi-echo data to calculate ϕ_0,j(r) explicitly (54,60). Specifically, when a double-echo sequence is used,

$${\varphi }_{0,j}\left(\mathit{r}\right)=\frac{\left[\mathrm{TE}2{\varphi }_{\mathrm{TE}1,\mathit{j}}\right(\mathit{r})-\mathrm{TE}1{\varphi }_{\mathit{TE}2,j}(\mathit{r}\left)\right]}{\mathrm{TE}2-\mathrm{TE}1}$$ [6].

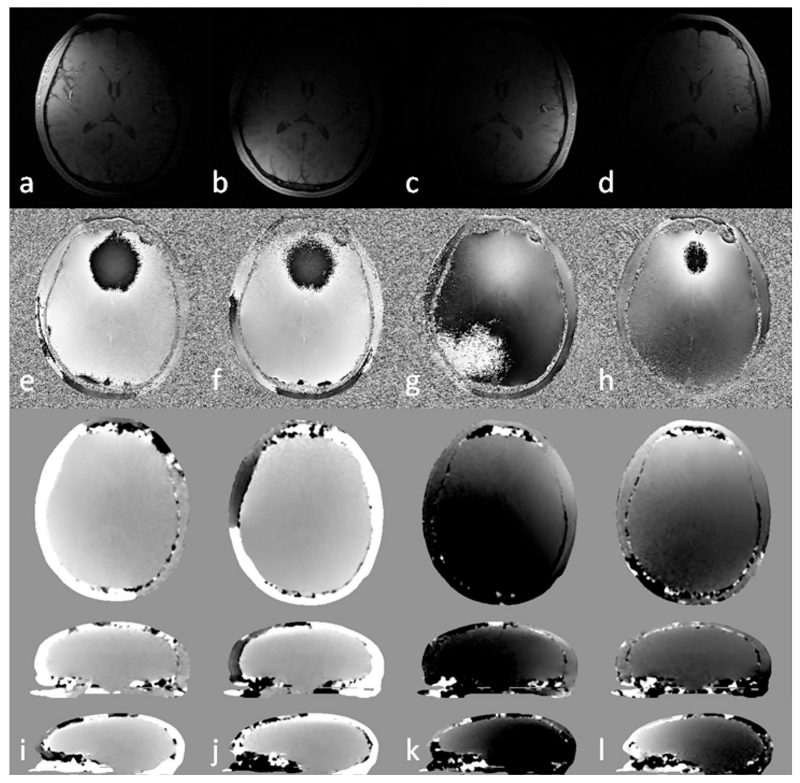
Figure 6.

Magnitude images (a to d), phase images (e to h) and the estimated coil sensitivity related phase in different views (i to l) for 4 different channels (columns). See the main text for details of the calculation of the coil sensitivity related phase. Images in sagittal view were scaled for better visualization. Multi-channel data combination without considering the variation in the sensitivity related phase components between different channels leads to singularities or cusp artifacts in the combined phase images.

However, this approach requires extra scans/echoes and time-consuming data processing such as unwrapping the phase of every channel (54). In this paper, we demonstrate an improved algorithm over the constant phase offset algorithm, referred to as echo center correction (ECC) algorithm. Particularly, the coil sensitivity induced phase component (Figure 6) is modeled as a 3D linear function which can be determined and corrected effectively in k-space (12,62). This is particularly convenient for integrating this algorithm into the image reconstruction pipeline of the MR scanner. When modeled as a 3D linear function, ϕ_0,j(r) can be approximated as:

$${\widehat{\varphi }}_{0,j}\left(\mathit{r}\right)={\beta }_j\mathit{r}+{\varphi }_{c,j}$$ [7].

The gradient β_j = [β_x,j, β_y,j, β_z,j] can be estimated from the position of the element with maximum magnitude value in k-space (denoted as k_max,j), using the Fourier shift theorem, while the constant phase offset ϕ_c,j can be estimated from ϕ_c,j = arg (k_max,j). After that, ${\widehat{\varphi }}_{0,j}\left(\mathit{r}\right)$ can be removed from the original phase images through complex division. In order to improve the accuracy of estimating the linear gradients, the central part of k-space can be interpolated by a factor of 2, through zero-filling in the image domain. Also note that it is only the peak of k-space that is of importance to this algorithm. Hence, the proposed algorithm can be applied using only the data in the central part of k-space, which also makes this algorithm both memory and time efficient. Finally, the phase images from all the N channels can be combined by averaging the complex data, weighted by the square of the magnitude:

$${\varphi }_{\mathit{comb}}\left(\mathit{r}\right)=\arg \left\{{\Sigma }_{j=1}^N{\mathit{mag}}_j^2\right(\mathit{r}\left)\exp \right[i{\varphi }_j\left(\mathit{r}\right)-i{\widehat{\varphi }}_{0,j}\left(\mathit{r}\right)\left]\right\}$$ [8].

The proposed algorithm was tested using in vivo data collected on a 3T Siemens system equipped with a 32-channel head coil, using a fully flow compensated double-echo sequence with the following imaging parameters: TE1=7.38ms, TE2=17.6ms, TR=30ms, FA=15°, BW/px=425Hz/px, voxel size=0.6×0.6×1.2mm³, matrix size=512×368×144, GRAPPA acceleration factor=2. In order to compare different coil combination algorithms, the phase images were combined using: 1) simple magnitude weighted averaging; 2) the constant phase offset algorithm, in which the differences between the ϕ_0,j(r) in each channel and the user-defined reference channel were estimated from 32×32×32 central voxels in image domain; 3) the double-echo phase combination: ϕ_0,j(r) was obtained using Eq. 6 for each channel (a 5×5×5 median filter was applied to ϕ_0,j(r), in order to reduce the random noise. Then the phase images were created following Eq. 8 for each echo); 4) the proposed ECC algorithm; and 5) a channel-by-channel high-pass filtering: 2D homodyne high-pass filter with k-space window size 64×64 was applied to the phase images of each channel, and then the filtered phase images were combined using magnitude weighted averaging similar to Eq. 8. For generating SWI and QSM data, the phase images combined using algorithm 5 were used directly, without further phase unwrapping or background phase removal, since the combined phase images were effectively high-pass filtered already. On the other hand, background phase removal is still required prior to generating the SWI and QSM data using the phase images combined through algorithms 1 to 4. For generating SWI data, homodyne high-pass filter (with 64×64 k-space window size) was applied. For generating QSM data, Laplacian phase unwrapping (9) was used for the phase images combined using algorithm 1, for better handling of the expected cusp artifacts; while 3D path-following phase unwrapping (63) was used for the phase images combined using algorithms 2 to 4. Next, SHARP was applied to remove the background phase and a geometry constrained iterative SWIM algorithm (64,65) was used to generate the susceptibility maps.

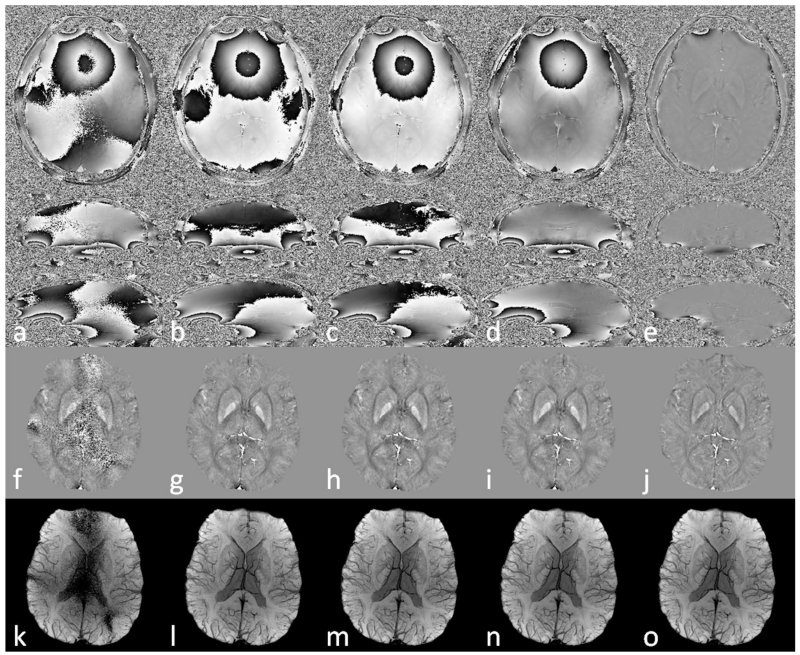
As shown in Figure 7, a simple magnitude weighted combination without considering the coil-sensitivity related phase components resulted in reduced SNR and cusp artifacts in the combined phase images. These artifacts propagated into QSM and SWI data. Using constant phase offset, double-echo combination and ECC algorithms, cusp artifacts were avoided from the combined phase images, leading to significantly improved quality in both QSM and SWI data. Comparing all the combined phase images in Figure 7, it can be concluded that the ECC algorithm eliminated the cusp artifacts and provided phase images with the most uniform profile, reflecting the proper handling of the coil sensitivity related phase components. On the other hand, the constant phase offset did not account for the spatial variation of the coil sensitivity and the combination was affected by the choice of the reference channel. Although ϕ_0,j(r) was determined using the double-echo method, the combined phase images had slightly lower SNR due to the noise amplification through Eqs. 6 and 8. It is also assumed that the ϕ_0,j(r) terms in different echoes are the same, without any additional background phase components such as those induced by eddy current effects; while the ECC algorithm can correct any linear background phase. This explains the differences between the results obtained using the double-echo combination and using the ECC combination. When a homodyne high-pass filter was applied to each channel prior to the combination, the combined phase images were not affected by cusp artifacts. However, this caused signal loss to the local phase and under-estimation in susceptibility quantification. For SWI, either the ECC algorithm or the channel-by-channel high pass filtering algorithm can be used.

Figure 7.

Comparison of the effects of different multi-channel data combination algorithms on phase images (a to e), QSM (f to j) and SWI (k to o). a, f, k: simple magnitude weighted averaging. b, g, i: constant phase offset algorithm. c, h, m: double-echo phase combination. d, i, n: echo center correction (ECC) algorithm. e, j, o: channel-by-channel high-pass filtering. Data were collected using a double-echo sequence with TE1=7.38ms and TE2=17.6ms. Only the results correspond to TE2 are shown here.

5. Clinical applications of SWI

5.1. Imaging stroke

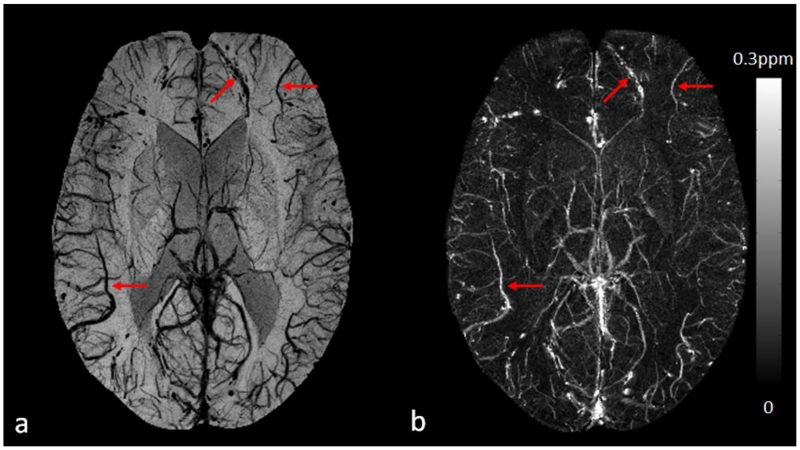
One of the most important recent applications of SWI is imaging stroke. It is well known that reliable detection of the ischemic penumbra has a significant impact on treatment and management, especially for acute stroke patients who might benefit from the thrombolytic therapy (66–69). The DWI-PWI mismatch is generally considered as the indicator of salvageable brain tissue with hypo-perfusion but preserved metabolic rate, despite the limitations such as the imprecise definition of perfusion deficit (68–74). In order to improve the detection of the penumbra, newer methods have been proposed exploiting T2* signal variation due to the change in deoxyhemoglobin/hemoglobin ratio, based on the fact that the oxygen extraction fraction in the ischemic penumbra is increased as a compensatory mechanism in response to misery perfusion (73–76). Because of its utilization of phase information, which is exquisitely sensitive to the changes in oxygen saturation of the blood, SWI could be a powerful tool for better detection of the ischemic penumbra (69,77). The potential of using SWI to image cerebral venous oxygen saturation is demonstrated in Figure 8 in which a clear trend of enhancing visibility of the veins on SWI can be observed, accompanied by increasing susceptibilities of the veins on QSM, from post acetazolamide administration, to normal state, and then to post caffeine administration, reflecting the increasing deoxyhemoglobin concentration in the veins.

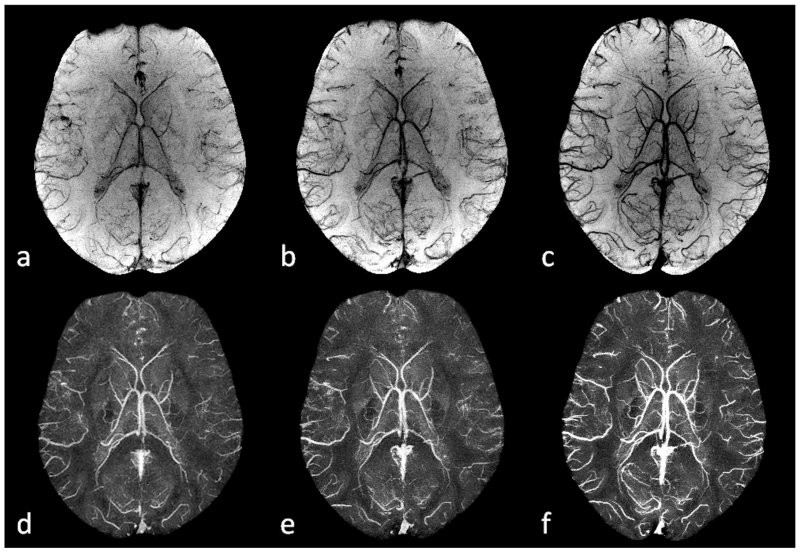
Figure 8.

Imaging cerebral venous oxygen saturation under different conditions using SWI and QSM. a and d: post acetazolamide administration. b and e: normal state. c and f: post caffeine administration. Here a to c are the minimum intensity projections of SWI, while d to f are the maximum intensity projections of the susceptibility maps generated using the geometry constrained iterative SWIM algorithm (65). The effective slice thickness is 20mm for all the images. Both the enhanced visibility of the veins on SWI from a to c and the increased susceptibilities on QSM from d to f reflect the increasing concentration of deoxyhemoglobin in the veins. The data for the acetazolamide and caffeine experiments were collected on different days, while the data for the normal state were collected before the caffeine administration during the caffeine experiment.

In fact, asymmetrically prominent cortical veins (APCVs) are usually observed on SWI in stroke patients, even in regions outside those with restricted diffusion on DWI (78–87). This is referred to as the DWI-SWI mismatch. Furthermore, it was found that the DWI-SWI mismatch correlates with the DWI-PWI mismatch and SWI could be a surrogate for PWI (80,81,86), as shown in the example in Figure 9. However, this correlation could be compromised in the presence of leptomeningeal arterial collateralization (84). Consequently, SWI could be an important technique in stroke imaging which provides high resolution local information of the oxygen extraction fraction yet does not require the use of a contrast agent. Nevertheless, further studies which include a sufficient number of subjects are still required.

Figure 9.

A 77-year-old male who suddenly had left limb weakness and paresthesia underwent an MR scan with PWI and SWI 3 hours after stroke. MTT (a) showed a large hypo-perfused region in the right lateral hippocampus and occipital lobe, while SWI (b) showed asymmetrically prominent cortical veins (APCV) in the corresponding region, as indicated by the red contour in b. Six days after intravenous rTPA treatment, with improved neurological symptoms, the patient underwent a second MR scan with PWI-MTT (c) and SWI (d), in which both MTT and SWI appeared normal.

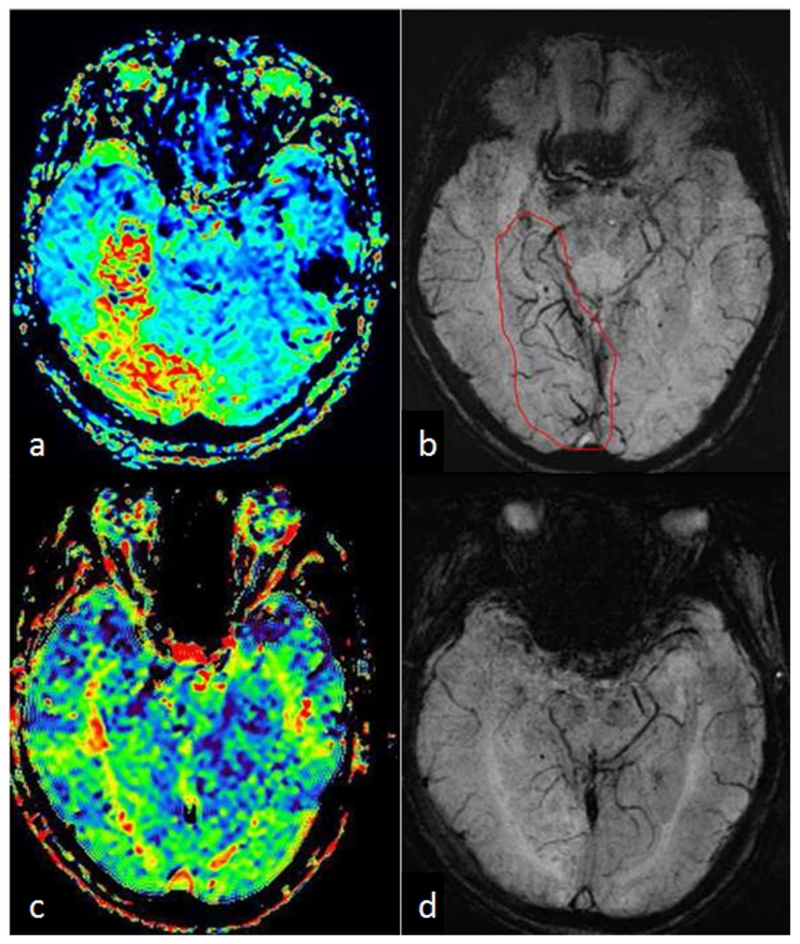
Moreover, the accuracy of detecting the penumbra using SWI could be affected by the orientation of the veins and imaging parameters (26). This problem can be solved by using QSM, the quantitative version of SWI (9,26). The potential of QSM has been demonstrated in a recent study, in which Xia et al. (88) compared the susceptibility value of cortical veins in the left and right hemispheres of healthy controls as well as in the contralateral hemisphere of stroke patients with APCVs. It was concluded that the occurrence of APCVs in ischemic stroke patients in SWI data was best explained by the increased deoxyhemoglobin concentration in the APCVs. In that study, a 16% to 44% decrease of the oxygen saturation of the APCVs was found, compared with that in the contralateral hemisphere (Figure 10). SWI has also been used to detect occlusive arterial thromboemboli (87,89,90). The sensitivity of SWI to arterial thrombus was found to be better than both CT and FLAIR images (89,90). In the disease of venous occlusion, there is collateral circulation and decreased oxygen saturation in the veins (91,92), as shown in Figure 11. The increased cerebral venous oxygen saturation may correspond to early recanalization or collateral venous drainage.

Figure 10.

Visualization and quantification of asymmetrically prominent cortical veins (APCV) in an ischemic stroke patient using SWI and QSM. a. DWI showed multiple high signal regions in the centrum semiovale and in the genu of the corpus callosum. b. Visualization of the APCV in the left hemisphere in the minimum intensity projection of SWI data. c. Maximum intensity projection of susceptibility maps showing cortical veins with increased susceptibility in the ischemic hemisphere, compared to those in the contralateral hemisphere. Susceptibility maps were generated using the geometry constrained iterative SWIM algorithm (65).

Figure 11.

Visualization and quantification of the susceptibility of bilateral cortical veins in a 19-year-old female patient with right transverse sinus thrombosis. The right transverse sinus is less hypo-intense than normal on T2WI (a) and markedly hypo-intense and dilated on SWI (b), suggestive of early thrombosis. Bilateral cortical veins were dilated and increased levels of deoxyhemoglobin were indicated on the minimum intensity projection (mIP) of the SWI data (c) and the maximum intensity projection (MIP) of the QSM data (d). In the follow-up scan, both the T2WI (e) and the original magnitude image in the SWI data (f) showed hyper-intensity in the right transverse sinus, possibly due to evolving blood products in the thrombus (white arrows). Although a normal flow void did not return on T2WI, the increased oxygen saturation of the cortical veins may suggest early recanalization or collateral venous drainage in the brain, as indicated by both the mIP of SWI data (g) and the MIP of QSM data (h). For a to d, the original data were acquired at 1.5T (where the echo time of the SWI data was 40ms); while for e to h, the original data were acquired at 3T (where the echo time of the SWI data was 20ms). Susceptibility maps in d and h were generated using a truncated k-space division algorithm (64) with a k-space threshold 0.2. The effective slice thickness is 24mm in c, d g, and h.

5.2. Imaging microbleeds with SWI

Cerebral microbleeds (CMBs), “small foci of chronic blood products in normal or near normal brain tissue” as described by Greenberg et al. (93), are commonly seen as round hypo-intense signal void on T2* weighted images (T2*WI). Multiple studies have shown that SWI is much more sensitive in detecting the presence of CMB than standard gradient-echo sequences (94–98). This is largely due to the sensitivity of SWI to blood products, the higher resolution in which SWI is usually collected, and the increased contrast SWI provides between normal parenchymal tissue and abnormal iron deposition (8,41). The detection of CMBs is usually based on the shape and the characteristics of the signal, such as signal intensity and blooming effects (93,99). Although the size of bleeding ranges between micro and macro hemorrhages, it is generally agreed that CMB can be defined as having a diameter of less than roughly 5mm (93). Other criteria based on T1 or T2 weighted images as well as the clinical history also help to improve the detection (93,100). In fact, the appearance of candidate CMBs are best confirmed when all components of SWI data (i.e., magnitude and phase images) are reviewed simultaneously, as demonstrated in Figure 12. The CMB should be partly surrounded by normal parenchyma and should be independent of vascular structures. In the phase image, a paramagnetic dipole effect should be associated with the CMB, and when reconstructed using QSM it should appear bright or highly paramagnetic. This differentiates CMBs from calcification which is diamagnetic (101). It should also be noted that the detection of CMBs may also depend on the imaging parameters such as field strength, echo time, and imaging resolution (93,102–104). While the first two parameters determine the phase information and blooming effects, imaging resolution may affect the accuracy of CMB detection through partial volume effects (9).

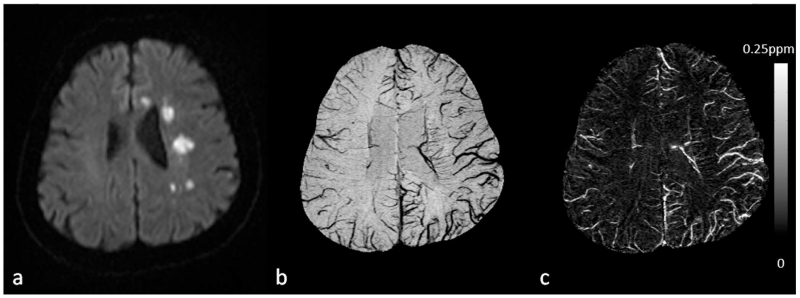
Figure 12.

Imaging cerebral microbleeds (CMB) using SWI and QSM. For this patient, there is a single CMB that is not visible in either T2WI (a) or FLAIR (d), but can be seen in the original magnitude (b) and filtered phase images (c) in the SWI data (white arrows). The CMB can be better visualized in the minimum intensity projection of SWI data (e) and the maximum intensity projection of susceptibility maps (f) (white arrows). The CMB appears as hypo-intense in b and e, while hyper-intense in c and f, indicating that it is paramagnetic. Note that the phase image shown in c was from a left-handed system. There is no connection between the CMB and vessels, as can be seen in both e and f. Susceptibility maps were generated using the geometry constrained iterative SWIM algorithm (65). The (effective) slice thickness is 2mm in a, 1.5mm in b and c, 0.5mm in d, 12mm in e and f.

Several diseases have benefitted from the use of SWI as a means for detecting CMB, including traumatic brain injury (TBI), stroke, and dementia (93,105–109). In TBI, Spitz et al. demonstrated that SWI detected far more TBI related lesions than FLAIR (110). In addition, it was found that the lesion volume on SWI correlated with the severity of the injury, while the lesion volume on FLAIR did not, although the lesion volumes measured by both techniques did show a positive correlation with the cognitive impairment. Liu et al. also demonstrated in a military cohort that had experienced TBI, SWI was the most effective method available compared to conventional MRI scanning to detect CMB. In their study, 77% of CMB appeared more clearly on SWI than on conventional MRI (111). This finding in the detection of CMB is quite common. While standard 2D gradient-echo sequence may find similar results in the prevalence of a sample who are CMB positive, the actual count of CMB which are identified using SWI may be almost doubled compared with 2D gradient-echo sequence (96,103,112). In addition to the detection of primary CMBs, SWI may also be used to evaluate the secondary CMBs and the oxygen saturation of local veins in areas suffered from ischemic hypo-perfusion due to diffuse axonal injury associated with head trauma (113,114), as shown in Figure 13. It was found that the susceptibilities of small hemorrhages were significantly higher than that of major veins, with a susceptibility threshold of 200ppb giving 92% for both sensitivity and specificity (114). In stroke, the presence of CMB must be evaluated for thrombolytic therapy to prevent secondary symptomatic intracranial hemorrhage (ICH). It was shown that SWI provide critical information for the treatment planning of antiplatelet therapy (115). It was also found that in patients affected by ischemic stroke or transient ischemic attack, multiple CMBs were associated with significantly increased risk of future ICH (116). The location of the CMBs may be associated with different pathologies, with deep CMBs being related to hypertensive vasculopathy while lobar CMBs being related to cerebral amyloid angiopathy (CAA) (93). For example, the presence of multiple or mixed CMBs was found to be correlated with increased risk in dementia (117,118). Even in normal elderly people with incidental cortical CMBs, significantly reduced cerebral blood flow (CBF) was observed which may be associated with increased risk of neurodegeneration (119). The increased rate of CMB proliferation can also be used as a method of diagnosis (106). In summary, the accurate detection and quantification of microbleeds is critical to the patient’s diagnosis and prognosis.

Figure 13.

Visualization and quantification of cortical veins on SWI (a) and QSM (b) in a 32-year-old male patient with diffuse axonal injury due to a traffic accident. The cortical veins near the cerebral microbleeds can be clearly seen in the frontal and parietal lobes (red arrows). Susceptibility maps were generated using the geometry constrained iterative SWIM algorithm (65).

5.3. Imaging the carotid vessel wall

Stroke is the second leading cause of death in the world, and carotid artery disease is one of most common causes of ischemic stroke (120,121). Symptomatic patients with high grade carotid stenosis may have vulnerable carotid plaques, as found in randomized controlled studies, the North American Symptomatic Carotid Endarterectomy Trial (NASCET) (122) and the European Carotid Surgery Trial (ECST) (123). However, vulnerable carotid plaques are not visible in angiography. Therefore, vessel wall imaging is indispensable for both the diagnosis and monitoring of treatment responses. In the field of cardiovascular disease, plaques with high-grade stenosis may not cause cardiovascular events, but those with low-grade stenosis may cause stroke (124). Better predictions of cardiovascular events can be achieved using carotid vessel wall imaging combined with the Framingham risk factors, including old age, male gender, high total cholesterol, low high-density lipoprotein (HDL), smoking, and high systolic blood pressure (125,126).

Both ultrasound and computed tomography (CT) have been applied to imaging carotid vessel wall. Using ultrasound, it is found that lipid-rich necrotic core and intraplaque hemorrhage (IPH) are components of vulnerable plaques, and echo lucent plaques are associated with high risk of stroke (127). Another important finding of vulnerable plaque is that the vasovasorum-derived neovascularization, which comes from inflammation, is well correlated with findings of contrast-enhanced ultrasound (128). However, ultrasound has limitations in evaluation of densely calcified plaques due to a limited acoustic window beyond calcification. Although CT is generally considered to be the best modality for imaging calcification, it has low CNR for soft tissue. Using a combination of MR sequences such as TOF-MRA, T1WI, T2WI, and proton density weighted imaging, advanced lesions can be distinguished from early and intermediate atherosclerotic plaques (129), and the results showed good correlation with the histological studies on carotid endarterectomy specimens (130).

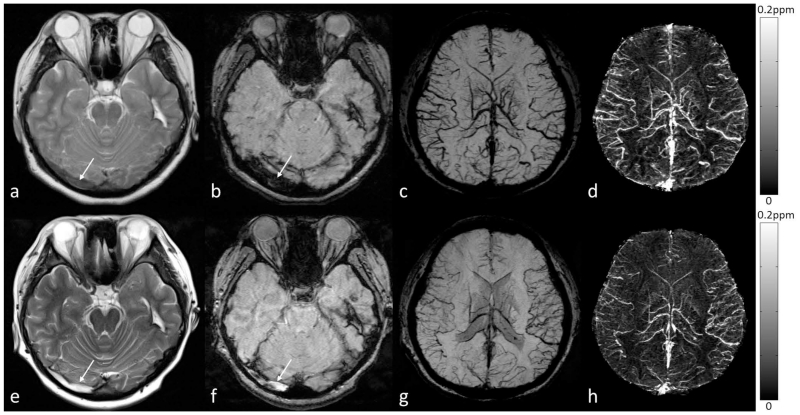
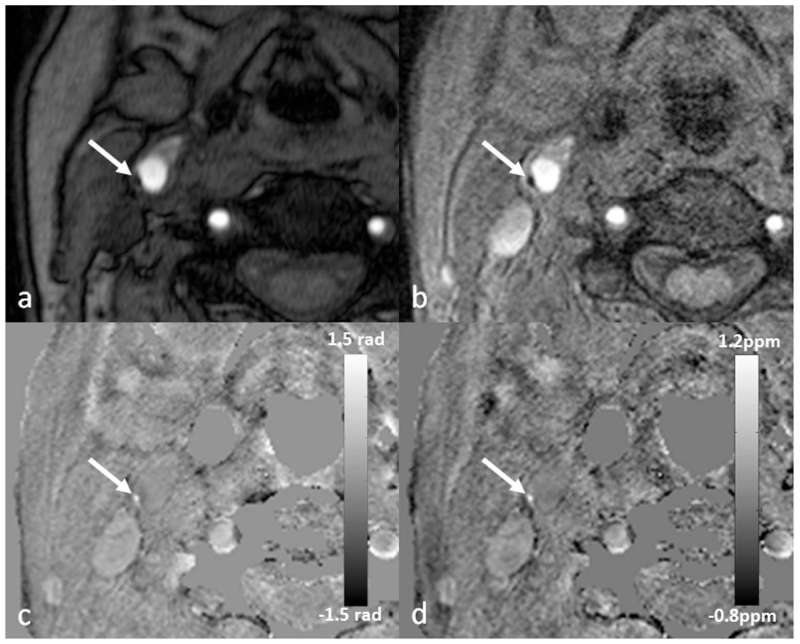
Nonetheless, for imaging complex plaques with features of large lipid-rich core, IPH, neovascularization, and inflammation (131–134), SWI has unique advantages over conventional techniques. IPH is usually defined as a two-fold hyper-intense signal within the carotid wall compared with adjacent sternocleidomastoid muscle. Normal vessel walls and calcification are diamagnetic (20,135), while IPH is paramagnetic. This leads to opposite phase polarities, which could be utilized in SWI and QSM for better differentiation of calcification from IPH (41,136,137). Although the detection and quantification of tiny foci of hemorrhage in asymptomatic carotid plaque is now possible using SWI (Figure 14), more research should be performed to investigate the sensitivity and specificity of SWI for imaging carotid plaques.

Figure 14.

Eccentric wall thickening (arrow) at the posterolateral aspect of the right common carotid artery on TOF-MRA (a). There is a dark spot on the magnitude image (b), which appears bright on both the filtered phase image (c) and the susceptibility map (d). This suggests that this is a tiny foci of intraplaque hemorrhage and may represent an example of vulnerable plaque. The original data for b, c and d were acquired using a multi-echo SWI sequence at 3T, although these images were generated using the data from the shortest echo with TE=5.18ms. Image c was generated using a homodyne high-pass filter with k-space window size 64×64, while d was generated using a truncated k-space division algorithm (64) with a k-space threshold 0.2.

5.4. Imaging siderotic nodules in cirrhotic liver

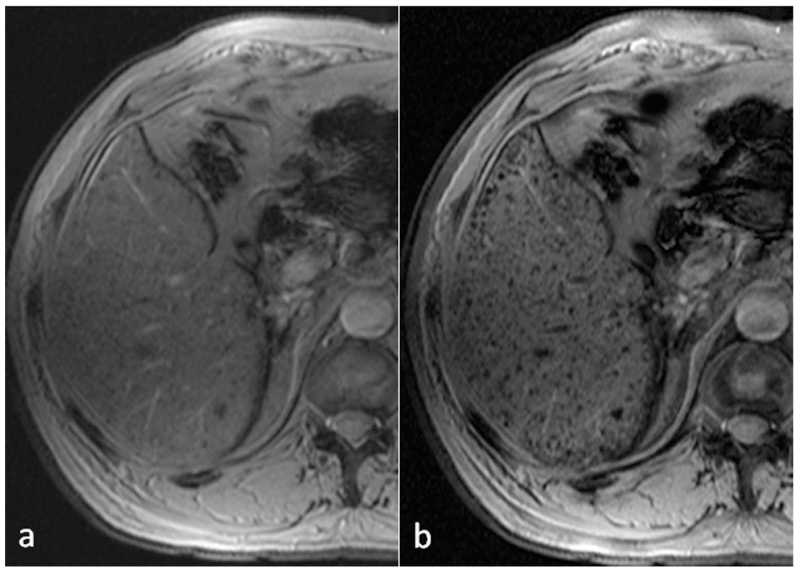
Inspired by the successful applications of SWI in neuro-imaging and motivated by the goal to improve the research and diagnosis of iron-related diseases, SWI has been extended to organs outside the brain (22,24,138,139). A typical abdominal application of SWI is imaging siderotic nodules in hepatic cirrhosis (22). It is well known that iron plays a significant role in the development of chronic hepatitis, hepatic cirrhosis, and hepatic carcinoma. For cirrhosis patients, liver iron may be accumulated within the siderotic nodules, even without iron overload disorders (22,140,141). However, the mechanism of iron deposition in the formation of siderotic nodule is still unclear, partly due to the inadequacy in detecting iron deposition in cirrhotic liver using conventional T2*WI (22), as demonstrated in Figure 15.

Figure 15.

Comparison of T2*WI (a) and SWI (b) for the detection of siderotic nodules (SN) in cirrhotic liver disease. The number of detected SN was 30 on T2*WI (a), and 139 on SWI (b). In the whole liver, the number of SN detected by SWI was nearly 5 times that detected by T2*WI (393 by T2*WI vs 1856 by SWI).

Different from the conventional three-dimensional gradient-echo sequence used in neuro-imaging, a two-dimensional multi-breath-hold gradient-echo sequence together with improved post-processing help to reduce the respiratory motion artifacts in liver imaging (22). As expected, SWI outperformed T2*WI in the detection of siderotic nodules, with SWI being approximately two times more sensitive to the presence of siderotic nodules than T2*WI. It was also observed that certain siderotic nodules with low iron content can only be detected by SWI. Besides the detection of siderotic nodules, SWI has been applied to detecting hemorrhage in hepatic lesions and grading liver cirrhosis (138,142). Using the phase information or the derived susceptibility distribution, it is also possible to quantify liver iron concentration using SWI and QSM (143,144).

5.5. Imaging prostate cancer and prostatic calcification

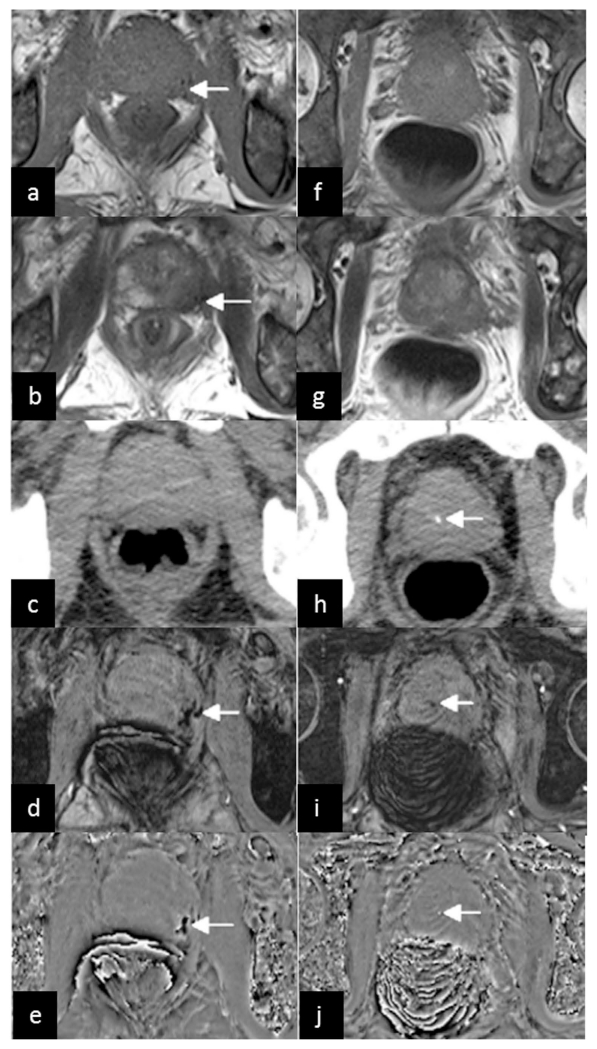
SWI has also been used to detect hemorrhage in prostate cancer and to measure prostatic calcification (145). Prostate cancer, commonly found in elderly men, has now become one of the major challenges to public health (146). Conventional MRI techniques (T1WI and T2WI) have been useful in detecting prostate cancer, despite the low specificity in distinguishing prostate cancer from benign prostatic diseases, especially in the prostate peripheral zone (145). Since prostate cancer tissues are prone to bleeding whereas noncancerous tissues are not, SWI may provide important information for the differentiation of prostate cancer from benign diseases. As reported in Bai et al. (145), most patients with prostate cancers had hemorrhages (Figure 16), whereas hardly any hemorrhage was detected in the noncancerous prostates. Using the hemorrhage of prostate on SWI as a biomarker, their results revealed higher sensitivity and specificity for SWI than conventional MRI in the diagnosis of prostate cancer.

Figure 16.

A 66-year-old man with prostate cancer in the peripheral zone of the prostate. Low signal on conventional T1WI (a) and T2WI (b) (arrows) indicates tumor hemorrhage. No hemorrhage is demonstrated on CT (c). The tumor hemorrhage was seen with SWI (d) and the filtered phase image (e) (arrows). The images in the second column came from another slice of the same patient. No prostatic calcification is demonstrated on conventional T1WI (f) and T2WI (g), but a dot-like high density on CT (h), low signal on SWI (i) and high signal on the filtered phase image (j) (arrows) indicates calcification. The filtered phase images (e and j) were from a right-handed system. Reproduced from ref. (145).

Prostatic calcifications were associated with several urological diseases and symptoms (147). Traditionally, CT has been used as the gold standard in detecting calcification. Nowadays, MRI is more commonly used in the prostate examination than CT because of its better soft tissue contrast. However, due to the complicated components and various proportions in calcification, the signal intensity of calcification on conventional T1WI and T2WI may vary greatly (148,149), making it difficult to detect prostatic calcification using conventional MRI techniques. Fortunately, the paramagnetic and diamagnetic materials have opposite signal intensities in filtered phase images (8,9). This enables the easy differentiation of calcification from hemorrhage using SWI and QSM (18,101,150). It has been shown that the filtered phase images could identify prostatic calcification equally well as CT, but were much better than using conventional MRI (Figure 16).

5.6. Imaging spinal cord injury

Although SWI has been shown to be far superior in detecting microbleeds compared to conventional T1WI, T2WI, or T2*WI in various conditions in the brain, such as stroke, trauma and vascular dementia etc., the susceptibility artifact renders imaging spinal cord a challenging problem. For patients with spinal cord injury (SCI), it is crucial to detect intraspinal hemorrhage for both treatment and management of the patients (151,152). The first SWI study on detecting hemorrhage in the spinal cord was performed by Wang et al. (21), in which the authors compared SWI with conventional T1WI, T2WI and T2*WI techniques. Out of the 23 patients included in that study, 6 cases with intramedullary hemorrhage were found by using either conventional MRI (T1WI, T2WI) or SWI. For another two cases, conventional T1WI and T2WI only revealed spinal cord contusion, while SWI showed low signal in the spinal cord which indicated intraspinal hemorrhage. In addition, all eight patients with hemorrhage, as demonstrated by SWI, had a poorer clinical outcome than those with spinal cord edema or contusion, which was consistent with previous studies. When comparing SWI with T2*WI, the contrast between hemorrhage to normal tissue on SWI was better than that on T2*WI, reflecting the superior sensitivity of SWI to detect intraspinal hemorrhage to the conventional imaging techniques. The ability of SWI to detect hemorrhages not seen by conventional imaging is of key importance to the prognosis for SCI patients. Moreover, this study also demonstrated the feasibility of including SWI as a routine MRI sequence for SCI patients, when the imaging parameters of SWI were properly chosen to balance the SWI data quality and acquisition time (see Table 1 for example imaging parameters).

5.7. Imaging intervertebral disc degeneration

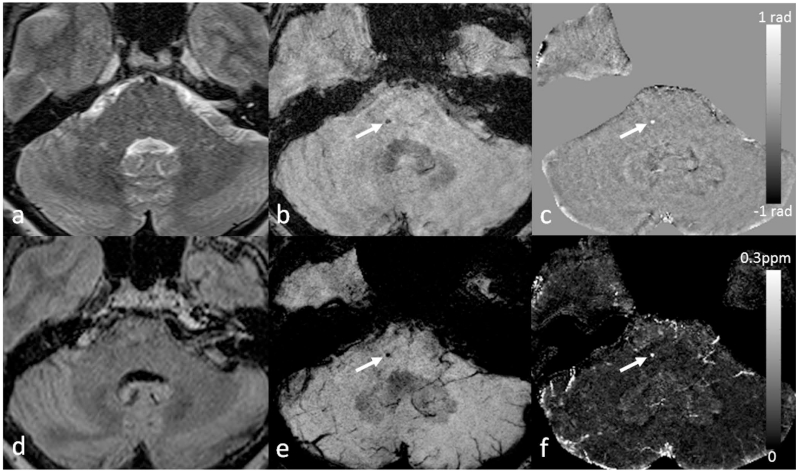
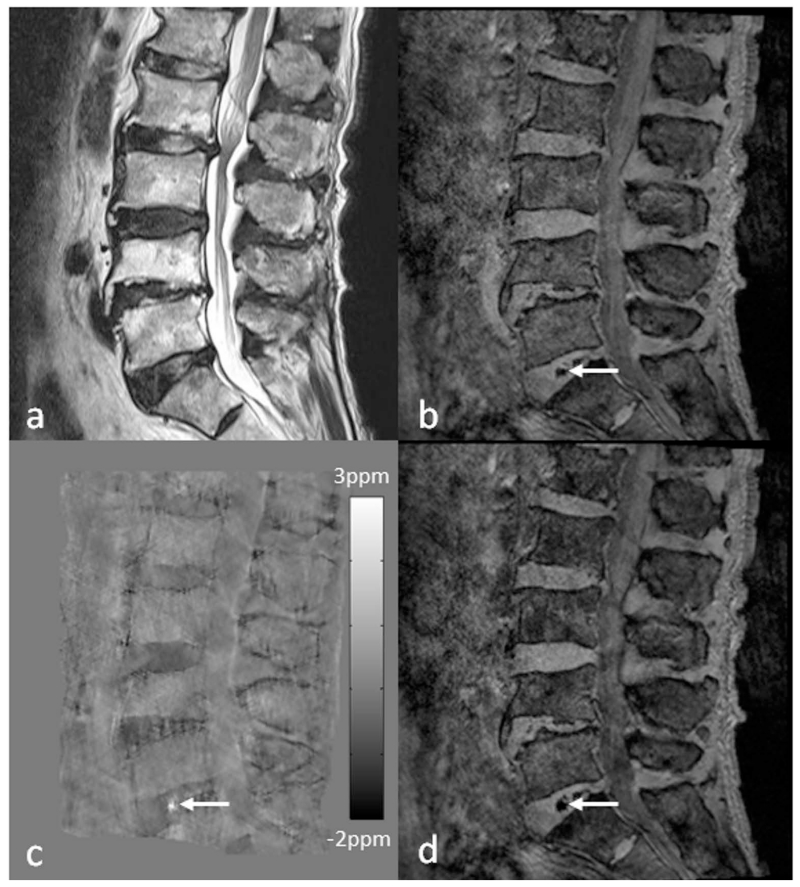
Lower back pain (LBP) is one of the most common health problems with a huge socioeconomic burden, in which intervertebral disc degeneration plays a significant role (153). It is generally acknowledged that the severity of degeneration is broadly associated with chronic symptoms (154). However, intervertebral disc degeneration is difficult to define, as it covers a variety of clinical, morphologic, and histologic manifestations. Adams et al. suggested a working definition that disc degeneration is an aberrant cell-mediated response to progressive structural failure (155). Simple as it seems, this definition connotes a wide range of changes from a biochemical level to functional consequences. During the aging process, the amount of proteoglycans and collagen type II slowly decreases with subsequent loss of water content in the nucleus pulposus, the inner gelatinous part of the disc. Meanwhile, defects or fissures develop in the annulus, the outer lamella of the disc (156,157). In contrast to normal aging, these changes manifest more rapidly and extensively in disc degeneration (156). Once a disc is structurally and functionally compromised, it further elicits the degenerative cascade, including changes of adjacent vertebral bodies, facet joints, uncovertebral joints, as well as supporting ligaments. Early change in the intervertebral disc architecture and its causal relationship with pain has been assessed with CT discography (158). However, owing to the invasiveness of the CT discography, MRI was established as a main diagnostic tool for intervertebral disc evaluation (159). Due to the differences in composition of collagen and water, nucleus pulposus and annulus fibrosus of intervertebral disc without degenerative change are clearly discriminated on T2-weighted images. As the degenerative process progresses, the distinction in signal intensity is effaced and structural changes such as bulging or height loss will appear (160). The Pfirrmann grading system of disc degeneration, which is most widely used in the clinical practice, is mainly based on the changes in T2-weighted images. However, the grading system has limitations in that it is relatively nondiscriminatory in elderly subject, and only has a weak correlation with the severity of symptoms (161). Recently, more advanced MRI techniques such as diffusion-tensor imaging, T1_ρ imaging, T2 mapping, and magnetic resonance spectroscopy have been applied to intervertebral disc, in order to gain insights in the biochemical and microstructural changes of the degenerating intervertebral disc prior to the morphologic changes (162–165). The use of SWI outside the brain is usually affected by the susceptibility artifacts due to air/bone-tissue interface. In the spine, SWI has been applied for evaluating traumatic cord hemorrhage or visualizing normal spinal vein (21,166). It is also a potential tool for evaluating degenerated discs. As discs degenerate, they undergo structural deterioration as well as accumulation of materials such as calcification and air (so-called vacuum phenomenon). SWI (both magnitude blooming effects and phase) and QSM can capture and quantitatively assess those changes in the disc under the degenerative process (Figure 17).

Figure 17.

Imaging advanced intervertebral disc degeneration more than grade 4 by the Pfirrmann grading system in the lumbar spine using SWI and QSM. Intradiscal air in the L5-S1 intervertebral discs (arrows) is better visualized on the magnitude image (b), susceptibility map (c) and tSWI (d), than on T2WI (a). Susceptibility maps were generated using the geometry constrained iterative SWIM algorithm (65).

6. Future directions

The potential of SWI has already been demonstrated in clinical applications focused on the brain. Using short TEs to reduce phase aliasing and T2* signal decay, it is also possible to image the structures with high susceptibilities such as air and bone using QSM (25). Through the marriage of SWI and QSM as tSWI, the geometry dependence of conventional SWI can be avoided and more accurate delineation of these structures can be obtained (26,27). In order to further apply SWI to other organs in the body, such as liver and kidney, one of the major challenges is handling motion artifact, especially when relatively high imaging resolution is desired. Fast imaging is the key to resolving this problem. In the past few years, a few techniques have been proposed which can be used for both SWI and QSM, such as 2D and 3D echo planar imaging (EPI) (167–172). However, conventional EPI techniques are known to be prone to geometric distortion, and segmented EPI (SEPI) partly solves this problem (172,173). Using similar field of view and resolution, 3D GRE with Wave-CAIPI provides significantly accelerated data acquisition, with the benefits in reducing the distortion and preserving the SNR (174,175). Compressed sensing (CS) has also been tested for both SWI and QSM. While the feasibility of applying CS to SWI data acquisition has been demonstrated, the reconstructed phase images may lead to additional artifacts in the susceptibility maps in QSM and better reconstruction algorithms are still needed (176–178). These techniques may play a significant role in the future applications of SWI, and will open the door for abdominal imaging using SWI such as fetal brain imaging (179–181).

Abbreviations

APCV

asymmetrically prominent cortical veins

CAA

cerebral amyloid angiopathy

CAIPI

controlled aliasing in parallel imaging

CBF

cerebral blood flow

CMB

cerebral microbleed

CNR

contrast-to-noise ratio

CS

compressed sensing

CT

computed tomography

DWI

diffusion weighted imaging

ECC

echo center correction

ECST

European Carotid Surgery Trial

EPI

echo planar imaging

FLAIR

fluid-attenuated inversion recovery

GRAPPA

generalized autocalibrating partially parallel acquisitions

HDL

high-density lipoprotein

ICH

intracranial hemorrhage

IPH

intraplaque hemorrhage

LBP

lower back pain

MRA

magnetic resonance angiography

MTT

mean transit time

NASCET

North American Symptomatic Carotid Endarterectomy Trial

PWI

perfusion weighted imaging

QSM

quantitative susceptibility mapping

SCI

spinal cord injury

SEPI

segmented echo planar imaging

SHARP

sophisticated harmonic artifact reduction for phase data

SN

siderotic nodules

SNR

signal-to-noise ratio

SWI

susceptibility weighted imaging

SWIM

susceptibility weighted imaging and mapping

TBI

traumatic brain injury

T1WI

T1 weighted imaging

T2WI

T2 weighted imaging

T2*WI

T2* weighted imaging

TOF

time of flight

tSWI

true susceptibility weighted imaging

VENC

velocity encoding