Properties of the two-dimensional heterogeneous Lennard-Jones dimers: An integral equation study

Abstract

Structural and thermodynamic properties of a planar heterogeneous soft dumbbell fluid are examined using Monte Carlo simulations and integral equation theory. Lennard-Jones particles of different sizes are the building blocks of the dimers. The site-site integral equation theory in two dimensions is used to calculate the site-site radial distribution functions and the thermodynamic properties. Obtained results are compared to Monte Carlo simulation data. The critical parameters for selected types of dimers were also estimated and the influence of the Lennard-Jones parameters was studied. We have also tested the correctness of the site-site integral equation theory using different closures.

I. INTRODUCTION

Two dimensional (2D) liquids can be different from three dimensional (3D) ones. The main difference can arise from the difference in number of degrees of freedom. For example, the rotational motion in 2D can be limited to rotation about only one axis, in contrast to a 3D liquid where rotations of molecules about multiple axes are possible. The properties of ionic fluids are strongly related to the systems’ dimensionality. One-dimensional electrolytes always form an insulating system, whereas 3D electrolytes are always conducting unless there is a strong ion pairing present. 2D electrolytes are very special since they have both the conducting and the insulating phases, depending on the density and the temperature. Such systems undergo a so-called Kosterlitz- Thouless (KT) transition between an insulating and a conductive phase. 2D fluids are also important because the monolayers of molecules absorbed on a solid substrate^1,2 or surfactant adsorbed on air/water interfaces behave as 2D fluids. Low pressure experiments of krypton adsorption on exfoliated graphite and graphitized carbon black indicated a behavior characteristic of 2D fluids.^3,4In comparison to the research of 3D^5–9 fluids, 1D¹⁰ and 2D fluids have attracted much less attention. Low dimensional systems have in addition to their interest as simple models for real situations, also important to understand the effect of dimensionality on phase transitions.^5,11–13

In 2D there exist many models with interesting features. One such water-like model is Mercedes Benz (MB) model.^14,15 It has been studied extensively by Monte Carlo simulations^16–18 and by integral equation methods^19–24 based on Wertheim’s theory for associating fluids.^25,26 The MB model can on simple way explain the water anomalous properties and solvation effects. In current work, we study 2D dimers which are of interest for two things. As first, they can be used as a model for diatomic molecules, e.g., N₂, O₂, HCl, HF, and CO absorbed on the surface. Monolayers of dimers adsorbed on the solid surfaces have been a field of intensive research.²⁷ As second, 2D dimers can be used to model amphiphilic molecules, e.g., methanol or lipids, when one segment of the dimer is hydrophilic and the other hydrophobic. If we take a 2D dimer and we add hydrogen bond interaction like in MB water, we can obtain models for alcohols like methanol and t-butanol. Most of the studies to understand the properties of dimers used computer simulations on a lattice^28–36 and some also on continuous-space.^27,37,38

This work is an extension of Ref. 39. In the previous paper, only homogeneous dimers were considered. Here we extended our calculation using the same version integral equation theory (IET) to heterogeneous dimers. IET is a fast and easy-to-implement method to calculate structure and thermodynamics of liquids and provides a rather good description of fluid-phase equilibria.⁴⁰ In this work, we applied the reference interaction site model (RISM) version of IET also known as the site-site integral equation theory.⁴¹ RISM is an extension of the Ornstein-Zernike (OZ) equation⁴² to a mixture of atoms, but with strong intramolecular correlations representing chemical bonds. The integral equation theory based on the RISM formalism has been applied successfully to obtain structural and thermodynamic properties of various chemical, biochemical, and biological systems.^43–47 The hard planar dumbell fluid has been previously studied using both RISM⁴⁸ and molecular integral equation theory.⁵⁵ Comparison between RISM and MC simulations for the planar dumbbell model showed that the theory accounts qualitatively for the structure of the planar dumbbell as described by radial distribution functions but this was not the case for computed pressures.⁴⁸ It has to be mentioned that methods based on RISM are not formally exact in that the graphical expansion of the RISM equations includes incorrect terms and excludes other correct ones. The proper interaction site method (PISM)^49,50 is a formal improvement over RISM and more accurately represents the graphical expression, but generally provides less accurate results.⁵¹ The other option is to use the integral equation theory based on Wertheim’s approach with complete association.^25,26,52,53

The paper is organized as follows. First, we present a short description of the model, i.e., the planar soft heterogeneous diatomic molecules. Second, details of the site-site integral equations theory with different closure relations and Monte Carlo (MC) simulations are presented. In Sec. V we present comparison of theoretical results with Monte Carlo simulations. We finish the paper with a summary of work in conclusion.

II. MODEL

The two-dimensional Lennard-Jones heterogeneous dimers are modeled as two Lennard-Jones disk at a fixed separation l. The two particles constitute sites 1 and 2 of the dimer. The potential energy for the interaction of two dimers U(R_i, R_j) is defined as the pairwise sum of Lennard-Jones energies U_LJ involving constituent sites, that is,

$$U({\text{𝐑}}_{\text{𝐢}},{\text{𝐑}}_{\text{𝐣}})=\sum _{\alpha ,\beta =1}^2{U}_{\text{LJ}}^{\alpha \beta }(|{\text{𝐫}}_{\text{𝐢}}\alpha -{\text{𝐫}}_{\text{𝐣}}\beta |),$$ (1)

where R_i and R_j are the vectors representing the coordinates and the orientation of the centers-of-mass of dimers i and j, respectively. ${\text{𝐫}}_{\text{𝐢}\alpha }$ is the position vector of site α in molecule i. A similar definition applies to ${\text{𝐫}}_{\text{𝐣}\beta }$. We use the standard form of the Lennard-Jones potential,

$$U_{\text{LJ}}^{\alpha \beta }(r)=4{\epsilon }_{\alpha \beta }\left({\left(\frac{{\sigma }_{\alpha \beta }}{r}\right)}^{12}-{\left(\frac{{\sigma }_{\alpha \beta }}{r}\right)}^6\right),$$ (2)

where ε_αβ denotes the well–depth and σ_αβ the contact parameter. In this work, we study the situation where constituent sites of the dimer are of different sizes (${\sigma }_{11}\ne {\sigma }_{22}$) or of different wall-depth (${\epsilon }_{11}\ne {\epsilon }_{22}$) or of both. The parameters for dissimilar segments are obtained from the Lorentz-Berthelot combining rules.⁵⁴

III. INTEGRAL EQUATION THEORY

As in our previous work,³⁹ we applied the site-site integral equation theory of Chandler and Andersen.⁴¹ This theory uses the Ornstein-Zernike-like equation which relates the direct site-site correlation functions, $c_{\alpha \beta }(r)$, the intramolecular site-site correlation functions, ${\omega }_{\alpha \beta }(r)$, and the intermolecular site-site correlation functions, $h_{\alpha \beta }(r)$, between sites α and β and can be written in a matrix form in Fourier space as

$$H(k)=\mathrm{\Omega }(k)C(k)\mathrm{\Omega }(k)+\rho \mathrm{\Omega }(k)C(k)H(k).$$ (3)

H(k), C(k), and $\mathrm{\Omega }(k)$ are the matrices whose elements are Fourier transforms of site-site correlation functions

$$H(k)=\left[\begin{array}{cc}{h}_{11}(k)\hfill & h_{12}(k)\hfill \\ h_{21}(r)\hfill & h_{22}(k)\hfill \end{array}\right],C(k)=\left[\begin{array}{cc}{c}_{11}(k)\hfill & c_{12}(k)\hfill \\ c_{21}(r)\hfill & c_{22}(k)\hfill \end{array}\right],\mathrm{\Omega }(k)=\left[\begin{array}{cc}{\omega }_{11}(k)\hfill & {\omega }_{12}(k)\hfill \\ {\omega }_{21}(r)\hfill & {\omega }_{22}(k)\hfill \end{array}\right].$$ (4)

${\omega }_{\alpha \beta }(k)$ are the Fourier transforms of the intramolecular correlation functions in form⁴⁸

$${\omega }_{\alpha \beta }(k)=J_0(k{l}_{\alpha \beta }),$$ (5)

$${\omega }_{\alpha \alpha }(k)=1.$$ (6)

$l_{\alpha \beta }$ is the distance between the sites α and β and J₀(x) is the zeroth Besel function. An additional relation between $h_{\alpha \beta }(r)$ and $c_{\alpha \beta }(r)$, called the closure relation, is needed in order to solve the set of equations. Closure relation can be written for the site-site correlation function $g_{\alpha \beta }(r)$ ($g_{\alpha \beta }(r)=h_{\alpha \beta }(r)+1$) as⁵⁶

$$g_{\alpha \beta }(r)=\text{exp}(-\beta U_{\alpha \beta }(r)+h_{\alpha \beta }(r)-c_{\alpha \beta }(r)+B_{\alpha \beta }(r)),$$ (7)

where $\beta =\frac{1}{kT}$, $U_{\alpha \beta }(r)$ is the interaction potential between sites, and $B_{\alpha \beta }(r)$ the bridge function, which is not known. The simplest approximation is the hypernetted chain (HNC) approximation, which neglects the bridge function ($B_{\alpha \beta }(r)=\mathrm{\hspace{0.17em}0}$). Percus and Yevick (PY) proposed the simple approximation^57,58 written as

$$g_{\alpha \beta }(r)=\text{exp}(-\beta U_{\alpha \beta }(r))(1+h_{\alpha \beta }(r)-c_{\alpha \beta }(r)).$$ (8)

HNC and PY closures have shortcomings like a narrow region of convergence and inherent thermodynamic inconsistency which lead to the development of several other closures. The Kovalenko-Hirata closure (KH)⁵⁹ was constructed to expand the convergence region and has the following form:

$$h(r)=\left\{\begin{array}{cc}\text{exp}(d_{\alpha \beta }(r))-1,\hfill & d_{\alpha \beta }(r)\le 0\hfill \\ d_{\alpha \beta }(r),\hfill & d_{\alpha \beta }(r)>0\hfill \end{array}\right\},$$

where $d_{\alpha \beta }(r)=-\beta U_{\alpha \beta }(r)+h_{\alpha \beta }(r)-c_{\alpha \beta }(r)$. Another way to expand the convergence region is by the soft mean-spherical approximation (SMSA). In this closure we divide the LJ part of potential into a short-range reference part $U_{\alpha \beta }^0(r)$ and a longer-range perturbation part $U_{\alpha \beta }^1(r)$,⁶⁰

$$U_{LJ}^{\alpha \beta }(r)=U_{\alpha \beta }^0(r)+U_{\alpha \beta }^1(r),$$ (9)

where

$$U_{\alpha \beta }^0(r)=\{\begin{array}{cc}{U}_{LJ}^{\alpha \beta }(r)+{\epsilon }_{\alpha \beta }\hfill & r\le r_{\alpha \beta }^m\hfill \\ 0\hfill & r>r_{\alpha \beta }^m\hfill \end{array}$$

and

$$U_{\alpha \beta }^1(r)=\{\begin{array}{cc}-{\epsilon }_{\alpha \beta }\hfill & r\le r_{\alpha \beta }^m\hfill \\ U_{LJ}^{\alpha \beta }(r)\hfill & r>r_{\alpha \beta }^m\hfill \end{array}.$$

The distance $r_{\alpha \beta }^m$ is the minimum of the LJ part of the potential function, i.e., $r_{\alpha \beta }^m=2^{1/6}{\sigma }_{\alpha \beta }$. The SMSA closure relation has at the end the following form:

$$g_{\alpha \beta }(r)=\text{exp}(-\beta U_{\alpha \beta }^0(r))(1+h_{\alpha \beta }(r)-c_{\alpha \beta }(r)-\beta U_{\alpha \beta }^1(r)).$$ (10)

The OZ equation together with the closure condition was solved by a direct iteration. The forward and inverse Bessel-Fourier transforms, needed to couple the correlation functions in real and Fourier spaces, have been performed by the method of Talman.^61,62 Knowledge of the site-site correlation functions allows us to calculate the thermodynamic properties of interest, including the internal energy, pressure, and compressibility, see our previous paper for details.³⁹

IV. MONTE CARLO SIMULATION DETAILS

Monte Carlo simulation of the 2D dimer model was performed in the canonical (N,V,T) ensembles in order to obtain data which were compared with the results from integral equation theory. We computed thermodynamic (energy and pressure) and structural properties (pair correlation functions) of the model. We used periodic boundary conditions and the minimum image convention to mimic an infinite system of particles. Starting configurations were selected at random. At each step, a dimer was chosen randomly and it was translated or rotated. Probability for translation, rotation was the same. In one cycle, we tried to translate and rotate each particle. The simulations were allowed to equilibrate for 100 000 cycles and averages were taken for 20 series each consisted for another 100 000 cycles to obtain well converged results. All simulations were performed with N = 200 or 400 molecules which are equivalent to about 8000 particles in 3D in case of 200 molecules in 2D. Thermodynamic quantities such as energy were calculated as statistical averages over the course of the simulations.⁶³ Pressure was calculated using the virial theorem. Increasing the number of particles had no significant effect on the calculated quantities. Cutoff of the potential was half-length of the simulation box.

V. RESULTS AND DISCUSSION

Results are given in reduced units: temperature and excess internal energy are normalized to the LJ interaction parameter ${\epsilon }_{11}=1$ ($U^{\ast }=\frac{E}{{\epsilon }_{11}}$, $T^{\ast }=\frac{k_{B}T}{{\epsilon }_{11}}$) and distances are scaled to the characteristic length ${\sigma }_{11}=\mathrm{\hspace{0.17em}1}$ ($r^{\ast }=\frac{r}{{\sigma }_{11}}$). ${\epsilon }_{22}$ and ${\sigma }_{22}$ were also in units of ${\epsilon }_{11}$ and ${\sigma }_{11}$. ${\sigma }_{22}$ = 2 means that ${\sigma }_{22}$ = 2${\sigma }_{11}$.

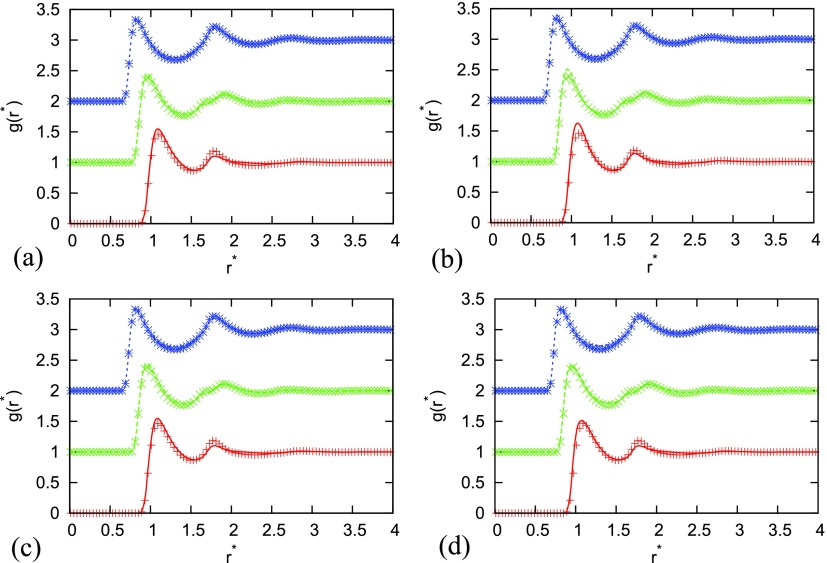
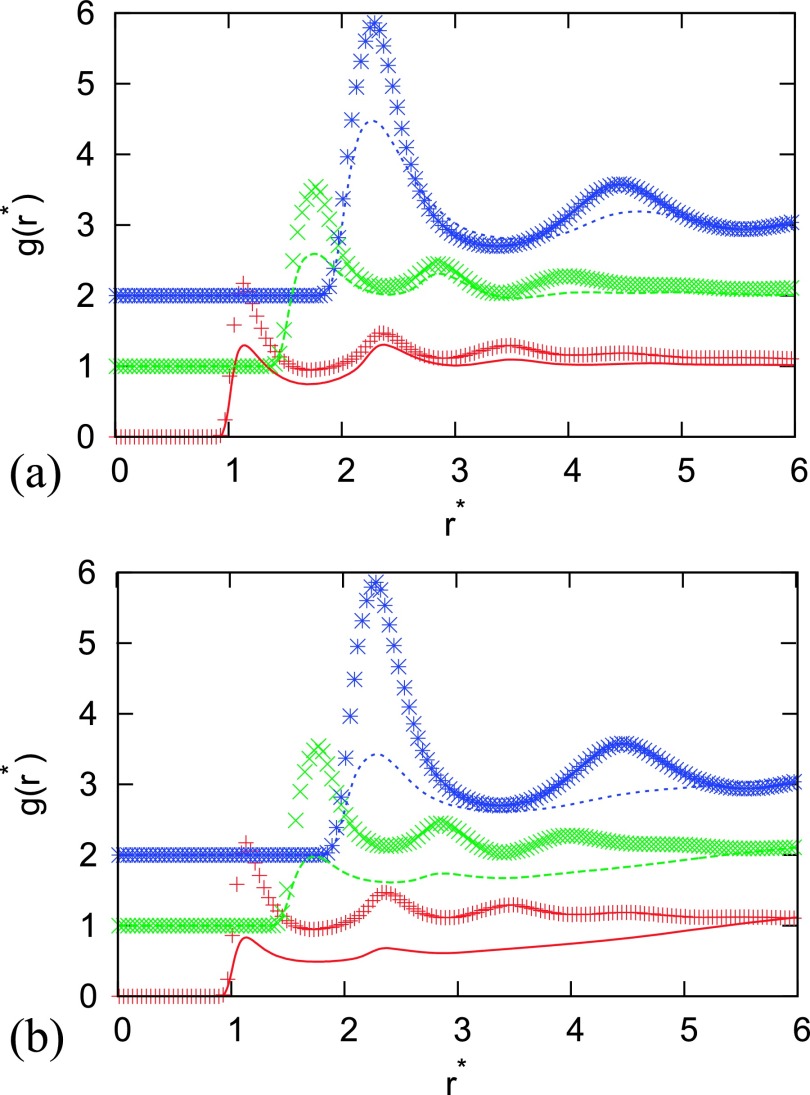
First, we checked how well the site-site integral equation with four closure relations, i.e., PY, HNC, KH, and SMSA, reproduces pair distribution functions that were computed at various densities, temperatures, and potential parameters in comparison with Monte Carlo simulations. Figures 1–6 show this comparison for different parameters. There are various asymmetries possible. We study the situation where constituent sites of the dimer are of different sizes (${\sigma }_{11}\ne {\sigma }_{22}$) (in Figures 1 and 2, the second particle is smaller ${\sigma }_{22}=0.75$ and ${\sigma }_{22}=0.25$ while in Figure 2 the second particle is bigger ${\sigma }_{22}=2.0$) or of different wall-depth (${\epsilon }_{11}\ne {\epsilon }_{22}$) (in Figures 4 and 6 the second particle has bigger wall-depth ${\epsilon }_{22}=2.0$) or of both (Figure 5). We were using the same asymmetry parameters as of Rzysko and Borowko in their work so that we can make the comparison of critical point temperatures and densities.²⁷ In Figures 1–6 we used symbols for Monte Carlo results and lines for IET results. Different site-site correlation functions are plotted and shifted for 1 in the y direction. Red line and symbols are for $g_{11}(r^{\ast })$, green for $g_{12}(r^{\ast })$ and blue for $g_{22}(r^{\ast })$. Agreement between MC and IET is very good for higher temperatures and moderate and high densities where all closures provide results (see Figure 1). When the temperature decreases and we are approaching the phase transition region, first HNC and later PY lack the convergence. At moderate temperatures, theoretical radial distribution functions reproduce only quantitatively simulation results. Positions of main peaks in the radial distribution function are found at a correct location but their intensities can be either over- or under-estimated. In Figures 2 and 3 we can see that the problems in agreement appear for a smaller particle in the dimer which is underestimated. The disagreement increases when asymmetry increases in both ways (the second particle becomes smaller or bigger). Asymmetry in wall-depth has no so huge affect as it can be seen in Figure 4, but it increases disagreement when the size asymmetry is present (see Figure 5). For the unrealistic situations where the dimer size is smaller than the sum of van der Waals radius of its constituent sites, i.e., $2l^{\ast }\ll {\sigma }_{11}+{\sigma }_{22}$, theoretical and simulated pair distribution functions show greater disagreement (Figure 6) which is greater comparing to the case of homogenous dimers. Somehow the best agreement is for the SMSA and KH closures. The incorrect behavior of the theory in the small $l^{\ast }$ limit is associated with the appearance of unallowed graphs in the cluster expansion of the distribution functions from the site-site IET.⁶⁴ In general, RISM reproduces a structure in a similar way as for homogeneous dimers, only that asymmetry in size causes more problems for IET in reproduction of the MC correctly. Wall-depth asymmetry is not that crucial.

FIG. 1.

Comparison of site-site correlation function for different closures with Monte Carlo simulation results for asymmetry ${\sigma }_{22}$ = 0.75, ${\epsilon }_{22}$ = 1.00, distance between sites $l^{\ast }=\mathrm{\hspace{0.17em}0.875}$, temperature $T^{\ast }=\mathrm{\hspace{0.17em}2.0}$, ${\rho }^{\ast }=\mathrm{\hspace{0.17em}0.4}$. Monte Carlo results are plotted with symbols, and IET by lines. Results are for closures (a) PY, (b) HNC, (c) SMSA, and (d) KH. Red line and symbols are for $g_{11}(r^{\ast })$, green for $g_{12}(r^{\ast })$, and blue for $g_{22}(r^{\ast })$. Different site-site correlation functions are shifted for 1 in the y direction.

FIG. 2.

Same as Figure 1, only for asymmetry ${\sigma }_{22}$ = 0.25, ${\epsilon }_{22}$ = 1.00, distance between sites $l^{\ast }=\mathrm{\hspace{0.17em}0.625}$, temperature $T^{\ast }=\mathrm{\hspace{0.17em}1.0}$, ${\rho }^{\ast }=\mathrm{\hspace{0.17em}0.45}$. Results are for closures (a) PY, (b) SMSA, and (c) KH. HNC does not converge.

FIG. 3.

Same as Figure 1, only for asymmetry ${\sigma }_{22}$ = 2.00, ${\epsilon }_{22}$ = 1.00, distance between sites $l^{\ast }=\mathrm{\hspace{0.17em}1.5}$, temperature $T^{\ast }=\mathrm{\hspace{0.17em}1.0}$, ${\rho }^{\ast }=\mathrm{\hspace{0.17em}0.125}$. Results are for closures (a) PY, (b) SMSA, and (c) KH. HNC does not converge.

FIG. 4.

Same as Figure 1, only for asymmetry ${\sigma }_{22}$ = 1.00, ${\epsilon }_{22}$ = 2.00, distance between sites $l^{\ast }=\mathrm{\hspace{0.17em}1.0}$, temperature $T^{\ast }=\mathrm{\hspace{0.17em}1.5}$, ${\rho }^{\ast }=\mathrm{\hspace{0.17em}0.1}$. Results are for closures (a) PY, (b) SMSA, and (c) KH. HNC does not converge.

FIG. 5.

Same as Figure 1, only for asymmetry ${\sigma }_{22}$ = 2.00, ${\epsilon }_{22}$ = 2.00, distance between sites $l^{\ast }=1.5$, temperature $T^{\ast }=1.5$, ${\rho }^{\ast }=0.025$. Results are for closures (a) PY, (b) HNC, (c) SMSA, and (d) KH.

FIG. 6.

Same as Figure 1, only for asymmetry ${\sigma }_{22}$ = 1.00, ${\epsilon }_{22}$ = 2.00, distance between sites $l^{\ast }=\mathrm{\hspace{0.17em}0.75}$, temperature $T^{\ast }=\mathrm{\hspace{0.17em}1.0}$, ${\rho }^{\ast }=\mathrm{\hspace{0.17em}0.1}$. Results are for closures (a) SMSA and (b) KH. PY and HNC do not converge.

In continuation we checked how well IET can reproduce the internal energy. Comparison was done for various temperatures, and selected asymmetries at low temperature $T^{\ast }=1.0$ are plotted in Figure 7. At this temperature, PY and HNC closures no longer have convergence so only data for SMSA and KH are presented in the figures. Both closures yield results that are in agreement with simulation data for distance between centers in molecule higher than $l^{\ast }>({\sigma }_{11}+{\sigma }_{22})/2$ at high temperatures and small asymmetry. Disagreement increases with a shorter distance between centers and with asymmetry in size and in well depth, while for a lower distance the internal energy by integral equation is too high which is similar as observed in our paper for homogeneous dimers.³⁹ SMSA closure is performing at lower temperatures slightly better than KH. In Figure 8 we are showing the comparison of different pressures as a function of density for selected closures, asymmetries, and bond distances at low temperature $T^{\ast }=1.0$. SMSA, PY, HNC, and KH yield different pressures when calculated via compressibility, energy, and virial route due to inconsistency in closures. In general, compressibility pressure is the most accurate for all closures, but it fails to predict phase transition like it was observed before for homogenous dimers. Isotherm compressibility pressure for all temperatures does not show Maxwell-like isotherm. Energy and virial predict liquid-gas phase transition, and Figure 9 shows dependence on critical temperature, density, and pressure as a function of energy parameter ${\epsilon }_{22}$ in dimer for selected asymmetries ${\sigma }_{22}$ for same parameters as reported by the Monte Carlo results by Rzysko and Borowko.²⁷ Results for KH and SMSA closures only are shown since those were the only closures converging in this region of temperatures and densities. Site-site integral equation theory predicts the critical temperature too high and the critical density too low when comparing to the Monte Carlo results by Rzysko and Borowko²⁷ which is in agreement with the results for the homogeneous dimers.³⁹ The results have systematic error, but trends are the same for both closures. SMSA closure even predicts intersection of curve for temperature at same ${\epsilon }_{22}$ as it is present in simulation. RISM provides quite good results for the structure and thermodynamics in the dense liquid region. However, it is less accurate for less dense liquids, as we have in the case of the vapor-liquid coexistence curve. Reason lies on the incorrect terms in the graphical expansion. Better agreement would require more complex treatments than first order perturbation theories considered thus far or application of better and more accurate versions of IET.

FIG. 7.

Density dependence of internal energy per particle for (a) ${\sigma }_{22}$ = 2.00, ${\epsilon }_{22}$ = 1.00, $l^{\ast }=1.5$, $T^{\ast }=1.0$, (b) ${\sigma }_{22}$ = 0.25, ${\epsilon }_{22}$ = 1.00, $l^{\ast }=0.625$, $T^{\ast }=1.0$, (c) ${\sigma }_{22}$ = 1.00, ${\epsilon }_{22}$ = 2.00, $l^{\ast }=1.0$, $T^{\ast }=1.0$, and (d) ${\sigma }_{22}$ = 1.00, ${\epsilon }_{22}$ = 2.00, $l^{\ast }=\mathrm{\hspace{0.17em}0.75}$, $T^{\ast }=\mathrm{\hspace{0.17em}1.0}$. Monte Carlo results are plotted with symbols, SMSA with a long-dashed green line, and KH with a dashed blue line.

FIG. 8.

Same as Figure 7 only, for density dependence of pressure calculated by virial (tick line) compressibility (bold line).

FIG. 9.

Virial pressure route results for the (a) critical temperature, (b) density, and (c) pressure as a function of ${\epsilon }_{22}$ in dimer for SMSA (solid line) and KH (dashed line) closure. Monte Carlo results by Rzysko and Borowko²⁷ are plotted with symbols. Red line is for size ${\sigma }_{22}=2$, blue for ${\sigma }_{22}=1$, and green for ${\sigma }_{22}=0.75$.

VI. CONCLUSIONS

We have examined the thermodynamics, structure, and phase transitions in 2D soft heterogeneous dimers, using the Monte Carlo computer simulations and the site-site integral equation theories with different closures: PY, HNC, SMSA, and Kovalenko-Hirata. The liquid-gas critical point was determined. The IET is faster from the computational point of view than the Monte Carlo simulations; however, it reproduces the structure only qualitatively. We systematically examined several closures and the results are as follows: the PY and HNC lose convergence at low temperatures. SMSA and KH fail at predicting the proper critical point for all studied geometries of dimers. All closures also fail at structure predicting at small densities. The reason is most probably due to the fact that RISM is not formally exact. RISM in the graphical expansion includes incorrect terms. So one can apply PISM^49,50 which is a formal improvement over RISM and more accurately represents the graphical expression, but in general does not provide more accurate results.⁵¹ Alternative option is to apply the Wertheim’s integral equation theory with complete association.^25,26,52,53