Relaxation Dynamics in Photoexcited Chiral Molecules Studied by Time-Resolved Photoelectron Circular Dichroism: Toward Chiral Femtochemistry

Abstract

Unravelling the main initial dynamics responsible for chiral recognition is a key step in the understanding of many biological processes. However, this challenging task requires a sensitive enantiospecific probe to investigate molecular dynamics on their natural femtosecond time scale. Here we show that, in the gas phase, the ultrafast relaxation dynamics of photoexcited chiral molecules can be tracked by recording time-resolved photoelectron circular dichroism (TR-PECD) resulting from the photoionization by a circularly polarized probe pulse. A large forward–backward asymmetry along the probe propagation axis is observed in the photoelectron angular distribution. Its evolution with pump–probe delay reveals ultrafast dynamics that are inaccessible in the angle-integrated photoelectron spectrum or via the usual electron emission anisotropy parameter (β). PECD, which originates from the electron scattering in the chiral molecular potential, appears as a new sensitive observable for ultrafast molecular dynamics in chiral systems.

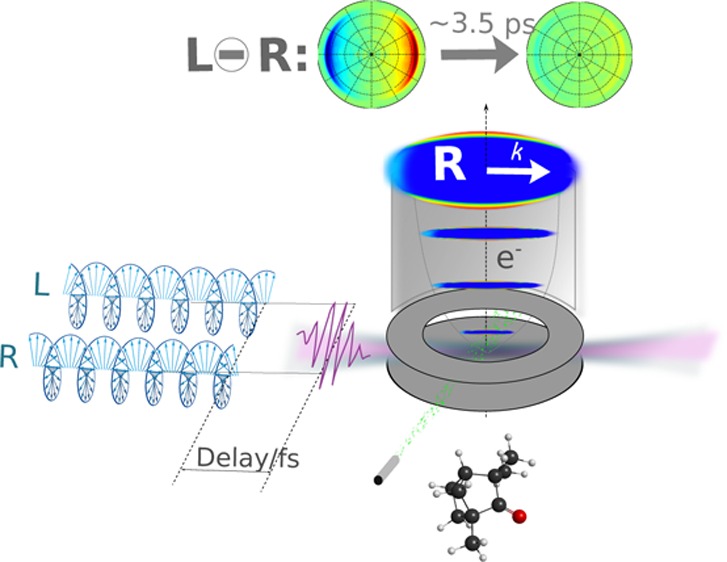
Chiral species exhibit enantio-specific properties when they are embedded into a chiral medium. For instance, chiral molecules interact with each other to form chiral complexes via the so-called chiral recognition process; this “molecular handshake” is at the basis of stereochemistry.¹ Enantio-specific properties also arise from the interaction of chiral molecules with “chiral light”, such as circularly polarized light (CPL), leading to various types of circular dichroism (CD).² As calculated^3,4 and experimentally demonstrated,⁵ CPL-induced photoionization of randomly oriented pure enantiomers gives rise to a forward–backward asymmetry of photoelectron emission along the photon propagation axis k, referred to as photoelectron circular dichroism (PECD). Based upon a differential measurement, this chiroptical effect can be fully described in the pure electric dipole approximation, leading to very strong asymmetries. The outgoing electron scatters in the mean chiral molecular potential involving all the other electrons, mostly the valence ones, which are the main actors of chemical reactivity. This electron scattering occurs in a space whose orientation is referenced by the circularly polarized ionizing field. Despite the random orientation of the molecules, the resulting photoelectron angular distribution shows an intense forward–backward asymmetry. The magnitude of this asymmetry, determined by the interferences between the different partial waves describing the outgoing electron wavepacket, can reach the order of several percent. The sign of this asymmetry reverses with the handedness of the enantiomer (e) or the helicity of the ionizing light (p). PECD is an orbital-specific effect that also depends on the final state, i.e., the photoelectron continuum. It is very sensitive to permanent (isomers, conformers, clustering) and dynamical (vibrational excitation) molecular structures.⁶ As such, PECD is a useful observable to investigate dynamics in chiral molecules. To date, experiments, mostly synchrotron radiation-based, have focused on the photoionization of molecules from their ground electronic state (S₀) in its equilibrium geometry. Recently, a laser-based one-color resonant enhanced multiphoton ionization (REMPI)-PECD scheme involving several intermediate states has been demonstrated; however, time resolution is not included.⁷⁻⁹ The possibility of observing PECD from excited states, for instance loosely bound electronic states, remains an open question. The present Letter focuses on the investigation of PECD from an electronic excited state to establish the sensitivity of PECD as a probe of the ultrafast relaxation taking place in this state. To record time-resolved PECD (TR-PECD), a linearly polarized femtosecond pump pulse photoexcites chiral molecules and a time-delayed circularly polarized femtosecond probe pulse photoionizes them. Key features of this two-color, two-photon experiment are schematized in Figure 1.

Figure 1.

(a) Schematic of the excitation scheme used to measure TR-PECD from the 3s Rydberg state of fenchone. The HOMO and the 3s orbitals are drawn to illustrate the difference in the initial wave function of the outgoing electron. (b) The photoelectron images recorded on (1R)-(−)-fenchone (e = −1) for each probe helicity (LCP-p = 1 or RCP-p = −1) are subtracted one from the other (LCP – RCP) to extract the unnormalized odd Legendre polynomial coefficients, while the sum of these images (LCP + RCP) provides the photoelectron spectrum (PES). These (LCP – RCP) and (LCP + RCP) images, called “difference” and “sum” images, respectively, are shown for three pump–probe delays. Note that the two photon beams are quasi copropagating with polarization axis parallel to the detector (see the Supporting Information).

The target molecule we investigate here is fenchone (C₁₀H₁₆O), a bicyclic ketone whose rigid structure ensures the existence of a single conformer. Fenchone has been extensively studied by vacuum ultraviolet (VUV)-PECD with and without coincidence detection,^10,11 by multiphoton,¹² above threshold or tunnel ionization⁹ PECD as well as by absorption circular dichroism.¹³ However, none of these experiments was time-resolved, and all of them probed a molecule in its ground electronic state defined by its equilibrium geometry, with a possible contribution from the excited states in the REMPI-PECD experiments. The absorption spectrum of fenchone is characterized by a weak valence band around 4.6 eV, followed by strong Rydberg bands starting around 6 eV.¹³ We chose to excite the molecules to their first Rydberg state (3s) in order to drastically change the initial orbital of the outgoing electron compared to the ground state, as illustrated in Figure 1. The pump pulse spectrum is centered at 6.17 eV with a 30 meV full width half-maximum bandwidth (201 nm, 80 fs duration if Fourier-transform-limited). The probe (403 nm, 35 meV with 70 fs duration) is chosen to photoionize the system ∼0.6 eV above the vertical ionization threshold (IP_v = 8.72 eV), in the energy range where the largest VUV PECD has been measured (15%).¹⁰ Because the pump pulse is linearly polarized, the sensitivity to chirality comes into play only in the ionization step, via the helicity of the probe pulse.

The photoelectron images are collected by a velocity map imaging detector for alternating probe helicities at each pump–probe delay, as described in Experimental and Computational Methods and the Supporting Information. The momentum distribution of the photoelectrons (angular resolved photoemission spectrum, ARPES) for a probe helicity p = ± 1 (left/right) and one given enantiomer (e) is defined by a function ARPES^(p,e)(φ, θ, E_kin) with θ the photoelectron ejection angle with respect to the probe propagation axis k, φ its azimuthal angle, and E_kin its kinetic energy. When a cylindrical symmetry in the emission angle φ of the photoelectron is achieved along an axis parallel to the detector, the ARPES^(p,e)(θ,E_kin) distribution is a simple sum of Legendre polynomials [B_i^(p,e)(E_kin)P_i(cos(θ))] and can be retrieved from its VMI 2D-projection PROJ^(p,e)(θ, E_kin) by using, for instance, a p-Basex analysis.¹⁴

Because the P_even Legendre polynomials are symmetric along the optical axis k, the B_even coefficients encode the angular distribution of the standard photoelectron image: the PES is the angle-integrated photoelectron intensity B₀(E_kin) and the anisotropy parameter b₂(E_kin) = −β/2 (with β the usual anisotropy parameter retrieved for a linearly polarized photoionization). These even parameters do not depend on the laser helicity (p) or enantiomer (e). The P_odd Legendre polynomials are antisymmetric along k; consequently, the B_odd^(p,e)(E_kin) coefficients are nonzero only for chiral molecules photoionized by elliptically polarized light (p ≠ 0) and encode the PECD. In a two-photon ionization, the sum of Legendre polynomials is expected to go up to P₄(cos(θ)), with a drastically reduced B₄ in a (1 + 1′) resonant ionization.

In the present experiment, the linear pump polarization as well as the circular probe polarization are defined by quantification axes perpendicular to each other and both parallel to the detector axis. The pump excitation along a well-defined transition dipole induces a loss of isotropy in the molecular target that breaks the φ cylindrical symmetry required to retrieve the ARPES distribution from its VMI 2D-projection PROJ. Nevertheless this cylindrical symmetry is restored in the “difference”-image, defined as PROJ^(+1,e)(θ, E_kin) – PROJ^(−1,e)(θ, E_kin), obtained by subtracting the images measured with left and right probe polarizations and called (LCP – RCP) images in Figure 1. Fitting this (LCP – RCP) difference-image by p-Basex provides the B_odd^(p,e)(E_kin) coefficients (see the Supporting Information).¹⁴

To extract PECD, which manifests itself as an asymmetry in the photoelectron yield emitted in the forward or backward hemisphere along the optical axis k for a given enantiomer and for a given light helicity, normalization by the PES needs to be done. The normalization of B_i observables yields the b_i coefficients (eq 1). As shown in the Supporting Information, the break of cylindrical symmetry prevents access to the “true” B₀(E_kin) via a p-Basex analysis of the “sum”-image, defined as PROJ^(+1,e)(θ, E_kin) + PROJ^(−1,e)(θ, E_kin) and called (LCP + RCP) images in Figure 1. Nevertheless, we will still use a p-Basex analysis on this (LCP + RCP) sum-image to obtain B̃₀(E_kin), and we use this coefficient to normalize the B_odd^(p,e)(E_kin) coefficients from which we calculate a circular dichroism of the 2D photoelectron projection. The quantity we calculate, 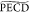, is thus not strictly the same as the PECD usually defined in the literature and that has been all recorded without a break of cylindrical symmetry. For (1R)-(−)-fenchone (e = −1), these definitions are

where

This yields, in terms of Legendre coefficients

with

with the cylindrical symmetry breaking

1

Figure 1 shows the difference- and sum-images measured at 1, 4, and 8 ps pump–probe delay. The time and energy dependences of the B_odd⁽⁻¹⁾ and B̃_even coefficients are extracted from these images. A significant forward PECD, i.e., preferential emission of the photoelectron in the k direction, is observed on the difference-images, demonstrating that loosely bound electronic excited states in chiral molecules can lead to strong asymmetric photoionization when driven by CPL. We also see that the sum-images show a preferential emission along the pump polarization. To obtain a time dependence of this anisotropy, we use also the B̃₂(E_kin) coefficient extracted from the p-Basex analysis of these sum-images. Similarly to the b̃_odd coefficients, normalization of B̃₂ by B̃₀ is required to obtain b̃₂. Note that the b̃₂ coefficient cannot be quantitatively used to evaluate the anisotropy of the ARPES, but it will show the same temporal evolution. The B̃₄ coefficient in these sum-images is zero, whatever the delay, as expected for a (1 + 1′) resonant photoionization.

Both enantiomers have been studied independently, and the sign of the B_odd⁽⁺¹⁾ of (1S)-(+) has been reversed to be compared to the (1R)-(−) ones. They are both positive for (1R)-(−) (negative for (1S)-(+)). Figure 2 shows the energy dependences of the B_odd and B̃_even for different pump–probe delays. The photoelectrons are emitted with a kinetic energy of 0.52 eV irrespective of the pump–probe delay. This 0.52 eV corresponds to the energy expected at the vertical ionization threshold (hν_pump + hν_probe – IP_v = 9.24–8.72 eV; see the Supporting Information).

Figure 2.

Unnormalized Legendre coefficients B_odd⁽⁻¹⁾ and B̃_even as a function of the photoelectron kinetic energy and the pump–probe delay in (1R)-(−)-fenchone.

Figure 3shows the time dependences of b̃_odd⁽⁻¹⁾ and b̃₂ coefficients, extracted from Figure 2 by averaging the B_i(E_kin) around E_kin = 0.52 eV over 30 meV and by normalizing these averages by B̃₀(E_kin) treated the same way. The B̃₀ coefficient, proportional to the total number of photoelectron, decays in 3.3 ps while the b̃₂ anisotropy slightly increases in magnitude with a faster rising time, around 2 ps. The asymmetric parameters b̃₁ and b̃₃⁽⁻¹⁾ show opposite trends, with a slow increase of b̃₁ over 3.2 ps while b̃₃⁽⁻¹⁾ decreases faster in only 1.4 ps. Using eq 1, the has the same sign and a magnitude similar to that observed at that same total energy in single-photon VUV photoionization (9.3 eV)¹⁰ even though the ionization process is different. In the experiments of ref (10), the outgoing electron was scattered from the highest occupied molecular orbital (HOMO) in the ground electronic state potential, while here, the outgoing electron is emitted from the 3s Rydberg wave function and scatters further from the ionic core.

Figure 3.

Temporal evolution of b̃_odd⁽⁻¹⁾, b̃₂, and b̃₀ with empty markers data recorded on (1R)-(−) enantiomer and filled ones on (1S)-(+) enantiomer (with a sign inversion on the b̃_odd): (a) b̃₀ in black and b̃₂ in green; (b) b̃₁⁽⁻¹⁾ in blue, b̃₃ in red, and in black. Table 1 summarizes the time constants extracted from the fits (see the Supporting Information). When the population in the 3s state starts to be less than 10% (delay ≥ 7 ps), the normalization by a small B̃₀ increases the dispersion of the normalized coefficients.

Table 1. Time Constants Extracted from the Fits of the Normalized Legendre Polynomial Coefficients b̃_i⁽⁻¹⁾ and b̃₂ Dependences Shown in Figure 3^a.

observable	time constant (ps)	converging value of the b̃i(−1) fit at long delay
B̃0	3.28 ± 0.05	0
b̃1(−1)	3.25 ± 0.5	0.073 ± 0.017
b̃2	2.0 ± 0.3	–
b̃3(−1)	1.4 ± 0.3	0

^aThe uncertainties correspond to 50% confidence bounds.

What are the dynamics revealed by these different time scales? The absorption of the pump pulse creates a vibrational wavepacket in the 3s Rydberg state. This wavepacket will undergo vibrational relaxation dynamics toward the equilibrium geometry of the 3s state as illustrated in Figure 4a. In addition, vibronic couplings may occur, leading to internal conversion toward either the lowest valence state (S₁) or the ground state (S₀), as shown in Figure 4c. Nothing is known about these two ultrafast processes. In the present excitation scheme, the vibrational energy in both S₁ (∼1.6 eV) and S₀ (∼6 eV) is too high to get significant Franck–Condon factors at only ∼0.5 eV above the IP_v. The probe energy is thus not high enough to photoionize molecules vibrationally excited in S₀ or in S₁.

Figure 4.

(a) Change in the nuclear structure of fenchone from the ground electronic state to the equilibrium geometry of the 3s Rydberg state. The most important relative changes of bond lengths are indicated. The arrow shows the direction of the 3s–S₀ transition dipole moment, and the orange axis shows the rotational axis with their rotational dephasing time for 30 K rotational temperature. (b) Different vibrational quantum of fenchone in the 3s state below 1000 cm^–1. (c) Relaxation processes revealed in the TR-PECD. (d) Lowest vibrational mode with a quantum of 84 cm^–1.

Consequently, the 3.28 ps B̃₀ decay mirrors the lifetime of the 3s Rydberg state and the internal conversion time scale from 3s to the lower valence states. The b̃₁ coefficient is mostly determined by the Rydberg-electron continuum transition dipole moment, while b̃₃, being a higher-order term, will depend on the anisotropy of excitation created by the pump pulse. Similarly, a β time dependence within a given electronic state is, in general, also associated with a decay of the anisotropy of excitation created by the pump.^15,16 The calculations presented in the Supporting Information predict that the 3s–S₀ transition dipole moment is aligned along the C1–C3 axis, as shown in Figure 4a. The free rotations of the excited molecules induce a loss of the anisotropy of excitation, over a time scale defined by the moments of inertia of the molecules and the rotational temperature of the gas.¹⁷ The moments of inertia of the asymmetrical top fenchone have been calculated from the S₀ geometry to I_x,y,z = 1159, 1555, and 1876 amu·bohr² with the axis represented in Figure 4a. The decay time due to the anisotropy loss is typically 1/3 of the dephasing time of the rotational periods , i.e., between 1.4 and 2.4 ps for T_rot ∼ 10–30 K as expected for an Even–Lavie pulsed valve source.^17,18 This is consistent with the 1.4 ps decay measured on b̃₃⁽⁻¹⁾ and the 2 ps on b̃₂, confirming the sensitivity of these two observables to the average laboratory-frame alignment created by the pump transition. Here, the 3s–S₀ dipole moment is almost aligned along the I_y rotational axis. Assigning the time dependence of b̃₃ and b̃₂ due to I_x and I_z rotations with periods similar to that of I_y, is a challenging task beyond the scope of this Letter. This would require a systematic study for different relative polarizations of the pump and probe pulses to extract the spherical tensor components of the photoionization matrix element.

Beyond these global picosecond dynamics, two different mechanisms can be inferred from Figure 3: b̃₁⁽⁻¹⁾ is found to reach a minimum, about 0.05 at 400 fs, and later attains a constant value of ∼0.073. Because of the 3s resonance, this b̃₁ coefficient, appearing in eq 1, is seen experimentally to be the dominant contribution to the . Consequently the same time dependence is visible on with a final value converging to +14.6 ± 3.3% for (1R)-(−) enantiomer (details in the Supporting Information). This asymmetry has the same sign and amplitude as that measured with a single VUV photon in this same energy range (+15.4%).¹⁰ More relevantly, the 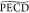value at ∼0 fs delay in this (1 + 1′) ionization can be also compared to the (2 + 1) fs-CPL one recorded on fenchone at 398 nm,^7,9 while the b̃_odd values can not be because the number and polarizations of photons used to reach the resonance are different. In both 0 fs-(1 + 1′) and (2 + 1) fs-CPL ionization, the PECD observed is in the range of +10%. More experiments are required before one can conclude whether or not intermediate resonances in REMPI fixes quantitatively the PECD.

To come back to the 400 fs time transient of b̃₁⁽⁻¹⁾, both TD-DFT and SA6-CASSCF(4,7)/aug-cc-pVDZ calculations predict that the vibrational wavepacket created by the pump pulse will be driven by the steepest descent path from the Franck–Condon region to the minimum-energy region of the 3s potential mostly along the stretching of the C1–C2 bond of the six carbon cycle, as illustrated in Figure 4a. This complex vibrational dynamics is expected to take place with energy flow between different vibrational modes, leading to a larger diversity of populated vibrational modes. PECD measurements on static molecules have revealed a high sensitivity to the vibrational excitation of the cation, with even the possibility of sign inversion, i.e., a flipping of the recorded asymmetry, upon excitation of certain vibrational modes.^9,19 In this context, we suggest that the first 400 fs decay observed on b̃₁ and 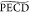reflects a part of intramolecular vibrational relaxation (IVR) taking place in the 3s Rydberg state. Indeed, the low degree of molecular symmetry does not restrain vibrational interaction such that fast IVR can take place. A lowering of the 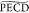in this short 400 fs window would result from the increasing number of populated vibrational modes, with a priori different contributions to b̃₁⁽⁻¹⁾, both in magnitude and sign, relative to the vibrational wavepacket created at 0 fs and thus leading to a blurring of the overall photoelectron asymmetry. This vibrational relaxation would involve, within the 0.25 eV kinetic energy available in the 3s state, principally the low frequency vibrational modes, for example, the bending of bicyclic skeleton, twisting modes, and methyl torsion, all of which are characterized by large anharmonic couplings. Figure 4b shows the vibrational quanta lower than 1000 cm^–1 (0.12 eV), while Figure 4d shows the vibrational mode with the lowest frequency (at 84 cm^–1). The 3s internal conversion onto lower valence states occurs, however, in a subset of the available degrees of freedom, meaning that all the vibrational modes populated directly or by IVR in the 3s state during the first 400 fs do not relax at the same time.^20,21 At long delay, we expect that only the less efficiently coupled vibrational modes, the spectator modes of the radiationless transition, will remain populated. It seems that in fenchone, these spectator modes are related to a larger PECD, as shown by the rising of the b̃₁ over ∼3.25 ps.

This interpretation requires theoretical support with calculations of TR-PECD that include vibrations; this is far beyond the present state-of-the-art. In particular, our results indicate that PECD would be very sensitive to the initial vibrational states, while previous investigations considered only the effect of vibrational excitation of the final cationic state.^19,22

The from the 3s Rydberg state (∼14.6 ± 3.3%) is as strong as the PECD recorded from the ground electronic state (15.4%). The 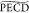magnitude obtained at large delays is rather impressive, considering that the 3s outgoing Rydberg electron scatters less often in the inner part of the molecular potential but more often at distance further from the chiral carbons compared to an electron outgoing from the HOMO ground-state orbital. This shows that the phases of partial wave functions can be determined by their values far from the ionic core and that PECD is thus a very long-range probe of the whole molecular potential, as already observed in one-photon PECD, for instance in clusters.^23,24 At the same time, by using a pump step, partial alignment is achieved, and when a Rydberg state is excited, a smaller number of angular momentum components are required to describe the photoelectron continuum. It would be interesting to investigate these two latter conditions to determine their respective impact on the large asymmetry that is observed here.

In conclusion, we have shown that a large (>10%) could be observed in photoionization from excited chiral molecules even if the outgoing electron is emitted from an extended wave function such as a Rydberg state. Furthermore, we have demonstrated that time-resolved PECD could be used as a sensitive probe of ultrafast dynamics in chiral molecules with femtosecond resolution. The different Legendre coefficients reveal dynamics related to alignment (b̃₃⁽⁻¹⁾), vibrational relaxation (b̃₁), as well as electronic conversion (B̃₀); all behave independently with different time constants. Only the b̃₁⁽⁻¹⁾ observable appears here sensitive to subpicosecond dynamics such as IVR.

In particular, odd coefficients, such as b̃₁ which is fully proportional to the sine of dephasing between adjacent outgoing waves,²⁵ are much more sensitive to the whole molecular potential than even parameters such as B̃₀. TR-PECD provides new and richer opportunities to template molecular dynamics in chiral systems in comparison to previous time-resolved angle-resolved PES on achiral samples involving only PES and the classical β anisotropy parameter. The ability to probe complex ultrafast relaxation in chiral systems opens up concrete possibilities for the investigation of molecular dynamics such as transient chirality or nuclear motions involved in chiral recognition. These results present a stepping stone for time-resolved chirality and more generally to establish a femtochemistry based on circular polarizations.

Experimental and Computational Methods

An Even–Lavie valve is used as a pulsed enantiopure fenchone source with helium as carrier gas to avoid cluster formation. The experiment was performed using the Aurore laser system at CELIA, which delivers 20 mJ, 25 fs, 800 nm pulses at 1 kHz. Only 2 mJ is used in the present experiment. The presented results are obtained by scanning the pump–probe delays typically 16 times, and at each delay, one helicity image is a record over 45 000 laser shots. For each scan, two background images corresponding to the probe pulse alone in each helicity are recorded and subtracted from each image of each delay for a given helicity. This background subtraction is required for the longest pump–probe delay when the signal reaches zero (see Figure S4 of the Supporting Information). High-level quantum chemistry calculations, using Gaussian 09, Molpro, and GAMESS-US quantum chemistry packages, have been performed on the ground and first five electronic excited states of fenchone to help in the interpretation of the experimental data. All the computational details and results can be found in the Supporting Information.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpclett.6b02065.

• Details of the calculations of the geometry and energies of the excited states, the experimental setup, the adiabatic ionization potential deduced experimentally by the energy balance of the PES, the effect of breaking cylindrical symmetry, and the fitting procedures used in Figure 3 (PDF)

The authors declare no competing financial interest.