Enhanced fold recognition using efficient short fragment clustering

Abstract

The main structure aligner in the CCP4 Software Suite, SSM (Secondary Structure Matching) has a limited applicability on the intermediate stages of the structure solution process, when the secondary structure cannot be reliably computed due to structural incompleteness or a fragmented mainchain. In this study, we describe a new algorithm for the alignment and comparison of protein structures in CCP4, which was designed to overcome SSM's limitations but retain its quality and speed. The new algorithm, named GESAMT (General Efficient Structural Alignment of Macromolecular Targets), employs the old idea of deriving the global structure similarity from a promising set of locally similar short fragments, but uses a few technical solutions that make it considerably faster. A comparative sensitivity and selectivity analysis revealed an unexpected significant improvement in the fold recognition properties of the new algorithm, which also makes it useful for applications in the structural bioinformatics domain. The new tool is included in the CCP4 Software Suite starting from version 6.3.

Introduction

The comparison and structural alignment of protein structures has attracted the attention of researchers and software developers for more than two decades. Over 50 different structure alignment algorithms have been designed (reviewed by Guerra & Istrali 2000), indicating that the problem is not yet solved in a commonly accepted manner. This is largely due to the absence of a universal and robust measure of structural similarity (Yang & Honig 2000), but also due to the high computational complexity, which requires a careful choice of various approximations, with a different balance between achievable quality and computation time.

The choice of a particular structure alignment algorithm is, in general, task-dependent. For example, the CCP4 Software Suite (Winn et al. 2011) includes several programs for structure comparison and the calculation of the best structure superposition: LSQKAB (Kabsch 1976), POLYPOSE (Diamond 1992) and SUPERPOSE (also known as Secondary Structure Matching, SSM, Krissinel & Henrick 2004). In addition, the 3D structure alignment and superposition may be calculated with MOLREP, a program for molecular replacement (Vagin & Teplyakov 1997). These programs are not functionally equivalent to each other; e.g. LSQKAB is extremely fast and efficient but needs a manual input of matching atom pairs, POLYPOSE performs multiple superpositions of a large number of structures but assumes them to be of the same length, with one-to one correspondence between their atoms. The actual structure alignment in CCP4 (i.e. 3D comparison based on the automatic computation of equivalent atom pairs) is done by SSM and MOLREP. SSM was recognized as the fastest and is considered to be a top-quality application in the field (Kolodny et al. 2005). Originally, this algorithm was designed for fast 3D searches in structural databases at the European Bioinformatics Institute (EBI). For this purpose, certain limitations were adopted. For example, SSM can only be applied to structures that contain a minimum number of secondary structure elements. In addition, SSM may underperform on fragmented chains and, in certain cases, it prunes search trees if speed is of essence. MOLREP is free from SSM limitations; however, structural alignment is not the main option for this application and comes as a by-product of a more general task. As a result, structural alignment in MOLREP is too slow for interactive applications and database searches.

GESAMT was developed as an attempt to complement the CCP4 Software Suite with a structure aligner that would be comparable to SSM by speed and quality, yet free of its limitations. The algorithm performs a fully automatic calculation of the correspondence between two ordered sets of 3D coordinates using SSM’s Q-score, which is equivalent to the identification of the largest common substructures, and performs the best superposition of the aligned structures. The algorithm is applicable to chains with undefined secondary structure, as well as incomplete and fragmented (broken) chains. This makes GESAMT a more convenient algorithm than SSM for the intermediate stages of the structure solution process when, e.g., only an outline of a protein backbone is known. Sensitivity vs selectivity analysis of GESAMT showed that it achieves a considerably higher alignment quality than SSM. The analysis also revealed a considerable (5-10 times) enhancement of fold recognition rate, which was not initially expected. The latter makes GESAMT a useful tool for various applications in structural bioinformatics, whenever an inference on structural similarity or homology is required.

The algorithm

Fundamentally, GESAMT has many similarities to other approaches, such as Combinatorial Extension (CE, Shindyalov & Bourne 1998) and FATCAT (Ye & Godzik 2003). Protein backbones (represented by C-alpha atoms in this study) of the compared protein chains A and B, of length N_A and N_B, respectively, are split into sets of overlapping short fragments of length M, $F_{A/B}=\left\{f_i^{A/B}\right\},$ such that there are L_A/B = N_A/B − M + 1 fragments in the corresponding sets. The optimal structure alignment of chains A and B may then be described as the identification of same-size subsets of non-overlapping fragments ${\tilde{F}}_{A/B}\subset F_{A/B},$ such that there is an unambiguous, one-to-one, correspondence between fragments $f_i^A\in {\tilde{F}}_A$ and $f_i^B\in {\tilde{F}}_B$ that maximizes the chosen score function $Q\left({\tilde{F}}_A,{\tilde{F}}_B\right).$

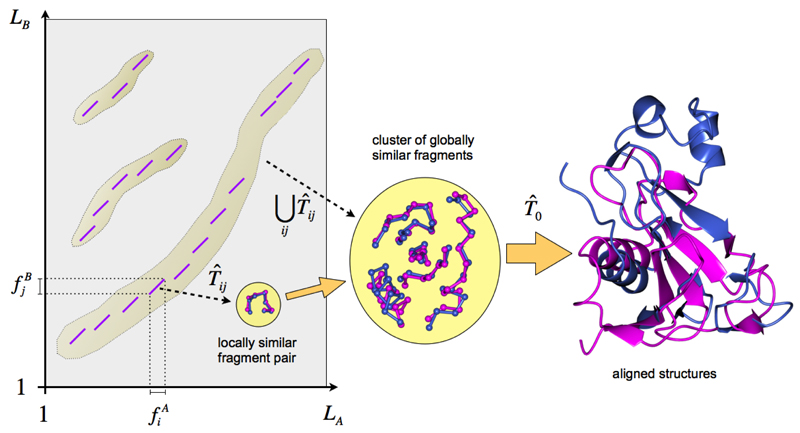
A straightforward approach to this problem includes the calculation of all L_A × L_B short fragment superpositions (SFS) and the identification of the largest subsets of non-overlapping fragment pairs with close superposition matrices T_ij, such that ${\widehat{T}}_{ij}\cdot f_j^B\approx f_i^A.$ The final solution is obtained by the appropriate “averaging” of superposition matrices $\left\{{\widehat{T}}_{ij}\right\}\to {\widehat{T}}_0,$ chosen to maximize the score function Q. Consider GESAMT’s version of this scenario in more detail (Figure 1).

Figure 1. Schematic of structure alignment process in GESAMT.

The left part of Figure 1 represents the fragment similarity matrix for the given chains A and B. Every short section in the matrix represents an SFS. SFSs with similar transformation matrices are collected into clusters, which after further refinement are brought to the common superposition matrix T₀.

As was found empirically, pre-calculation of all L_AB = L_A × L_B SFSs with further clustering is considerably (hundreds of times) slower than fusing these operations as in the following approach. At each time point, GESAMT keeps a list of clusters (that is initially empty). Each cluster contains the list of short fragments, the superposition matrix T_K (where K stands for cluster number) and the Q-score of the fragment superposition (see the definition of the Q-score in Krissinel & Henrick 2004). Each new fragment pair $\left\{f_i^A,f_i^B\right\}$ is tested for suitability for each cluster, for which the pair is added to the cluster with the corresponding recalculation of T_K and Q-score. If the new Q-score is not smaller than the previous one, the pair is left in the cluster. Note that, as a result of this procedure, a fragment pair may be included in more than one cluster. Note also, that a properly designed algorithm allows the incremental calculation of correlation matrices for individual clusters (cf. superposition matrix calculations from Krissinel & Henrick 2004), which makes the testing of fragment pairs as fast as the calculation of individual SFSs. If a fragment pair cannot be added to any existing cluster, a new cluster is generated. As observed, this algorithm results in a relatively small number of clusters (typically around 0.01·L_AB). If an excessive number of clusters is generated (over 0.1·L_AB), the smallest clusters that grow slower than their similar-sized equivalents, are abandoned.

Structural alignments, represented by the resulting clusters, are not optimal in most cases. This is because the fragment pairs $\left\{f_i^A,f_i^B\right\}$ are added to clusters in the order of i,j -counting, and the fact that addition of one pair may result in the rejection of a whole branch of suitable pairs on later stages is completely ignored. This simplified approach was taken only because of performance considerations. More specifically, trying all combinations of fragment pairs for each cluster would result in an optimal alignment but also make the problem NP-complete, which is computationally intractable. Instead, GESAMT attempts to repair the deficiency of the chosen approach by further refining the alignments in the largest clusters. After refinement, the alignment with the highest Q-score is reported as the final result.

The refinement procedure attempts to choose a superposition matrix T₀ that would increase the Q-score of an alignment. This is achieved by the iterative addition of new atom pairs into the alignment, but also by the removal of atom pairs if they render an increase in Q-score impossible, and recalculation of T₀ after each iteration. Conceptually, this task is similar to conventional sequence alignment, which is solved rather efficiently with the Smith-Waterman algorithm (Smith & Waterman 1981). This algorithm places the elements of the two sequences in an optimal correspondence that minimizes the difference between individual elements (such as residue types). In a structural context, the difference between the individual backbone atoms i and j is a function of their space separation w_ij = w(d_ij) at a given superposition matrix T₀. Firstly, T₀ is calculated using the initial set of corresponding atom pairs in the chosen cluster. Then, a new set of pairwise atom relations is calculated by the Smith-Waterman algorithm with the appropriately chosen function w(d_ij). The new set of atom pairs may be used for the calculation of the corrected superposition matrix T₀, and this process is iterated until the results cease to change (Gerstein & Levitt 1996).

Using atomic separations d_ij as the sole measure of difference for the Smith-Waterman algorithm would result in the optimization of a purely distance-related score. For example, the following function:

$$w\left(d_{ij}\right)=\text{max}\left(0,d_0^2-d_{ij}^2\right)$$ (1)

will produce alignments with minimal rmsd for pairs separated by distances less than d₀ angstroms. In general, rmsd is not the most convenient score for structural alignments. With this score, the best alignments (zero rmsd) may be always achieved with the superposition of just one or two C-alpha atoms from each chain. SSM’s Q-score (Krissinel & Henrick 2004):

$$Q=\frac{N_{align}^2}{(1+{(rmsd/R_0)}^2)N_A{N}_B}$$ (2)

was found to be a far better measure, because it takes both r.m.s.d. and the number of aligned atoms N_align into account. In Eq. (2), R₀ is an empirical parameter (set to 3 Å), which balances the effects of the alignment length and r.m.s.d. on the score. Chain lengths N_A and N_B are added into the denominator in order to generate a score in the region of 0 (completely dissimilar structures) to 1 (identical structures).

The Smith-Waterman algorithm utilizes elemental scores w_ij to measure the effect of putting the ith and jth elements of the two sequences into correspondence. Since the Q-score cannot be factored into a sum of individual effects w_ij, it cannot be used directly in the Smith-Waterman algorithm. In order to overcome this difficulty, we represent the Q-score in the following form:

$$Q=\frac{N_{align}}{N_A{N}_B}{\displaystyle {\sum }_{ij}\left(1-\frac{d_{ij}^2}{R_0^2+rms{d}^2}\right)}$$ (3)

where summation is made over all aligned pairs. Assuming that N_align and rmsd do not change significantly from iteration to iteration, the difference function w(d_ij) may be written as

$$w\left(d_{ij}\right)=1-\frac{d_{ij}^2}{R_0^2+rms{d}^2}$$ (4)

such that $Q=\frac{1}{N_A{N}_B}{\displaystyle {\sum }_{ij}w\left(d_{ij}\right)}.$ In Eq. (4), rmsd is calculated on every iteration using the superposition matrix T₀ and the N_align atom pairs produced by the Smith-Waterman algorithm in the previous iteration. As described in the next section, the refinement procedure converges to alignments with higher, when compared to the SSM algorithm, Q-scores.

GESAMT is implemented as a C++ application and is operationally identical to SUPERPOSE from the CCP4 Software Suite. As any other application of its kind, GESAMT has a few semi-empiric parameters, such as thresholds for Q-score variations in the clustering procedure and parameters for keeping the number of clusters on a reasonable level. These parameters control the extensiveness of the search and balance the achieved quality (as measured by the Q-score) and computation time. For simplicity, these parameters have been combined in two sets, called Normal and High mode. In Normal mode, a reasonable balance between quality and speed is negotiated, while in High mode, quality considerations are ultimately preferred. GESAMT is released by CCP4 (Winn et al. 2011) starting from version 6.3.

Results and Discussion

The assessment of structure alignment algorithms presents a problem on its own (see, e.g., Kolodny et al. 2005, Mayr et al. 2007). This is partially due to differences in the score functions used by the different algorithms, but also because of the fact that any assessment procedure requires benchmark sets of “similar” and “dissimilar” structure pairs, which cannot be comprehensive and may be inadvertently biased. In order to minimize the chances of having a biased result, we have chosen to use a benchmark set from elsewhere and provide score-based comparisons only with the SSM algorithm, which optimizes the same Q-score as GESAMT. Neither SSM nor GESAMT were calibrated (trained) on this data set.

The benchmark set was produced by the authors of the FATCAT structure alignment software (Ye & Godzik 2003). It consists of 6233 similar and 8769 dissimilar pairs of protein structures, where similarity and dissimilarity may be identified on all 4 levels of SCOP hierarchy (Murzin et al. 1995): family, superfamily, fold and class. This set was successfully used in other studies (see, e.g., Friedberg et al. 2007) and is available from http://fatcat.burnham.org/fatcatbench/benchmark/benchvalue.txt together with FATCAT’s figures of performance, which are used in this study for reference.

First, consider the discrimination properties of the structure alignment algorithms. Usually, structure similarity is measured by a continuous score S. Introduce function P(S) as the probability of obtaining an alignment of similar structures with a score lower than S. Likewise, let function N(S) be the probability of getting a score higher than S in the alignment of dissimilar structures. The score S₀, such that E₀ = N(S₀) = P(S₀), is the optimal discrimination score, and the lower the discrimination error E₀, the higher the discrimination power of the algorithm.

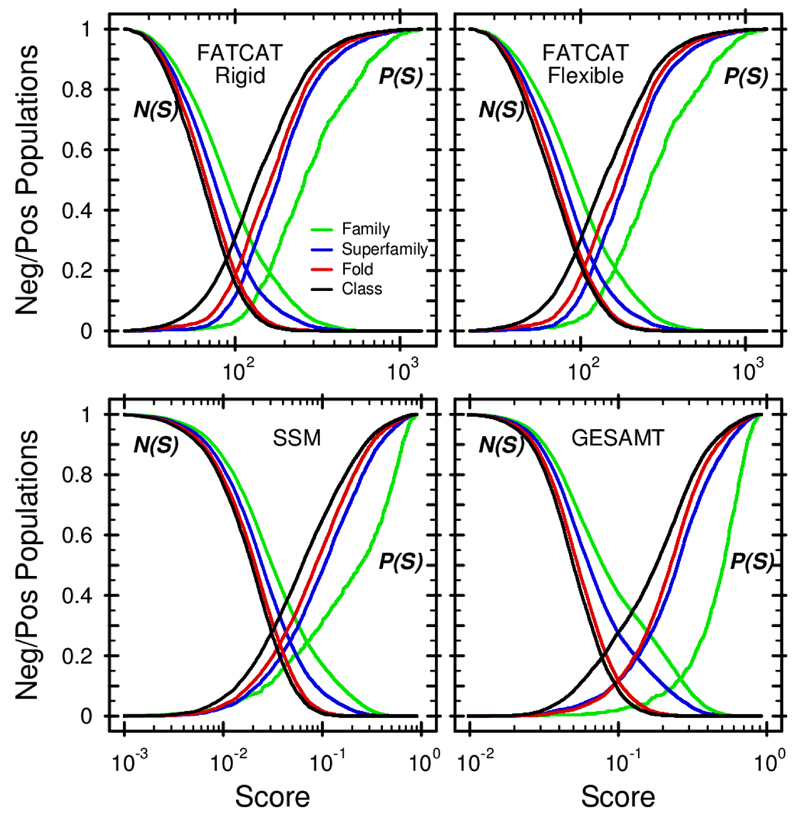
Figure 2 shows the discrimination properties of FATCAT-Rigid, FATCAT_Flexible, SSM and GESAMT. Predictably, all N(S) curves are monotonically decreasing and P(S) monotonically increasing. The intersection point S₀, as well as the value of the discrimination error E₀, appear to be different for all algorithms and similarity levels (which correspond to the levels of SCOP hierarchy). An ideal discrimination between similar and dissimilar structures would occur in case of E₀ = 0, which is not observed in Figure 2. It is therefore obvious that neither FATCAT’s “raw” scores nor the Q-score can unambiguously indicate structure similarity. Table 1 suggests that GESAMT provides the best similarity detection in all cases, while SSM’s performance is the worst. As the similarity detection is performed using the same score in both SSM and GESAMT, the forementioned result indicates a considerable advantage of the latter algorithm. More specifically, in the Family and Fold similarity classes, GESAMT outperforms other algorithms by a substantial margin, while in the case of Superfamilies, it offers only a marginal improvement, when compared to FATCAT-Rigid.

Figure 2. Discrimination properties of selected structure alignment algorithms.

FATCAT-Rigid, FATCAT-Flexible (Ye & Godzik 2003), SSM (Krissinel & Henrick 2004) and GESAMT (present study) are compared. N(S) gives the probability of getting a score higher than S for dissimilar structures, P(S) corresponds to the probability of getting a score lower than S for similar structures. For FATCAT, S corresponds to the “raw” scores, contained in the FATCAT benchmark set. For SSM and GESAMT, the Q-score was used. Different-color curves correspond to similarity detected at various levels of SCOP hierarchy, as indicated in the figure.

Table 1.

Discrimination errors E₀ for selected structure alignment algorithms, corresponding to the intersection points in Figure 2.

	Family	Superfamily	Fold	Class
FATCAT-Rigid	0.19	0.20	0.19	0.24
FATCAT-Flexible	0.21	0.22	0.21	0.26
SSM	0.25	0.25	0.24	0.28
GESAMT	0.12	0.19	0.12	0.19

Discrimination between similar and dissimilar structures is used in a more rigorous, score-independent, test on sensitivity and specificity. A good structure alignment algorithm is both sensitive and specific. The algorithm is said to be sensitive if it tends not to identify similar structures as dissimilar. The sensitivity is measured by the True Positive Rate:

$$SNS=\frac{TP}{TP+FN}$$ (5)

where TP stands for the probability to identify similar structures as similar (True Positives), and FN is the probability to identify similar structures as dissimilar (False Negatives). Similarly, a specific algorithm is one with a high True Negative Rate:

$$SPC=\frac{TN}{TN+FP}$$ (6)

where TN and FP are probabilities to identify dissimilar structures as dissimilar and similar, respectively (True Negatives and False Positives).

In order to evaluate the sensitivity and specificity of an algorithm on a wide range of scores, the Coverage vs. Error plot is used (Brenner et al. 1998). All alignments are sorted by decreasing score, and the values of TP, TN, FP and FN are calculated as functions of the sort index n. E.g., TP(n) is the number of true positives detected in alignments 1 to n. Finally, SNS(n) called Coverage, and SPC(n) are calculated. However, for presentation purposes, the False Positive Rate: FPR(n) = 1 − SPC(n) is used instead (Brenner et al. 1998). Lower and longer FPR(n) curves indicate a more specific and sensitive similarity detector.

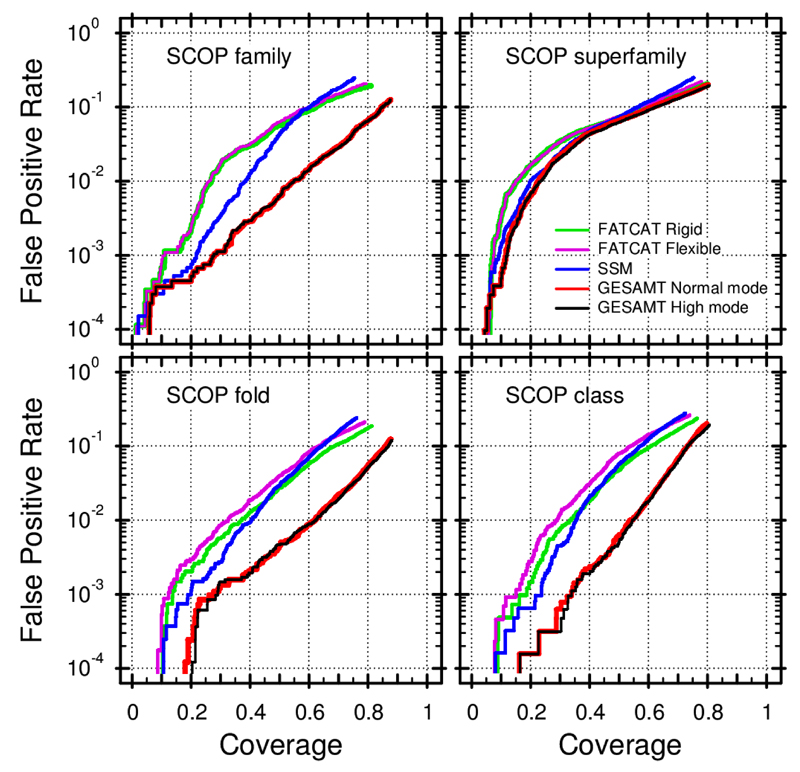
Figure 3 presents the Coverage vs Error plots for selected algorithms. The curves were calculated using the optimal discrimination scores from Figure 2 (listed in Table 2) and, therefore, reflect the best possible results for each algorithm on the benchmark set used. As seen in the figure, SSM appears to be generally more specific at lower and medium coverages comparing to FATCAT, but is marginally outperformed by the latter at high coverages i.e. SSM is a slightly more specific tool. This may be partially explained by the fact that SSM was designed and tuned for fast database screening, which is based on the aggressive removal of non-promising (True Negative) hits. The most significant difference between SSM and FATCAT is seen on the level of SCOP families, which means that SSM is better at a finer discrimination of generally similar structures.

Figure 3. Coverage vs. Error plots (Brenner et al. 1998) for selected structure alignment algorithms.

FATCAT-Rigid (green lines), FATCAT-Flexible (magenta lines), SSM (blue lines) and GESAMT in Normal (red lines) and High (black lines) mode are compared. The optimal discrimination scores from Table 2 were used as similarity thresholds. Different plots correspond to similarity detection at various levels of SCOP hierarchy, as indicated in the figure.

Table 2.

Optimal discrimination scores corresponding to data in Figure 2 and Table 1.

	Family	Superfamily	Fold	Class
FATCAT-Rigid	161	117	101	88
FATCAT-Flexible	162	121	105	93
SSM	0.070	0.047	0.037	0.031
GESAMT	0.262	0.134	0.100	0.078

GESAMT is an absolute winner in this series of tests. On Family, Fold and Class similarity levels, GESAMT provides considerably and consistently more specific and sensitive results (with the exception of a narrow region of coverages between 0.6 and 0.15 on Family level, where GESAMT is as good as SSM). In selected coverages, GESAMT gives up to 10 times fewer false positives, when compared to SSM and FATCAT. On average, GESAMT results appear to be 3 to 5 times more accurate. In the case of fold-level and class-level similarity detection, GESAMT shows a stunning difference from the other algorithms compared. This result suggests that GESAMT may be useful for various applications in the structural bioinformatics domain, where structural similarity is used to infer on homology or functional properties of structures. As seen in Figure 3, there is little difference in the results produced by GESAMT in the Normal and High modes. Therefore, for the majority of practical applications, the Normal mode is an appropriate choice.

Curiously, all algorithms perform nearly equally in the Superfamily similarity level, where they reach a relatively high number of false positives at low coverages. It is difficult to give any definite reason for this behavior. It is not very likely that this is caused by particular design or implementation features in the 4 different methods. This could rather be an artifact originating from the composition of the benchmark set. Another possible explanation is that SCOP classification could be less perfect on the level of superfamilies. One can note in this regard that the classification of SCOP superfamilies is defined by a probable common evolutionary origin (Murzin et al. 1995), and could thus be less related to structural features, compared to other levels of SCOP hierarchy.

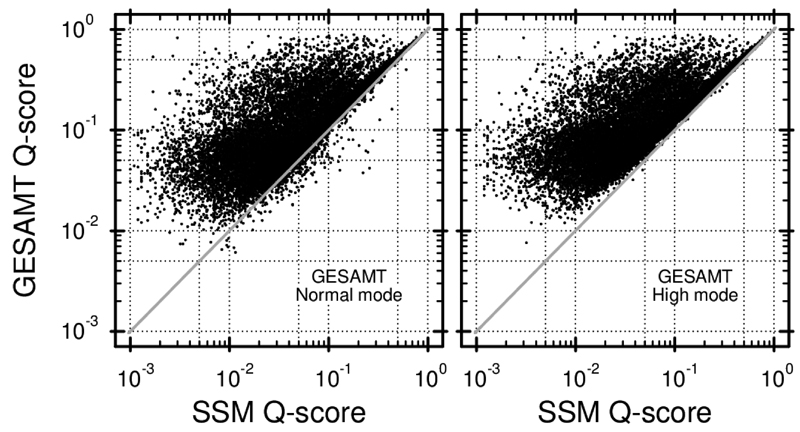
It is interesting to perform a direct comparison of SSM and GESAMT, which is facilitated by the fact that they are based on the optimization of the same score. As seen in Figure 4, GESAMT produces considerably higher Q-scores. On average, Q-scores from GESAMT are 2-3 times higher than SSM’s. This means that GESAMT finds longer alignments at lower rmsd. In many cases, GESAMT produces scores that are 10 and even 100 times higher. These cases correspond to SSM failures. As seen in the figure, only a small percentage of GESAMT’s alignments in Normal mode are worse than the ones produced by SSM. In very few instances, GESAMT fails (i.e. produces Q-scores that are 5-10 times lower than SSM’s).

Figure 4. Comparison of Q-scores produced by SSM and GESAMT in Normal (left panel) and High (right panel) mode.

Each dot represents a pair of alignments, produced by SSM and GESAMT for the same protein pair from the benchmark set used.

In High mode, less than 10 of GESAMT’s alignments have superficially lower than SSM’s Q-scores, while approximately 95% percent of the other results are very similar or identical to those obtained in Normal mode. As mentioned before, higher Q-scores in High mode are achieved by a wider exploration of the search space, which involves additional computational costs. Figure 5 presents a comparison of the computation time used by SSM and GESAMT for producing individual alignments. As seen in the figure, in the majority of cases GESAMT is faster than SSM in Normal mode and slower in High mode. The gross computation times suggest that, on average, SSM takes 0.3 secs per alignment while GESAMT in Normal mode is 4.3 times faster and in High mode approximately 2.5 times slower. These results indicate that a marginal (in less than 5% of cases) quality decrease in the Normal mode is accompanied by a 10-fold gain in speed. These figures justify the choice of internal parameters configured to the Normal mode and leave the use of the High mode to special (doubtful and difficult) cases.

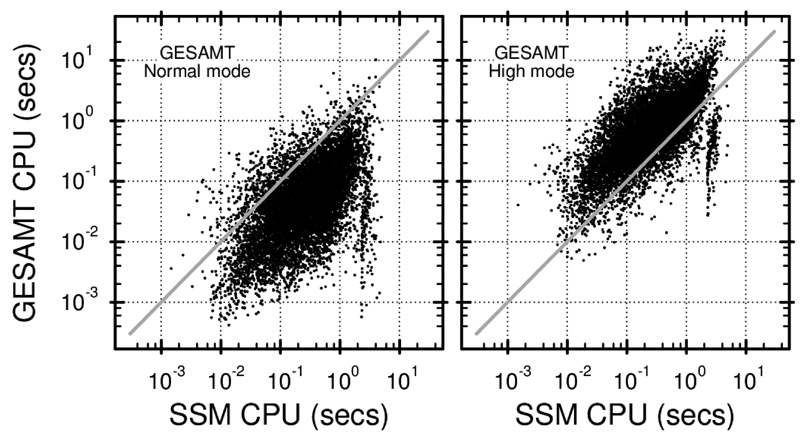
Figure 5. Comparison of computation times used by SSM and GESAMT in Normal (left panel) and High (right panel) modes for individual alignments.

Each dot represents a pair of alignments, produced by SSM and GESAMT for the same protein pair from the benchmark set used. Total computation time used by SSM is 4,746 secs, GESAMT in Normal mode: 1,107 secs, GESAMT in High mode: 12,167 secs.

It is worth noting here, that this test is not truly indicative of SSM’s speed. As its essential feature, SSM allows for efficient precompilation of structural data, which is then used for fast database screening. With this precompilation in force, SSM’s speed is significantly (20–30 times) faster than indicated in Figure 2. This particular feature of the SSM algorithm cannot be used for pairwise comparisons and, therefore, is not engaged in CCP4’s SUPERPOSE. However, precompilation of structural data is an essential feature of the SSM web-server running at the European Bioinformatics Institute (http://www.ebi.ac.uk/pdbe/ssm). In addition, SSM makes use of controlled complexity, which allows for a further 20-30 times speed-up by pruning the search tree so that only alignments with higher than an a priori specified similarity level are looked at.

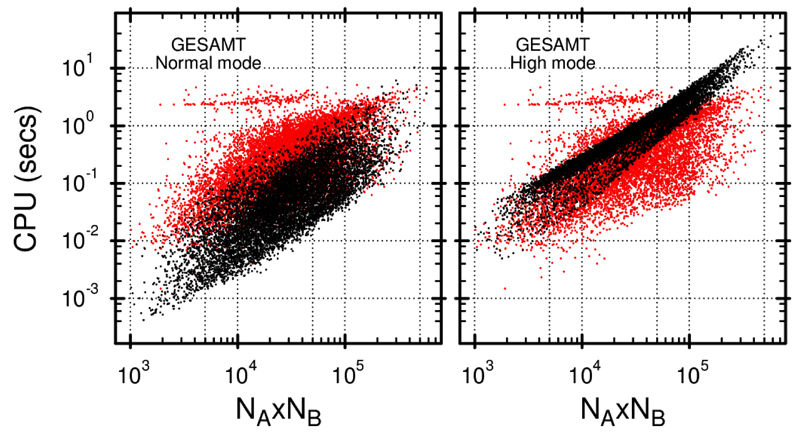
The structure size is one of the major factors affecting the computation times of structure alignment algorithms. Figure 6 shows the correlation between the computation time and the product of chain lengths for SSM and GESAMT. As seen in the figure, in the Normal mode, GESAMT outperforms SSM in cases of medium to small-sized structures (100-200 residues) and shows a comparable performance in the case of larger structures (more than 400 residues). In the High mode, GESAMT is considerably slower than SSM for larger structures. The theoretical complexity of GESAMT is estimated as O(N_A × N_B), which is generally confirmed by data shown in Figure 6. A linear correlation between the measured CPU time and the product of chain lengths is seen rather clearly in the High mode, while the Normal mode shows a higher extent of variation from the estimate. This is explained by the previously mentioned fact that GESAMT utilizes much more liberty in pruning the search tree when running in the Normal mode, subject to the particular situation and structural features. This often results in shorter than theoretical computation times. On the contrary, in the High mode, most of the search space is forcefully explored, which results in a narrower configuration of black dots, as if they were pulled up to the top limit.

Figure 6. Correlation between computation time and product of chain lengths for SSM (red dots) and GESAMT (black dots).

Each dot represents a pair of alignments, produced by SSM and GESAMT for the same protein pair from the benchmark set used.

In its current form, GESAMT solves the very basic problem of a rigid-body alignment of linear structures. This is applicable in most practical situations. Yet, there are a few important cases where a rigid-body alignment does not provide an easy answer: alignment of structures with hinges, branches, loops and reverse inclusions and multiple alignments. Application of a rigid-body technique to a pair of structures with hinge motion between the domains results in the identification of a single domain pair that aligns with the highest score, while, typically, a researcher would like to have a complete list of the matching domains. Branching and looping mainchains break the original assumption of linear structures, which makes results dependent on the indexing of monomeric residues. Sometimes, two structures may have a similar spatial orientation of the larger construction units (e.g., secondary structure elements), but differ in the way these units are interconnected. This represents the case of reverse inclusions which are not suitable for rigid-body aligners. A multiple alignment (MA) refers to the identification of common structural features in n>2 molecules (see Krissinel & Henrick 2005, Micheletti & Orland 2009, Shatsky et al. 2004). This technique allows one to draw higher-confidence conclusions from comparative studies in structural bioinformatics. Also, MA is receiving an increasing interest associated to the selection of models for molecular replacement in protein crystallography. In general, MA does not reduce to a set of pairwise alignments and requires simultaneous consideration of all the structures involved. This cannot therefore be achieved with GESAMT in its present form. However, based on the impressive results on the structure recognition rate that were demonstrated by GESAMT, it would be interesting to extend the algorithm to all or some of the tasks listed above. This would represent a promising direction for future developments.

Conclusion

We present GESAMT, a new algorithm for the structural alignment of polypeptide chains. The initial motivation for this development was to overcome the limitations of SSM, a primary structure alignment tool in the CCP4 Program Suite, without losing its strengths. SSM only works with structures that have at least a few secondary structure elements and is sensitive to the completeness of data. This limits SSM’s applicability on the intermediate stages of the structure solution process, when a secondary structure pattern may still be undefined and the model may be partially incomplete (fragmented). GESAMT is free from these limitations. In this study, we applied GESAMT only to protein structures. However, it is equally applicable to any ordered sets of points in 3D space; for example, representing a backbone of RNA chains. Likewise, we only used C-alpha based fragments but the method allows for a straightforward generalization on fragments of an arbitrary level of details, e.g. those including C-beta or C-gamma atoms.

The assessment of the new algorithm has confirmed that it is at least as fast and efficient as the (pairwise) SSM. What came out as a surprise is GESAMT’s enhanced ability to discriminate between similar and dissimilar structures. Compared to SSM, GESAMT makes up to 10 times fewer errors at the same coverages and produces 5-10 times higher Q-scores. We also confirmed these findings in respect to another popular algorithm, FATCAT. A comprehensive comparative study with numerous other algorithms is beyond the scope of this paper but an enthusiastic reader may get the general points of reference from the comparisons made in this paper and from similar studies that involve SSM and FATCAT elsewhere (see Kolodny et al. 2005). The enhanced ability to discriminate between structure families, folds and classes makes GESAMT a recommended substitution to SSM in bioinformatics-related studies.

GESAMT is as fast as SSM at pairwise comparisons but is not competitive at database screening, where SSM is 10 to 100 times faster. This is due to its ability to filter out non-promising matches and efficiently prune whole branches of the search trees in early stages, without their exhaustive exploration. Also, GESAMT does not compute multiple alignments, for which there is a growing demand from the area of ensemble modeling for molecular replacement. Addressing these problems represents the future direction of GESAMT development.