A promising new mechanism of ionizing radiation detection for positron emission tomography: Modulation of optical properties

Abstract

Using conventional scintillation detection, the fundamental limit in positron emission tomography (PET) time resolution is strongly dependent on the inherent temporal variances generated during the scintillation process, yielding an intrinsic physical limit for the coincidence time resolution of around 100 ps. On the other hand, modulation mechanisms of the optical properties of a material exploited in the optical telecommunications industry can be orders of magnitude faster. In this paper we borrow from the concept of optics pump-probe measurement to for the first time study whether ionizing radiation can produce modulations of optical properties, which can be utilized as a novel method for radiation detection. We show that a refractive index modulation of approximately 5 × 10⁻⁶ is induced by interactions in a cadmium telluride (CdTe) crystal from a 511 keV photon source. Furthermore, using additional radionuclide sources, we show that the amplitude of the optical modulation signal varies linearly with both the detected event rate and average photon energy of the radiation source.

1. Introduction

1.1. Impact of better PET detector time resolution

For the last three decades, a significant amount of research has focused on improving scintillation crystal properties and other factors in a PET system to go beyond simple 511 keV photon coincidence detection to time-of-flight (ToF) capability which requires much better timing resolution. Researchers have been searching for crystal materials with faster rise time, shorter decay time and higher light output that are more suitable for ToF-PET systems (Yeom et al 2013a). Crystals including lanthanum bromide (LaBr₃) and cerium-doped lutetium orthosilicate (LSO) are good candidates (Melcher and Schweitzer 1992). Different crystal geometries and surface treatments have been studied in order to improve PET time resolution (Kronberger et al 2008). Photodetectors including silicon photomultiplier (SiPM) have been developed to achieve the detection of scintillation light with higher quantum efficiency and faster response time (Yeom et al 2013b). Different read electronics and time pick off methods have been studied (Yeom et al 2013c, Bieniosek et al 2013). Other electronics components needed in a ToF-PET system are also improved to achieve smaller time jitter (Conti 2009).

A dramatically improved 511 keV photon coincidence time resolution will bring substantial signal amplification over existing systems (Karp et al 2008). This increased signal-to-noise ratio (SNR) in reconstructed PET images enables an advanced ability to visualize and quantify a fewer number of diseased cells in the presence of diffuse background signal that is typical in any PET study (Surti et al 2006). Alternately, patient injected dose and patient scan duration, two major limitations of clinical PET systems, may both be substantially reduced with much better ToF performance (Fazel et al 2009). If less than 20 picosecond (<20 ps) time resolution were possible, image reconstruction time would also be greatly reduced (Presotto et al 2015, Mehranian et al 2016), enabling PET for real time imaging applications including guiding diagnostic interventions and surgical treatments for diseases. Additionally, significantly higher SNR enabled by better time resolution paves the way for advanced clinical PET systems designed with significantly smaller photon detector elements to increase spatial resolution for patient studies (Levin and Hoffman 1999).

1.2. Limits on the coincidence time resolution of conventional scintillation based PET detectors

Even though a dramatically improved time resolution is desired as discussed in section 1.1, the coincidence time resolution of conventional PET detectors utilizing scintillation detection is largely limited by the scintillation process, which is essentially a form of “spontaneous emission”. In Lecoq et al (2006) and Lecoq et al (2014), the evolving process of the charge carriers created by ionizing radiation photons in scintillation crystals is reviewed and can be summarized as in table 1.

Table 1.

The evolving process of the charge carriers excited by high energy radiation photons in scintillation crystals (Lecoq et al 2006, Lecoq et al 2014).

Time Scale (s)	Process
10−16 – 10−14	Production of primary charge carriers from interactions with ionizing radiation photons, production of secondary charge carriers through inelastic electron-electron scattering and Auger processes
10−14 – 10−12	Thermalization of charge carriers, along with the production of phonons
10−12 – 10−10	Localization of charge carriers through interactions with material defects and impurities, leading to the production of polarons
10−10 – 10−8	Migration of charge carriers, radiative and/or non-radiative carrier recombination, production of scintillation light
10−10 – 10−9	Typical optical transport time

The production of primary charge carriers happens at the first stage after the interaction between ionizing radiation photons and scintillation crystals. High kinetic energy is transferred to the primary charge carriers and they immediately further excite a large number of secondary charge carriers through inelastic electron-electron scattering and Auger processes. This multiplication of charge carriers occurs within the femtosecond range. At the second stage within the sub-picosecond time scale, the electron multiplication process stops and the thermalization of charge carriers starts with the production of phonons. The energy of charge carriers decreases to below the threshold for inelastic electron-electron scattering. The third stage features the localization of charge carriers through their interactions with stable defects and impurities in the scintillation crystal. This stage is at the picosecond time scale. At the last stage within nanosecond time scale, charge carriers migrate to the luminescent centers and scintillation light is produced through radiative carrier recombination. Non-radiative decay happens simultaneously. We have also added a typical optical transport time for scintillation light to reach photodetectors in table 1 as a reference.

The production and emission of scintillation light occurs only at the last stage. The stochastic nature of the processes occurring before scintillation emission leads to significant statistical fluctuations for the generation of the first scintillation photons. Consequently the coincidence time resolution achievable by a scintillation based PET detector has an intrinsic limit which is estimated to be on the order of 100 ps in Lecoq et al (2014).

Apart from the intrinsic scintillation process, other influencing factors on the timing properties of scintillation based PET detectors have also been extensively investigated, including the intrinsic light yield, decay time, scintillation light transit time variations (a function of crystal element length and photon interaction depth), surface treatment, the photon detection efficiency and time jitter of the photodetector, and the properties (bandwidth and time jitter) of readout electronics (Spanoudaki and Levin 2011, Derenzo et al 2014, Gundacker et al 2014, Cates et al 2015). These factors determine the limitation for the coincidence time resolution of a realistic scintillation based PET detector. The current performance of “clinically relevant” PET scintillation detectors (with crystal length larger than or equal to 20 mm) is greater than 100 ps (Nemallapudi et al 2015, Cates et al 2015, Cates and Levin 2016).

However, an order of magnitude improvement (e.g. 10 ps or better coincidence time resolution) would enable substantial gains in reconstructed image quality and accuracy using ToF PET methodology. It will also lead to many other benefits as discussed in section 1.1. To dramatically improve the coincidence time resolution in PET and achieve a performance far below 100 ps, the intrinsic limitations placed by the scintillation process need to be overcome. Therefore in this work, we circumvent the scintillation based detection mechanism by borrowing from the field of ultrafast optics to study a novel concept for radiation detection in PET.

1.3. Concept of optics pump-probe measurement for radiation detection

One way to overcome the limitation for coincidence time resolution placed by the scintillation mechanism is to utilize the ultrafast charge carrier transient phenomena occurring before scintillation (as stated in table 1) to generate ultrafast time stamps for radiation detection. The optics pump-probe method utilizing the mechanisms of optical property modulation, as widely exploited in the optical telecommunications industry (Hecht 2015, Keiser 2003, Almeida et al 2004, Slavík et al 2010), shows great potential for the measurement of these ultrafast processes. First, unlike standard ionizing radiation detection methods, the optics pump-probe measurement introduces no extra time delay or variation. It is an “in place” and “instantaneous” detection method that has been widely used to observe femtosecond scale dynamical processes (Weiner 2011, Tomimoto et al 2002). Second, for the optical modulation material studied in this paper (CdTe) with an electron-hole pair creation energy of approximately 5 eV, it can be estimated that the total number of charge carriers generated by one 511 keV photon is around 10⁵. This relatively small number of carriers induces a very subtle modulation signal in the detector material. In optics pump-probe measurement, it is possible to make use of an optical resonant cavity with a high quality factor (high-Q) that would enable the observation of very weak signals. For example, single molecule detection has been achieved with high-Q optical microcavities (Armani et al 2007, Vollmer and Yang 2012).

In this work, we borrow the idea of optics pump-probe measurement to explore a totally new optics based method for 511 keV photon detection in PET using the modulation of optical properties due to ionization. Our motivating questions for this work are: Can we detect the modulation of optical properties in a detector material from the ionization charges created by an ionizing radiation source? Can faster timing and/or higher temporal resolution for PET be accomplished using mechanisms of optical property modulation instead of using scintillation detection? This paper focuses on the first question.

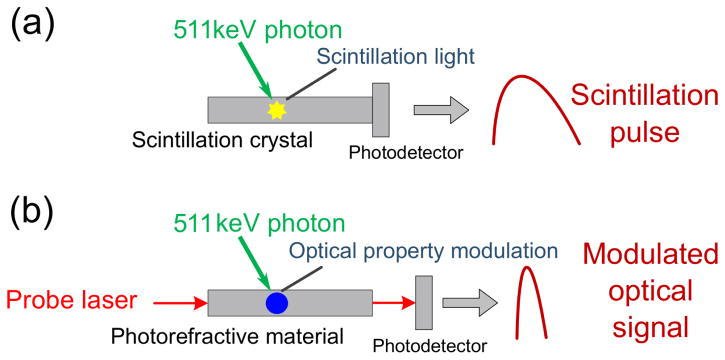
A basic comparison of a conventional scintillation based PET detection element and the proposed optics based detection method is shown in figure 1. In a scintillation based PET detector, the ionization charges created by 511 keV photons are converted to scintillation light which is detected by a photodetector. The time resolution is limited by the scintillation mechanism and other factors as discussed in section 1.2. In the proposed method, a probe laser is used for the detection of a small change in the local electric field resulting from the ionization charges created from high energy (e.g. 511 keV) photon interactions. Significant changes in optical properties (such as refractive index, absorption coefficient, reflectivity, nonlinear susceptibility, etc.) induced by the electric field change will modulate the characteristics (such as amplitude and phase) of the probe laser light. Therefore, by monitoring the probe laser state with a photodetector, we can detect the interactions of ionizing photons.

Figure 1.

(a) Conventional scintillation based PET annihilation photon detection element; (b) optics pump-probe based detection method.

Although combining optics pump-probe measurement with radiation detection still remains a mostly unexplored research concept, rising efforts and attention have been drawn to this field as a promising way to dramatically improve the timing properties of radiation detection. Ultrafast low energy X-ray detection based on optical modulation has been achieved (Lowry et al 2004, Vernon and Lowry 2006). Electro-optic neutron detectors have also been realized (Nelson et al 2010, Nelson et al 2012). Transient processes in scintillation crystals have been studied with ultrafast optical spectroscopy as an alternative way to generate fast time stamps for radiation detection (Auffray et al 2014, Auffray et al 2015). However all these studies require a very high flux, precisely synchronized radiation source as the pump source, which is impossible in realistic PET systems since the 511 keV photons arrive asynchronously and normally in relatively low flux. Some of these previous research efforts require ultrashort pulse lasers as the probe source (Auffray et al 2014, Auffray et al 2015), which is also highly impractical in PET. To date, the optics pump-probe approach has never been studied for radionuclide photon detection, where individual photon events are processed for time, energy, and spatial information. This work describes the first efforts to explore the feasibility of this concept.

2. Materials and methods

2.1. Detector material selection

The optics pump-probe based radiation detection method proposed in this paper depends on the electro-optic modulation effect (Sturman 1992, Günter et al 1989, Yeh 1993). We identified CdTe as a prototype detector material to use in a proof-of-principle study of this proposed approach. CdTe is a high Z and high density material, which provides sufficient interaction probability with ionizing radiation photons. Additionally, CdTe has the largest linear electro-optic coefficient among II–VI compound crystals (Adachi 2009) and it has been widely used as an electro-optic modulator (Bell 1977, Shcherbin et al 2013). A large modulation coefficient is favorable for improving the detection sensitivity. Moreover, bulk CdTe crystal has been demonstrated as an effective ultrafast nonlinear optical switch using the electro-optic effect (Tatsuura et al 2005). This characteristic of undergoing fast optical property modulations is desirable in our application and shows the potential of CdTe to generate very fast time stamps in radiation detection.

Our detector material is a 5× 5 × 5 mm³ undoped CdTe crystal [Gooch & Housego, Moorpark, CA, USA] with gold electrodes deposited on two opposite surfaces for supplying bias voltage, and the remaining four surfaces fine polished for probe laser reflection.

2.2. Experimental setup for optics pump-probe based measurement method

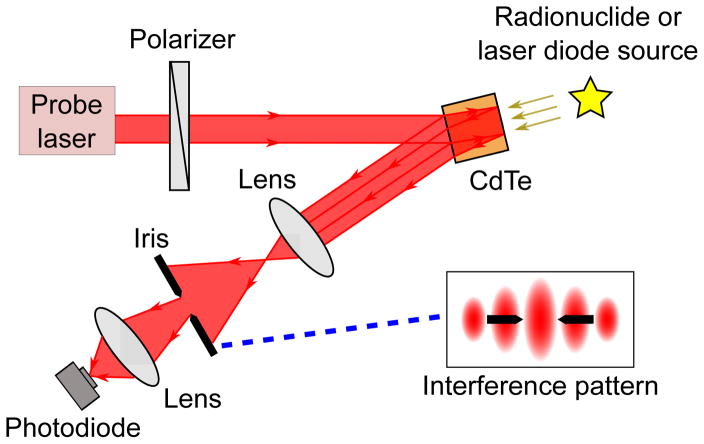
In this work, we make use of a two beam interference setup to achieve the optics pump-probe measurement. The schematic for the optical setup is shown in figure 2. The experimental layout of the detection system is shown in figure 3. A tunable C-band (with central wavelength around 1550 nm) probe laser (Agilent N7714A Tunable Laser Source) first goes through a linear polarizer and then illuminates the CdTe crystal. The laser beams reflected back from the front and rear surfaces of the crystal interfere with each other and generate a stable interference pattern (shown in the inset). The interference pattern is expanded with a lens. An optical iris is placed after the lens to allow only a fixed portion of the interference pattern to pass through (shown by the black arrows in the inset). The light transmitted through the iris is further focused by another lens and detected with a photodiode detector. The detected light intensity is the signal being monitored during the experiment.

Figure 2.

Schematic of optical setup. The “signal” is represented by a spatial shift in the interference pattern caused by the creation of charge carriers in the crystal.

Figure 3.

Experimental layout of detection system. This layout is shown with laser diode radiation as an illustration. An isotope source can be placed beside the crystal holder instead of the laser diode (and associated focusing lens) to measure the isotope source radiation induced modulation signal.

The CdTe crystal is DC biased at 1000 V (according to the manufacturer-specified working voltage) and the entire setup is put in a light tight box during the experiment. When ionizing radiation photons interact with the crystal, the charge carriers generated will modulate the crystal’s refractive index via Pockels effect (discussed in section 2.3). The interference fringes start to move consequently, which leads to a spatial shift of the transmitted interference fringe (e.g., from one bright fringe to one dark fringe). The intensity of the light passing through the iris and detected by the photodiode changes in response. Therefore, by monitoring the light intensity transmitted through the iris, we can detect the interaction of ionizing radiation.

Compared to conventional interference setups (e.g., Michelson or Mach-Zehnder interferometers), using two surfaces of the CdTe crystal as reflectors minimizes sensitivity of the setup to the vibrations of optical components, therefore significantly improves the stability of the setup without sacrificing sensitivity. It is also much more compact, thus more practical for potential usage in a future PET detector design. Considering the fact that an ionizing radiation source is asynchronous in PET, a continuous wave (CW) probe laser is employed. In comparison, a pulsed probe laser (as used in Auffray et al 2014 and Auffray et al 2015 to measure transient phenomena relative to scintillation) can only probe the effects of ionizing radiation when the laser pulses are emitted, and therefore will likely miss a large portion of the information during the relatively long time delays between laser pulses.

2.3. Modulation of optical properties from ionizing radiation interactions

The ionization-induced optical property modulation mechanism employed in this work is the linear electro-optic effect (i.e., Pockels effect) in CdTe crystal (Bell 1977). The index of refraction for a Pockels medium can be expressed as (1) (Saleh et al 1991)

$$n(E)\approx n_0-\frac{1}{2}\gamma {n_0}^{3}E$$ (1)

where n(E) is the material’s index of refraction under a certain applied electric field, n₀ is the index with no electric field present, E is the applied electric field amplitude, γ is the Pockels coefficient or the linear electro-optic coefficient. The refractive index of a Pockels medium is linearly dependent on the applied electric field strength.

The optical phase difference between the two interfering beams in the experimental setup can be calculated as (2)

$$\varphi =\frac{2\pi n(E)L}{\lambda }$$ (2)

where ϕ is the optical phase difference, n(E) is the refractive index of the interference medium (CdTe) under a certain applied electric field, λ is the vacuum wavelength of the probe laser, L is the geometric path length difference between the two interfering beams, which is a fixed value and approximately equals twice the crystal thickness here.

When ionizing radiation photons interact with the CdTe crystal, charge carriers are created through impact ionization. These carriers drift towards the two electrodes at the crystal surface due to applied bias voltage. Consequently, local charge separation and current flow occur, and thus a change in the local electric field strength is generated. During this process, some of the charge carriers also have the chance to be captured by long lifetime traps (due to crystal defects, imperfections, and surface states) inside the crystal and establish an additional perturbation on the local electric field strength. According to (1), the refractive index of CdTe is changed as a result. This also modifies the optical phase difference between the two interfering beams according to (2). Since the interference pattern is determined by the optical phase difference, interference fringes (see figure 2) shift in space accordingly, and then shift back as the space charge clears. The detected intensity of the light passing through the iris is modulated in response. Therefore monitoring the detected light intensity modulations allows us to detect the interaction of ionizing radiation photons.

2.4. Testing setup feasibility and choosing the operating point

In order to test the setup feasibility and to choose the optimal operating point, we first study the dependence of the signal magnitude on the bias voltage at a fixed operating wavelength (1550.000 nm), then keep the bias voltage fixed (1000 V) and study the signal magnitude dependence on the operating wavelength. No ionizing radiation source is present in these studies. The optimal operating point is chosen based on the results of these studies and is discussed in section 3.1.

2.5. Estimating the detection sensitivity of the setup

The detection sensitivity of the setup around the operating point can be estimated based on the results of the setup feasibility and operating point studies. By taking the derivatives of both sides in (2), we arrive at (3) (we have denoted n(E) in (2) with n here for simplification and the negative sign is omitted):

$$\begin{array}{l}\mathrm{\Delta }\varphi =\frac{2\pi L}{\lambda }·\mathrm{\Delta }n\\ =\frac{2\pi nL}{{\lambda }^2}·\mathrm{\Delta }\lambda .\end{array}$$ (3)

By equating the two derivative expressions, we have (4):

$$\frac{\mathrm{\Delta }n}{n}=\frac{\mathrm{\Delta }\lambda }{\lambda }.$$ (4)

Equation (4) relates the tuning of the operating wavelength (Δλ) to an effective modulation in the refractive index (Δn). After choosing the operating point, we can acquire the values of the operating wavelength (λ) and the corresponding refractive index (n) of CdTe. In addition, the minimum detectable wavelength tuning resolution (Δλ) corresponding to the minimum detectable signal modulation amplitude around the operating point can be decided. Taking these back into (4), we can estimate the detection sensitivity for refractive index modulation of the setup (Δn).

2.6. Using laser diode as the source of ionization

A 405 nm laser diode (CEL NV4V31SF) is first used as the source of ionization to prove the capability of the experimental setup (shown in figure 2 and 3) to detect refractive index modulation since its timing properties and emitting power are controllable.

2.6.1. Observing the modulation signal

We shine laser diode light pulses onto CdTe crystal and record the signal magnitude change under illumination. The oscilloscope used to record the signal is triggered by the drive voltage of the laser diode. Based on the estimated detection sensitivity of the setup, we can calculate how much refractive index change is induced by the laser diode source.

2.6.2. Measuring carrier clear time in the CdTe crystal

The carrier clear time is a crucial factor for the timing performance of the detector crystal. To estimate the carrier clear time in CdTe crystal, we utilize its characteristic of photoconductivity (Pierret et al 1996). The cause for the modulation of the refractive index of CdTe crystal discussed in section 2.3 can be alternatively understood as a change in its photoconductivity. In section 2.3, we state that when ionizing radiation interacts with the crystal and creates free charge carriers (electron-hole pairs), these carriers will introduce a modulation in the local current flow (or local electric field strength). The effect of these charge carriers is an increase in the material’s photoconductivity, which further leads to the modulation of the local current flow (or local electric field strength). This modulation finally results in the change of the material’s index of refraction due to its photorefractive property as described by (1).

As discussed in Pierret et al (1996), the carrier lifetime in a semiconductor material can be measured by introducing a perturbation in its carrier concentration, therefore photoconductivity, by shining light pulses onto the semiconductor. The light pulse gives rise to a carrier excess inside the semiconductor material and thus a detectable change in the photoconductivity. Once the light is removed, the excess carriers are gradually eliminated via recombination (and absorption at the electrodes when the crystal is biased) and the photoconductivity decays exponentially back to its value in the dark. The carrier lifetime is determined by the decay constant of the exponentially decaying signal indicating the change of the photoconductivity. The change of the signal can be approximated by (5)

$$v_L\approx V_L+v_0{\mathrm{e}}^{-t/\tau }$$ (5)

where v_L is magnitude of the exponentially decaying signal after the light is removed, V_L is the DC component of the signal (the stable signal level in the dark), v₀ is the maximum (or starting) value of the exponentially decaying signal, t is the time variable, and τ is the decay constant indicating the carrier lifetime.

A closer inspection reveals that the measurement method for the modulation signal induced by laser diode radiation described in section 2.6.1 is exactly the same as the carrier lifetime measurement method described in Pierret et al (1996). With the setup described in section 2.2, the perturbation in the photoconductivity of CdTe crystal is converted to a modulation in its refractive index and that modulation is measured by monitoring the interference pattern (as discussed in section 2.2 and 2.3). Therefore analyzing the decay constant of the modulation signal induced by laser diode radiation amounts to an appropriate estimation for the carrier clear time in the CdTe crystal.

Using a similar method as in section 2.6.1, we shine laser diode light pulses onto the CdTe crystal and record the signal magnitude change under illumination. The frequency of the drive voltage for the laser diode is set to 10 Hz here to allow complete recovery of the signal back to the level in the dark.

2.7. Using radionuclide source as the source of ionization

After using a laser diode as the source of ionization, we switch to experiment with radionuclide sources.

2.7.1. Observing the modulation signal

We first observe the modulation signal induced by radionuclide sources. A 10 μCi Ge-68 source is used for this experiment. The source is repetitively placed 15 mm from the CdTe crystal and removed. We observe the signal level change between source present and source removed to see how radionuclide sources modulate the signal. The selected data point for each measurement was the stable signal level observed at five minutes after placing or removing the source. Each data point (the stable signal level) was recorded as a histogram of the signal magnitudes for 30 s. The value corresponding to the histogram peak is taken as the magnitude of the stable signal level, and the peak width (full width at half max, FWHM) is used as the error bar which reflects the noise level of the system. All the data points are taken consecutively in time.

Based on the estimated detection sensitivity of the setup, we can calculate how much refractive index change is induced by the radionuclide source.

2.7.2. Studying the modulation amplitude dependence on detected event rate and photon energy

A practical PET detector should produce a signal that depends on incoming photon detected event rate and energy, therefore we take the difference between the signal levels with radionuclide source present and no source as the modulation signal amplitude, and study its dependence on detected event rate and photon energy.

We first study the detected event rate dependence of the modulation signal. The inverse square law governing the event rate detected by the detector is shown in (6)

$$I\propto \frac{A_0}{r^2}$$ (6)

where I is the detected event rate at the observing point (the position of the crystal), A₀ is the current radioactivity of the source, and r is the distance between the source and the detection point. According to this, we acquire different detected event rates by varying the distance between the radionuclide source and the CdTe crystal. The closest distance possible between the crystal and the source is 11 mm in our setup. In order to avoid potential high voltage breakdown issues, the source is not put in contact with the crystal holder. Instead, the distance between the crystal and the source is incremented from 13 mm to 25 mm in 2 mm steps during the experiment to create different detected event rates. When plotting the result, we normalize all event rates to the detected event rate when the separation between the crystal and the source is 11 mm. Both a 9 μCi Ba-133 and a 10 μCi Ge-68 source are used for this experiment.

We continue to study the dependence of the modulation signal amplitude on photon energy. Besides the Ba-133 and Ge-68 sources discussed above, we use a 10 μCi Co-57 source to acquire different photon energies. Since the radionuclide sources are not monochromatic, to study the relation between the modulation signal amplitude and the source photon energy, we first calculate an average photon energy based on source energy spectra to represent the average energy deposition by a photon emitted from the corresponding source.

The source energy spectra for Ba-133 and Ge-68 are measured by a cadmium zinc telluride (CZT) PET detector (Gu et al 2011), with the assumption that the energy deposition processes and resulting energy spectra are similar in CZT and CdTe. Based on the energy spectra, an average photon energy is calculated as the mean value for the energy deposition distribution for Ba-133 and Ge-68. The results represent the average energy deposited in the CdTe crystal by a photon emitted from the corresponding source, taking into account both photoelectric absorption and Compton scattering.

With a minimum detectable photon energy of around 150 keV, the CZT PET detector cannot be used to measure the energy spectrum for the Co-57 source whose emission photon energy centers around 122 keV. For Co-57, the source energy spectrum is acquired from radionuclide data sheet (Stanford University 2016), and the average photon energy is calculated as in (7)

$$E_{\text{avg}}=\sum _i{q}_i{E}_i$$ (7)

where E_avg is the average photon energy, q_i is the decay probability of a certain energy gamma ray in one disintegration, and E_i is the corresponding gamma ray energy. From the comparison between the total attenuation coefficient and photoelectric attenuation coefficient (National Institute of Standards and Technology 2016) of CdTe for photon energy of 122 keV, we can see that more than 85% of the interaction events are photoelectric absorption instead of Compton scattering. Therefore we take the average photon energy calculated by (7) for Co-57 as the average energy deposited in the CdTe crystal by a photon emitted by Co-57.

Due to the sensitivity limit of the experimental setup, the modulation signal induced by radionuclide sources that we observe results from the integration of ionization charges produced from interactions by multiple incoming photons (We know this since the carrier generation rate is faster than the clearing rate, which is discussed in more detail in section 4.7). To study the relation between photon energy and modulation signal amplitude, we normalize the total modulation signal amplitude by the total event rate to estimate the average modulation induced by a photon interaction event. Equation (8) calculates the total event rate:

$$I_{\text{tot}}\propto A_0\sum _i{q}_i(1-{\mathrm{e}}^{-{\mu }_{i}t})$$ (8)

where I_tot is the total event rate used for normalization, A₀ is the source activity as in (6), q_i is the decay probability for a given energy gamma ray in a disintegration as in (7) (Stanford University 2016), μ_i is the total linear attenuation coefficient for a specific energy gamma ray in CdTe (National Institute of Standards and Technology 2016), and t is the interaction length or the thickness of CdTe crystal in this case. It should be noted here that although as described, the average photon energy is calculated from the source spectra acquired with CZT based PET detector (for Ba-133 and Ge-68) to account for the average energy deposition, the radionuclide data sheet is used (for all sources) here to calculate the total event rate, since we want to account for the total number of photon interaction events occurring in the CdTe crystal based on the original gamma ray decay energies, not on the energy deposited.

During the experiment, we keep the distance between the crystal and the three different radionuclide sources (Ge-68, Ba-133, and Co-57) fixed as 15 mm (the same as discussed in section 2.7.1). Also, we keep the data point acquisition duration the same for the three sources (see section 2.7.1). Therefore, the total event rate calculated from (8) represents (is proportional to) the total number of interaction events occurring in the CdTe crystal for the corresponding sources. Normalizing the total modulation signal amplitude by this value, we obtain the estimation for the average modulation amplitude induced by a photon interaction event. By comparing that with the average photon energy calculated, i.e., the average energy deposited in the CdTe crystal by a photon interaction, we arrive at the relation between modulation signal amplitude and photon energy. Five experiments were performed for each data point and the error bars were acquired from the standard deviation between the results acquired from these multiple experiments.

3. Results

3.1. Setup feasibility and operating point

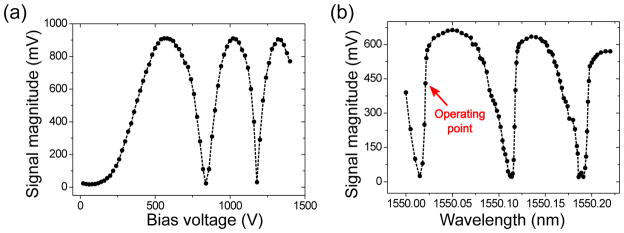
The results of the setup feasibility and operating point studies discussed in section 2.4 are shown in figure 4(a) and figure 4(b) respectively.

Figure 4.

(a) Dependence of signal magnitude on bias voltage at operating wavelength equal to 1550.000 nm; (b) dependence of signal magnitude on operating wavelength at bias voltage equal to 1000 V.

First, according to (1), changing the bias voltage (thus the electric field) changes the refractive index of CdTe. Therefore, according to (2), the optical phase difference between the two interfering beams is modulated as the bias voltage is tuned. This modulation results in a spatial shift of the transmitted interference fringe as discussed in section 2.3. Therefore bright and dark fringes pass through the optical iris successively and are detected. This explains the oscillating pattern in the signal magnitude corresponding to bias voltage tuning as shown in figure 4(a). This result proves the Pockels effect in CdTe crystal and also shows the feasibility of this setup for detecting a modulation in the refractive index of the detector material.

Second, according to (2), it can be seen that tuning the operating wavelength has a similar effect on the optical phase difference as does changing the refractive index (by changing bias voltage). Therefore oscillations in the signal magnitude are observed again corresponding to operating wavelength tuning as shown in figure 4(b) similar to figure 4(a). For the operating point, we keep the bias voltage at 1000 V, which is the manufacturer-specified working voltage for the detector crystal, and choose the operating wavelength at the point with the largest slope in signal magnitude (denoted with the red arrow in figure 4(b)) to guarantee the highest sensitivity.

3.2. Detection sensitivity of the setup

According to (4) and based on the estimation method described in section 2.5, at the chosen operating point, we take λ as 1550.000 nm. At this wavelength, the refractive index (n) of CdTe is around 2.74 (Martínez et al 2008). The wavelength tuning resolution (Δλ) of the Agilent tunable laser source is 0.001 nm at 1550 nm. When the operating wavelength is tuned by this resolution, the modulation induced on the signal magnitude is detectable, which means that the modulation amplitude evidently exceeds the total noise level (generated by the sum of the noise from the photodetector, oscilloscope, probe laser source, and other devices involved) of the system, and thus is detectable on the scope. We take the effective refractive index change (Δn) corresponding to this wavelength tuning resolution as the detection sensitivity for refractive index modulation of the setup. According to (4), it is estimated that a change in the refractive index (Δn) as small as 10⁻⁶ is detectable.

3.3. Results with laser diode as the source of ionization

3.3.1. Modulation signal

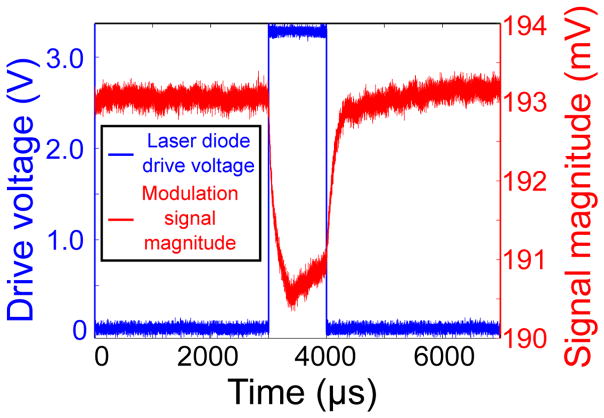
Figure 5 shows the modulation signal with a laser diode as the source of ionization acquired by the method described in section 2.6.1. The blue line shows the drive voltage of the laser diode and the red line shows the signal level change in response. We can see that the signal magnitude is modulated by each laser diode light pulse. This result shows that the optical property (i.e. refractive index) of CdTe can be modulated by the laser diode radiation and our setup can detect this modulation.

Figure 5.

Modulation signal with laser diode as the source of ionization.

Based on the estimated detection sensitivity of the setup discussed in section 3.2, it can be calculated that the refractive index change corresponding to the signal modulation amplitude induced by the laser diode source is around 10⁻⁷. This value is estimated in the following way. As discussed in section 3.2, the minimum detectable modulation signal magnitude corresponds to the wavelength tuning resolution of 0.001 nm, which decides the refractive index detection resolution of 10⁻⁶. At the chosen operating point, when tuning the wavelength by 0.001 nm, we measure the modulation amplitude of the signal as around 30 mV. Therefore a signal modulation with amplitude of 30 mV corresponds to a refractive index change of 10⁻⁶ at the chosen operating point. As shown in figure 5 (red line), the induced pulse modulation amplitude by the laser diode is around 3 mV, and it thus corresponds to a change in the refractive index of 10⁻⁷.

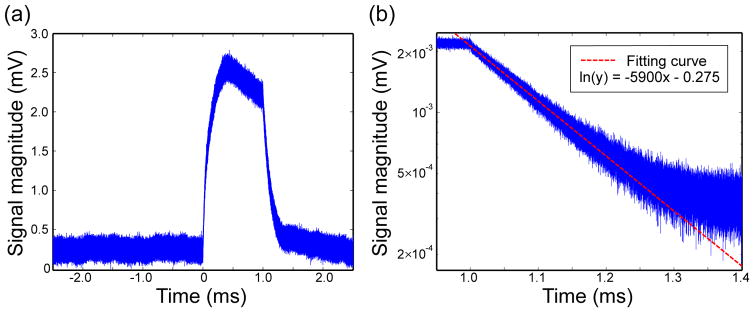
3.3.2. Carrier clear time in the CdTe crystal

Based on the method described in section 2.6.2, the pulse modulation signal induced by laser diode radiation is shown again in figure 6(a). It is just the inverted plot (for easier interpretation) of the signal data shown in figure 5 (red line). The DC component representing the stable signal level in the dark is subtracted from the total signal magnitude in figure 6(a). By comparison to (5), the remaining value represents v_L − V_L. Figure 6(b) shows the decay edge of the signal with the y axis plotted on logarithmic scale (natural logarithm). By simply taking the natural logarithm of both sides in (5), we can see that the slope of the straight line region shown in figure 6(b) corresponds to −1/τ. Therefore by analyzing this slope we can estimate the carrier clear time in the CdTe crystal used in this paper as 170 μs.

Figure 6.

(a) Pulse modulation signal induced by laser diode radiation; (b) decay edge of pulse modulation signal induced by laser diode radiation, y axis plotted on logarithmic scale.

3.4. Results with radionuclide source as the source of ionization

3.4.1. Modulation signal

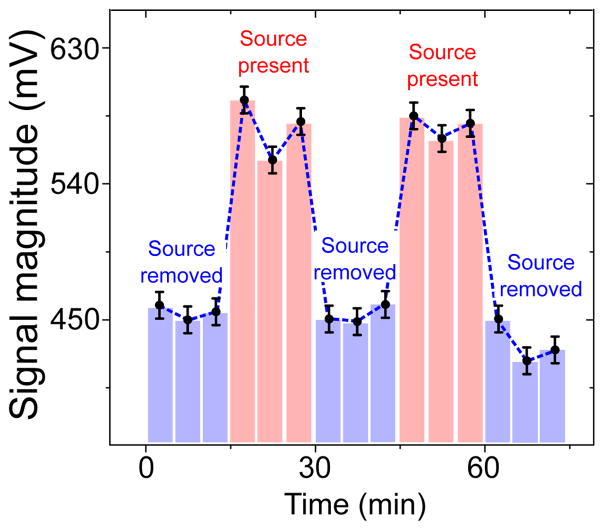
Using the method discussed in section 2.7.1, we acquire figure 7 which shows the signal magnitude modulated by a Ge-68 source. The red bars indicate the signal magnitude when the source is placed close to the detector crystal, and the blue bars indicate the signal magnitude when the source is removed.

Figure 7.

Modulation signal with radionuclide source as the source of ionization.

From figure 7, it can be seen that the signal magnitude is modulated by the presence of the radionuclide source. From similar considerations as presented in section 3.3.1, a signal modulation with amplitude of 30 mV corresponds to a refractive index change of 10⁻⁶ at the chosen operating point. As shown in figure 7, the total induced modulation signal amplitude by Ge-68 is around 150 mV, and it thus corresponds to a change in the refractive index of 5 × 10⁻⁶.

3.4.2. Modulation amplitude dependence on detected event rate and photon energy

Based on the method discussed in section 2.7.2, we acquire figure 8 which shows the relation between the modulation signal amplitude and the normalized detected event rate for Ba-133 and Ge-68 source. The error bars are acquired from the FWHM of the histogram (which is used to record the stable signal magnitude) peak as discussed in section 2.7.1. In both cases, a linear dependence is observed with an R value larger than 0.9. Here the R value, alternatively written as r² value, is a measure of goodness-of-fit of linear regression.

Figure 8.

Modulation signal amplitude dependence on detected event rate. The error bars are acquired from the FWHM of the histogram (which is used to record the stable signal magnitude) peak as discussed in section 2.7.1.

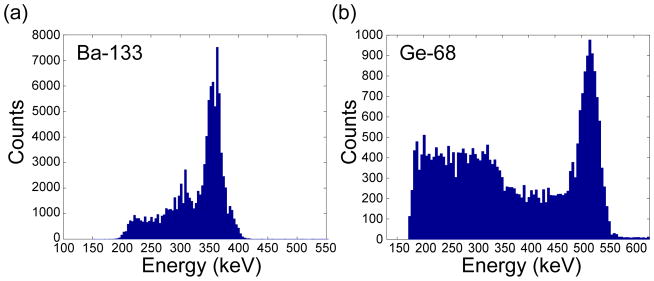
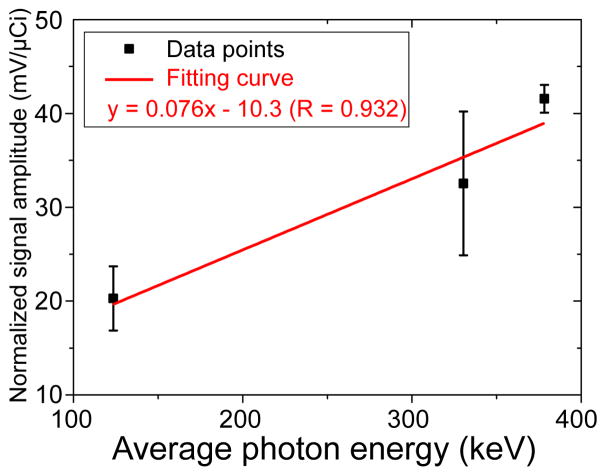
With the method discussed in section 2.7.2, the energy spectra measured by a CZT PET detector for Ba-133 and Ge-68 are shown respectively in figure 9 (a) and (b). An average photon energy is calculated as 330.4 keV for Ba-133 and 378.3 keV for Ge-68. Based on (7), we obtain an average photon energy of 123.5 keV for Co-57. Figure 10 shows the dependence of the modulation signal amplitude on average photon energy. The values of the data points are acquired from the peak value difference of the histograms recording the stable signal magnitude with source present and without source (discussed in section 2.7.1). As stated in section 2.7.2, the error bars represent the standard deviation between the results acquired from five experiments for each data point. We can see that the normalized signal amplitude is linearly proportional to the average photon energy. The fitting curve has an R value larger than 0.9.

Figure 9.

Energy spectrum for (a) Ba-133 source; (b) Ge-68 source measured with a CZT detector (Gu et al 2011).

Figure 10.

Modulation signal amplitude dependence on average photon energy. The error bars represent the standard deviation between the results acquired from five experiments for each data point.

4. Discussion

4.1. Potential of the optics-based radiation detection method for dramatically improving PET time resolution

With the setup described in section 2.2, theoretically, the monitored light intensity changes as soon as charge carriers are created and begin to drift towards the electrodes. As stated in table 1, this process is very fast (femtosecond scale). However the timing properties of this detection method ultimately depend on its sensitivity. The sensitivity of the measurement setup, including the noise level, determines how many carriers are needed before a detectable signal shows up; therefore the experimental sensitivity determines the time delay and variance between the creation of the first charge carrier and the appearance of a measurable signal. The long lifetime traps in the detector crystal and the resulting persistent electric field established by trapped carriers adds complexity to this relation. The bandwidth and temporal jitter of the photodetector and other electronic devices involved are also important influencing factors on the timing properties. However, compared to 100 ps for scintillation based detectors, the intrinsic physical limit for the time resolution of the proposed method is expected to be at the femtosecond time scale. As discussed in section 1.3, possibilities exist to make use of ultra high-Q optical detection cavities and explore other configurations to push the detection sensitivity towards the intrinsic physical limit for timing. Therefore this method seems promising for dramatically improving PET time resolution.

This report has described studies with CdTe as the detector crystal material to study ionization induced modulation of optical properties. However this method does not rely on the use of CdTe. We are also studying other crystals such as bismuth silicon oxide (BSO). BSO has similar density and effective atomic number as bismuth germanate (BGO), which is an appropriate crystal for efficient detection of 511 keV photons. Other materials with larger electro-optic coefficient (thus better detection sensitivity) will also be considered and researched.

Other than the linear electro-optic effect (Pockels effect) studied in this paper, there are other potential mechanisms of optical property modulation that can be exploited to achieve ionizing radiation detection. For example, nonlinear electro-optic modulation effects including the Kerr effect (Saleh et al 1991) will be studied. The photo-induced phase transition (Nasu 2004) is another potential effect that will be explored.

4.2. The operating point

As shown in figure 4(b) (denoted with the red arrow), we choose the operating wavelength at the point with the largest slope in signal magnitude. This is because this point represents the setting where the changing rate of the signal magnitude is the largest if we tune the operating wavelength. Since tuning the wavelength has a similar effect on the optical phase difference (see (2)) as tuning the refractive index, and since the optical phase difference decides the signal magnitude by affecting the interference pattern (discussed in section 2.3), this point also represents the setting where the changing rate of the signal magnitude is the largest if we tune the refractive index. Therefore operating at this point guarantees the highest detection sensitivity for the refractive index modulation induced by ionizing radiation sources.

As discussed in section 2.4, the studies for testing the setup feasibility and choosing the operating point are done when no ionizing radiation source is present. Based on the results presented in this paper, ionizing radiation sources can introduce only a small modulation around the operating point. By “small modulation”, we mean that the phase shift corresponding to the refractive index modulation induced by ionizing radiation sources is far below π, so that the results shown in figure 4(a) and (b) do not change much when an ionizing radiation source is present. Therefore we keep using the operating point chosen based on the studies when no ionizing radiation source is present for the experiments involving a radiation source, since the operating point still represents the point with highest detection sensitivity.

4.3. Estimation of the detection sensitivity

It should be noted that the value of the detection sensitivity for refractive index modulation of the setup estimated in section 3.2 (10⁻⁶) is a conservative estimation due to the limited wavelength tuning resolution at the operating point. If the tuning resolution is better, the estimated sensitivity could be improved. Thus the refractive index detection resolution estimated in section 3.2 establishes an upper bound for the sensitivity of the setup. The detection sensitivity will eventually be determined by the total noise level of the system.

4.4. Modulation signal with laser diode as the source of ionization

The pulse modulation signal induced by laser diode light pulses shown in figure 5 is built on top of a baseline level change when the crystal is under illumination, i.e., apart from the pulse modulations, we also observe a baseline level change of the signal magnitude when the laser diode illuminates the CdTe crystal. Only the pulse modulation is shown in figure 5 for emphasis and the baseline change is omitted. Therefore, the value of the signal modulation amplitude discussed in section 3.3.1 (3 mV) only accounts for the amplitude of the pulse modulation, without considering the baseline level change.

In addition, we should note that the estimated measured refractive index change induced by laser diode experiments (10⁻⁷) as discussed in section 3.3.1 is even smaller than the refractive index measurement sensitivity estimated in section 3.2 (10⁻⁶). There are two reasons for that. First, in the result shown in figure 5 (red line), due to the synchronized nature of the laser diode light, the “Average” function of the scope is applied to the data so that the noise level is significantly reduced over multiple averaging cycles. As discussed in section 4.3, we know that the measurement resolution of the refractive index is dependent on the detection sensitivity of the modulation amplitude, both of which are determined by the total noise level of the system. Therefore the reduced noise level by the “Average” function of the scope helps to improve the measurement sensitivity of the refractive index modulation. Second, as also discussed in section 4.3, the estimated sensitivity value of 10⁻⁶ itself is a conservative estimation because the wavelength tuning resolution of the Agilent tunable laser source is limited to 0.001 nm at 1550 nm. If the wavelength tuning resolution is better or if we can utilize other mechanisms to modulate the interference pattern with better resolution (as with the laser diode radiation here), we should arrive at a lower estimated value for the refractive index detection sensitivity.

4.5. Carrier clear time in the CdTe crystal

It should be noted that we did not simply use the carrier drift time (i.e., the time it takes for the charge carriers to drift from the position they are created to the electrodes) to estimate the carrier clear time in the CdTe crystal, but instead used the method discussed in section 2.6.2. Two reasons account for that. First, the general value of the carrier mobility in CdTe crystals provided by manufacturer or literature may not correctly account for the value of this specific piece of crystal we use. The traps, imperfections, recombination centers, surface states and other characteristics of the CdTe crystal may result in this deviation. Second, under the bias voltage used in this paper, the drift velocity may have already saturated, so that the linear relation between the drift velocity and the electric field strength may no longer be valid. Therefore the method described in section 2.6.2 establishes a more accurate estimation for the carrier clear time in the CdTe crystal than the simple drift time estimation.

4.6. Modulation signal with radionuclide source as the source of ionization

As discussed in section 2.7.1, for the measurement of the modulation signal induced by radionuclide source, we choose to read each data point as the stable signal level at five minutes after placing or removing the source. This is because during the transition between placing the source close to the CdTe crystal and taking the source away, the signal does not change instantaneously. Instead, the response to the presence or removal of the source takes several seconds to several minutes depending on the source activity. After this settling time, the signal level will remain stable around a fixed value. Therefore, we choose to wait five minutes for the signal to stabilize and then read each data point as the stable signal level.

From figure 7, we can see that a non-zero (around 450 mV) baseline signal level exists when the radionuclide source is removed. This non-zero baseline results from the operating point we choose. As shown in figure 4(b) (denoted with the red arrow), we choose the operating wavelength at the point with the largest slope in signal magnitude to guarantee the highest detection sensitivity for refractive index modulation measurement. This operating point corresponds to a non-zero baseline signal level.

In addition, as discussed in section 2.7.1, the error bar in figure 7 is acquired from the histogram peak width (FWHM) which reflects the noise level of the system. This noise comes from the probe laser source (output power and wavelength noise), the vibrations of the optical components, the intrinsic thermal noise of the CdTe crystal, and the noise from the photodetector, the oscilloscope, and other electronic devices involved.

4.7. Charge carrier pile-up in the CdTe crystal

The average activity of the radionuclide sources used in the experiments is around 10 μCi, which corresponds to 3.7 × 10⁵ disintegrations every second. If we calculate for the situation when the distance between the source and the crystal is 15 mm (see section 2.7.1), and take into account the solid angle from the source to the crystal surface and the absorption probability in the CdTe crystal, it can be estimated that around 10% of the disintegrations turn into absorbed photons by the crystal. That leads to roughly 3.7×10⁴ absorbed photons every second. Therefore, it can be estimated that on average, one ionizing photon is absorbed by the CdTe crystal every 30 μs.

According to the result presented in section 3.3.2, the charge carrier clear time in the CdTe crystal is 170 μs. From the comparison between the photon emission rate of the isotope source (one photon every 30 μs) with the carrier clear time in the CdTe crystal (170 μs), it can be seen that on average multiple photon interaction events occur before the carriers clear away in the crystal. As discussed in section 2.7.1 and 2.7.2, when observing the modulation signal induced by radionuclide sources and when studying the dependence of the modulation amplitude on average photon energy, we keep the distance between the crystal and the source fixed as 15 mm (which corresponds to one absorbed photon every 30 μs). Therefore the modulation signal induced by radionuclide sources results from multiple photon interaction events and we need to normalize the total modulation signal amplitude by the total event rate to estimate the average modulation induced by a photon interaction event (discussed in section 2.7.2).

From figure 8, we can see that when the normalized detected event rate is around 0.2, the modulation signal starts to become undetectable, which means that the total noise level of the system begins to exceed the modulation amplitude. The normalized detected event rate of 0.2 corresponds to a distance between the source and the crystal of 25 mm as discussed in section 2.7.2. This distance corresponds to one absorbed photon every 83 μs. This photon absorption rate is still faster than the carrier clear rate, therefore still results in charge carrier pile-up in the CdTe crystal. Since the modulation signal starts to disappear when the normalized detected event rate is below 0.2, we conclude that the setup described in this paper needs the charge carriers to pile up before observing a detectable signal. This is limited by the detection sensitivity and the total noise level of the current setup.

As discussed in section 2.7.1, during the transition between placing the source close to the CdTe crystal and taking the source away, the signal does not change instantaneously. Instead, the response to the presence or removal of the source takes several seconds to several minutes depending on the source activity. After this settling time, the signal level will remain stable around a fixed value. The transitions can be understood as a gradual build-up of an equilibrium between charge carrier generation and clearance. The carrier clear time depends on the carrier concentration in the CdTe crystal. Specifically, the carrier recombination rate is higher when the carrier concentration is higher, and the rate at which carriers are captured by the traps, imperfections, recombination centers, and surface states in the CdTe crystal also becomes higher with increasing carrier concentration. Both of these lead to a shorter carrier clear time. Therefore the carrier clearance rate will eventually be balanced with the carrier generation rate during the carrier pile-up process, which leads to an equilibrium in the CdTe crystal and a stable signal level.

As described in section 2.7.1, we choose to wait for five minutes and read out the stable signal level after the equilibrium is established in the CdTe crystal. However, this does not mean that the setup proposed is limited to the five minutes readout delay. Since the signal level starts to change as soon as an ionizing radiation source is placed close to the detector crystal, faster readout methods are possible. This will be a subject for our future study. Our ultimate goal would be to establish a setup (and develop an appropriate readout method) that is sensitive enough to measure the modulation signal from the ionization charges created by one individual 511 keV photon with measured response time and variance both on the order of picoseconds.

4.8. The dependence of modulation signal amplitude on detected event rate and photon energy

Due to the charge carrier pile-up effect in the CdTe crystal during the observation of the modulation signal induced by radionuclide sources, it should be expected that the amplitude of the modulation signal depends on the carrier generation rate. Specifically, the modulation signal amplitude depends on both the detected event rate and average photon energy of the radiation source. Therefore we see that higher event rates (more interactions per unit time) and higher energy photons (more photoinduced carriers generated in one interaction) lead to stronger signal, as indicated in figure 8 and 10.

Several points are worth mentioning concerning figure 8 and 10. First, in figure 8, it should be noted that the absolute values of the Ba-133 (blue) and Ge-68 (red) data points are not comparable due to different operating conditions. The linear relation observed from these two sets of data is the key point of this figure. Second, the relatively large error bar for the Ba-133 source as shown in figure 10 is related to the large variation in gamma ray emission energies for that source. Lastly, the absolute value of the normalized signal amplitude shown in figure 10 does not match exactly to the modulation amplitude induced by a photon interaction, but is proportional to it. Normalizing the total signal modulation amplitude by the total event rate calculated from (8) results in a signal modulation amplitude induced by a 1 μCi source after the fixed data point acquisition duration (see section 2.7.1). Therefore the normalized signal amplitude shown in figure 10 has a unit of “mV/μCi”. To acquire the exact value estimation for the signal modulation amplitude induced by a photon interaction, we need to divide this value by a constant representing the total number of disintegrations from a 1 μCi source within the fixed data point acquisition duration.

4.9. Possible structure of a practical PET detector module built with the proposed detection concept

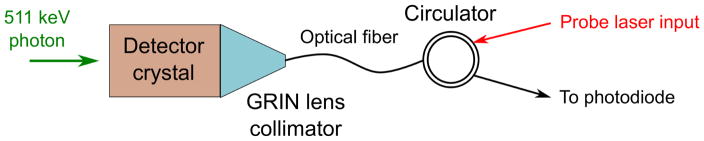
As discussed in section 4.7, our ultimate goal would be to establish a setup (and develop an appropriate readout method) that is sensitive enough to measure the modulation signal from the ionization charges created by one individual 511 keV photon with measured response time and variance both on the order of picoseconds. When this goal is achieved, we will take steps towards designing a practical PET detector module that employs the proposed optical property modulation based detection concept as depicted in figure 1(b). The exact structure of the detector module will depend on the final choice of the experimental setup, but it should have a low profile to enable assembly of detector modules with high crystal packing fraction relative to incoming photons. A possible structure is shown in figure 11 to give the readers a basic concept.

Figure 11.

Possible structure of a practical PET detector module built with the proposed optical property modulation based detection concept.

For the structure shown in figure 11, a detector crystal with electro-optic modulation effect is used to sense the interactions of 511 keV photons. The crystal’s optical properties will be changed by the ionization charges created from 511 keV photon interactions. A small GRIN lens and an optical fiber are used to collimate the probe laser light and to collect the reflected laser beam from the detector crystal. The intensity of the reflected laser light will be changed as a result of the optical property modulation of the detector crystal. A small optical circulator is used to separate the input probe laser from the reflected light and to guide the reflected laser beam into a photodiode detector that monitors the reflected light intensity change. This structure could be used similarly as conventional scintillation detector elements and be integrated to form a practical compact PET detector module.

5. Conclusions and future work

5.1. Conclusions

In this paper, the concept of utilizing the idea of optics pump-probe measurement for ionizing radiation detection is explored. Having the potential to dramatically improve the detection time resolution, this approach could be a promising future research direction for PET detector technology.

Our data indicate that ionizing radiation produces a measurable change in the optical properties (specifically the refractive index) in a CdTe crystal, and by using a two beam interference setup we can detect this modulation. The work reported here is the first experimental demonstration of utilizing the optics pump-probe concept for energy-resolving radionuclide photon detection as required in PET systems. Our data indicate that the strength of the modulation signal is linearly dependent on the detected event rate and photon energy of the ionizing source. By avoiding dependence on the scintillation mechanism or electron migration to an impurity site, this optics based detection is promising since it has a much lower intrinsic temporal variance compared to conventional scintillation based radiation detectors. We plan to further investigate this hypothesis in future studies.

5.2. Future work

Efforts will be made to optimize the setup described in this paper, aiming to improve its detection sensitivity and reduce the total noise level in order to become sensitive to the effect of single ionizing photon interactions and optimize time resolution. A thorough search for potentially better detector materials is one important aspect. Vanadium doped CdTe crystal has been identified to have a largely enhanced photorefractive effect which can potentially lead to much stronger optical modulation signal under the same radiation condition (Shwartz et al 2006).

In addition, many other parameters in the proposed setup can be tuned to lead to better detection sensitivity. The probe laser wavelength is one important parameter. We plan on both trying 850 nm, which is close to CdTe’s bandgap energy and should lead to a much stronger refractive index modulation, and 10 μm, where most commercial CdTe based electro-optic modulators operate at (Bell 1977, Shcherbin et al 2013). Moreover, different CdTe crystal geometries and different electrode types will be tested.

Faster readout methods will also be studied to achieve the detection of individual 511 keV photon interactions. We plan to utilize low noise broadband linear amplifiers, tunable bandpass electronic filters and a microwave spectrum analyzer as part of the detection scheme, along with the use of a real time oscilloscope which does not require a trigger signal and works better with non-periodic signal detection.

Other higher Z, higher density crystal materials will also be considered and researched. Additionally, we will study other potential mechanisms of optical property modulation that can be exploited to achieve ionizing radiation detection. Finally, efforts will be devoted to developing theoretical models to understand the ionization charge creation and transportation processes in the detector crystal, and how that modulates the optical properties of the material.