Qualitative longitudinal analysis of symptoms in patients with primary and metastatic brain tumours

Summary

Primary and metastatic brain tumour patients are treated with surgery, radiation therapy and chemotherapy. Such treatments often result in short- and long-term symptoms that impact cognitive, emotional and physical function. Therefore, understanding the transition of symptom burden over time is important for guiding treatment and follow-up of brain tumour patients with symptom-specific interventions. We describe the use of a hidden Markov model with person-specific random effects for the temporal pattern of symptom burden. Clinically relevant covariates are also incorporated in the analysis through the use of generalized linear models.

1. Introduction

This paper studies the temporal pattern of symptom experience in brain tumour patients from a multidimensional perspective. The approach that we adopt in this paper differs from the two most commonly used statistical methods for analysing longitudinal data—mixed linear or nonlinear models, which are based on likelihood methods, and marginal models, which are based on generalized estimating equations (Diggle et al., 2002). Although the mixed model and generalized estimating equation approaches are distinct with respect to their goals and techniques, they are both based on quantitative approaches that are applicable to only a single or a few outcome measures, which are often framed in a regression setting. The brain tumour symptom data that we shall analyse involved more than a dozen outcome measures, each concerning how a particular symptom was bothersome to the patient. Thus, the data seem amenable to neither generalized estimating equation nor mixed model analysis unless the symptom experience is summarized by a weighted sum score, which may lead to losing information on synergistic effects.

To incorporate full information from the entire set of outcome measures—in this case, brain cancer symptoms—we employ a qualitative analysis in which the symptoms are assumed to be explained by symptom states. To model the qualitative symptom state variable we shall use the multiple-indicator hidden Markov model (HMM) (Baum and Petrie, 1966; Rabiner, 1989; MacDonald and Zucchini, 1997) as the ‘workhorse’. Under an HMM, a categorical latent variable is incorporated to account for qualitatively distinct patterns of manifestation of the entire set of symptoms. To capture the serial correlation of symptoms over time, it is assumed that the latent (symptom) state of a patient at time t + 1 depends on his or her latent state at time t. Physicians are often trained to think and make decisions in terms of discrete outcomes that affect decisions on treatment and follow-up of disease states like brain tumours. The results from HMMs, which appear in the form of probability tables for disease states and transition probabilities between disease states, may be more consistent with the physicians’ mental models and thus may help them to think differently about disease states that they encounter.

There are many reported applications of HMM or HMM-type models to biomedical data in the literature (Bureau et al., 2003; Jackson and Sharples, 2002; Le Strat and Carrat, 1999; Smith and Vounatsou, 2003; Dunson and Herring, 2005; Scott et al., 2005). More recently, two- and three-state inhomogeneous HMMs were applied for modelling lesion counts in multiple-sclerosis patients (Altman and Petkau, 2005). Lesion count is assumed to have a Poisson distribution, with the mean being dependent on the patient’s unobserved state. The HMM was also used to characterize the trajectory of side effects in a population of schizophrenia patients in a randomized control trial (Scott et al., 2005). In both applications, no covariate was included in the model. In this paper, we propose to incorporate two important groups of covariates into the model: patient characteristics and symptom attributes. This way, the model can account for the fact that different patients received different treatments on the one hand, and for symptom cluster (domain) information on the other hand. Both types of covariates are incorporated through a logistic regression model for the conditional probabilities of the responses.

In addition, the model also incorporates random effects to account for possible clustering effects of symptoms within specific disease states. The random-effects approach allows the relaxation of the assumption that the conditional probabilities of the responses are the same for all patients within the same health or disease state. This assumption is likely to be violated in the case of brain tumours because, even after taking into account patient characteristics, brain tumour patients form quite a heterogeneous group based on factors that include tumour type (primary versus metastatic), location and size of the tumour, among others. Consequently, individual differences between patients in overall proneness to symptoms are to be expected, i.e. a patient who suffers more than other patients in his or her disease state from one symptom is expected to have other more severe symptoms as well (Gleason et al., 2007). In this paper, we propose to incorporate random effects to account for these individual differences in overall proneness to symptoms that are not captured by observed patient profiles, so that the states of the HMM solely reflect qualitatively distinct health or disease states.

The remainder of the paper is organized as follows. In the next section, we describe the background and the data. It is followed by a discussion of the statistical methodology. Then we report the results of the analysis. The final section provides a brief discussion and conclusion.

2. Background

Primary and metastatic brain tumours are a significant cause of morbidity and mortality in cancer patients world wide. In the USA alone, approximately 20000 primary and 200000 metastatic brain tumours are diagnosed annually (Jemal et al., 2005; Shaw, 2000). The most common primary brain tumour, glioblastoma multiforme, is treated with surgery, radiation therapy and chemotherapy and has a median survival time of 9–15 months. Metastatic brain tumours, which are usually treated with surgery and radiation therapy, have a median survival time of only 2–7 months (Shaw, 2000). Quality of life (QOL) is affected by numerous tumour- and treatment-associated symptoms. In general, these symptoms can be classified as physical (e.g. fatigue), emotional (e.g. depression and anxiety) and cognitive (e.g. decreased attention and concentration, poor short-term memory and expressive language problems). Various pharmacologic interventions can be used to improve the QOL of brain tumour patients (Shaw and Robbins, 2006).

Several challenges exist for analysing symptom data that are collected from brain tumour patients. First, although symptom experience is often measured by summing the presence or absence or the frequency of symptom occurrence, this method for measuring symptom severity has been criticized for providing only a one-dimensional view of the symptom experience that limits our ability to test for possible synergistic effects on patient outcomes (Miaskowski et al., 2004). Second, there is a poor understanding of how brain tumour symptoms change over time. Thus, any data analysis method that is only applicable to cross-sectional data may not be representative. Finally, although symptoms tend to be concurrent and to occur in combination, much of the symptom literature is focused only on single symptoms (Butler et al., 2007; Dodd et al., 2001). The characteristics of symptom measurement for brain tumour patients—multidimensionality, temporal pattern, inclusion of covariates and the formation of clusters—motivate this HMM analysis. The proper analysis of data that are generated from the evolution of symptoms over time can provide valuable information for developing strategies for understanding and managing QOL issues for brain tumour patients.

3. Description of the data

100 patients with either a primary brain tumour or brain metastases were treated in two different studies, A and B. Study A was a prospective randomized double-blind phase III trial for patients undergoing a 2–6-week course of partial or whole brain radiation. They were randomly assigned to two groups, one receiving the central nervous system stimulant d-methylphenidate (d-MPH), and the other receiving a placebo, during and for 12 weeks following radiation. The primary end point of the study was the effect of d-MPH on fatigue (Butler et al., 2007). Study B was an open label phase II study of brain tumour survivors who had completed a 2–6-week course of brain radiation at least 6 months before entry to the study. These patients were treated with a 6-month course of the acetylcholinesterase inhibitor donepezil (Aricept). The primary end point of this study was cognitive function (Shaw et al., 2006). The d-MPH, placebo and donepezil groups respectively had 32, 34 and 34 patients, for a total of 100 patients. Eligibility criteria that were in common between the studies were inclusion of adult (age ≥ 18 years) primary and metastatic brain tumour patients, Karnofsky performance status score (a physician-scored assessment of QOL ranging from 100 (asymptomatic) to 0 (dead)) of 70 and over) and absence of significant medical comorbidities such as cardiac or psychiatric diseases. A common battery of self-reported QOL measures in both studies was the functional assessment of cancer therapy (FACT) (Cella et al., 1993) and the brain-tumour-specific sub-scale. Both the FACT and its brain subscale have been validated in brain tumour patients (Weitzner et al., 1995). An example of an FACT brain subscale item is ‘I am bothered by side effects of treatment’. Patients rated each item on a five-point Likert scale (0, not at all, and 4, very much).

Because some items exhibited flooring or ceiling effects and some cells were sparse, we dichotomized the responses (0, ‘not at all’, ‘a little bit’ and ‘somewhat’, and 1, ‘quite a bit’ and ‘very much’). Although patients in the two studies completed their FACT brain subscale assessment at different time points following initiation of their study intervention with donepezil, d-MPH or the placebo (study A at the end of radiation, then 4, 8 and 12 weeks following onset of d-MPH or placebo, and study B at 6, 12, 24 and 30 weeks following onset of donepezil), the symptoms that were experienced by patients in both studies were similar (Gleason et al., 2007). Furthermore, we inspected the patterns of change in symptoms over time within each study and did not find detectable differences. After weighing issues regarding sample size and possible bias from combining studies A and B, we decided to pool them and to align their time points, labelling them 1–5. Table 1 shows how the time points were aligned for the two studies. Because of patient dropout from brain tumour progression, mortality and other factors, not every patient had complete data at all five time points. For study A, the d-MPH and placebo groups had 17 complete cases, and for study B, in the donepezil group, there were 21. However, for time points at which patients had observations, the amount of partially missing data was less than 3%.

Table 1.

Time alignment for studies A and B

Time point	Value for study A (d-MPH) (weeks)†	Value for study B (donepezil) (weeks)‡
t1§	Baseline	Baseline
t2	8–12	6
t3	12–16	12
t4	16–20	24
t5	20–24	30

^†Study A participants completed radiation therapy during the first 8 weeks after baseline.

^‡Study B participants completed radiation therapy before baseline and within a short window of about 2–4 weeks.

^§Both study A and study B participants started the drug right after baseline.

We focused on FACT brain subscale items that described symptoms that were directly linked to brain tumour. Items that are related to consequences or concerns that arise from the disease but are not necessary symptoms were excluded. For example, items such as ‘I am (not) able to work’ (a consequence of disease) or ‘I am afraid of having a seizure’ (a concern arising from disease) were not included. Items that exhibited a high level of flooring or ceiling effect were also excluded. As a result, 13 items from the FACT brain subscale were included in the final analysis. A factor analysis unambiguously separates the items into three domains (Gleason et al., 2007), which we labelled cognition problems (six items), emotional problems (four items) and physical and functional problems (three items). We provided a representative item for each domain: ‘I am losing hope in the fight against my illness’ (emotional domain), ‘I have difficulty expressing my thoughts’ (cognitive domain) and ‘I have a lack of energy’ (physical domain).

The result of the factor analysis suggested that the symptom domains may be consistent with the location of the tumour. For example, a site in the frontal lobe may affect the emotions of the patient, and a site in the left temporal lobe may cause problems with memory.

Fig. 1 shows the trend lines for the domain scores. For the three domains that have been measured, only symptoms that were related to the emotional domain tend to decline slightly over time. Symptom stresses arising from both the cognitive and the physical domains remain almost constant on average. However, as we shall see later, the averaged effect may be misleading. Patients do move from one type of symptom experience to another over time, even though the population effect appears to remain relatively constant.

Fig. 1.

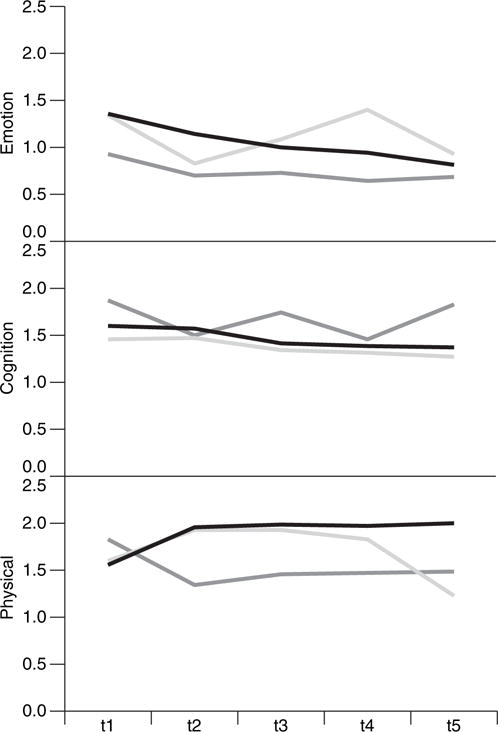
Trend lines for the emotional, cognition and physical domains by treatment group: ■, d-MPH arm; , donepezil; , placebo

4. Statistical model and estimation

4.1. Model

The multiple-indicator HMM is defined as follows. Let y_itj denote the discrete response of patient i at occasion t on item j, i=1,…, n, j =1,…, J, t = 1,…,T. The corresponding random variables are denoted by capitals. Specifically, y_it = (y_it1,…, y_itj,…, y_itJ)′ denotes the response vector of person i at occasion t, and y_i =(y′_i1,…, y′_it, …, y′_iT)′ represents the complete response pattern of patient i. z_it, z_it = 1,…,s,…,S, is the categorical latent state of patient i at occasion t, and thus z_i = (z_i1,…,z_it,…,z_iT)′ is the trajectory of patient i through the latent space over time. Assuming a first-order Markov chain for the latent variable, the latent state at occasion t + 1 depends on the past latent states through the latent state at occasion t only, Pr(z_it+1|z_i1,…,z_it) = Pr(z_it+1|z_it). The latent Markov model contains three basic sets of parameters, as follows:

1. τ = (τ_rs), the matrix of time homogeneous transition probabilities between latent states, Pr(Z_it = s|Z_it−1 = r) = τ_rs for t = 2,…,T;

2. α₁ = (α₁₁,…, α_1S)′, the vector of marginal state probabilities at occasion 1 (initial state probabilities); marginal state probabilities at occasion t =2,…,T are given by the recursive formula ${\alpha }_t^{\prime }={\alpha }_{t-1}^{\prime }\tau$;

3. Π=(π_js), the matrix of state conditional response probabilities, π_js=Pr(Y_itj =1|Z_it =s).

Assuming conditional independence between responses, given the latent state, the marginal probability of a response pattern y_i is then

$$\text{Pr}({\mathbf{y}}_i)={\displaystyle \sum _{{\mathbf{z}}_i}\text{Pr}({\mathbf{z}}_i){\displaystyle \prod _{t=1}^T\text{Pr}({\mathbf{y}}_{\mathit{it}}|{\mathit{Z}}_{\mathit{it}}=z_{\mathit{it}}),}}$$ (1)

where the summation is over S^T terms,

$$\text{Pr}({\mathbf{y}}_{\mathit{it}}|Z_{\mathit{it}}=\mathit{s})=\prod _{j=1}^J{\mathrm{\pi }}_{\mathit{js}}^{y_{\mathit{it}j}}{(1-{\mathrm{\pi }}_{\mathit{js}})}^{1-y_{\mathit{it}j}}$$

and

$$\text{Pr}({\mathbf{z}}_i)={\alpha }_{z_{i1}}{\displaystyle \prod _{t=2}^T{\tau }_{z_{\mathit{it}-1}{z}_{\mathit{it}·}}}$$

The multiple-indicator HMM was extended in two ways in this paper. First, observed patient characteristics and symptom attributes were incorporated through a logistic regression model for the conditional response probabilities (Vermunt et al., 1999):

$$\text{logit}({\mathrm{\pi }}_{\mathit{itjs}})={\mathbf{x}}_j^{\prime }{\mathit{\beta }}_s+{\mathbf{w}}_{\mathit{it}}^{\prime }\mathrm{\gamma },$$ (2)

where β_s indicates the vector of fixed symptom effects within state s, and γ represents the vector of fixed patient effects. The vectors x_j and w_it contain respectively the values of symptom j on the symptom attributes (e.g. symptom domain) and the values of patient i on the patient characteristics. The latter are allowed to be varying over time. Note that π_{it js} has an index for patients and time as well, since incorporation of (time varying) patient characteristics results in patient- (and time-)specific conditional response probabilities.

A second extension consisted of the incorporation of random effects for patients to capture the heterogeneity between patients in overall proneness to symptoms that are not accounted for by the patient covariates:

$$\begin{array}{cc}\text{logit}({\mathrm{\pi }}_{\mathit{itjs}})={\mathbf{x}}_j^{\prime }{\mathbf{\beta }}_s+{\mathbf{w}}_{\mathit{it}}^{\prime }\mathrm{\gamma }+{\theta }_i,& {\theta }_i\sim N(0,{\sigma }^2).\end{array}$$ (3)

Including patient effects (fixed and/or random) has the conceptual advantage that two sources of heterogeneity between patients are distinguished. The first source of heterogeneity arises from between-patient variation in overall proneness to symptoms. Part of this may be explained by observed patient characteristics ( $w_{it}^{\prime }\mathrm{\gamma }$), whereas the remaining part is taken into account by the random patient effect (θ_i). A second source of heterogeneity is variation in symptom patterns: one group of patients may suffer more from emotional distress, whereas another group may show more cognitive deficits. The second source of heterogeneity is of a qualitative nature and is modelled through the state-specific effects of the symptom attributes ( ${\mathbf{x}}_j^{\prime }{\mathit{\beta }}_s$). This extension of the multiple-indicator HMM was proposed in a psychometric context by Rijmen et al. (2005).

The assumption of missingness at random is generally applied for handling missing values. Specifically, missing values do not enter the likelihood equation. The missingness at random assumption allows patients with partially recorded data to be included.

4.2. Estimation

The extended HMM model is estimated by using the EM algorithm (Dempster et al., 1977), implemented in MATLAB. The E- (expectation) step can be carried out by making use of graphical model theory (Lauritzen, 1995). In brief, we first create a directed acyclic graph for the associated statistical model. The directed graph, which consists of nodes (variables) and arcs (Hunter et al., 1986), is a pictorial representation of the conditional dependence relations of the statistical model. The directed acyclic graph is then transformed into a so-called junction tree, which is the basis of efficient computational schemes (Jensen et al., 1990). Fig. 2 provides a schematic illustration of the directed acyclic graph that was used in this study.

Fig. 2.

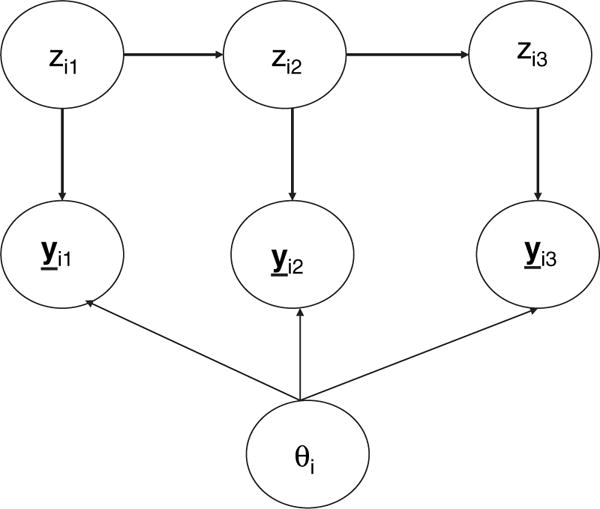
Simplified directed acyclic graph for the HMM with random effects (fixed effects covariates are not shown)

To construct the directed acyclic graph, and to transform the graph into a junction tree, we used the Bayes net toolbox (Murphy, 2001), which can be downloaded from http://www.cs.ubc.ca/∼murphyk/Software/BNT/bnt.html.

The EM algorithm was implemented through a second set of modular MATLAB functions that we developed. Detailed technical description of these implementations can be found in Rijmen et al. (2008). These functions model the conditional probabilities through a multinomial logistic regression model, allowing for the inclusion of covariates (for the patient and/or the symptoms, time constant as well as time varying). In the E-step, the posterior probabilities of the latent variables are computed through a propagation scheme that was defined on the junction tree. In the M-step, parameters are updated by using Fisher scoring. For models with normally distributed, continuous latent variables (e.g. individual-specific θ_i), the method of Gaussian quadrature was used in integration. The second set of MATLAB functions is available as a toolbox and can be obtained from a MATLAB exchange server, which is described in Rijmen (2006). We have also built an easy-to-use graphical interface and added regression features. The version is described in Ip et al. (2007) and the program can be obtained from the contact author.

5. Results

The issue of how many states must be included in the model is an important and actively researched area in HMMs (Scott, 2002) and in finite mixture models in general (McLachlan and Peel, 2000). The strategy that we used was to examine models with a varying number of states within the same level of model complexity and to select the number of states according to the Bayesian information criterion BIC (Schwarz, 1978). Then we compared models with different levels of complexity (e.g. with and without covariates). Our approach is similar to that used in the literature for latent class models (Bandeen-Roche et al., 1997), in which the number of latent states was selected on the basis of a model without any covariate.

We started with the simple multiple-indicator model without any covariate. Table 2 (top part) shows the deviance at the maximum likelihood solution, the number of parameters and BIC for the basic model for S = 2,…,5. The model with four classes had the lowest value of BIC. From a reviewer’s suggestion, we also used the log-marginal-likelihood (Kass and Raftery, 1995) for validating the selection. The log-marginal-likelihood involves an integral, which can be evaluated through a Laplace approximation, over a prior distribution. Following the specification in Scott et al. (2005), we used the Dirichlet distribution with count vector μ, for the HMM parameters, such that the value of each element in μ was set to 1.0. This specification represents a uniform prior over the probabilities for a multinomial distribution. The log-marginal-likelihood criterion also had the lowest value, at S = 4 (Table 2). The evidence based on various model selection criteria tended to converge, and therefore we selected S =4 as the basic model.

Table 2.

Number of parameters, deviance, BIC and log-marginal-likelihood for the estimated model

	Number of states	Number of parameters	Deviance	BIC	Log-marginal likelihood
Plain HMM	2	29	3650.6	3784.2	3767.0
	3	47	3502.8	3719.2	3684.7
	4	67	3399.3	3707.9	3669.1
	5	89	3321.2	3731.0	3712.2
Domain effects	2	19	3676.5	3764.0	—
	3	27	3558.0	3682.4	—
	4	37	3471.3	3641.7	—
	5	49	3433.0	3658.6	—
Domain effects, continuous latent variable	2	20	3526.3	3618.4	—
	3	28	3454.8	3583.7	—
	4	38	3401.0	3576.0	—
	5	50	3371.9	3602.1	—
Domain effects, continuous latent variable, treatment effects after first time point	2	22	3511.7	3613.0	—
	3	30	3447.2	3585.3	—
	4	40	3395.9	3580.2	—
	5	52	3362.0	3601.5	—

A second model was obtained by including symptom attributes as covariates for the conditional responses of the symptoms. Specifically, the differences between states in the logit of the conditional response probabilities were restricted to be the same for all items pertaining to the same domain:

$$\text{logit}({\mathrm{\pi }}_{\mathit{js}})={\beta }_j+{\beta }_{\text{domain}s},$$ (4)

where β_j is a parameter to be interpreted as the general proneness of a symptom j, and β_{domain s} is a state-specific effect that is common to all items belonging to the same domain. We set β_{domain 1} =0 for all three domains such that the model can be identified. In the restricted model, the JS conditional item–response probabilities are modelled as a function of J +3(S −1) model parameters. Again, models with S = 2,…,5 were estimated. The model with four states also had the lowest BIC (Table 2, second part).

In a third model, random patient effects were incorporated to capture patient effects:

$$\begin{array}{cc}\text{logit}({\mathrm{\pi }}_{\mathit{ijs}})={\beta }_j+{\beta }_{\text{domain}s}+{\theta }_i,& {\theta }_i\sim N(0,{\sigma }^2).\end{array}$$ (5)

Once again, the model with four states emerged as the model with the best fit (Table 2, third part).

The final family of models was obtained by adding treatment as a patient covariate. Because treatment only started after the first time point, it was included as a time varying patient characteristic in that its effect was not incorporated for the first time point:

$$\begin{array}{cc}\text{logit}({\mathrm{\pi }}_{i1\mathit{js}})={\beta }_j+{\beta }_{\text{domain}s}+{\theta }_i,& {\theta }_i\sim N(0,{\sigma }^2),\\ \text{logit}({\mathrm{\pi }}_{\mathit{itjs}})={\beta }_j+{\beta }_{\text{domain}s}+{\mathrm{\gamma }}_{\text{treatment}d}+{\theta }_i,& {\theta }_i\sim N(0,{\sigma }^2)\text{for}t=2,\dots ,T,\end{array}$$ (6)

where γ_{treatment d} is the effect of treatment d, d = 1, 2, 3. To identify the model, the effect of the placebo treatment was set to 0. The model with four states showed the lowest BIC (Table 2, bottom part), but its value (3580.2) was slightly higher than that of the random-intercept model that did not include the treatment effects (BIC = 3576). Nevertheless, a Wald test revealed a significant difference between the d-MPH group and the placebo group (d-MPH coefficient, 0.49, SE = 0:21; z = 2:30; p = 0:02). The direction of the effects was such that d-MPH patients had suffered more from symptoms than the placebo group. No significant effect was found between the donezepil group and the placebo group (donepezil coefficient, −0.08; SE = 0:26; z = −0.29; p = 0:77). Because it was important, from a clinical perspective, to include the treatment effect in the model, the four-state random patient with treatment effect HMM was selected as our final model, despite its slightly inferior BIC-value.

The patient-specific random effects play an important role in the final selected model. The variance of the distribution of the random effects had an estimated value of 1.25. This implies that for a specific symptom, if the conditional probability of having the symptom of a patient i with a random effect that is equal to the mean (θ_i = 0) is 0.5, a patient k within the same state who has a random effect that is 1 standard deviation above the mean (θ_i =1.12) has a probability of having that symptom of 0.75. This represents a rather substantial change in the response probability. Note that the value of θ_i for patient i remains constant when he or she transitions from one state to another.

To assess the normality assumption of θ, the final model was also estimated by using a nonparametric approach in which the distribution of the random effects was approximated with a discrete distribution for which the mass points and proportions were estimated from the data (Aitkin, 1999). The model was estimated with 3–5 categories. The deviances for θ were slightly lower than for the model with a normal distribution, with values of 3391, 3387 and 3387 respectively. However, the BIC-values were higher owing to the introduction of additional parameters, with values of 3589, 3595 and 3604. These results suggest that the assumption of a normally distributed θ was reasonable.

For the final model, the profiles for the four states are graphically displayed in Fig. 3. We noted that the profiles of the three separate groups—d-MPH, donepezil and placebo—are similar across the identified states, with the profile for the donepezil group almost identical to that of the placebo group. This is somewhat comforting because of our initial concerns about combining data across studies to boost sample size. For ease of reading, the profile of the donepezil group is not shown in Fig. 3.

Fig. 3.

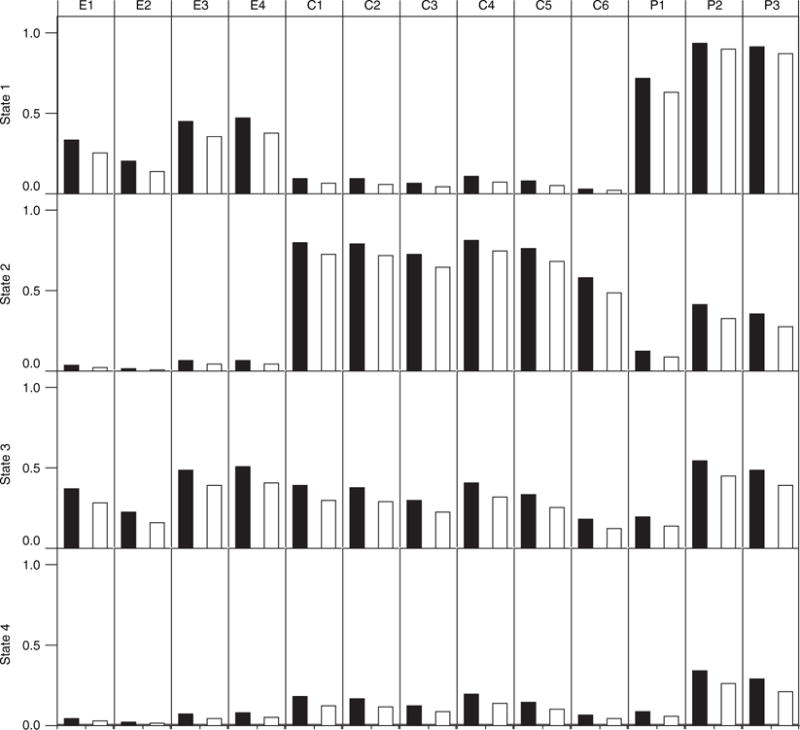
Profiles for the four latent states, as identified by the model (E1–E4 are items from the emotion domain, C1–C6 are from the cognition domain and P1–P3 are from the physical domain):■, d-MPH arm;□, placebo arm

In Fig. 3, each bar represents the conditional probability given the latent state. The random effects were integrated out when computing the conditional probabilities, and the treatment effect was only included in the model from the second time point on. We have tested models that include other covariates such as gender, but none of the covariate effects appeared significant, and results from these models are not reported here.

Patients in state 3 are characterized by general suffering from almost all symptoms—cognitive, emotional and physical. Patients in state 4 had only minor symptom experience across all three domains. Both state 1 and state 2 are interesting in their divergence among the manifestation of symptom groups. State 1 patients were almost unaffected in their cognitive functioning but complained about lack of energy and other side effects. They also experienced some emotional symptoms. In contrast, state 2 patients are characterized by severe cognitive symptoms, but they had only mild emotional symptoms. Among the four states, state 2 and state 4 patients form the most emotionally stable group. State 2 seems to consist of optimists who maintain a positive view even when they suffer from cognitive dysfunction.

The transition probability matrix in Table 3 reveals that state 4 is the most stable state. The probability of remaining within state 4 between consecutive time points is 0.86. This is in accordance with the clinical observation that if a patient does not have severe symptoms at time t − 1 he or she would have a good chance of staying that way at time t. State 3 patients had symptoms across the three domains, but most of them over time tended to improve and move out of this state. Indeed, the probability of remaining in state 3 between consecutive time points is only 0.18, but the probability of transitioning from state 3 to state 4 is 0.65. Being in state 2, the optimistic state, a patient would have the highest chance (0.51) of staying within the same state but also a good chance (0.43) of transitioning to the almost-symptom-free state, which is state 4. State 1 patients are most likely to stay within the same state (0.65). Note that the transition probabilities between the two states with the most divergent profiles (states 1 and 2) are quite low (for state 1 to 2 and state 2 to 1 respectively they are 0.05 and 0.00).

Table 3.

Estimated marginal state probabilities and state transition probabilities for the model incorporating domain effects, treatment and random patient effects

Probability	Results for the following states:
	State 1	State 2	State 3	State 4
Initial state probabilities α1	0.03	0.11	0.52	0.34
State probabilities at time point 2, α2	0.11	0.09	0.12	0.68
State probabilities at time point 3, α3	0.11	0.10	0.08	0.72
State probabilities at time point 4, α4	0.10	0.10	0.07	0.73
State probabilities at time point 5, α5	0.10	0.10	0.07	0.73
State transition probabilities τ†	0.65	0.05	0.15	0.16
	0.00	0.51	0.06	0.43
	0.15	0.02	0.18	0.65
	0.03	0.06	0.05	0.86

^†Rows, state at time point t−1; columns, state at time point t.

Fig. 4 shows the evolution of states over time. The most salient feature in Fig. 4 is the rapid growth of state 4 patients, which indicates that this state may be the state in which most patients end up in the long run. The growth of state 4 comes mostly at the expense of state 3, which reflects the general trend that there is a reduction of symptoms over time. The benefits also seem to come early in the process (time 2). In contrast, the growth of state 1 (high physical domain symptoms) indicates that, over time, there is an increasing subgroup of patients with severe physical limitations. Hence, most patients start with general symptoms in all domains, but over time most of them improve in all domains, except for a subgroup that only improves in the cognitive domain and has to face more severe physical limitations.

Fig. 4.

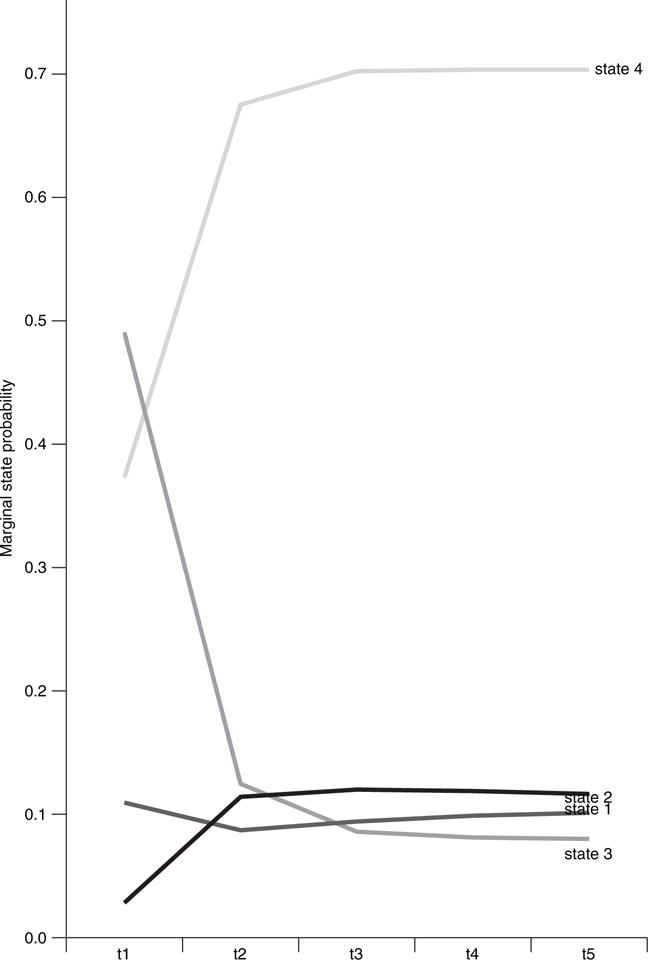
Evolution of the four states over time

We also note that the proportion of patients in state 2 remains quite stable. These optimistic patients tend to remain rather robust in maintaining their positive emotional status over time because they either remain within this state or, if they do transition, they tend to transition to state 4, which also has low emotional symptoms. Furthermore, because of the relative small size of this group (about 10% of the population), receiving the rather small amounts from the other states (see Table 3) is sufficient to balance and maintain the size of this state over time. The transition matrix reveals this interesting dynamic regarding state 2 patients: although the transition out into state 4 (0.43) is high, the low transition rates (0.02 and 0.06 respectively) from two relatively large groups—state 3 and state 4 (respectively 0.52% and 0.34% of the population at baseline)—offset the loss.

Fig. 4 also suggests that it is quite likely that different states have reached an equilibrium status at around time point 3. The proportions of the states in equilibrium are approximately 0.10, 0.10, 0.07 and 0.73 respectively for states 1, 2, 3 and 4. The trend lines that are shown in the time plots in Fig. 4 show that the extended HMM model effectively captures the drop between time points 1 and 2 for symptoms in the emotional domain (see Fig. 1)—a sudden increase of state 4, which is characterized by low emotional symptoms, and a sudden decrease of state 3, which is characterized by high emotional symptoms.

6. Discussion

The application of the HMM that was described in this paper has helped to provide a concise and qualitative summary of the evolution of symptoms due either to disease or to its treatment in brain tumour patients. Clinicians are used to working with discrete health states. The qualitative approach in this paper thus has the appeal of providing a meaningful interpretation of different psychosocial profiles of symptom stress and the evolution of such experience over time. Our findings should also add to the existing literature that concerns QOL issues for brain tumour patients. Historically, the literature on symptom management and QOL issues for the brain tumour population is quite sparse. Fox and Lantz (1998) noted that fewer than 20 references reflecting QOL in the adult brain tumour population were published in the period 1978–1998. Although more attention is now given to QOL issues in this population, the evolution of the patients’ experience is still not very well understood. Some recent work suggests that depressive symptoms are prevalent among brain tumour patients, with 38% scoring in the clinically depressed range (Pelletier et al., 2004). Pelletier et al. (2004) also reported that in their sample (n=60) depression is the single most important predictor of QOL. This is consistent with findings in Mainio et al. (2006), which has a sample size of 77. The finding in this work suggests that brain tumour patients as a group tend to improve emotionally over time, even though in our study a significant proportion remained depressed over the course of treatment. Emotional burdens, we found, also tend to correlate with physical limitations (Fig. 3). In contrast, cognitive symptoms tend to affect patients differentially—more severely for some but less for others. The implication is that different strategies need to be developed for handling patients with different symptom profiles.

In terms of analytic methodology, our work in this paper is related to prior work on applying HMMs to biomedical data, which has focused on using the data to delineate the structure of homogeneous classes for the purpose of classification and prediction (Jackson and Sharples, 2002; Altman and Petkau, 2005). Other recent work has used hierarchical models and structural equation modelling (Daniels and Normand, 2006) for examining profiles and trajectories. In contrast with the aforementioned work, the method that is proposed in this paper focuses on the interpretation of latent states and the modelling of possible sources of heterogeneity that affect the trajectory of the latent states. The method also enables us to incorporate covariates at both the item and the person levels. Random effects were also incorporated in the model to accommodate individual differences. In terms of model structure, our approach is closely related to the concomitant latent class models (Bandeen-Roche et al., 1997), latent transition analysis (Lanza et al., 2003) and latent trajectory analysis (Jones et al., 2001). Each of these approaches aims to serve a different purpose and does not necessarily contain all of the functionalities that are featured in the HMM proposed.

Our application of the method to this specific data set has several limitations. First, not unlike many studies of brain tumour patients, the sample size may limit the generalizability of our findings. The limitation due to the small number of cases that are available at later time points in this work is somewhat alleviated by the model assumption that latent state profiles and the transition matrix are invariant over time. Information is shared across time points for defining the latent structure and the transition mechanism. A second limitation is the rather artefactual alignment of time points across the two studies. Fortunately, as Table 1 suggests, the alignment does have some face validity, and empirical evidence also suggests that the distribution of latent states remains relatively stable after time point 2, which means that results after this time point are not likely to be affected by potential time matching bias. An alternative approach would have been to arrange chronologically the time points of the two studies and to treat values from some time points as missing by design. However, when the number of latent classes is more than 3 this approach would have given unstable results for our available data set. As a result, we did not implement this approach in the current paper. A third limitation of this application is that covariates can only affect either the person or the item but not the temporal structure of the Markov model. The transition probabilities are not affected; nor are the starting probabilities of the states. Creating a separate transition matrix at each time point might create too many parameters. One possibility would be to apply a Bayesian approach that allows deviation from a mean transition probability matrix at each time point (Scott et al., 2005). Other inhomogeneous Markov models and the associated issues have also been considered in the literature (Altman and Petkau, 2005). Efforts to incorporate covariates that can affect transition probabilities through the Bayesian model are currently on going.