Development of a rhesus monkey lung geometry model and application to particle deposition in comparison to humans

Abstract

The exposure-dose-response characterization of an inhalation hazard established in an animal species needs to be translated to an equivalent characterization in humans relative to comparable doses or exposure scenarios. Here, the first geometry model of the conducting airways for rhesus monkeys is developed based upon CT images of the conducting airways of a 6-month-old male, rhesus monkey. An algorithm was developed for adding the alveolar region airways using published rhesus morphometric data. The resultant lung geometry model can be used in mechanistic particle or gaseous dosimetry models. Such dosimetry models require estimates of the upper respiratory tract volume of the animal and the functional residual capacity, as well as of the tidal volume and breathing frequency of the animal. The relationship of these variables to rhesus monkeys of differing body weights was established by synthesizing and modeling published data as well as modeling pulmonary function measurements on 121 rhesus control animals. Deposition patterns of particles up to 10 μm in size were examined for endotracheal and and up to 5 μm for spontaneous breathing in infant and young adult monkeys and compared to those for humans. Deposition fraction of respirable size particles was found to be higher in the conducting airways of infant and young adult rhesus monkeys compared to humans. Due to the filtering effect of the conducting airways, pulmonary deposition in rhesus monkeys was lower than that in humans. Future research areas are identified that would either allow replacing assumptions or improving the newly developed lung model.

Introduction

Nonhuman primates have often been used as surrogates to study the health effects from exposure to harmful agents, particularly for aerosolized agents that produce a variety of biological responses that can be expected to also occur in humans following inhalation of these agents. Exposure characteristics and ensuing biological endpoints can be characterized and used in the development of a risk assessment model to estimate dose-response functions and exposure levels that are unlikely to result in adverse effects in humans. The nature and severity of most biological end points are a function of the retained dose in the lung, which is often difficult to determine experimentally. Hence, to study the potential for human health effects, the exposure-dose-response characterization of inhaled gases, vapors, and aerosols established in nonhuman primates needs to be translated to predict biologically equivalent doses in humans. This translation involves the use of mathematical dosimetry models that allow the calculated doses in nonhuman primates to be extrapolated to estimate human lung doses and, thus, equivalent human exposure scenarios.

Various disease models and pathobiological conditions have been studied in nonhuman primates. Plopper et al. (2007) have shown that remodeling of the epithelial-mesenchymal trophic unit of the tracheobronchial airway wall is altered in postnatal development of rhesus monkey lungs exposed to ozone and challenged with house dust mites as the allergen. Cynomolgus and rhesus macaques have been used in the study of severe acute respiratory syndrome (Haagmans & Osterhaus, 2006). Indeed, macaques are the major nonhuman primate used in biomedical research and serve as models for more than 70 human infectious agents of diverse etiologies, including bacteria, viruses, fungi, parasites, and prions (Gardner & Luciw, 2008). Nonhuman primate studies involving therapeutic drug research targeting subregions of the intrathoracic airways benefit from knowledge of particle deposition patterns in the lower respiratory tract (LRT) as a function of aerodynamic size.

In principle, inhalation studies must be conducted to measure the deposited dose of inhaled toxicants or therapeutic drugs in the lungs of primates. However, only a limited number of such studies can be conducted due to the high costs of developing inhalation exposure systems, monitoring and maintaining a stable aerosol over the duration of the exposure period, and evaluating all of the biological endpoints that may be involved in the mode of action of the compound. Even then, measurements will not encompass all desirable exposure scenarios and deposition/absorption ranges. Hence, available deposition measurement information is used in the construction of a dosimetry model in conjunction with mathematical expressions and differential equations that allow one to examine the deposition/absorption and removal of the material in the respiratory tract in a costand time-effective manner.

Deposition/absorption calculations of inhaled materials (vapors, gases, aerosols, mixtures,) involve simultaneous solutions of the airflow and material transport equations in realistic geometries of the respiratory tract for various lung and breathing parameters. However, anatomically correct models of the respiratory system are currently limited to either discrete regions of the respiratory system or, if they include conducting airways of both the upper and lower respiratory tract, do not extend into the alveolar spaces that are important for many inhaled materials. To achieve the needed calculations, the process can be broken down into four independent steps. First, semi-empirical predictive models for the inhalability of airborne materials into and deposition/absorption in the upper respiratory tract (URT) are developed based on either laboratory measurements or computational fluid dynamics studies. Second, the LRT geometry is constructed from available, selected measurements of conducting and alveolated airways of the lung by assuming that each airway is shaped as a cylindrical tube. Third, a model for lung ventilation is developed based on airway resistance and lung compliance to allow distribution of inhaled materials throughout the LRT. Finally, an account of the fate of inhaled materials is accomplished by performing a mass balance on the inhaled materials in each airway of the LRT. Calculated airway losses are combined to obtain local and regional deposition fractions and deposited masses.

Steps 3 and 4 of the above process are fairly generic and share many common elements and procedures across material types and species. Thus, modifications are made to existing models in order to develop similar models in a new species or for a new material. Steps 1 and 2 have been carried out in detail for humans, but not for rhesus monkeys. Therefore, the development of mathematical models for head losses and lung geometry accompanied by breathing parameters for rhesus monkeys constitute a major thrust of the current study.

The only previous attempt to model particle deposition in rhesus monkeys was done by Martonen et al. (2001). Since these investigators did not provide any measurements of LRT airway dimensions for the rhesus monkey, they made a number of assumptions to create a rhesus lung model, among them being: (1) the symmetric dichotomously branching system of Soong et al. (1979) for human airway lengths and diameters could be scaled to the size for a rhesus monkey using the ratios of the human trachea to that of a rhesus monkey that had been measured by Phalen and Oldham (1983), (2) the airway branching angles for major and minor daughters were assumed equal to a value of 41°, which represented an average of the 20° for the major daughter and 62° for the minor daughter reported in Table 2 of Phalen and Oldham (1983), and (3) the alveolar volume was set equivalent to the alveolar volume for a cynomolgus monkey of 121 cm³ measured by Hislop et al. (1984). Values of physiologic variables such as tidal volume and breathing frequency were taken from Phalen (1984), who reported values from the study by Crosfill and Widdicombe (1961) for monkeys (type of monkey not specified).

Currently, there are three major dosimetry models for deposition of particles in human lungs where the software is available for use by most investigators: (1) the National Council on Radiation Protection and Measurements (NCRP) deposition model (NCRP, 1997), (2) the International Commission on Radiological Protection (ICRP) deposition model (ICRP, 1994), and (3) the multiple path particle deposition (MPPD) model (Anjivel & Asgharian, 1995; Asgharian et al., 2001; Asgharian & Price, 2007). In a review of the performance of these models, Rostami (2009) noted that the models produce similar regional deposition results in humans for particles larger than about 0.1 μm in diameter but that the MPPD model is more user friendly due to its menu driven data input format.

To calculate the deposition of particles in various respiratory tract regions, a dosimetry model requires inputs for the aerosol: concentration, particle density, particle diameter (count median, mass median, or mass median aerodynamic), the geometric standard deviation, and whether a correction is to be made for inhalability. Inputs that relate to the route and pattern of breathing must also be specified. These include: initial lung volume at the start of the breath, which is termed functional residual capacity (FRC); the volume of air inhaled broken down into the tidal volume and the breathing frequency; the fraction of the breathing cycle due to inspiration and due to pause; and the route of breathing. In addition, the user must specify an airway morphometry model to be used and the volume of the nasal and oral passages.

The objectives of the current study were three-fold. The first was to develop a LRT geometry model for the lungs of rhesus monkeys using computed tomography (CT) images of the tracheobronchial (TB) airways to construct a conducting airway tree and synthesizing morphometric data from the literature to construct the alveolar region geometry. The second objective was to develop relationships between various physiologic variables and the body weight/age of rhesus monkeys to be able to specify values of input variables needed in deposition model calculations of inhaled particles and to scale the LRT geometry model to monkeys of different sizes. The final objective was to examine the deposition of particles in the lungs of rhesus monkeys and make comparisons to deposition patterns and values in humans. To accomplish these objectives, various tasks were undertaken, as described in the following sections.

Development of lung geometry model

Constructing the conducting airway tree

Rhesus monkeys 1 to 12 months of age are considered to be infants and are young adults when they are 4 to 8 years of age (Golub & Gershwin, 1984). The lungs of a 6-month old, male rhesus monkey weighing 1.79 kg were removed from the chest and via a tracheal cannula instilled with a 1% glutaraldehyde/1% paraformaldehyde fixative in cacodylate buffer (330 mosm, pH 7.4) at 25 cm H₂O pressure overnight and then stored in fixative. Fixed lungs were placed in buffered saline prior to casting. Silicone RTV mixed with silicone oil was introduced to the lung through the trachea under a slight negative pressure (−80 mm Hg) until it reached the distal airways. The silicone RTV was allowed to cure for 48 h, after which the airway tissue was removed with bleach. Silicone RTV diluted with low viscosity silicone oil penetrates well to the level of the terminal bronchioles and alveolar ducts without causing overdistention. The shrinkage rate for the casting material was negligible at 0.32% after 7 days (Perry et al., 2000).

Post mortem lung CT data were obtained after removing airways containing alveoli. Serial-section scan images of the lungs were made from the trachea down to reconstruct the lung geometry for visualization and inhaled dose calculations. The coronal images of lung airway cross sections were assembled and digitized to create a 3-D structure, as described by Carson et al. (2010).

The reconstructed 3-D lung geometry was converted to a binary tree made up of parent-daughter branches with each branch assumed to have the shape of a cylinder. Cylindrical representation of non-cylindrically-shaped lung airways allows average predictions of deposited dose for various possible shapes of the airway and is consistent with the first-order, accuracy level of the constructed model for deposition predictions. Airway parameters including length, diameter, branching and bifurcating angles were calculated and reported along with parent-daughter connectivity to create an asymmetric tree geometry for the conducting airways of the lung. The TB geometry contained over 20,000 airways.

The reconstructed conducting tree was made from a dataset containing 24,846 airway records, with each record specifying the length, volume, [x,y,z] coordinate, and basic connectivity information (Jiao et al., 2010). These records of the 6-month old, male rhesus monkey were analyzed for development of the lung geometry into a single path airway branching model. The airway tree dataset was not a dichotomous branching network. There were a few cases where a parent airway split into several daughter branches. The number of daughter branches reached as many as 10 in several instances, which is unrealistic and has not been observed anatomically. The false extra-branching observations were primarily due to the lack of adequate resolution of the scanned images that affected the automated medial curve algorithm. Hence, a reassignment of airway branching was necessary for branches with more than 2 siblings.

An algorithm was developed to reorganize the airway branching patterns established by the initial medial curve analysis based on the premise of a steady decrease in airway diameter with increasing lung depth. First, the number of daughter pathways was examined at each bifurcation. Pathways exceeding 3 at a junction were removed and reattached to other bifurcations. Each removed pathway, consisting of a detached (root) airway and its subsequent bifurcations, was reattached to a nearby bifurcation. The criterion for reattachment of a removed pathway was based on the diameter of its root airway. The diameter of the root airway was compared with the airway diameters of the intact conducting airway tree. The removed pathway could belong to a bifurcation if its root airway diameter was closest to but smaller than the parent airway diameter. The maximum number of daughter pathways was kept to 3 at each bifurcation. Third, the comparison of the root airway diameter of a removed pathway with the conducting tree airway diameters was repeated for all removed pathways until all were reassigned to different bifurcations and a new conducting tree emerged. Finally, the branching and gravity angles of all airways were recalculated. The resulting new TB tree geometry was made up solely of bifurcations and trifurcations.

The reconstructed geometry of the conducting airway tree had an asymmetric structure (i.e., airway parameters at a given generation had different values). Initially, a typical-path, symmetric lung geometry for the rhesus monkey was developed, with the realization that more information on the variability among lobes in airway dimensions of various monkeys is needed before more detailed geometry models might be developed. The following steps were taken to create a symmetric lung geometry of the conducting airways:

1. Average airway parameters (diameter, length, and branching and gravity angles) were calculated for each airway generation of the conducting airway tree. In addition, the average generation number was found for the entire tree by dividing the sum of generation numbers for all pathways by the number of pathways. The average generation number was calculated to be N = 15.

2. A functional relationship was adopted between each airway parameter and airway generation number [e.g. d = f(i), where d was the airway diameter and f(i) was the functional relationship, which depended on generation number, i]. The coefficients of the function were found by fitting the function to the corresponding averaged airway parameter. Hence, an airway parameter value (e.g. diameter) was found by inserting a value for the generation number i in function f(i).

3. The predictive curve-fit models developed in step 2 gave airway parameters from generations i=0 to the last generation number, I, which was found to be 33. However, the symmetric lung geometry stretched from generation 0 to average generation number, N. Hence, the functional relationships were rescaled by i = (I / N) × n or i = (33 / 15) × n.

While the initial rhesus monkey deposition model was developed from data on a 6-month-old male, rhesus monkey weighing 1.79 kg, the deposition model can be extended over a wide range of body weights and ages for both male and female monkeys by rescaling lung dimensions and replacing age-specific values of lung and breathing parameters with values obtained from equations developed in subsequent sections of this paper. The lungs of the rhesus monkey imaged were fixed at a pressure of 25 cm of H₂O, ensuring fixation at total lung capacity (TLC). Since deposition calculations are done with an animal taking a breath starting at FRC, the TB geometry data were scaled from TLC to FRC using isotropic scaling methods.

To develop a LRT geometry for animals of different body weights, the ratio of FRC to TLC must be used to scale the airway dimensions appropriately. Since FRC/ TLC changes in value as animals grow from birth to adulthood, the relationship of FRC/TLC as a function of body weight in rhesus monkeys must be established and this is done in a subsequent section.

Constructing the pulmonary airway tree

A number of relationships between variables such as alveolar duct volume or alveolar volume and the animal’s body weight, age or lung volume are needed to construct the alveolar region lung geometry, as well as to scale their values and dimensions to animals of different sizes or to scale the dimensions for a given animal to animals with a different lung volume. Here, we describe how the needed relationships were estimated.

The lung volume (V_L) represents the cumulative sum of the volume of the trachea and all of the airway volumes proceeding distally from the trachea down every lung path until terminating at an alveolar sac. As noted above, data on V_L are critical for assessing the reasonableness of the generations of respiratory bronchioles and alveolar ducts and partitioning the total volume among the TB airways, respiratory bronchioles, and alveolar ducts and sacs. In pulmonary physiology studies, a good estimate of V_L is provided by the measurement of TLC. In lung morphometry studies, lung volume is typically estimated from the buoyancy of the lungs (minus the trachea and extrapulmonary bronchi) after they are placed in a physiologically-buffered saline solution. In lung morphometry studies, the pressure used for fixation, the materials present in the fixative solution, and the length of time allowed for fixation all influence the volume at which the lungs become fixed. If the fixation procedure results in lungs fixed at a volume near TLC, the estimates of V_L from lung morphometry and pulmonary function studies will be close to each other.

Hyde et al. (2007) examined a number of alveolar variables in the lungs of male and female rhesus monkeys ranging in age from a few days to more than 7 years, with body weights ranging from 0.41 to 12.66 kg. They determined the number of alveoli, the volume of the airway portion of the alveolar ducts, the volume occupied by the alveoli, and a number of other parameters reflective of lung structure. Their measurements of V_L as a function of body weight for their male rhesus monkeys are shown in Figure 1 together with the TLC values for male animals that served as controls in various studies at the California National Primate Research Center. Most of the morphometric study animals had body weights less than 4 kg, and their values for V_L agree quite well with the estimates of V_L obtained in pulmonary function animals. The variability around the fitted curve increases as body weight increases.

Figure 1.

Lung volume as a function of body weight in male rhesus monkeys. The open triangles are total lung capacity measurements of lung volume from pulmonary function studies. The closed circles are lung volume data from the morphometry study of Hyde et al. (2007). A quadratic fit to all of the data is shown.

Since the animal used to develop the conducting airway geometry weighed 1.79 kg, we elected to restrict the regression analyses of the various morphometric variables to animals at the lower end of the body weight range (i.e., <4 kg). The best fitting models for variables needed to develop the pulmonary generations of a lung model for male rhesus monkeys are given in Table 1 with plots of the raw data and fitted curves presented in the various panels of Figure 2. Fits for these same variables for female rhesus monkeys are provided in Appendix A.

Table 1.

Best fitting regression models in male rhesus monkeys for various pulmonary variables.

Dependent Y-Variable	Independent X-Variable	Modela	Model parameters		R2
			β0	β1
Lung Volume, mL	Body Wt., kg	Linear	27.497	53.326	0.936
Duct Volume, mL	Body Wt., kg	Linear	4.8231	17.243	0.796
Volume of Alveoli, mL	Lung Volume, mL	Linear	−0.12747	0.5735	0.959
Log No. of Alveoli	Lung Volume, mL	Exponential	8.0389	0.00014507	0.744

^aLinear model: β₀ +β₁ * X; Exponential model: Y = β₀ * exp(β₁ * X).

Linear models fit to data for animals <4 kg body weight; exponential fit to data for all animals.

Figure 2.

For male rhesus monkeys, best fitting regression models showing the relationships among lung variables, body weight and lung volume. Panel A: Lung volume vs. body weight, with linear curve; Panel B: Alveolar duct volume vs. body weight, with quadratic curve; Panel C: Alveolar volume vs. lung volume, with linear curve; Panel D: Log of the number of alveoli vs. lung volume, with an exponential curve. See Table 1 for the coefficients of the fitted regression models.

Based on the regression models in Table 1, we computed the predicted values of various variables for the male, rhesus monkey used to develop the lung geometry model. All pulmonary volumes were calculated at TLC; the equations in Table 1 were used to obtain the values in Table 2 for a male rhesus monkey weighing 1.79 kg having a TLC of 123.1 mL (i.e., the size of the monkey whose CT scans were used to construct the conducting airway geometry). The values of the variables given in Table 2 provided constraints that our pulmonary airways scaling approach had to meet.

Table 2.

Values of variables used to develop the pulmonary airway geometry for a 6-month-old male rhesus monkey weighing 1.79 kg with a TLC of 123.1 mL.

Variable	Value
Duct Volume, mL	35.69
Volume of alveoli, mL	70.38
Log number of alveoli	8.18357169
Number of alveoli	81,835,717

We compared the resulting rhesus monkey anatomic data with comparable data for cynomolgus monkeys (Hislop et al., 1984). In the Hislop et al. (1984) study, a mixture of barium sulfate and gelatin at 60°C at a pressure of 70 mmHg was injected into the pulmonary arteries. Subsequenly, 10% buffered formol saline was injected at a pressure of 30 cm of H₂0 and the trachea clamped. The lungs were then immersed in formol saline for at least 1 week. As the data in Table 3 clearly show, the values for V_L are consistently about 30% greater for rhesus monkeys compared to cynomolgus monkeys, with the difference being about 50% for the largest monkey (i.e., body weight of 6.7 kg). Injecting hot gelatin into the pulmonary arteries at 70 mmHg likely deformed the airways, thereby creating considerable artifacts and errors in intrapulmonary airway dimensions. In addition, Hislop et al. (1984) do not make it clear whether the perfusion pressure was maintained at 30 cm H₂0, which would have further confounded any artifacts or errors. Thus, we would not recommend substituting this cynomolgus lung volume data for rhesus data.

Table 3.

Comparison of fixed total lung volume in cynomolgus and rhesus monkeys.

Body weight (kg)	Lung volume, mL
	Reported by Hislop et al. (1984)	Predicted from linear fit to Hyde et al. (2007) rhesus data
2.9	114	163
3.2	136 ± 30.8a	175
4.3	182	220
6.7	155	317
Average	143	204
SD	30.2	58.7

^aMean and standard deviation of three monkeys weighing 3.2 kg.

SD: Standard deviation.

With no information on airway dimensions in the pulmonary region for rhesus monkeys, the values for the duct volume and volume of the alveoli in Table 2 were used to reconstruct the pulmonary airway tree. In addition, due to the lack of data on the distribution of the number of alveoli per generation in monkey lungs, the measured values in humans (Weibel, 1963) were used to apportion the volume of alveoli among the respiratory bronchioles and alveolar ducts of rhesus monkeys. Finally, the calculated TLC of the rhesus monkey lung compared against reported measurements was used as a final confirmation for the accuracy of pulmonary dimensions and structure.

To complete the geometry model for the rhesus monkey, generations of respiratory bronchioles (RBs) and alveolar ducts have to be added to the terminal bronchioles from the symmetric lung geometry. Hislop et al. (1984) examined the structural development of the lung of cynomolgus monkeys. They reported 6–9 generations of respiratory bronchioles and at least five generations of alveolar ducts. However, for the rhesus monkey, four generations of RBs are typically seen (Phalen & Oldham, 1983).

Relative to the number of alveolar generations, a restriction on their number is imparted by literature data on the number of alveoli and their volume, as well as on the volumes and lengths of alveolar ducts. We used data on duct volume to help determine the reasonableness of the number of added alveolar generations. The pulmonary airway tree was constructed with 4 generations of respiratory bronchioles and 4 generations of alveolar ducts and sacs. Thus, the entire lung geometry consisted of 23 airway generations: 15 generations of the conducting airways and eight generations of the alveolar airways. Airway diameters of the symmetric pulmonary tree for generations 16–23 were obtained by assuming changes in airway diameter and length from generation to generation are the same in humans and monkeys.

The pulmonary airway tree of rhesus monkeys excluding the alveoli was constructed based on a Wiebel type airway volume distribution and calculated total duct volume of rhesus monkeys (35.69 mL; Table 2). In addition, the airway tree structure and shape were assumed to be the same for humans and rhesus monkeys. Thus, airway length to diameter ratio was the same in humans and rhesus monkeys for corresponding airway generation numbers. Airway dimensions of rhesus monkeys were determined in several steps. First, volume fraction of human pulmonary airways (excluding the volume of alveoli) was calculated per airway generation and used to find the cumulative airway volume fraction in the human pulmonary region. The cumulative volume fraction was assumed to be the same for humans and rhesus monkeys. Thus, the volume fraction and cumulative volume fraction in each generation of the rhesus monkey lung was obtained by linear interpolation (Figure 3). Next, accumulative and airway volumes in each generation of the rhesus monkey pulmonary tree were found by multiplying volume fractions by an arbitrary volume scale. The volume scale was selected such that the duct volumes (i.e. volume of the last 4 generations of the pulmonary tree) added to 35.69 mL. Finally, airway length and diameter were calculated from airway volume per generation of the rhesus monkey and the corresponding airway length-to-diameter ratio.

Figure 3.

Pulmonary duct volume fraction versus airway generation number in rhesus monkeys and humans.

Once the pulmonary airway tree was constructed, the alveoli were attached to different generations of the pulmonary airway tree. There are limited data on the number, volume, and distribution of acini in monkeys, which hampers the construction of the monkey alveolar structure. Given that the structure and distribution of airway parameters are similar between humans and monkeys (Mercer et al., 1994), we used the relationship in humans for the number of alveoli per duct to construct the pulmonary acinus structure in the rhesus monkey. The alveoli number distribution versus generation number in humans was used to distribute 70.38 mL (Table 2) of alveolar volume among respiratory bronchioles and alveolar ducts of the rhesus monkey airway generations. The fraction and accumulative fraction of the alveoli volume of the human respiratory tree was calculated per airway generation number in the pulmonary region. The alveoli volume fraction and cumulative volume fraction were assumed to be the same for humans and rhesus monkeys (Figure 4). The volume fraction and volume of alveoli per generation of the rhesus monkey lung was consequently obtained by linear interpolation. The volume of alveoli per airway generation in rhesus monkeys was found by multiplying the volume fraction per generation by the total volume of alveoli in the pulmonary region.

Figure 4.

The pulmonary volume fraction and cumulative volume fraction versus airway generation number in the lungs of monkeys and humans.

The completed alveolar airway tree was then attached to the conducting airway tree to form the complete lung geometry. Airway dimensions of the symmetric lung tree are listed in Table 4 and a comparison between rhesus monkeys and humans for airway dimension as a function of airway generation is shown in Figure 5. The typical-path lung geometry model for the rhesus monkey has the same number of airway generations as humans except for one fewer conducting airway generation and one additional alveolar airway generation.

Table 4.

Airway dimensions for the rhesus monkey symmetric lung geometry at TLC.

Generation number	Number of airways	Length (cm)	Diameter (cm)	Bifurcation angle (°)	Gravity angle (°)	Total volume (cm3)	Accumulated volume (cm3)
0	1	1.62900	0.48990	0	9.57	0.307	0.307
1	2	1.17490	0.34130	51.97	55.1	0.215	0.522
2	4	0.78420	0.22970	45.76	66.26	0.130	0.652
3	8	0.43060	0.16790	44.76	70.98	0.076	0.728
4	16	0.31090	0.12420	46.77	73.23	0.060	0.789
5	32	0.22900	0.09140	51.16	77.02	0.048	0.837
6	64	0.17590	0.06940	55.94	83.81	0.043	0.879
7	128	0.14350	0.05650	56.21	84.94	0.046	0.925
8	256	0.12100	0.04920	58.44	84.32	0.059	0.984
9	512	0.11020	0.04340	58.82	85.44	0.083	1.068
10	1,024	0.10130	0.04060	59.36	87.2	0.134	1.202
11	2,048	0.09400	0.03910	59.21	85.02	0.231	1.433
12	4,096	0.09100	0.03760	60.21	86.8	0.414	1.847
13	8192	0.08950	0.03730	60.71	85.6	0.801	2.648
14	16,384	0.08530	0.03600	60.07	85.11	1.423	4.071
15†	32,768	0.08120	0.03480	60.63	86.08	2.531	6.601
16	65,536	0.05578	0.02136	45	60	1.400	8.001
17	131,072	0.04445	0.01869	45	60	1.843	9.844
18	262,144	0.03727	0.01715	45	60	2.953	12.797
19	524,288	0.03113	0.01591	45	60	5.371	18.168
20	1,048,576	0.02590	0.01479	45	60	9.571	27.739
21	2,097,152	0.02156	0.01370	45	60	16.474	44.213
22	4,194,304	0.01799	0.01278	45	60	28.809	73.023
23	8,388,608	0.01491	0.01223	45	60	48.059	121.082

^†Terminal bronchioles.

Figure 5.

Change of airway parameters as a function of airway generation number in the lungs of a 6-month-old, male rhesus monkey and 3-month-old human infant.

Estimating values of physiologic variables

As noted earlier, calculating lung deposition of inhaled particles or the absorption of an inhaled gas requires knowledge of a number of physiologic variables. These include the route, rate, and depth of breathing, the volume of the URT, and the volume of the lungs at FRC. Subsequent sections provide how values of these variables were estimated for rhesus monkeys.

URT volume

Particle- or gas-laden inhaled air is diluted by the volume of air initially in the URT. The mixture of dilution air and inhaled air make up the tidal volume air that travels to various locations of the lung. In addition to the route and depth of breathing, the volume of the URT influences LRT deposition. Thus, the URT volume must be known to assess losses of particles in various locations of the lung. To obtain an estimate of URT volume, data were integrated from a number of sources: (1) nasal measurements of MRI scans of 6-month-old rhesus monkeys, (2) computational fluid dynamics (CFD) model of a 6-month old monkey, and (3) volume measurements of URT molds of rhesus monkeys that had been used in airflow studies conducted by investigators at the Chemical Industry Institute of Toxicology (CIIT, currently named the Hamner Institutes for Health Sciences).

Nasal volume and surface area measurements were made from MRI scans of the nose of 8 rhesus monkeys that had been exposed to either filtered air or cyclic ozone for a period of 6 months that did not result in any nasal structural alterations. Since the scans were only of the left side of the nose, the value for each animal was obtained by doubling the value of volume or surface area for the imaged side (Table 5). The volume and surface area measurements reported in Table 5 also include the maxillary sinuses. Since the URT region represents from the nares down to and including the larynx, the volume of the nasopharynx, the oropharynx, and the larynx must be added to the nasal volume to derive an estimate of URT volume for these animals.

Table 5.

Nasal plus maxillary sinus volume and surface area of 6-month-old male rhesus monkeys exposed to clean air or cyclic ozone for 6 months.

Group	Age (days)	BWT (kg)	Nasal + maxillary sinus		Nasal only		SA to volume ratio
			Volume (cm3)	Surface area (cm2)	Volume (cm3)	Surface area (cm2)
Air	180	1.3	1.06	20.6	0.96	18.73	19.55
	179	1.498	1.28	27.8	1.18	25.93	22.01
	176	1.55	2.44	76.2	2.34	74.33	31.79
	177	1.39	2.54	82.6	2.44	80.73	33.11
Ozone	179	1.548	1.18	26.8	1.08	24.93	23.12
	178	1.32	1.24	27.4	1.14	25.53	22.43
	182	1.363	2.12	54.4	2.02	52.53	26.03
	177	1.43	2.62	98.6	2.52	96.73	38.41
Ave. & Std. Air		1.43 ± 0.11			1.73 ± 0.77	49.93 ± 32.11	26.62 ± 6.83
	Ozone	1.42 ± 0.10			1.69 ± 0.70	49.93 ± 33.75	27.50 ± 7.44
	All Animals	1.42 ± 0.10			1.71 ± 0.68	49.93 ± 30.50	27.06 ± 6.63

Since the study by Morgan et al. (1991) showed there was no evidence of flow into the maxillary sinuses in the rhesus monkey mold, we needed to be able to “back out” an estimate of the maxillary sinus volume for the volumes derived from the MRI scans. This is important to do because the filtration efficiency of the nose for particle deposition is highly dependent upon the rate of airflow. The recent study of Ge et al. (2012) of local deposition fractions of ultrafine particles in a human nasal-sinus cavity CFD model showed that, even with very low flow rates, there is a lack of particle deposition within the maxillary sinuses. This further supports obtaining URT volume estimates that do not include the volume of the maxillary sinuses when examining the URT deposition of particles.

To obtain an estimate of the amount to subtract from the volume and surface area data of the maxillary sinuses for the MRI scanned animals, a three-dimensional reconstruction of one side of the nasal cavity of a 180-day-old, male rhesus monkey (1.3 kg) was created as described by Carey et al. (2007). The reconstruction was imported in STL format into the meshing software package ICEM-CFD version 12.1 (ANSYS, Inc., Canonsburg, PA) and the maxillary sinus and adjacent ostium were isolated from the main nasal cavity and meshed using 56,154 tetrahedral elements. The resulting mesh was imported into the CFD software Fluent version 12.1.4 (ANSYS, Inc.), and the volume and surface area of the maxillary sinus (one side only) were calculated using Fluent’s volume and surface integral utilities. The result of these computations was a volume of 0.051 cm³ and a surface area of 0.0936 cm² for a single maxillary sinus. These values were doubled and then subtracted from the nasal plus maxillary sinus data to obtain nasal only values that appear in the last three columns of Table 5.

Should others in the future obtain estimates of the nasal plus maxillary sinuses volume for rhesus monkeys and wish to estimate only the nasal volume portion, one can use measurements of the maxillary sinuses volume in macaque monkeys made by Kocon & Stephen (1967). Using metal casts of the URT, they studied monkeys between the ages of 1 and 8 years of age. Their data on the volume of the maxillary sinuses are given in Table 6, together with the value we determined here for a 6-month old rhesus. The value of 1.86 cm³ for the maxillary sinus volume in 6- to 8-year-old macaques given by Kocon and Stephen (1967) is in reasonably good agreement with the value of 2.25 cm³ reported by Gross et al. (1987) for rhesus monkeys likely to be of a similar age (Table 7). While the maxillary sinuses probably represent about 22 to 27% of the nasal region volume in animals 1 to 8 years of age, they represent less < 10% of the nasal region volume in 6-month old rhesus monkeys.

Table 6.

Maxillary sinus volume in rhesus monkeys as a function of age.^a

Age (years)	Maxillary sinuses volume (cm3)
0.5	0.102
1–2	0.35
3–4	0.51
5–6	1.2
6–8	1.86

^aValue for 0.5 years determined here; other data derived from Table 11 in Gross and Morgan (1992), which is based on data in Kocon & Stepien (1967).

Table 7.

Surface area and volume of the nasal cavity and maxillary sinuses in rhesus monkeys.^a

Variable	Average	Standard deviatonb
Body weight (kg)	7.17	0.16
Surface area (cm2)
Nasal cavity	64.30	13.94
Maxillary sinus	11.06	3.95
Total	75.36	16.64
Volume (cm3)
Nasal cavity	6.18	1.88
Maxillary sinus	2.25	1.39
Total	8.43	2.60

^aBased on Gross et al. (1987).

^bStandard deviation based on n = 3.

To our knowledge, there are no data in the literature on the volume of the nasopharynx, oropharynx, or larynx in rhesus monkeys less than one year of age. Thus, we used data from other ages and body weights for these regions and then applied a scaling relationship to obtain estimates of volumes for these regions for infant rhesus monkeys. Schreider and Raabe (1981) made serial step sections through a silicone rubber cast of the URT of a male rhesus monkey weighing 7 kg. From these detailed sections, they determined the perimeter and area of each section. By linking the sections together and taking into account the distance between sequential step sections, one can calculate the surface area and volume between any two sections via a forward or a backward process. The resulting data for surface area and volume were averaged for the forward and backward calculation process and are given in Table 8, providing another source of data for obtaining URT volume estimates for rhesus monkeys of different sizes.

Table 8.

Cross-sectional dimensions of serial sections of a rhesus monkey URT cast.^a

Anatomical region	Section number	Distance (mm)	Perimeter (mm)	Area (mm2)	Surface area (mm2)	Volume (mm3)
External Nares	1	0	45.8	55.6	133.7	159.9
	2	3	43.3	51.0	264.0	280.0
	3	8	62.3	61.0	340.3	368.0
	4	13	73.8	86.2	423.5	479.5
				Subtotal	1161.4	1287.4
Maxillo-Turbinate	5	18	95.6	105.6	537.3	666.8
	6	23	119.3	161.1	240.3	316.1
	7	25	121.0	155.0	435.2	503.7
	8	28	169.1	180.8	905.0	866.0
				Subtotal	2117.7	2352.6
Ethmo-Turbinate	9	33	192.9	165.6	1011.8	827.3
	10	38	211.8	165.3	383.6	329.4
	11	40	171.8	164.1	472.8	488.7
	12	43	143.4	161.7	648.8	785.8
	13	48	116.1	152.6	436.5	610.3
				Subtotal	2953.4	3041.4
Nasopharynx	14	53	58.5	91.5	258.8	361.8
	15	58	45.0	53.2	207.3	228.0
	16	63	37.9	38.0	154.8	142.0
	17	68	24.0	18.8	132.5	115.3
				Subtotal	753.3	847.0
Oropharynx	18	73	29.0	27.3	167.3	233.3
	19	78	37.9	66.0	124.4	290.9
	20	80	86.5	224.9	240.2	717.0
				Subtotal	531.8	1241.2
Larynxb	21	83	73.6	253.1	410.3	1290.3
	22	88	90.5	263.0	165.9	519.4
	22	88	75.4	256.4	194.2	513.7
	23	90	118.8	257.3	229.4	451.7
	24	93	34.1	43.8	61.7	59.6
	25	95	27.6	15.8	85.7	51.0
	26	98	29.5	18.2	161.3	225.5
	27	103	35.0	72.0	68.3	147.4
	28	105	33.3	75.4	153.0	328.8
				Subtotal	1529.6	3587.3
				Totals	9,047.2	12,356.7

^aLast two columns computed here are the average of forward and backward calculations using adjacent serial section data; others based upon Schreider and Raabe (1981).

^bSections 21–24 contain the laryngopharynx.

Since we only have data in Table 5 for the nasal region of 6-month-old rhesus monkeys averaging 1.42 kg, we still had to obtain volume estimates for the nasopharynx, oropharynx and laryngeal regions for the 1.79 kg monkey for which we had the CT data. We elected to use as a scaling factor for these regions the ratio of the nasal airway volume for a 1.42 kg monkey to that of the 7 kg rhesus that Schreider and Raabe (1981) studied. The volumes for these regions calculated by the backward and forward process for the data in Table 8 were divided by 1000 to convert to cm³ and then multiplied by the scaling ratio to yield the volume estimates given in Table 9.

Table 9.

Volume estimates for various regions of the URT of a rhesus monkey weighing 1.79 kg.

Volume (cm3) of nares to Nasopharynx for a 7 kg Rhesus Monkeya	Nasal Airway Ratiob 1.79 to 7 kg	Regional URT Volume (cm3) Estimates for a Rhesus Monkey Weighing 1.79 kg				URT Volume (cm3)
		Nasalc	Nasopharynxd	Oropharynxd	Larynxd
6.6	0.244	1.71	0.245	0.230	0.931	3.117
6.76	0.238	1.71	0.163	0.366	0.797	3.037
	Average	1.71	0.204	0.298	0.864	3.077

^aValues of 6.6 and 6.76 come from forward and backward calculations, respectively, of volume from data in Table 8.

^bNasal ratios derived, for example, as 0.244 = 1.71/6.6 and similarly for the other row.

^cValue taken from all animals average given in Table 5 for 6-month-old monkeys.

^dForward and backward calculation values from data in Table 8 divided by 1000 and then multiplied by nasal airway ratio.

URT molds for two adult rhesus monkeys, a 7-yr old female weighing 4.74 kg and a 15-yr old male weighing 10 kg, were examined to determine their URT volume. These molds had been used in airflow and particle deposition studies conducted at CIIT (Morgan et al., 1991). The nostrils of the molds were plugged with silly putty prior to filling the molds with ethanol and then weighing the molds. Ethanol was used to more easily eliminate air bubbles compared to using water. The filling and weighing process was repeated three times for each URT mold. The average weight of the ethanol was 6.36 g (0.11 std. dev.) and 13.39 g (0.09 std. dev.), respectively, for the mold from the animal weighing 4.74 kg and the one weighing 10 kg. Taking into account the density of pure ethanol, which is 0.789 g/cm³, the URT volume estimates for the 4.74 and 10 kg monkeys were 8.06 and 16.97 mL, respectively. Since the molds of these animals contained a portion of the trachea, the URT volume after adjusting for the tracheal volume of the mold was 7.61 and 15.32 mL for the animals weighing 4.74 and 10 kg, respectively.

Utilizing the data sources described above, estimates of URT volume in relationship to body weight were obtained for animals ranging in weight from 1.79 kg to 10 kg. The relationship between URT volume and the body weight of rhesus monkeys is highly linear over this body weight range (Figure 6A), with the linear fit explaining 98.2% of the variability in the data. While a quadratic polynomial gave a slightly better R² (i.e., 0.99), the concept of parsimony argues for using the linear fit since the quadratic fit requires estimating the value of an additional parameter while yielding essentially the same R².

Figure 6.

Relationship of body weight of rhesus monkeys to the volume of the upper respiratory tract (Panel A) and the surface area to volume ratio of the nasal region (Panel B). The URT volumes in Panel A and the nasal surface area to volume ratios in Panel B do not include the maxillary sinuses.

Surface area to volume ratio of the nasal passages

The surface area of the complex nasal airways affects the filtration efficiency of the nose to remove inhaled particles, which serves to protect insults to sensitive LRT tissues. The surface area to volume ratio of this region appears in equations that account for the effects of impaction and diffusion mechanisms, which are presented later in this paper. Here, we will consider the nasal passages as only those comprising the nasal cavity absent the paranasal sinuses.

Various models were fit to the data for the relationship between the nasal passages surface area to volume ratio and body weight using data for the animals in Tables 5, 7, and 8 plus the data for an adult monkey weighting 11.9 kg that had been used in a nasal deposition modeling analysis and the data for rhesus monkeys in the study by Yeh et al. (1997a). For animals less than 2 kg in body weight, the nasal passages surface area to volume ratio is highly variable, having an average value of 27.06 with a standard deviation of 6.63. For the adult animals, the nasal surface area to volume ratio is much smaller and is less variable (i.e., 9.67 ± 1.58). A quadratic model provided an R² of 77.2, but the predicted values steadily increase for animals with body weights greater than about 10 kg. Thus, an exponential decreasing model was judged to provided the best fit to the data in Figure 6B, explaining 76.4% of the variability and yielding the following equation:

$$\text{Nasal}\text{Passages}\text{SA}/\text{Volume}=6.23+30.306\ast exp(-0.2658\ast \text{Body}\text{Wt})$$ (1)

Rhesus breathing parameters

Deposition of inhaled materials in the lung depends on the ventilation rates of the animal. Laboratory measurements of ventilation rates include the tidal volume (V_T) and frequency of breathing (f), which together determine the respiratory minute volume (V̇_E). The subdivision of V̇_E into its two components is necessary for accurate deposition modeling because the inhaled particles have varying patterns of deposition depending upon the combination of V_T and f. Thus, values of V_T and f are needed to calculate material loss in the respiratory tract of rhesus monkeys. While a number of studies have reported group means for V_T, f, and V̇_E, only 3 studies have reported values of these variables on individual rhesus monkeys where the sex was specified (Karel & Weston, 1946; Brooks et al., 1957; Binns et al., 1972). One animal was judged to be an outlier in each of the studies reporting individual values for these variables, and none of the data for these animals was used in our analyses (Appendix B).

Breathing frequency

Values of breathing frequency and body weight for the male and female rhesus monkeys studied by Karel and Weston (1946), Brooks et al. (1957), and Binns et al. (1972) are shown in Figure 7A and 7B, respectively. For animals weighing up to 4.5 kg, the scatter plots clearly show that there is no relationship between breathing frequency and body weight for either sex. The overall average breathing frequency for the males and females in these 3 studies was 39.7 and 39.6 bpm, respectively, with the standard deviation of the 31 males being 6.8 and being 10.1 for the 36 females.

Figure 7.

Scatter plots of breathing frequency versus body weight for male (Panel A) and female (Panel B) rhesus monkeys. The horizontal lines correspond to the overall mean breathing frequency for each sex.

Given that a number of other rhesus monkey studies have reported group mean breathing frequency, we elected to use the averages of the Karel and Watson (1946), Brooks et al. (1957) and Binns et al. (1972) studies together with these other study means to determine an overall mean breathing frequency based upon a larger number of animals (Table 10). The study by Kelly et al. (1974) was not included in Table 10 because the minute volume for the female animals in that study was basically the same as the minute volume in the Guyton (1947) and Crosfill and Widdicombe (1961) studies that used animals about 2 kg less in size.

Table 10.

Body weight and physiologic variables for rhesus monkeys.

Study	Anesthesia	Sex	n	Body weight (kg)			Breathing Frequency (bpm)			Minute Volume (L/min)
				Range	Mean	Standard deviation	Range	Mean	Standard deviation
Karel & Weston (1946)	No	Male	19	1.99–3.55	2.58	0.42	20–49	38.8	6.9	1.133
	No	Female	19	2.19–3.54	2.65	0.34	27–48	36.8	6.5	0.937
Binns et al. (1972)	No	Male	7	2.4–4.3	3.48	0.59	33–51	38.3	5.8	1.481
	No	Female	8	2.8–3.9	3.33	0.38	29–57	39.8	9.7	1.820
Brooks et al. (1957)	Yes	Male	5	3.44–5.35	4.05	0.78	28–53	47.6	5.0	2.010
	Yes	Female	9	3.07–4.5	3.81	0.52	32–71	45.3	14.6	1.907
Crosfill & Widdicombe (1961)a	Yes	NSb	4	1.8–3.05	2.45	NS	27–47	33.0	NS	0.700
Guyton (1947)	No	NS	6	2.05–3.08	2.68	NS	31–52	40.0	NS	0.863
Lees et al. (1965)	Yes	NS	14	4.2–6.7	5.80	0.86	31–52	42.7	7.0	1.791
Liu and DeLauter (1977)	No	Male	4	3.6–4.5	NS	NS	NS	28.0	6	1.100e
Howell (1995)	No	Both	6c	7–14.8	NS	NS	NS	21.4	1.6	2.000
Howell et al. (1995)	No	Both	3d	7.2–14.2	NS	NS	NS	18.9	1.7	2.000
						Overall values		39.0	7.8
						Sample size		91

^aThe authors did not state the monkeys were rhesus but Liu and DeLauter (1977) included their data in a table for rhesus monkeys.

^bNS: not reported by the author(s).

^cFive males and one female.

^dTwo males and one female.

^eValue is mean after 1 hr; the 6 hr mean was 1.082.

Since the sample size of the groups studied varied between 3 and 21 animals, we calculated a weighted mean and pooled standard deviation to use for male and female rhesus monkeys. Using the studies in Table 10 that reported a mean and a standard deviation for breathing frequency, the weighted mean of male and female rhesus monkeys was calculated to be 39 bpm with a standard deviation of 7.8 based upon a sample size of 91. If the 2 studies that did not report a standard deviation are also included in the weighted mean calculation, the weighted mean has a value of 38.8 bpm.

Assuming the overall average breathing frequency is the same for male and female rhesus monkeys is consistent with the absence of gender differences in this variable for a number of animal species. For example, Alexander et al. (2008) reported for cynomolgus monkeys a bpm value of 72 for males and 69 for females. These same investigators found a value of 259 bpm for both male and female CD1 mice, and the weighted mean for Beagle dogs using their Table 2 data gave mean breathing frequencies of 30 and 29 for males and females, respectively. Similarly, Costa and Tepper (1988) show no gender difference in breathing rates for rats.

Minute volume

Ideally, one would like to have measurements of tidal volume to calculate minute volume as the product of the breathing frequency times the tidal volume. In addition, tidal volume and breathing frequency are required input variables in most dosimetry models to calculate particle deposition. If tidal volume is not known but the body weight is known, an estimate of tidal volume can be derived using the analyses presented below.

For the 3 studies discussed above where individual data were collected, only 4 male and 4 female rhesus monkeys had body weights above 4 kg. In addition to the study means for the 3 studies where individual values were reported, Table 10 provides the average minute volume data for 6 additional studies. The body weight range in several of these other studies included at least 26 animals that weighed greater than 4 kg, with 9 of these animals having body weights between 7 and 14.8 kg. The data of Kelly et al. (1974) on 21 female rhesus monkeys were not used because the minute volume for animals weighing about 2 kg less in other studies was the same as that reported by Kelly and colleagues. Also, while Liu and Delauter (1977) studied both conscious and anesthetized rhesus monkeys, the conscious animals were all males and had a tighter body weight range than those that were anesthetized over the 6-hour study period. Thus, we elected to report in Table 10 the mean minute volume data for the conscious male monkeys during the first hour of the 6-hr exposure period.

Since we want to develop relationships for breathing parameters over a large range of body weights, we elected to examine the relationship between minute volume and body weight via two approaches. First, we fit the data from the 3 studies that reported individual minute volume values and body weights for monkeys that were mostly < 4 kg in body weight. Second, we used the study minute volume means in Table 10 together with the body weight means if the authors reported them or we used the midpoint of the body weight range if the average body weight was not reported. The separate analyses were necessary since the individual measurements and means should not be used simultaneously to fit a regression model. Various regression models were fit to the individual data as well as to the group mean data.

Among the 3 studies where individual measurements were reported, there is significant variability in the value of minute volume for body weights in the range of 2.5 to 3.5 kg. A linear regression explained 72% of the variability in the data, while a logarithmic model explained 73.7% of the variability (Figure 8A). Other models (e.g. quadratic, exponential rising) also explained about 73% of the variability but typically required the use of more parameters. Thus, the logarithmic model was judged the best model and is given by:

$$\text{Minute}\text{volume}=-0.44051+3.8434\ast \text{Log}(\text{body}\text{weight})$$ (2)

where minute volume is in L/min and body weight is in kg

Figure 8.

Relationship between minute volume and body weight in rhesus monkeys. Panel A shows a logarithmic model fit to the male rhesus data for studies where individual measurements were reported. Panel B provides a 3-parameter asymptotic exponential model fit to the means for all the studies in Table 10. Panel C provides a comparison of the predicted model fits for the two models for animals between 1.7 and 5 kg in body weight.

For the models fit to the minute volume study means in Table 10, a 3-parameter exponential rising model with body weight gave the best fit, explaining 73% of the variability in the study means. Various other models were also fit (i.e., quadratic, exponential, logarithmic, power law), but these models only explained anywhere from 37 to 63% of the variability in the data. The exponential rising model is of the form [m₁ – (m₁ – m₂) * exp (-m₃ * Body Weight)]. The fitted curve parameters are given by Equation (3).

$$\begin{array}{l}\text{Minute}\text{volume}=1.9108-(1.9108\text{to}-22.827)\ast exp(-1.2479\ast \text{body}\text{weight})\\ =1.9108-24.7378\ast exp(-1.2479\ast \text{body}\text{weight})\end{array}$$ (3)

where minute volume is in L/min and body weight in kg. The model fit to the study means in shown in Figure 8B.

A comparison of the logarithmic fit from Eq. (2) and the 3-parameter exponential rising model from Eq. (3) is shown in Figure 8C. For body weights within the range of 3 to 4 kg, the two models provide very similar estimates of the minute volume. For body weights outside of this range, the models start to differ in their estimates of minute volume. Given that the logarithmic curve is a fit of individual animal values and had most of the animals with body weights < 4 kg and no animals above 5.35 kg, we recommend that Eq. (2) be used to estimate minute volume when the body weight of the rhesus monkeys is < 4 kg and that Eq. (3) be used for animals with body weights ≥ 4 kg.

Tidal volume

In most instances where dosimetry calculations are of interest, tidal volume is seldom measured. Since minute volume is the product of the breathing frequency and the tidal volume, one can determine an estimate of tidal volume (V_T) in mL by solving for the minute volume using Eq. (2) or Eq. (3), depending upon the body weight of interest, multiplying the result by 1000 to convert to mL, and then dividing that value by the overall breathing frequency of 39 bpm. For example, for a 3 kg rhesus monkey, Eq. (2) gives a value of 1.393 L/min. So an estimate of tidal volume is 35.7 mL (i.e., 1.393 * 1000/39). Likewise, for a 7 kg rhesus monkey, Eq. (3) yields a value of 1.907 L/min. Thus, an estimate of tidal volume for this animal would be 48.9 mL [i.e., (1.9108−(1.9108+22.827)* exp(−1.2479*7)*1000/39) = 1.907*1000/39].

For animals < 4 to 5.5 kg in body weight, an alternative way to estimate V_T is discussed in Appendix B. This alternative method is based upon regression analyses of the tidal volume data reported for individual animals in the studies of Karel and Weston (1946), Binns et al. (1972), and Brooks et al. (1957). In addition, if one has experimentally measured V_T, the regression models in Appendix B allow one to determine how far above or below the predicted mean V_T for a given body weight their animals are. While the focus of the main body of this paper is on male rhesus monkeys, Appendix B also provides analyses of the relationship between tidal volume and body weight for female rhesus monkeys as well as equations for minute volume and body weight.

TLC and FRC volumes

The critical lung volumes for the structure of the lung geometry used in the deposition model are the lung volumes at TLC and FRC for an animal of a given body weight. The deposition calculations are initiated using the tidal volume to expand the lungs from the lung volume at the end of a breath, which is termed FRC, and calculate the impact of each mechanism of particle deposition (e.g. impaction, sedimentation, and diffusion) in each lung generation. Thus, the lung geometry structure that was derived from CT and morphometric data obtained at or near TLC must be scaled to the dimensions and volumes associated with FRC. For an animal having a body weight different from that of the animal used to develop the initial lung geometry structure, then the ratio of FRC to TLC for the animal of interest is used to obtain the necessary dimensions and volumes at their FRC.

From the California National Primate Research Center database, we had available pulmonary function data for 107 male and 14 female rhesus monkeys ranging in body weight from 0.76 to 14.26 kg that had served as control animals in various studies conducted at UC Davis. Lung volumes were measured in sedated and anesthetized monkeys that were intubated and placed in a whole body plethysmograph with the cuffed endotracheal tube attached to an automated valve assembly (Buxco Research Systems). Vital capacity, inspiratory capacity, and expiratory reserve volume were measured after inflating the lungs to an airway pressure of 30 cm H₂O and then slowly deflating them to an airway pressure of −20 cm H₂O (Likens & Mauderly, 1982). FRC was measured using airway occlusion and Boyle’s law (Dubois et al., 1956). TLC and residual volume were calculated using inspiratory capacity, expiratory reserve volume and FRC.

Various models were fit to the data on TLC and FRC to examine the relationship between these variables and body weight. The quadratic fit for the male rhesus monkeys is given in Figure 9A. While a scatter plot of the TLC data for the 14 female monkeys showed no relationship with body weight, the body weights of the female monkeys were in a very narrow range compared to that for the male monkeys. This is illustrated in Figure 9B, which contains the quadratic curve obtained combining the data for both sexes. The quadratic fit to only the data for the males explains 90.4% of the variability in the data (Table 11, part A), while the curve for both sexes explains 87.2% of the variability (Table 11, part B). If there were data for females over as broad a range of body weights as there is for males, female rhesus monkeys might well exhibit an altered pattern of TLC with changes in body weight; however, there currently are insufficient data for females to examine this possibility.

Figure 9.

The relationship between Total Lung Capacity (TLC) and body weight in rhesus monkeys. Panel A shows a quadratic fit for the data for male monkeys, while Panel B provides a quadratic fit for the combined data of both sexes.

Table 11.

A comparison among various models for the relationship between TLC and body weight in rhesus monkeys.

A. Males		Coefficients				R2
Model type	Model form	M0	M1	M2	M3
Linear	Y = M0 + M1*X	20.685	61.279			0.849
Quadratic	Y = M0 + M1*X + M2*X2	−51.304	104.02	−3.6788		0.904
Cubic	Y = M0 + M1*X + M2*X2 + M3X3	−55.726	108.16	−4.5431	0.044156	0.905
Power law	Y = M0*XM1	59.672	1.094			0.831
Logarithmic	Y = M0 + M1*Log(X)	16.921	516.27			0.857
Exponential	Y = M1 * exp(-M2*X))		67.841	0.2628		0.454
Exponential rising	Y = M1 - (M1 - M2)*exp(-M3*X)		859.92	−66.379	0.12947	0.904
B. Both sexes		Coefficients				R2
Model type	Model form	M0	M1	M2	M3
Linear	Y = M0 + M1*X	25.318	60.24			0.824
Quadratic	Y = M0 + M1*X + M2*X2	−42.086	99.336	−3.5443		0.872
Cubic	Y = M0 + M1*X + M2*X2 + M3X3	−80.836	134.44	−10.554	0.35295	0.877
Power Law	Y = M0*XM1	60.457	1.0707			0.812
Logarithmic	Y = M0 + M1*Log(X)	19.245	508.6			0.846
Exponential	Y = M1 * exp(-M2*X)	68.772	0.26298			0.425
Exponential rising	Y = M1 - (M1 - M2)*exp(-M3*X)		779.51	−66.778	0.14483	0.875

Several other models were also fit to the TLC data, with some models explaining a slightly greater percentage of the variability (Table 11). However, the concept of parsimony argues for selecting the model that requires the least number of fitted parameters, all other things being equal. Since the cubic and exponential rising models give large deviations from the leveling off trend of the experimental data, the quadratic curve was deemed the best overall mathematical fit to the experimental data in combination with desired behavior at the upper end of the body weight range. Thus, Equation (4) can be used to estimate the value of TLC for a male rhesus monkey of a specified body weight:

$$\text{TLC}=-51.304+104.02\ast \text{body}\text{weight}-3.6788\ast \text{body}{\text{weight}}^2$$ (4)

where TLC is in mL and body weight is in kg. Since Eq. (4) typically gives a TLC value no more than 4% greater than the value obtained using a quadratic model for fitting the combined sexes data (Figure 9B) for animals weighing up to 11.4 kg, it is probably reasonable to use Eq. (4) to estimate TLC even when female rhesus monkeys are used, at least until there are sufficient data available to fit accurately a separate curve for female monkeys.

The same types of models were fit for FRC as were fit for TLC. For the male rhesus monkey data, the cubic model gave a slightly higher R² than the quadratic curve, and the R² for the exponential rising model was very close to the value for the quadratic model (Table 12, Part A). The same findings held for comparisons among models fit to the combined sex data for FRC (Table 12, Part B). However, for both data sets, the quadratic curve followed a gently increasing trend up to a body weight of about 16 kg, while the cubic and exponential rising models quickly departed from a plateau at the higher body weight values. Thus, overall, the quadratic model was judged to be the most useful for estimating the value of FRC over a range of body weights from 0.76 to 16 kg. Equation (5) gives the quadratic regression for FRC as a function of body weight and explains 91.4% of the variability in the data.

Table 12.

A comparison among various models for the relationship between FRC and body weight in rhesus monkeys.

A. Males		Coefficients				R2
Model type	Model form	M0	M1	M2	M3
Linear	Y = M0 + M1*X	9.3409	42.971			0.872
Quadratic	Y = M0 + M1*X + M2*X2	−52.593	68.651	−2.2103		0.914
Cubic	Y = M0 + M1*X + M2*X2 + M3X3	−46.454	62.906	−1.0105	−0.061294	0.914
Power law	Y = M0*XM1	24.903	1.3243			0.811
Logarithmic	Y = M0 + M1*Log(X)	−9.2574	354.63			0.844
Exponential	Y = M1 * exp(-M2*X))		28.992	0.31921		0.417
Exponential rising	Y = M1 - (M1 - M2)*exp(-M3*X)		651.93	−58.517	0.10603	0.912
B. Both sexes		Coefficients				R2
Model type	Model form	M0	M1	M2	M3
Linear	Y = M0 + M1*X	−6.8435	42.757			0.843
Quadratic	Y = M0 + M1*X + M2*X2	−49.212	67.331	−2.2279		0.882
Cubic	Y = M0 + M1*X + M2*X2 + M3X3	−63.411	80.193	−4.7962		0.883
Power law	Y = M0*XM1	25.184	1.3072			0.790
Logarithmic	Y = M0 + M1*Log(X)	−8.6051	354.89			0.837
Exponential	Y = M1 * exp(-M2*X))		29.344	0.32239		0.365
Exponential rising	Y = M1 - (M1 - M2)*exp(-M3*X)		−94424	−6.6142	−4.509E-04	0.843

$$\text{FRC}=-52.593+68.651\ast \text{body}\text{weight}-2.2103\ast \text{body}{\text{weight}}^2$$ (5)

The quadratic fits for the male only and combined sex models for the relationship between FRC and body weight are provided in Figure 10A and 10B, respectively. As with TLC, there are insufficient data to fit a FRC model separately for females. Also, given that Eq. (5) predicts FRC values that are only about 2% greater than the equation for both sexes when body weights are ≤ 6.7 kg and never more than 4.2% greater when body weights are between 6.7 and 15 kg, Eq. (5) can be used even when female rhesus monkey values are of interest. The current analyses of TLC and FRC in relationship to body weight based upon 107 male and 14 female rhesus monkeys provide equations that have a broader and statistically more robust application than the equations developed by Kosch et al. (1979) based upon 12 monkeys.

Figure 10.

The relationship between functional residual capacity (FRC) and body weight in rhesus monkeys. Panel A shows a quadratic fit for the data for male monkeys, while Panel B provides a quadratic fit for the combined data of both sexes.

Airway scaling guidance using TLC and FRC data

While airway measurements are often made at TLC, lung airway dimensions and volumes are needed at FRC since the FRC volume is the starting point for calculating deposition of inhaled particles or absorption of inhaled gases and is a required input variable for dosimetry models such as the MPPD model. Therefore, estimates of FRC and TLC as well as their ratio are required to construct the pulmonary geometry. The ratio of FRC to TLC against body weight provides guidance on how much the TLC measurements and volumes must be scaled to relate accurately to the corresponding FRC values.

Using the pulmonary function database for control animals at the UC Davis National Primate Research Center, various regression models were fit to examine the relationship between FRC/TLC and body weight. The body weight range for the 14 females of 5.21 to 8.3 kg was not wide enough to estimate any relationship between body weight and FRC/TLC. Thus, the regression models were fit for male rhesus monkeys (Table 13, Part A) as well as for the combined data of both sexes (Table 13, Part B). While for each case the quadratic curve explained about 0.5% more of the variability in the data compared to an exponential rising model, the quadratic curve estimates decrease for body weights greater than about 10 kg. Since one would expect TLC to plateau at the upper end of the body weight range for any given species, an exponential rising model is more in line with the expected trend in FRC/TLC.

Table 13.

A comparison among various regression models for the relationship between FRC/TLC and body weight in rhesus monkeys.

A. Males		Coefficients				R2
Model type	Model form	M0	M1	M2	M3
Linear	Y = M0 + M1*X	0.43193	0.029522			0.374
Quadratic	Y = M0 + M1*X + M2*X2	0.35941	0.072578	−3.7059E-03		0.482
Cubic	Y = M0 + M1*X + M2*X2 + M3X3	0.34002	0.090722	−7.4957E-03	1.9361E-04	0.484
Power law	Y = M0*XM1	0.41738	0.2302			0.455
Logarithmic	Y = M0 + M1*Log(X)	0.42087	0.27386			0.458
Exponential	Y = M1 * exp(-M2*X))		0.42738	0.056391		0.321
Exponential Rising	Y = M1 - (M1 - M2)*exp(-M3*X)		0.71801	0.32678	0.28282	0.477
B. Both sexes		Coefficients				R2
Model type	Model form	M0	M1	M2	M3
Linear	Y = M0 + M1*X	0.43076	0.031293			0.439
Quadratic	Y = M0 + M1*X + M2*X2	0.36068	0.071936	−3.6846E-03		0.542
Cubic	Y = M0 + M1*X + M2*X2 + M3X3	0.33919	0.091404	−7.5722E-03		0.545
Power law	Y = M0*XM1	0.41661	0.2365			0.517
Logarithmic	Y = M0 + M1*Log(X)	0.41949	0.28362			0.520
Exponential	Y = M1 * exp(-M2*X))		0.42672	0.059401		0.379
Exponential rising	Y = M1 - (M1 - M2)*exp(-M3*X)		0.72359	0.32487	0.28113	0.538

Predicted FRC/TLC values for the males only and the combined sexes exponential rising models differ at most in the 3^rd digit after the decimal point. Given this and the fact that the combined data set provides an R² of 0.538 compared to an R² of 0.477 for the males, the recommended equation for examining the relationship between FRC/TLC and body weight is given by Equation (6) obtained from measurements on both sexes.

$$\text{FRC}/\text{TLC}=0.72359-0.39872\ast exp\left(-0.28113\ast \text{body}\text{weight}\right)$$ (6)

where body weight is in kg. Figure 11 corresponds to a plot of the data that generated Eq. (6).

Figure 11.

FRC/TLC as a function of body weight in rhesus monkeys.

Mode of breathing and particle deposition

With lung deposition models such as MPPD one can investigate the influence of many factors on the dosimetry of inhaled particles in rats and humans, and now with the development of a lung geometry for rhesus monkeys, regional LRT deposition can also be examined in this species. Recall that with deterministic models one studies the fate of inhaled materials based on the laws of physics that govern the transport of inhaled materials and on particle physicochemical properties influencing their fate once deposited. Two modes of breathing were examined: endotracheal and spontaneous nasal breathing.

Endotracheal breathing

With endotracheal breathing, a tube is placed either through the nose or the oral cavity and inserted down to the beginning of the trachea. For the purpose of deposition studies, the endotracheal tube defeats the filtering effect of the nose or mouth in removing particles before they can enter the LRT via the trachea. This enables interspecies comparisons of deposition fractions that are a function only of LRT structure.

Spontaneous nasal breathing

Breathing through the nose spontaneously is the most common mode of breathing in rodents, nonhuman primates, and most resting humans. While rodents are obligatory nose breathers, humans and nonhuman primates can engage in oral and oronasal breathing as well. Oronasal breathing typically occurs when the ventilatory demand due to work or exercise becomes large. The oronasal switching point in adult humans occurs when minute ventilation is at about 35 L/min (Niinimaa et al., 1981). Currently, data on the oronasal switching point in rhesus monkeys is not known. Thus, here we will examine deposition in rhesus monkeys breathing spontaneously through the nose. In order to use MPPD for examining LRT deposition with this scenario, we need to determine the extent of nasal deposition of inhaled particles.

Particle filtration efficiency of the rhesus monkey nose

Particle losses in the nasal airway passages of rhesus monkeys occur by inertial impaction for micrometer and larger particles and by Brownian diffusion for submicron particles. The travel time in these airways is insufficient to allow losses due to the gravitational settling of particles. Measurements for losses of particles in the rhesus monkey nasal passages by the above loss mechanisms are typically reported at a specific age. To extend the results to different ages, we take notice of the fact that except for the first 3 months after birth, nasal passages of rhesus monkeys grow in size while the structure and shape remain intact. Thus, the same semi-empirical formulas derived for the measured age of rhesus monkeys can be used to calculate deposition efficiency at different ages if the coefficients of the fit are adjusted by a correction factor.

In Vivo measurements on particle losses in the nasal passages of rhesus monkeys are scarce. Yeh et al. (1997b) measured deposition of 0.005, 0.014, and 0.1 μm thoron progeny and ⁵⁹Fe₂O₃ particles in head and lung airways on a total of 8 anesthetized rhesus monkeys ages between 5 and 8 years (n = 2 for 0.005 μm, n = 2 for 0.014 μm, and n = 4 for 0.1 μm). Exposure duration was kept brief (5 to 8 minutes) to minimize particle clearance, and the mouths of the monkeys were taped to ensure that they breathed only through the nose. Yeh et al. (1993) measured deposition of 0.005 to 0.2 μm particles in a clear replica cast of an 8.5 kg monkey under various inspiratory and expiratory flow rates. Losses of particles by diffusion in nasal passages are related to the flow rate (Q) and particle diffusion coefficient (D). Thus, Yeh et al. (1993) fit to the experimental measurements a semi-empirical model for deposition efficiency as a function of these two variables. The semi-empirical model can be extended to other ages when corrected by the nasal passages volume and surface area ratios according to the equation below:

$${\mathrm{\eta }}_{\mathrm{d}}=1-{\mathrm{e}}^{-\mathrm{k}\times {\left(\frac{\mathrm{S}/\mathrm{V}}{{\mathrm{S}}_0/{\mathrm{V}}_0}\right)}^{-0.219}\times {\mathrm{D}}^{0.543}\times {\mathrm{Q}}^{-0.219}}$$ (7)

where η_d is the deposition efficiency by Brownian diffusion defined as the fraction of the inhaled particles through the nasal airway that are deposited, parameter K values are −13.3 and −14.6 during inhalation and exhalation respectively, V₀ and S₀ are the nasal passages volume and surface area at the age where deposition measurements were made (i.e., data for the 8.5 kg monkey from Yeh et al., 1993), and V and S are the nasal passages and volume and surface area at the age for which deposition efficiency by diffusion is to be calculated.

Inertial losses of particles depend primarily on particle Stokes number and secondarily on the flow Reynolds number. The Stokes number is equivalent to ρd²Q in the nasal passages of a given monkey for which ρ is the mass density of the particle and Q is the inhalation flow rate. Kelly et al. (2005) measured particle losses in the rhesus monkey nasal replica at four different inhalation flow rates with values of an impaction parameter (ρd²Q) between 100 and 5000 μm² cm³/s. They used particle sizes from 1 to 10 μm in diameter. Kelly et al. (2005) found excellent agreement between the deposition efficiency in two human nasal molds and their rhesus monkey nasal mold for inspiratory flow rates corresponding to resting breathing in both species.

Using the data in Kelly et al. (2005), a semi-empirical function for particle losses was developed. The model can be extended to different ages by correcting for the volume and surface area ratios:

$${\mathrm{\eta }}_{\mathrm{i}}=1-{\mathrm{e}}^{-{\left(3.227\times {10}^{-4}\frac{\mathrm{S}/\mathrm{V}}{{\mathrm{S}}_0/{\mathrm{V}}_0}\mathrm{\rho }{\mathrm{d}}^2\mathrm{Q}\right)}^{2.162}}$$ (8)

where η_i is the deposition efficiency by inertial impaction in the nasal passages. Here, V₀ and S₀ correspond to the data for the 12 kg monkey used by Kelley et al. (2005).

Since losses by impaction and diffusion occur for different ranges of particle sizes, it can be assumed that net loss of particles in the nasal passages is the sum of deposition efficiency by each mechanism. Thus,

$${\mathrm{\eta }}_{\text{net}}={\mathrm{\eta }}_{\mathrm{d}}+{\mathrm{\eta }}_{\mathrm{i}}$$ (9)

Eqs. (7) to (9) were implemented in MPPD to find losses of particles in rhesus monkey nasal airway passages.

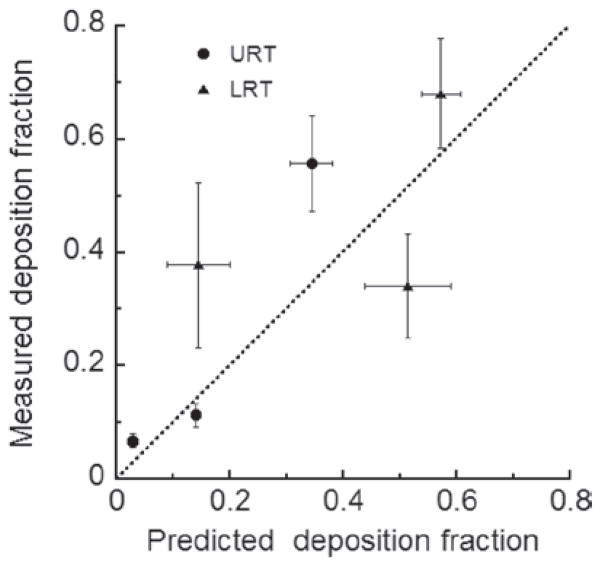
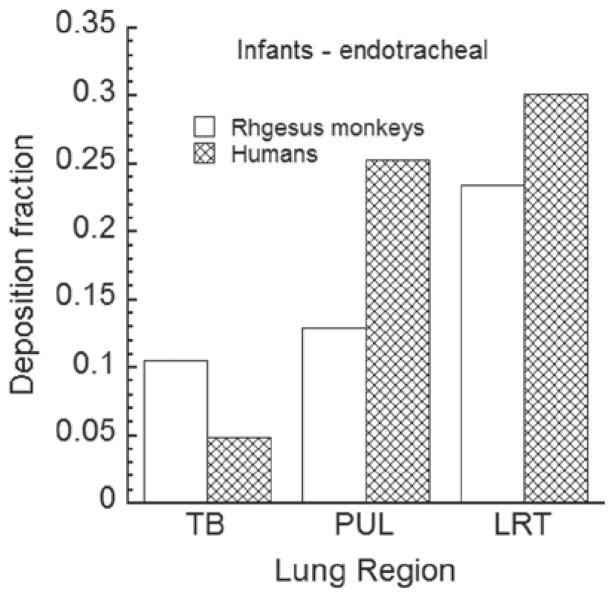
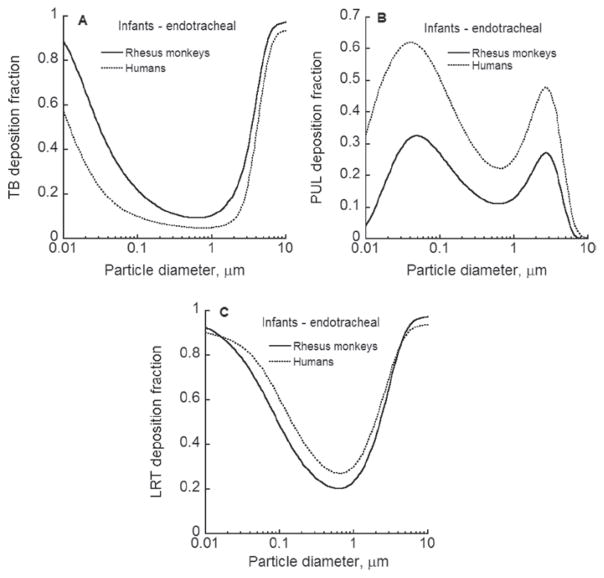
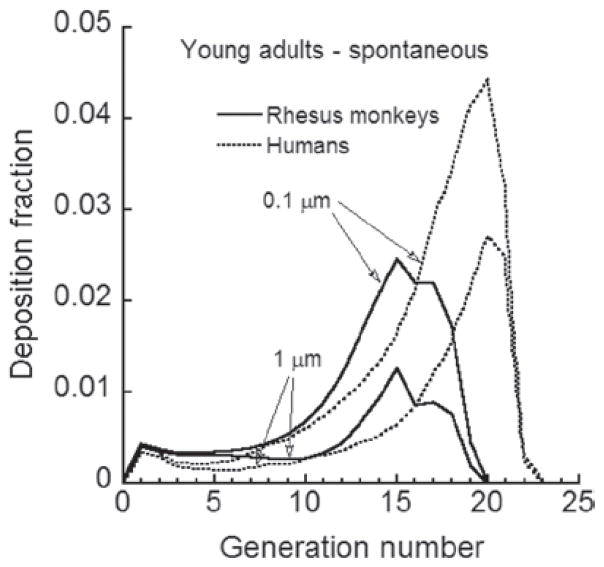
Model predicted lung deposition vs experimental data

There are limited published data involving the deposition of inhaled particles in the lungs of monkeys with which to compare predicted deposition using the model that has been developed here. Palm et al. (1956) studied total and alveolar deposition of 0.3 to 5 μm particles in rhesus and cynomolgus monkeys, but did not separate the results for the two. Since we showed earlier (Table 3) that one should probably not substitute cynomolgus lung volume data for rhesus data, the Palm et al. (1956) study was not used to evaluate lung deposition predictions of the rhesus deposition model.

There are no published data on lung deposition fractions in rhesus monkeys for particles ≥2 μm in aerodynamic diameter. However, Yeh et al. (1997b) measured both nasal and lung deposition in the ultrafine particle experiments they conducted. A comparison of their experimental deposition fraction measurements with the deposition fractions obtained using the lung geometry model developed here are shown in Figure 12. If there were perfect agreement between the predicted and measured deposition fractions, the values would fall on the line of identity. The mean experimental values on the Y-axis are plotted with the vertical bars representing ± one standard deviation. The predicted deposition fractions on the X-axis are mean values obtained using the average body weight of the animals in the Yeh et al. (1997b) study. The horizontal bars represent results obtained using body weights ± two standard deviations from the mean body weight. Given the large variability in measured deposition fractions and the small sample sizes used by Yeh et al. (1997b), there is reasonable agreement between the predicted and experimentally measured deposition fractions.

Figure 12.

Comparison of model predicted deposition fractions in rhesus monkeys with experimental measurements. Horizontal bars represent results for ± 2 standard deviations of body weight. Vertical bars represent ± one standard deviation of experimentally measured deposition fractions.

Figure 12 also provides some insights as to the level of uncertainty in the predicted deposition fractions. When 2 standard deviations above and below the mean body weight are used, this results in a new computation of the values for TLC, FRC, FRC/TLC, minute volume, and V_T using Eqs. (3–6) and the average breathing frequency of 39 breaths per minute. In addition, this results in the need to isotropically scale the lung geometry airway dimensions to the size appropriate for the newly specified body weight. The mean values plotted in Figure 12 can be considered as population means with the lines above and below the means reflecting the impact of the variability of different physiologic variable values on the deposition fraction since animals of the same body weight can vary in the values of their physiologic variables. The uncertainty about the URT deposition fractions is much less than it is for the pulmonary region deposition fractions. Based on the limited experimental deposition data available for rhesus monkeys, one standard deviation around the mean deposition fraction can give predicted deposition fractions that are larger or smaller than the mean value by about 0.1–0.15 (Figure 12).

Results and discussion

To study particle deposition characteristics in the lungs of rhesus monkeys, the hypothetical case of breathing via the trachea was first examined by bypassing the URT region. In addition, since monkey and human lung deposition predictions have often been used interchangeably due to the resemblance of lung geometries between these species, MPPD model predictions for humans (Asgharian et al., 2001) with endotracheal breathing are also provided for comparison. Next, deposition fractions and patterns with spontaneous nasal breathing were examined as spontaneous breathing is the most common route of breathing, and this route incorporates the filtration efficiency of the URT in lessening the insult of inhaled material to the sensitive tissues of the LRT. For all deposition calculations we assumed the particles were spherical with a density of 1 g/cm³. Hence, all particle diameters are aerodynamic particle diameters.

Deposition in infants via endotracheal breathing

Figure 13 gives predicted deposition fractions of 1 μm particles in different regions of the lungs of a 6-month-old rhesus monkey with an FRC of 63 mL, tidal volume of 13.6 mL, and breathing frequency of 39 breaths per minute. For humans, a 21-month old child having an FRC of 38.4 mL, tidal volume of 81.2 mL, and breathing frequency of 28 breaths per minute was used. Losses of 1 μm particles are predominantly by gravitational settling in the pulmonary (PUL) region (i.e., alveolar region). The pulmonary deposition fraction is about the same as the TB region deposition fraction for infant monkeys compared to about a 5-fold increase for human infants. Figure 13 shows that there is a lower overall particle deposition fraction in the lungs of an infant rhesus monkey compared to that of an infant human, which is primarily due to the pulmonary deposition fraction being about 2.5 times larger in human infants than in rhesus infants.

Figure 13.

Predicted regional deposition of 1 μm particles in the lungs of infant rhesus monkeys and humans with endotracheal breathing.

Particle deposition in the lung depends on lung geometry dimensions, branching and gravity angles, airway and carinal shape, and branching patterns as well as on physiologic parameters. A comparison of generation-by-generation predicted deposition fraction betweens monkeys and humans reveals information regarding interspecies similarities and differences. Hence, deposition fractions for 0.1 μm and 1 μm particles were calculated for different generations of the infant human and rhesus monkey lungs using the values for lung and breathing parameters stated above. While Figure 14 shows that the general trend of particle deposition versus generation number is similar overall for the two geometries for both 0.1 μm and 1 μm particles, there are differences that can be attributed to species differences in airway dimensions. The predicted deposition fraction in the infant human lung for both particle sizes shows a steady enhanced deposition in the TB region, reaching a peak deposition fraction in about the 21st or 22nd generation in the alveolar region and then rapidly declining in value. The maximum deposition fraction is much larger for the ultrafine particle (i.e. 0.1 μm) compared to the 1 μm particle (0.1 vs. 0.06).

Figure 14.

Predicted deposition fractions for 0.1 and 1 μm particles versus lung generation in infant rhesus monkeys and humans with endotracheal breathing.

The deposition fraction versus generation trend indicates increasing losses due to sedimentation as particle size increases. In the infant monkey, the particle deposition fractions increase steadily in the TB region and reach a peak in the pulmonary region in about the 18th or 19th generation before plummeting to zero. These particle deposition results show that the smaller size of the monkey lung directly influences the mechanisms and distribution of particle losses. Hence, the differences between infant humans and monkeys in lung geometry warrant separate predictive deposition models for these species. The monkey lung cannot be treated by simply scaling down the geometry of a human lung, as was done by Martonen et al. (2001).

Comparisons of particle deposition in Figure 14 were made for only a couple of particle sizes. To generalize, deposition fractions of particles between 0.01 μm and 10 μm were calculated in the lungs of infant humans and monkeys at the same breathing and lung conditions noted above. Figure 15 presents predicted deposition fractions in the TB and PUL regions, as well as for the LRT with endotracheal breathing. Particle deposition fractions in the infant monkey TB region are higher than those in infant humans (Figure 15A) and are substantially lower than infant humans in the PUL region for particles <3 μm in diameter (Figure 15B). For both species, the peaks for PUL deposition occur at about the same particle sizes (i.e., about 0.04–0.05 μm and at about 2.7 μm). The similarity in deposition fraction trends for the LRT region (Figure 15C) demonstrates that the deposition model findings seen in Figure 14 can be extended to a wide range of particle sizes, but with the deposition fractions having region specific differences in value.

Figure 15.

Lower respiratory tract deposition fractions of particles in the lungs of infant rhesus monkeys and humans as a function of particle size for endotracheal breathing. Panel A compares tracheobronchial deposition, while Panel B compares alveolar deposition. The lower respiratory tract deposition pattern for the two species is shown in Panel C.

However, there is a notable difference between human and monkey results that has implications for data extrapolation between these species. TB deposition in monkey lungs approaches 100% for particles larger than 6 μm. Consequently, pulmonary deposition of particles larger than 6 μm is negligible. Given that particles > 6 μm are not completely removed by humans from the inhaled air, finding comparable exposure atmospheres for pulmonary deposition mass of particles for infant humans and monkeys for endotracheal breathing becomes more difficult if the exposure atmosphere contains many particles greater than 5 to 6 μm.

Deposition in young adults via endotracheal breathing

Analogous to what was done in the previous section, this section examines the deposition model predictions in young adult monkeys and humans. Figure 16 gives predicted deposition fractions of 1 μm particles in different regions of the lungs of a young adult rhesus monkey weighing 6.5 kg with an FRC of 300 mL, tidal volume of 48.8 mL, and breathing frequency of 39 breaths per minute. For humans, a young adult having a FRC of 3300 mL, tidal volume of 625 mL, and breathing frequency of 15 breaths per minute was used.

Figure 16.

Predicted regional deposition of 1 μm particles in the lungs of young adult rhesus monkeys and humans with endotracheal breathing.

In contrast to infants, the TB and pulmonary deposition fraction for 1 μm particles are not similar in value in young adult monkeys. The TB deposition fraction in young adult monkeys is substantially greater than the PUL deposition fraction. Moreover, there is slightly less of a difference in LRT deposition between young adult monkeys and humans (Figure 16 compared to Figure 13). Generation specific deposition fractions for the LRT for young adult monkeys and humans are given in Figure 17 for 0.1 μm and 1 μm particles. As with infants, the pattern of deposition fractions is similar between the two species, but the values of the deposition fractions are lower than in infants, particularly distal to generation 15 (Figure 17 compared to Figure 14).

Figure 17.

Predicted deposition fraction of 0.1 μm and 1 μm particles versus lung generation in young adult rhesus monkeys and humans with endotracheal breathing.

The results of extending the deposition calculations to a broad range of particle sizes are shown in Figure 18 where the particle size was varied from 0.01 to 10 μm. The overall shape of the TB, PUL, and LRT deposition fraction curves for the young adult monkey and human were quite similar to the shapes of these curves for an infant. However, there was a shift downward in TB deposition fraction values (Figure 18A) for particles <2 μm in size in young adults compared to infants and a downward shift as well of the pulmonary deposition fraction values (Figure 18B). The net result was a downward shift in the magnitude of the deposition fraction values for the LRT for particles less than about 2 μm such that the overall LRT deposition fractions are quite similar in value for the two species for particles <2 μm in diameter (Figure 18C). Pulmonary deposition in the young adult rhesus monkey is minimal for particles >5 μm, similar to what was seen for infant monkeys. Thus, the same issues about interspecies comparisons that were made above for infant monkeys also apply to young adults. Since the above comparisons were for endotracheal breathing, deposition fractions arising from nasal breathing will have different values than those appearing in Figures 15 and 18, but the overall shapes of the curves will remain the same.

Figure 18.

Lower respiratory tract deposition fractions of particles in the lungs of young adult rhesus monkeys and humans as a function of particle size for endotracheal breathing. Panel A compares tracheobronchial deposition, while Panel B compares alveolar deposition. The lower respiratory tract deposition pattern for the two species is shown in Panel C.

Deposition with spontaneous nasal breathing in young adults

By examining spontaneous nasal breathing, the filtration efficiency of the URT comes into play such that differences in the deposition patterns between species may be more pronounced for certain particle sizes. Since there currently are no published experimental data to be able to estimate the probability of particles of a given size being able to be inhaled in rhesus monkeys, we elected to restrict deposition calculations to particles no greater than 5 μm in diameter as particles less than this size are most likely nearly 100% inhalable in rhesus monkeys, and they are basically 100% inhalable by humans.

In addition, given that there are only limited data on nasal deposition in rhesus monkeys and that these data were obtained in an adult, we will not estimate particle deposition in infant monkeys at this time. The need for more experimental data on URT deposition of particles in rhesus monkeys of different ages is discussed more in the Future Research section below.

On a regional basis, the TB deposition fraction of 1 μm particles in the young adult rhesus monkey is about 30% greater than it is in the young adult human TB region, with a deposition fraction of 0.068 compared to 0.052 in humans (Figure 19). However, for the pulmonary region, the deposition fraction in young adult humans is four times that of young adult monkeys (0.1 vs. 0.025). The net result is that total LRT deposition fraction is about 45% greater in young adult humans than it is in young adult rhesus monkeys.

Figure 19.

Predicted regional deposition of 1 μm particles in the lungs of young adult rhesus monkeys and humans with spontaneous nasal breathing.

Deposition fractions per LRT generation for young adult monkeys and humans are shown in Figure 20 for 0.1 μm and 1 μm particles. Since diffusion is the dominant mechanism for deposition of 0.1 μm particles, TB deposition (i.e., generations 0 to 15) is minimal, with the pulmonary region deposition fraction being at least 4-fold higher in both species. Overall, the LRT deposition fraction pattern is quite similar between the two species for 0.1 μm particles, but peaks earlier in the lungs of young adult monkeys compared to humans (generation 15 vs. 20).

Figure 20.

Deposition fraction per lower respiratory tract generation for young adult rhesus monkeys and humans for particles 0.1 μm and 1 μm in size.

For particles 1 μm in diameter, there are not significant differences between young adult rhesus monkeys and humans in the deposition fraction for the first 10 generations of the TB region. After the 10th generation, the TB deposition fraction rises more rapidly in monkeys compared to humans. For more distal generations, the pattern of the deposition fractions is quite similar for the two species for 1 μm particles, but the value of the peak pulmonary deposition fraction in humans is more than twice that of monkeys and the peak occurs in generation 20 compared to generation 17 (Figure 20).

Regional deposition in adult rhesus monkeys and humans is shown in Figure 21 for particles between 0.01 and 5 μm. Deposition fractions for particles >5 μm are not depicted because inhalability may well be an issue in monkeys for these larger particles. The impact of the filtration efficiency of the nose is clearly seen in the TB region for both species (Figure 21A). There is a substantial decrease in the deposition fraction for ultrafine particles (i.e., 0.01 to 0.1 μm) for spontaneous nasal breathing compared to endotracheal breathing, most likely due to the high diffusivity of these particles in combination with the complex geometry of the nasal passages (Figure 21A vs. Figure 18A). For particles above 1 μm in diameter, the deposition fraction in the TB region in adult rhesus monkeys rapidly increases to 0.165 for 2.9 μm particles before rapidly declining; in adult humans, the deposition fraction for particles >1 μm increases gradually from about 0.05 to 0.09 (Figure 21A).

Figure 21.

Lower respiratory tract deposition fractions of particles in the lungs of young adult rhesus monkeys and humans as a function of particle size for spontaneous nasal breathing. Panel A compares TB deposition, while Panel B compares alveolar deposition. Panel C reflects the total LRT deposition pattern for the two species.

For the pulmonary region, Figure 21B shows peak deposition of ultrafine particles occurs in both species at about 0.03 μm. However, the peak deposition fraction is about 0.3 in humans compared to only about 0.13 in monkeys. For particles >1 μm, the pulmonary deposition fraction in young adult rhesus monkeys spontaneously breathing through the nose rapidly falls from a maximum of about 0.062 for 2.5 μm particles before rapidly declining towards zero. However, in adult humans with spontaneous nasal breathing, the peak pulmonary deposition fraction is about 0.2, declining to about 0.1 for 5 μm particles. Overall, the similarity in shapes of the LRT deposition fraction patterns shown in Figure 21C supports being able to conduct inhalation studies in monkeys for particles <5 μm in diameter and that interspecies dosimetric adjustments can be made to translate biologically effective dose-response relationships in young adult monkeys to humans.

There are no published LRT experimental deposition data in rhesus monkeys for particles >2 μm in diameter with which to compare the deposition fractions predicted using the lung geometry model developed here. The alveolar deposition fraction of 0.12 measured in cynomolgus monkeys by Cheng et al. (2008) for 2.3 μm particles compares well with the value predicted here for male rhesus monkeys. However, their value for 5.1 μm particles is 2 to 3 times greater than what the new model for rhesus monkeys predicts. Recall that lung volumes differ significantly between the two types of monkeys, so there is not a solid basis for expecting the deposition fractions to be similar for all particle sizes. Clearly, experimental measurements in rhesus monkeys are needed to evaluate and refine the rhesus lung geometry and dosimetry models developed here.

Future research

A combination of data from the literature and previously unpublished data were used in estimating relationships between various physiologic variables and body weight to serve as input variables for the deposition model that was developed. In addition, some morphometric data were used to complete the pulmonary airway tree after constructing the TB tree from data on CT scans of a male, rhesus monkey weighing 1.79 kg. Inherent in the development of the deposition model, various assumptions and decisions had to be made that could be replaced by data if the research to develop the needed data had been done. Here, some of the areas are described that additional research would help improve the particle deposition model as well as extend the model to handle the clearance of particles. The listing and discussion of topics are not in any prioritized order nor is the list exhaustive.

• Inhalability: Deposition of inhaled particles in the lungs of rhesus monkeys depends on the amount that is able to penetrate into the nasal or oral cavity, escape deposition in the URT, and reach the lungs. While inhalability in monkeys is 100% for submicrometer particles, for micrometer and larger particles, inhalability will decrease as particle size increases beyond probably 4 to 5 μm. Currently, there is no information on the inhalability of particles for rhesus monkeys. The results of the current study generally imply that particle inhalability is lower for monkeys than for humans. Thus, inhalability equations for humans cannot represent those for monkeys, and there is a need to develop such a database for monkeys.

• URT volume: When inhalation initiates, the volume of air in the head airways enters the lung as part of the tidal volume. There are limited data on the volume of the URT as a function of body weight in monkeys. Currently, there are no data in the literature on the volume of the nasopharynx, oropharynx, or larynx in rhesus monkeys less than one year of age, and there are limited data on these volumes in larger sized monkeys.

• Particle losses in URT airways: The filtering efficiency of the head is a critical aspect of limiting the exposure of sensitive pulmonary tissues to the adverse effects of inhaled particles. Experimental as well as computationally-generated data on nasal and oral deposition as a function of particle size and airflow rate are needed to be able to verify or improve equations for the removal of particles in the URT of rhesus monkeys and to establish input levels for the deposition model that was developed here for the LRT.

• Tidal volume measurements: The available data for estimates of tidal volume in rhesus monkeys are limited to animals with body weights <5 kg. However, monkeys with body weights up to about 15 kg are used in various research studies. Specification of the tidal volume value is a necessary input variable for calculating the deposition of particles or examining the uptake of gases. Experimental measurements of tidal volume in rhesus monkeys of varying body weights are needed to ascertain whether one can linearly extrapolate beyond the range of the currently available data.

• Pulmonary airway geometry: In the absence of data on pulmonary airways, four generations of respiratory duct and four generations of alveolar ducts were assumed in this study based on measured duct and lung volumes. However, detailed morphometric studies are needed to measure airway number and shape for rhesus monkeys of different ages and weights. These data could be used to improve or replace the geometry selected in this study and to enable more accurate reconstructions of the pulmonary region.

• Pulmonary compliance and resistance: Deposition of inhaled particles is directly related to the airflow distribution in the lung. While the current model assumed a uniform airway expansion and contraction, it is not known whether such an arrangement is equally valid in rhesus monkeys. Lung compliance and airway resistance data are needed to develop an airflow-specific model for rhesus monkey lungs.

• Regional particle deposition data: Experimental deposition studies for a range of particle sizes would provide the data needed to evaluate the accuracy of the deposition model developed here and provide insights into how the model can be improved. Since particle deposition mechanisms depend upon aerodynamic diameter, the deposition fractions determined from these experimental studies will be applicable to any particle having the same aerodynamic properties. However, the resulting toxicity or therapeutic effects will be specific to a given particle.

• Individual variation in LRT morphometry and uncertainty analyses: The LRT airway geometry for the conducting airways model developed here is based upon data for only one monkey. Similarly, human conducting airway geometries are only available for a few children (Ménache et al., 2008) and a few adults (Weibel, 1963; Horsfield & Cumming, 1968; Yeh & Schum, 1980) with values for the alveolar airways either based on a few measurements or developed from morphometric studies of various alveolar components. With new imaging techniques and enhanced computation speeds, more airway geometry models need to be developed for both rhesus monkeys and humans so that the uncertainty in estimated deposition values can be characterized via sensitivity analyses. Given that the range of deposition fractions among individuals most likely overlaps between rhesus monkeys and humans, the uncertainty around the mean values in the population can be quantified with various sensitivity analyses. For example, Figure 22 provides the results for infant and young adult monkeys for endotracheal breathing at a frequency that is ±2 standard deviations from the mean of 39 breaths per minute. One sees that there is little impact on TB deposition fraction from variation in breathing frequency for any particle diameter (Figure 22A and 22C). However, variation in breathing frequency has a significant impact on deposition fractions for the alveolar region for particles between about 0.02 and 4 μm in diameter (Figure 22B and 22D).

Figure 22.

Lower respiratory tract deposition fractions of particles in the lungs of infant and young adult rhesus monkeys as a function of particle size for endotracheal breathing at the mean value of 39 breaths per minute and at ±2 standard deviations from the mean.

Comparing Figure 18B with Figure 22D, one sees that the plus two standard deviations curve for pulmonary deposition fractions in young rhesus monkeys is similar to the mean curve for young adult humans for particles <3 μm in diameter, inferring there may well be a differences between the two species in population average deposition fractions, with some overlap at the extremes of breathing frequency. However, for particles >3 μm in diameter, these same figures show that there is likely a real difference between the two species in population average pulmonary deposition fractions. These simulation results also demonstrate the importance of measuring various physiologic variables (e.g. minute volume, tidal volume, breathing frequency) on individual animals when conducting experimental particle deposition studies if one wants to make more accurate interspecies dosimetric comparisons.

Summary

Here, the first geometry model of the conducting airways for rhesus monkeys is developed based upon CT data on the conducting airways of a 6-month-old male rhesus monkey (i.e. Macaca mulatta). An algorithm was developed for adding the alveolar airways using criteria based upon published rhesus morphometric data such as the volume of alveolar ducts and the number of alveoli per lung as a function of the body weight. The resultant lung geometry model can be used as the lung morphometry model in mechanistic dosimetry models to predict the deposition of inhaled particles or the absorption of inhaled gases

Implementing these dosimetry models for a given monkey of a specific body weight requires estimating the URT volume, FRC, tidal volume, and breathing frequency of the animal. The relationship of these variables to rhesus monkeys of differing body weights was established by synthesizing and modeling published data as well as modeling pulmonary function measurements in the California National Primate Research Center data base on 121 rhesus monkeys that had served as control animals in various studies. Equations that were developed for the relationships of physiologic variables to the body weight of male and female rhesus monkeys are given in Table 14, while relationships of various alveolar morphometric variables to lung volume are presented in Parts A and B of Table 15 for male and female rhesus monkeys, respectively.

Table 14.

Summary of equations relating physiologic variables to the body weight of rhesus monkeys.

Dependent variable, Y	Model	Comments
URT volume, mL	Y = 0.56973 + 1.5336 * BWt	Use for BWt ≤ 12 kg
Nasal passages SA/Vol, 1/cm	Y = 6.23 + 30.306 * exp(−0.2658 * BWt)	Use for BWt ≤ 12 kg
Breathing frequency	Y = 39	Use for both sexes
Minute volume, L/min	Y = −0.44051 + 3.8434 * Log(BWt)	Males, use for BWt ≤ 4 kg
	Y = 1.9108 – 24.7378 * exp(−1.2479 * BWt)	Both sexes, use for BWt > 4 kg
	Y = −2.5302 + 1.7744 * BWt – 0.15866 * BWt2	Females, use for BWt < 4 kg
TLC, mL	Y = −51.304 + 104.02 * BWt – 3.6788 * BWt2	Both sexes, use for BWt ≤ 15 kg
FRC, mL	Y = −52.593 + 68.651 * BWt – 2.2103 * BWt2	Both sexes, use for BWt ≤ 15 kg
FRC/TLC	Y = 0.72359 – 0.39872 * exp (−0.28113 * BWt)	Both sexes, use for BWt ≤ 15 kg
Tidal volume, mL	Y = −23.818 + 26.093 * BWt – 2.1946 * BWt2	Males, use for BWt < 5.5 kg
	Y = −61.578 + 45.391 * BWt – 4.3842 * BWt2	Females, use for BWt < 4.5 kg
	Y = 1000*minute Vol/39	Both sexes, BWt ≤ 5.5 kg for males & BWt ≤ 4.5 kg for females

Table 15.

Summary of equations relating morphologic variables to the body weight and lung volume of rhesus monkeys.

A. Males
Dependent Variable, Y	Modela
Lung Volume (LV), mL	Y = 27.497 + 53.326 * BWt
Duct Volume, mL	Y = 4.8231 + 17.243 * BWt
Volume of Alveoli, mL	Y = –0.12747 + 0.5735 * LV
Log No. of Alveoli	Y = 8.0389 * exp(0.00014507 * LV)

B. Females
Dependent Variable, Y	Modela
Lung Volume (LV), mL	Y = −15.17 + 100.84 * BWt
Duct Volume, mL	Y = 6.3733 + 11.867 * BWt + 4.1392 * BWt2
Volume of Alveoli, mL	Y = −7.814 + 0.65711 * LV
Log No. of Alveoli	Y = 7.7808 + 0.0025813 * (LV)

^aLinear models fit to data for animals <4 kg body weight; exponential fit to data for all animals.

^aModel fits for females with body weights <4 kg.

Using the lung geometry model that was developed, the lower respiratory tract deposition pattern of particles up to 10 μm in diameter was examined for endotracheal breathing and up to 5 μm in diameter for spontaneous breathing in infant and young adult monkeys and the resulting deposition patterns compared to those for humans. The deposition fraction of respirable size particles was found to be higher in the conducting airways of infant and young adult rhesus monkeys compared to humans. Due to the filtering effect of the conducting airways, pulmonary deposition in rhesus monkeys was lower than that in humans. The lung geometry model and the relationships between various physiologic variables developed in this paper have been added to the MPPD model software program. A new release of the MPPD model will be available free to the public in the fall of 2012 for both MacIntosh and PCs and can be downloaded at the following address: http://www.ara.com/products/mppd.htm.

Appendix A. Female rhesus monkey relationships among various variables

Figure A–1.

For female rhesus monkeys, best fitting regression models showing the relationships among various variables and body weight or lung volume. Panel A: lung volume vs. body weight, with linear curve. Panel B: alveolar duct volume vs. body weight, with quadratic curve. Panel C: alveolar volume vs. lung volume, with linear curve. Panel D: log of the number of alveoli vs. lung volume, with a linear curve. See Table A-1 for the coefficients of the fitted regression models.

Table A–1.

Best fitting regression models in female rhesus monkeys for various pulmonary variables.

Dependent Y-variable	Independent X-variable	Modela	Model parameters			R2
			β0	β1	β2
Lung volume, mL	Body weight., kg	Linear	−15.17	100.84		0.846
Duct volume, mL	Body weight., kg	Quadratic	6.3733	11.867	4.1392	0.955
Volume of alveoli, mL	Lung volume, mL	Linear	7.814	0.65711		0.974
Log number of alveoli	Lung volume, mL	Linear	7.7808	0.0025813		0.899

^aLinear model: β₀ +β₁ * X; Quadratic model: Y = β₀ + β₁ * X + β₂ * X².

Appendix B. Relationships of rhesus breathing parameters with body weight

Tidal volume

Of the three studies reporting individual measurements of tidal volume on rhesus monkeys, two did not anesthetize the animals (Karel & Weston, 1946; Binns et al., 1972), while the study by Brooks et al. (1957) was on anesthetized animals. In that study, intraperitoneal injections of a mixture of 25% urethan solution and paraldehyde to give 1 g of urethan plus 0.2 mL of paraldehyde per kg of body weight were used. The body weight range of the animals in these three studies was 1.99–5.35 kg for male monkeys and was 2.19–4.5 kg for female monkeys.

Scatter plots of the V_T data for each sex were used to identify animals whose data were well beyond the normal variability that one can expect in animals of a given body weight. If an animal was agitated or deeply anesthetized, the resulting alteration in breathing pattern would result in V_T values not reflective of normal respiration. One male animal from each study was deleted from the V_T data set: (1) an animal in the Karen and Weston (1946) study whose body weight was 53% greater than that of another animal, but still had about the same V_T value, (2) an animal in the Binns et al. (1972) study that had a body weight of 3.45 kg had a V_T only about 50% of that of another animal of similar size, while the other animal’s value was in line with trend line for animals of this and higher body weights, and (3) an animal in the Brooks et al. (1946) study had a V_T value more than 50% greater than the V_T value of other animals of similar body weight. The scatter plots for female rhesus monkeys did not reveal any animals whose tidal volume values should be considered as outliers.

Table B–1.

Mathematical models fit to tidal volume data for male and female rhesus monkeys.

A. Males		Model Coefficients				R2
Model Type	Model Form	M0	M1	M2	M3
Linear	Y = M0 + M1*X	−0.53403	11.321			0.763
Quadratic	Y = M0 + M1*X + M2*X2	−23.818	26.093	−2.1946		0.796
Exponential	Y = M0 *exp(M1*X)	11.442	0.34163			0.675
Power Law	Y = M0*XM1	9.6299	1.1206			0.757
Logarithmic	Y = M0 + M1*Log(X)	−5.4402	83.776			0.793
Exponential Rising	Y = M1 – (M1 – M2)*exp(-M3*X)		65.867	−38.208	0.40302	0.795
B. Females		Model Coefficients				R2
Model Type	Model Form	M0	M1	M2	M3
Linear	Y = M0 + M1*X	−16.446	16.679			0.537
Quadratic	Y = M0 + M1*X + M2*X2	−61.578	45.391	−4.3842		0.553
Exponential	Y = M0 *exp(M1*X)	7.1648	0.48581			0.492
Power Law	Y = M0*XM1	5.6256	1.5727			0.525
Logarithmic	Y = M0 + M1*Log(X)	−24.167	123.12			0.549
Exponential Rising	Y = M1 – (M1 – M2)*exp(-M3*X)		74.004	−87.081	0.47315	0.551

A number of mathematical models were fit to the tidal volume data for each sex. Part A of Table B–1 provides the model coefficients and R² values for the models fit to the male V_T data, while Part B provides the results for the female monkeys. As can be seen from the table, a quadratic polynomial and an exponential rising model provided almost the same percentage of explanation of the variability in the data for both sexes as reflected by the R² values. Given that the models are not to be used to predict V_T values above the upper range of the data (i.e., about 5.35 kg), the simpler to evaluate quadratic model is recommended.

The fitted curves and experimental data for the 3 studies are given in Figure B–1, and the regression equations for males and for females are given in Equations (B-1) and (B-2), respectively.

$$\text{Males:}{\mathrm{V}}_{\mathrm{T}}=-23.818+26.093\ast \text{Body}\text{Wt}-2.1946\ast \text{Body}{\text{Wt}}^2$$ (B-1)

$$\text{Females:}{\mathrm{V}}_{\mathrm{T}}=-61.578+45.391\ast \text{Body}\text{Wt}-4.3842\ast \text{Body}{\text{Wt}}^2$$ (B-2)

where V_T is in mL and body weight is in kg.

Figure B–1.

The relationship between tidal volume and body weight for male and female rhesus monkeys over a body weight range of about 2 to 5 kg from analyses of studies reporting measurements on individual monkeys.

Table B–2.

Mathematical models fit to minute volume data for male and female rhesus monkeys.

A. Males		Model Coefficients				R2
Model Type	Model Form	M0	M1	M2	M3
Linear	Y = M0 + M1*X	−0.22706	0.52322			0.720
Quadratic	Y = M0 + M1*X + M2*X2	−0.93338	0.97133	−0.066572		0.733
Exponential	Y = M0 *exp(M1*X)	0.37742	0.3992			0.645
Power Law	Y = M0*XM1	0.31007	1.3049			0.708
Logarithmic	Y = M0 + M1*Log(X)	−0.44051	3.8434			0.737
Exponential Rising	Y = M1 + (M1 – M2)*exp(-M3*X)		3.2294	−1.4199	0.30928	0.735
B. Females		Model coefficients				R2
Model Type	Model Form	M0	M1	M2	M3
Linear	Y = M0 + M1*X	−0.89685	0.73531			0.582
Quadratic	Y = M0 + M1*X + M2*X2	−2.5302	1.7744	−0.15866		0.594
Exponential	Y = M0 *exp(M1*X)	0.21307	0.56779			0.527
Power Law	Y = M0*XM1	0.16296	1.825			0.564
Logarithmic	Y = M0 + M1*Log(X)	−1.2273	5.4071			0.590
Exponential Rising	Y = M1 + (M1 – M2)*exp(-M3*X)		3.5433	−2.9997	0.36558	0.592

Relative to extrapolating beyond the range of the experimental data to lower body weights, the data contained in Crosfill and Widdicombe (1961) provided support that going as low as 1.4 kg in body weight is probably okay for male monkeys. These investigators examined tidal volume in rhesus monkeys weighing as little as 1.8 kg, but they did not state which sex was used or if animals of both sexes were used. They reported a V_T value of 9 mL as the lowest measurement, which likely was at this body weight; Eq. (B-1) gives a value of 8.4 mL for a body weight of 1.4 kg. If one has used females, extrapolation below 2 kg using Eq. (B-2) is not advised as this quadratic equation begins to provide V_T estimates that rapidly decline and become negative. Thus, for female monkeys between 1.4 and 2 kg, use of the linear equation given in Part B of Table B-1 is recommended.

Minute volume

In the main body of this paper, the relationship between minute volume and body weight was examined for male rhesus monkeys. A logarithmic curve was shown to best describe the relationship between minute volume and body weight when the body weight was <4 kg, based upon a regression using the 3 studies that reported individual measurements of minute volume.

Figure B–2.

The relationship between minute volume and body weight of female rhesus monkeys over a body weight range of about 2 to 5 kg.

Here, a similar analysis is presented for female rhesus monkeys. Scatter plots of the 3 studies reporting individual measurements of minute volume did not reveal any animals whose minute volume values should be considered as outliers. The parameter estimates for various models fit to the female minute volume data set are given in Part B of Table B–2. For completeness, the analogous results for the male monkeys are presented in Part A of the table. A quadratic polynomial also provided the best fit to the minute volume data for the female rhesus monkeys, although the logarithmic and exponential rising models were essentially as good as the quadratic over the range of the experimental data. The fitted curve and individual data points for the quadratic fit are given in Figure B–2 and the corresponding equation for female minute volume as a function of body weight is given by Eq. (B-3).

$$\text{Minute}\text{Volume}=-2.5302+1.7744\ast \text{Body}\text{Wt}-0.15866\ast \text{Body}{\text{Wt}}^2$$ (B-3)

where minute volume is in L/min and body weight is in kg.