Comparison of Patient-Specific Computational Modeling Predictions and Clinical Outcomes of LASIK for Myopia

Abstract

Purpose

To assess the predictive accuracy of simulation-based LASIK outcomes.

Methods

Preoperative and 3-month post-LASIK tomographic data from 20 eyes of 12 patients who underwent wavefront-optimized LASIK for myopia were obtained retrospectively. Patient-specific finite element models were created and case-specific treatment settings were simulated. Simulated keratometry (SimK) values and the mean tangential curvature of the central 3 mm (K_mean) were obtained from the anterior surfaces of the clinical tomographies, and computational models were compared. Correlations between K_mean prediction error and patient age, preoperative corneal hysteresis (CH), and corneal resistance factor (CRF) were assessed.

Results

The mean difference for K_mean between simulated and actual post-LASIK cases was not statistically significant (−0.13 ± 0.36 diopters [D], P = 0.1). The mean difference between the surgically induced clinical change in K_mean and the model-predicted change was −0.11 ± 0.34 D (P = 0.2). K_mean prediction error was correlated to CH, CRF, and patient age (r = 0.63, 0.53, and 0.5, respectively, P < 0.02), and incorporation of CH values into predictions as a linear offset increased their accuracy. Simulated changes in K_mean accounted for 97% of the variance in actual spherical equivalent refractive change.

Conclusions

Clinically feasible computational simulations predicted corneal curvature and manifest refraction outcomes with a level of accuracy in myopic LASIK cases that approached the limits of measurement error. Readily available preoperative biomechanical measures enhanced simulation accuracy. Patient-specific simulation may be a useful tool for clinical guidance in de novo LASIK cases.

Laser in situ Keratomileusis (LASIK) is among the most frequently performed surgeries in the world and is associated with high global patient satisfaction rates.¹ However, LASIK and other forms of corneal refractive surgery that rely on tissue incision or removal induce corneal biomechanical changes.^2–4 These changes to the corneal structure and individual differences in the mechanical response to them are important potential drivers of residual postoperative refractive error, postoperative refractive regression, and postoperative corneal ectasia.

Although the outcomes of LASIK are among the best of any elective procedure, enhancement procedures are often required for residual or induced refractive error. Residual refractive error and the need for retreatment are significant sources of uncompensated cost, risk, and patient dissatisfaction.¹ A variety of risk factors for retreatment after primary refractive surgery have been identified, including the type and magnitude of preoperative refractive error, depth of ablation, patient age, and higher degrees of preoperative astigmatism.^5–7 In addition to the cost and intrinsic risks of additional surgery, retreatments have been associated with an increased risk of corneal ectasia.^8,9 Although historic nomograms have been useful for improving refractive outcomes through regression-based guidance of treatment offsets,¹⁰ they are generally agnostic to individual corneal shape variations and other important drivers of the structural response to surgery. A surgical planning tool that can increase the accuracy of surgical algorithms for routine and atypical cases has the potential to reduce cost while increasing patient safety and satisfaction.

Finite element analysis (FEA)-based computational simulation is being investigated as a predictive tool to enhance clinical decision-making in an increasing number of clinical disciplines.¹¹ Structural analysis using the FEA method has the potential to account for the biomechanical impact of a complex three-dimensional (3D) surgical intervention while accounting for the patient's particular corneal geometric configuration and biomechanical properties. The sensitive link between the cornea's geometry, biomechanical behavior, and the optical function of the eye presents significant advantages for leveraging simulation-based engineering in keratorefractive applications. Furthermore, the cornea's accessibility with commercially available imaging systems makes creation of patient-specific models more feasible than in other tissues requiring invasive or ionizing imaging techniques.

The approach to corneal finite element modeling has progressed from homogenous material formulations^12,13 to more microstructurally representative models^14–21 that account for preferred collagen orientations from x-ray diffraction data,²² axially inclined collagen fibers in the anterior stroma characterized by two-photon microscopy²³ and corneal hydration behavior.¹⁸ Only a limited number of studies have modeled the optical effects of both flap creation and ablation in the context of LASIK,^24,25 and no prior publication has performed a direct clinical comparison of computationally predicted refractive outcomes. The goal of the present study was to assess the predictive accuracy of case-specific finite element simulations of LASIK procedures through comparison to clinical topographic and refractive outcomes.

Methods

Patient Selection and Surgery

Consecutive charts of 20 eyes of 12 subjects that underwent LASIK for myopia or myopic astigmatism on the Refractive Surgery service of the Cleveland Clinic Cole Eye Institute (Cleveland, OH, USA) and that were followed for at least 3 months after surgery were included in the study. Patients were selected by a retrospective review of corneal tomography under an institutional review board (IRB)-approved research protocol (Cleveland Clinic IRB protocol #13-213). Eyes with at least 10 mm of corneal coverage in Scheimpflug-based anterior segment scans (Pentacam HR; Oculus Optikgerate GmbH, Wetzlar, Germany) were chosen for the study from a consecutive series of refractive surgery screening candidates who had LASIK performed. Charts of patients not meeting all of these criteria were excluded. The treatments were performed by two fellowship-trained refractive surgeons (WJD, RK) using an FS200 femtosecond laser (Alcon, Fort Worth, TX, USA) or IntraLase fs60 femtosecond laser (AMO, Santa Ana, CA, USA) for flap creation and an Allegretto Eye Q 400 excimer laser system (Alcon) with a 6.5-mm optical zone in a 9-mm total ablation zone with a 1.25-mm annular transition zone. Programmed refractive correction was determined individually by each surgeon using their standard practice pattern of reviewing commercial nomogram software suggestions for each case (IBRA; Zubisoft GmbH, Oberhasli, Switzerland). As described in more detail below, case-specific surgical parameters for flap creation and excimer laser ablation were incorporated into the simulations. Only preoperative corneal tomography was used to construct computational models, and posttreatment data was used to assess model accuracy.

Corneal Anisotropy and Material Model

For modeling purposes, the cornea was represented as a nonlinear, anisotropic, hyperelastic, nearly incompressible material with depth-dependent material properties.^14,26,27 To simulate this spectrum of behavior, a microstructural fiber-reinforced material model representing collagen fibers was combined with an isotropic Neo-Hookean solid extrafibrillar matrix to produce a composite corneal stroma.^28–30 Collagen crimping behavior was accounted for by representing each collagen fibril as a 3D spring proposed by Freed et al.^28,29 where H is the axial distance between two turns of the helix, R is the radius of the helix, and r is the radius of the fiber thickness. The microstructural helical spring model requires three parameters: Ho/Ro (the ratio between initial axial distance between two turns within the helix and the initial radius of the helix), Ro/ro (the initial radius of the helix and the radius of the fiber thickness), and Ef (the elastic modulus of the fiber when it is uncrimped and behaves in its linear region).^15,28 The resulting fiber behavior was calculated using the algorithm given elsewhere by Freed et al.²⁹

Corneal material strength is dependent on stromal fiber distributions and their preferred orientations.^22,31–33 The material formulation proposed by Freed et al.²⁹ was limited to reflect this behavior in the fiber splay. Therefore, the algorithm was combined with the equation given by Pinsky et al.¹⁵ to more realistically simulate the corneal stroma (Equations 1–4). At each integration point within the model, splay of fibers was modeled and angularly integrated to represent a gradual change in fiber orientation from the center to the periphery of cornea. The equations are partially reproduced here to demonstrate how fiber and matrix components are accounted for in the total strain energy density function (Equation 1) and how the fiber component is defined using the probability density function (Φ) to describe the presence of fiber population as a function of rotational angle (θ) and radial distance from the corneal center (R) (Equations 2–4). The separate treatment of fiber orientation for central (Equation 3) and peripheral (Equation 4) cornea allows representation of the transition from predominantly orthogonal to more circumferential/tangential orientation near the limbus. A linear combination of Equations 3 and 4 was used in the transition zone between central and peripheral regions. The details of the components of this equation including n, c₁, and c₂ were explained by Pinsky et al.¹⁵

Depth-dependent properties of the cornea were simulated by linearly scaling the ground matrix material constant, C₁₀, in the material model down to 50% from anterior to posterior regions of the stroma to approximate experimental data in human corneal explants.³⁴ The material model was implemented in an Abaqus v611 UMAT subroutine (Dassault Systemes Simulia Corp., Providence, RI, USA).³⁰ The pretreatment corneal material constants were obtained by performing an inverse FEA³⁰ on previously published experimental inflation and tensile test data from a 50-year-old excised human cornea.³⁵ This analysis produced material constants that were then used in the models to represent the normative preoperative stroma. Preoperative material constants were defined as follows: the shear modulus of isotropic ground matrix C₁₀ = 0.04 MPa, the compressibility constant D = 0.0001 MPa⁻¹, the ratio of the axial length of the collagen fibers spring to the diameter of the collagen fiber H₀r₀ = 30.5, the unitless ratio of radial diameter of the collagen fiber to the diameter of the collagen fiber R₀r₀ = 1.51, and the elastic modulus of the collagen fibers Ef = 32 MPa. Epithelium was modeled as a uniformly thick 50-μm isotropic hyperelastic neo-Hookean material. The shear modulus of the epithelium was set as 1% of the shear modulus of the stroma, and the fiber component was omitted due to absence of continuous collagen elements and the epithelium's negligible contribution to the corneal structural response.

Model Generation

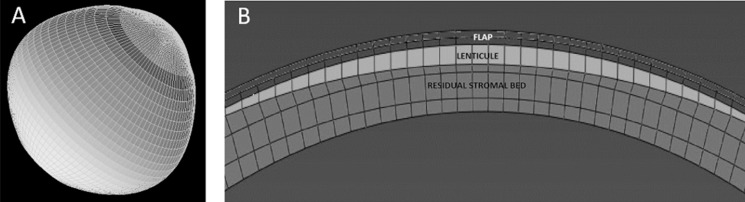
Patient-specific preoperative Cartesian coordinates of the anterior and the posterior surfaces were exported from Pentacam as grid format comma separated value files. The data were interpolated and meshed with eight-node hexahedral brick elements (Fig. 1A) with SpecifEye v0.1 (Optoquest, Cleveland, OH, USA).²⁰ The preoperative geometry was divided into four regions in depth (Fig. 1B): epithelium (50 μm), stromal component of the flap (50 μm), flap interface wound (10 μm), and posterior stroma (defined as the remaining patient-specific thickness).³⁶ A generic sclera, with an anterior thickness matched to the patient-specific peripheral corneal thickness, was generated to form the posterior portion of the eye in order to capture the effects of limbal displacement within the simulation.^20,24 The posterior surface of the corneoscleral globe was then subjected to a homogenous IOP of 15 mm Hg.

Figure 1.

(A) Representative side-view of cornea-scleral finite element mesh. (B) Representative cross-section of a corneal mesh to demonstrate myopic LASIK correction applied to the cornea with LASIK flap, ablated lenticule, and residual stromal bed.

Surgical Simulation and Stress-Free Geometry Calculation

Myopia with astigmatism treatments were simulated with their patient-specific treatment settings recorded in operation reports. These treatment settings were translated from the spectacle plane to the corneal plane.³⁷ The patients received wavefront optimized treatments. The ablation profile calculation and equations were given by Mrochen et al.³⁷ Finite element analysis were run using a commercial FEA solver Abaqus v6.11 (Dassault Systemes Simulia Corp.). The amount of ablation was calculated for each node in the 3D finite element model and the nodes were repositioned according to their ablation magnitudes in the geometry with a custom Python script. Because the corneal Scheimpflug scans were acquired under physiological IOP, the stress-free geometries were calculated by an iterative technique given elsewhere by Pandolfi et al.^14,38 and modified by our group.^25,39 The corneal surface coordinates of the unoperated mesh (X₀) depend on the patient specific tomographies acquired under pressure. The nodal coordinates of the mesh within the treatment zone were modified from X_pre to X_post according to the ablation algorithm. The coordinates of the postoperative mesh (including the treatment zone and the peripheral cornea, limbus, and sclera) were taken as a reference (X_ref). A negative pressure with amplitude 90% lower than the physiologic IOP (15 mm Hg) was applied to the posterior surface of the postoperative corneoscleral model (X_ref). The displacements that were calculated from the negative pressure (u_deflation) were added to X_ref to obtain the initial set of coordinates (X₀) to start the iterative no-load calculation (Equation 5). Following the deflation, the physiologic IOP (15 mm Hg) was iteratively applied and error (e) was calculated as the root mean square (RMS) of the distances between the nodes in the whole corneoscleral structure from the reference and the calculated geometries (Euclidian norm). The iterations were stopped once RMS error was less than 1 × 10⁻⁵, which typically required six or seven iterations.

The wound region peripheral to the flap was simulated to represent the restored strength resulting from healing at the femtosecond laser interfaces. The width of the wound region was defined as 305° arc (360° minus hinge width of 55°) with a 10-μm thickness.⁴⁰ The side cut was simulated with a 50% weakening in the isotropic component and omitting the fiber component of the strain energy equation (Equation 6). The flap was simulated by omitting the fiber component of the strain energy equation (Equation 7).³⁶ All patients were operated on using a circular flap with 9-mm diameter and 90° side cut angle. Hinge width was reported as 55° for all patients at 12 o'clock position. All simulations conformed to these reported surgical parameters for each patient.

A wound region beneath the flap was also defined in the model. This region was simulated by a 90% weakening of the isotropic region and omitting the fiber component from the strain energy equation (Equation 8) to approximate the cohesive weakening measured in ex vivo post-LASIK corneas.⁴¹ The material properties of the posterior cornea remained unchanged for the LASIK simulation.

Data Analysis

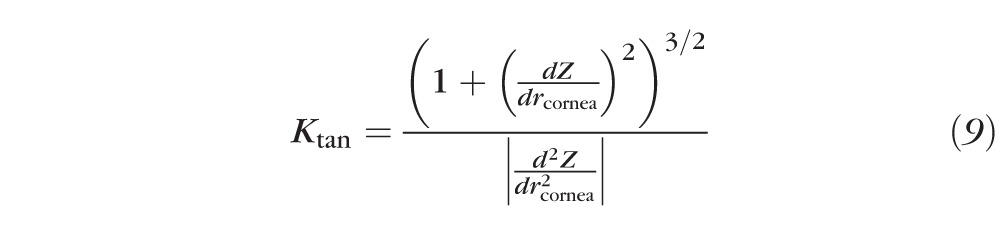
Following the simulations, anterior corneal surface coordinates of pre- and posttreatment geometries were exported from Abaqus Version 6.11 (Dassault Systemes Simulia Corp.). Using the pre- and posttreatment anterior surface coordinates from both simulated and clinical geometries, simulated K values including mean tangential curvature from the central 3-mm region (K_mean), the average curvature of the steepest meridian (K₁), and the average curvature of the flattest meridian (K₂) of the anterior corneal surface were calculated. Tangential curvature at each point (K_tan) on the cornea was calculated using the first and second derivative of an 8^th order Zernike fit (Z) of the anterior corneal surface with respect to distance from the center of the cornea (r_cornea) (Equation 9). The constants of Zernike polynomials (Z) were calculated with a linear regression analysis using a custom Python script. The calculated tangential curvature values were converted to diopters (D) using Snell‘s law with a corneal refractive index of 1.3375 (the keratometric index, which estimates the total corneal power assessed at the anterior corneal surface). Pretreatment clinical K₁ and K₂ values were directly taken from Pentacam tomographies for comparison. Pretreatment model, posttreatment clinical, and simulated K₁ and K₂ values were calculated using SpecifEye. The pairwise differences of these variables for clinical and simulated geometries were calculated. Statistical significance was determined by paired Student's t-tests for nonindependent samples with P less than 0.05 indicating significance (MINITAB, Minitab, Inc., State College, PA, USA).

Corneal hysteresis (CH) and corneal resistance factor (CRF) obtained at each preoperative screening exam with the Ocular Response Analyzer (ORA; Reichert Ophthalmic Instruments, Buffalo, NY, USA) were recorded. Correlations between these variables and the difference in predicted versus actual curvature values were investigated using Pearson correlation. Programmed change in central anterior corneal curvature was calculated as the spherical equivalent (SE) of the programmed correction following the vertex calculation with a 12.5-mm vertex distance. Actual and simulated changes were calculated by subtracting preoperative K_mean from postoperative K_mean for actual and simulated cases, respectively. Treatment and prediction errors were calculated as differences between actual – programmed changes and predicted – actual changes, respectively.

Results

The mean patient age averaged across eyes was 39.3 ± 12.7 years. Clinical tomographic characteristics of the simulated eyes included a mean maximum curvature (maximum K) of 44.12 ± 1.21 D (mean ± SD), mean apical corneal thickness of 570.5 ± 21.9 μm, and mean minimum corneal thickness of 568.1 ± 21.7 μm.

The mean programmed refraction correction was −3.18 ± 1.69 D for the spherical component and −0.50 ± 0.35 D for the cylindrical component. Tables 1 and 2 show individual K₁, K_2, corneal astigmatism (K₁–K₂), steep axis, and K_mean values and comparisons of actual and simulation values for the preoperative and post-LASIK states, respectively. Preoperative model fidelity was verified by comparing each value from clinical tomography to that of the associated finite element model, and none of the differences were statistically significant. The mean difference in K_mean (ΔK_mean) between actual outcomes of the surgeries and the predictions produced by their corresponding LASIK simulations was not statistically significant (−0.13 ± 0.36 D, P = 0.1 by paired Student's t-test). The only statistically significant difference between clinical and simulated values across the preoperative and postoperative comparisons was for K₂ (+0.13 ± 0.28 D, P = 0.03). Errors in the agreement of the axis of steep astigmatism were also insignificant and were higher in individual cases with very low magnitudes of astigmatism where axis identification (both by refraction and by keratometric analysis) is anticipated to be error prone but of minimal clinical consequence.

Table 1.

Comparison of Anterior Curvature Values for Pre-LASIK Clinical Cases and Modeled Pre-LASIK Geometries for Model Verification

Table 2.

Comparison of Absolute Curvature Values for Post-LASIK Clinical Cases and Post-LASIK Models

To address the possibility of statistical error from the inclusion of both eyes of some patients, we performed a correlation analysis of the prediction error (ΔK_mean) between right and left eyes of the eight patients who had both eyes enrolled. The analysis suggested no significant intraclass correlation (r = 0.11, P = 0.95). The minimum detectable difference for K_mean was 0.23 D for a paired t-test using values n = 20, α = 0.05, and β = 0.2 (80% statistical power) by post-hoc calculation. All predicted K_mean values were within 1.00 D of the clinical postoperative value, with 55%, 85%, and 95% of the cases demonstrating prediction errors within 0.25, 0.50, and 0.75 D, respectively (Fig. 2). Figure 2 also presents a prediction error frequency based on an adjustment for preoperative biomechanical measurement and is further described below.

Figure 2.

Percentage of cases with less than or equal to 0.25, 0.50, 0.75, and 1.00 D of error in the actual versus predicted anterior tangential curvature of the central 3 mm (K_mean, D). Green: prediction error, Blue: CH-adjusted prediction error.

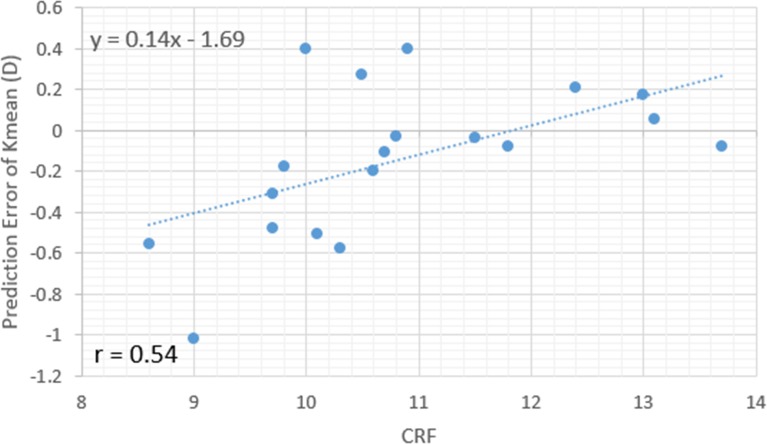
Figures 3, 4, and 5 illustrate the case-specific prediction error in K_mean expressed as a function of CRF, CH, and age. Forty percent of the variance in K_mean prediction error was accounted for by interindividual differences in preoperative CH. Twenty-nine percent was accounted for by CRF, and 25% by age (P = 0.016, 0.004, and 0.02, respectively). ΔK_mean values were confirmed to be normally distributed, and a one-sided outlier analysis using Grubbs' test for the null hypothesis that all data points come from the same normally distributed population did not suggest that the largest prediction error, −1.02 D, was a statistical outlier (P = 0.08). When the linear regression equation for the strongest preoperative predictor of prediction error (CH) was used as a linear adjustment to the model-predicted curvature, the magnitude and frequency of observed error improved (Fig. 2).

Figure 3.

Scatterplot and linear regression of the case-specific prediction error in mean central corneal curvature (D) as a function of preoperative corneal resistance factor (CRF, mm Hg) indicating a trend toward overestimation of myopic correction in subjects with lower CRF.

Figure 4.

Scatterplot and linear regression of the case-specific prediction error in mean central corneal curvature (D) as a function of preoperative corneal hysteresis (CH, mm Hg) indicating a trend toward overestimation of myopic correction in subjects with lower CH.

Figure 5.

Scatterplot and linear regression of the case-specific prediction error in mean central corneal curvature (D) as a function of age (years) indicating a trend toward overestimation of myopic correction in older subjects.

Table 3 reports attempted, actual, and predicted changes in central corneal curvature (K_mean) and assesses treatment error and prediction errors. The treatment error, expressed as the difference between programmed refractive change calculated at the anterior corneal plane and actual change in K_mean, was statistically significant (+0.40 ± 0.30 D, P < 0.05). However, the model prediction error in K_mean was not statistically significant (−0.11 ± 0.34 D, P = 0.2).

Table 3.

Accuracy of Predicted LASIK Outcomes Expressed as the Change in Anterior Tangential Corneal Curvature Averaged Over the Central 3 mm (K_mean)

Table 4 shows the value for pre- and postoperative manifest refraction for each patient, as well as the model-predicted curvature change and the vertex-corrected change after LASIK. The Pearson correlation coefficient for these last two variables is high (P = 0.99) and the scatterplot graph (Fig. 6) also demonstrates a strong correlation between predicted changes in corneal curvature and corneal vertex–corrected changes in actual SE manifest refraction.

Table 4.

Comparison of Model-Predicted Outcomes Expressed as the Change in Anterior Tangential Corneal Curvature Averaged Over the Central 3 mm (K_mean) and the Actual Vertex-Corrected SE Change in Manifest Refraction, Calculated Using the Difference Between Pre- and Post-Operative SE and Assuming Vertex Distance of 12.5 mm

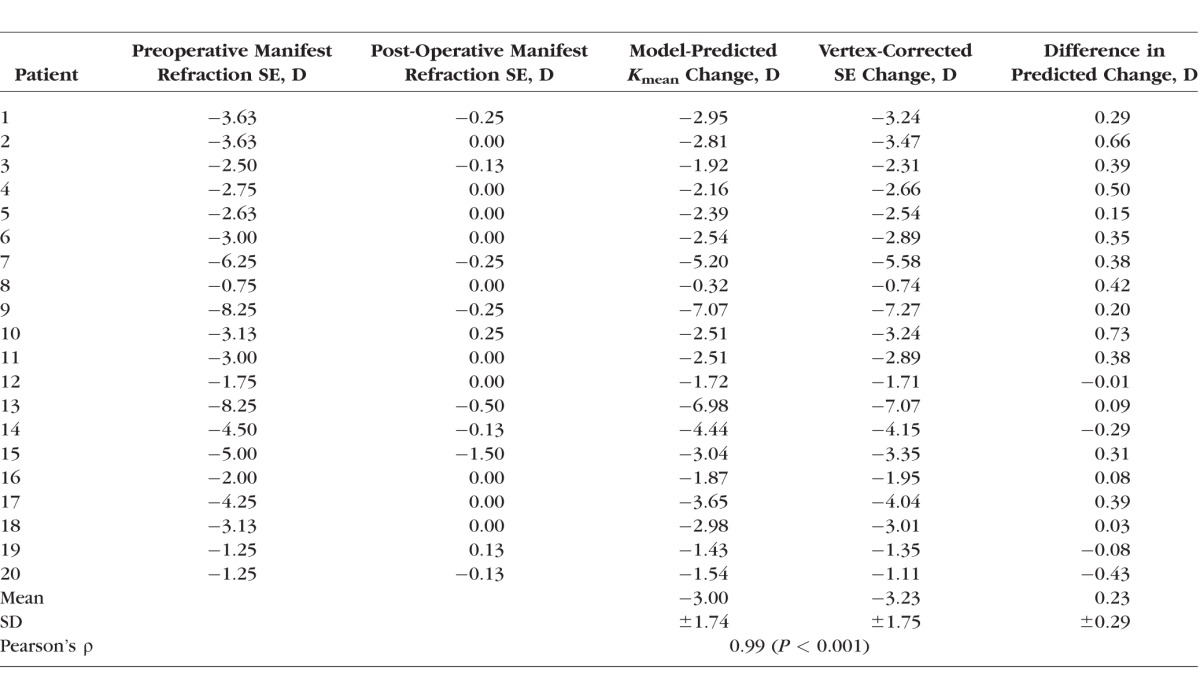
Figure 6.

Scatterplot and linear regression comparing case-specific predictions of mean central corneal curvature (K_mean) change to actual change in vertex-corrected SE manifest refraction.

Discussion

LASIK is one of the world's most commonly performed procedures and is associated with high levels of patient satisfaction.¹ Surgeons frequently use personal nomograms or commercial software-based equivalents as a guide for modifying the laser input to reduce the risk of outcome variability. Although planning systems vary in complexity, the process involves entry of a small number of patient- and surgery-specific variables, interrogation of a regression formula developed from historic outcome data as a function of some subset of those inputs, and generation of a predicted refractive outcome and/or suggested treatment entry for generating the desired correction. These tools have been an important part of outcomes analysis and optimization since the inception of corneal refractive surgery, and analogous methods are also widely used in incisional keratotomy, intraocular lens calculation, intracorneal ring implantation, and other forms of ocular surgery.

Nomogram-based guidance accounts for several sources of systematic variability using a retrospective, empirical fit to the response data. However, there are limitations to a probabilistic approach. Regression models are fit to the average response and typically intersect only a minority of the actual responses. Regression models are historic in nature and optimized for the data used to fit the model; predictive performance beyond the range of previous observations and in prospective forecasting involves additional uncertainty.⁴² The variables represented in nomograms are sparse representations of the patient and the procedure and do not leverage potentially predictive 3D corneal tomography datasets. The statistical associations produced by regression models do not explicitly reflect the biophysical mechanisms of variability and are therefore of limited utility for de novo inferences in complex or atypical cases. Also, aside from surrogate associations related to patient age, nomograms do not explicitly account for the biomechanical impact of the intervention on corneal geometry and optical outcome.^2,4,26

In this study, we investigated the ability of a computational modeling method that directly incorporates patient-specific 3D corneal geometry, case-specific treatment geometry, and evidence-based corneal anisotropy and depth-dependent material property assumptions to simulate actual clinical LASIK outcomes. While previous studies have suggested a role for finite element modeling in enhancing the predictability of refractive surgery procedures by accounting for intrinsic patient characteristics and the biomechanical nature of the surgery,^24,36,43 the current study is the first to assess the predictive performance of a model in a series of keratorefractive surgery patients. This is a critical step in assessing computational modeling as a potential clinical decision support tool in the surgical planning process.

The comparison of model predictions and clinical outcomes was performed in a series of cases with myopic LASIK corrections as high as 8.25 D (SE) and up to 1.50 D of refractive astigmatism, and conclusions about predictive performance should be limited to the range of refractive errors assessed in the current study. The mean pairwise difference in central anterior corneal curvature (K_mean) derived from each computational model from the same metric measured in the actual post-LASIK tomographies—an absolute comparison of predictive accuracy—was insignificant (−0.13 ± 0.36 D, P = 0.1). In relative terms, the mean difference between the surgically induced clinical change in K_mean and the model-predicted change was also insignificant (−0.11 ± 0.34 D, P = 0.2). The keratometric variable K_mean was selected as the primary outcome measure because it was thought to represent the most optically important changes within a typical photopic entrance pupil and because the data directly represent the input and output of the modeling process. However, to relate the predictive performance of the model more directly to clinical refractive outcomes, a direct comparison of predicted changes in model K_mean to the vertex-adjusted SE manifest refractive change was performed and produced close agreement across the range of corrections (Table 4; Fig. 6) with a mean error of +0.23 ± 26 D. While K_mean considers only corneal first-surface changes in curvature, simulation results compared favorably with subjective manifest refraction results that depend on whole-eye optics. Ray tracing analysis is being incorporated into the modeling software to account for additional sources of refractive change such as axial length and posterior corneal surface changes.

Overall, the differences between the model predictions and clinical outcomes were statistically insignificant and within the precision limits of topographic measurement and clinical refraction (±0.25 D) for most cases. When the clinical error in achieved versus programmed K_mean change (0.40 ± 0.30 D) was compared with the prediction error in the same metric (−0.11 ± 0.34 D), the ranges of clinical and prediction error were comparable. However, the model prediction was closer in magnitude to the actual K_mean change than the programmed correction by a factor of 4. Individual comparisons of these differences in Table 3 suggest that preoperative adjustments to the surgical plan based on case-specific model predictions would potentially have improved treatment accuracy in 16 of 20 cases. The actual programmed correction for each case was used to drive each associated simulation and included any spherical and/or cylindrical treatment offsets incorporated by the surgeon after reviewing commercial nomogram software output.

The analysis of model prediction error as a function of preoperative air-puff–derived biomechanical metrics is the first to directly associate the predictability of LASIK outcomes with these variables. The case with the largest discrepancy between programmed and achieved change in K_mean (an apparent 1.18-D myopic undercorrection) and also the largest prediction error in K_mean (−1.08 D) also had the lowest preoperative CH value. While CH is not a measure of the corneal elastic modulus, the trend toward undercorrection of myopia in eyes with lower CH and overcorrection in those with higher CH reflects earlier FEA-based sensitivity analyses suggesting greater anterior displacement of the residual stromal bed and thus myopic undercorrection in eyes with lower corneal stiffness properties.⁴⁴ For simulation purposes, every patient was assumed to have identical, normative initial material properties at the anterior stroma. The isotropic component of these properties were then reduced as a function of depth as described in the methods, and thus produced different depth-dependent property profiles due to differing patient-specific corneal thicknesses. However, the absence of knowledge regarding actual patient-specific material properties is a potential source of prediction error in these simulations, and the finding that a linear adjustment for CH could improve prediction fidelity is important evidence that incorporation of individual measures of corneal properties in the future could enhance model performance. On average, the models predicted slightly flatter corneas than were observed in actual cases, and this could be due to a slightly stiff corneal material assumption.

Another important source of variance in the simulations is the test–retest repeatability of the corneal surface elevation data derived from clinical tomography scans. The current study suggests that a high level of predictive fidelity can be achieved even within the context of a typical clinical workflow involving capture of a single preoperative scan. Selection of optimal scans from a set of replicate measurements may support even stronger predictive performance, and improvements in repeatability with OCT-based tomography methods^45,46 coupled with the ability of emerging OCT and high-frequency ultrasound devices to generate patient-specific epithelial thickness maps⁴⁷ will provide even greater opportunities for improved model accuracy.

In summary, a clinically feasible approach to computational simulations predicted corneal curvature and manifest refraction outcomes with a high level of accuracy in myopic LASIK cases. An automated workflow for the steps described in this study is in place to allow software-driven tomography file transfer and treatment data entry, cloud-based finite element analysis simulation, and electronic delivery of simulation results in under 30 minutes with the goal of providing a useful tool for clinical guidance in de novo LASIK cases.