Perceived image quality with simulated segmented bifocal corrections

Abstract

Bifocal contact or intraocular lenses use the principle of simultaneous vision to correct for presbyopia. A modified two-channel simultaneous vision simulator provided with an amplitude transmission spatial light modulator was used to optically simulate 14 segmented bifocal patterns (+ 3 diopters addition) with different far/near pupillary distributions of equal energy. Five subjects with paralyzed accommodation evaluated image quality and subjective preference through the segmented bifocal corrections. There are strong and systematic perceptual differences across the patterns, subjects and observation distances: 48% of the conditions evaluated were significantly preferred or rejected. Optical simulations (in terms of through-focus Strehl ratio from Hartmann-Shack aberrometry) accurately predicted the pattern producing the highest perceived quality in 4 out of 5 patients, both for far and near vision. These perceptual differences found arise primarily from optical grounds, but have an important neural component.

1. Introduction

Simultaneous vision corrections are increasingly used to treat presbyopia [1, 2], the age-related loss of accommodation by the crystalline lens (i.e. the ability to change its shape to focus at near distances). These corrections aim at restoring the capability to see near and far objects by providing the eye with two or more superimposed foci, for near and far vision [1]. Simultaneous vision is normally provided in the form of contact lenses, intraocular lenses or presbyopic LASIK [1, 3]. In some cases, extended depth of focus is achieved by increasing aberrations [4–6]. Multiple foci may be achieved through diffractive optics, where the design parameters primarily control the power of the lens (to correct for far refractive error), the dioptric distance between the far and near foci (near addition power), and the energy balance between foci [1, 3, 7]. Other lenses follow a refractive design, where some parts of the lenses are dedicated for far and others are dedicated for near, in some cases with a blending zone between both.

Despite the widespread use of simultaneous vision corrections, there is a lack of systematic studies investigating visual perception with those corrections. Most studies in the literature are limited to clinical studies investigating visual function with a certain lens, or a clinical comparison of visual performance in groups of patients implanted with different multifocal lenses [8–10]. However, simultaneous vision is a new and unusual visual experience for the patient, and it is very likely that a particular lens design can be optimized through a better understanding of the optical and neural aspects involved in simultaneous vision corrections.

We have recently reported a simultaneous vision simulator capable of providing the patient with a simultaneous vision experience [11, 12]. The system consists of two channels which project on the patient's retina superimposed images of the same visual scene, one corrected for far (with the required spherical correction) and the other corrected for near (with the desired addition). Unlike real bifocal corrections, the system is not affected by features associated with specific clinical usage, such as flexure or conformity of contact lenses to the cornea, or tilt and decentration with intraocular lenses. The system allows unhindered testing of aspects related to a specific bifocal design, in the presence of the natural aberrations of the eye. Using this system, we studied the effect of near addition on visual acuity (high contrast and low contrast), and found that moderate additions (~2 D) produced the largest compromise of visual acuity [11]. In a subsequent study, using a custom-developed adaptive optics simulator we explored the effects of simultaneous vision with different near additions and near/far energy balances on visual perception, and the capability of the visual system to adapt to these corrections, indicating that neural aspects also play a role in vision with bifocal corrections [13].

Another unexplored aspect in refractive simultaneous vision lenses is the effect of pupillary distribution for near and far. In a recent computational study on diffraction-limited eyes we found that there are in fact differences in the optical performance and depth-of-focus produced by different multifocal segmented lenses with different zonal distributions, with angular patterns generally providing better performance [14]. The presence of the natural high order aberrations of the eye is likely to enhance the differences in performance across multifocal patterns and produce intersubject variability. While optical computer simulations neglect neural contributions, experimental visual simulations of bifocal designs on subjects incorporate both optical and neural factors, isolated from the sources of variability associated to particular implementations (contact lenses, intraocular lenses, refractive surgery pattern).

In this study, we have adapted our previously developed simultaneous vision instrument to simulate, in the same patient, refractive bifocal corrections with different pupillary distributions of near and far vision zones, by use of a transmission spatial light modulator. As the same patient is provided with alternative designs, which can be rapidly programmed in the spatial light modulator, direct comparisons can be made, without the limitations involving comparison of different groups of patients each implanted with a lens design. The patterns tested in this study include designs reminiscent of lenses existing in the market (i.e. bi-segmented angular patterns such as that found in the M-Plus IOL, Oculentis Inc [15, 16] tested in different orientations, or concentric bifocal patterns such as those found in the ReZoom, AMO [17]). A psychophysical paradigm was implemented to answer the following questions: Do some bifocal patterns provide better perceived quality than others? If so, is performance similar across patients, or can bifocal vision be optimized by the choice of the best pattern for each individual? Psychophysical tests were performed on normal cyclopleged patients using a modified custom simultaneous vision instrument. Measurements of the optical aberrations in these patients were used in optical simulations that studied the optical contributions of the perceptual results.

2. Methods

2.1 Subjects

Five subjects, aged between 29 and 42 years and with spherical refractive error ranging from −5.50 D to + 0.75 D, participated in the study. None of the subjects had astigmatism > 1 D. All subjects had good ocular health, as confirmed in an ophthalmological checkup before the measurements, and had prior experience in participating in psychophysical experiments. The measurements were performed in one eye, with dilated pupils and paralyzed accommodation, induced with instillation of tropicamide 1%. All protocols met the tenets of the Declaration of Helsinki and had been approved by the Institutional Review Boards. Subjects signed an informed consent after receiving explanation regarding the nature of the study.

2.2 Simultaneous vision instrument

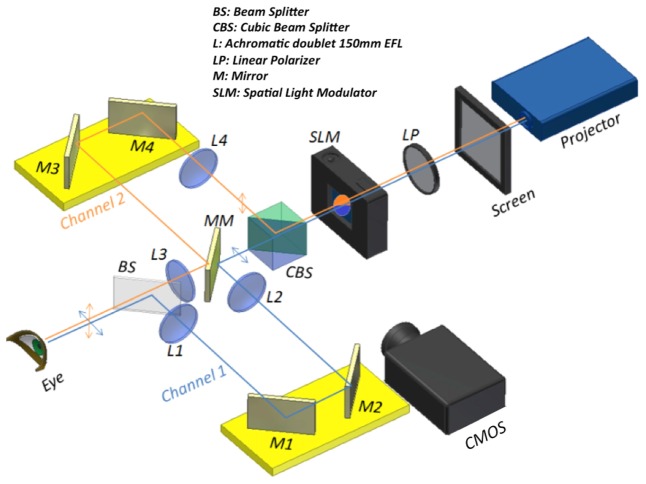
The psychophysical measurements were performed with a modified version of the simultaneous vision simulator, described elsewhere [11, 12]. The instrument allows the simulation of ideal bifocal corrections, by projecting simultaneous bifocal images on the subject’s retina. Figure 1 shows a schematic diagram of the system. The instrument consists of two visual channels capable of achieving different vergences by means of respective Badal optometers, with one channel focused for far vision, and the other for near vision, with a given addition. A CMOS camera (Thorlabs Inc, Germany) allows monitoring the subject’s pupil centration, achieved by use of a bite bar. A Pico-Projector (DLP, Texas Instruments) projects visual stimuli to allow performing psychophysical experiments with the instrument.

Fig. 1.

Simultaneous vision simulator with two Badal Channels (Channel 1: lenses L1 and L2 and mirrors M1 and M2. Channel 2: L3, L4, M3, M4) and a transmission liquid crystal spatial light modulator (SLM) optically conjugated with the pupil of the subject’s eye. Both channels are split using a polarizing cube beam splitter (CBS) in combination with a linear polarizer (LP) and the SLM, and recombined using a double mirror (MM), and a Beam Splitter (BS).

Previous versions of the instrument used the entire pupil for both far and near corrections. For this study, the system was modified by incorporating a transmission spatial light modulator (SLM) in a plane optically conjugate with the subject’s pupil, a linear polarizer (LP) and a polarizing cube beam splitter (CBS). The SLM (LC2002 Holoeye, Germany) is based on a liquid crystal microdisplay (1024 x 768 pixels in 36.9 x 27.6 mm), and is able to change the polarization angle of a linearly polarized incident light beam. In combination with the LP, the SLM was configured to produce a pupillary pattern such that light going through different areas will show perpendicular polarizations, according to an input binary image. The CBS, after the SLM, selectively reflects or transmits the incident light, depending on its polarization angle, and therefore directs the beam passing through different areas of the pupil through the far or near visual channels of the simultaneous vision instrument.

Visual stimuli are projected by the DLP pico projector onto a back-illuminated diffusing screen (Novix technologies, Australia). The projected stimulus was a gray-scale image of a face, with a maximum luminance of 32 cd/m². The screen target is focused on a retinal image plane inside the system, subtending a 0.75-deg retinal angle.

Calibrations revealed that each channel transmits 44% of the light coming from the stimulus, when the maximum transmittance was programmed in the SLM for either channel. The light efficiency of each channel was equivalent, with less than 2% differences in the measured luminance of each channel, measured separately. The measured residual transmission was 1.36%, through the channels, when zero transmittance was programmed in the SLM, in good agreement with the SLM specifications (an intensity ratio of 1000:1 at 633 nm) and the nominal efficiency of the CBS (1000:1 for transmission and 100:1 for reflection). No significant chromatic shifts were measured in the images projected by each channel, in the presence of the SLM.

2.3 Pupillary bifocal patterns

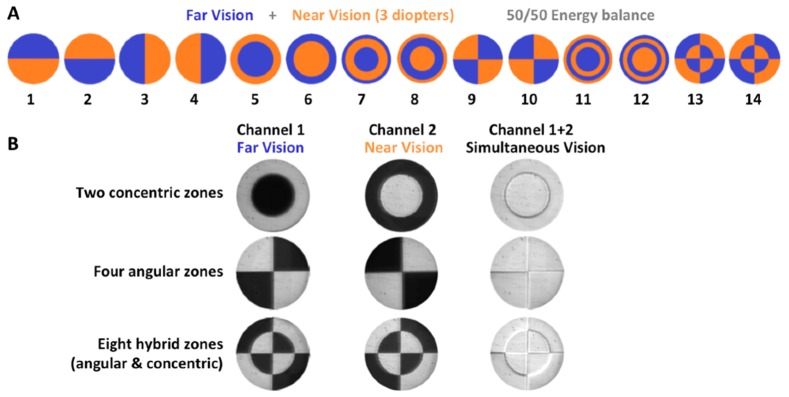
Fourteen different Bifocal Pupillary Patterns (BPP) were simulated in this study. A program written in C++ controlled automatically the presentation of black-and-white images onto the SLM. Figure 2(A) shows the patterns programmed in the system, with blue representing the regions for far vision and orange the regions of near vision.

Fig. 2.

(A) Bifocal pupillary patterns (BPPs) simulated in this study. Far (in blue) and near (in orange) regions have equal area and energy. (B) Image of BPP#6 (2 zones), BPP#10 (4 zones) and BPP#14 (8 zones) captured with a CCD camera at pupil plane through only the far vision channel (left) only the near vision channel (center) and through both channels (right).

The far and near vision pupillary zones were arranged in different angular (BPPs #1-4; #9-10), radial (#5-8; #11-12) or hybrid angular-radial (#13-14) distributions, with up to 8 zones. In all patterns the energy distribution was 50/50 between far and near vision channels. Initially, the vergence of the far vision channel was set to correct for the subject’s refractive error (simulating vision at far distance), while the vergence of the near vision channel was set to induce an additional refractive power of + 3 D (simulating near distance). To simulate bifocal vision at different distances, both channels are moved. The far vision channel (corresponding to the regions of far vision at the BPPs) induces the vergence determined by far, intermediate or near distances, and the power difference between both channels (which represents the addition) remains constant at every test distance. An artificial pupil of 6 mm was placed next to the SLM.

A linear CCD image sensor (Retiga, QImaging, Canada), placed at the subject’s pupil plane, was used to test the relative efficiency, and alignment, of the channels in this experimental implementation, and also the capability of the system to project the BPPs created in the SLM. Figure 2(B) shows images of BPP #3: the far channel (left), the near channel (center), and the combination of both (right). These images illustrate the complementarity of the channels, filling the whole pupil.

2.4 Psychophysical experiments

The psychophysical experimental paradigm is described in Fig. 3. Subjects viewed the face image through different BPPs, and their task was to compare the quality of the perceived face image over pairs of successive BPPs, in a two-alternative-forced-choice procedure with a weighted choice. The subjects responded whether the first or the second image (shown for 1.5s each) was best perceived and the certainty of the response (very certain, quite certain, not certain), using a custom keyboard with six buttons. A Matlab function using PsychToolbox [18, 19] was developed to synchronize the image presentation at the DLP and the pattern presentation at the SLM and for response acquisition. A total of 315 pairs of images were randomly presented to the subjects, representing all possible combinations of the 14 BPPs, repeated three times. Thus, each segmented bifocal pattern was evaluated 39 times (compared against all the other 13 patterns, 3 times) at any given distance. All subjects repeated the experiment in three different conditions representing far, near and intermediate observation distances (i.e. with the far vision channel set to 0 D, −3 D, and −1.5 D, respectively, tested in this order, and the near vision channel adjusted accordingly to maintain the 3-D addition). On average, each subject took ~4 hours to complete the measurements. The subject was given frequent breaks and cycloplegia was ensured by hourly instillation of 1% tropicamide. The centration of the lens pattern within the pupil was periodically checked.

Fig. 3.

Illustration of the method for assessing subjective preferences to segmented bifocal patterns.

2.5 Pattern selection & statistical significance

The statistical significance of the perceptual differences across patterns was explored comparing the number of times that each pattern was selected with the expected values of a Bernoulli cumulative distribution function [20]. We tested the null hypothesis that if all the patterns were perceptually similar, the image comparisons and the corresponding scores would be driven just by chance (with probability 0.5). Thus a BPP is considered to produce a significant perceptual selection if the cumulative number of positive responses (when compared with other BPPs) represents a probability above 0.95 (indicating significant preference) or below 0.05 (significant rejection). Alternatively, all responses with a probability between 0.05 and 0.95 are not significant, hence the hypothesis cannot be rejected and the BPP is considered neutral to the subject.

For a given subject and observation distance (far, intermediate or near), any BPP is presented 39 times paired with other BPPs. A BPP is significantly preferred if the cumulative score is more than 24 and rejected if it is less than 14 (what makes the Bernoulli cumulative density function for 39 tosses higher that 0.95 or lower than 0.05, respectively). Similarly, considering all subjects at a specific distance (195 trials per BPP), a BPP is significantly rejected or preferred if the total cumulative response lie outside 86 and 108, respectively. Considering all subjects and observation distances (585 trials), statistically significant responses are outside 273 and 311.

2.6 Differences in perceived quality across subjects

To evaluate the differences and similarities across subjects in their responses, the perceptual strength of responses was considered [21]. A perceived quality score of a given BPP was obtained by adding the responses given to the each BPP across trials, assigning perceptual weights associated to subject’s certainty of the response (10, 5 and 1 for the positive responses with increasing uncertainty, and likewise −10, −5 and −1 for the negative). The average perceived quality of a given BPP was obtained by averaging the score across subjects and observation distances.

A Multivariate ANOVA analysis (3-way) was performed to test the influence of subjects, BPPs and observation distances on the mean of the perceptual quality. The analysis was performed for two (far and near) and three (including intermediate) distances.

2.7 Ocular aberrations measurement

The ocular aberrations of the subjects were measured in order to investigate the potential optical coupling effects between each BPP and each eye’s optics. Subjects’ ocular aberrations were measured using a Hartmann-Shack wavefront sensor (HASO32, Imagine Eyes, France) integrated in a custom developed Adaptive Optics system, described elsewhere [22], while spherical error was corrected with a Badal optometer. The ocular aberrations were measured under pupil dilation with tropicamide 1%, and described by 7th order Zernike polynomials in a 6 mm pupil diameter.

2.8 Optical predictions

We used Strehl Ratio to evaluate the optical quality of the BPP design. The pupil function was calculated by adding the BPP phase map and the subject’s wave aberration map, for 6 mm pupils and for different observation distances. For far vision the BPP was simulated with zero phase in the far vision zones and a spherical wave aberration (corresponding to the + 3 D addition) in the near vision zones. The Strehl Ratio was calculated as the maximum of the corresponding Point Spread Functions (PSFs) using Fourier Optics [23]. A diffraction limited eye was also simulated, as a reference. The predicted BPP responses from optical computations were correlated with the subjective BPP responses, across subjects and conditions, and for each subject and condition individually.

3. Results

3.1 Pattern preferences and statistical significance

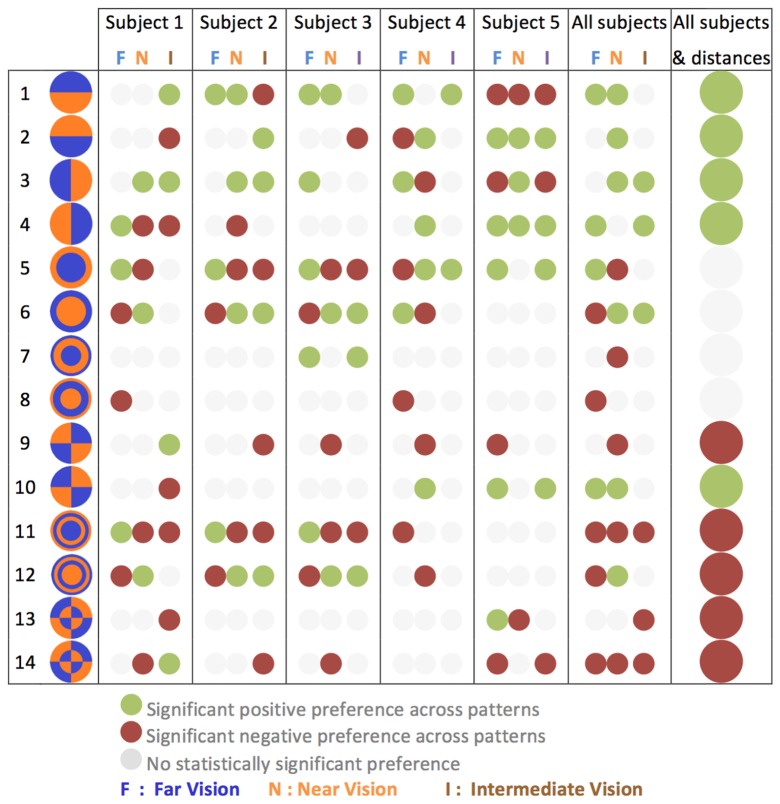
Figure 4 summarizes the pattern preference results and their statistical significance, for each subject and observation distance and on average. Green circles indicate significant preferences, red circles indicate significant rejections and gray circles indicate non-significant responses.

Fig. 4.

Preference maps for all subjects across far, intermediate and near distances. Pooled preferences subjects and across subjects and distances is given in last column. Red dots indicate significant rejection, green dots indicate significant preference and gray dots indicate non-significant preferences at p<0.05.

As seen in Fig. 4, there was a relatively high number of significant selections (colored circles) of BPPs across subjects and distances. Across the 5 subjects, 3 distances (N = 3) and 14 BPPs, 101 out of a total of 210 comparisons (48%) were significant. 25% BPPs were significantly preferred (green circles), and 23% BPPs were significantly rejected (red circles) when compared to all the other patterns under the same conditions. Despite intersubject variability, BPPs providing significant responses tended to be consistent across subjects. In fact, the pooled responses across subjects and across subjects and distances (last two columns in Fig. 4) revealed significant positive and negative responses in 10 out of the 14 BPPs.

3.2 Comparison of perceived quality across subjects

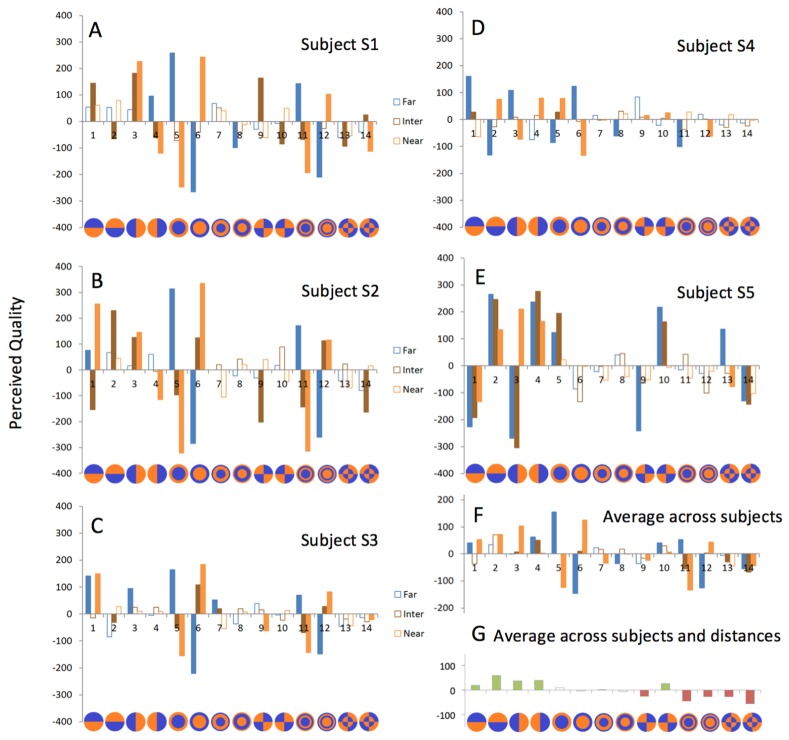
Figure 5 shows the perceived quality score for each of the 14 BPPs for each subject (A to E), and the average across subjects (F), for far (blue), intermediate (brown) and near (orange) distances. Empty and solid columns represent statistically non-significant (gray dots in Fig. 4) and statistically significant (colored dots in Fig. 4) selections, respectively. The maximum possible perceived quality is 390 (13 comparisons with other patterns, 3 repetitions, scored with 10 perceptual points each). The average perceived quality (absolute value) of the patterns with significant selections was 71 ± 92 (18 ± 24 for patterns with non-significant selections). The strength of the score varied across subjects, ranging from 64 ± 57 for S4 to 120 ± 90 for S5 (averaging across BPPs and distances).

Fig. 5.

Perceived optical quality to BPP for far (blue), intermediate (brown) and near distances (orange). A-E shows data for individual subjects, F shows the average across subjects and G shows average across subjects and distances.

A subject to subject correlation analysis revealed that subjects S1, S2, S3 provided statistically similar perceived quality judgments (R>0.6; p<0.0001) to most BPPs, which differed from those provided by S4 and S5. In fact, the scores of S4 showed a strong negative correlation (R<-0.4; p<0.01) with subjects S1 and S3. These correlations are likely driven by the responses to radial BBPs #5, #6, #11 and #12, strong and almost identical in subjects S1, S2 and S3 (determining the average values of Fig. 5(F)), and almost opposed to that of S4. The strength of the scores to other radial BPPs (#7 and #8) is small (neutral) or non-significant in all subjects. Also, except for S5 who provided consistent scores at all distances (BPPs #2 and #4 were preferred for all distances and BPP #1 rejected, with high absolute values, >200), the scores for the same BPP at far and near correlated strongly and negatively (r = −0.54, p<0.00001) indicating a reversal of preference between far and near.

On average across subjects and distances (Fig. 5(G)), BPPs #1-4 and #10 were significantly preferred (green columns, corresponding to the green dots of the last column of Fig. 4), although with small average values of perceived quality, and #9 and #11-14 were significantly rejected.

Figure 6 shows the perceived quality averaged across distances for each subject, and averaged across distances and subjects (blue line). In this figure, the BPPs (x-axis) have been re-ordered according to the ranking of patterns in the average condition (all subjects, all distances). The scores from individual subjects (symbols) follow similar trends as the average, with most subjects (but not all) preferring or rejecting patterns as predicted by the average. On the other hand, while the best perceptual quality corresponds on average to BPP #2, this was not the best pattern for most subjects (which is BPP #3 for S1, BPP#9 for S3, BPP#1 for S4 and BPP#4 for S5).

Fig. 6.

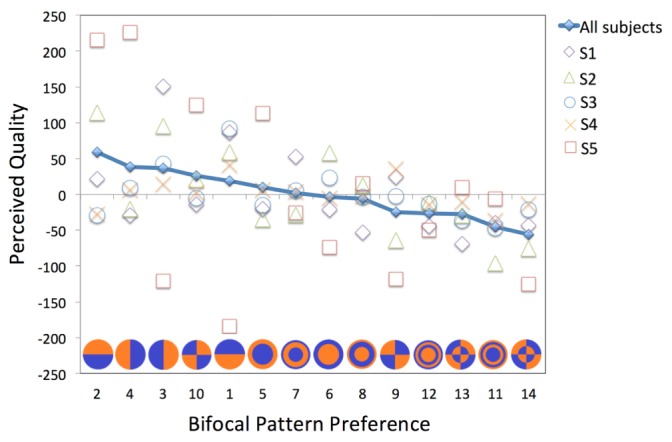
Perceived quality on an average across distances for each subject and for on an average across subjects (blue line).

While the average score was low (mean of absolute values = 32, range + 59 to −56), some subjects (S5, mean abs = 85) showed strong preferences (+ 226) and rejections (−184) and other subjects much weaker preferences (S3; mean abs = 18).

3.3 ANOVA

We studied the influence of subject, observation distance and BPP on the perceived quality score, using ANOVA. If all distances were considered, observation distance was, by far, the strongest statistical factor (p = 0) on perceived quality. However, if the data set from intermediate distance was removed from the analysis, the observation distance was not a significant factor (far and near vision are equivalent conditions, on average), and the patient factor was significant (p = 0). In both cases (considering intermediate distance or not), BPP design and observation distance had a significant combined effect (p = 0.01). Patient and observation distance also had a significant interaction (p = 0) in all cases.

3.4 Ocular aberrations

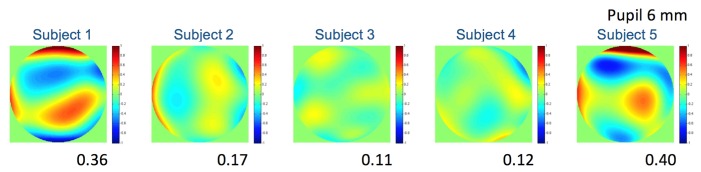
Figure 7 shows the ocular high order aberration wavefront maps (with their respective RMS) of the five subjects. Coma was the prediminant aberration in S1, S2, S4 and S5, while trefoil was the predominant aberration in S3.

Fig. 7.

Ocular wave aberration maps, and corresponding RMS in microns, for the five subjects.

3.5 Perceived quality vs optical quality

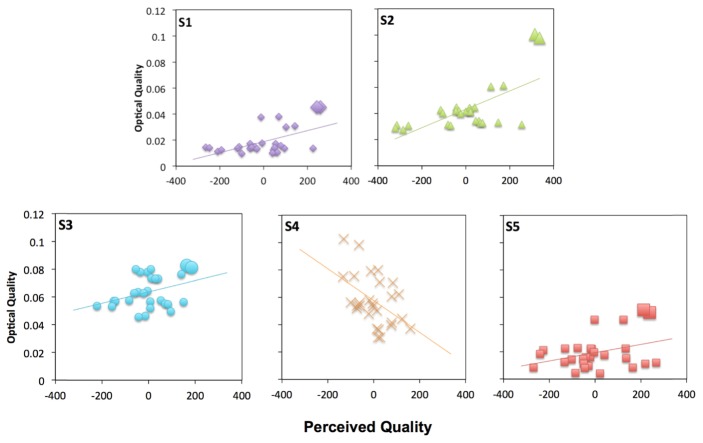
Figure 8 shows correlation plots between the measured perceived quality and the simulated optical quality for all the BPPs, both at near and far distances. In 4 out of the 5 subjects (S1, S2, S3 and S5) the BPP producing the highest optical quality score (big symbols) matched the subjectively most preferred pattern. The correlation between perceived and image quality was highly statistically significant for subjects S1 and S2 (R>0.54 and p<0.005), and marginally significant for S3 and S5 (R<0.34 and p = 0.07). However, subject 4, with high optical quality, showed a negative correlation (R = −0.47, p = 0.01), and the optical simulation did not predict the preferred pattern.

Fig. 8.

Perceived Quality vs Optical Quality (Strehl Ratio) for all subjects at far and near distances. Each symbol represents a different pattern.

4. Discussion

The Simultaneous Vision Simulator allows simulating non-invasively bifocal corrections in subjects before the implantation or fitting of the multifocal correction, or even before a particular correction is manufactured. In a previous study we simulated pure simultaneous vision [11], an ideal situation in which the entire pupil is used for far vision and near vision at the same time, as it occurs in diffractive designs. On the other hand, computational studies have shown that the specific pupillary distribution for near and far produces differences in the thru-focus optical performance both in diffraction-limited eyes with multizone radial and angular distributions [14, 24]), and in real eyes with angular bifocal patterns at different orientations [16, 25]. The new simultaneous vision simulator presented in this study is capable of simulating any bifocal pupillary pattern, optically programmed by means of a Spatial Light Modulator, expanding the capability of simulating any refractive bifocal design. This capability of switching from one BPP to another allows direct psychophysical comparisons of pairs of corrections in the same subject and without the need of fitting or implanting corrections.

We simulated 14 radial and angular segmented patterns (all of them with same addition and energy split between far and near vision) and found strong systematic perceptual differences across patterns, subjects, and observations distances. In general, patterns with semicircular far and near zones were preferred over other designs (BPPs #1-4, Fig. 4) and the preferences tended to change between far and near distances. However, we also found these preferences to be patient-specific (Figs. 5 and 6).

Differences in pattern preferences across subjects seem at least in part be driven by differences in the ocular aberrations. The low, but significant correlation between optical and perceived visual quality indicates some predictive power of Strehl Ratio as an estimator of pattern preference. The multifocal pattern producing the best perceived quality was well predicted by optical simulations in 4 out of 5 subjects. Optical predictions failed to predict the responses in one subject with very low amounts of aberrations.

Interestingly, high differences in performance were found with the same pattern at different orientations (i.e. BBP #1 - 4 in subjects S1, S2, S4 and S5, and BPPs #9-10 in subjects S1, S2 and S5), likely due to the differences arising from different optical interactions of the near and far zones with an asymmetric wavefront. Incidentally, the subject showing the strongest orientation preferences (S5, Fig. 5(E)), is the subject with the largest amounts of coma. The effect of pattern orientation, and the interaction with the ocular wavefront, is a matter of interest that has been further investigated using the simultaneous vision simulator developed here [26].

The experiments and simulations were conducted at a 6-mm diameter pupil. While the study indicates that the technique can differentiate across lens designs, further work may focus on potential differences in natural viewing conditions (generally with smaller pupil diameters).

The two-channel nature of the simultaneous vision simulator used in this study limited the tested patterns to bifocal corrections. However, other designs beyond bifocal are penetrating the market, i.e. Trifocal e.g., FineVision (PhysIOL Inc), AT LISA (Zeiss) [27, 28] and extended depth of focus [4]. Also, studies based on optical simulations [14] predict differences in performance when increasing the number of zones in multizonal patterns (i.e. 3- and 4- zone angular designs outperforming other configurations). Simulation of multifocal patterns needs to be addressed integrating alternative technology into visual simulations, such as phase masks [29, 30] phase inducing SLMs [31, 32] or temporal multiplexers [33, 34].

5. Conclusions

Significant perceptual differences were found across the different far/near pupillary distributions of bifocal corrections, which varied across subjects and distances. The best perceived pattern can be predicted to a large extent from the ocular aberrations. A two-channel simultaneous vision simulator allows subjective validation of the bifocal patterns producing the best visual quality by including both optical aberrations and potential neural effects.

Funding

European Research Council (ERC) (ERC-AdG-294099) and Spanish Government. Plan Nacional de I+D+i (FIS2011-264605, FIS2014-56643-R) to SM; EU FP7 Marie Curie Initial Training Network OpAL (PITN-GA-2010-264605) to AR; CSIC JAE-Pre Program to PdG; Spanish Government. MEyC FPI Predoctoral Fellowship to LS.