Intracellular dynamics measurements with full field optical coherence tomography suggest hindering effect of actomyosin contractility on organelle transport

Abstract

Intracellular motion can be quantitatively monitored in tissues using coherence-gated microscopic techniques. With full-field optical coherence tomography (FFOCT), the use of high numerical aperture microscope objectives provides a high resolution mapping of intracellular dynamics that are probed with subwavelength sensitivity. In the upper temporal bandwidth that we have used (1-6 Hz) the main contribution to the dynamic signal arises from the overall dynamical, optically heterogeneous cytoplasm. We propose a method to specifically study the impact of actomyosin contractility on the intracellular dynamic signal by performing high throughput, comparative measurements of multicellular aggregates with and without blebbistatin action, a selective inhibitor of class-II myosins that disrupts actomyosin contractile activity. Our results indicate a significant increase in the fraction of the signal that decorrelates within 1 second after inhibition of contractility. This observation mitigates the anticipated importance of actomyosin contractile forces to directly move organelles, but highlights their role in hindering organelle transport via their stiffening effect of the viscoelastic cytoplasm.

Introduction

Morphological changes of living cells during cellular processes (such as motility, division, and differentiation) partly result from the active remodeling of the cytoskeleton. Using a large range of exogenous probes and force sensing, microrheology of cells has brought multiple evidences that the cytoskeleton plays a pivotal role in cell mechanics [1]. The dense actin-cortex confers its elasticity to the cytoplasm, and is then expected to hinder the motion of these probes. However this is not what is observed in living cells. The trajectories of probes do not follow the expected characteristic of subdiffusive, hindered, transport but rather follow fast diffusive motions. This is due to cytoskeletal forces driven by molecular motors activity, which dominate their motion [2,3]. Fast, apparently diffusive, motions are generated by the “stirring” forces of the cytoskeleton. Inhibition of class-II myosin motors with blebbistatin treatment [4] lead to a major reduction in the apparent diffusion of injected nanoparticles and endogenous vesicles that can be tracked with high numerical aperture bright field microscopy [5]. Little is known, however, to which extend the myosin II-generated forces drive the motion of micron-sized organelles, because their motion is not easily tracked with adequate accuracy using conventional tracking techniques based on time-lapse imaging. Other motor proteins, and in particular dyneins, are known to directly move organelles and this can be observed with fluorescence microscopy.

The myosin II-generated displacement of 100 nm particles and vesicles is small and diffusive, in the order of 10⁻² μm².s⁻¹ [5]. For larger organelles, it is expected to be smaller, and less accurately measurable with fluorescence microscopy. Microrheology of embedded probes also show that inhibition of myosin II activity also leads to a 2-3 fold softening of the cytoplasm due to the annihilation of the actin tensile forces [5,6], which may actually ease the motion of large organelles through the cytoskeletal mesh [2]. To investigate whether the active forces generated by class-II myosin motors mostly drive or hinder the motion of intracellular components, we performed a comparative study of intracellular dynamics with/without blebbistatin treatment in multicellular aggregates. Intracellular dynamics were measured with Full-Field Optical Coherence Tomography (FFOCT) [7], a coherent-gated interferometric microscopy with high spatial resolution and nanometric phase sensitivity.

Coherent-gated interferometric microscopy techniques, namely Digital Holographic Optical Coherence Imaging [8] (DHOCI) and Optical Coherence Tomography [9] (OCT) have the ability to measure intracellular dynamics in label free tissues, via temporal analysis of the coherent signal [10–14]. At each pixel, the interferometric nature of the signal provides the sensitivity to measure intracellular motion at the nanometer scale. Coherent-gated microscopies probe non-specifically cellular components that scatter light, and provide a spatially-averaged measurement of the temporal dynamics of scatterers weighted by their scattering efficiency. Robust methodologies have been recently introduced to quantitatively compare intracellular dynamics over large data sets in different experimental conditions. They rely on the use of reproducible biological models, such as multicellular aggregates, and a correct data interpretation. In particular, the influence of the signal strength is generally addressed by computing normalized motility metrics. It allows comparison of data acquired with non-optimal instrumentation, at increased imaging depth in the tissue, or in regions of tissues that scatter more light [10–13]. Alternatively, the response of multicellular aggregates to a variety of anti-cancerous drugs has been monitored as normalized change of the entire temporal spectrum of DHOCI, with respect to the initial spectrum before drugs were injected [14]. This provides time-frequency normalized spectrograms of drug-induced perturbation of intracellular dynamics in large multicellular aggregates, with high potential for improving cancer treatment [15].

With FFOCT, a dynamical contrast unravels the cytoplasm of individual cells in tissues [16]. Here, we studied the influence of actomyosin contractility on the dynamics of the cellular components probed by FFOCT. The analysis is based on the spatial average of the temporal autocorrelation function (ACF) of the FFOCT signal computed on pixel basis, which is a straightforward and standard approach for analyzing dynamical signals with coherent-gated interferometric microscopy [17]. We will start by describing our analysis of the ACF, and in particular the contrast that it carries when it is analyzed as a 2D image, at fixed short-time lag (<1s). We demonstrate that the ACF alone fulfill many of the requirements generally associated to the analysis of interferometric signal. After proper normalization by the overall signal strength, the amplitude of the fast decay of the ACF quantifies the relative fraction of cellular component that undergo fast motion. We provide experimental evidences that the inhibition of actomyosin contractility after blebbistatin treatment increases the dynamics of the FFOCT signal, and that this effect is important for intracellular components with a strong FFOCT signal. Our work therefore suggests that the actomyosin contractile activity represents more an obstacle rather than a motor for organelle transport, and demonstrate the capability of FFOCT to quantify the motion of intracellular components after specific changes in biophysical conditions.

Methods

Optical setup

The FFOCT system used in this study is a commercially available system manufactured by LLTECH (Paris, France, Princeton USA). It uses a halogen lamp (KL 1500 compact, Schott) as a spatially and temporally incoherent illumination light source. The overall spectral response of the system sets the depth resolution of the microscope to a 1 μm optical thickness (full width at half maximum), which in combination to the 0.3 numerical aperture of the microscope objective gives an isotropic resolution close to 1 μm³ at the central 625 nm wavelength. The recently updated CMOS camera (Adimec, the Netherlands) has a 2 million electron full well capacity, which is mostly illuminated by the light coming from a silicon reference mirror (reflectivity 0.175). These two parameters set the noise level for a single FFOCT acquisition to −80 dB when operating in the two-phase mode. In this mode, one FFOCT image is obtained from the subtraction of two consecutives CMOS images acquired with the reference mirror axially shifted with a piezoelectric actuator by ±λ/8 from the focus position of microscope objective of the reference arm. We obtain a mapping of the backscattered light at a 1 μm³ resolution, with a minor −5 dB drop in signal at the 60 microns imaging depth in a spheroid.

Spheroid preparation and observation

The multicellular aggregates were produced using the cellular capsules technology, an high throughput microfluidic system to produce and grow multicellular spheroids (MCS) inside hollow, permeable, elastic alginate shells [18]. Spheroids were produced either with human colorectal adenocarcinoma (HT29) or murine colon carcinoma (CT26) cell lines. Spheroids were grown and imaged in a temperature and pH controlled environment (Fig. 1). Few days after the encapsulation step, small spheroids are formed with a typical diameter of 100 microns.

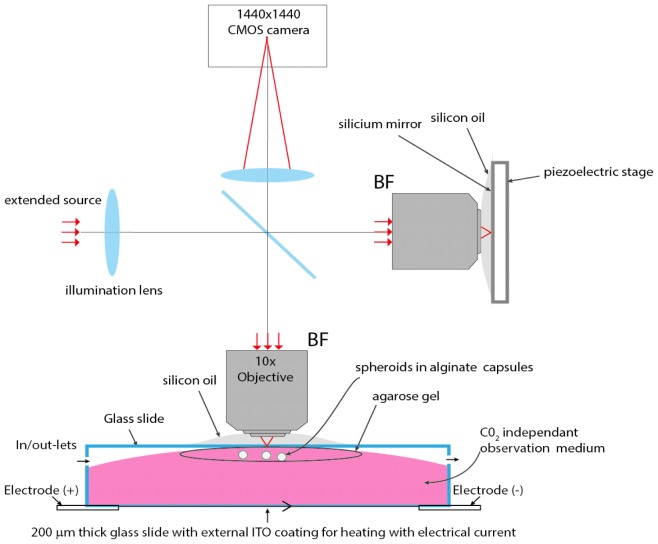
Fig. 1.

Experimental setup to image encapsulated spheroids. A spatially and temporally incoherent light source is imaged at the back focal plane BF of two identical microscope objectives using an illumination lens. The spatial extend of the source generates small and isotropic (1μm³) observation volumes (voxel) from which light is backscattered and interferes with the beam reflected by a silicon reference mirror. Encapsulated spheroids are mechanically stabilized in an agarose gel, and maintained at 37°C temperature via an active temperature control performed at the lower glass side, which is coated with ITO.

In the FFOCT setup, tissues are continuously exposed to a red light irradiance of 5mW/mm², with negligible phototoxicity. More than 50 aggregates were observed within two hours at each experimental condition, in a CO₂ independent culture medium, with no noticeable change of intracellular dynamics during the time course. We equipped the microscope with a temperature-controlled chamber (Delta T system, Bioptechs Inc.) to maintain suitable cellular metabolism during observation. The system consists of a glass window with a conductive Indium Tin Oxyde (ITO) coating that heats the observation medium. The coating is located 6 mm below spheroids, so that fast temperature changes that occurs during the active control of the temperature do not introduce measurable optical path length difference.

Alginate capsules are transparent to visible light, which enables conventional microscopy. It nevertheless provides a weak FFOCT signal that allowed us to avoid analyzing spheroids that are confluent to the capsule, and to check that the optical system had reached thermal equilibrium. Thirty minutes after the spheroids were placed below the microscope and the heating started, thermal drift were still observable as a slow decorrelation of the FFOCT signal in approximatively 20 seconds. This drift eventually disappeared approximatively 30 minutes later, and was then found to introduce negligible decorrelation over the 80 second acquisition time. We were able to image spheroids with minimal dead time between measurements. We carefully investigate the imaging chamber following a raster pattern to prevent from measuring the same spheroid twice. The 60 μm imaging depth was set relative to each spheroid apex with a fast in-depth screening of the spheroid at a 10 μm axial step.

30μM of blebbistatin was added to the 5ml observation medium 30 minutes before placing the spheroids under the microscope, and we waited another one hour to reach thermal equilibrium. We were confident that this time should be sufficient, as previous reports on the effect of blebbistatin on the dynamics of the cytoskeleton indicate noticeable changes 20 min after the drug injection.

Data analysis

Series of 500 FFOCT images were acquired at a 6.25 Hz rate, with the CMOS camera working at a 125 Hz frame rate. Each FFOCT image is computed from the accumulation of 10 frames for each of the two piezo positions:

$$OC{T}_{ij}\left(t\right)\approx 2\sqrt{I_{ij}^r\times I_{ij}^s\left(t\right)}\cos \left({\varphi }_{ij}\left(t\right)\right)$$ (1)

where I^r is the dominant, homogeneous intensity reflected from the reference arm. I^s and ϕ are respectively the intensity and phase of the backscattered light from the sample at pixel i,j on the camera. The ±λ8 shift of the piezo introduces a phase difference, which removes the D.C. term of the detected intensity after subtraction of the two accumulated frames. Due to the tissue dynamics, the OCT signal averages to zero when observed over a significantly long period of time (typically a few seconds). It is a time-varying signal that arises from the coherent sum of light backscattered from an ensemble of sub-wavelength scatterers located within the 1 μm³ voxel of the microscope.

For each pixel ij of the camera, we estimate the ACF of the FFOCT signal:

$$AC{F}_{ij}(\tau =m\times dt)=\frac{1}{N-m}{\displaystyle \sum _{k=0}^{k=N-1-m}OC{T}_{ij}(k)\times OC{T}_{ij}(k+m)}$$ (2)

N = 500 is the total number of FFOCT frames per acquisition, and dt = 0.16 s the time lag between two consecutive FFOCT frames.

In the cytoplasm, the FFOCT signal was found to be homogeneously distributed, and highly dynamic. On a typical acquisition, the FFOCT signal partly decorrelates over a time scale in the order of 1 second. This decorrelation can be imaged by investigation of a 2D image, M_ij=ACF_ij(τ=dt)-ACF_ij(τ=1 s). Figure 2(b) shows a typical M_ij images of individual cells in a CT26 spheroid, with the FFOCT setup used in this study. The lack of specificity is definitely the main challenge of coherent microscopies. We interpret the FFOCT signal as originating from organelles (except the nuclei), without being able to distinguish them. The nuclei are visible as circular regions with fainter dynamic signal (Fig. 2(b)). Membranes also are found to marginally contribute to the dynamic signal, as there is a dark intercellular space between neighboring cells (Fig. 2(b)). From a geometrical perspective, the 1 µm axial resolution of the microscope is much smaller than a cell (10-20 µm) and cellular membranes are therefore expected to marginally contribute to the signal. Protein complexes are not expected to significantly contribute to the FFOCT signal, which in general drastically diminishes with the size of the scatterer.

Fig. 2.

Dynamic contrast with FFOCT provided by the fast decay of the ACF, M_ij. (a) Spheroid imaged at the 60 μm imaging depth of this study, with the LLTECH setup. (b) Individual cells imaged with the LLTECH setup (linear gray map with 2 dynamic range).

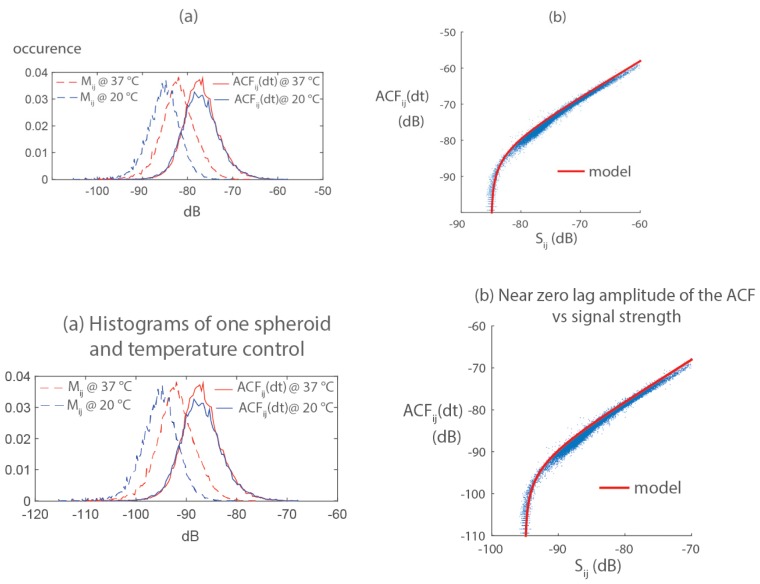
For a given spheroid, the mean value of M_ij increases by 3dB when the temperature of the experimental setup varies from 20°C (room temperature) to 37°C, but this effect does not appear on ACF_ij(dt) (histograms of Fig. 3(a)). M_ij depends on both the strength and the dynamics of the signal, because the autocorrelation as defined in Eq. (2) is not normalized. Being not modified by the temperature change, we concluded the near zero lag amplitude ACF_ij(dt) mostly carries the information of the strength of the FFOCT signal and little about its dynamics. This observation is confirmed by the correlation, for a given acquisition at each pixel ij, between the signal strength $S_{ij}={\displaystyle \sum _{k=1}^{k=N}\left|OC{T}_{ij}\left(k\right)\right|}$ and$AC{F}_{ij}(dt)$, in agreement to the following model (Fig. 3(b)):

Fig. 3.

The near zero lag amplitude of the ACF_ij(dt) carries the information of signal strength: (a) Histograms of the fast decorrelation M_ij and the zero lag amplitude of correlation ACF_ij(dt), for the same spheroid at 20°C and 37°C. ACF_ij(dt) is not affected by change in temperature that promotes intracellular motion. (b) ACF_ij(dt) is strongly correlated to signal strength S_ij.

$$S_{ij}^2=\frac{2}{\pi }\left({\mathit{\text{ACF}}}_{ij}(dt)+n^2\right)$$ (3)

where n² corresponds to the noise floor of the microscope in the acquisition settings of our experiment, $n^2={10}^{-96/10}$. Equation (3) indicates that the FFOCT signal $OC{T}_{ij}$ follows the $\mu =\sqrt{2/\pi }\times \sigma$ rule of a zero-mean, normally distributed random variable of standard deviation$\sigma$and mean of the absolute value μ. The variance of the FFOCT signal is the sum of the noise-filtered variance $AC{F}_{ij}(dt)$ and the variance of the noise n². The overall variance mostly depends on the strength of the scatterer located around pixel ij, and is barely affected by intensity fluctuations at the pixel ij.

In this work we have used ACF_ij(dt) as a metric of signal strength to normalize the ACF. The normalization was performed after spatial averaging, in order not to increase the noise. With coherent-gated microscopies, proper normalization with signal strength is a key step to quantitatively compare the dynamics of intracellular motion probed [10–13]. It reduces the variability in signal strength due to non-optimal instrumental setting during image acquisition. We have analyzed the dynamics of the FFOCT macroscopically, invoking the small size and limited imaging depth of the spheroids, for which no major biophysical inhomogeneity was expected. We spatially averaged the ACF of all pixels ij in the image of a spheroid: $ACF(\tau )={\langle ACF(\tau )\rangle }_{ij\in spheroid}$ . Spheroid contours were manually defined during a first pre-processing step. The normalized ACF were robustly adjusted with a biexponential function over the [dt-10 s] interval:

$$\frac{ACF\left(\tau \right)}{ACF(dt)}=\alpha e^{-\tau /T_1}+\left(1-\alpha \right)e^{-\tau /T_2}$$ (4)

T₁ is a fast decorrelation time, in the order of 0.5-1 s, and T₂ is a slower decorrelation time in the order of 3-10 seconds. The fit parameter α is the overall fraction of the ACF that decorrelates within T₁. It is independent of the strength of the signal thanks to the normalization by the ACF at zero lag, and was interpreted in this work as a metric of intracellular dynamics normalized by signal strength. The α parameter was typically in the 0.1-0.4 range.

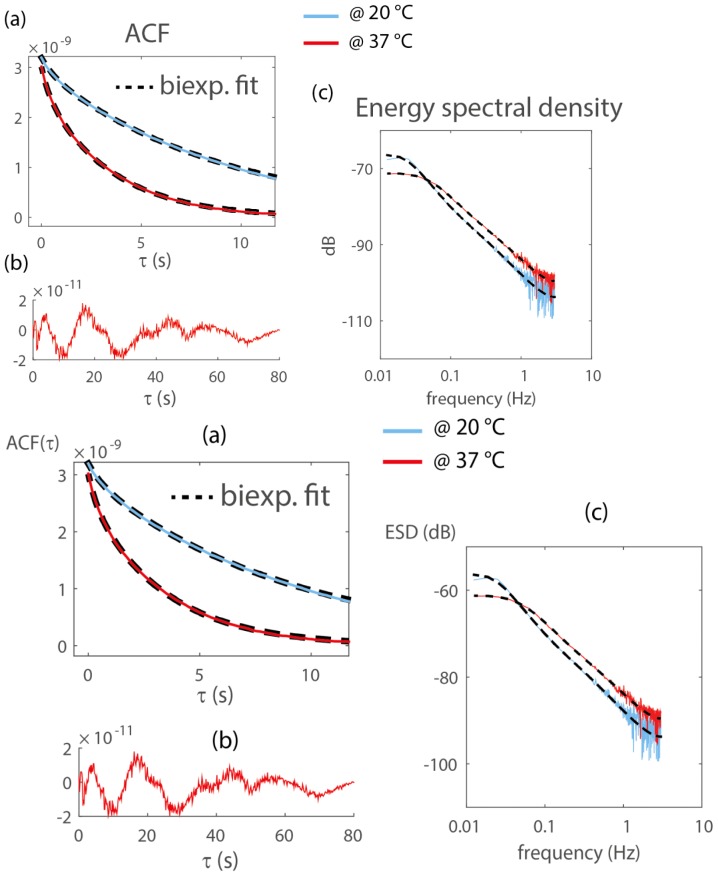
Figure 4(a) shows the spatially averaged ACF and the biexponential fit of the same data as Fig. 3(a) (same spheroid at 37°C and 20°C). Here, no normalization was performed to highlight the independence of the near-zero lag ACF with signal dynamics, as discussed above. Typical residual of the fit show a 1% discrepancy over the [0.16-80] s time lags covered by this experiment (Fig. 4(b)). Biexponential fits allow for a fairly accurate representation of the ACF with 3 parameters, but are also known in many field of physics to accurately fit continuous distribution of characteristic times. Alternatively, intracellular dynamics can be analyzed in the frequency domain [11,13,14]. Fourier transform of Fig. 4(a) (invoking the Wiener–Khinchin theorem) reveals that increased intracellular dynamics increases the higher frequency content of the Energy Spectral Density (ESD) by 5 dB, and induce a change of slope in its linear decay in the 0.1-1 Hz band, from −1.7 to −1.6 (Fig. 4(c), on a double logarithmic scale). These two effects are captured by the Fourier transform of the biexponential fits.

Fig. 4.

(a) Spatially-averaged ACF function of the same spheroid at 37°C and 20°C. The ACF are not normalized to illustrate that increased intracellular motion does not modify the near zero lag amplitude, which is a measure of signal strength. Temperature control at 37°C increases α (0.08 to 0.13), and reduce the fast T₁ (0.7 to 0.36 s) and slow T₂ (9 to 3.4 s) decorrelation times. (b) Typical residual from the biexponential fit, which show fluctuations of normalized amplitude 1%. (c) Same data as (a) in the frequency domain. Increased intracellular motion at 37° increase the slope of the spectrum in the [0.1-1] Hz band, and its high frequency plateau by 5dB.

Results and discussion

Normalization of the ACF by a metric of signal strength reduces the variability related to non-optimal conditions in the image acquisition, and allows to compare population-averaged values of the dynamic metric α, as the previously reported motility metric [10–13]. After inhibition of myosin II after treatment with blebbistatin, we measured a consistent increase of α for the two cellular phenotypes (Fig. 5). Consistently with previous reports of motility metric measurements with DHOCI [10], a fairly large variability is obtained in each experimental condition and different cell types give different distribution in the α measurements. The more proliferative and motile phenotype (CT26 in this work) gives higher values of α. In comparable experimental conditions, no difference between the two cell types was found in the decorrelation times T₁ and T₂. Control experiments 7 days after the spheroid encapsulation gave T₁0.47s (0.35/0.57) and T₂ = 4.2 s (3.4/4.8) for the CT26 cells (71 spheroids), T₁0.47s (0.38/0.58) and T₂ = 3.6 s (3.3/3.9) for the HT29 cells (57 spheroids). (Brackets give the 66% quantiles). In contrary to the α measurements, decorrelation times were later found to be correlated with the day after the aggregate synthesis.

Fig. 5.

Distribution of the α values with and without blebbistatin for two cell types. (71 and 75 CT26 spheroids were measured in the control and in the experiment with blebbistatin respectively. 57 and 47 HT29 spheroids were measured in the same experimental conditions).

The increase in α after blebbistatin treatment can unambiguously be related to an overall increase in the speed of transport of intracellular components. Two interpretations lead to the same conclusion that lower α values are a landmark of reduced dynamics. We can either interpret α as the fraction of cellular components with dynamics at the (fast) T₁ scale, and (1-α) represents the fraction of other components at the (slow) T₂ scale. With this interpretation, enhanced values of α with blebbistatin show the transfer of a fraction of cellular components from the T₂ to the T₁ scale. Alternatively, α can be interpreted as a partial decorrelation of the signal of an ensemble of cellular components with similar (but possibly uncorrelated) dynamics. In this case lower α values (without blebbistatin) indicate longer lasting correlation of the FFOCT signal, which is a landmark of hindered (possibly subdiffusive) transport. The transport of cellular components that backscatter light above the noise floor of the FFOCT instrument is significantly faster after annihilation of actomyosin contractility. At similar blebbistatin concentration, a 2-fold reduction of the cytoplasmic stiffness was reported on single cell using optical tweezer [5] and atomic force microscopy [6]. Elastic stiffness is known to hinder particle transport in a viscoelastic medium at short timescale (1-5 seconds for the cytoplasm). Our results may therefore have mechanical origins. How this observation correlates to the increased cellular migration in confined environments after blebbistatin treatment [19] remains an open question. Our results appear compatible with this observation, yet at the intracellular scale.

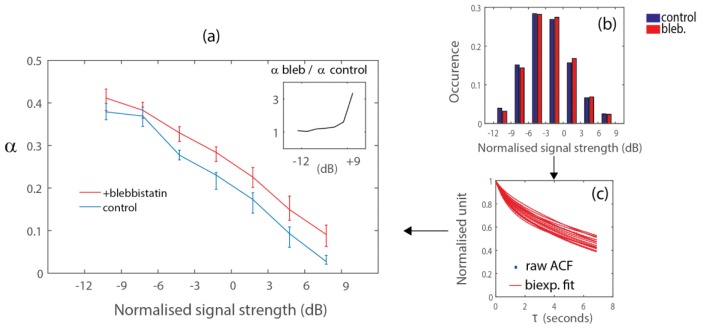
Recent microrheology experiments have highlighted the role of the actomyosin contractility in the dynamics of embedded particles of size 100-500 nm and endogenous vesicles [5]. The conclusion that many organelles should also experience the same stirring effect driven by the actin network is not validated by our FFOCT experiments. Whether the actomyosin contractility has a hindering or driving effect in cellular components most probably depends on the size of the intracellular components. With coherent-gated microscopy, the contribution of the light backscattered by large cellular components is expected to hide the contribution of smaller components within the same detection voxel. Because we spatially averaged the ACF, we also tend to exacerbate this effect. Consequently, the fraction of signal from small cellular components for which tensile forces have a predominantly stirring effect might have been hidden by the process of spatial averaging. An alternative approach to investigate this question is to average the ACF in bins of signal strength, after normalization by the overall signal strength of all pixels. We can then compare population-averaged α values, with/without blebbistatin, for cellular components that yield similar signal strength (Fig. 6(a)). We defined the normalized signal strength as the ratio$AC{F}_{ij}(dt)/ACF(dt)$, i.e. after normalization by the overall signal strength in the spheroid. Histograms of normalized signal strength show that this distribution is not affected by blebbistatin treatment (Fig. 6(b)). Within each group of the histogram, we adjusted a biexponential fit to the ACF of each spheroid (Fig. 6(c), for normalized signal strength of 4.5 dB). Figure 6(a) shows the median value and the 66% quantile of parameter α, for the control and blebbistatin experiment with CT26 cells. The ratio of α values (with/ without blebbistatin, inset of Fig. 6(a)) is above unity, which shows that the motion of all cellular components probed with FFOCT are actually hindered by tensile forces. The increase of the ratio with signal strength (inset) indicates that the transport of large, highly scattering, cellular components is actually more hindered by the stiff cytoplasm in the control experiment. A ratio below 1 would correspond to the stirring effect of actomyosin contractile forces on intracellular motion, and was not detected in our experiment. We expected to observe this in the domain of weak scattering strength in Fig. 6(a), where microtubules and vesicles might contribute significantly to the FFOCT signal.

Fig. 6.

(a) Population-averaged α response to blebbistatin treatment for CT26 aggregates, as a function of the normalized scattering strength. Error bars represent the 66% quantile, for 71 (control) and 75 (with blebbistatin) CT26 spheroids. All cellular components probed with FFOCT undergo faster transport after blebbistatin treatment (α values are higher with blebbistatin, for all values of signal strength. Inset: The transport of strongly scattering, most probably larger, cellular components is more affected by blebbistatin treatment. (b-c) Processing steps to plot (a): (b) sort pixels in bin of signal strength, normalized by the overall signal strength of the acquisition; (c) adjust biexponential parameters for each spheroid, at a given normalized signal strength.

The analysis described in Fig. 6 is a promising approach to simultaneously unravel the two antagonist effects of actomyosin contractile forces on the motion of intracellular components. We anticipate that the use of a FFOCT prototype at higher numerical aperture (0.8) might give the sufficient sensitivity and spatial resolution to detect the motion of smaller intracellular components, for which the actomyosin contractile forces have a stirring effect. With this FFOCT prototype, we obtain a 30 dB signal increase of M_ij in comparable experimental conditions (Fig. 7, versus Fig. 2). The physical explanation for this effect is that subwavelength scatterers are predominant in living cells, so that the mostly isotropic backscattered light is better collected by high numerical aperture objectives. This remark makes the FFOCT technic a very good approach to investigate tissue dynamics. The LLTECH commercial microscope uses a 0.3 numerical aperture microscope, which is still 5 to 10 times higher than conventional point scanning OCT. With the observed increase 30dB increase in signal at 0.8 numerical aperture, the stirring effects of the cytoskeleton on microtubules and vesicles might appear on the analysis of Fig. 6(a). It may provide a global picture of the role of actomyosin contractile forces in intracellular dynamics. This implies additional technical improvement to use our FFOCT prototype for high-throughput measurements of spheroids in a thermalized environment.

Fig. 7.

Dynamic contrast with FFOCT provided by the fast decay of the ACF, M_ij. (a) Spheroid imaged at the 60 μm imaging depth of this study with the 0.8 numerical aperture FFOCT prototype. (b) Individual cells imaged with the prototype (linear gray map with 2 dynamic range).

The shape of the ACF does not bear unambiguous information about the type of transport, especially in the heterogeneous cytoplasm. Coherent microscopy probes non-specifically cellular components that scatter light, and the measurement of spatially averaged ACF provides an overall measurement of all dynamical components weighted by their scattering efficiency [20]. Assuming that intracellular motions are mostly sensed along the z-axis of the microscope, i.e. with respect to the backscattering wavevector$q=4\pi /\lambda$, exponential decays with characteristic time T can be attributed to diffusion $D=1/q^{2}T$ or direct transport of cellular components with uncorrelated velocities in the order of $V=1/qT$ [13,20,21]. We interpreted the α parameter as the fraction of the FFOCT signal emitted by intracellular components that undergo transport at the T₁ 1 s scale. As Brownian motion, it corresponds to a diffusivity of $1.4\times {10}^{-3}\mu m^2/s$, which is smaller than the lower bound of diffusive like transport in cells [22]. Interpretation of the T₁ dynamics as direct transport is therefore more likely. It corresponds to a characteristic velocity of $4\times {10}^{-2}\mu m/s$, i.e. in the order of organelle transport [23]. At the $3<T_2<10$ s scale, the slow dynamics of intracellular components might also originate from a direct transport compatible with organelle motion$(3.7\times {10}^{-3}<V<1.2\times {10}^{-2}\mu m/s)$, or could alternatively be attributed to the long lasting correlation of subdiffusive motions [24].

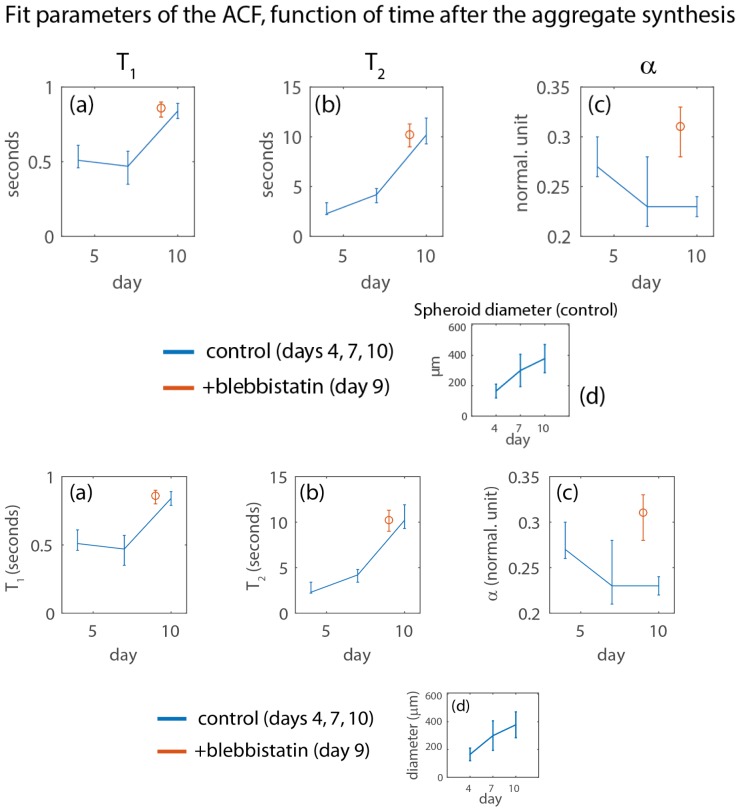
We found that the measured decorrelation times T₁ and T₂ are highly correlated with the time after the aggregate formation (Fig. 8(a)-8(b), data in blue), but marginally influenced by blebbistatin treatment (red circle in Fig. 8(a)-8(b)). These results do not mitigate the significance of the change in α parameters after blebbistatin treatment (Fig. 8(c)). They suggest significant changes at the cellular level during the first week after the aggregate formation, which to our knowledge, have never been observed in previous studies. We carefully measured all spheroids at a fixed 60 μm imaging depth from the aggregate apex, i.e. at an average distance of around 30 μm from the periphery of the aggregates, to ensure that no significant gradient of oxygen or nutrients would affect our study [25]. The diameter of each spheroid was estimated form the knowledge of the imaging depth and the area covered by the spheroid on the FFOCT image, under the assumption that it is spherical. In agreement to previous studies using the same methodology to form aggregates of CT 26 cells [18], the aggregates doubled their diameter within a week, indicating that there was no anomaly in their culture (Fig. 8(d)). From a mechanistic point, reduced intracellular dynamics as the spheroid growths may be induced by the increased confinement of individual cells. Increased cellular density is observed in the peripheral region of a growing spheroid (“proliferative rim”, of typical thickness 70 μm for CT26 aggregates), where cell divisions occur faster than the spheroid growth [26]. Alternatively, our data could indicate an unreported phenotypic change of the aggregated cells. Discerning between the two scenarios will require to design new experiments in which our methodology will play a pivotal role.

Fig. 8.

(a-c) Fit parameters measured during the first week after aggregate synthesis, for the CT26 cells. Median values are represented, and the error bars limits the 66% quantiles. (d) Estimated diameter of the CT26 spheroid during one week. Numbers of measured CT26 spheroids are 38, 71, and 44 for the control experiment on days 4, 7, and 10. We measured 75 spheroids for the blebbistatin experiment on day 9.

Given the limited depth at which we performed our measurements, we are confident that multiple scattering marginally influence our data. Hence, the FFOCT signal result from cellular components located in the detection voxel. Our data indicate that the temporal dynamics are homogenous at the 60 µm imaging depth in the spheroids, away from their necrotic cores. The applicability of our method to probe intracellular dynamics deeper in the spheroids and in heterogeneous tissues remains to be validated. In general, we do not expect to observe regions in the spheroid where the signal decorrelates orders of magnitude faster than in other regions, so that the shadowing effect observed in blood flow Doppler-OCT should not occur. At the 60 µm imaging depth, we are confident that the motion of organelles inside the coherence volume decorrelates the FFOCT signal, while the motion above the coherence gate introduces spatio-temporal variation of the optical path with second order effect on the dynamics of the FFOCT signal.

Conclusion

With FFOCT, we have analyzed in multicellular aggregates a dynamic signal that mostly originates from the cytoplasm. The potential of FFOCT to reveal cellular activity was previously reported [16] with a technique named Dynamic FFOCT (DFFOCT). By revealing only moving scatterers, DFFOCT highlights subcellular activity in complex heterogeneous tissues and adds a complementary contrast to the traditional mapping of signal strength with FFOCT. Here in this work, we have analyzed multicellular aggregates at a limited distance from the periphery, where cells have a high activity and the FFOCT signal is dynamical everywhere in the aggregates. We investigated the motion of intracellular components over two temporal decades through the analysis of the ACF. In a bandwidth limited to [0.01-6] Hz, we measured significantly different temporal dynamics of intracellular components in different experimental conditions.

For this study, LLTECH improved the sensitivity of their FFOCT microscope with a new CMOS camera, which decreases the noise floor of the system by 10 dB. At the imaging depth of 60 μm, the dynamic signal of the cytoplasm was consistently above the noise floor of the LLTECH system when the acquisition rate was reduced to 6 Hz, with a 10 frames averaging. Correlation-based data analysis also reduces the impact of noise by temporal filtering. As previous associates in the field of coherence gated microscopy, we have noted the necessity to spatially average the ACF in order to obtain smooth, quantifiable profiles. We also investigated a method to normalize the dynamic signal by the signal strength, in order to quantitatively compare large data sets. After spatial averaging over the entire cell aggregate, the normalized dynamical contrast corresponds to a fraction (0.1<α<0.4) of the ACF that decorrelates within approximatively 1 second. Measurements at a fixed imaging depth of 60 μm in multicellular aggregates revealed interesting differences in the measurement of α parameters. In particular, it indicates that the annihilation of actomyosin contractility on overall increases the motion of intracellular components.

Funding

This research is supported by the INSERM program-Physique-Mathématiques-Sciences de l’ingénieur et Cancer and the Fondation Pierre-Gilles de Gennes.