Abstract
Measurement of the double-pass (DP) point-spread function (PSF) can provide an objective and non-invasive method for estimating intraocular scatter in the human eye. The objective scatter index (OSI), which is calculated from the DP PSF images, is commonly used to quantify intraocular scatter. In this article, we simulated the effect of higher-order ocular aberrations on OSI, and the results showed that higher-order ocular aberrations had a significant influence on OSI. Then we developed an adaptive optics DP PSF measurement system (AO-DPPMS) which was capable of correcting ocular aberrations up to eighth-order radial Zernike modes over a 6.0-mm pupil. Employing this system, we obtained DP PSF images of four subjects at the fovea. OSI values with aberrations corrected up to 2nd, 5th and 8th Zernike order were calculated respectively, from the DP PSF images of the four subjects. The experimental results were consistent with the simulation, suggesting that it is necessary to compensate for the higher-order ocular aberrations for accurate intraocular scatter estimation.
OCIS codes: (170.4460) Ophthalmic optics and devices, (110.1080) Active or adaptive optics, (170.0110) Imaging systems
1. Introduction
It has long been known that the human eye suffers from intraocular scatter that degrades retinal image quality. Intraocular scatter consists of forward scatter and backward scatter. In ophthalmology, forward scatter is of more importance [1], because it produces a veiling light over the retina and a reduction in retinal contrast, whereas backscattered light theoretically only reduces the amount of light reaching the retina [2]. The forward scatter is especially relevant to specific situations [3,4], such as cataracts [3] or post-surgery eyes [5–7], where the ocular media transparency and/or the regularity of the optical surfaces of the ocular system could be affected [1]. It is valuable to quantify ocular scatter to aid in better understanding of the visual performance of the patient.
The double-pass (DP) technique provides combined information of both aberrations and small-angle intraocular scatter [8]. Based on this technique, measurement of small-angle intraocular scatter can be performed by calculating a parameter called ocular scatter index (OSI) [9]. OSI is defined as the ratio of the amount of light within an annular area of 12 and 20 arcmin to that recorded within a circular area with a one arcmin radius centered on the central peak of the acquired DP PSF image [9]. This method has been applied for estimating intraocular scatter in cataract eyes [9] and dry eyes [10].
The accuracy of intraocular scatter estimation using OSI depends on several factors. DP point-spread function (PSF) contained all the relevant information including pupil diffraction, ocular aberrations and scatter [1]. Hence, to accurately quantify intraocular scatter, the effect of aberrations and pupil diffraction needs to be minimized. Regarding the effect of ocular aberrations, P. Artal et al. [9] measured the OSI of DP PSF images as a function of defocus to get the acceptable range of uncorrected refractive errors (defocus and astigmatism). Meanwhile, compared with the values calculated from the measured aberration data in the same eye, they selected the peripheral zone where the effect of scatter was significant and the effect of aberrations was small. However, the effect of aberrations on the peripheral zone of PSF would lead to a misleading estimate of intraocular scatter in situations where a significant amount of higher-order aberrations is presented [1], such as in diseased eyes which have larger higher-order aberrations than healthy eyes [11, 12]. On the other hand, to obtain complete optical transfer function of the eye, most DP systems were based on an unequal pupil configuration with a 1.5-mm or 2-mm diameter in the entrance pupil and a 4-mm diameter in the exit pupil [9, 13]. The light distribution in the peripheral zone of PSF increases with smaller pupil size because of pupil diffraction. Hence, small pupil sizes may affect the intraocular scatter estimation through OSI values. Employing the DP technique, M. A. Nanavaty et al. [4] quantified the amount of light scatter in patients with uveitis. They suggested that larger pupil sizes could be more appropriate for the specific case of uveitis. P. Artal et al. [9] used the OSI values to classify cataracts. They found that there was minor variability in the PSF images due to the small entrance pupil and pointed out that this problem could be avoided with a larger entrance pupil. However, ocular aberrations increased with the pupil size, so the effect of the ocular aberrations over large pupils should not be neglected. Therefore, it is interesting to investigate the effect of higher-order aberration on OSI and whether more accurate OSI values can be achieved by measuring the DP PSF with higher-order ocular aberrations corrected over a large pupil. To achieve retinal phase contrast imaging, E. Logean et al. [14, 15] measured double-pass PSF over a large 6.7-mm pupil with ocular aberrations corrected by adaptive optics (AO). Their results showed that DP PSFs with ocular aberrations corrected by AO had higher image quality than those obtained without AO correction. However, they used a 35-element bimorph deformable mirror (DM) to correct ocular aberrations, which could not meet the requirement of ocular aberrations correction to reach near diffraction-limited imaging [16].
In this article, we first simulated the effect of ocular aberrations on OSI. To validate the simulation results, we developed an AO DP PSF measurement system (AO-DPPMS) with a 145-element PZT deformable mirror, which was capable of correcting ocular aberrations up to eighth-order radial Zernike modes over a 6.0-mm pupil. Employing this system, we obtained near diffraction-limited DP PSF images of four subjects at the fovea and calculated the half-width at half-maximum (HWHM) for each DP PSF image. OSI values with ocular aberrations corrected to either the 2nd, 5th or 8th Zernike order were obtained to evaluate the effect of ocular aberrations on intraocular scatter estimation.
2. Methods
2.1 Simulating the effect of ocular aberrations on OSI
To quantify the effect of ocular aberrations on intraocular scatter estimation, we simulated the DP process using Matlab (Mathworks, Natick, Massachusetts). This simulation was based on the theory that the DP image is proportional to the cross-correlation between the PSF of the first-pass and that of the second-pass [17, 18]. In order to quantify the effect of ocular aberrations on OSI for both large and small pupils, the DP PSFs were calculated based on the optical parameters of two systems. In the first system (System 1), the entrance pupil was 6-mm in diameter with its central 1.5-mm obscured, and the exit pupil was a 6-mm diameter clear aperture, corresponding to the actual configuration of the adaptive optics ophthalmoscope in our lab [11]. The second system (System 2) was based on an unequal pupil configuration with a 2-mm entrance pupil and a 4-mm the exit pupil described as refs. [9, 13]. The data of ocular aberrations in this study included 300 virtual healthy eyes (normal group) and 300 virtual diseased eyes (abnormal group). These virtual eyes were generated by two statistical wavefront aberration models which were constructed as a multivariate, Gaussian, random variable with known mean, variance and covariance [19] based on normative data from 332 healthy eyes and 344 diseased eyes [11], respectively.The single-pass PSFs were first calculated by the optical parameters and data of the ocular aberrations. Then DP PSFs were achieved by the cross correlation of the single-pass PSFs [17, 18].
The OSI values with aberrations corrected up to different Zernike orders were calculated for each eye. These OSI values were divided into four groups by system and eye group. Group 1 was calculated based on the configuration of System 1 with aberrations in abnormal group. Group 2 was calculated based on the configuration of System 1 with aberrations in normal group. Group 3 was calculated based on the configuration of System 2 with aberrations in abnormal group. Group 4 was calculated based on the configuration of System 2 with aberrations in normal group. The statistical results were calculated for each group.
2.2 AO-DPPMS system
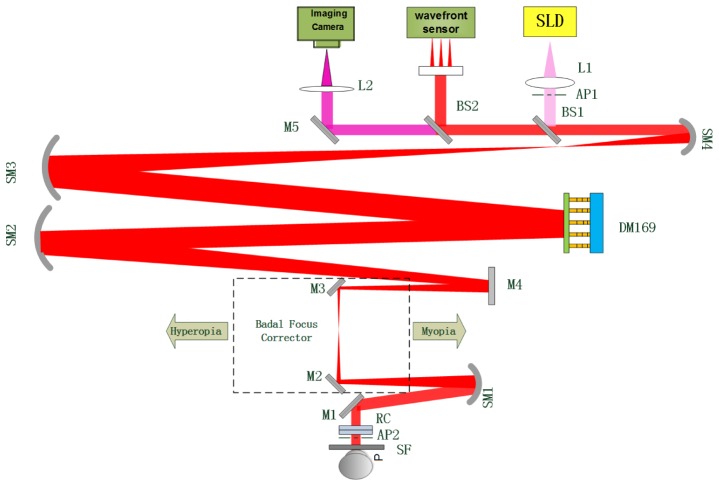
In order to validate the simulation results, an AO DP measurement system was developed. Figure 1 is the schematic diagram of the AO-DPPMS system, which consists of an illumination path, an observation path and a wavefront sensing path. In the illumination path, the light from a super-luminescent diode (SLD, λ = 795nm, Δλ = 18.8nm) was collimated by a lens L1. The use of near-infrared light provided more comfortable viewing conditions and higher retinal reflectance, and the SLD was used to reduce speckle in the DP images [17]. After reflected by a beam splitter BS1, the light passed through the 145-element PZT DM and a series of relay optics (SM 1-4, M2-4) for pupil matching, and was directed into the eye by a reflecting mirror M1. The optical path was folded by a mirror M4 to make the system more compact. In the observation path, the reflected light from the eye fundus passed along the reverse optical path to BS1. Then it travelled by BS2, a mirror M5 and an imaging lens L2 before forming the DP PSF image on the CCD camera (View Works Inc., Korea). In the wavefront sensing path, part of the light from the eye fundus was reflected by the beam splitter BS2 onto a 16 × 16 SHWS. The wavefront slope data measured by the SHWS were processed to reconstruct wavefront and the direct slope control algorithm was used to drive the DM to correct ocular aberrations in real-time over a 6.0 mm pupil. In this system, defocus and astigmatism were corrected by means of a pair of rotating cylinders (RC) in combination with a Badal focus corrector. The range of correction was ± 4 D spherical and ± 3D cylindrical.
Fig. 1.
Schematic diagram of the AO-DPPMS system. SLD, super-luminescent diode; SM, spherical mirror, BS, beam splitter; M, mirror; DM, 145-element PZT deformable mirror; L, lens; AP1, artificial entrance pupil; AP2, artificial exit pupil; RC, rotating cylinders; SF, scatter filter.
In the system, the artificial entrance pupil AP1 was a 6-mm diameter aperture with its central 1.5-mm obscured to avoid corneal reflection, and the artificial exit pupil AP2 was a 6-mm diameter clear aperture. The SLD was pre-corrected by the DM prior to focusing on the subject’s retina, so that the ocular aberrations were corrected in the entrance pupil. The aberration correction capability of the DM was previously demonstrated [11].
2.3 Calculation of the diffraction-limited DP PSF
For comparison with the measured DP PSF, a theoretical diffraction-limited DP PSF of our system was calculated based on optical parameters. We first calculated the single-pass PSF of the illumination path and the observation path, respectively. The single-pass PSF images of the illumination path and the observation path are shown in Fig. 2(a) and Fig. 2(b), respectively. The DP PSF of a diffraction-limited optical system can be achieved by the cross correlation of its single-pass PSFs [17, 18]. The calculated diffraction-limited DP PSF (DL-PSF) for the AO-DPPMS system is shown in Fig. 2(c). The HWHM of the DL-PSF was 0.30 arcmin.
Fig. 2.
Single-pass PSF image of the illumination path (a) and observation path (b), and calculated DP PSF image (c) of our system.
To assess the influence of diffraction (pupil size) on DP PSF measurement, the theoretical diffraction-limited DP PSF of the system (DPPMS) with a 2-mm diameter entrance pupil and a 4-mm diameter exit pupil was also calculated. The single-pass PSF images of the illumination path and observation path are shown in Fig. 3(a) and Fig. 3(b), respectively. The DL-PSF for the DPPMS system is shown in Fig. 3(c). The HWHM of the DL-PSF was 0.77 arcmin.
Fig. 3.
Single-pass PSF image of the illumination path (a) and observation path (b), and calculated DP PSF image (c) of the DPPMS system.
2.4 Measurement of the DP PSF images and calculation of the OSI values
Four subjects (CH, HSY, LB, ZLN) aged between 23 and 39 years participated in this study. The subjects had refractive errors between −4.0 and 4.0 diopters. Informed consent was obtained from the subjects after a full explanation of the procedures and possible consequences of this study. Pupil was dilated with 1% cyclopentolate solution before data collection. The power of the SLD at the pupil was always kept no more than 60 μW during the experiment, which was far below the maximum permissible exposure for continuous viewing at this wavelength [20]. The short 10-ms exposure helped to prevent motion blur resulting from the movement of the retina during each exposure.
Three series of DP PSF were obtained in the experiment, all of which were taken at the fovea. Series 1 was achieved with defocus and astigmatism corrected. Series 2 was obtained with aberrations corrected up to the 5th Zernike order. Series 3 was obtained with aberrations corrected up to the 8th Zernike order. A constant bias level obtained from an unexposed corner of the CCD camera was subtracted for each image.
Then we calculated OSIs of the subjects for different values of intraocular scatter. Five DP PSF images were taken to calculate the OSI values for each eye. These five OSI values were averaged as the final value of the OSI.
3. Results
3.1 Calculating OSI values with ocular aberrations based on optical parameters of two systems
The statistical OSI values calculated with aberrations corrected up to different Zernike orders based on the optical parameters of System #1 are shown in Table 1. OSI values in the abnormal group were larger than those in the normal group. This was because higher-order aberrations in the abnormal group were larger than those in the normal group [11]. It can be seen that correction of aberrations up to the 5th Zernike order was necessary to reduce the OSI value to 0.5 (mean value plus one standard deviation (std)) or less for the normal group, while correction of aberrations up to the 6th order was needed for the abnormal group. In addition, to reduce the OSI value to 0.1 or less, correction of aberrations up to the 7th Zernike order was necessary for both groups.
Table 1. OSI values calculated with aberrations corrected up to different Zernike orders based on optical parameters of System 1.
| OSI values |
Zernike orders |
||||||
|---|---|---|---|---|---|---|---|
| 2 | 3 | 4 | 5 | 6 | 7 | ||
| Normal | mean std |
1.31 | 0.46 | 0.13 | 0.09 | 0.05 | 0.02 |
| 2.02 | 1.00 | 0.64 | 0.60 | 0.37 | 0.03 | ||
| Abnormal | mean std |
2.18 | 1.13 | 0.33 | 0.12 | 0.08 | 0.03 |
| 2.46 | 1.66 | 0.65 | 0.19 | 0.15 | 0.04 | ||
Table 2 shows statistical OSI values calculated with aberrations corrected up to different Zernike orders based on the optical parameters of System #2. Correction of aberrations up to the 3th Zernike order was necessary to reduce the OSI value to 0.5 or less for both the normal and abnormal group. To reduce the OSI value to 0.1 or less, correction of aberrations up to the 4th Zernike order was necessary for both the normal and abnormal group.
Table 2. OSI values calculated with aberrations corrected up to different Zernike orders based on optical parameters of System 2.
| OSI values |
Zernike orders |
||||||
|---|---|---|---|---|---|---|---|
| 2 | 3 | 4 | 5 | 6 | 7 | ||
| Normal | mean std |
0.59 | 0.08 | 0.04 | 0.04 | 0.04 | 0.04 |
| 1.27 | 0.09 | 0.010 | 3.40e-3 | 3.14e-4 | 2.80e-5 | ||
| Abnormal | mean std |
0.89 | 0.09 | 0.05 | 0.04 | 0.04 | 0.04 |
| 2.87 | 0.07 | 0.02 | 2.33e-3 | 6.60e-4 | 7.50e-5 | ||
3.2 Correction of the ocular aberrations in AO-DPPMS system
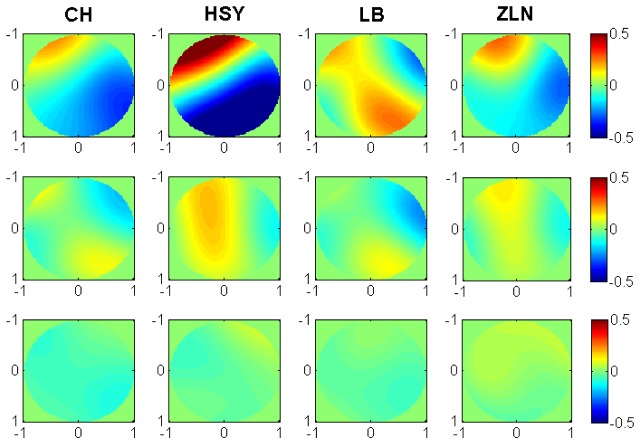
Figure 4 shows the residual wavefront profiles of the left eyes of the four subjects for different aberration correction strategies. The wavefront with defocus and astigmatism corrected is shown in the first row. The root mean square (RMS) aberration except tip and tilt was 0.51, 0.42, 0.24 and 0.39μm for Subject CH, HSY, LB and ZLN, respectively. In the second row, the images were the wavefront with aberrations corrected up to the 5th Zernike order, and the RMS aberration for each subject was 0.091, 0.094, 0.075 and 0.104μm, respectively. The images in the third row were wavefront with aberrations corrected up to the 8th Zernike order, and the RMS values for each subject were 0.047, 0.049, 0.043, and 0.046 μm, respectively. These values were smaller than λ/14 (0.057μm) for all subjects, demonstrating that the AO-DPPMS system had the ability to accomplish near diffraction-limited imaging.
Fig. 4.
Wavefront for the left eyes of the four subjects (CH, HSY, LB and ZLN) with different aberration correction strategies for a 6-mm pupil (with pupil coordinate normalized). First row, wave aberration for subjects CH, HSY, LB and ZLN with defocus and astigmatism corrected; second row, wave aberration for subjects CH, HSY, LB and ZLN with aberrations corrected up to the 5thZernike order; third row, wave aberration for subjects CH, HSY, LB and ZLN with aberrations corrected up to the 8thZernike order. The unit of the legend is μm.
3.3 Effect of ocular aberrations on DP PSF measurements in AO-DPPMS system
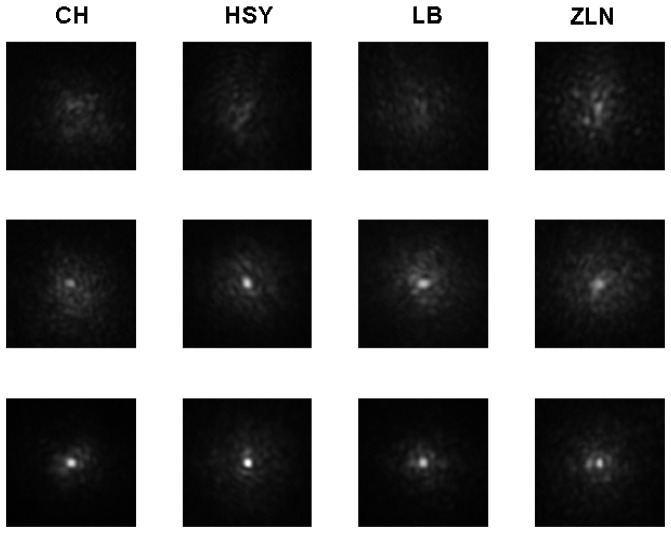
We acquired the DP PSF images for both eyes of all subjects at the fovea through the AO-DPPMS system. The typical images for the left eyes of the subjects are shown in Fig. 5. The images with defocus and astigmatism corrected (Series1) are shown in the first row. In the second row, the images were obtained with aberrations corrected up to the 5th Zernike order (Series 2). The images in the third row were achieved with aberrations corrected up to the 8th Zernike order (Series 3).
Fig. 5.
The typical DP PSF images measured at the fovea for the left eyes of subjects in AO-DPPMS system with different aberration correction strategies. First row, DP images for subjects CH, HSY, LB and ZLN with defocus and astigmatism corrected in the AO-DPPMS system; second row, DP images for subjects CH, HSY, LB and ZLN with aberrations corrected up to the 5th Zernike order with AO-DPPMS system; third row, DP images for subjects CH, HSY, LB and ZLN with aberrations corrected up to the 8th Zernike order with AO-DPPMS system. The image width was 8 arcmin.
Compared to Series 1, Series 2 and 3 had obvious reductions in PSF spatial extent and increases in contrast, suggesting that higher-order aberrations degraded the DP PSF. To make a quantitative assessment of the DP PSF, the HWHM of the measured DP PSF was calculated for each subject. Each HWHM value was the average result of five DP PSF images. The HWHM values of all subjects for different aberration correction strategies are shown in Table 3. The values of HWHM in Series 1 and Series 2 were larger than those in Series 3. Hence, correcting the ocular aberrations up to 8th Zernike order was necessary to achieve high-resolution DP PSF image. The HWHM values in series 3 were close to the DL-PSF, manifesting that AO-DPPMS has the ability to provide near diffraction-limited DP PSF measurement.
Table 3. HWHM in arcmin of all subjects with different aberration correction strategies.
| Subject | CH | HSY | LB | ZLN | ||
|---|---|---|---|---|---|---|
| HWHM | 2nd (Series1) | 1.13 | 1.09 | 1.17 | 1.75 | |
| 5th (Series 2) | 0.46 | 0.49 | 0.46 | 0.52 | ||
| 8th (Series 3) | 0.34 | 0.37 | 0.35 | 0.39 | ||
3.4 Effect of the ocular aberrations on estimating intraocular scatter
To assess the effect of ocular aberrations on estimating intraocular scatter, we calculated the OSI values from the DP PSF images of each subjectfor different aberration correction strategies. As OSI is intended for eyes with significant amounts of scatter, two scatter filters SF1 (Tiffen, BPM 1/2) and SF2 (Tiffen, Pro Mist 1/2) were used in front of one normal eye to simulate the scatter effect in cataract [21]. The results with ocular aberrations corrected up to the 2nd, 5th and 8th Zernike order are shown in Table 4. Series1 and Series 2 were commonly larger than Series 3. Series 1 were 1.5~2.7 times larger than Series 3, and the difference between Series 2 and Series 3 were in the range of 0.19~0.47.
Table 4. OSI values for both eyes of subjects with different aberration correction strategies.
| Subject | Eye | OSI values | ||
|---|---|---|---|---|
| 2nd(series1) | 5th(series2) | 8th(series3) | ||
| CH | LE | 2.42 | 1.37 | 0.90 |
| CH | RE | 2.2 | 1.26 | 0.88 |
| HSY | LE | 1.98 | 0.99 | 0.82 |
| HSY | RE | 2.04 | 1.16 | 0.91 |
| LB | LE | 2.18 | 1.55 | 1.12 |
| LB | RE | 2.05 | 1.31 | 0.96 |
| ZLN | LE | 1.75 | 1.29 | 0.83 |
| ZLN | RE | 1.91 | 1.05 | 0.82 |
| HSY + SF1 | LE | 4.24 | 3.18 | 2.98 |
| HSY + SF2 | LE | 4.76 | 3.67 | 3.48 |
4. Discussion
OSI values were achieved with higher-order ocular aberrations uncorrected in previous studies [4, 9, 10]. In the current work, we simulated the effect of higher-order ocular aberrations on OSI. The simulation results showed higher-order ocular aberrations had a significant influence on OSI values. For the system used in previous studies [4, 9, 10], correction of aberrations up to the 3th Zernike order was necessary to reduce the OSI value introduced by aberrations to 0.5 or less for both normal and abnormal eyes. Our result showed that the OSI values achieved with only defocus and astigmatism corrected may be suspicious. To validate the simulation results, we acquired the OSI values from the DP PSF images achieved with different aberration correction strategies using the proposed AO-DPPMS system. The difference between the OSI values with aberrations corrected up to the 5th Zernike order and the 8th Zernike order was in the range of 0.17~0.47, which was consistent with the simulation results. The average value of OSI with aberrations corrected up to the 2nd Zernike order was about 2 times of the value expected from healthy eyes without defocus and astigmatism with the DPPMS system. This phenomenon may be caused by the large pupil in our system. Large pupil allowed more scattered light to be detected, and the effect of higher-order aberrations on OSI increased with pupil sizes. In addition, previous studies [11,12] showed that there were larger amounts of higher-order aberrations in the diseased eyes than in the healthy eyes. Presumably, the effect of higher-order aberrations on the OSI value should be larger in diseased eyes. Therefore, it is necessary to correct higher-order aberrations for accurate estimate of intraocular scatter. In order to simulate the scatter effect in cataract [21], OSI values with two scatter filters SF1and SF2 in front of one normal eye were obtained with different aberration correction strategies. The results also showed that higher-order ocular aberrations had a significant influence on OSI values, suggesting that simulation results were suitable for eyes with significant amounts of scatter in clinical situations.
To assess the accuracy of our results, we compared our OSI values with that reported in a previous study. To establish an objective gradation for cataracts, P. Artal et al. [9] calculated the OSI values in 53 eyes including 15 normal eyes. Their results showed that the OSI values in normal eyes were 0.7 ± 0.3 (mean ± standard deviation). The OSI values obtained with aberrations corrected up to the 8th Zernikeorder in our study were 0.92 ± 0.14. The mean value in our study was larger than that reported by P. Artal et al.. One possible reason for this phenomenon is that a larger pupil size allows more scatter light to be measured. However, it should be noted that the number of subjects involved in this studyis limited and future work is needed for further verification. In addition, the annular aperture in the entrance pupil may lead to an underestimate of intraocular scatter.
Employing our system, near diffraction-limited DP PSF images can be achieved, and the effect of aberrations on estimating intraocular scatter is reduced. To the best of our knowledge, no similar near diffraction-limited DP PSF images have been reported and this is the first report on intraocular scatter estimation with higher-order ocular aberrations corrected. However, our system is limited to measuring small-angle intraocular scatter. To measure wide-angle scatter and stray-light, a modification of the DP method using an optical integration approach was proposed by H. Ginis et al. [22, 23]. It is interesting that they extended the measurement of intraocular scatter to angles up to 7 degrees. They used small sub-apertures (2 mm) to minimize the effect of aberrations and assumed that the central part of the PSF corresponded to a diffraction-limited system for both the illumination and the imaging arm. However, in cases of non-uniform distribution of scatters such as in corneal scars or localized cataract opacities, their approach might lead to an overestimation or underestimation of scattering depending on whether these defects were on the measurement paths or not [22]. Using large sub-apertures with aberrations corrected by the AO technique may be a choice to deal with this problem.
5. Conclusion
In this article, we first simulated the effect of higher-order ocular aberrations on OSI. The results suggested that higher-order ocular aberrations had a significant influence on OSI. Then an adaptive optics DP PSF measurement system was developed and established. We achieved DP PSFs for four subjects at the fovea with ocular aberrations corrected up to 8th Zernike order. The HWHMs of the PSFs were 1.13 to 1.3 times larger than the width expected from diffraction alone. The results showed the ability of AO-DPPMS to provide near diffraction-limited DP PSF measurement. Finally, we calculated OSI values from the DP PSF for four subjects with aberrations corrected up to different Zernike orders. The experimental results were consistent with the simulation, which suggested that it is necessary to compensate for higher-order ocular aberrations for intraocular scatter estimation.
Acknowledgments
The authors would like to thank Professor Wenhan Jiang for his critical comments and thoughtful suggestions. We also thank all subjects for their positive supports in this work.
Funding
National Natural Science Foundation of China (61378064); National High Technology Research and Development Program of China (2015AA020510).
References and links
- 1.Piñero D. P., Ortiz D., Alio J. L., “Ocular scattering,” Optom. Vis. Sci. 87(9), E682–E696 (2010). 10.1097/OPX.0b013e3181e87da6 [DOI] [PubMed] [Google Scholar]
- 2.Atchinson D. A., Smith G., Optics of the Human Eye (Oxford, UK: Butterworth-Heinemann, 2000). [Google Scholar]
- 3.de Waard P. W., IJspeert J. K., van den Berg T. J., de Jong P. T., “Intraocular light scattering in age-related cataracts,” Invest. Ophthalmol. Vis. Sci. 33(3), 618–625 (1992). [PubMed] [Google Scholar]
- 4.Nanavaty M. A., Stanford M. R., Sharma R., Dhital A., Spalton D. J., Marshall J., “Use of the Double-Pass Technique to Quantify Ocular Scatter in Patients with Uveitis: A Pilot Study,” Ophthalmologica 225(1), 61–66 (2011). 10.1159/000316690 [DOI] [PubMed] [Google Scholar]
- 5.McCally R. L., Freund D. E., Zorn A., Bonney-Ray J., Grebe R., de la Cruz Z., Green W. R., “Light-scattering and ultrastructure of healed penetrating corneal wounds,” Invest. Ophthalmol. Vis. Sci. 48(1), 157–165 (2007). 10.1167/iovs.06-0935 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Lohmann C. P., Fitzke F., O’Brart D., Muir M. K., Timberlake G., Marshall J., “Corneal light scattering and visual performance in myopic individuals with spectacles, contact lenses, or excimer laser photorefractive keratectomy,” Am. J. Ophthalmol. 115(4), 444–453 (1993). 10.1016/S0002-9394(14)74445-9 [DOI] [PubMed] [Google Scholar]
- 7.Hindman H. B., McCally R. L., Myrowitz E., Terry M. A., Stark W. J., Weinberg R. S., Jun A. S., “Evaluation of deep lamellar endothelial keratoplasty surgery using scatterometry and wavefront analyses,” Ophthalmology 114(11), 2006–2012 (2007). 10.1016/j.ophtha.2007.01.009 [DOI] [PubMed] [Google Scholar]
- 8.Díaz-Doutón F., Benito A., Pujol J., Arjona M., Güell J. L., Artal P., “Comparison of the retinal image quality with a Hartmann-Shack wavefront sensor and a double-pass instrument,” Invest. Ophthalmol. Vis. Sci. 47(4), 1710–1716 (2006). 10.1167/iovs.05-1049 [DOI] [PubMed] [Google Scholar]
- 9.Artal P., Benito A., Pérez G. M., Alcón E., De Casas A., Pujol J., Marín J. M., “An Objective Scatter Index Based on Double-Pass Retinal Images of a Point Source to Classify Cataracts,” PLoS One 6(2), e16823 (2011). 10.1371/journal.pone.0016823 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Benito A., Pérez G. M., Mirabet S., Vilaseca M., Pujol J., Marín J. M., Artal P., “Objective optical assessment of tear-film quality dynamics in normal and mildly symptomatic dry eyes,” J. Cataract Refract. Surg. 37(8), 1481–1487 (2011). 10.1016/j.jcrs.2011.03.036 [DOI] [PubMed] [Google Scholar]
- 11.Zhao J., Xiao F., Kang J., Zhao H., Dai Y., Zhang Y., “Statistical analysis of ocular monochromatic aberrations in Chinese population for adaptive optics ophthalmoscope design,” J. Innov. Opt. Health Sci. 10(1), 1650038 (2016). 10.1142/S1793545816500383 [DOI] [Google Scholar]
- 12.Pantanelli S., MacRae S., Jeong T. M., Yoon G., “Characterizing the wave aberration in eyes with keratoconus or penetrating keratoplasty using a high-dynamic range wavefront sensor,” Ophthalmology 114(11), 2013–2021 (2007). 10.1016/j.ophtha.2007.01.008 [DOI] [PubMed] [Google Scholar]
- 13.Artal P., Iglesias I., López-Gil N., Green D. G., “Double-pass measurements of the retinal-image quality with unequal entrance and exit pupil sizes and the reversibility of the eye’s optical system,” J. Opt. Soc. Am. A 12(10), 2358–2366 (1995). 10.1364/JOSAA.12.002358 [DOI] [PubMed] [Google Scholar]
- 14.Logean E., “On Phase Contrast Imaging of the Inner Retina,” Galway: National University of Ireland; (2009). [Google Scholar]
- 15.Logean E., Dalimier E., Dainty C., “Measured double-pass intensity point-spread function after adaptive optics correction of ocular aberrations,” Opt. Express 16(22), 17348–17357 (2008). 10.1364/OE.16.017348 [DOI] [PubMed] [Google Scholar]
- 16.Miller D. T., Roorda A., Handbook of optics, 3th ed. (McGraw Hill, 2010). [Google Scholar]
- 17.Guirao A., Lopez-Gil N., Artal P., “Double-pass measurements of retinal image quality: a review of the theory, limitations and results,” in Vision Science and its Applications, Vol. 35 of 2000 OSA Technical Digest Series (Optical Society of America, 1996), paper NW4. [Google Scholar]
- 18.Artal P., Marcos S., Navarro R., Williams D. R., “Odd Aberrations and Double-Pass Measurements of Retinal Image Quality,” J. Opt. Soc. Am. A 12(2), 195–201 (1995). 10.1364/JOSAA.12.000195 [DOI] [PubMed] [Google Scholar]
- 19.Thibos L. N., Bradley A., Hong X., “A statistical model of the aberration structure of normal, well-corrected eyes,” Ophthalmic Physiol. Opt. 22(5), 427–433 (2002). 10.1046/j.1475-1313.2002.00059.x [DOI] [PubMed] [Google Scholar]
- 20.ANSI Standard Z136.1, American National Standard for the Safe Use of Lasers (American National Standards Institute, 1993).
- 21.de Wit G. C., Franssen L., Coppens J. E., van den Berg T. J., “Simulating the straylight effects of cataracts,” J. Cataract Refract. Surg. 32(2), 294–300 (2006). 10.1016/j.jcrs.2006.01.048 [DOI] [PubMed] [Google Scholar]
- 22.Ginis H., Pérez G. M., Bueno J. M., Artal P., “The wide-angle point spread function of the human eye reconstructed by a new optical method,” J. Vis. 12(3), 20 (2012). 10.1167/12.3.20 [DOI] [PubMed] [Google Scholar]
- 23.Ginis H., Sahin O., Pennos A., Artal P., “Compact optical integration instrument to measure intraocular straylight,” Biomed. Opt. Express 5(9), 3036–3041 (2014). 10.1364/BOE.5.003036 [DOI] [PMC free article] [PubMed] [Google Scholar]