Abstract
Human tissue is one of the most complex optical media since it is turbid and nonhomogeneous. We suggest a new optical method for sensing physiological tissue state, based on the collection of the ejected light at all exit angles, to receive the full scattering profile. We built a unique set-up for noninvasive encircled measurement. We use a laser, a photodetector and finger tissues-mimicking phantoms presenting different optical properties. Our method reveals an isobaric point, which is independent of the optical properties. We compared the new finger tissues-like phantoms to others samples and found the linear dependence between the isobaric point's angle and the exact tissue geometry. These findings can be useful for biomedical applications such as non-invasive and simple diagnostic of the fingertip joint, ear lobe and pinched tissues.
OCIS codes: (290.0290) Scattering, (120.5820) Scattering measurements, (160.4670) Optical materials
1. Introduction
Human tissue is one of the most complex optical media since it is turbid and nonhomogeneous. Optical methods of sensing physiological tissue state based on light-tissue interactions are non-invasive, inexpensive and simplistic and therefore are very useful. Most of the optical methods focus on the reflected light from the tissue [1–6], which is described as a semi-infinite medium, while very few use the transmitted light [7–9].
We suggest a new optical method for sensing the physiological state of cylindrical tissues. This method is based on the collection of the ejected light at all exit angles, to receive the full scattering profile (FSP), which is the angular distribution of light intensity. The scattered light from cylindrical tissues such as fingertip, earlobe or any pinched tissue is a signature of the whole tissue.
Extracting optical properties of tissue is very important for diagnosis and therapy [10]. It is assumed that the absorption and scattering characteristics of tissue change during the progression of disease [11]. The main phenomenon that we present here is the isobaric point that we reveal by the FSP [12,13]. This point is a common point for different profiles of cylindrical tissues which are characterized by different optical properties. In other words, a single central angle where we can predict the light intensity value, which is independent of the optical properties and linearly-depends on the exact tissue geometry. In addition to the discovery of this point, the isobaric point can be useful as a reference point in optical measurement methods of sensing physiological tissue state [14]. Hence, the FSP method allows measuring in a single wavelength, so that calibration is not required.
In this paper we are presenting, for the first time, experimental results from finger tissue-like phantoms made from a silicone elastomer polydimethylsiloxane (PDMS) and glycerol mixture, what gives us the possibility to obtain phantoms mimicking biological tissue without using any nanoparticles. In many cases, the sedimentation or clustering of nanoparticles causes uncontrolled inhomogeneity of phantom properties due to uneven distribution of scattering centers. Methods which solve these problems require additional equipment; increase the time, cost, and difficulty of phantom fabrication. The particle-free phantoms, with intrinsic scattering, are perfectly homogeneous and usually easier to produce. However, a drawback of phantoms with intrinsic scattering lies in their short lifetime and reduced possibilities for introducing structures and creating multiple layers.
We fabricated particle-free optical phantoms with intrinsic scattering arising from the matrix material itself. This phantom has effective optical properties ( = homogeneous phantom), has a long lifetime of months, is stable at room temperature, flexible, inexpensive, easy to produce and easy to control scattering properties during the manufacturing process. The phantom comprises a PDMS mixed with glycerol. Both composing materials are transparent in the VIS-NIR wavelength range. This mixture creates an emulsion which is stable after curing.
Altering the optical properties of phantoms was achieved during the manufacture procedure by changing the content of glycerol in the mixture. The phantoms are designed as stable, flexible phantoms with the possible introduction of structural inhomogeneities. The procedure of producing as well as optical properties of phantoms with intrinsic scattering was described in details in a previous paper [15].
2. Materials and methods
Our suggested method measures the light from all possible angles by placing a photodiode detector on a rotation stage adjacent to an irradiated cylindrical tissue in order to measure the reemitted light, as shown in Fig. 1. The experimental set-up includes a He-Ne gas laser (Thorlabs, Newton, USA) with an excitation wavelength of λ = 632.8nm and maximum power of 5mW. The waist of the laser beam is = 0.63mm. We use a portable fixed gain silicon detector as a photo detector (PD). The PD has an active area of 0.8mm2. The voltage is measured every 5 degrees from to 1450. The scattered light between 1450 and 1800 cannot be measured due to the PD's size, which blocks the light source.
Fig. 1.
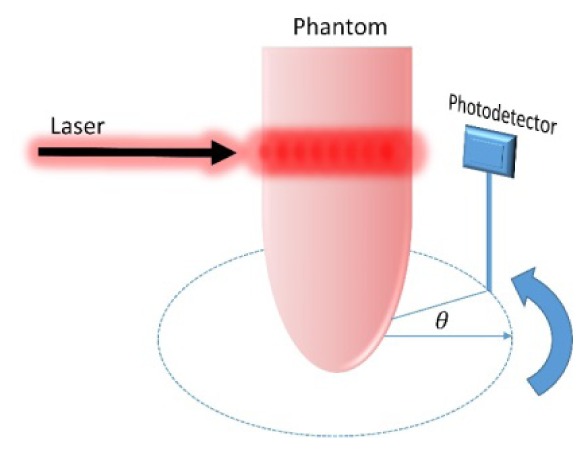
Scheme of the experimental system, where is the detector's angle.
We prepared a new type of phantoms made from PDMS and glycerol mixture. Typically, to obtain dedicated optical properties of phantoms a special set of nanoparticles are used during phantom preparation [16,17]. The uniqueness of the described phantoms is that we obtain a phantom, without using nanoparticles, with intrinsic scattering centers consisting of micron-sized cavities formed by a silicone-glycerol mixture. Such phantoms are comprising of two materials: the PDMS (Sylgard® 184, Dow Corning, USA) and glycerol (1,2,3-propanetriol) (≥ 99.5% Sigma-Aldrich). The PDMS is a two-component organic silicone which cures at room temperature over 48 hours. We have prepared three finger-shaped phantoms with different optical properties (µs' = 1.626 ± 0.015 mm–1, and 2.535 ± 0.014 mm–1; g = 0.975 at 630 nm wavelength, for the third phantom we have no data about its optical properties) without any absorbers to focus solely on the scattering profile. The phantoms were fabricated in molds with a 14mm diameter. The measurements for the optical properties of the new phantoms were conducted on thin reference samples made during the same fabrication process from the same batch of materials, as described in previous works [15,17]. We prepared different types of phantoms in order to simulate tissues with different optical properties. The new phantoms and the optical system are presented in Fig. 2. As a control we compared the new phantoms to liquid phantoms with different reduced scattering coefficients [18–20]. Those phantoms were prepared using varying concentrations of Intralipid (IL, Lipofundin MCT/LCT 20%, B. Braun Melsungen AG, Germany), as a scattering component. The IL was diluted with water. The values of the reduced scattering coefficient for four different phantoms that we choose (µs' = 0.8, 1, 1.6, 2.6 mm−1) represent the range of the human tissue values [10,21]. The phantoms are placed in test tubes with different diameters.
Fig. 2.
An irradiated finger phantom placed in the full scattering profile system. A portable photodetector collects the light intensity from all scattering directions.
3. Results
3.1 The full scattering profile and the isobaric point phenomenon
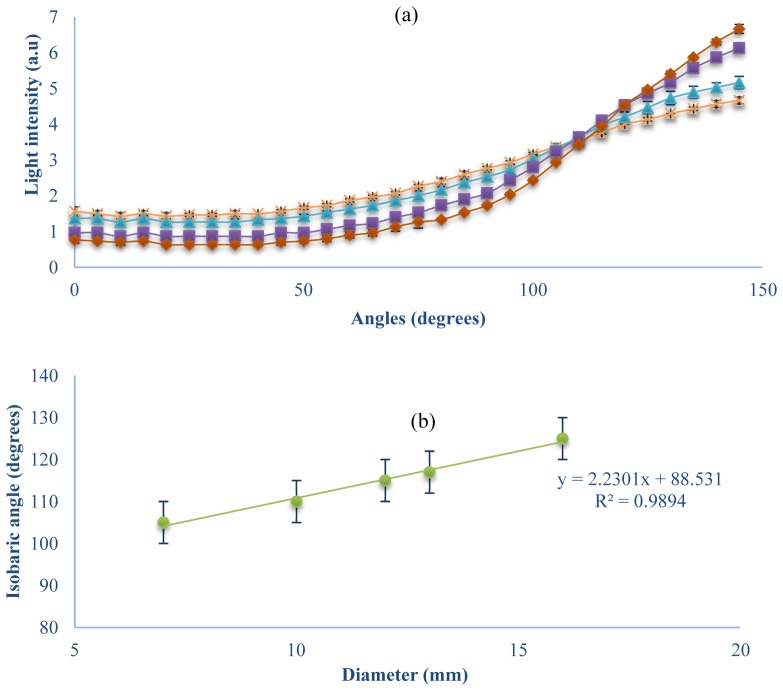
We report, an experimental observation of a typical reflected light intensity behavior of a cylindrical structure characterized by the isobaric point, in accordance to our previous works that simulated this phenomenon [12,24]. Our method allows measuring in a single wavelength with no calibration. For examining the influence of optical properties on the full scattering profile, we measured the full scattering profile of liquid phantoms with different reduced scattering coefficients between 0.8mm−1 to 1.6mm−1. The experimental results for a 10mm diameter phantom are presented in Fig. 3(a). We found a constant light intensity at one angle, even though the tissue optical properties are different, and we named it the isobaric point. This isobaric point is common for various reduced scattering coefficients at 110°. Furthermore, a linear dependence (99% fit) between the phantom diameter and the isobaric point angle was found (Fig. 3(b)).
Fig. 3.
(a) Influence of reduced scattering coefficient on the full scattering profile; Intensity of light at each angle between 0 to 145 degrees for different reduced scattering coefficients (diamond, square, triangle and x in respect to 2.6, 1.6, 1, and 0.8mm−1), where phantom diameter is 10mm. (b) Influence of phantom diameter on the isobaric point angle. A linear dependency is presented between the central angle of the isobaric point and the phantom diameter.
3.2 The full scattering profile of finger tissue-like phantoms
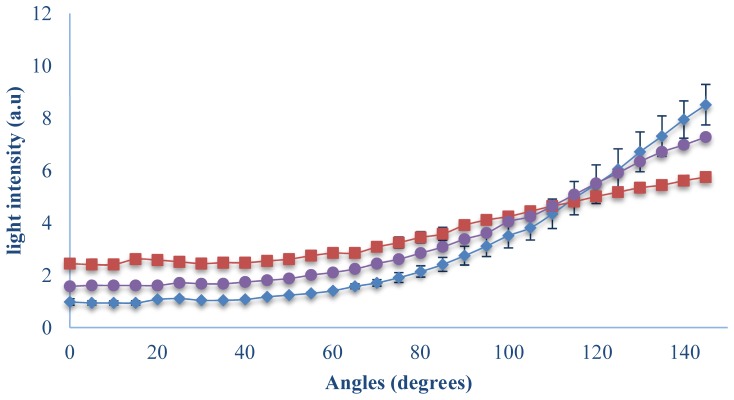
Next we measured the new finger tissue-like phantoms in the unique optical setup and the results are presented in Fig. 4. The FSPs of the known phantoms (µs' = 1.626 ± 0.015mm−1 and µs' = 2.535 ± 0.014mm–1) cross and their isobaric point is at 115°. Furthermore, although there is no optical information about the third finger-phantom, which operates as a test phantom, it has a common isobaric point, and its FSP was measured in the range between the FSPs of the two others. Hence, by using the comparison between them we can say that the reduced scattering coefficient of the testing phantom is in the range of 1.626mm−1 to 2.535mm–1.
Fig. 4.
Measurements of the full scattering profile of finger tissue-like phantoms with different reduced scattering coefficients; Intensity of light at each angle between 0 to 145° for different reduced scattering coefficients (squares circles and diamonds in respect to µs' = 1.626 ± 0.015 mm–1, testing phantom and µs' = 2.535 ± 0.014mm–1).
Moreover, the gradation of the reduced scattering coefficients of the PDMS phantoms is according to the FSP simulation and experiments of IL phantoms; at the smaller angles (transmission light) the light intensity is lower for the higher µs', and at the higher angles (reflected light) the opposite is true, so the higher light intensity is for the higher µs'.
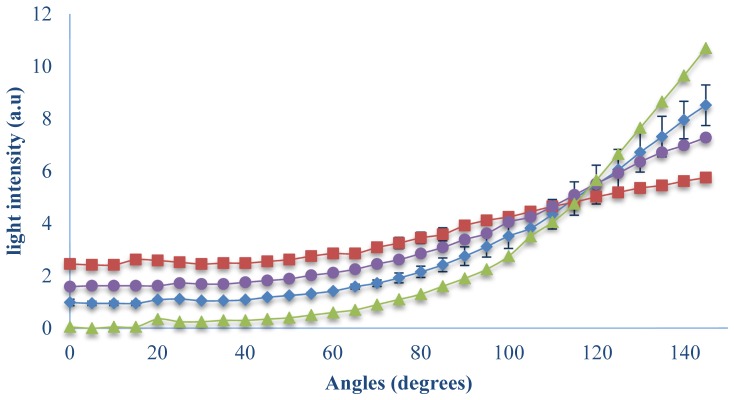
While comparing the results to the IL phantoms in a glass test tube (Fig. 3), one can see that the isobaric point fit to diameter of 13mm. This phantom characterized by µs' = 1mm−1 and contained Agarose powder in order to convert the solution into gel. The common angle is shown in Fig. 5, at 115°. At the linear fit equation of the liquid phantom experiment, the isobaric point of this diameter range is 117°.
Fig. 5.
Comparison between the full scattering profiles of PDMS finger tissue-like phantom and IL phantoms (triangles, squares, circles and diamonds represent IL phantom, PDMS phantoms: µs' = 1.626 ± 0.015 mm–1, testing phantom and µs' = 2.535 ± 0.014mm–1).
4. Discussion
Most of the optical methods for extracting optical properties deal with the light reflection, and few of them use the light transmission. At the reflection region, the light intensity is higher for a medium with higher reduced scattering coefficient, due to the fact that the light experiences more scattering events and has a high probability to back-scattering. This phenomenon has been discussed in the literature, for example in diffusion reflection articles [19, 22]. The reflection region is defined from the isobaric point to 180° in the FSP system, because of the same tendency between the profiles of different optical properties; light intensity is higher for higher µs’. The transmission region is defined between 0 degrees and the isobaric point. In this region, a higher intensity is measured in the case of a lower reduced scattering coefficient. This is in accordance with the literature, since in a lower reduced scattering coefficient the quantity of scattering events decreases and more photons succeed in crossing the medium [1,23]. When we use the full scattering profile for cylindrical tissue, we can collect the photons at all exit direction. Hence, we can use the isobaric point to define the tendency of the profiles in each region, above and below the isobaric point, in accordance with the optical properties of the cylindrical phantoms. The human tissue includes different layers and areas that are characterized by different optical properties. The homogeneous phantom is unlike the natural structure in order to simplify the experiment in its early stages. This phantom has a uniform structure that represents the effective optical properties that the photons experience through all different layers of a real tissue on average. Having presented the results for this simple structure, we can further study, a more complex model, i.e. non-homogeneous model, which claims to be more like real tissue. Hence, it is important to notice that the isobaric point has no dependence on the materials of the phantom. However, we should investigate the different material properties in relation to their absolute values in reflection and transmission.
5. Conclusion
In this work we presented experimental results of our unique set up for noninvasive simple encircled optical measurements of the angular distributions of the emitted light from cylindrical tissues. In the experimental field, using one low power CW laser and a simple detector we measured the angular distributions of the emitted light from an irradiated phantom. We present the full scattering profile of cylindrical homogeneous phantoms that mimic finger-shaped tissues. By using phantoms made from a silicone elastomer polydimethylsiloxane with different reduced scattering coefficients, we simulate different physiological states of tissues. The comparison between the angular distributions of tissues with different optical properties reveals the isobaric point, which has no dependence on the optical properties of the finger tissue-like phantom. Moreover, this isobaric point is common for phantoms that have the same diameter yet composed of different materials. These experimental results verify what we proposed in our previous work, in the simulation model of full scattering profiles and the isobaric point [12, 24].
Furthermore, it enables to obtain unknown optical properties of our phantoms which will allow us to improve their structures so that they will mimic biological tissues more precisely in the future [25]. The findings of the experimental results that we presented are relevant to cylindrical tissues such as fingertip, earlobe, lips or any pinched tissue. It can be useful for detecting physiological states using the different optical properties in the different states, like changes in the blood vessel diameters or the changes in skin scattering upon laser treatment [26, 27] that influences the full scattering profile. This new technique can be implemented in various optical methods such as NIR spectroscopy [28, 29] PPG experiments, and improves analyzing of oxygen saturation values, blood perfusion and blood pressure. The measurement of the full scattering profile during respiration, for example, will produce a range of profiles that are affected by the blood vessel diameters that change during inhalation and exhalation.
Funding
This study was partially supported by the National Science Center, Poland under the grants 2011/03/D/ST7/03540 and 2016/20/T/ST7/00380; DS Programs of the Faculty of Electronics, Telecommunications and Informatics, Gdańsk University of Technology; and European Cooperation in Science and Technology (COST) Action BM1205.
References and links
- 1.Tuchin V. V., “Light scattering study of tissues,” Phys. Uspekhi 40(5), 495–515 (1997). 10.1070/PU1997v040n05ABEH000236 [DOI] [Google Scholar]
- 2.Schmitt J. M., Knüttel A., Bonner R. F., “Measurement of optical properties of biological tissues by low-coherence reflectometry,” Appl. Opt. 32(30), 6032–6042 (1993). 10.1364/AO.32.006032 [DOI] [PubMed] [Google Scholar]
- 3.Lee P., Gao W., Zhang X., “Performance of single-scattering model versus multiple-scattering model in the determination of optical properties of biological tissue with optical coherence tomography,” Appl. Opt. 49(18), 3538–3544 (2010). 10.1364/AO.49.003538 [DOI] [PubMed] [Google Scholar]
- 4.Levitz D., Thrane L., Frosz M., Andersen P., Andersen C., Andersson-Engels S., Valanciunaite J., Swartling J., Hansen P., “Determination of optical scattering properties of highly-scattering media in optical coherence tomography images,” Opt. Express 12(2), 249–259 (2004). 10.1364/OPEX.12.000249 [DOI] [PubMed] [Google Scholar]
- 5.Schmitt J., Knüttel A., “Model of optical coherence tomography of heterogeneous tissue,” J. Opt. Soc. Am. A 14(6), 1231–1242 (1997). 10.1364/JOSAA.14.001231 [DOI] [Google Scholar]
- 6.Thrane L., Yura H. T., Andersen P. E., “Analysis of optical coherence tomography systems based on the extended Huygens-Fresnel principle,” J. Opt. Soc. Am. A 17(3), 484–490 (2000). 10.1364/JOSAA.17.000484 [DOI] [PubMed] [Google Scholar]
- 7.Pickering J. W., Prahl S. A., van Wieringen N., Beek J. F., Sterenborg H. J., van Gemert M. J., “Double-integrating-sphere system for measuring the optical properties of tissue,” Appl. Opt. 32(4), 399–410 (1993). 10.1364/AO.32.000399 [DOI] [PubMed] [Google Scholar]
- 8.Arridge S. R., Cope M., Delpy D. T., “The theoretical basis for the determination of optical pathlengths in tissue: temporal and frequency analysis,” Phys. Med. Biol. 37(7), 1531–1560 (1992). 10.1088/0031-9155/37/7/005 [DOI] [PubMed] [Google Scholar]
- 9.Spinelli L., Botwicz M., Zolek N., Kacprzak M., Milej D., Sawosz P., Liebert A., Weigel U., Durduran T., Foschum F., Kienle A., Baribeau F., Leclair S., Bouchard J. P., Noiseux I., Gallant P., Mermut O., Farina A., Pifferi A., Torricelli A., Cubeddu R., Ho H. C., Mazurenka M., Wabnitz H., Klauenberg K., Bodnar O., Elster C., Bénazech-Lavoué M., Bérubé-Lauzière Y., Lesage F., Khoptyar D., Subash A. A., Andersson-Engels S., Di Ninni P., Martelli F., Zaccanti G., “Determination of reference values for optical properties of liquid phantoms based on Intralipid and India ink,” Biomed. Opt. Express 5(7), 2037–2053 (2014). 10.1364/BOE.5.002037 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Jacques S. L., “Optical properties of biological tissues: a review,” Phys. Med. Biol. 58(11), R37–R61 (2013). 10.1088/0031-9155/58/11/R37 [DOI] [PubMed] [Google Scholar]
- 11.Lu G., Fei B., “Medical hyperspectral imaging: a review,” J. Biomed. Opt. 19(1), 010901 (2014). 10.1117/1.JBO.19.1.010901 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Duadi H., Feder I., Fixler D., “Linear dependency of full scattering profile isobaric point on tissue diameter,” J. Biomed. Opt. 19(2), 026007 (2014). 10.1117/1.JBO.19.2.026007 [DOI] [PubMed] [Google Scholar]
- 13.Feder I., Duadi H., Fixler D., “Experimental system for measuring the full scattering profile of circular phantoms,” Biomed. Opt. Express 6(8), 2877–2886 (2015). 10.1364/BOE.6.002877 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Feder I., Duadi H., Dreifuss T., Fixler D., “The influence in the full scattering profile from cylindrical tissues following changes in vessels diameter: experimental evidence for the shielding effect,” J. Biophotonics 9, 1001–1008 (2015). [DOI] [PubMed] [Google Scholar]
- 15.Wróbel M. S., Popov A. P., Bykov A. V., Tuchin V. V., Jędrzejewska-Szczerska M., “Nanoparticle-free tissue-mimicking phantoms with intrinsic scattering,” Biomed. Opt. Express 7(6), 2088–2094 (2016). 10.1364/BOE.7.002088 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Wróbel M. S., Popov A. P., Bykov A. V., Kinnunen M., Jędrzejewska-Szczerska M., Tuchin V. V., “Multi-layered tissue head phantoms for noninvasive optical diagnostics,” J. Innov. Opt. Health Sci. 08(03), 1541005 (2015). 10.1142/S1793545815410059 [DOI] [Google Scholar]
- 17.Wróbel M. S., Popov A. P., Bykov A. V., Kinnunen M., Jędrzejewska-Szczerska M., Tuchin V. V., “Measurements of fundamental properties of homogeneous tissue phantoms,” J. Biomed. Opt. 20(4), 045004 (2015). 10.1117/1.JBO.20.4.045004 [DOI] [PubMed] [Google Scholar]
- 18.Ankri R., Taitelbaum H., Fixler D., “On Phantom experiments of the photon migration model in tissues,” The Open Optics Journal 5(1), 28–32 (2011). 10.2174/1874328501105010028 [DOI] [PubMed] [Google Scholar]
- 19.Ankri, R., H. Duadi, and D. Fixler. “A new diagnostic tool based on diffusion reflection measurements of gold nanoparticles,” SPIE BiOS. (2012). [Google Scholar]
- 20.R. Ankri, “Non Invasive Optical Technique for the Investigation of Tissue Structure and Physiology,” Ph.D. Thesis, 4–11 (2012). [Google Scholar]
- 21.Friebel M., Roggan A., Müller G., Meinke M., “Determination of optical properties of human blood in the spectral range 250 to 1100 nm using Monte Carlo simulations with hematocrit-dependent effective scattering phase functions,” J. Biomed. Opt. 11(3), 034021 (2006). 10.1117/1.2203659 [DOI] [PubMed] [Google Scholar]
- 22.Reif R., A’Amar O., Bigio I. J., “Analytical model of light reflectance for extraction of the optical properties in small volumes of turbid media,” Appl. Opt. 46(29), 7317–7328 (2007). 10.1364/AO.46.007317 [DOI] [PubMed] [Google Scholar]
- 23.Jacques S. L., Pogue B. W., “Tutorial on diffuse light transport,” J. Biomed. Opt. 13(4), 041302 (2008). 10.1117/1.2967535 [DOI] [PubMed] [Google Scholar]
- 24.Duadi H., Fixler D., Popovtzer R., “Dependence of light scattering profile in tissue on blood vessel diameter and distribution: a computer simulation study,” J. Biomed. Opt. 18(11), 111408 (2013). 10.1117/1.JBO.18.11.111408 [DOI] [PubMed] [Google Scholar]
- 25.Duadi H., Nitzan M., Fixler D., “Simulation of oxygen saturation measurement in a single blood vein,” Opt. Lett. 41(18), 4312–4315 (2016). 10.1364/OL.41.004312 [DOI] [PubMed] [Google Scholar]
- 26.Wróbel M. S., Jedrzejewska-Szczerska M., Galla S., Piechowski L., Sawczak M., Popov A. P., Bykov A. V., Tuchin V. V., Cenian A., “Use of optical skin phantoms for preclinical evaluation of laser efficiency for skin lesion therapy,” J. Biomed. Opt. 20(8), 085003 (2015). 10.1117/1.JBO.20.8.085003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.M. Jędrzejewska-Szczerska, M. S. Wróbel, S. Galla, A. P. Popov, A. V. Bykov, V. V. Tuchin, and A. Cenian, “Investigation of photothermolysis therapy of human skin diseases using optical phantoms,” SPIE Proc. 9447, 944715 (2015). [Google Scholar]
- 28.Hyttel-Sorensen S., Kleiser S., Wolf M., Greisen G., “Calibration of a prototype NIRS oximeter against two commercial devices on a blood-lipid phantom,” Biomed. Opt. Express 4(9), 1662–1672 (2013). 10.1364/BOE.4.001662 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Fixler D., Garcia J., Zalevsky Z., Weiss A., Deutsch M., “Pattern projection for subpixel resolved imaging in microscopy,” Micron 38(2), 115–120 (2007). 10.1016/j.micron.2006.07.007 [DOI] [PubMed] [Google Scholar]