Nonlinear characterization of elasticity using quantitative optical coherence elastography

Abstract

Optical coherence elastography (OCE) has been used to perform mechanical characterization on biological tissue at the microscopic scale. In this work, we used quantitative optical coherence elastography (qOCE), a novel technology we recently developed, to study the nonlinear elastic behavior of biological tissue. The qOCE system had a fiber-optic probe to exert a compressive force to deform tissue under the tip of the probe. Using the space-division multiplexed optical coherence tomography (OCT) signal detected by a spectral domain OCT engine, we were able to simultaneously quantify the probe deformation that was proportional to the force applied, and to quantify the tissue deformation. In other words, our qOCE system allowed us to establish the relationship between mechanical stimulus and tissue response to characterize the stiffness of biological tissue. Most biological tissues have nonlinear elastic behavior, and the apparent stress-strain relationship characterized by our qOCE system was nonlinear an extended range of strain, for a tissue-mimicking phantom as well as biological tissues. Our experimental results suggested that the quantification of force in OCE was critical for accurate characterization of tissue mechanical properties and the qOCE technique was capable of differentiating biological tissues based on the elasticity of tissue that is generally nonlinear.

1. Introduction

Optical coherence tomography (OCT) can be used to aid in the identification of diseased tissue such as cancerous tissue, for clinical diagnosis and surgical guidance [1, 2]. In addition to structural imaging, OCT has a functional extension referred as optical coherence elastography (OCE) that could be used to assess tissue stiffness [3–10]. OCE measures the mechanical response (deformation, resonant frequency, elastic wave propagation) of biological tissues under external or internal mechanical stimulation, and extracts mechanical properties of tissue related to its pathological and physiological status. Therefore, OCE has great potential in tissue characterization for various biomedical applications. It is generally accepted that the elasticity of tissue changes in pathological processes, as in the cases of breast or prostate cancer, and has the potential to be a discriminative biomarker for cancer diagnosis [11–14].

The most conventional way to describe the elasticity of a material is the Young’s modulus measured at small strains. The Young’s modulus can be directly measured using the stress-strain relationship through a compression process. Researchers also investigated indirect methods to quantify the Young’s modulus of tissue. One of the indirect measurement technologies is dynamic elastography that generates dynamic excitation and propagating mechanical wave in tissue [15, 16]. In dynamic OCE, OCT imaging system is used to measure the propagation parameters of shear wave or surface wave for the estimation of Young’s modulus. The mechanical excitation in dynamic OCT can be introduced by focused ultrasound or by photothermal effects, providing great opportunity for loading at depth. However, indirect measurement of tissue Young’s modulus has limited spatial resolution and limited access to deep tissue. Conventional compression OCE that measures spatially resolved tissue displacement under compression has the potential to achieve high spatial resolution and can be implemented as an instrument with a small form factor. However, conventional compression OCE lacks the mechanism for force or stress quantification. This can limit its application in tissue characterization, because most of the biological tissues have different elastic behavior under large loads as compared to small loads. Strain stiffening is frequently observed in biological tissue at large loads, and the linear stress-strain relationship is limited to few tissues such as bone tissue in a very limited deformation regime. In other words, the displacement of tissue measured by OCE not only depends on the mechanical characteristics of the tissue, but also depends on the magnitude of loading [17]. Therefore, it is critical for OCE measurement to consider the nonlinear elasticity of tissue to achieve effective tissue differentiation, which has not been investigated extensively before [18].

In our previous work, we demonstrated a miniature quantitative OCE (qOCE) instrument which simultaneously measured the force exerted to tissue and the resultant tissue deformation [19]. We also demonstrated that our qOCE technique was able to provide depth resolved stiffness assessment in a muti-layer structure [20]. In this study, we explored the significance of force quantification in OCE for the characterization of nonlinear elasticity. We measured the apparent stress and the apparent strain of the tissue when the qOCE probe was used to slowly apply compressive load to the tissue, assuming the tissue is isotropic, homogeneous, elastic and incompressible within the volume interrogated by qOCE. Mechanical contrast between different biological tissues can be revealed using a calibrated qOCE instrument. Particularly, we used our qOCE technology to study the nonlinear elasticity of an elastic phantom and biological tissues, by characterization the apparent stress-strain relationship under different loading conditions.

2. qOCE system

The quantitative OCE (qOCE) system (Fig. 1(a)) utilizes a spectral domain OCT (SD OCT) engine operated at 1300nm. A detailed description of the system can be found in our previous publication [19, 21]. Briefly, the system has a 91 kHz Ascan rate and a ~7.5μm axial resolution. The phase noise of the SD OCT system has been measured to be 0.01 rad, corresponding to a 1nm sensitivity in displacement tracking. The output of the broadband light source illuminates the reference and sample arm of a fiber-optic Michelson interferometer through a fiber-optic coupler. When the system is used for mechanical characterization, we attach the fiber optic qOCE probe to the sample arm of the Michelson interferometer. When the system is used for 2D or 3D structural imaging, we interface the sample arm of the interferometer with a beam scanning system that consists of a collimator, a pair of galvanometers, and a scanning lens. Light returned from the interferometer is detected by a CMOS InGaAs camera (SUI1024LDH2, Goodrich). A frame grabber (PCIe-1433, National Instrument) streams the signal from the camera to the host computer (Dell Precision T7600) where the OCT signal is processed in real-time using graphic processing units (GPU).

Fig. 1.

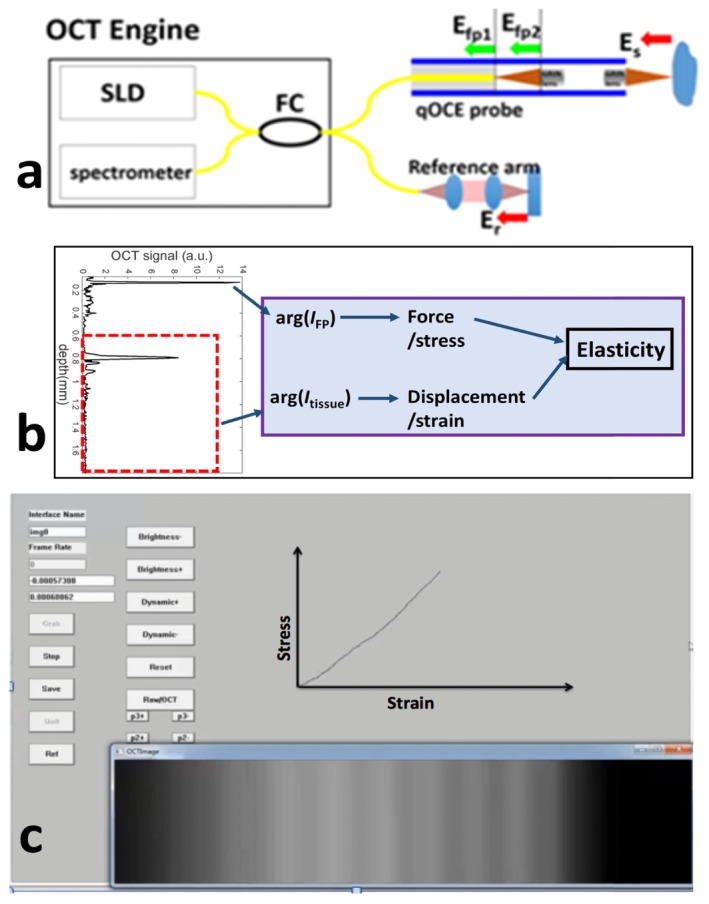
(a) Illustration of qOCE system (FC: fiber optic coupler; SLD: superluminescent diode; (E)_fp1, optical reflection from the tip of single mode fiber; (E)_fp2, optical reflection from the proximal end of the first GRIN lens; (E)_s, sample light; (E)_r, reference light; (b) multiplexed signal for simultaneous probe and tissue deformation tracking; (c) software interface for real-time stress-strain characterization (Visualization 1 ^{(6.1MB, MP4)} ).

A miniature fiber optic qOCE probe integrated with a Fabry-Perot (FP) interferometer is used to indent the tissue sample and collect optical signal for elasticity assessment [19]. The probe has a lead-in single mode fiber connected to its proximal end and a pair of GRIN lenses (1.8mm diameter) attached to its distal end. A low finesse Fabry-Perot (FP) cavity with two end surfaces (the cleaved SMF tip and the foremost surface of the first GRIN lens) are formed for force sensing. We used a polyimide tube with 1.8mm inner diameter as the probe shaft. Interference of the optical signals reflected from the end surfaces of the FP cavity produces a peak in the OCT A-scan (I_FP in Fig. 1(b)). The force exerted through the probe causes deformation of the probe which in turn generates a detectable phase shift in the complex valued OCT signal. The sample is illuminated by the incident light from the broadband source through the probe. The backscattered light from the sample (E_s) generates a complex valued OCT signal (I_tissue). The displacement of the tissue can be quantified from the Doppler analysis of the complex valued OCT signal (arg(I_tissue)) in response to compression. Notability, I_tissue is derived from the Michelson interferometer consisting of the reference arm and the sample arm, and I_FP is derived from the common path interferometer (the FP cavity). Therefore, I_tissue and I_FP can be multiplexed in the same OCT Ascan without spatial overlapping by choosing appropriate optical path length for the reference arm, as shown in Fig. 1(b). In addition, the deformation of probe for force quantification has negligible impact on the measurement of tissue deformation, because the stiffness of the probe is orders of magnitude larger than that of soft tissue (GPa versus kPa). Therefore, the mechanical property of the tissue can be obtained by measuring the force and the depth resolved displacement simultaneously from the space-division-multiplexed OCT signal in our qOCE system. On the other hand, due to the large stiffness of the probe, the measurable sample stiffness has a lower limit. However, the small deformation of the stiff qOCE probe can still be quantified with high accuracy, if the Doppler phase is calculated using OCT signals acquired with larger time interval. In our future study, we will investigate a data-driven adaptive Doppler analysis method to achieve a larger dynamic range for stiffness assessment.

As illustrated in Fig. 1(b), we simultaneously measured the apparent stress and strain for the elastic characterization of biological tissue. These quantities are referred as apparent stress and strain in our description, because our measurement assumed a uniform spatial distribution of the stress and the strain within the tissue. The qOCE probe was used to perform slow indentation on the sample and OCT signals were acquired for mechanical characterization. We were able to quantify the probe-tissue interaction force (F) using Φ_FP, the accumulated phase shift at the signal peak for I_FP, because Φ_FP was proportional to probe shaft deformation and thus the force. Briefly, we calculated the Doppler phase shift ϕ_FP(τ) between A-scans and integrated the Doppler phase shift over time (${\Phi }_{FP}\left(t\right)={\displaystyle {\int }_0^t{\varphi }_{FP}(\tau )}d\tau$). Full force transfer from the sample to the FP sensor was not expected. To quantify the force, we performed a calibration experiment to extract the constant (α) that correlated the probe tip force (F) with the phase shift (Φ_FP) due to FP cavity displacement: F = αΦ_FP. The apparent stress was then obtained: σ = F/A. Here A indicates the area of the GRIN lens at the tip of the qOCE probe and A = 2.5mm², calculated using the radius of the GRIN lens. On the other hand, we used I_tissue to quantify tissue displacement and the apparent strain. We calculated tissue displacement (δl) using Doppler phase shift at depth d₀: δl = δϕ_tissue(d₀,τ)λ₀/(4π) and integrated tissue displacement over time: $\Delta d={\displaystyle {\int }_0^t\delta l(d_0,\tau )}d\tau$. This allowed us to calculate the apparent strain assuming uniform distribution of the displacement: ε = Δd/(Δd + d₀). In this study, d₀ was chosen to be 0.63 mm where the tissue deformed substantially and the signal to noise ratio (SNR) of OCT signal was satisfactory. Notably, the apparent stress (σ) and the corresponding apparent strain (ε) were both obtained by integrating the Doppler phase from the beginning of indentation (τ = 0) to the observation time point t (τ = t). The fundamental data acquisition frequency for stress and strain signal was 10 kHz, determined by an external trigger source.

As described in our recent publication, we have calibrated our qOCE instrument and demonstrated force and displacement measurement with high linearity and accuracy [19]. We have developed high-speed software based on GPU to quantify stress and strain for our quantitative study of linear and nonlinear elasticity of tissue, as shown in Fig. 1(c) and Visualization 1 ^{(6.1MB, MP4)} .

To perform elastic characterization as shown in Fig. 1(c) and Visualization 1 ^{(6.1MB, MP4)} , we attached the qOCE probe to a high precision linear motor (Newport, ILS100CC DC) and translated the qOCE probe at small speed (~0.1 mm/s) in axial direction for indentation. This relatively slow motion was introduced to minimize any viscoelastic effects. The apparent stress-strain data were obtained during the indentation process for linear and nonlinear characterization of elastic properties of the material.

3. Results

To demonstrate qOCE’s capability in linear and nonlinear mechanical characterization, we first performed qOCE measurement on an in-house fabricated elastic phantom. The phantom material was a room temperature platinum cure silicone rubber called RTV-22 purchased from Raw Material Suppliers. The solid material was prepared by mixing equal parts of base and catalyst, with titanium dioxide to provide scattering. The mixture was then thoroughly mixed, degassed for 15 minutes, and then cured on a 6-inch square glass plate overnight. From the cured sheet, specimens were cut using circular dies with a 0.5-inch diameter. Results obtained from qOCE characterization of the phantom are shown in Fig. 2. The apparent stress-strain relationship is linear when the apparent strain is small (Fig. 2(a)) and becomes nonlinear when the apparent strain increases (Fig. 2(b)). Using data obtained in linear regime of the apparent stress-strain curve (ε<0.1), we were able to evaluate the Young’s modulus (E) of the material by fitting the linear model σ = E_linearε, where σ indicates the apparent stress, ε indicates the apparent strain and E_linear indicates the Young’s modulus for the linear material model. We performed regression analysis and obtained the value of E_linear: E_linear = 84.85kPa. The R² statistics of the regression was 0.9971. Using data obtained from a larger range of apparent strain as shown in Fig. 2(b), we extracted the Young’s modulus of tissue by fitting a Neo-Hookean model: σ = E_nonlinear(λ-1/λ²)/3. Here λ indicates the magnitude of stretch and λ = 1-ε. The Neo-Hookean model is the simplest non-linear model possible. In the limit where the deformations are small, it reduces to linear elasticity [22, 23]. We performed regression to extract E_nonlinear, using the nonlinear material model. E_nonlinear turned out to be 85.64kPa and was highly consistent with E_linear. The R² statistics of the regression was 0.9787. The fitting results are shown as the black curve in Fig. 2(b). For comparison, we also plot the linear stress-strain curve (blue curve) assuming a Young’s modulus of E_linear in Fig. 2(b). Clearly, the experimental data became significantly different from the prediction made by the linear model for strain larger than 0.2.

Fig. 2.

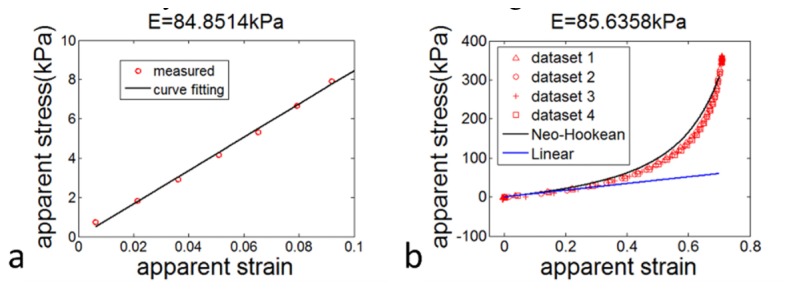
(a) Linear stress-strain relationship at small strain; (b) nonlinear stress-strain relationship and curve fitting based on Neo-Hookean model.

To demonstrate that the qOCE technology could be used to study the nonlinear elasticity of biological tissue, we performed in vivo qOCE measurement of human skin tissue. Quasi-static indentation was applied to volar and dorsal skin of the forearm of a 32 years old healthy volunteer. To minimize the motion artifacts during the measurement, the arm was rested on a flat rigid surface. B-scan and en face images of volar skin are shown in Fig. 3(a) and 3(b), respectively. B-scan and en face images of dorsal skin are shown in Fig. 3(c) and 3(d), respectively. We selected a depth range of interest as indicated by the arrows in Fig. 3(a) and 3(c) assuming uniform distribution of tissue strain, for the analysis of dermis deformation and hence dermis stiffness. To calculate the apparent stress using the probe tip force, we assumed that equilibrium was achieved at arbitrary time during the indentation process. Experimentally acquired apparent stress-strain curves (black dashed curve: volar forearm skin; red dashed curve: dorsal forearm skin) are shown in Fig. 3(e). Clearly, both curves are nonlinear. The slope of the skin stress-strain curve increases with the magnitude of mechanical loading, because the dermis collagen fibers realign their orientations in response to the compression and the stiffness of the skin becomes larger [24]. As shown in Fig. 3(e), dorsal forearm skin has larger slope compared to volar skin over the entire range of loading, which is consistent with previous findings based on OCE [25]. Using data obtained at linear elasticity regime (apparent strain<0.1), we were able to derive the Young’s moduli of dermis for volar (E_volar = 79.7 kPa) and dorsal skin (E_dorsal = 116.7 kPa). In other words, with the same qOCE system and measurement geometry, the apparent stress-strain curves obtained from different tissues were different. This validated the qOCE system’s tissue differentiation capability. In comparison, structural OCT images in Fig. 3 do not show significant difference between volar and dorsal skins of the forearm, suggesting qOCE can potentially provide another dimension of information for tissue characterization. To further demonstrate that the elastic behaviour of skin tissue is nonlinear, we performed linear regression using the apparent stress-strain data obtained in the entire range of apparent strain. The resultant values of R-square statistics of the regression were 0.7616 and 0.8898, for the volar skin and the dorsal skin, respectively, suggesting a linear model could not provide satisfactory description of the apparent stress-strain relationship. In addition, we used the acquired apparent stress and apparent strain values to fit an existing nonlinear elastic model for skin tissue: σ = 2µ₀(λ²- λ⁻¹){exp[γ(λ² + 2λ⁻¹-3)]-1/(2λ)}, where σ indicates the stress and λ indicates the stretch [35, 36]. The model is known as Veronda-Westman Constitutive Law. It was originally developed for skin tissue and has been successfully used to fit experimental data. In the Veronda–Westman Constitutive Law, μ₀ is directly related to linear elasticity E = 3μ₀ and γ determines the rate at which the apparent stress-strain curve departs from linear behaviour. The fitting results are shown as solid curves in Fig. 3(e). The resultant value of µ₀ was 14 kPa for volar skin and 38 kPa for dorsal skin, suggesting the nonlinear elastic behaviour characterized by qOCE could be used for tissue characterization, while the value of γ was approximately the same for both dorsal and volar skin: γ≈5.3. For dorsal skin, E extracted from linear regime of elasticity and µ₀ extracted from Veronda–Westman model approximately satisfy the following relationship: E = 3µ₀. However, this relationship is not satisfied for volar skin, due to the limited data points within the linear elasticity regime to estimate the Young’s modulus.

Fig. 3.

Human skin at volar forearm: cross-sectional image (a) and (b) en face image; human skin at dorsal forearm: cross-sectional image (c) and (d) en face image; (e) stress-strain curve for volar (black) and dorsal (red) skin. In Fig. 3(a) and 3(c), E indicates epidermis and D indicates dermis.

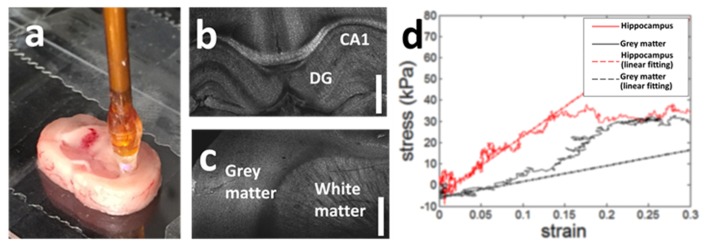
We also performed a pilot study on ex vivo rat brain tissues using qOCE. 10-week-old Sprague Dawley rats (320-360 g in weight) from Charles River Labs were used. We harvested the brain from a rat that was sacrificed for other research purposes, and used a coronal brain slicer to cut the brain into slices with 3mm thickness. The miniature qOCE probe could perform localized mechanical characterization on hippocampus and other anatomical regions due to its small form factor (Fig. 4(a)). As shown in Fig. 4(a), the dimensions of hippocampus and cortex regions of the rat were comparable to the dimension of the qOCE probe and could be visually identified. Therefore, we performed visual inspection before the measurement started to make sure that the mechanical characterization was performed on anatomical structures of interest. We performed quasi-static indentation using the qOCE probe on the brain slice. Hippocampus (Fig. 4(b)) and cortex grey matter (Fig. 4(c)) were interrogated. In Fig. 4(b) and 4(c), the scale bars indicate 1mm. Hippocampus of the brain is thought to be the center for memory, emotion and spatial navigation and hippocampal damage in traumatic brain injury (TBI) is incredibly disabling. The mechanical contrast between hippocampus and other parts of the brain is directly related to the damage of hippocampus in TBI [26, 27]. Therefore, the mechanical properties of the hippocampus are of great interest. Before acquiring qOCE data, we translated the qOCE probe for 0.6mm to apply pre-compression. The apparent stress-strain curves obtained from the hippocampus (red) and the cortex (black) are shown in Fig. 4(d) as solid curves. Using data obtained at small apparent strain (strain<0.1) where the brain tissue had linear elasticity, we were able to determine Young’s moduli for hippocampus (E_H) and cortex (E_C): E_H = 276 kPa and E_C = 74 kPa. This is consistent with results of previous studies that suggested the hippocampus tissue had larger stiffness compared to cortex [28]. The linear fittings of stress-strain relationships are shown as dashed curves in Fig. 4(d). The discrepancy between solid and dashed curves in Fig. 4(d) suggests the nonlinear stress-strain relationship for brain tissues. The loading could not be applied to the tissue when strain was larger than 0.2 due to material failure. This is consistent with published results [29]. We used the apparent stress-strain data corresponding to strain ranging from 0 to 0.2 to fit a linear model through regression and obtained the R² statistics to evaluate the quality of the fitting. The values of R² were 0.9472 and 0.8094 respectively for the hippocampus, and the grey matter, suggesting the elastic behaviour of hippocampus was approximately linear while the grey matter deviates from linear elastic behavior at a smaller strain.

Fig. 4.

(a) qOCE probe and brain slice; (b) en face OCT image of hippocampus obtained from the coronal plane (DG: dentate gyrus; CA1: Cornu Ammonis 1); (c) en face OCT image of cortex obtained from the coronal plane; (d) stress-strain curve for cortex grey matter (black) and hippocampus (red) of rat brain. Solid curves are experimental data and dashed curves are linear fitting of the stress-strain curve.

4. Discussion and conclusion

Unlike many engineered materials, biological tissues often exhibit nonlinear elastic behavior. Therefore, understanding the nonlinear elasticity is critical for elastography imaging and mechanical characterization of biological tissue. However, conventional OCE techniques lack the mechanism for force sensing. As a result, the nonlinearity of tissue elasticity has not been fully investigated and it remains challenging to establish the consistency in tissue stiffness obtained from different OCE measurements. In this study, we demonstrated the capability of qOCE in characterizing the nonlinear elasticity of biological tissue. We validated the effectiveness of our qOCE system by correlating its measurements with published values.

In our qOCE measurement, we used the qOCE probe to apply indentation on biological tissues and characterized the response of tissue in terms of depth resolved displacement and force. A significant advantage of depth resolved measurement of displacement enabled by the qOCE system is its potential in accurate strain measurement. In conventional apparatus for indentation test, the indenter displacement is measured. The measured displacement may be due to tissue deformation that generates stress, or due to the global motion of tissue that does not generate stress. This can be a source of inaccuracy when in situ measurement is conducted. In our qOCE system, we performed Doppler analysis on depth resolved OCT signal to extract depth resolved tissue displacement. As a result, the tissue deformation that generated the stress could be obtained by estimating the spatial derivative of the displacement, in other words, the strain. Moreover, qOCE technology will offer great opportunity for early detection of deep tumors that cannot be detected through manual palpation, because the miniature qOCE probe can be conveniently delivered to various tissue sites of interest for direct mechanical characterization. We will further optimize our instrument and miniaturize its dimension for such applications. The feasibility of such needle-based probes for mechanical characterization has been demonstrated before [9]. In summary, qOCE measurement of biological tissue, along with statistical analysis performed on qOCE data, will be able to reveal the difference in mechanical properties between different tissues.

Notably, the stress and strain fields within the sample under the compression of qOCE probe are generally nonuniform. However, we deliberately chose to estimate the strain using data obtained from a limited range of depth where the displacement varies as the axial depth in an approximately linear manner. In other words, in the limited depth range we considered, the axial strain and stress remain constant. As the strain and stress simply diminishes beyond the region effectively compressed by the qOCE probe, mechanical heterogeneity of tissue in a large scale would not affect the accuracy of qOCE characterization. Therefore, for accurate qOCE characterization, the elastic material (tissue) has to be incompressible, isotropic and homogeneous within the volume interrogated by qOCE, although the material does not have to be homogeneous beyond the region effectively compressed by the qOCE probe where the strain and stress simply diminish.

In the current study, the accuracy of the measurement is limited by the heterogeneous spatial distribution of actual stress and strain under indentation test, as well as the heterogeneous mechanical properties of tissue [30]. In principle, our qOCE technology can be used to study nonlinear elasticity with considerable spatial resolution [20]. However, accurate mechanical characterization of inhomogeneous sample is not trivial, even when the elastic behavior of the sample is linear. For a sample with microscopic mechanical heterogeneity, it is very challenging to determine the stress field within the sample based on the force measurement at the probe tip. In our future work, the Young’s modulus of tissue will be extracted accurately using an inverse finite element approach where the impact of measurement geometry is considered [31–33]. In addition, a model-based approach will be developed to extract the spatial distribution of elasticity from inhomogeneous tissue, as demonstrated in ultrasound elastography [34]. The inter- and intra-sample and inter-measurement variability will be also investigated in our future study.

In this study, the elasticity of biological tissue is considered. However, most biological tissues have time dependent mechanical behavior and are essentially viscoelastic. To minimize the impact of viscoelasticity in our measurement, we translated the qOCE probe at a small speed such as 0.1 mm/s for tissue indentation and assumed the material achieved equilibrium at any time during the indentation process. qOCE measurement performed at different indentation speeds will allow more comprehensive mechanical characterization of biological tissues in both elasticity and viscoelasticity.

To conclude, we studied the nonlinear elastic property of tissue by the qOCE based system on a miniature probe with an integrated Fabry-Perot force sensor. We performed qOCE characterization on silicone rubber phantom, in vivo human skin tissues and ex vivo rat brain tissues. Our results have demonstrated the capability of our qOCE technology in characterizing nonlinear elasticity of biological tissue.