BEHAVIOR OF POST-INSTALLED ANCHORS TESTED BY STEPWISE INCREASING CYCLIC LOAD PROTOCOLS

Abstract

Cyclic loads are a characteristic feature of actions acting on structures and anchorages during earthquakes. For this reason, seismic qualification of post-installed concrete anchors according to the internationally recognized American Concrete Institute (ACI) standard ACI 355 is based on cyclic load tests. The protocols for these tests, however, have limited scientific basis. Therefore, in the present paper newly-developed test protocols with stepwise-increasing load amplitudes are utilized to more realistically evaluate anchor seismic performance. The study focuses on the load-displacement behavior of common anchor types installed in cracked concrete and subjected to both cyclic tension and cyclic shear actions. The results confirmed robust behavior for anchors loaded in cyclic tension even in the presence of crack widths in the anchorage material larger than currently required by ACI 355. In addition, the critical influence of low cycle fatigue on the performance of anchors loaded in cyclic shear is demonstrated.

INTRODUCTION

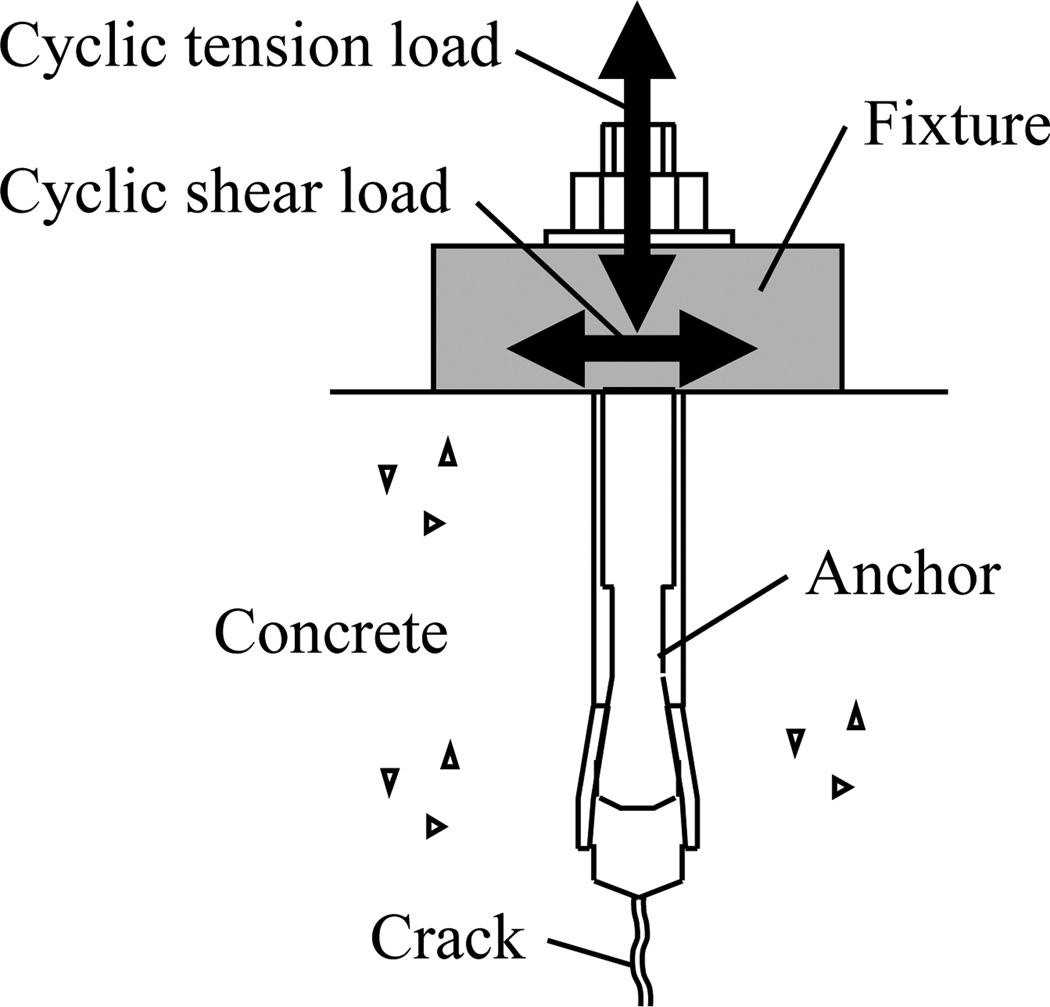
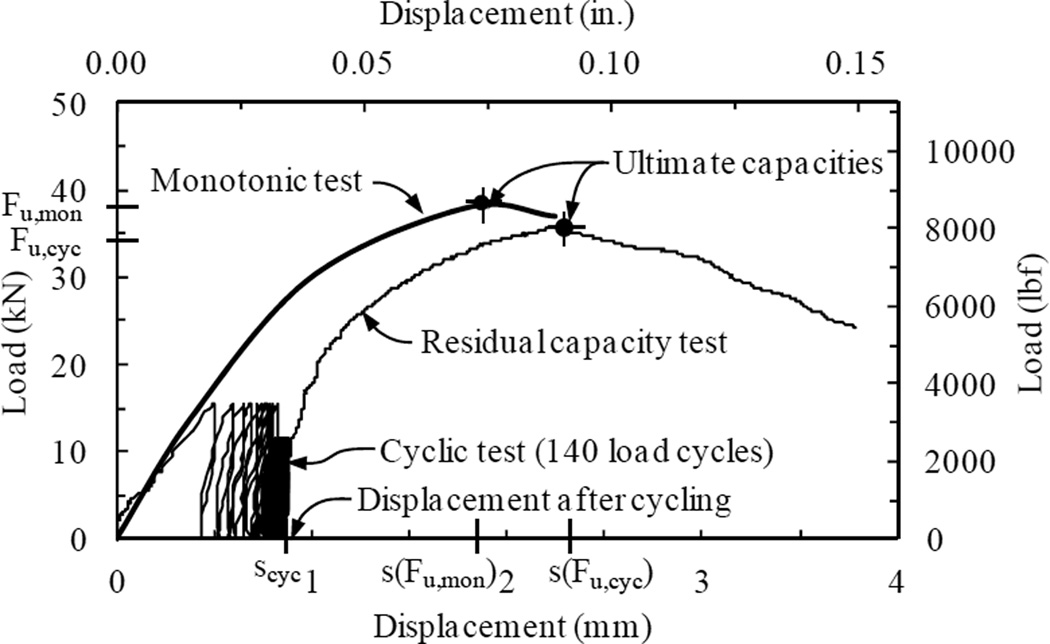
During seismic events, anchors used to connect structural and nonstructural elements to concrete are subjected to cyclic tension and cyclic shear loads (Fig. 1). Incorrectly designed or inadequately qualified anchors have caused severe damage and fatalities^1,2,3,4. To ensure safe anchorages, the American Concrete Institute (ACI) design code ACI 318⁵ Appendix D requires anchor products to be qualified according to ACI 355.2⁶ for mechanical anchors and ACI 355.4⁷ for adhesive anchors. First implemented in 2001, ACI 355 includes seismic anchor qualification based on simulated seismic tests. The cyclic load regimes given therein are primarily founded on research by Tang and Deans⁸ for the Canadian nuclear industry and consist of 140 cycles, imposed in three blocks of decreasing amplitudes. Other loading patterns are feasible, namely constant load cycling amplitudes, e.g., the German guideline for anchorages in nuclear power plants⁹ or stepwise increasing load cycling amplitude, e.g., the Structural Engineers Association of Southern California (SEAOSC) anchor testing guideline¹⁰. While it has been demonstrated that the sequence effect of amplitudes on the overall performance is typically negligible for tension loads^11,12,13, stepwise-increasing protocols are preferable for product evaluation since the evolving stiffness of the anchor can be determined throughout the entire loading range¹⁴. The decreasing load cycle amplitudes in ACI 355 simulated seismic tests do not allow direct comparison to the steadily increasing monotonic load-displacement curve and the influence of low amplitude cycles on the anchor behavior is to a great extent hidden by the large amplitude cycles (Fig. 2). The European Technical Approval Guideline (ETAG) for post-installed anchor qualification ETAG 001¹⁵ historically did not recognize seismic qualification. This limitation was a major catalyst for the presented research.

Fig. 1.

Concrete anchor subjected to cyclic tension and shear loads.

Fig. 2.

Load-displacement diagram for simulated seismic test (cyclic and residual capacity test) and corresponding mean curve of monotonic reference tests according to ACI 355 (example after Mahrenholtz³⁵).

Previous research showed that for anchors loaded in tension, a substantial resistance to cycling can generally be assumed for post-installed anchors and in general the backbone curve of the cyclic load-displacement path follows that of the mean monotonic curve obtained from corresponding reference tests^16,17. These behavioral attributes are also true for tension loads for which a large number of load cycles at load levels below peak or a considerable number of load cycles near ultimate load can be performed without failure¹³. Tension cycling well below the ultimate monotonic capacity does not significantly influence the residual load capacity of mechanical anchors, however, the performance of axially loaded anchors is in general highly dependent on the width of cracks in the concrete that pass through an anchorage¹⁸.

For shear load cycling, early studies draw a more complex picture. While some researchers found that a small number of shear load cycles has no significant influence on the shear capacity¹⁹, others concluded that the cyclic load path does not generally follow the monotonic mean envelope and that the cyclic load capacity is smaller than the monotonic load capacity²⁰. Pulsating shear cycling is not as demanding for anchors as alternating shear cycling and achieved strengths are substantially higher^21,22. A reason for the variability in results is the different demand with respect to load level and cycle number to which the anchor is subjected. Depending on this, the occurrence of low cycle fatigue due to accumulated plastic steel strains may govern performance. In the event low cycle fatigue occurs during shear load cycling, the strength may be substantially reduced¹⁷ and the completion of a seismically relevant number of cycles requires a reasonably low shear load level²³.

State-of-the-art guidelines for performance verification of structures and components recommend early evaluations with relatively small cyclic demands, which are gradually increased until the test specimen is subject to the maximum force demand²⁴. The stepwise-increasing load cycling protocols developed at the University of California, San Diego (UCSD)²⁵ for example reflect an effort to lay the foundation for improved investigations of seismically loaded anchors. To further characterize seismic performance of post-installed anchors and to support the development of qualification tests representing the loading conditions relevant for seismic applications, an extensive research program was carried out at the Institut für Werkstoffe im Bauwesen, Universität Stuttgart (IWB). The tests were conducted using the stepwise-increasing anchor load protocols proposed by UCSD (Wood et al.²⁶). To compare the suitability of these load controlled test protocols to that of displacement controlled test protocols, additional cyclic tests were carried out according to the Federal Emergency Management Agency (FEMA) guideline FEMA 461²⁷. In this paper, these tests are described and the behavior of the investigated anchors are discussed.

RESEARCH SIGNIFICANCE

This paper presents a comprehensive research program involving cyclic load tests of concrete anchors covering a wide range of post-installed anchor types and associated failure modes. The test results provide insight about how to design safer structural and nonstructural anchorages. This unique dataset demonstrates the influence of crack width on the performance of anchors subject to stepwise increasing cyclic tension and cyclic shear load. Complementary data from seismic tests carried out according to the FEMA 461 standard confirms the advantage of using stepwise increasing cyclic load protocols for the seismic qualification of anchor products.

EXPERIMENTAL INVESTIGATION

A total of 91 cyclic and monotonic tests series were conducted. In general, three test repeats were performed, which is the minimum required to calculate a coefficient of variation. While additional test replicates would be preferable, three test repeats were sufficient to differentiate trends in anchor behavior. The primary objective of the tests was to investigate the performance of different anchor types installed in static cracks and subjected to either cyclic tension or cyclic shear loads. The aim was to study the cyclic load-displacement behavior for all key failure modes and to demonstrate the efficacy and benefits of the stepwise increasing load cycling protocol.

Anchors and concrete

Seven post-installed anchor products of medium size and from various manufacturers were investigated. Five of which were mechanical and two adhesive anchor types (Table 1). One undercut anchor (UA1), one screw anchor (SA1, tested only in shear), two sleeve-type expansion anchors (EAs1 and EAs2), one bolt-type expansion anchor (EAb1), and two bonded anchors (BA1 and BA2, both epoxy mortar type with threaded rod) were tested. The EAs2 anchor did not hold any product performance qualification, the SA1 was qualified according to ETAG 001 for use in uncracked and cracked concrete and all other anchor products, namely UA1, EAs1, EAb1, BA1 and BA2, were qualified according to ACI 355 including seismic applications. Fig. 3 illustrates the tested types and their load transfer mechanisms.

Table 1.

Investigated anchors.

Anchor designationa	Anchor type	Nominal size	Steel element diameter, mm (in.)	Embedment depth hef, mm (in.)
UA1	Undercut	M10	10 (0.39)	90 (3.54)
SA1	Screw	Ø16	16 (0.63)	105 (4.13)
EAs1	Expansion, sleeve-type	M10	10 (0.39)	80 (3.15)
EAs2		5/8”	15.9 (0.625)	85 (3.35)
EAb1	Expansion, bolt-type	1/2”	12.3 (0.5)	83 (3.25)
BA1	Bonded, epoxy-type	M12b	12 (0.47)	96 (3.78)
BA2		M12b	12 (0.47)	96 (3.78)

^aUA: Undercut anchor; SA: Screw anchor; EAs: Expansion anchor – sleeve-type; EAb: Expansion anchor – bolt-type; BA: Bonded anchor

^bThreaded rod with f_y = 900 MPa (130 ksi) and f_u = 1000 MPa (145 ksi)

Fig. 3.

Tested anchor types with indicated tensile load transfer mechanism: a) Undercut anchor (UA); b) Screw anchor (SA); c) Expansion anchor – sleeve-type (EAs); d) Expansion anchor – bolt-type (EAb); e) Bonded anchor (BA).

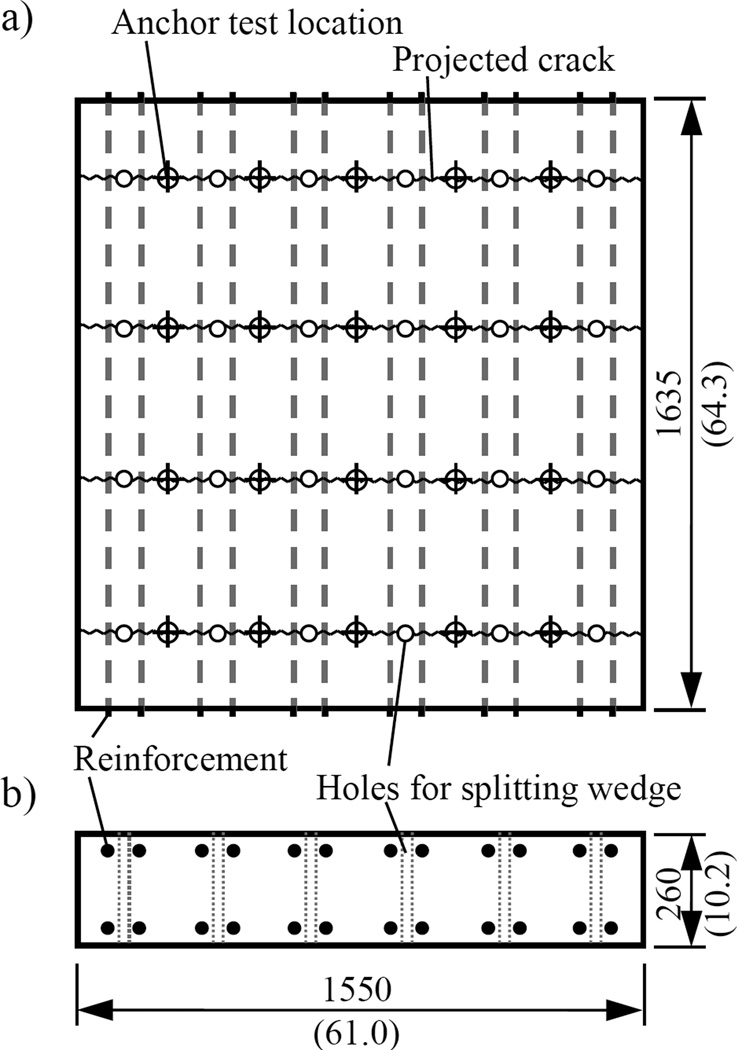
The concrete slabs used as anchorage material were 1635 mm x 1550 mm x 260 mm (64 in. x 61 in. x 10 in.) and made of normal weight concrete with a nominal compressive strength of f’_c = 20 MPa (2900 psi). The concrete slabs were designed to allow for the generation and control of static cracks by means of steel wedges driven into sleeves placed in preformed holes in the slab (Fig. 4). The unidirectional 12 mm (0.47 in.) steel reinforcing bars resulted in a reinforcement ratio perpendicular to the cracks of 0.8 %. The cracks were generated after drilling and cleaning of the anchor borehole. Then the wedges were removed to allow the crack to close, and the anchors were installed according to the manufacturer’s published installation instructions with the specified embedment depth h_ef. Prior to testing, the installation moment was reduced to 50 % to account for relaxation of the preload typically observed in practice. All tests were performed on single anchors with large edge distances. Concrete slab design and anchor installation procedures were in accordance with ACI 355 and ETAG 001 requirements. It is noted that due to position and direction, neither the longitudinal reinforcement nor the holes for the splitting wedges influenced the test results.

Fig. 4.

Wedge split concrete slab: a) Top view; b) Side view (all units in mm and (in.)).

Load protocol, target load and crack width

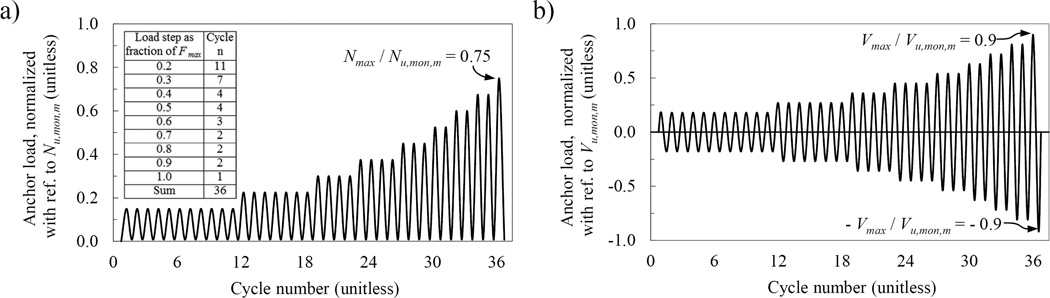
The protocols used for the load cycling tests were developed from extensive nonlinear numerical simulations of representative reinforced concrete structures²⁶. After subjecting a suite of seven buildings of various heights (2 to 20-stories) to 21 earthquakes, the floor level accelerations were used as input to a suite of elastic single-degree-of-freedom (SDOF) oscillators with frequencies ranging from 5 Hz to 20 Hz. The oscillator frequencies were selected to represent the response of attached mechanical and electrical equipment in commercial buildings²⁸. The protocols were generated using Rainflow counting of the oscillator responses and rearranging them with respect to their amplitudes. The protocols have a total of 36 load cycles with force amplitude increased in nine steps to attain a target maximum force demand F_max (Fig. 5). For cyclic shear tests, the protocol had symmetrically alternating load amplitudes targeting a maximum shear load of V_max. For cyclic tension tests, only positive excursions were used with a maximum tension load of N_max.

Fig. 5.

Load controlled cyclic load protocols: a) Cyclic tension tests; b) Cyclic shear tests (after Hutchinson and Wood²⁵).

The definition of the maximum anchor load assumes that to achieve qualification with an unreduced seismic strength the anchor must complete all load cycles with a maximum anchor load N_max or V_max corresponding to the characteristic monotonic strength F_Rk,mon of an anchor installed in cracked concrete. The characteristic strength was taken as the 5 % fractile of the mean ultimate load capacity F_u,mon,m from monotonic reference tests. The characteristic strength was calculated as F_Rk,mon = F_u,mon,m (1 – k_s · v) with the statistical k-factor taken as k_s = 1.645 (n = ∞) and a coefficient of variation v corresponding to the maximum value that may be assumed for the test¹⁷. For anchors loaded in tension, the maximum coefficient of variation was assumed for concrete related failure modes to be v = 15 %, which is also the maximum acceptable coefficient of variation according to ACI 355. For anchors loaded in shear, shear failure of the anchor steel is the predominant failure mode and the maximum variation was assumed to be v = 6 % based on experience. Using these assumptions, F_Rk,mon yields maximum anchor loads corresponding to 75 % of the mean ultimate monotonic capacity for cyclic tension tests and 90 % for cyclic shear tests.

The crack width was constant for all tests. For tension tests, the anchors were installed in w = 0.5 mm (0.02 in.) wide cracks, which is the relevant crack width for simulated seismic tests according to ACI 355. Some anchors were also tested in w = 0.8 mm (0.03 in.) cracks to investigate their behavior under more severe seismic conditions²⁹. For shear tests, the anchors were loaded parallel to the direction of the crack, which is more critical for load capacity and displacement behavior compared with loading perpendicular to the crack³⁰. Since the influence of the actual crack width on the anchor behavior in shear is small¹⁷, the anchors were conservatively tested in w = 0.8 mm (0.03 in.) cracks only.

Test setup and procedures

After the installation of transducers to measure crack width at the surface of the concrete slab, wedges were sequentially hammered into the sleeves in the concrete slabs until the desired crack width was reached. The cracks were opened by the specified crack width of 0.5 mm or 0.8 mm (0.02 in. or 0.03 in.). For tension tests, a 250 kN (56 kip) servo-hydraulic actuator was used to load the anchor. The actuator rested on two beams (Fig. 6a). Mechanical anchors were tested under unconfined conditions with a clear distance between the beams of 4h_ef. Adhesive anchors were tested under confined condition to ensure bond failure. For this configuration, a sheet of Polytetrafluoroethylene (PTFE) and a steel plate with a clearance hole equal to approximately two times the borehole diameter (≈ 2d₀) were placed around the anchor on which the beams rested. For shear tests, a 630 kN (142 kip) servo-hydraulic actuator was used to load the anchor by means of a shear load device which was mechanically held down to avoid uplift of the anchor during testing (Fig. 6b). The concrete slab was braced against the strong floor and frontal supports acted as horizontal bearing. Bushings made of hardened steel were inserted in the fixture of the shear load device, providing a clearance gap of 2 mm (0.08 in.). To minimize friction, a sheet of PTFE was placed between slab and shear load fixture (dynamic and static coefficient of friction µ ≈ 0.05 for steel on PTFE).

Fig. 6.

Test setups: a) Tension load tests; b) Shear load tests.

Prior to testing, displacement transducers were installed at the top of the anchor for tension tests and orthogonal to the fixture for shear tests. Load measurements were captured by the load cells of the actuators. The cyclic tests were run load-controlled at quasi-static frequencies of about 0.2 Hz. It has been shown that this loading rate is appropriate for simulated seismic anchor tests^13,31,32. For cyclic tension tests, the servo control program consisted of sinusoidal load cycles in which the minimum load level was 0.1 kN (22 lbf) to avoid control problems due to slackness between anchor nut and slab. For cyclic shear tests, the load cycles were split into two half-sinus cycles with interconnecting displacement-controlled ramps to avoid servo control conflicts due to the gap between anchor and loading fixture. Similar to tests according to ACI 355 (refer to Fig. 2), the anchors were unloaded after completion of the load cycles, and then loaded to failure to determine the residual anchor capacity. These residual capacity tests as well as the reference tests were run displacement-controlled and the ultimate load was reached within 1 min to 3 min (quasi-static). Anchor load, anchor displacement, and crack width were measured and recorded at a sampling rate of 5 Hz. Details on the test setup and testing procedures can be found in Mahrenholtz³³.

EXPERIMENTAL RESULTS AND DISCUSSION

It is noted that the test conditions in respect to maximum crack width as well as maximum cyclic anchor load were more demanding than the conditions for which the anchors have been qualified. Any adverse load-displacement behavior does not disqualify the tested anchors with respect to current qualification guidelines.

Tension performance and influence of crack width

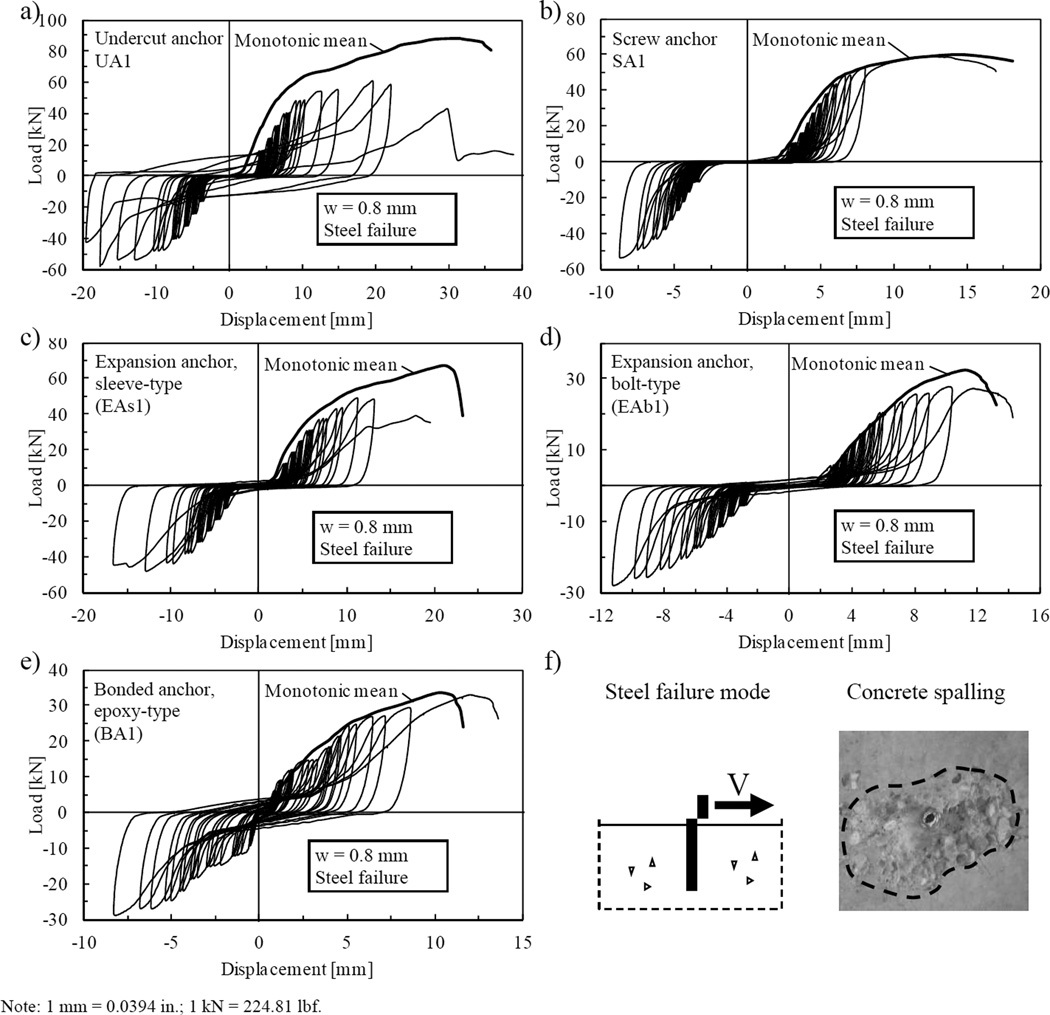
The tension test program and the key test results are given in Table 2. Note that the subscripts u, mon, cyc and m stand for ultimate (capacity), monotonic, cyclic and mean. For each cyclic test series, Fig. 7 shows typical load-displacement curves and the corresponding monotonic mean curve calculated as the average of the monotonic reference test series. Observed failure modes are schematically depicted in Fig. 7j. For a detailed explanation of failure modes, reference is made to Eligehausen et al.¹⁷. All anchors completed load cycling and were subsequently tested to failure to determine the residual capacity. Sufficient steel strength and the specific embedment depth prevented steel failure.

Table 2.

Tests conditions and key test results of tension load tests with stepwise increasing protocol (load and displacement values given as average of all test repeats).

Anchor designationa	Crack width w, mm	Load. typeb	Number of tests	Failure modec	Target load Nmax ,kN	Nu,m, kN	vd(Nu,m), %	Nu,cyc,m/ Nu,mon,m	sN,cyc, mm	s(Nu)m, mm	vd(s(Nu)m), %	s(Nu,cyc)m/ s(Nu,mon)m
UA1	0.5	mon	3	C	-	39.4	11.0	1.13	-	3.9	67.2	1.23
		cyc	3	C	34.9	44.5	4.8		1.4	4.8	53.1
	0.8	mon	3	C	-	34.2	5.7	1.07	-	3.3	11.8	1.20
		cyc	3	C	30.0	36.7	19.6		2.9	3.9	49.0
EAs1	0.5	mon	3	C	-	38.9	15.3	0.96	-	6.5	62.6	0.64
		cyc	3	C	29.2	37.2	3.9		1.7	4.2	49.1
EAs2	0.5	mon	3	C	-	23.4	7.4	1.13	-	8.3	4.5	0.74
		cyc	3	C	17.6	26.4	2.5		2.0	6.1	40.1
EAb1	0.5	mon	3	P	-	25.2	6.6	0.98	-	7.9	13.0	1.22
		cyc	3	P	19.0	24.6	9.4		3.8	9.7	25.0
	0.8	mon	3	P	-	21.8	7.3	1.08	-	11.0	10.1	1.23
		cyc	3	P	16.4	23.5	2.7		5.9	13.5	7.5
BA1	0.5	mon	3	P	-	78.2	8.1	0.98	-	1.2	29.5	1.13
		cyc	2	P	65.9	76.4	6.1		1.0	1.4	16.1
	0.8	mon	3	P	-	62.6	10.3	1.08	-	1.9	32.5	0.92
		cyc	3	P	49.7	67.4	15.4		0.9	1.7	30.2
BA2	0.5	mon	3	P	-	44.2	16.6	1.05	-	0.8	21.8	0.74
		cyc	2	P	29.6	46.2	1.4		0.3	0.6	39.5

^aUA: Undercut anchor; SA: Screw anchor; EAs: Expansion anchor – sleeve-type; EAb: Expansion anchor – bolt-type; BA: Bonded anchor

^bmon = monotonic; cyc = cyclic

^cFailure mode: C = Concrete failure; P = Pullout failure

^dCoefficient of variation

Note: Refer to Fig. 2 for explanation of variables; 1 mm = 0.0394 in.; 1 kN = 224.81 lbf.

Fig. 7.

a) to i) Sample load-displacement curves of load controlled cyclic tension load tests on anchors as well as corresponding mean curve of monotonic reference tests (0.5 mm and 0.8 mm (0.02 in. and 0.03 in.) crack width); j) Failure mode schematics.

The load-displacement curves of the cyclic tests on the undercut anchor UA1 followed the corresponding monotonic mean curve (Figs. 7a and b). The concentrated load transfer at the anchor base by mechanical interlock allowed a deep concrete cone to develop at failure. Also the load-displacement curves of the cyclic tests on the sleeve-type expansion anchors EAs1 and EAs2 with relatively thick expansion elements followed the corresponding monotonic mean curves (Figs. 7c and d) and both products failed by concrete breakout. Expansion anchors transfer the tension loads by friction between anchor body and expansion element, and expansion element and concrete. The bolt-type expansion anchor EAb1 predominantly failed by being pulled completely through its relatively thin expansion elements. This pullout failure mode shows the characteristic bell-shaped curve which envelopes the load-displacement curves of the cyclic tests (Figs. 7e and f). Bonded anchors transfer tension loads via the adhesive mortar into the concrete. For the tests on the anchors BA1 and BA2, the confined test setup prevented concrete breakout failure and the high strength threaded rod was pulled out with some of the mortar when the bond of the adhesive mortar ultimately failed. The cyclic load-displacement curves followed the corresponding monotonic mean curves (Figs. 7g and i). Since for both bonded anchors, BA1 and BA2, the same type of threaded rod was used, any difference in the performance of the anchors can be attributed to the individual characteristics of the mortars or their installation. The mortars used for BA1 and BA2 result in load-displacement curves of similar stiffness; however, the ultimate load and displacement capacity of BA1 is greater than that of BA2.

The residual load capacities after tension load cycling N_u,cyc,m were approximately equal to the respective monotonic capacity N_u,mon,m. Taking into account the coefficient of variation v of the failure loads, which in all test series was relatively high and for some test series close to 20 %, ratios of N_u,cyc,m / N_u,mon,m at around 1.00 indicate that tension load cycling does not have a negative influence on the residual load capacities of mechanical anchors. In some cases the residual load capacities were significantly greater than the corresponding monotonic capacity. This has been observed in earlier studies^30,34,35 and it is attributed to the setting of the expansion mechanism or compaction of the concrete near the anchor head. Also the adhesive anchors showed no reduction in failure load due to cyclic loading although half of the bond has to be assumed destroyed for bonded anchors located in cracks¹⁷, giving greater importance to the load transfer via mechanical interlock between mortar and concrete.

The effect of tension load cycling on the anchor displacement was not consistent and the displacement at ultimate residual load capacity s(N_u,cyc)_m as well as the displacement at ultimate monotonic load capacity s(N_u,mon)_m exhibited large scatter with a maximum coefficient of variation v of 67 %. The displacement after tension load cycling s_N,cyc ranged from less than 1 mm (0.04 in.) for bonded anchors to 5 mm (0.20 in.) at maximum for expansion anchors failing in pull-through. Expansion anchors are pulled further into their expansion elements when loaded (follow-up expansion) and therefore the tested expansion anchors experienced larger displacements than other anchor types like undercut or bonded anchors. Bonded anchors developed the smallest displacements as their load transfer mechanism does not allow substantial deformation.

The tests showed that all anchor types resisted the tension load cycles. The tension load cycling did not deteriorate the load-displacement response of any tested anchor, regardless of anchor type and observed failure mode. It is known that high load amplitudes, relative to the capacity, or large numbers of cycles potentially damage the anchor steel or the concrete base material and cause high cycle fatigue failure³⁶, but here the number of load cycles and load amplitudes of the tested load protocol were too moderate to result in any material damage. The diagrams in Fig. 7 further illustrate that hysteretic behavior and associated ability for energy dissipation were nearly nonexistent for the investigated anchors under tension load cycling independent of anchor type and failure mode. For the anchor products tested in 0.5 mm and 0.8 mm (0.02 in. and 0.03 in.) cracks (UA1, EAb1 and BA1) the overall load cycling behavior was consistent for both crack widths. The response of anchors tested in 0.8 mm (0.03 in.) cracks to load cycling was as stable as that of anchors tested in 0.5 mm (0.02 in.) cracks. However, it is noted that the cyclic load level for tests in 0.8 mm (0.03 in.) cracks was lower than that for tests in 0.5 mm (0.02 in.) cracks since the maximum load amplitude depends on the monotonic reference capacity (N_max = 0.75 · N_u,mon,m) and the monotonic reference capacity N_u,mon,m decreases with increasing crack widths. The mean residual capacity in 0.8 mm cracks compared to the value measured for 0.5 mm cracks was reduced by about 15 % to 20 %. This result is in line with earlier studies¹⁸. Since the relative reduction of the residual capacity after load cycling N_u,cyc,m was approximately the same, the ratio of cyclic and monotonic capacity (N_u,cyc,m / N_u,mon,m) was nearly constant for tests in 0.5 mm and 0.8 mm (0.02 in. and 0.03 in.) cracks. The effect of increased crack widths on the displacement behavior depended on the anchor type. The displacement after completion of load cycles (s_N,cyc) increased for mechanical anchors (UA1, EAb1) installed in cracks of increased width, whereas the displacement of the adhesive anchor (BA1) proved to be insensitive to the crack width due to its bond and mechanical interlock load transfer mechanism. It is noted, however, that with continued increase of crack width, the mechanical interlock will become insufficient and the anchor can fail rapidly. Taking the large scatter of the displacements at ultimate load, a clear trend for the displacements for crack widths increased from 0.5 mm (0.02 in.) to 0.8 mm (0.03 in.) cannot be inferred for the tested anchors. This observation was comprehensively investigated and confirmed by Mahrenholtz and Eligehausen³⁷.

Shear performance and effect of low cycle fatigue

The shear test program and the key test results are given in Table 3. For each cyclic test series, Fig. 8 shows typical load-displacement curves and the corresponding monotonic mean curves calculated as the average of the reference test series. All anchors failed by steel rupture of the anchor either during load cycling or in the subsequent residual load capacity test. The steel failure mode is schematically depicted in Fig. 8f. The anchors were located far from edges to exclude concrete edge failure and deep enough to exclude pry-out failure.

Table 3.

Tests conditions and key test results of shear load tests with stepwise increasing protocol (load and displacement values given as average of all test repeats).

Anchor designationa	Crack width w, mm	Load. typeb	Number of tests	Failure modec	Target load Vmax, kN	Vu,m, kN	vg(Vu,m), %	Vu,cyc,m / Vu,mon,m	sV,cyc, mm	s(Vu)m, mm	vg(s(Vu)m), %	s(Vu,cyc)m/ s(Vu,mon)m
UA1	0.8	mon	3	S	-	89.2	4.7	0.64	-	31.2	25.2	0.63
		cyc	3	Sd	80.3	56.7	10.9		-e	19.7f	10.1
SA1	0.8	mon	3	S	-	59.7	6.2	1.01	-	14.4	8.0	0.84
		cyc	3	S	53.7	60.1	5.9		7.7	12.1	3.0
EAs1	0.8	mon	3	S	-	68.1	6.9	0.72	-	21.1	11.1	0.66
		cyc	3	Sd	62.5	49.0	13.4		-e	13.8f	16.5
EAb1	0.8	mon	3	S	-	32.4	4.6	0.82	-	11.2	10.5	1.10
		cyc	3	S	29.2	26.7	2.3		10.7	12.4	5.9
BA1	0.8	mon	3	S	-	33.4	5.7	1.01	-	10.3	22.1	0.94
		cyc	3	S	30.6	33.8	2.9		6.7	9.7	21.6

^aUA: Undercut anchor; SA: Screw anchor; EAs: Expansion anchor – sleeve-type; EAb: Expansion anchor – bolt-type; BA: Bonded anchor

^bmon = monotonic; cyc = cyclic

^cFailure mode: S = Steel failure

^dLow cycle fatigue before completion of load cycles

^eNo displacement value after load cycling available since all anchor samples failed during load cycling

^fMean value of the displacements at peak load during load cycling

^gCoefficient of variation

Note: Refer to Fig. 2 for explanation of variables; 1 mm = 0.0394 in.; 1 kN = 224.81 lbf.

Fig. 8.

a) to e) Sample load-displacement curves of load controlled cyclic shear load tests on anchors as well as corresponding mean curve of monotonic reference tests (0.8 mm (0.03 in.) crack width); f) Failure mode schematic, photo of spalling.

The load-displacement curves of the cyclic shear tests on the undercut anchor UA1 were clearly below the corresponding monotonic mean curve (Fig. 8a) and all replicates failed during cycling in steel. First, the sleeve surrounding the bolt broke in the shear plane, then, few cycles later, the anchor bolt followed. The screw anchor SA1, representing an anchor type with ductile core but hardened and therefore potentially brittle surface, showed a high resistance to cycling. All samples completed the shear cycles and their load-displacement curves followed the corresponding monotonic mean curve (Fig. 8b) and the anchors failed in steel during the residual load capacity test. The cyclic load-displacement curves of the sleeve-type expansion anchor EAs1 were again clearly below the corresponding monotonic mean curve and all anchors failed during cycling (Fig. 8c). The anchor bolt and sleeve, which was installed flush with the fixture, ruptured at concrete surface. The load-displacement curves of the cyclic shear tests on the bolt-type expansion anchor EAb1, followed the corresponding monotonic mean curve (Fig. 8d) and all replicates failed after cycle completion when being loaded to failure to test the residual capacity. Also the load-displacement curves of the shear cycling tests on the bonded anchor BA1 followed the corresponding monotonic mean curve. All anchors completed all cycles (Fig. 8e) and failed in steel during the residual capacity test.

The mean residual load capacities after shear load cycling V_u,cyc,m were significantly lower than the respective monotonic capacity V_u,mon,m for anchors undercut anchors UA1, as well as expansion anchors EAs1 and EAb1. Only for the screw anchors SA1 and bonded anchors BA1, the residual load capacities agreed with the monotonic load capacities with ratios V_u,cyc,m / V_u,mon,m close to 1.00. Clearance gap and concrete spalling, a shell shaped concrete breakout caused by the stress concentration at the contact between anchor and concrete at the surface (Fig. 8f), led to increased anchor bending and ultimately reduced the shear failure load of the anchor as described in earlier studies^38,39. Concrete spalling was much less pronounced for screw and bonded anchors with direct contact between the anchor and the concrete along their entire length reducing bending of the anchor and ensuring a less localized load transfer. Compared to cyclic tension tests, the scatter was relatively low for the cyclic shear tests with a coefficient of variation v generally below 6 % due to the steel failure mode. Larger variations can be attributed to concrete spalling.

The anchor displacements generated during shear load cycling s_V,cyc are relatively large in comparison to those of cyclic tension tests. The displacements at ultimate load were in the range of 10 mm (0.40 in.) to more than 30 mm (1.20 in.). The scatter of the displacements was relatively small with a maximum of variation v of 25 %. Anchors accompanied with pronounced concrete spalling during loading (UA1 and EAs1) showed large displacements at ultimate monotonic load s(V_u,mon)_m.

The diagrams in Fig. 8 show closely spaced hysteretic loops and characteristic pinching. Despite the prevalent steel failure mode, the energy dissipation was small, though larger than under tensile load cycling. In general, the tested anchors resisted shear load cycling with a considerable number of load cycles. However, for some anchor types the backbone curve of the load path deviated early during cycling from the monotonic mean curve and the anchors failed then by low cycle fatigue prior to completion of load cycles. Anchors loaded by shear loads are generally more prone to fatigue than tension loaded anchors because they experience large plastic deformations in alternating directions, which is not the case for anchors in tension. Furthermore, anchors experience highly-localized plastic deformation along the shear plane under shear loads⁴⁰. For the anchor tests presented in this paper, most of the pretension of the anchor and therefore the friction between fixture and concrete was already gone when the crack was opened and the anchor lost some of its stiffness. For undercut and sleeve-type anchors, UA1 and EAs1, failure occurred shortly before completion of load cycling during cycle 32 to 35 out of 36. The ultimate load was reduced by approximately 30 % if compared to the ultimate load of the corresponding monotonic test series. Bolt-type anchors EAb1 sustained load cycling but the mean residual load capacity was approximately 20 % lower compared to the mean ultimate load of the corresponding monotonic test series. This indicates that the bolt was damaged during cycling and low cycle fatigue was imminent. Screw and adhesive anchors, SA1 and BA1, did not experience any strength reduction due to load cycling. It is interesting to note that the investigated anchors experiencing low cycle fatigue failure during cycling were products with sleeves. The stiff sleeve attracts more shear load than the bolt, which can move within the sleeve, and is therefore subjected to higher shear load amplitudes causing low cycle fatigue failure. Moreover, the high monotonic capacity of these anchor types result in relatively large target load amplitudes during cycling (V_max = 0.90 · V_u,mon,m).

Displacement controlled tests and tests with continued load cycles

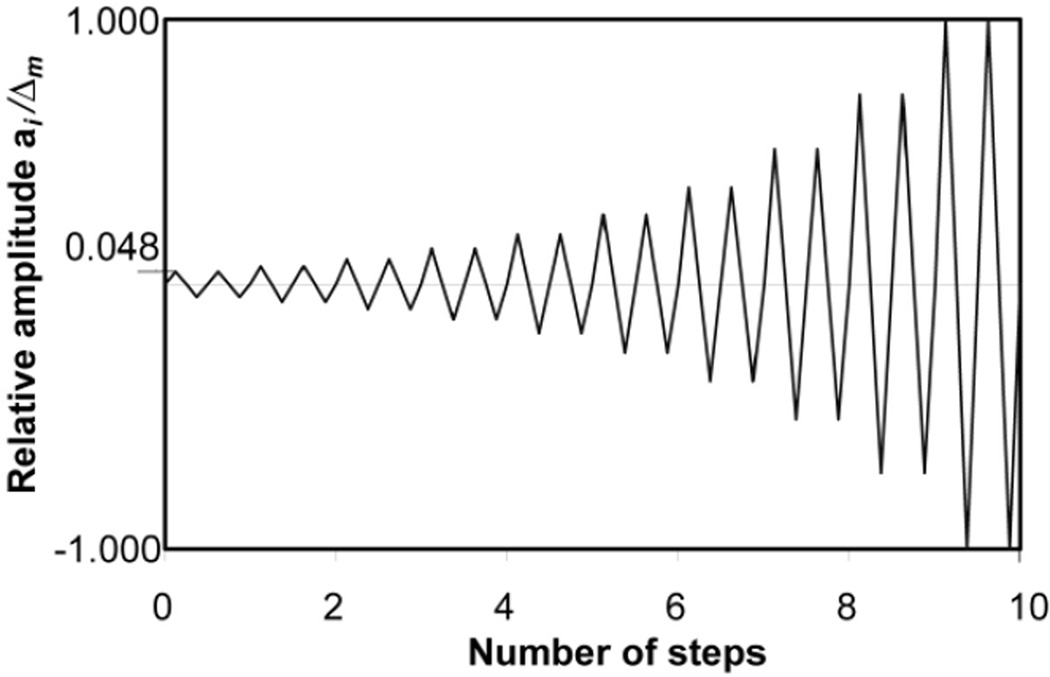
Historically, anchor qualification tests are run under load control like the simulated seismic tests according to ACI 355. For the seismic approval of nonstructural components, however, the use of displacement controlled test protocols is generally recommended²⁴. Also the FEMA 461 guideline for determining the seismic performance characteristics of structural and nonstructural components²⁷ stipulates displacement controlled fragility tests. Its test protocol defines relative displacement amplitudes a_i / Δ_m with a_i+1 = 1.4a_i and the maximum amplitude Δ_m, and defines 10 steps with 2 cycles each (Fig. 9). To investigate the applicability of displacement controlled cyclic tests on anchors and to compare the test results with those gained in the load controlled tests with stepwise increasing load cycling, the study presented in this paper included a limited number of tests conducted according to the FEMA 461 testing protocol.

Fig. 9.

Relative amplitude protocol according to FEMA 461²⁷ for displacement controlled cyclic test (a_i: amplitude of step i; Δ_m: displacement target).

FEMA 461 defines the target displacement Δ_m for the cyclic test as the estimated value for which the most severe damage is expected to initiate. To establish this threshold, monotonic tests may be carried out but are not explicitly required. To ensure direct comparability within this study, however, the target displacement after completion of the 20 cycles was taken as the mean monotonic displacement at the target load used for the load controlled tests (Δ_m = s(V_max) = s(0.90 · V_u,mon,m)). The displacement signal of the actuator was used as control signal. Since the above discussed load controlled tests proved that alternating shear cycling is more critical than pulsed one direction tension cycling, only cyclic shear tests are reported herein. The simple control program solely comprising regular sinusoidal displacements with increasing amplitudes led to an accelerated testing because the time consuming intermediate displacement controlled ramps required for the load controlled tests could be omitted. Particular attention had to be paid to the annular gap around the anchors as uneven gaps result in asymmetric load-displacement curves. The tests were carried out on undercut and bolt-type expansion anchors, UA1 and EAb1, installed in 0.8 mm (0.03 in.) cracks. The test setup was identical to that used for the load controlled tests. The test program and key test results are presented in Table 4. Refer to Table 3 for monotonic shear reference data.

Table 4.

Tests conditions and key test results of displacement controlled cyclic shear load tests after FEMA 461²⁷ (load and displacement values given as average of all test repeats).

Anchor designationa	Crack width w, mm	Load. typeb	Number of tests	Failure modec	Target displ. s(V)max, kN	Vu,m, kN	vg(Vu,m), %	Vu,cyc,m / Vu,mon,m	V,cyc, mm	s(Vu)m, mm	vg(s(Vu)m), %	s(Vu,cyc)m/ s(Vu,mon)m
UA1	0.8	cyc	3	S	21.79	67.4	18.5	0.76	54.1	26.9	42.1	0.86
EAb1	0.8	cyc	3	S	9.08	28.1	2.2	0.87	23.2	11.4	11.1	1.02
EAb1	0.8	cont cyc	3	Sd	-	31.2	10.1	0.96	-e	11.3f	25.4	1.01

^a–gRefer to Table 2

Note: Refer to Fig. 2 for explanation of variables; 1 mm = 0.0394 in.; 1 kN = 224.81 lbf.

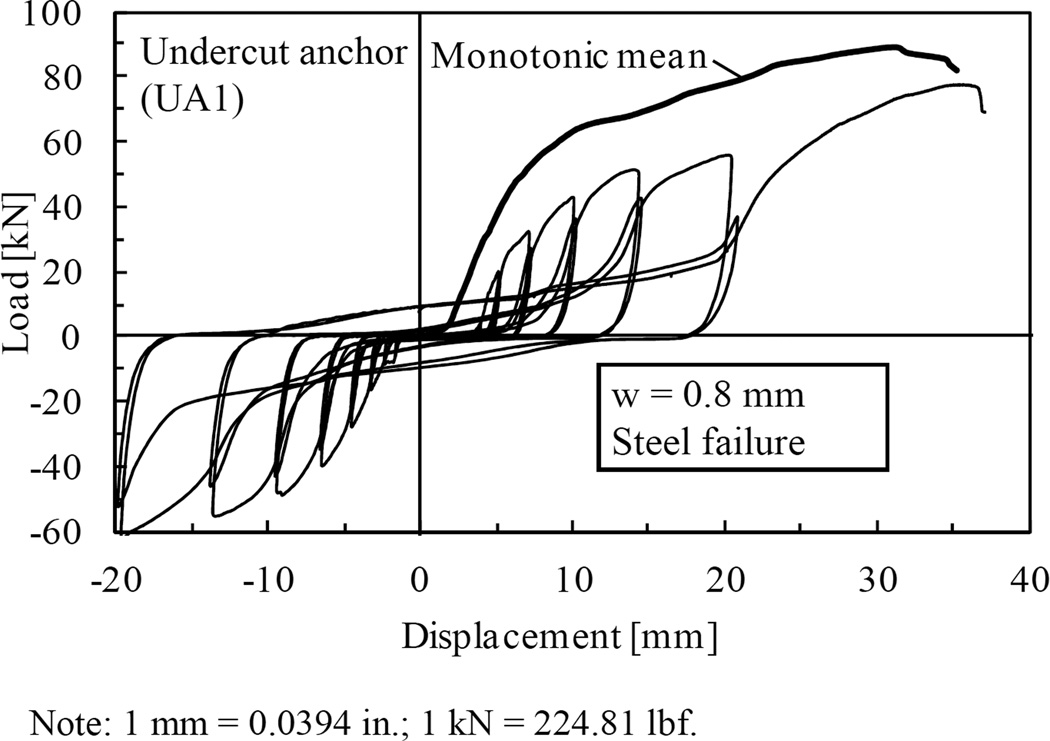
Fig. 10 plots an example load-displacement curve of the undercut anchor (UA1) tested cyclically to the targeted displacement. For comparison, the monotonic load-displacement curve is also shown. The load response steadily increased with increasing displacement demands. In contrast to load controlled tests with increasing displacements within a load step, the displacement controlled tests showed decreasing loads within a displacement step. The backbone curve of the cyclic load-displacement path was clearly below the monotonic mean curve and the load measured during the last displacement cycle V_cyc was significantly below the corresponding monotonic load measured for that anchor displacement. This loss in strength, however, is less pronounced compared to that measured during the corresponding load controlled cyclic tests (Figs. 8a). Moreover, the UA1 anchor did not fail in low cycle fatigue but showed substantial residual capacity. The reason for the different fatigue behavior in the tests with stepwise increasing load cycles and the tests according to FEMA 461 is the different stress regime the test protocols impose on the anchor. Assuming a simple damage rule based on the number of load cycles i and their load amplitudes a, the stress accumulating during cycling (Σ_i a_i) is for the tests with stepwise increasing load cycles (36 cycles) roughly twice as large compared to that of the FEMA 461 tests (20 cycles). In this sense, the stepwise increasing load cycling protocol was more demanding than the displacement controlled tests according to the FEMA 461 protocol and it better allows for detection of low cycle fatigue behavior and better differentiates the behavior of various anchor types.

Fig. 10.

Sample load-displacement curve of displacement controlled cyclic shear load test after FEMA 461²⁷ and corresponding mean curve of monotonic reference test (0.8 mm (0.03 in.) crack width).

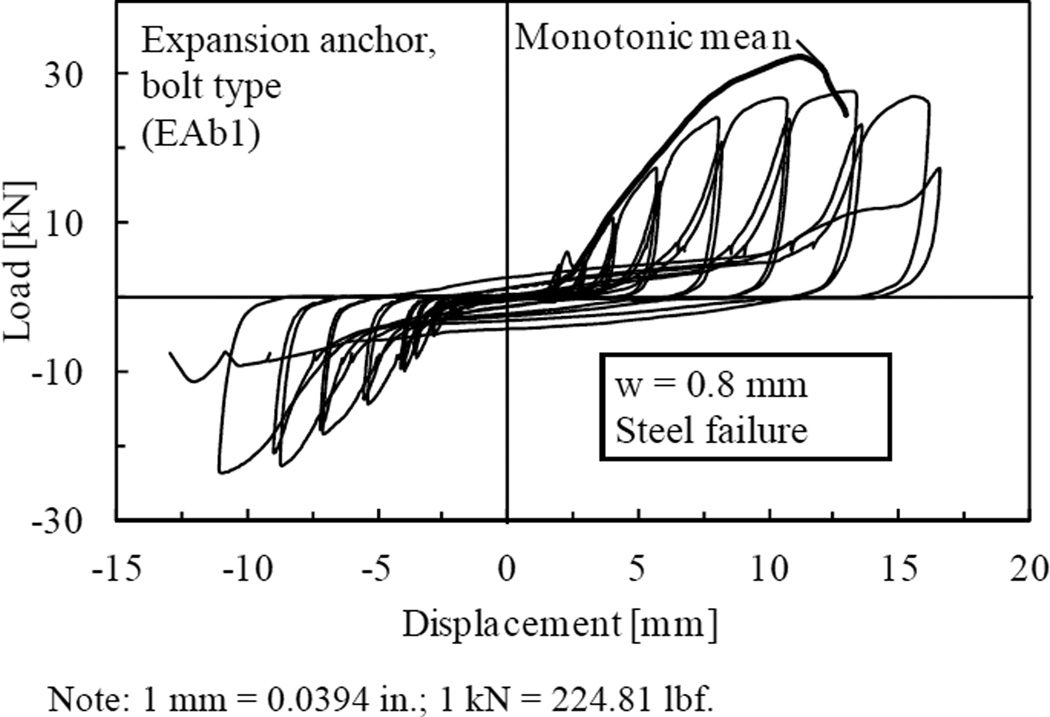
To cover near ultimate load behavior for specimens not failing within the basic test cycles, FEMA 461 proposes to prolong cycling beyond the original target displacement by stepwise increased displacement cycles until failure. This methodology was checked by an exploratory cyclic shear test series on the bolt-type anchor EAb1. The displacement increments after the achievement of the original target displacement were chosen according to the FEMA 461 recommendations as 30 % of the target displacement. The envelope of the example cyclic load-displacement curve with continued cycles shown in Fig. 11 coincides well with the envelopes derived from the other displacement controlled tests on the bolt-type anchor EAb1 until it ultimately failed in steel due to low cycle fatigue. Failure occurred at a displacement larger than the mean displacement at peak monotonic load. The mean peak load is approximately equivalent to the residual strength determined in the other displacement controlled tests. Furthermore, testing with prolonged cycling until failure does not allow for the evaluation of anchor performance based on a required number of completed cycles and limits the assessment to the overall load-displacement behavior and the peak strength achieved during cycling. The FEMA 461 guideline allows for cyclic testing without determining the monotonic capacity of the tested component, however, to relate the seismic to the static performance, monotonic reference tests as proposed for the stepwise increasing load cycling protocols are essential for eliciting the difference in performance of different anchor products.

Fig. 11.

Sample load-displacement curve of continuous shear load cycling test after FEMA 461²⁷ and corresponding mean curve of monotonic reference test (0.8 mm (0.03 in.) crack width).

SUMMARY AND CONCLUSIONS

Cyclic load tests on post-installed anchors using new stepwise-increasing load protocols, which are based on an extensive study of the nonlinear response of anchored components in buildings, were carried out. The tests resulted in load-displacement curves representative for common anchor types and failure modes.

For cyclic tension tests, the envelope of the load-displacement curves followed the mean curve of corresponding monotonic tests. For the tested load regime, the number of cycles and the load levels were sufficiently low to prevent damage in the anchor or concrete during tension load cycling. For this reason, tensile load cycling did not produce large anchor displacements during cycling and did not affect anchor load capacity. In all residual capacity tests, concrete-related failure modes occurred (concrete breakout or pullout). The effect of crack width on the ultimate tension capacity was clearly visible for monotonic and cyclic tests. Tests in larger cracks consistently resulted in reduced load capacities. For the tested anchors, the reduction for tests in 0.8 mm (0.03 in.) cracks was about 20 % compared to the capacities in 0.5 mm (0.02 in.) cracks. The investigated adhesive anchors exhibited suitable resistance to tensile load cycling in 0.8 mm (0.03 in.) wide cracks.

For cyclic shear tests, in general, the envelope of the load-displacement curves followed the mean curve of corresponding monotonic tests. The anchor displacements during cycling were larger than for tension cycling, but generally in the range of displacements corresponding to monotonic tests at that load level. However, depending on the anchor type and applied target load, the anchors bent plastically during shear load cycling, and the surrounding concrete experienced spalling. When this occurred, the envelope of the cyclic load-displacement curves was lower than the monotonic mean curve and the anchors were prone to low cycle fatigue failure prior to completion of the cyclic load protocol. This behavior was particularly prevalent for anchors with sleeves in the shear plane presumably owing to their larger monotonic capacities, which dictates a higher load cycling demand, and uneven distribution of the applied shear load between the anchor sleeve and bolt. To complete all cycles with these anchors, a reduction of the maximum cyclic anchor load level relative to the monotonic capacity would be required.

The displacement controlled cyclic tests conducted on anchors according to the FEMA 461 guideline exhibited anchor behavior similar to that during the load controlled tests with stepwise increasing load cycles. The damage potential of the FEMA 461 test protocol is less than that of the investigated stepwise increasing load cycling protocol, resulting in delayed material degradation and higher low cycle fatigue strength. Furthermore, the lack of a clearly defined displacement target and absence of required monotonic reference tests, make the assessment of anchor behavior for product qualification difficult using the FEMA 461 standard.

The results showed that despite the variations in performance, in principle, each anchor type is suitable for seismic applications with respect to tension and shear load cycling under the investigated conditions, provided they function well in cracked concrete with large cracks (w ≥ 0.5 mm (0.02 in.)) under monotonic loading and during crack cycling. However, the ratio of seismic to static anchor strength may be different for different anchor types. Furthermore, the tests demonstrated that energy dissipation during cycling is insignificant for tension loading and very small for shear loading, irrespective of the anchor type.

The approach to test anchors by stepwise increasing load protocols proved to be practical and resulted in load-displacement curves displaying the anchor behavior throughout the relevant loading range. These advantages make stepwise increasing load protocols the preferred choice for anchor qualification procedures. Together with crack cycling tests, the tests described in this paper contributed to the development of the recently published ETAG 001 Annex E⁴¹ anchor qualification guideline, which introduces a new, more stringent seismic performance category to augment the seismic performance tests currently in ACI 355.

LIST OF NOTATIONS

d₀

Borehole diameter

f’_c

Concrete compression strength

h_ef

Effective embedment

k_s

Statistical factor

s(N)

Axial displacement

s(V)

Shear displacement

s_cyc

Residual displacement after load cycling

v

Coefficient of variation

w

Crack width

F_u,m

Mean ultimate load

F_Rk

Characteristic resistance

N_u,m

Mean ultimate tension load

N_max

Target tension load

V_u,m

Mean ultimate shear load

V_max

Target shear load

Biographies

Philipp Mahrenholtz is the Engineering Manager at Stanley Black & Decker – Powers Fasteners Europe in Frankfurt, Germany. He received his diploma in civil engineering from the University of Aachen (RWTH), Aachen, Germany, and his PhD from the University of Stuttgart, Stuttgart, Germany. His research interests include metal and fiber reinforced polymer anchors, in particular, for use in seismic applications.

Rolf Eligehausen, FACI, is a Professor Emeritus at the Institute of Construction Materials at University of Stuttgart, Stuttgart, Germany. He is a member of ACI Committees 349, Concrete Nuclear Structures, 355, Anchorage to Concrete, and Joint ACI-ASCE Committee 408, Development and Splicing of Deformed Bars and is chairman of the fib Task Group 2.9 “Fastenings to Concrete and masonry Structures”. His research interests include anchorage to concrete as well as bond and detailing of reinforcement.

Tara C. Hutchinson is a Professor at the University of California, San Diego. She received her MS from the University of Michigan, Ann Arbor, MI, and her PhD from the University of California, Davis. Her research interests include earthquake engineering, including the performance evaluation of soil-foundation systems, concrete components, nonstructural systems and components, and development of damage-monitoring strategies.

Matthew S. Hoehler is a Research Structural Engineer at the National Institute of Standards and Technology in Gaithersburg, Maryland (formerly with Hilti Corporation). He received his BS from Princeton University, his MS from the University of California, Berkeley, and his PhD from the University of Stuttgart, Germany. His research interests include experimental testing and analysis of the performance of materials, components, and structures associated with structural collapse, natural disasters, or human-initiated events.