Abstract
Despite the important role that mechanical forces play in tumor growth and therapy, the contribution of swelling to tumor mechanopathology remains unexplored. Tumors rich in hyaluronan exhibit a highly negative fixed charge density. Repulsive forces among these negative charges as well as swelling of cancer cells due to regulation of intracellular tonicity can cause tumor swelling and development of stress that might compress blood vessels, compromising tumor perfusion and drug delivery. Here, we designed an experimental strategy, using four orthotopic tumor models, to measure swelling stress and related swelling to extracellular matrix components, hyaluronan and collagen, as well as to tumor perfusion. Subsequently, interventions were performed to measure tumor swelling using matrix-modifying enzymes (hyaluronidase and collagenase) and by repurposing pirfenidone, an approved antifibrotic drug. Finally, in vitro experiments on cancer cell spheroids were performed to identify their contribution to tissue swelling. Swelling stress was measured in the range of 16 to 75 mm Hg, high enough to cause vessel collapse. Interestingly, while depletion of hyaluronan decreased swelling, collagen depletion had the opposite effect, whereas the contribution of cancer cells was negligible. Furthermore, histological analysis revealed the same linear correlation between tumor swelling and the ratio of hyaluronan to collagen content when data from all tumor models were combined. Our data further revealed an inverse relation between tumor perfusion and swelling, suggesting that reduction of swelling decompresses tumor vessels. These results provide guidelines for emerging therapeutic strategies that target the tumor microenvironment to alleviate intratumoral stresses and improve vessel functionality and drug delivery.
Introduction
Finding the cure for cancer is a true challenge undertaken by hundreds of research groups worldwide, each one focusing on different aspects of the disease in an attempt to better understand the mechanism of cancer progression and identify a more effective therapy. From the mechanical point of view, all tumor components interact with each other, resulting in generation of mechanical stresses between them that could elucidate disease pathogenesis. Mechanical stresses stem either from the solid components of a tumor, mainly cancer and stromal cells and the extracellular matrix (ECM), or from the interstitial fluid. In the former case, the stress of the solid, structural tumor components is known as solid stress, whereas the stress from the interstitial fluid is referred to as the interstitial fluid pressure (IFP) [1]. Solid stress can be further divided into three components: stress owing to reciprocal interactions between the tumor and the host tissue, residual stress, and swelling stress [2], [3]. Solid stress is usually elevated in tumors because of tumor growth in the confined space of the host tissue, which in turn resists tumor expansion. Another cause of solid stress is the stiffening of the tumor, observed in many cancers during tumor progression and the accumulation of residual stresses [1], [2], [3]. Additionally, tumors rich in hyaluronan (e.g., breast and pancreatic cancers and sarcomas) are characterized by a high-net negative charge density owing to the negatively charged groups of hyaluronan, quantified as the fixed charge density (FCD) [4]. Because of its negative charge, hyaluronan immobilizes interstitial fluid forming gel-like regions within the tissue [5]. Repulsive electrostatic forces among the closely spaced negative groups cause the swelling of these regions — an effect known as chemical expansion — which in turn generates a swelling solid stress (or swelling stress for brevity) because it is generated by solid components of a tumor. IFP is also elevated owing to the hyperpermeability of some tumor blood vessels, which allows excessive plasma to enter the tumor, and due to the dysfunction of most intratumoral lymphatic vessels, which cannot drain adequately the interstitial fluid [6], [7]. Additionally, in hyaluronan-rich tumors, because of the presence of FCD and in order for the tumor to meet the electroneutrality condition, a large number of counter ions must be present within the interstitial space. Therefore, there might be an excess of cations within the tumor interstitial space, creating a Donnan osmotic fluid pressure difference between the internal and external environment of the tissue [8], [9].
Elevated solid and fluid stresses determine in large part tumor progression and response to treatment [2], [10]. On one hand, elevated solid stresses can directly compress cancer cells to reduce their proliferation rate and increase their invasiveness and metastatic potential [11], [12], [13], [14], [15], [16]. These stresses can also compress intratumoral blood and lymphatic vessels and thus cause hypoxia and hypoperfusion [1], [17], [18]. Hypoxia, among other effects, imposes a survival advantage for cancer cells, enhances their ability to invade and metastasize, harbors the cancer stem cells, and compromises the efficacy of radiotherapy [19]. Hypoperfusion drastically reduces the systemic delivery of drugs to the tumor site and, consequently, the efficacy of chemo- and nanotherapeutics [20]. On the other hand, elevated IFP poses an additional barrier to the delivery of nanoscale drugs and facilitates transport of growth factors and cancer cells from the tumor to the surrounding tissue, fueling tumor growth, progression, and lymphatic metastasis [21], [22]. Alleviation of solid and fluid stresses by targeting specific components of the tumor microenvironment has emerged as a new therapeutic strategy to enhance cancer therapy with promising preclinical data [3], [20], [23], [24], [25], [26], [27] and the first clinical trial being already in progress (clinicaltrials.gov identifier NCT01821729). Preclinical studies have shown that therapeutic depletion of collagen and/or hyaluronan alleviates mechanical stresses and thus decompresses tumor blood vessels, improving perfusion and the efficacy of chemotherapy [23], [24], [25], [26], [27], [28]. Despite these encouraging findings, there are no established guidelines on the use of stress alleviation strategies yet owing in large part to our limited knowledge of tumor mechanical behavior and its relation to tumor pathophysiology [2], [29], [30]. Therefore, it is high time for in-depth understanding, analysis, and better characterization of all mechanical components of the tumor microenvironment that contribute to the acquisition of malignant properties and drug resistance to develop new and effective therapeutic interventions.
Interestingly, little is known regarding the swelling behavior of tumors, as there are only a few studies reporting osmotic fluid pressure measurements [31], whereas to the best of our knowledge, there is no study to measure and characterize the swelling stress. To this end, we designed and performed a series of experiments and developed a mathematical model to quantify the swelling behavior of tumors, hereafter referred to as tumor swelling. Our objectives were to relate tissue swelling to the composition and organization of the tumor ECM and the functionality of the tumor vessels, compare swelling stress and osmotic pressure to the total solid stress and IFP, investigate how modifications of the ECM affect swelling and perfusion, and identify the contribution of cancer cells to tumor swelling. In that regard, we employed four orthotopic tumor models: three xenograft models using the human breast MCF10CA1a, pancreatic MiaPaCa2 and fibrosarcoma HT1080 cell lines and a syngeneic model using the mouse 4T1 breast cancer cell line. Furthermore, cancer cell spheroid models were generated to measure swelling of cancer cells in vitro. Finally, because the component of the solid stress owing to interactions with the host tissue and the osmotic fluid pressure cannot be measured experimentally, we developed a triphasic biomechanical mathematical model of tumor growth, which accounted for the solid and fluid phase of the tumor as well as the transport of ions and the fixed charged density. The model was informed and specified using our experimental data and predicted the contribution of each stress type to the mechanics of cancer during progression.
Materials and Methods
Cell Culture
MCF10CA1a human breast cancer cell line was obtained from the Karmanos Cancer Institute (Detroit, MI) and maintained as previously described [32]. 4T1 mouse mammary carcinoma, HT1080 human fibrosarcoma, and MiaPaCa2 pancreatic cell lines were purchased from ATCC. 4T1 cells were maintained in RPMI medium supplemented with 10% fetal bovine serum and 1% penicillin/streptomycin, whereas the other cell lines were maintained in Dulbecco's modified Eagle's medium supplemented with 10% fetal bovine serum and 1% penicillin/streptomycin.
Animal Tumor Models and Experimental Protocols
All experimental protocols were approved by the Cyprus Veterinary Services, the Cyprus national authority for monitoring animal research, under a license (no. CY/EXP/PR.L1/2014). Orthotopic xenograft breast tumors were generated by implantation of 5 × 105 human MCF10CA1a cells resuspended in 40 μl of serum-free medium into the mammary fat pad of 6-week-old female CD1 nude immunodeficient mice. Orthotopic syngeneic models were generated by implantation of 105 4T1 mouse mammary cancer cells into the mammary fat pad of 6-week-old BALB/c female mice. Orthotopic fibrosarcoma tumors and ectopic pancreatic tumors were established by subcutaneous implantation of 5 × 106 human HT1080 cells or 2 × 106 MiaPaCa2 cells, respectively, into the left flank of 6- to 8-week-old NOD/SCID mice. Tumor growth was monitored every second day, and the planar dimensions (x, y) were measured with a digital caliper. Tumor volume was calculated using the volume of an ellipsoid and assuming that the third dimension, z, is equal to . The establishment of human orthotopic pancreatic tumors was performed by surgical implantation of MiaPaCa2 cells directly into the pancreas of 6-week-old male CD1 nude mice that were anesthetized by intraperitoneal injection of Avertin (250 mg/kg). Briefly, an incision of the skin was performed in the area above the spleen, followed by a small cut on the surface of the abdominal cavity. Then, the spleen along with the underlying pancreas was gently pulled out, and the entire pancreatic body was exposed. The organ was slightly spread using forceps, and 2.5 × 106 MiaPaCa2 cells resuspended in 20 μl of serum-free medium were implanted in the pancreas [33]. Upon implantation, the abdominal surface and skin were sutured.
Measurement of Swelling Solid Stress and Elastic Modulus in Murine Tumors
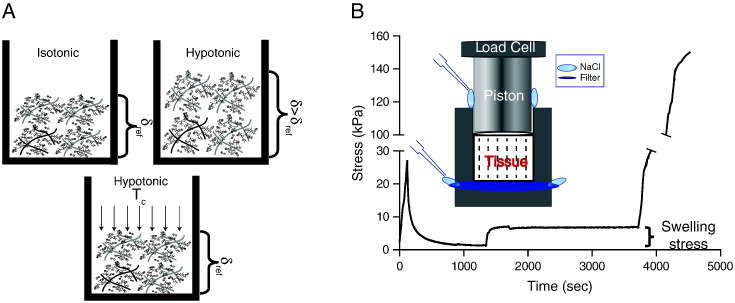
The experimental setup was in line with other studies [8] and based on the confined compression experiment using a high-precision mechanical testing system (Instron 5944, Norwood, MA). Tumors were excised with a scalpel into specimens of cylindrical shape, 4 mm in diameter and 5 mm long, and they were placed into a chamber (Figure 1 and Supplementary Figures S1 and S2). Therefore, each tumor was divided into three to four pieces, and experiments were performed on all of them. In total, 20 tumors were used from each tumor type (n = 20). At the top side of the chamber, a piston was adjusted to compress the specimen. At the bottom side of the chamber, a filter paper (Whatman, 20- to 25-μm pore size) was placed to allow fluid flow. Special care was taken to ensure that the tumor was never in direct contact with fluid during storage so as to minimize potential leakage of FCD from the specimen before testing. The sample was initially compressed to 10% strain in a period of 2 minutes to make sure the piston applies well on the specimen and that the specimen's response to deformations is measurable. Afterward, the specimen was held for 20 minutes until the stress relaxed and reached an equilibrium. Subsequently, the specimen was kept at the same strain, and NaCl dissolved in ultrapure water was added to the chamber at concentrations ranging from 0.001 to 0.3 M (Figure 1). Upon addition of NaCl, the stress increased and reached a new equilibrium. Swelling stress was quantified as the change in stress following NaCl addition (Figure 1). Finally, the sample was compressed to 30% strain. This allowed for the measurement of the elastic modulus of the specimen from the slope of the stress-strain curve between 10% and 15% compression (Figure 1). As a reference condition for all measurements, we used the physiological ionic concentration (0.15 M) where tumor swelling is considered to be zero [8].
Figure 1.
Measurement of tumor swelling. (A) δref is defined as the thickness attained when NaCl concentrations are isotonic enough to shield electrostatic interactions; δ > δref tumor swelling in hypotonic solutions (the thickness of the sample increases); the stress required to compress the sample from thickness δ to δref defines the swelling stress, Tc. (B) The tumor specimen was initially compressed to 10% strain and allowed to relax. Subsequently, NaCl solution of specified concentration was added, causing the swelling of the tissue, which reached a new equilibrium. Finally, the specimen was compressed for another 20% strain. The difference in the stress between the two equilibriums was quantified as the swelling stress. Islet shows a schematic of the experimental set up.
Cancer Cell Spheroids Formation and Swelling Measurement
MiaPaCa2 and HT1080 cell spheroids were formed using the “hanging drop” technique, as described previously (Supplementary Material [34], [35]). Subsequently, formed spheroids were transferred into wells of a 96-well plate containing 1% agarose using a glass Pasteur pipette. Pictures were then taken using a Nikon Eclipse optical microscope; this was considered as time zero. Subsequently, NaCl solutions of different molarity were added on top of the spheroids, and they were incubated for an additional hour at 37°C. Hypotonic NaCl solution had a concentration of 0.001 M; isotonic, a concentration of 0.15 M; and hypertonic, a concentration of 0.3 M. Pictures were taken at the 1-hour time point, as this proved to be sufficient for cells to equilibrate, and changes in spheroids' size (average of the major and minor axis length) were measured using the ImageJ software. Two independent experiments were performed, and at least six spheroids were monitored for each NaCl condition.
Fluorescent Immunohistochemistry
Seven minutes prior euthanization and tumor removal, mice were slowly injected with 100 μl of 1 mg/ml of biotinylated Lycopersicon esculentum (tomato) lectin (Vector Labs) via intracardiac injection. Following swelling measurements, tumor specimens were fixed with 4% paraformaldehyde in PBS for 20 minutes at room temperature followed by overnight incubation at 30% sucrose in PBS at 4°C. The samples were then embedded in optimal cutting temperature compound (Tissue-Tek) and frozen.
Collagen and Hyaluronan Analysis
Transverse 40-μm–thick tumor sections were cut and immunostained with collagen I antibody (ab4710, Abcam 1:100 dilution) and hyaluronan (ab53842, Abcam 1:100 dilution) counterstained with 4′,6-diamidino-2-phenylindole (Vector Labs). Collagen I was detected with Alexa Fluor-647 Goat Anti-Rabbit IgG (H + L) secondary antibody (A-21244, Invitrogen, 1:800 dilution), and hyaluronan was detected using Alexa Fluor-647 donkey Anti-sheep IgG (H + L) secondary antibody (A-11015, 1:800 dilution).
Blood Perfusion Analysis
Transverse 60-μm–thick tumor sections were prepared and counterstained with antibody against the endothelial marker CD31 (MEC13.3 antibody, Biosciences [BD], 1:100 dilution). Lectin staining was detected using the Streptavidin Alexa Fluor 488 conjugate (Molecular Probes, S11223, 1:400 dilution), and CD31 signal was detected with Alexa Fluor-647 Goat Anti-Rat IgG (H + L) secondary antibody (Molecular Probes, A-21247, 1:800 dilution). Perfused vessel fraction was calculated as the ratio of the perfused vessel area (lectin and CD31-positive vessels) to the total area of vessels (CD31-positive vessels). For image analysis, the calculation of collagen and hyaluronan area fractions and fraction of perfused vessels was performed automatically using a previously developed in-house code in MATLAB (MathWorks, Inc., Natick, MA) to avoid any associated bias [3], [23]. Furthermore, to deal with the spatial heterogeneity of the tissues, five sections were taken from each specimen starting from tumor center toward the periphery.
IFP Measurement
IFP was measured in vivo with the wick-in-needle technique [36].
Statistical Analysis
The data are presented as means with standard errors. Groups were compared using Student's t test.
Mathematical Model
Based on our previous work [1], [29], [30], [37], [38], a mathematical model was developed and informed by our experimental data to calculate the Donnan osmotic pressure and the solid stress exerted by the host tissue on the tumor, which cannot be measured experimentally. The model consisted of three phases: the solid and fluid phase and the ions (positive and negative). Furthermore, it employed the multiplicative decomposition of the deformation gradient tensor to model tumor growth, accounting also for the effect tumor oxygenation and solid stress on cancer cell proliferation [38], [39], [40]. A detailed description of the mathematical model is given in the Supplementary Material.
Results
Swelling Stress Is Evident in All Tumor Models and Increases with Hypotonic Conditions
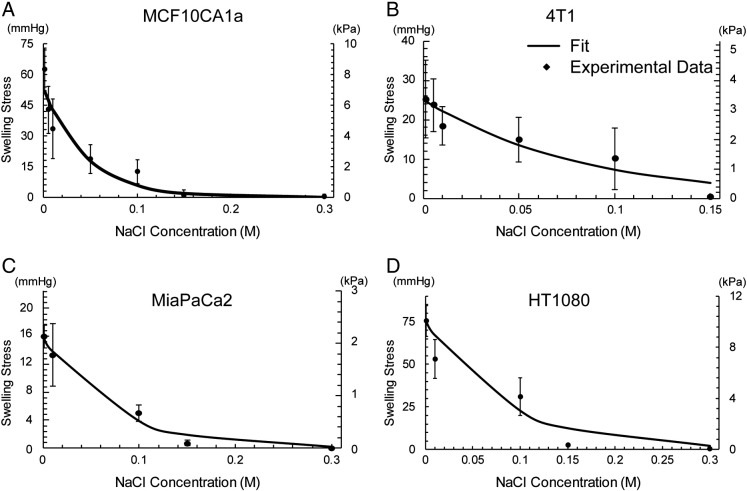
To measure the swelling stress of the four orthotopic tumor models as a function of the concentration of electrolytes, we designed an experimental approach as depicted in Figure 1, A and B. A typical tissue response is shown in Supplementary Figure S2. The swelling stress increased upon addition of hypotonic saline, whereas it remained stable at zero upon addition of isotonic or hypertonic solutions (Figure 2). As hypotonic solutions exhibit low ionic strength, the Debye length that defines the range of electrostatic interactions increases. For NaCl concentrations closer to or higher than the physiological value of 0.15 M, the electrostatic repulsive forces become negligible owing to the small value of the Debye length (~0.8 nm), and thus, no swelling was observed. For the lowest concentration of NaCl, the swelling stress ranged from 16.01 ± 1.66 mmHg (2.13 ± 0.22 kPa) for the MiaPaCa2 tumors to 75.38 ± 9.03 mmHg (10.05 ± 1.20 kPa) for the HT1080. To confirm that the experimental measurements of the swelling stress did not include any component of Donnan osmotic pressure, we simulated the experimental procedure using our mathematical model. The simulations showed that Donnan osmotic pressure should be negligible (Supplementary Figure S3).
Figure 2.
Experimental data of tumor swelling. Swelling stress as a function of NaCl concentration for the four orthotopic tumor models employed in the study. The experimental data were fitted to Eq. (S14) (solid line) and values of the fitting parameters are shown in Supplementary Table S1.
As far as the elastic modulus is concerned, in all tumor types, it exhibited a dependence on NaCl concentration (Supplementary Figure S4). The modulus was higher at low electrolyte concentrations, whereas it dropped to a constant value at higher concentrations, with the exception of MiaPaCa2 tumors in which it remained unaltered for all spectra of electrolyte concentrations. Swelling stress and elastic modulus fitted well to phenomenological expressions previously employed for cartilage swelling (Supplementary Equations S5 and S14) [8]. The values of the parameters of the equations are given in Supplementary Table S1.
Tumor Swelling Increases Linearly with the Ratio of Hyaluronan to Collagen Area Fraction
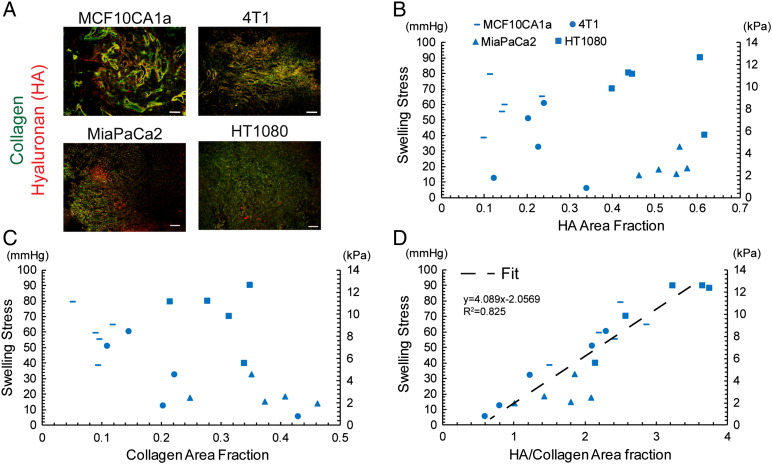
To investigate the ECM structure of the tumor types studied, immunofluorescence analysis of collagen and hyaluronan was performed. Even though other types of glycosaminoglycans might contribute to tumor swelling, we focused on the examination of hyaluronan owing to its abundance in the tumors tested and because it has been reported to be a target for stress-alleviating therapeutic strategies [23], [24], [25]. MiaPaCa2 and HT1080 tumors had higher levels of collagen and hyaluronan compared with the two breast tumor types, MCF10CA1a and 4T1 (Figure 3A and Supplementary Figure S5). As the data of the lowest electrolyte concentration (0.001 M) exhibited the largest variation in swelling, they were selected for further analysis. Thus, correlations between the swelling stress and the composition of the tumor ECM were sought. There was no correlation between swelling and hyaluronan or collagen content alone (Figure 3, B and C). Interestingly however, when swelling stress was plotted as a function of the relative area fraction of hyaluronan to collagen, a strong linear correlation was revealed that was verified in all tumor types tested (Figure 3D), indicating a dependence of tissue swelling on tumor's collagen and hyaluronan composition. This finding is in accordance with in vivo studies in cartilage tissue as well as with studies using in vitro models [41], [42], [43].
Figure 3.
Effect of ECM composition on swelling stress. (A) Representative immunofluorescence staining sections for hyaluronan (HA) and collagen (scale bar 100 μm), (B) Swelling stress as a function of HA area fraction, and (C) collagen area fraction showing no correlation. (D) Swelling stress is linearly proportional to the ratio of HA/collagen area fraction (y = 4.089x − 2.057, R2 = 0.825). Five tumor specimens (n = 5) from each tumor type were used.
Swelling Contributes to Tumor Mechanical Function Contrary to Negligible Donnan Osmotic Pressure
Contrary to swelling stress and IFP that can be measured experimentally, there is no in vivo or ex vivo technique to measure the solid stress owing to mechanical interactions of the tumor with the host tissue and the Donnan osmotic pressure. As mentioned above, to assess all components of mechanical stress and investigate their contribution to tumor mechanics, we developed a triphasic biomechanical model of tumor growth (details in Supplementary Material). The solid phase was modeled as a compressible neo-Hookean material with a Poisson's ratio of 0.45 [1], and the elastic modulus was taken by the experimental data accounting for the dependence on ion concentration (Supplementary Figure S4 and Equation S5). The fluid phase was modeled as ideal (i.e., of no viscosity) and governed by Darcy's law [1]. The hydraulic conductivity of the tumor appearing in Darcy's law was defined by fitting the model to the IFP experimental data (Supplementary Figure S6). To determine the values of model parameters related to tumor growth rate, we fitted the model to our experimental data of tumor growth (Supplementary Figure S7 and Table S1).
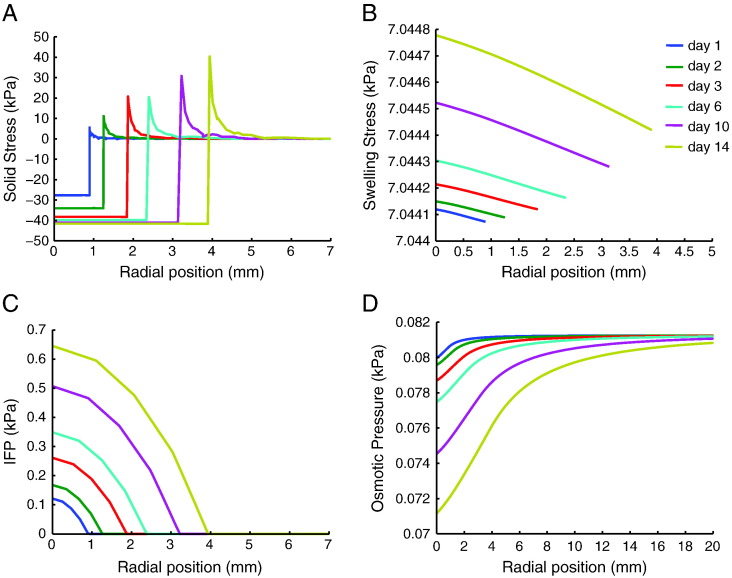
Model predictions for the solid stress, swelling stress, IFP, and osmotic pressure during tumor progression are shown in Figure 4 and Supplementary Figure S8 for MCF10CA1a and 4T1 tumors, respectively. In both tumor types, the compressive solid stress exerted externally on the tumor by the host was in the order of 300 mmHg (40 kPa), and the swelling stress was ~52.5 mmHg (7 kPa) for MCF10CA1a and ~25.13 mmHg (3.35 kPa) for the 4T1 tumors. IFP calculations were similar to the experimental measurements, i.e., in the range of 4.5 to 5.2 mmHg (0.6-0.7 kPa) (Figure 4 and Supplementary Figure S6), and the calculated Donnan osmotic pressure ranged from 0.52 to 0.6 mmHg (0.07-0.08 kPa). Therefore, our calculations indicated that solid stress (external and swelling) is much larger than interstitial fluid pressure and that swelling stress can be important to tumor mechanics, whereas Donnan osmotic pressure is negligible.
Figure 4.
Model predictions of (A) solid stress applied externally to the tumor by the host tissue, (B) swelling stress, (C) IFP, and (D) Donnan osmotic fluid pressure as a function of the radial position from tumor center at different times. Model was specified for the MCF10CA1a tumors. External solid stress is compressive in the tumor interior and becomes tensile at the periphery, swelling stress remains spatially and temporally uniform, IFP increases with time owing to increased vessel permeability and drops to normal (zero) values at the periphery, whereas osmotic pressure is negligible.
To further explore the predictive capabilities of the model, a parametric analysis was performed varying the hydraulic conductivity of the tumor and the initial concentration of fixed charges that mostly affect model predictions (Supplementary Figures S9 and S10). From the analysis, we conclude that model results only change quantitatively.
Enzymatic and Drug-Mediated Reduction of ECM Components Modulates Tumor Swelling
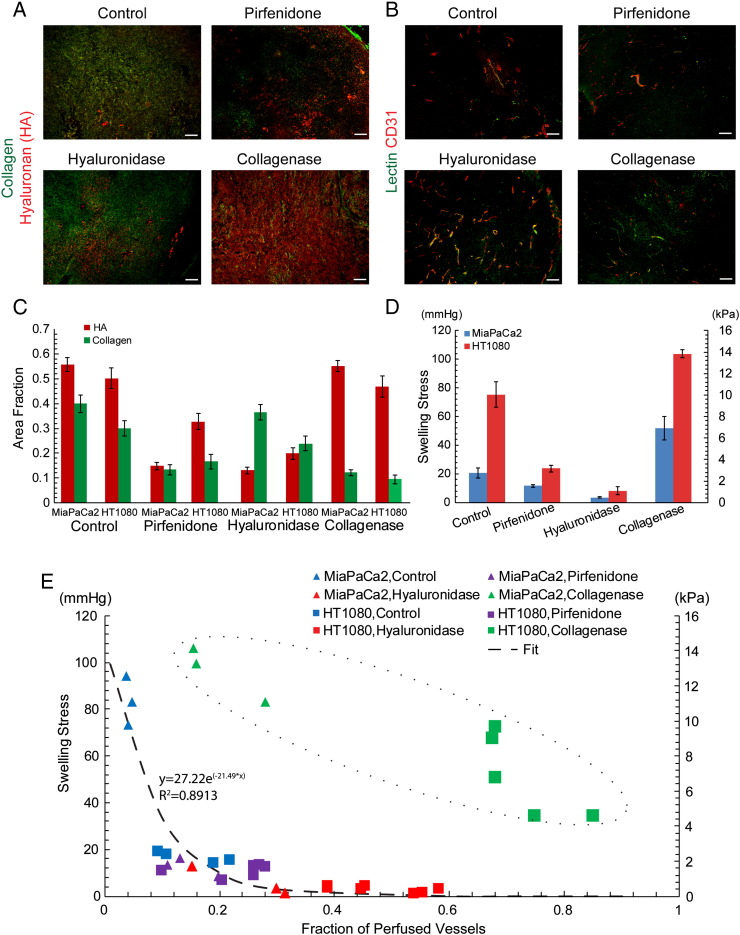
To further investigate the contribution of collagen and hyaluronan to tumor swelling, we treated ectopic MiaPaCa2 and orthotopic HT1080 tumors with enzymes (collagenase and hyalurodinase) as well as with pirfenidone (Esbriet), a drug prescribed for idiopathic pulmonary fibrosis. Intratumoral injection of 1000 U in 50 μl of collagenase or 25 μg in 50 μl of hyaluronidase 2 hours prior to tumor removal significantly reduced collagen and hyaluronan levels (P<.05) respectively, whereas daily oral administration of 500 mg/kg pirfenidone reduced significantly levels of both constituents, P<.05 (Figures 5, A–C). Interestingly, our results show that swelling of hyaluronidase-treated tumors reduced drastically to negligible levels, that of pirfenidone-treated tumors decreased, whereas the swelling of collagenase-treated tumors increased (Figure 5D). Hence, the observed swelling response is exclusively due to hyaluronan, and collagen itself restricts swelling.
Figure 5.
Effect of tissue swelling on vessel perfusion. (A) Representative immunofluorescence staining sections for hyaluronan (HA) and collagen (scale bar 100 μm), (B) typical immunofluorescence staining sections for lectin and CD31 (scale bar 100 μm), (C) area fraction of collagen and HA, and (D) swelling stress for the control and treated tumors tested. Changes in stress between the control and each of the treated groups are statistically significant (P < .05) for both tumor types. (E) Fraction of perfused vessels as a function of tumor swelling showing their exponential decay relationship (dash line, y = −27.22e(−21.49x), R2 = 0.8913) and also the different mechanism of collagen reduction to improve perfusion (dash circle).
Tumor Swelling Inversely Correlates with Blood Vessel Functionality
Solid stress can compress intratumoral blood vessels, reducing their diameter and tumor perfusion [6], [44]. To investigate any potential correlation of swelling to tumor perfusion, we examined perfused vessels by administering biotinylated lectin to mice via intracardiac injection prior to tumor removal for all tumor types and treatment conditions tested. Interestingly, there is an inverse relationship, well expressed by an exponential decay function, between the perfused vessel fraction and the swelling stress (Figure 5E). A similar inverse correlation between tumor perfusion and the tumor ECM fraction has also been shown previously in pertinent research [23]. Interestingly, hyaluronidase treatment radically reduced tumor swelling to negligible levels and significantly improved perfusion. Collagen reduction following collagenase treatment, on the other hand, was associated with improved perfusion even though the tumor exhibited increased swelling stress, thus implying a different mechanism of action. This could be due to the fact that collagen fibers restrict tissue swelling and their depletion allows the tumor to further swell and relax, alleviating intratumoral swelling stresses. Pirfenidone treatment also resulted in improved perfusion, showing that repurposing of common antifibrotic drugs can be used to enhance perfusion and drug delivery, ultimately improving therapy.
Cancer Cell Swelling Does Not Contribute to Tissue-Level Effects
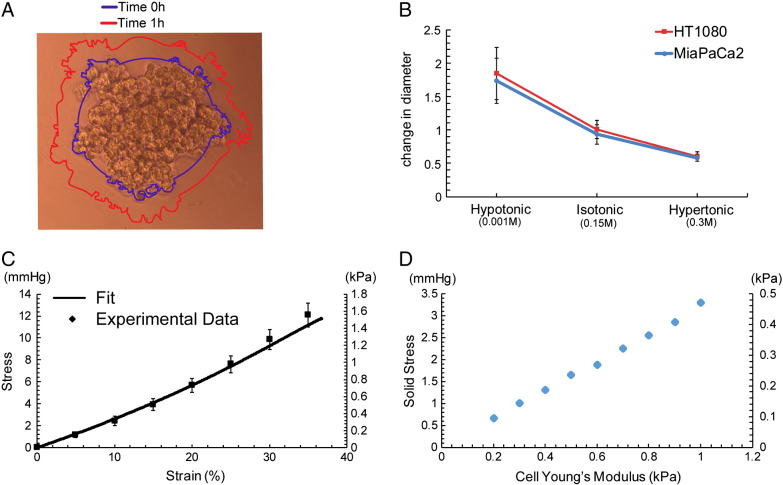
Recent work by McGrail et al. showed that cancer cells regulate their tonicity and swell to survive and resist compressive forces that are developed in the tumor's interior [45]. To determine whether cancer cell swelling can account for the changes we observe in tumor swelling, we employed an in vitro model. Specifically, MiaPaCa2 and HT1080 cancer cells were used to generate tumor spheroids that were embedded in a 1% agarose matrix, and changes in the spheroids' size were recorded in relation to changes in osmolarity. Our findings show that cancer cell spheroids swelled by approximately 70% to 80% for a hypotonic solution (0.001 M, NaCl) and shrunk by 60% to 70% when the solution was changed to hypertonic (0.3 M, NaCl) (Figure 6, A and B). To convert the observed deformations to stresses, we measured the mechanical properties of the agarose gel and found the Young's modulus to be 3.6 ± 0.56 kPa (Figure 6C). Subsequently, using our mathematical model, the growth of the spheroids within the agarose matrix was simulated, and the stress developed in the spheroids was calculated. Figure 6D presents the calculated by the model stress for varying the elastic properties (Young's modulus) of cancer cell spheroids with values taken from the literature [40]. According to our calculations, cancer cell swelling should not contribute to tissue-level swelling of the tumor.
Figure 6.
Cancer cell swelling (A) microscope image of a spheroid. Lines depict the perimeter of the spheroid before (0 hour) and an hour after addition of electrolyte solution. (B) Change in spheroid's diameter as a function of the tonicity for HT1080 and MiaPaCa2 cancer cells, (C) stress strain curve of 1% agarose gel, and (D) stress developed on the spheroids as a function of their elastic modulus.
Discussion
It has been well established that mechanical forces modulate the tumor microenvironment and pathophysiology and determine in large part tumor progression and response to therapy [2], [46]. However, there has been no study to date to describe the swelling behavior of tumors, the magnitude of swelling stress and Donnan osmotic pressure, the dependence of swelling on tissue composition, and its contribution to tumor perfusion, which play a critical role in the efficacy of cancer therapy [47], [48]. Here, we performed a series of in vivo and in vitro experiments coupled with mathematical modeling to elucidate these issues. We found that swelling is evident in breast, pancreatic, and sarcoma cell lines and that it is high enough to compress intratumoral blood vessels and affect tumor perfusion. Interestingly, our analysis revealed the same linear correlation between swelling stress and the ratio of hyaluronan to collagen content for all tumor types tested, suggesting that tumor swelling is mainly due to the ECM composition. This conclusion was further supported by the finding that tumors treated with hyaluronidase exhibited negligible swelling, whereas swelling was increased in tumors treated with collagenase. This can be explained by the fact that collagen fibers are stressed during swelling and hinder tissue expansion owing to their property to resist tensile loads. Moreover, this observation regarding the role of collagen is consistent with pertinent studies on cartilage [42], [43] and a recent in vitro study [41]. Last but not least, in vitro experiments on tumor spheroids showed that cancer cell swelling should not significantly contribute to tumor swelling.
More importantly, we found that swelling affects tumor perfusion and thus could be a significant factor affecting drug delivery. Perfusion is compromised in many tumor types, particularly in desmoplastic tumors (e.g., breast and pancreatic cancers and sarcomas) that are considered to be rich in collagen and/or hyaluronan, because of intratumoral blood vessel compression [3], [23], [48]. Hypoperfusion in turn causes hypoxia, which promotes tumor growth in multiple ways, and reduces the efficacy of radiation therapy, immunotherapy, and chemo-/nanotherapy because of the inability of oxygen, immune cells, and drugs to reach the tumor site in sufficient amounts [19], [47], [48], [49]. In previous research, we proposed and proved experimentally that alleviation of solid stresses has the potential to decompress tumor blood vessels and thus improve perfusion [3], [23]. In this work, we found that swelling stress is high enough to cause vessel compression and that modulation of swelling stress levels can result in vessel decompression (Supplementary Figure S12) and improved perfusion. Interestingly, our data indicated that alleviation of tumor swelling by hyaluronan depletion and increase in tumor swelling by reduction of collagen levels are two different mechanisms to improve perfusion. Furthermore, we demonstrated that the repurposing of commonly used antifibrotic drugs could comprise a novel approach to improve delivery of cytotoxic agents by enhancing perfusion.
Conclusively, this is a comprehensive study that provides new insights on the mechanopathology of solid tumors, highlighting the effect of tumor structure on the tissue function and pathophysiology and the role of ECM components in tumor mechanical response and tissue swelling in particular. Our findings and especially the direct, linear correlation of swelling stress to tumor ECM content as well as the inverse correlation of perfusion to tumor swelling provide novel considerations for the use of stress alleviation strategies to modify the microenvironment of solid tumors to enhance therapeutic outcome.
Author Contributions
C. V. and T. S. designed research; C. V. performed research; C. V. and T. S. analyzed data, C. P. provided assistance with immunohistochemistry, P. P. prepared the animal tumor models, V. G. provided assistance with the tumor spheroid formation assay; all authors wrote the paper.
Footnotes
Disclosure statement: There is no financial or other competing interest in the work.
The research leading to these results has received funding from the European Research Council under the European Union's Seventh Framework Programme (FP7/2007-2013)/ERC grant agreement no. 336839–Reengineering Cancer and the Research Promotion Foundation of Cyprus under a new researcher award grant agreement (no. ΚΟΥΛΤΟΥΡΑ/ΒΡ-ΝΕ/0514/08).
Supplementary Material to this article can be found online at http://dx.doi.org/10.1016/j.neo.2016.10.001.
Contributor Information
Chrysovalantis Voutouri, Email: tstylian@ucy.ac.cy.
Christiana Polydorou, Email: polydorou.christiana@ucy.ac.cy.
Panagiotis Papageorgis, Email: p.papageorgis@euc.ac.cy.
Vasiliki Gkretsi, Email: vasso.gkretsi@gmail.com.
Triantafyllos Stylianopoulos, Email: tstylian@ucy.ac.cy.
Appendix A. Supplementary Material
Supplementary material.
References
- 1.Stylianopoulos T, Martin JD, Snuderl M, Mpekris F, Jain SR, Jain RK. Coevolution of solid stress and interstitial fluid pressure in tumors during progression: Implications for vascular collapse. Cancer Res. 2013;73:3833–3841. doi: 10.1158/0008-5472.CAN-12-4521. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Jain RK, Martin JD, Stylianopoulos T. The role of mechanical forces in tumor growth and therapy. Annu Rev Biomed Eng. 2014;16:321–346. doi: 10.1146/annurev-bioeng-071813-105259. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Stylianopoulos T, Martin JD, Chauhan VP, Jain SR, Diop-Frimpong B, Bardeesy N, Smith BL, Ferrone CR, Hornicek FJ, Boucher Y. Causes, consequences, and remedies for growth-induced solid stress in murine and human tumors. Proc Natl Acad Sci U S A. 2012;109:15101–15108. doi: 10.1073/pnas.1213353109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Wiig H, Swartz MA. Interstitial fluid and lymph formation and transport: physiological regulation and roles in inflammation and cancer. Physiol Rev. 2012;92:1005–1060. doi: 10.1152/physrev.00037.2011. [DOI] [PubMed] [Google Scholar]
- 5.Alexandrakis G, Brown EB, Tong RT, McKee TD, Campbell RB, Boucher Y, Jain RK. Two-photon fluorescence correlation microscopy reveals the two-phase nature of transport in tumors. Nat Med. 2004;10:203–207. doi: 10.1038/nm981. [DOI] [PubMed] [Google Scholar]
- 6.Boucher Y, Jain RK. Microvascular pressure is the principal driving force for interstitial hypertension in solid tumors: implications for vascular collapse. Cancer Res. 1992;52:5110–5114. [PubMed] [Google Scholar]
- 7.Jain RK, Stylianopoulos T. Delivering nanomedicine to solid tumors. Nat Rev Clin Oncol. 2010;7:653–664. doi: 10.1038/nrclinonc.2010.139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Eisenberg SR, Grodzinsky AJ. Swelling of articular cartilage and other connective tissues: electromechanochemical forces. J Orthop Res. 1985;3:148–159. doi: 10.1002/jor.1100030204. [DOI] [PubMed] [Google Scholar]
- 9.Wilson W, van Donkelaar CC, van Rietbergen R, Huiskes R. The role of computational models in the search for the mechanical behavior and damage mechanisms of articular cartilage. Med Eng Phys. 2005;27:810–826. doi: 10.1016/j.medengphy.2005.03.004. [DOI] [PubMed] [Google Scholar]
- 10.Swartz MA, Fleury ME. Interstitial flow and its effects in soft tissues. Annu Rev Biomed Eng. 2007;9:229–256. doi: 10.1146/annurev.bioeng.9.060906.151850. [DOI] [PubMed] [Google Scholar]
- 11.Helmlinger G, Netti PA, Lichtenbeld HC, Melder RJ, Jain RK. Solid stress inhibits the growth of multicellular tumor spheroids. Nat Biotechnol. 1997;15:778–783. doi: 10.1038/nbt0897-778. [DOI] [PubMed] [Google Scholar]
- 12.Kaufman LJ, Brangwynne CP, Kasza KE, Filippidi E, Gordon VD, Deisboeck TS, Weitz DA. Glioma expansion in collagen I matrices: analyzing collagen concentration-dependent growth and motility patterns. Biophys J. 2005;89:635–650. doi: 10.1529/biophysj.105.061994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Demou ZN. Gene expression profiles in 3D tumor analogs indicate compressive strain differentially enhances metastatic potential. Ann Biomed Eng. 2010;38:3509–3520. doi: 10.1007/s10439-010-0097-0. [DOI] [PubMed] [Google Scholar]
- 14.Egeblad M, Rasch MG, Weaver VM. Dynamic interplay between the collagen scaffold and tumor evolution. Curr Opin Cell Biol. 2010;22:697–706. doi: 10.1016/j.ceb.2010.08.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Cheng G, Tse J, Jain RK, Munn LL. Micro-environmental mechanical stress controls tumor spheroid size and morphology by suppressing proliferation and inducing apoptosis in cancer cells. PLoS One. 2009;4:e4632. doi: 10.1371/journal.pone.0004632. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Tse JM, Cheng G, Tyrrell JA, Wilcox-Adelman SA, Boucher Y, Jain RK, Munn LL. Mechanical compression drives cancer cells toward invasive phenotype. Proc Natl Acad Sci. 2012;109:911–916. doi: 10.1073/pnas.1118910109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Griffon-Etienne G, Boucher Y, Brekken C, Suit HD, Jain RK. Taxane-induced apoptosis decompresses blood vessels and lowers interstitial fluid pressure in solid tumors: clinical implications. Cancer Res. 1999;59:3776–3782. [PubMed] [Google Scholar]
- 18.Padera TP, Stoll BR, Tooredman JB, Capen D, di Tomaso E, Jain RK. Pathology: cancer cells compress intratumour vessels. Nature. 2004;427:695. doi: 10.1038/427695a. [DOI] [PubMed] [Google Scholar]
- 19.Wilson WR, Hay MP. Targeting hypoxia in cancer therapy. Nat Rev Cancer. 2011;11:393–410. doi: 10.1038/nrc3064. [DOI] [PubMed] [Google Scholar]
- 20.Stylianopoulos T, Jain RK. Combining two strategies to improve perfusion and drug delivery in solid tumors. Proc Natl Acad Sci U S A. 2013;110:18632–18637. doi: 10.1073/pnas.1318415110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Jain RK, Tong RT, Munn LL. Effect of vascular normalization by antiangiogenic therapy on interstitial hypertension, peritumor edema, and lymphatic metastasis: insights from a mathematical model. Cancer Res. 2007;67:2729–2735. doi: 10.1158/0008-5472.CAN-06-4102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Swartz MA, Lund AW. Lymphatic and interstitial flow in the tumour microenvironment: linking mechanobiology with immunity. Nat Rev Cancer. 2012;12:210–219. doi: 10.1038/nrc3186. [DOI] [PubMed] [Google Scholar]
- 23.Chauhan VP, Martin JD, Liu H, Lacorre DA, Jain SR, Kozin SV, Stylianopoulos T, Mousa A, Han X, Adstamongkonkul P. Angiotensin inhibition enhances drug delivery and potentiates chemotherapy by decompressing tumor blood vessels. Nat Commun. 2013:4. doi: 10.1038/ncomms3516. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Liu J, Liao S, Diop-Frimpong B, Chen W, Goel S, Naxerova K, Ancukiewicz M, Boucher Y, Jain RK, Xu L. TGF-beta blockade improves the distribution and efficacy of therapeutics in breast carcinoma by normalizing the tumor stroma. Proc Natl Acad Sci U S A. 2012;109:16618–16623. doi: 10.1073/pnas.1117610109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Provenzano PP, Cuevas C, Chang AE, Goel VK, Von Hoff DD, Hingorani SR. Enzymatic targeting of the stroma ablates physical barriers to treatment of pancreatic ductal adenocarcinoma. Cancer Cell. 2012;21:418–429. doi: 10.1016/j.ccr.2012.01.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Gkretsi V, Stylianou A, Papageorgis P, Polydorou C, Stylianopoulos T. Remodeling components of the tumor microenvironment to enhance cancer therapy. Front Oncol. 2015;5:214. doi: 10.3389/fonc.2015.00214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Papageorgis P, Stylianopoulos T. Role of TGFbeta in regulation of the tumor microenvironment and drug delivery (review) Int J Oncol. 2015;46:933–943. doi: 10.3892/ijo.2015.2816. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Diop-Frimpong B, Chauhan VP, Krane S, Boucher Y, Jain RK. Losartan inhibits collagen I synthesis and improves the distribution and efficacy of nanotherapeutics in tumors. Proc Natl Acad Sci U S A. 2011;108:2909–2914. doi: 10.1073/pnas.1018892108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Pirentis AP, Polydorou C, Papageorgis P, Voutouri C, Mpekris F, Stylianopoulos T. Remodeling of extracellular matrix due to solid stress accumulation during tumor growth. Connect Tissue Res. 2015;56:345–354. doi: 10.3109/03008207.2015.1047929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Voutouri C, Mpekris F, Papageorgis P, Odysseos AD, Stylianopoulos T. Role of constitutive behavior and tumor-host mechanical interactions in the state of stress and growth of solid tumors. PLoS One. 2014;9:e104717. doi: 10.1371/journal.pone.0104717. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Tong RT, Boucher Y, Kozin SV, Winkler F, Hicklin DJ, Jain RK. Vascular normalization by vascular endothelial growth factor receptor 2 blockade induces a pressure gradient across the vasculature and improves drug penetration in tumors. Cancer Res. 2004;64:3731–3736. doi: 10.1158/0008-5472.CAN-04-0074. [DOI] [PubMed] [Google Scholar]
- 32.Papageorgis P, Ozturk S, Lambert AW, Neophytou CM, Tzatsos A, Wong CK, Thiagalingam S, Constantinou AI. Targeting IL13Ralpha2 activates STAT6-TP63 pathway to suppress breast cancer lung metastasis. Breast Cancer Res. 2015;17:98. doi: 10.1186/s13058-015-0607-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Qiu W, Su GH. Development of orthotopic pancreatic tumor mouse models. Methods Mol Biol. 2013;980:215–223. doi: 10.1007/978-1-62703-287-2_11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Kelm JM, Timmins NE, Brown CJ, Fussenegger M, Nielsen LK. Method for generation of homogeneous multicellular tumor spheroids applicable to a wide variety of cell types. Biotechnol Bioeng. 2003;83:173–180. doi: 10.1002/bit.10655. [DOI] [PubMed] [Google Scholar]
- 35.Del Duca D, Werbowetski T, Del Maestro RF. Spheroid preparation from hanging drops: characterization of a model of brain tumor invasion. J Neurooncol. 2004;67:295–303. doi: 10.1023/b:neon.0000024220.07063.70. [DOI] [PubMed] [Google Scholar]
- 36.Fadnes HO, Reed RK, Aukland K. Interstitial fluid pressure in rats measured with a modified wick technique. Microvasc Res. 1977;14:27–36. doi: 10.1016/0026-2862(77)90138-8. [DOI] [PubMed] [Google Scholar]
- 37.Voutouri C, Stylianopoulos T. Evolution of osmotic pressure in solid tumors. J Biomech. 2014;47:3441–3447. doi: 10.1016/j.jbiomech.2014.09.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Mpekris F, Angeli S, Pirentis AP, Stylianopoulos T. Stress-mediated progression of solid tumors: effect of mechanical stress on tissue oxygenation, cancer cell proliferation, and drug delivery. Biomech Model Mechanobiol. 2015 doi: 10.1007/s10237-015-0682-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Rodriguez EK, Hoger A, McCulloch AD. Stress-dependent finite growth in soft elastic tissues. J Biomech. 1994;27:455–467. doi: 10.1016/0021-9290(94)90021-3. [DOI] [PubMed] [Google Scholar]
- 40.Roose T, Netti PA, Munn LL, Boucher Y, Jain RK. Solid stress generated by spheroid growth estimated using a linear poroelasticity model. Microvasc Res. 2003;66:204–212. doi: 10.1016/s0026-2862(03)00057-8. [DOI] [PubMed] [Google Scholar]
- 41.Lai VK, Nedrelow DS, Lake SP, Kim B, Weiss EM, Tranquillo RT, Barocas VH. Swelling of collagen-hyaluronic acid co-gels: an in vitro residual stress model. Ann Biomed Eng. 2016 doi: 10.1007/s10439-016-1636-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Mow VC, Ratcliffe A, Poole AR. Cartilage and diarthrodial joints as paradigms for hierarchical materials and structures. Biomaterials. 1992;13:67–97. doi: 10.1016/0142-9612(92)90001-5. [DOI] [PubMed] [Google Scholar]
- 43.Maroudas AI. Balance between swelling pressure and collagen tension in normal and degenerate cartilage. Nature. 1976;260:808–809. doi: 10.1038/260808a0. [DOI] [PubMed] [Google Scholar]
- 44.Chauhan VP, Boucher Y, Ferrone CR, Roberge S, Martin JD, Stylianopoulos T, Bardeesy N, DePinho RA, Padera TP, Munn LL. Compression of pancreatic tumor blood vessels by hyaluronan is caused by solid stress and not interstitial fluid pressure. Cancer Cell. 2014;26:14–15. doi: 10.1016/j.ccr.2014.06.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.McGrail DJ, McAndrews KM, Brandenburg CP, Ravikumar N, Kieu QM, Dawson MR. Osmotic regulation is required for cancer cell survival under solid stress. Biophys J. 2015;109:1334–1337. doi: 10.1016/j.bpj.2015.07.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Shieh AC. Biomechanical forces shape the tumor microenvironment. Ann Biomed Eng. 2011;39:1379–1389. doi: 10.1007/s10439-011-0252-2. [DOI] [PubMed] [Google Scholar]
- 47.Jain RK. Normalizing tumor microenvironment to treat cancer: bench to bedside to biomarkers. J Clin Oncol. 2013;31:2205–2218. doi: 10.1200/JCO.2012.46.3653. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Jain RK. Antiangiogenesis strategies revisited: from starving tumors to alleviating hypoxia. Cancer Cell. 2014;26:605–622. doi: 10.1016/j.ccell.2014.10.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Facciabene A, Peng X, Hagemann IS, Balint K, Barchetti A, Wang LP, Gimotty PA, Gilks CB, Lal P, Zhang L. Tumour hypoxia promotes tolerance and angiogenesis via CCL28 and T(reg) cells. Nature. 2011;475:226–230. doi: 10.1038/nature10169. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary material.