Mendelian Randomization Analysis of a Time-varying Exposure for Binary Disease Outcomes using Functional Data Analysis Methods

Abstract

A Mendelian randomization (MR) analysis is performed to analyze the causal effect of an exposure variable on a disease outcome in observational studies, by using genetic variants that affect the disease outcome only through the exposure variable. This method has recently gained popularity among epidemiologists given the success of genetic association studies. Many exposure variables of interest in epidemiological studies are time-varying, for example, body mass index (BMI). Although longitudinal data have been collected in many cohort studies, current MR studies only use one measurement of a time-varying exposure variable, which cannot adequately capture the long-term time-varying information. We propose using the functional principal component analysis method to recover the underlying individual trajectory of the time-varying exposure from the sparsely and irregularly observed longitudinal data, and then conduct MR analysis using the recovered curves. We further propose two MR analysis methods. The first assumes a cumulative effect of the time-varying exposure variable on the disease risk, while the second assumes a time-varying genetic effect and employs functional regression models. We focus on statistical testing for a causal effect. Our simulation studies mimicking the real data show that the proposed functional data analysis-based methods incorporating longitudinal data have substantial power gains compared to standard MR analysis using only one measurement. We used the Framingham Heart Study data to demonstrate the promising performance of the new methods as well as inconsistent results produced by the standard MR analysis that relies on a single measurement of the exposure at some arbitrary time point.

Introduction

The risk of complex diseases is influenced by multiple genetic factors, as well as behavioral and environmental factors, and their interactions. In the past ten years, tremendous progress has been made in genetic studies for complex diseases [Stranger, et al. 2011]. In addition to genetic factors, studying the effect of behavioral and environmental factors on the risk of complex diseases has been the focus of conventional observational epidemiology studies. Although the observational epidemiology studies have made considerable contributions to identifying possible factors affecting the risk of complex diseases, many of these observational findings cannot be confirmed by randomized clinical trials (RCTs). For example, the association between Vitamin E intake and coronary heart disease (CHD) risk identified in an observational study cannot be confirmed by an RCT [Hooper, et al. 2001]. The inability to establish causality in observational studies is mainly due to unadjusted confounders [Vandenbroucke 2004]. Is it possible that the success of genetic studies can be helpful for establishing the causal effect of exposure variables on the risk of complex diseases in observational studies? Mendelian randomization (MR), a principle originally described by Katan [Katan 1986], is used to study the exposure-outcome causal relationship in observational studies using genetic variants that affect the disease outcome only through the exposure variable [Lawlor, et al. 2008].

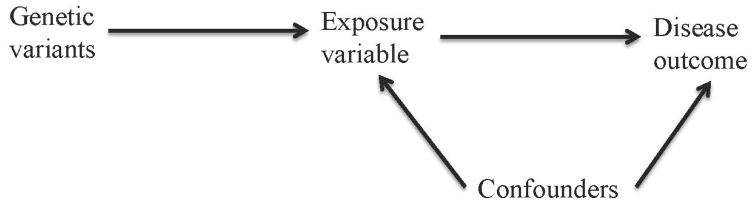
By the Mendel’s second law of independent assortment, the inheritance of two different traits is independent, with the exclusion of linkage disequilibrium (LD). Due to the independent and random allocation of alleles during gamete formation, the allele inherited from each parent is randomly determined. Therefore, at the population level, the associations between genetic factors and exposure variables are generally not confounded, in particular, by socioeconomic status and behavioral factors [Smith, et al. 2007]. In addition, the association between genetic factors and disease risk cannot be due to reverse causality [Lawlor, et al. 2008]. Therefore, genetic variants can be used as an instrument for an exposure variable to study its effect on a disease outcome. MR study is an application of instrumental variable (IV) analysis, which uses genetic variants as IVs to study the causal effect of an exposure variable on a disease outcome. IV analysis is commonly used in econometrics to make causal inference in observational studies. As depicted in Fig. 1, in order to be valid IVs, genetic variants must satisfy three assumptions: 1. the genetic variants are associated with the exposure variable; 2. the genetic variants are independent of the confounders that confound the association between the exposure variable and the disease outcome; 3. the genetic variants only affect the disease outcome through the exposure variable. The third assumption is also known as the exclusion restriction assumption and indicates the independence between genetic variants and disease outcome given the exposure variable and other observed confounders in the analysis. The three assumptions are necessary for testing the causal effect of the exposure variable on the disease outcome. At least another assumption, that is, all the associations in Fig. 1 are linear and are not subject to interactions, is needed for causal effect size estimation in MR analysis [Lawlor, et al. 2008].

Fig. 1.

Directed acyclic graph of MR analysis assumptions.

The disease outcomes in epidemiology studies are often binary, for example, type 2 diabetes (T2D). One of the most commonly used IV analysis methods for a binary outcome is the two-stage residual inclusion (2SRI) [Holmes, et al. 2014b; Terza, et al. 2008]. Specifically, a linear regression model is fitted in the first stage for the exposure variable using the IV(s) and measured covariates. In the second stage, a nonlinear model is fitted for the binary disease outcome using the exposure variable, measured covariates, and residuals from the first stage linear regression model. In theory, 2SRI uses the residuals from the first stage regression as a proxy for the unmeasured confounders. 2SRI is also known as the control function method for IV analysis [Wooldridge 2010] and has been used in MR studies with binary disease outcomes [Holmes, et al. 2014b]. A Wald test using robust standard errors, an adjusted closed form solution for the standard errors, or bootstrapped standard errors is recommended for testing the significance of the causal effect in 2SRI [Terza, et al. 2008; Wooldridge 2010].

MR analysis is a very attractive approach for causal inference analysis in observational studies, especially for the exposure variables that are difficult to be studied using RCTs, such as body mass index (BMI). However, MR studies are subject to strong assumptions. Although the first two assumptions are not difficult to satisfy as described above, there may be violations of the exclusion restriction assumption, including pleiotropy, LD, and population stratification [Lawlor, et al. 2008; VanderWeele, et al. 2014]. The exclusion restriction assumption is often very difficult to validate and can only be statistically tested when there is over-identification. Moreover, a single genetic variant, usually a single nucleotide polymorphism (SNP), only explains a small proportion of the total variation in the exposure variable. Hence the genetic variant might turn out to be a weak IV, which can be a challenge in the MR studies, leading to inconclusive and insignificant results. Multiple SNPs or a genetic risk score (GRS), which is a weighted count of the effect alleles of multiple SNPs, have been used to resolve the weak IV problem and increase the statistical power in MR studies [Holmes, et al. 2014b; Palmer, et al. 2012; Pierce, et al. 2011]. In addition, the possible violation of the exclusion restriction assumption can be alleviated by using multiple SNPs instead of just one SNP in MR studies [Lawlor, et al. 2008].

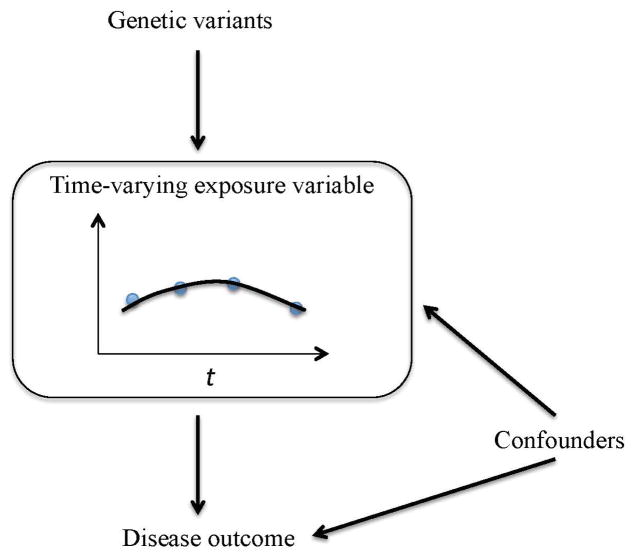
Another challenge in MR studies is that the exposure variables of interest are often time-varying (Fig. 2), for example, BMI and high-density lipoprotein (HDL) levels. Current MR analyses only use the exposure variable data from a single arbitrary time point, usually at the baseline level [Holmes, et al. 2014b; Voight, et al. 2012], even though longitudinal data of the time-varying exposures have been collected in many prospective cohort studies, for example, the Framingham Heart Study (FHS) [Splansky, et al. 2007]. A time-varying exposure may vary substantially over time, and a single measurement is often not adequate to capture the time-varying information. Furthermore, the exposure variables that change continuously over one’s lifespan might have a cumulative effect on the risk of a disease, e.g., lifelong reduced plasma levels of triglycerides-rich lipoproteins reduce the risk of CHD, but a reduced level of triglycerides-rich lipoproteins at an arbitrary baseline time point might not always reduce the risk of CHD because the CHD risk will also depend on triglycerides-rich lipoproteins at other time points in life [Crosby, et al. 2014]. Davis et al. pointed out that using a single measure of a time-varying exposure could underestimate the relationship between the exposure variable and the outcome variable, not only due to the measurement error in the exposure, but also failure to capture its long-term change [Davis, et al. 1990]. More importantly, it is the lifetime genetic effect on the exposure that is assumed and estimated in the MR analysis framework, which, however, is unlikely to be obtained with cross-sectional exposure data [Evans and Davey Smith 2015]. Given this limitation, how should the longitudinal data of a time-varying exposure variable be incorporated in an MR analysis? Here we propose modeling longitudinal data using functional data analysis methods. Specifically, the underlying individual curve of the time-varying exposure variable is recovered using the functional principal component analysis through conditional expectation (PACE) method, which is designed for modeling irregular and sparse longitudinal data [Yao, et al. 2005]. Then MR analysis is performed by assuming that the time-varying exposure variable has a cumulative effect or burden on the risk of the disease. We propose two methods. For the first method, the cumulative effect of the time-varying exposure variable is calculated from the recovered curves and standard MR analysis is then performed using the cumulative effect of the exposure variable. The second method further assumes a time-varying genetic effect on the exposure variable, for which the functional regression models are used. Note that here we focus on testing if a time-varying exposure variable has a causal effect on the risk of a disease, rather than effect size estimation. Our simulation studies mimicking real data show that the proposed functional data analysis-based methods incorporating longitudinal data have higher statistical power than the standard MR analysis using a single measurement of the time-varying exposure variable. The proposed method that assumes a time-varying genetic effect has the highest statistical power. We also demonstrate promising performance of the proposed methods by investigating if BMI has a causal effect on the risk of T2D and CHD, and if HDL has a causal effect on the risk of CHD, using the FHS longitudinal data. To the best of our knowledge, this is the first work aiming to incorporate longitudinal data of a time-varying exposure variable in MR analysis to test its causal effect on a binary disease outcome.

Fig. 2. Directed acyclic graph of MR analysis with a time-varying exposure variable.

Blue points represent observed longitudinal data. The black line represents unobserved level that changes continuously over time.

Methods

Notation

We consider a cohort study for MR analysis. Suppose the cohort study has a total sample size of n subjects. Let y_i be the binary disease outcome recorded at time T_i, y_i = 0 or 1, for i = 1, …, n. Let X_i = (x_i1, x_i2, …, x_iJi)^T, be the longitudinal data vector of the time-varying exposure variable of subject i. The time when x_ij is recorded is t_ij, where t_ij < T_i for j = 1, …, J_i. G_i denotes the vector of multiple SNPs or the GRS of subject i. Z_i is the vector of observed covariates of subject i. Neither G_i nor Z_i is time-varying.

MR analysis using baseline measurement of a time-varying exposure variable

Conventional MR analysis for a time-varying exposure variable involves performing a 2SRI using only one measurement from the longitudinal data, usually at the baseline, for example, x_i1. Specifically, a linear regression model is fitted for x_i1 in the first stage: x_i1 = β₀ + β₁G_i + β₂Z_i + v_i to obtain the fitted residual v̂_i. Then a logistic regression model is fitted in the second stage: $log(\frac{E(y_i)}{1-E(y_i)})={\alpha }_0+{\alpha }_1{x}_{i1}+{\mathit{\alpha }}_{\mathbf{2}}{\mathit{Z}}_{\mathit{i}}+{\alpha }_3{\widehat{v}}_i$, where E(y_i) is the expected value of y_i. To test the null hypothesis that the baseline level of the time-varying exposure variable has no effect on the disease outcome, i.e., H₀: α₁ = 0, a Wald test using the robust standard error (Huber-White standard error), an adjusted closed form solution for the standard error, or a bootstrapped standard error can be performed [Cai 2010; Holmes, et al. 2014b; Palmer, et al. 2011; Terza, et al. 2008]. The limitation of the conventional analysis method is that a single measurement is not adequate to capture the information in the exposure variable that changes over time, leading to possible loss of power and biased results.

Functional data analysis methods for MR analysis with a time-varying exposure variable

A time-varying exposure variable changes continuously over time. It is intrinsically functional data with longitudinal observations collected only at certain time points, as shown in Fig. 2. Therefore, we propose to use functional data analysis techniques to incorporate longitudinal data in MR analysis. Of note, we previously employed functional data analysis approaches to model longitudinal exposures in the context of gene-environment interactions (GxE) that may modify the risk of complex disease [Wei, et al. 2014].

PACE

Longitudinal data from observational studies are often sparse and collected at irregular time points. In addition, different subjects may have different numbers of observations. Given the characteristics of the longitudinal data, we propose to use the PACE method [Yao, et al. 2005] to recover the underlying curves for the exposure variable. The PACE method was developed specifically for modeling sparse longitudinal data with irregular observations by assuming that the longitudinal observations of each subject are sampled from an underlying curve with noise and the curves of all the subjects are independent with the same mean function and covariance function [Müller 2009; Yao, et al. 2005]. Let μ(t) be the mean function and R(s, t) = cov[x(s), x(t)] be the covariance function of the collection of curves in a closed time interval 𝒯, where s, t ∈ 𝒯. Eigen decomposition can be performed to expand the covariance function as $R(s,t)={\sum }_{k=1}^{\infty }{\lambda }_k{\varphi }_k(t){\varphi }_k(s)$, where λ_k’s are nonnegative eigen-values (λ₁ ≥ λ₂ ≥ ···) and ϕ_k(t)’s are eigen-functions. Then the curve of subject i can be expressed as $x_i(t)=\mu (t)+{\sum }_{k=1}^{\infty }{\xi }_{ik}{\varphi }_k(t)$ by the Karhunen-Loève theorem [Yao, et al. 2005]. ξ_ik is the kth functional principal component (FPC) score of subject i with a mean of 0 and a variance of λ_k, where ξ_ik = ∫_𝒯[x_i(t) − μ(t)]ϕ_k(t)dt. The numerical integration method for FPC score calculation works well for densely observed data, but not for sparse longitudinal data. To solve this problem, Yao et al. [Yao, et al. 2005] introduced additive measurement errors into the model as $x_{ij}=\mu (t_{ij})+{\sum }_{k=1}^{\infty }{\xi }_{ik}{\varphi }_k(t_{ij})+{\epsilon }_{ij}$, where the measurement error ε_ij is assumed to follow the classical measurement error assumption with a mean of 0 and a variance of σ² [Carroll, et al. 2006]. For sparse data, the best prediction of ξ_ik is the conditional expectation ${\stackrel{\sim }{\xi }}_{ik}=E({\xi }_{ik}\mid {\mathit{X}}_{\mathit{i}})={\lambda }_k{\mathit{\varphi }}_{\mathit{ik}}^{\mathit{T}}{\mathit{\sum }}_{{\mathit{X}}_{\mathit{i}}}^{-\mathbf{1}}({\mathit{X}}_{\mathit{i}}-{\mathit{\mu }}_{\mathit{i}})$ by assuming that ξ_ik and ε_ij are jointly normally distributed, where ϕ_ik = (ϕ_k(t_i1), …, ϕ_k(t_iJi))^T, Σ_Xi = cov(X_i, X_i), and μ_i = (μ(t_i1), …, μ(t_iJi))^T [Yao, et al. 2005]. When applied to real data, μ̂(t) and R̂(s, t) are estimated by pooling all the observations x_ij (i = 1, …, n; j = 1, …, J_i) together. The mean function μ̂(t) is estimated using a local linear smoother. The covariance function R̂(s, t) is estimated by smoothing the sample covariance function (x_ij − μ̂(t_ij))(x_il − μ̂(t_il)) using a local linear smoother in the direction of the diagonal and a local quadratic smoother in the direction orthogonal to the diagonal to take into account measurement errors. Eigen decomposition is then performed for R̂(s, t) after discretization and ξ̂_ik can be calculated by plugging in the parameter estimates from the previous steps. The last step is to recover the individual curve using the leading eigen-functions as ${\widehat{x}}_i(t)=\widehat{\mu }(t)+{\sum }_{k=1}^K{\widehat{\xi }}_{ik}{\widehat{\varphi }}_k(t)$ for t ∈ 𝒯. The selection of the number of eigen-functions K can be based on the fraction of variance explained (FVE), Akaike information criterion (AIC), or Bayesian information criterion (BIC) [Yao, et al. 2005]. The PACE method has been implemented in R package “PACE”.

MR analysis is subject to strong assumptions. For effect estimation, a more strict assumption that all the associations in Fig. 1 are linear is required [Lawlor, et al. 2008]. For a binary disease outcome, the linear association assumption cannot be satisfied. Therefore, we focus on testing if a time-varying exposure variable has a causal effect on a binary disease outcome, and do not focus on the effect size estimation. This is consistent with the fact that the focus of MR analysis is to identify causal risk factors for a disease, not to obtain precise estimation of the effect size [Burgess 2013]. We propose two methods for testing the causal effect.

New Method I: PACE+2SRI

The first method assumes that the time-varying exposure variable has a cumulative effect on the risk of the disease. The cumulative value of the time-varying exposure variable x_i can be calculated from the recovered curve by integration:

$$x_i={\int }_{T_0}^{T_i}({\widehat{x}}_i(t)-\widehat{\mu }(t))dt$$ (1)

where T₀ is the lower bound of the time interval 𝒯 and T_i is the disease incidence time or the time that the follow-up of y_i is censored. Then standard 2SRI can be performed using the cumulative value x_i. A linear regression model is fitted in the first stage:

$$x_i={\beta }_0^{\prime }+{\mathit{\beta }}_{\mathbf{1}}^{\prime }{\mathit{G}}_{\mathit{i}}+{\mathit{\beta }}_{\mathbf{2}}^{\prime }{\mathit{Z}}_{\mathit{i}}+w_i$$ (2)

to obtain the fitted residual ŵ_i. A logistic regression model is then fitted in the second stage:

$$log\left(\frac{E(y_i)}{1-E(y_i)}\right)={\alpha }_0^{\prime }+{\alpha }_1^{\prime }{x}_i+{\mathit{\alpha }}_{\mathbf{2}}^{\prime }{\mathit{Z}}_{\mathit{i}}+{\alpha }_3^{\prime }{\widehat{w}}_i$$ (3)

A Wald test based on the robust standard error (Huber-White standard error) is used to test the null hypothesis that the time-varying exposure variable has no effect on the disease risk, i.e., $H_0:{\alpha }_1^{\prime }=0$. We denote this method as PACE+2SRI.

New Method II: PACE+2SFRI

As gene expression levels change over time, the genetic effect on a time-varying exposure variable might change over time as well. To take this phenomenon into account, we propose the second method for conducting MR analysis for the recovered functional data using functional regression techniques. Specifically, let D_i(t) = x̂_i(t) − μ̂(t) be the functional data of the time-varying exposure variable with trend removed. A two-stage functional residual inclusion (2SFRI) can be performed. In the first stage, we fit a functional linear model for the time-varying exposure variable as:

$$D_i(t)={\beta }_0(t)+{\mathit{\beta }}_{\mathbf{1}}(t){\mathit{G}}_{\mathit{i}}+{\mathit{\beta }}_{\mathbf{2}}(t){\mathit{Z}}_{\mathit{i}}+r_i(t),t\in \mathcal{T}$$ (4)

to obtain the fitted residual r̂_i(t), where β₁(t) is the time-varying genetic effect on the exposure. The functional linear model has been implemented in the R package “fda” [Ramsay, et al. 2009]. In the second stage, a functional logistic regression model is fitted to assess the effect of the time-varying exposure variable on the binary disease outcome:

$$log\left(\frac{E(y_i)}{1-E(y_i)}\right)={\gamma }_0+{\int }_{T_0}^{T_i}{\gamma }_1(t)D_i(t)dt+{\mathit{\gamma }}_{\mathbf{2}}{\mathit{Z}}_{\mathit{i}}+{\int }_{T_0}^{T_i}{\gamma }_3(t){\widehat{r}}_i(t)dt$$ (5)

For hypothesis testing purposes, we assume a time-constant effect for both the exposure variable and the fitted residual so that the functional logistic regression model (5) can be simplified to a logistic regression model:

$$log\left(\frac{E(y_i)}{1-E(y_i)}\right)={\gamma }_0+{\gamma }_1{\int }_{T_0}^{T_i}{D}_i(t)dt+{\mathit{\gamma }}_{\mathbf{2}}{\mathit{Z}}_{\mathit{i}}+{\gamma }_3{\int }_{T_0}^{T_i}{\widehat{r}}_i(t)dt={\gamma }_0+{\gamma }_1{x}_i+{\mathit{\gamma }}_{\mathbf{2}}{\mathit{Z}}_{\mathit{i}}+{\gamma }_3{\widehat{r}}_i$$ (6)

where $x_i={\int }_{T_0}^{T_i}{D}_i(t)dt$, and ${\widehat{r}}_i={\int }_{T_0}^{T_i}{\widehat{r}}_i(t)dt$. To test the null hypothesis that the cumulative time-varying exposure has no effect on the disease outcome, i.e., H₀:γ₁ = 0, we use a Wald test with the robust standard error (Huber-White standard error). We denote this method as PACE+2SFRI. Of note, the simplified model (6) is in line with the “burden test” in association testing for rare variants [Li and Leal 2008].

IV-outcome association test in MR analysis

If the objective of a MR analysis is only to test if an exposure variable has a causal effect on a disease outcome, it has been suggested that it suffices to test the association between the IV(s) and the disease outcome given that the IV(s) are valid [Holmes, et al. 2014b; VanderWeele, et al. 2014]. This is analogous to “intent-to-treat” in an RCT. Specifically, a logistic regression model is fitted: $log(\frac{E(y_i)}{1-E(y_i)})={\theta }_0+{\mathit{\theta }}_{\mathbf{1}}{\mathit{G}}_{\mathit{i}}+{\mathit{\theta }}_{\mathbf{2}}{\mathit{Z}}_{\mathit{i}}$, where E(y_i) is the expected value of y_i. Given the validity of G_i, rejecting H₀: θ₁ = 0 amounts to rejecting the null hypothesis that the exposure variable has no causal effect on the disease outcome. Although the IV-outcome association test can maintain the Type I error rate in the absence of causal effect, its power can be different from that of the two-stage methods when there is a causal effect as demonstrated in our method comparison detailed below.

Simulation Studies

We performed simulation studies to evaluate the performance of the two proposed functional data analysis-based methods in comparison with the standard MR analysis, which uses only the baseline measurement of a time-varying exposure variable and the IV-outcome association test method. We considered two simulation set-ups.

Simulation Set-up I

We simulated data by assuming that genetic variants have time-varying effects on the exposure variable and the exposure variable has a cumulative effect on the disease risk. To mimic the real data, we used the parameter estimates obtained from studying the effect of BMI on the risk of T2D using the GRS as the IV in the FHS data analysis as described in the next section. We simulated the time-varying exposure of subject i as: x_i(t_i) = β₀(t_i) + β₁(t_i)G_i + β₂(t_i)sex_i + β₃ (t_i)u_i + v_i(t_i), where t_i ∈ [31, T_i] and T_i ∈ [51,60]. T_i was the age that the disease outcome y_i was recorded, which was randomly sampled from the age interval of 51 to 60. G_i, the GRS of subject i, was simulated from N(0,0.45²). Sex was simulated from a Bernoulli (0.5) distribution and then standardized to have a mean of 0. u_i represents the unmeasured confounders, simulated from the standard normal distribution. We further let β₀(t_i) = μ̂(t_i), which was the mean BMI function over time estimated from the PACE procedure. β̂₁(t) and β̂₂(t) were the estimated time-varying coefficients of GRS and sex from the first stage of 2SFRI when analyzing the effect of BMI on the risk of T2D using the FHS data. We simulated data using β₂(t_i) = β̂₂(t_i) and β₁(t₁) = β̂₁(t_i), 2β̂₁(t_i) or 4β̂₁(t_i) to assess the performance of different methods using different IV strength levels. In addition, β₃(t_i) = 1+ 0.2(sin(πt_i/20) +cos(πt_i/20)). The residual v_i(t_i) was resampled from the BMI residuals estimated from the first stage of 2SFRI. Then the binary disease outcome was simulated from a binomial distribution Binom(1, p_i), where $p_i=\frac{exp(0.06+0.0054h{\int }_{31}^{T_i}\left(x_i(t_i)-\widehat{\mu }(t_i)\right){dt}_i+0.2u_i-0.04T_i-0.35\times {\mathit{sex}}_i)}{1+exp(0.06+0.0054h{\int }_{31}^{T_i}\left(x_i(t_i)-\widehat{\mu }(t_i)\right){dt}_i+0.2u_i-0.04T_i-0.35\times {\mathit{sex}}_i)}$. The estimated coefficient of the cumulative effect of BMI was 0.0054, based on analyzing its effect on the risk of T2D using the FHS data. We let h = 1 or 2 to simulate data with different causal effect sizes. We also simulated data with h = 0 to check if Type I error rates of the functional data analysis-based methods can be well controlled. To simulate sparse and irregular longitudinal measurements of the time-varying exposure variable, we randomly selected two to five observations at different age points for each subject from the simulated time-varying exposure variable (x_i(t_i)) as the observed data. We analyzed each simulated data set using four methods, 2SRI using only the first measurement of the time-varying exposure variable, PACE+2SRI, PACE+2SFRI, and the IV-outcome association test. G_i was used as the IV, and sex and T_i were included as observed covariates in all the analysis. The number of FPCs in the PACE procedure was selected based on at least 95% of FVE. We fixed the sample size of each simulated data set at n=1000. Using the significance level of 0.05, we conducted 2000 replications for empirical Type I error rate evaluation and1000 replications for empirical statistical power evaluation. For different IV strength levels, we calculated the mean F-test statistic for testing the association between the GRS and longitudinal exposure data using linear mixed models (LMMs).

Simulation Set-up II

To mimic the real data, we simulated the longitudinal data of the time-varying exposure variable and genetic variants by resampling from the FHS data. We further simulated the binary disease outcome using FPC scores instead of assuming a cumulative effect of the exposure variable on the disease risk. Let data_i = (x_i1, x_i2, … x_i7, SNP_i1, SNP_i2,…, SNP_i14, sex_i, T_i, FPC_i1, FPC_i2, FPC_i3)^T be the data vector of subject (i = 1, …, 1722) in the FHS data, which was used to analyze the effect of BMI on the risk of T2D. The vector (x_i1, x_i2, … x_i7)^T was the longitudinal BMI data collected from seven clinical visits. Many subjects had missing BMI values, meaning that not all the subjects had seven measurements. (SNP_i1, SNP_i2,…, SNP_i14)^T were the 14 SNPs used for constructing the GRS, and T_i was the time that the disease outcome was recorded. FPC_i1, FPC_i2, and FPC_i3 were the top three FPC scores selected in the PACE procedure to recover the BMI curve. More detailed information on the FHS data is described in the next section. The data vectors in the simulated data sets were resampled with replacement from the observed FHS data vectors data_i (i = 1,…,1722). We fixed the sample size of each simulated data set at n=1722, the same as the real data. We used parameter estimates from the real data analysis to simulate binary disease outcomes. For statistical power evaluation, the binary disease outcome of subject l in a simulated data set was generated from the binomial distribution Binom(1,p;), where $p_l=\frac{exp(-0.61+a_1{\mathit{FPC}}_{l1}+a_2{\mathit{FPC}}_{l2}+a_3{\mathit{FPC}}_{l3}-0.029T_l-0.34\times {\mathit{sex}}_l)}{1+exp(-0.61+a_1{\mathit{FPC}}_{l1}+a_2{\mathit{FPC}}_{l2}+a_3{\mathit{FPC}}_{l3}-0.029T_l-0.34\times {\mathit{sex}}_l)}$. This amounts to assuming a time-varying causal effect with $p_l=\frac{exp(-0.61+{\int }_{\mathcal{T}}\alpha (t)X_l(t)dt-0.029T_l-0.34\times {\mathit{sex}}_l)}{1+exp(-0.61+{\int }_{\mathcal{T}}\alpha (t)X_l(t)dt-0.029T_l-0.34\times {\mathit{sex}}_l)}$, where $\alpha (t)={\sum }_{k=1}^3{\alpha }_k{\widehat{\varphi }}_k(t)$ and $X_l(t)={\sum }_{k=1}^3{\mathit{FPC}}_{lk}{\widehat{\varphi }}_k(t)$ was the time-varying causal effect and exposure, respectively. We simulated data in three cases. In the first case, we let a₁ = 0.027, a₂ = −0.006, and a₃ = −0.064, where the effect sizes are the same as the ones estimated from the real data. In the second case, we doubled the effect sizes and let a₁ = 0.054, a₂ = −0.012, and a₃ = −0.128. In the third case, we let a₁ = 0.027, and a₂ = a₃ = 0, meaning only FPC1 affects the disease outcome. For empirical Type I error rate evaluation, the binary disease outcome of subject l in a simulated data set was generated from a binomial distribution Binom(1,p_l), where $p_l=\frac{exp(0.6-0.04T_l-0.6\times {\mathit{sex}}_l)}{1+exp(0.6-0.04T_l-0.6\times {\mathit{sex}}_l)}$. We analyzed the simulated data sets using either the 14 SNPs as IVs or the GRS as a single IV. Sex and T_i were included as covariates in all the analysis. For the IV-outcome association test, a Wald test was used when the GRS was used as the IV and a likelihood ratio test (LRT) was used when the 14 SNPs were used as IVs. With a significance level of 0.05, we simulated 2000 data sets for empirical Type I error rate evaluation and 1000 data sets for empirical statistical power evaluation.

Application to the FHS data

To demonstrate the proposed functional data analysis-based methods for testing the causal effect of a time-varying exposure variable on a binary disease outcome, we analyzed the effect of BMI on the risk of T2D and CHD, and the effect of HDL on the risk of CHD using the FHS data. The FHS is a family-based prospective cohort study with subjects from three generations: the Original Cohort, the Offspring Cohort, and the Third Generation Cohort [Splansky, et al. 2007]. The Offspring Cohort is the largest cohort with both genetic information and longitudinal phenotype measurements collected from seven clinical visits [Cupples, et al. 2009]. We performed MR analyses using unrelated individuals from the Offspring Cohort. The FHS data was downloaded from NCBI dbGaP. We selected the age interval from 25 to 75 years to recover the BMI curves and HDL curves from the longitudinal data using the PACE method. We chose such an age interval that at least 50 measurements of an exposure variable were collected at each age point when the data were pooled together to ensure stable estimation of both the mean function and the covariance function in the PACE procedure. The disease outcomes were censored at the last clinical visit that was at or before 75 years of age. The subjects included in the analysis had at least two measurements of the exposure variable in the age interval from 25 to 75 years before the disease incidence or censoring. The sample size for analyzing the effect of BMI on the risk of T2D was 1722 with 171 cases, while those for analyzing the effects of BMI and HDL on the risk of CHD were 1709 with 113 cases and 1669 with 110 cases, respectively. Following the previous MR analyses of the causal effect of BMI on cardiometabolic traits and events [Holmes, et al. 2014b], we used the 14 selected BMI SNPs identified from large-scale meta-analyses [Guo, et al. 2013]. The SNP data were extracted from the FHS Candidate Gene Association Resource (CARe) study. The weights used for the BMI GRS calculation were the same as those used by Holmes et al. [Holmes, et al. 2014b]. To analyze the causal effect of HDL on the risk of CHD, we used the 14 HDL SNPs as used in a previous MR study [Voight, et al. 2012]. We extracted 2 of the 14 HDL SNPs from the FHS CARe study data and imputed the rest of the 14 SNPs from the FHS Affymetrix 500K array using the 1000 Genomes Project haplotypes as the reference panel. We used SHAPEIT for phasing [Delaneau, et al. 2012] and IMPUTE2 for imputation [Howie, et al. 2012]. The HDL GRS was constructed following Voight et al. [Voight, et al. 2012]. We conducted MR analyses using the functional data analysis-based methods, the standard MR method using only the baseline measurement, and the IV-outcome association test. We used the first measurement of the time-varying exposure variable in the age interval from 25 to 75 years as the baseline measurement. We used either the GRS as a single IV or the SNPs used in GRS calculation as multiple IVs. We included sex and age when the disease outcome was recorded as covariates. The same covariates were included in the observational analysis, where the exposure variable’s effect on the disease outcome was assessed using logistic regression models.

Results

Simulation Studies

In simulation set-up I, we simulated data by assuming that the time-varying exposure variable has a cumulative effect on the disease risk. Table 1 shows the empirical Type I error rates of the different analysis methods in the presence of unmeasured confounders. At the significance level of 0.05, all the MR analysis methods were able to control Type I error rates at the nominal level, while direct observational analyses had inflated Type I error rates. Table 2 shows the empirical power of the four MR analysis methods, i.e., 2SRI using only the baseline measurement, PACE+2SRI, PACE+2SFRI, and the IV-outcome association test, for a time-varying exposure variable, at varying IV strength levels and different cumulative effect sizes of the time-varying exposure variable on the disease risk. As expected, the power increased as either the IV strength or the causal effect size increased. The two functional data analysis-based methods always had higher statistical power than either the MR analysis method that uses only the baseline measurement or the IV-outcome association test in each of the simulated scenarios (Table 2). The IV-outcome association test had much lower power than the other three MR analysis methods.

Table 1.

Empirical Type I error rates of different analysis methods in simulation set-up I.

IV strength	Mean F-test statistic from LMM	MR analysis				Observational analysis
		Baseline 2SRI	PACE+ 2SRI	PACE+ 2SFRI	IV-outcome test	Baseline	PACEa
β̂1(ti)	8.34	0.053	0.056	0.056	0.046	0.076	0.083
2β̂1(ti)	30.29	0.053	0.056	0.057	0.046	0.073	0.081
4β̂1(ti)	118.02	0.053	0.054	0.052	0.046	0.073	0.079

^athe cumulative effect of the exposure variable calculated from PACE-recovered curve was tested.

Table 2.

Empirical statistical power of different MR analysis methods in simulation set-up I.

IV strength	Cumulative effect of xi(ti) on yi	MR analysis
		Baseline 2SRI	PACE+2SRI	PACE+2SFRI	IV-outcome test
β̂1(ti)	α1	0.133	0.135	0.139	0.073
	2α1	0.269	0.278	0.277	0.141
2β̂1(ti)	α1	0.258	0.268	0.272	0.143
	2α1	0.586	0.593	0.603	0.398
4β̂1(ti)	α1	0.588	0.596	0.601	0.438
	2α1	0.980	0.986	0.986	0.922

In simulation set-up II, we simulated the longitudinal measurements of the time-varying exposure variable by resampling from the FHS real data. The disease outcomes were simulated using the FPC scores without assuming a cumulative effect from the exposure variable. Table 3 shows the empirical Type I error rate and power of different MR analysis methods using either the GRS as the IV or the 14 SNPs as multiple IVs. All the methods were able to control the Type I error rates at the nominal level except that the type I error rate of baseline 2SRI using 14 SNPs as multiple IVs was slightly larger (0.059). We observe substantial power gain by using the functional data analysis-based methods, especially the PACE+2SFRI method. When comparing MR analysis using the GRS as a single IV with that using the SNPs which were included in the GRS calculation as multiple IVs, the IV-outcome association test method had power loss, while the other methods had substantial power gain when the SNPs were used as multiple IVs in all the three simulated cases. We also performed MR analysis at each visit (see supplemental methods for details) in simulation set-up II. To use the minimum p-value (minP) obtained from analyzing the exposure variable data in each of the seven visits individually, we observe that the Bonferroni correction is necessary to control the Type I error rate (Table S1). The power of the Bonferroni corrected minP method was much lower than that of the baseline method only method, PACE+2SRI, and PACE+2SFRI.

Table 3.

Empirical Type I error rates and statistical power of MR analysis methods in simulation set-up II.

Simulation effect size			IV	MR analysis
FPC1	FPC2	FPC3		Baseline 2SRI	PACE+2SRI	PACE+2SFRI	IV-outcome test
Empirical Type I error rate
0	0	0	GRS	0.041	0.041	0.046	0.050
			14 SNPs	0.059	0.056	0.053	0.055
Empirical statistical power
0.027	−0.006	−0.064	GRS	0.188	0.206	0.259	0.121
			14 SNPs	0.380	0.417	0.450	0.113
0.054	−0.012	−0.128	GRS	0.435	0.485	0.557	0.300
			14 SNPs	0.783	0.816	0.827	0.250
0.027	0	0	GRS	0.188	0.199	0.258	0.133
			14 SNPs	0.326	0.384	0.430	0.133

The FHS Data Analysis

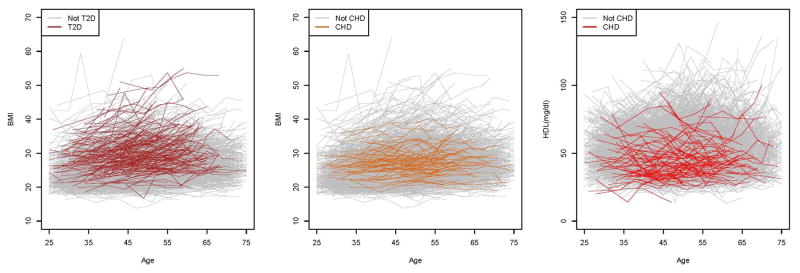
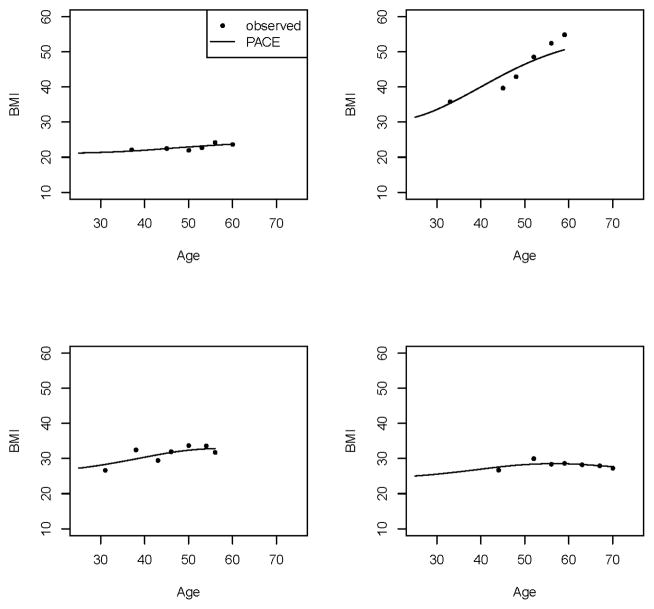
We performed MR analyses of the causal effect of BMI on the risk of T2D and CHD, and the causal effect of HDL on the risk of CHD, using data from the FHS Offspring Cohort. Fig. 3 shows the longitudinal BMI data and HDL data that were included in MR analyses. For both BMI and HDL, the individual fluctuation patterns could be very different. While some subjects had relatively stable trajectories over time, others had substantial changes across visits, hence establishing that the time-varying information cannot be adequately captured by a single measurement. We used the PACE method to recover the individual BMI curves and HDL curves from the longitudinal data. The smoothed mean BMI function increased slowly over time. The smoothed mean HDL function was almost constant over time (Fig. S1). We used the leading three eigen-functions (Fig. S2) and their corresponding FPC scores in BMI functional data recovery, which explained 84.7%, 13.6%, and 1.5% of the variation, respectively, with a total of 99.8% variation explained. The first eigen-function shows an almost constant shift from the mean curve. The second eigen-function shows a slowly increasing trend over time, while the third one increases from 25 to approximately 50 years of age, and then decreases. Fig. 4 shows the observed longitudinal BMI data and the corresponding underlying time-varying curves recovered using PACE of four randomly selected subjects. Although the trajectories of different subjects varied, the PACE-recovered curves were able to capture the different patterns. The recovered curves either went through or were adjacent to the longitudinal data points, confirming that majority of the variation in the observed data were well captured. For HDL, we used the leading two eigen-functions (Fig. S2) and their corresponding FPC scores in the functional data recovery, which explained 99% and 0.9% of the variation, respectively, with a total of 99.9% variation explained. The first eigen-function shows a slowly increasing trend over time. The second eigen-function shows an increasing trend up to approximately 55 years of age, followed by a decrease. Fig. S3 shows the observed longitudinal HDL data and the recovered time-varying underlying curves of four randomly selected subjects. Again, the PACE method was able to recover the time-varying information for the subjects with different patterns.

Fig. 3. The observed FHS longitudinal data.

For the plot on the left and the plot in the middle, each line represents the longitudinal BMI data of a subject included in MR analysis. For the plot on the right, each line represents the longitudinal HDL data of a subject included in MR analysis.

Fig. 4. PACE-predicted vs. observed BMI data.

Each plot shows the BMI data of a randomly selected subject.

Before performing the MR analyses, we checked the strength of the association between the GRS and longitudinal exposure data using an LMM. The F-test statistic for the association between the BMI GRS and longitudinal BMI data was 13.25, higher than the weak IV threshold of F-test statistic of 11 [Pierce, et al. 2011]. The F-test statistic for the association between the HDL GRS and longitudinal HDL data was 8.94, below the weak IV threshold. We did not perform the test for the exclusion restriction with the FHS data because such a test cannot be performed when only one IV is used for one exposure variable (exact-identification). In addition, there are no consistent ways to test the exclusion restriction in our two proposed MR analyses combined with the functional data analyses, even when we have multiple IVs (over-identification) because there are no validated exclusion restriction tests for these new methods yet in the literature.

The MR analysis results of the FHS data are shown in Table 4. When analyzing the causal effect of BMI on the risk of T2D using the GRS as the IV, PACE+2SRI had the smallest p-value of 0.008, more significant than the baseline only analysis (p-value of 0.014), the IV-outcome association test (p-value of 0.026), and the PACE+2SFRI analysis (p-value of 0.057). When using the 14 BMI associated SNPs as IVs, MR analysis using the baseline BMI data, PACE+2SRI, PACE+2SFRI, and the IV-outcome association test had p-values of 0.061, 0.026, 0.089, and 0.033, respectively. We did not identify a significant causal effect of either BMI or HDL on the risk of CHD, irrespective of whether we used the GRS as the IV or the SNPs as multiple IVs in the MR analyses. When performing direct observational analysis of the association between BMI and the risk of CHD, the baseline BMI had a significant association, while the cumulative BMI did not. The direct observational analysis of the association between HDL and the risk of CHD shows a significant association with the cumulative HDL level, but not the baseline HDL level. We also analyzed the effect of BMI on the risk of T2D and CHD, and the effect of HDL on the risk of CHD by individual clinical visits (Table S3, S4, and S5). We only used the exposure data collected between 25 and 75 years of age, to be consistent with the data used for functional data analysis-based methods. The sample sizes of different visits were different, but comparable. However, the results are not consistent across clinical visits. For example, in MR analysis of the causal effect of BMI on the risk of T2D using the GRS as the IV (Table S3), the result based on the BMI measurement from the 6^th clinical visit was very significant (p-value of 0.002), while the result based on the BMI measurement from the 7^th clinical visit was not significant (p-value of 0.097).

Table 4.

Analysis of the causal effect of BMI on the risk of T2D and CHD, and the effect of HDL on the risk of CHD using the FHS data.

Exposure	Disease	MR analysis p-value					Observational analysis p-value
		IV	Baseline 2SRI	PACE +2SRI	PACE+ 2SFRI	IV-outcome test	Baseline	PACEa
BMI	T2D	GRS	0.014	0.008	0.057	0.026	< 2E-16	< 2E-16
		14 SNPs	0.061	0.026	0.089	0.033
BMI	CHD	GRS	0.396	0.397	0.510	0.793	0.005	0.708
		14 SNPs	0.438	0.467	0.532	0.414
HDL	CHD	GRS	0.518	0.531	0.239	0.967	0.114	0.005
		14 SNPs	0.783	0.790	0.489	0.083

^athe cumulative effect of the exposure variable calculated from PACE-recovered curve was tested.

Discussion

In this work, we have proposed two novel functional data analysis-based methods, i.e., PACE+2SR and PACE+2SFRI, for incorporating longitudinal data of a time-varying exposure variable in the MR analysis when the disease outcome is binary. We have shown that the new methods outperform the current MR analysis that uses a single measurement at some arbitrary time point and the IV-outcome association test.

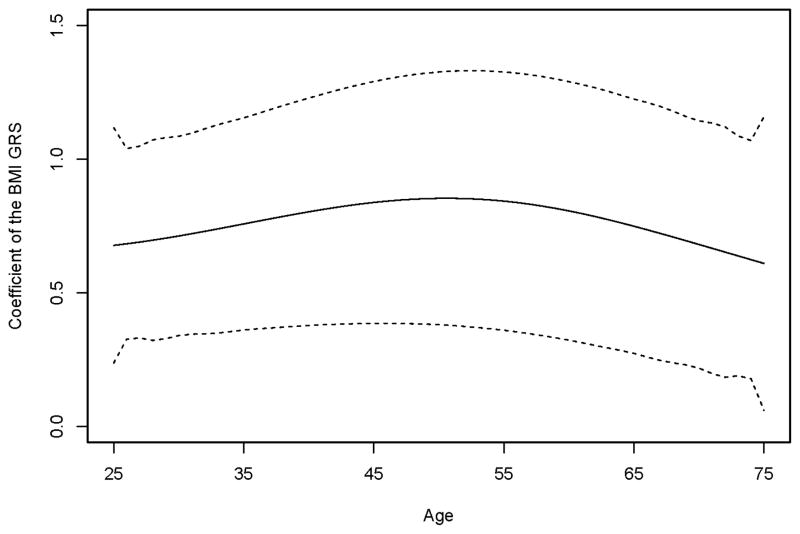
MR studies have been widely used in recent years to identify causal risk factors in observational studies, especially for the factors that cannot be studied using RCTs, for example, BMI, HDL and alcohol consumption [Holmes, et al. 2014a; Holmes, et al. 2014b; Voight, et al. 2012]. Many of these risk factors change continuously over one’s lifespan, and consequently a single measurement cannot capture such time-varying information. In addition, MR analysis inherently assumes that genetic variants affect these time-varying exposure variables, e.g., BMI, for the entire lifetime [Evans and Davey Smith 2015]. However, longitudinal data have not been taken into account in current MR studies, and only one measurement of a time-varying exposure variable, usually at the baseline, is used. The functional data analysis methods we introduce here incorporate longitudinal data in the analysis, and assume that the time-varying exposure variable has a cumulative effect on the risk of developing a disease. We have seen an increase in statistical power in our simulation studies using the functional data analysis-based methods, regardless of whether the data were simulated with or without the cumulative effect assumption. The PACE+2SFRI method had substantially higher power in simulation set-up II, where the longitudinal data of the exposure variable was resampled from the FHS real data. This may imply that the genetic variants have a time-varying effect on the exposure variable, which leads to a power gain in the statistical analysis that takes the time-varying information into account. In the FHS data analysis, the estimated functional coefficient of the BMI GRS changes over time (Fig. 5). The estimated effect of the GRS on BMI increases slowly from age 25 to 50 years, followed by a slow decrease. The estimated combined genetic effect of the 14 SNPs on BMI also changes over time (Fig. S4). Overall subjects with more effect alleles have higher fitted BMI values across their lifetime.

Fig. 5. The estimated functional coefficient of the BMI GRS from the first stage of 2SFRI.

The dotted lines indicate the point-wise 95% confidence limits.

The GRS is widely accepted in current MR studies to increase IV strength by combining the effect of multiple SNPs [Holmes, et al. 2014b; Palmer, et al. 2012; Proitsi, et al. 2014; Voight, et al. 2012], where the weights used to construct the GRS are effect estimates from previous large-scale association studies. For example, Holmes et al. [Holmes, et al. 2014b] constructed the BMI GRS using SNP effect estimates from an association study with 108,912 subjects [Guo, et al. 2013]. In our simulation set-up II, we observed a statistical power increase by using the SNPs in the GRS as separate IVs, compared to using the GRS as a single IV (Table 3). The SNP weights used in the GRS calculation, estimated from 108,912 subjects, may not represent the SNP effect sizes well for the FHS data with 1722 subjects that we used in the simulation studies. This might have led to a power loss in the GRS-based MR analyses. Extensive simulation studies conducted by Pierce et al. [Pierce, et al. 2011] found that using multiple genetic variants as separate IVs may result in weak IVs, while combining them could lead to statistical power loss, which is in agreement with our simulation results. Weak IVs may lead to inflated type I error rate in stage II testing due to poor estimation in stage I [Burgess, et al. 2015]. Therefore, we suggest that researchers conduct an MR analysis using both IV methods, i.e., the first method using the GRS as a single IV and the second method using the multiple SNPs from the GRS computation as separate IVs.

In the FHS data analysis, we identified a significant causal effect of BMI on the risk of T2D using the PACE+2SRI method. When using the PACE+2SFRI method, the effect was not significant based on a significance level of 0.05, but the p-values were close to 0.05. We did not identify a significant causal effect of either BMI or HDL on the risk CHD. Our analysis results are generally consistent with previous MR study results based on much larger sample sizes. Holmes et al. showed that BMI had a causal effect on the risk of T2D, but not on the risk of CHD in a MR study with a sample size of 34,538 [Holmes, et al. 2014b]. Voight et al. showed that HDL did not have a causal effect on the incidence of myocardial infarction in a MR study with a sample size of 53,813 [Voight, et al. 2012]. In addition, randomized clinical trials have shown that HDL increasing therapy does not reduce cardiovascular risk [Landray, et al. 2014]

The limitation of this work is that the two new proposed methods are only aimed for hypothesis testing, not for causal effect size estimation. Our simulation studies showed that the new methods were able to control the Type I error rates well, confirming that the new methods are valid for testing purpose. However, statistical models that are valid for testing may not provide consistent estimates [Dai, et al. 2014]. Consistent effect size estimation is challenging in causal inference and is subject to strong assumptions. Nevertheless, the main focus of MR studies is to identify disease risk factors, rather than effect size estimation [Burgess 2013].

Although the MR analysis is subject to strong assumptions, it is a very useful method to identify potential causal risk factors from observational studies [Evans and Davey Smith 2015]. The two proposed methods for incorporating longitudinal data of a time-varying exposure will help improve the versatility of the MR analysis. These novel methods are readily applicable to existing longitudinal cohort studies, such as the FHS, and new large-scale electronic health record (EHR)-based longitudinal cohorts, for example, the Genetic Epidemiology Research on Adult Health and Aging (GERA) Cohort of 100,000 individuals [Lapham, et al. 2015], and, in principle, can be applied to the planned Precision Medicine Initiative longitudinal cohort of one million individuals [Collins and Varmus 2015]. R programs implementing the proposed methods will be posted on our website at: https://sites.google.com/site/utpengwei/