Non-Equilibrium Cytoquake Dynamics in Cytoskeletal Remodeling and Stabilization

Abstract

The cytoskeleton (CSK) is a tensed fiber framework that supports, shapes and stabilizes the cell. The CSK is in a constant state of remodeling, moreover, which is an active non-equilibrium thermodynamic process. We report here that cytoskeletal remodeling involves reconfigurations that are not only sudden but also are transmitted to great distances within the cell in a fashion reminiscent of quakes in the Earth's crust. Remarkably, these events in the cell conform both qualitatively and quantitatively to empirical laws typical of earthquakes, including hierarchical fault structures, cumulative energy distributions following the Gutenberg-Richter law, and rate of after-shocks following Omori's law. While it is well-established that remodeling and stabilization of the cytoskeleton are non-equilibrium process, these new unanticipated observations establish that these processes are also remarkably non-local and strongly cooperative.

Introduction

The analogy between quake-like dynamics within biologic versus geologic systems is not new. Ansari et al.¹ used the term “proteinquake” to explain large and sudden reconfigurations of the myoglobin molecule. Myoglobin is found in abundance in skeletal muscle of vertebrates, and can attach and detach to O₂ and CO in a way that implies the existence of a large number of configurational substates (CS).^1,2 The motion between equilibrium substates they called a protein-equilibrium fluctuation (EF), whereas motion between an equilibrium state and an intermediate non-equilibrium state they called a functionally important motion (FIM). For EFs, fluctuations in internal energy and entropy can be determined by equilibrium statistical mechanics, whereas for FIMs, being nonequilibrium states, this cannot be done. As such, studies of EFs can be based upon resting proteins undergoing thermal agitation alone whereas study of FIMs requires protein excitation as might be driven by photodissociation, for example. The strain energy suddenly released during return of the molecule to equilibrium is dissipated in the form of waves of deformation that propagate across it.¹ Hence the analogy between the proteinquake and the earthquake.

The living CSK at rest metabolizes adenosine triphosphate (ATP) at an appreciable basal rate and is therefore a non-equilibrium system.³ It has been suggested previously that the living CSK can attain a large number of configurational substates defined by a rugged free-energy landscape.⁴ The ruggedness of this energy landscape is imagined to originate from short range interactions that form barriers and traps. We define as a substate any group of barriers locally connected in the energy landscape with an energy of order k_BT or smaller. Thus the CSK can jump between substates through the agency of thermal agitation alone. However, when barriers are substantially greater than k_BT, the CSK might become trapped. But to overcome the barrier, escape the trap, and jump to another state, the CSK can use energy release from hydrolysis of ATP, which is about 20–25 k_BT.³

Rugged energy landscapes are typified by non-equilibrium materials such as glasses,^2,5 which for such systems provide a unifying language.² Irreversible structural relaxations in a glass are characterized by dynamic heterogeneity and appreciable cooperativity.^6–8 Indeed, the CSK of the adherent cell exhibits features of soft glasses, including power law rheology fluidization by shear, and structural rearrangements that are intermittent, non-Gaussian and cooperative.^3,4,9,10 In this connection, a recent study of unfolding of a protein molecule emphasizes that sequential events are discrete and independent, as in Markovian processes.¹¹ On the other hand, if transitions between states of the protein fiber network, at the level of the cytoskeleton, are cooperative rather than Markovian, then the metaphor with quake-like behavior is deeper than previously imagined. The adherent cell generates ATP-dependent contractile forces that are transmitted to remote sites along stress fibers that can span the breadth of the cell.¹² These contractile forces, in turn, lead to the storage of appreciable elastic strain energy within the S2 subfragments of the myosin motor, within the backbone of cytoskeletal myosin, within actin fibers and filaments,¹³ and within the elastic substrate to which the cell adheres. And just as this elastic strain energy can build-up in various cellular compartments, so too it cannot be ruled out that at least some part of that strain energy might at times be released in a sequence of discontinuous but cooperative events similar to fault-slips and resulting seismic waves in the crust of the Earth. Here we test that idea.

The surface of the Earth is not homogeneous, but rather is subdivided into tectonic plates each of which is under different stress conditions. Resulting plate motions lead to buildup of elastic strain energy near plate junctions. Once the stored energy reaches a given threshold, which varies with the geological region, there is a fault rupture with the consequent release of part of this stored strain energy. Since the accumulation of strain energy is more common at the interface of the tectonic plates, earthquakes are spatially clustered. And since after an earthquake there are many local slow geological accommodations, much slower than the shock propagation itself, aftershocks are also clustered in time. In a similar fashion, the accumulation and sudden release of energy is widespread in other physical systems, such as snow avalanches,¹⁴ particle gels,¹⁵ catastrophic rupture events,¹⁶ magnetism,¹⁷ and in physiology, such as pressure volume instabilities,^18,19 and crackling lung sounds.^20,21

Earthquakes are known to conform to three empirical laws: (i) their spatial distribution clusters along hierarchical fault structures;²² (ii) the Gutenberg-Richter law^22,23 states that, over a fixed time interval, the number of earthquakes in a given region, with energies exceeding some reference energy, follows a power law, decaying as M^−B, where M is the magnitude of the quake; and (iii) the modified Omori’s law²⁴ states that the rate of after-shocks n(t) (the number per unit time) also follows a power law, n(t) = bt^−a, although here we ignore the time offset in Omori’s law.

The cytoskeleton network of the eukaryotic cells is a complex non-homogeneous fiber network that is mostly in tension and is constantly remodeling. Both tension buildup and cytoskeletal remodeling events require ATP hydrolysis. The tension in cytoskeleton network is generated by ATP-dependent acto-myosin interactions. Actin polymerization, one of the key remodeling events, also requires ATP hydrolysis. The non-homogeneity in these ATP driven processes may lead to localized accumulation of elastic strain energy, which may abruptly be released as fibers breaks or rearranges or as a myosin fibers slips on an actin fiber. Such sudden changes in structure and energy in the cytoskeleton network would propagate via serial rearrangement events which we referred as after-shocks. Just as probes are placed at the Earth’s surface to measure spontaneous earthquake events, here we attached microbeads to the cell surface to meaure spontaneous nanoscale cytoquake events. Because each microbead becomes tightly bound to the F-actin structure of the cytoskeleton, the bead cannot move unless the structure to which it is attached rearranges.^3,25 Here we report that nano-scale structural rearrangements of the CSK of the airway smooth muscle cell follow these same three empirical laws.

Measuring the remodeling events

To evaluate nano-scale remodeling events we plated cells sparsely on a well-defined substrate while we followed the position of microbeads attached to the cell.²⁶ We used 15 µm membrane-based micro-patterning (MEMPAT) to place the cell in a square island (Fig. 1a). Each cell was micropatterned onto a single 50 µm square, which was chosen based on the average area of the isolated human airway smooth muscle cell (Fig. 1a), see Ref.²⁶ for more details.

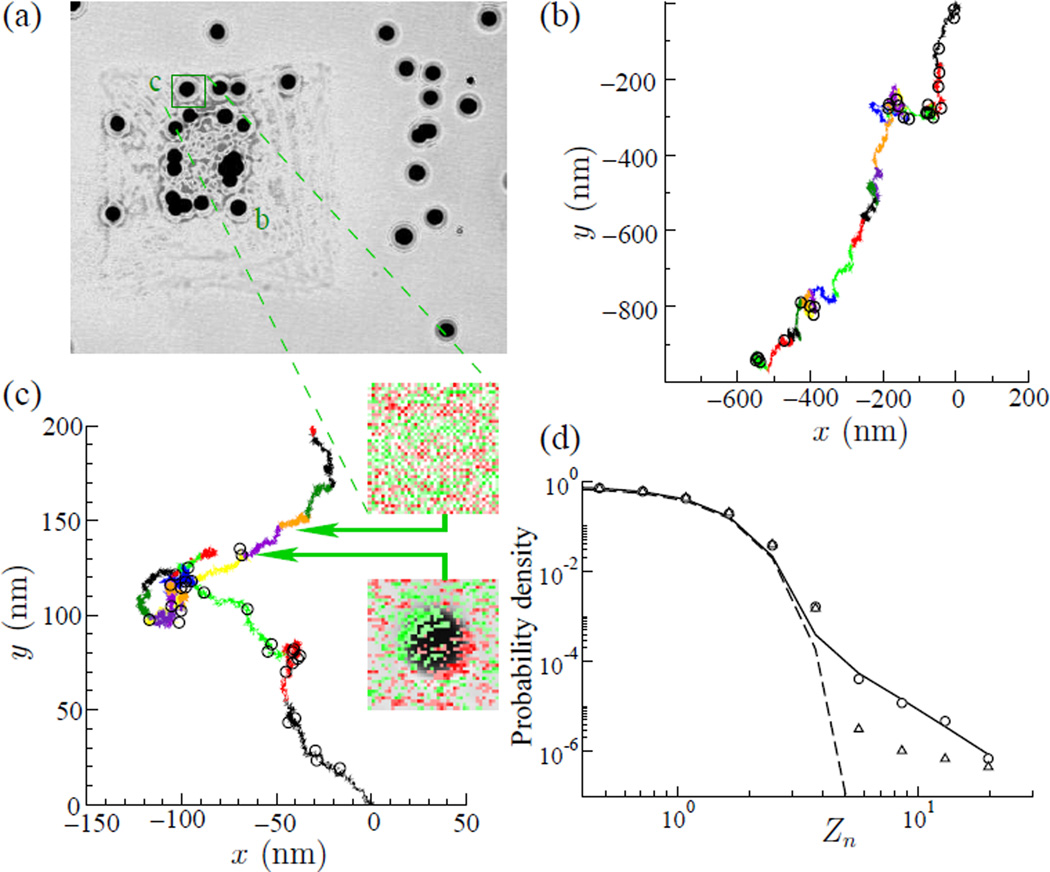
Fig. 1.

(a) Microbeads probes attached in micro-patterned Airway Smooth Muscle Cell were tracked using images at 12 Hz recorded by a CCD camera attached to an inverted microscope. (b,c) Ten minutes of bead trajectory. Each colored line in (b,c) represents 40 seconds of trajectory. (b) bead labeled “b” and (c) bead “c”, circles in the trajectory indicate large values of Z_n > 3. The insets in (c) are images originally from (a) which were digitally processed to highlight differences between consecutive images. Red color indicates the reduction of the gray scale level of the image while green indicate an increase. The top inset shows the typical fluctuation of gray scale in a position occupied by a bead, see arrows from (a). The bottom inset shows a “cytoquake”, note the red-green shadow in the superimposed image of the bead indicating a fast motion in the NW direction. The open circles on top of the graph show the 30 biggest jumps in this series, all of them Z_n > 3. (d) Histogram of the normalized bead displacements Z_n (circles) in a log-log graph. The continuous line shows the best-fit using $P(Z_n)=B{e}^{-Z_n^2/\beta }+A{(Z_n+Z_G)}^a$, with B=0.79, β = 1.80, A=0.05, Z_G=0.87 and α=3.62. The dashed line shows a Gaussian fit, and the triangles is ATP depleted. The graph shows two regions: the first region, for small Z_n where the histogram of all combined data follows a Gaussian distribution (dashed line), associated with thermal motion; and a second region, the tail of the graph, rare events, follows a power law.

To probe motions at the surface of the cell, microbeads (4.1 µm diameter) were coated with a synthetic peptide containing the Arg-Gly-Asp (RGD) sequence and allowed to adhere randomly to the apical surface of the smooth muscle cell.^3,4,26 These beads become tightly tethered to the F-actin through transmembrane integrin receptors, mostly α₅β₁.^27,28 It has been demonstrated that membrane stiffness has little effect on the cytoskeletal remodeling dynamics probed through integrin bound beads.^29,30 We then monitored the spontaneous motion of these ferrimagnetic beads during an average of 400 s using an algorithm that calculates the center of the mass of the beads from the images recorded by a CCD camera through an optical microscope with nanometer accuracy. Positions r⃗_n along each bead trajectory were measured at 12 Hz, and displacements d_n were calculated as the Euclidean distance between sequential points, d_n = |r⃗_n − r⃗_n−1|. Displacements d_n were normalized using the averaged value 〈d〉 and the standard deviation σ, Z_n = (d_n − 〈d〉)/σ, where σ² = 〈d²〉 − 〈d〉², and 〈․〉 denotes averages over each bead trajectory.

Here we define a cytoquake as being a normalized displacement which satisfies Z_n > Z_M, where Z_M is a threshold value denoting a main quake. Aftershocks are defined for subsequent displacements that satisfy Z_A < Z_n < Z_M, where Z_A is a second event threshold. If a subsequent displacement exceeds Z_M, it is taken to be a new cytoquake (this is analogous to Omori’s law, but with a fixed threshold for determining the presence of a main quake). Trajectories of two typical microbeads are shown in Figs. 1b and 1c. The color of the traces have been changed every 40 s for clarity in visually tracking the bead motions. Events with Z_n > Z_M = 3 are indicated by circles. The cumulative number of occurrences of aftershocks N_A(t) following a cytoquake depends on the two thresholds Z_M and Z_A, and for any given Z_M and Z_A, N_A(t) can be computed. These data can then be compared with cumulative number of aftershocks predicted from the integrated form of Omori’s equation, N_Omori(t) = b(1 − a)⁻¹t^1−a.

In addition to measuring N(t), and computing N_Omori(t), from the best fit to the data with respect to Omori parameters a and b, we also calculated the cumulative probability of the occurrence of at least one aftershock as a function of time following a cytoquake, based on a random arrivals model given by a Poisson process with intensity λ. The probability of exactly n occurrences in time t is given by p(t, n) = (λt)ⁿe^−λt/n!, and so the probability of at least one aftershock is simply

$$P=1-e^{-\lambda t}.$$ (1)

These probabilities were computed as follows. Lets call the total number of elements of the normalized displacement series Z_n as N_n. The number N_n is very large compared with the number of cytoquakes, which is the sum of aftershock N_A and the number of main quake N_M. Thus, the probability to have a cytoquake is p = (N_A + N_M)/N_n, and we can replace λ ≈ p in Eq. 1, and use it to compare with experimental data.

Results

Bead displacements showed multiple large jumps (Z_n > 3) indicated by circles (Fig. 1b and 1c). As quantified below these jumps were clustered in space and in time. The histogram of Z_n revealed two regimes. For small Z_n, the probability distribution can be fitted by a Gaussian (dashed line, Fig. 1d); we associate these Gaussian motions with thermal fluctuations of the cytoskeleton. For large Z_n, however, the distribution departs markedly from Gaussian and approximates a power law distribution, $P(Z_n)\approx A{Z}_n^{-\alpha }$; we associate these larger non-Gaussian motions with non-equilibrium fluctuations. These results and conclusions are consonant with those first reported in colloidal glass transition, and in cells.^3,31 Similar results were subsequently confirmed in reconstituted networks.^32,33

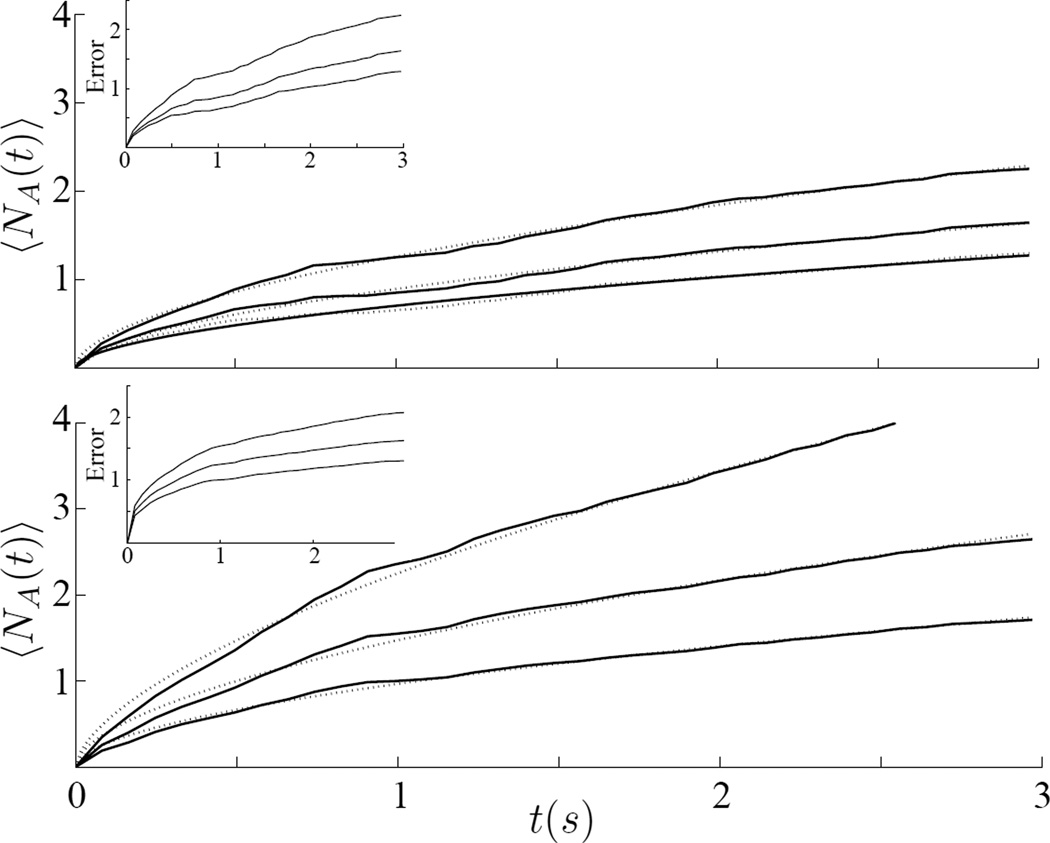
The distribution of Z_n (Fig. 1d) shows two regions. We chose to focus on the part of the distribution where Z_n departs from a Gaussian distribution, or Z_n = 3, where Z_A is chosen to be always smaller then Z_M. Figure 2 shows the average number of aftershock events 〈N_A(t)〉 for cells at 24°C using two values of Z_M: (top) shows data for fixed Z_M = 5, and for three aftershock thresholds, Z_A =3, 3.5 and 4; (bottom) shows data for fixed Z_M = 4 and for three others aftershock thresholds, Z_A =2, 2.5 and 3. Shown as dotted lines are the cumulative aftershock numbers from Omori’s equation, Eq. 2, with its parameters a and b determined by least squares best fit. The data was also fitted assuming Poisson error using Generalized Linear Regression,³⁴ results not shown, and the data fall within the 95% confidence interval.

Fig. 2.

The average cumulative number 〈N_A(t)〉 of jumps Z_n larger than a threshold Z_A for a given initial trigger Z_M: (top) Z_M=5, and from top to bottom the continuous lines were obtained for Z_A= 3, 3.5 and 4 respectively. The dashed lines are the best fit of the Eq. 2, and the parameter a found were 0.45, 0.44 and 0.45 respectively; (bottom) Z_M = 4, and from top to bottom the continuous lines were obtained for Z_A = 2, 2:5 and 3 respectively. The dashed lines are the best fit of the Eq. 2, and the parameter a found were 0.39, 0.44 and 0.46 respectively. The inset show the Poisson error counting of the experimental data.

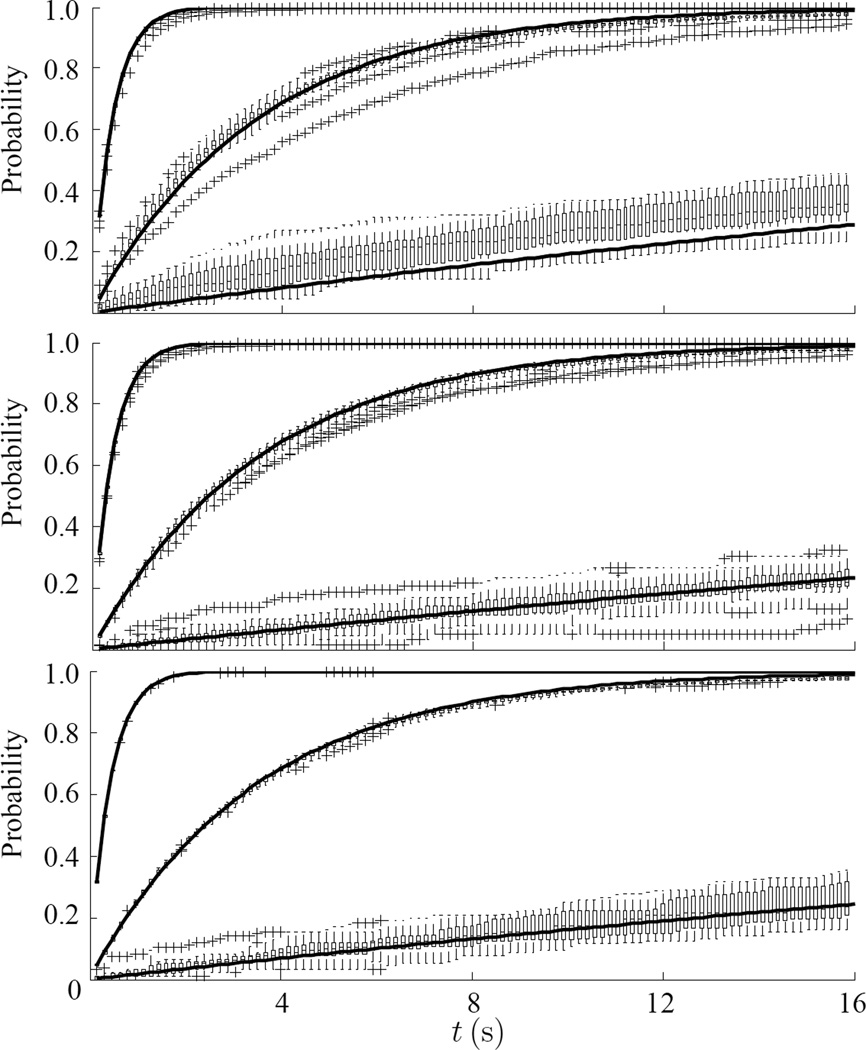
We compared predictions for a Poisson process (Eq. 1) to experimental data for cells at 24°C, for thermal noise from beads glued to the substrate, and for ATP-depleted cells, to a Poisson process (Figs. 3a, b and c). The data from 23, 27 and 18 experiments, respectively, are shown using box and whisker plot with asterisks as the outliers. For each of these situations, we used three values of Z_M = Z_A = 1 (top), 2 (middle) and 3 (bottom).

Fig. 3.

Given one large event, Z_n ≥ Z_M, the probability to have at least one additional event greater than Z_A within a time window of t, for Z_A = 1 (top), Z_A = 2 (middle) and Z_A = 3 (bottom). Data are shown as a box and whisker plot with asterisks as the outliers. The continuous black lines are the predicted values of a Poisson distribution with the same number of events according with Eq. 1. (a) Cells at 24°C, λ =0.187±0.006, 0.023±0.001 and 0.0017±0.0002, (b) noise from beads glued to the substrate, λ =0.189±0.005, 0.023±0.001 and 0.0013±0.0001, and (c) ATP-depleted cell, λ = 0.189±0.002, 0.023±0.001 and 0.0014±0.0001.

We measured the cumulative number of events N(t) larger then a given threshold Z_A after an initial event of Z_n > Z_M; we did this for 15 to 25 beads per experiments in 23 experiments (Fig. 2). As Z_A decreases N(t) increased, and this was true both for Z_M = 4 and 5. Given one large event, the probability to have at least one additional jump greater than Z_A within a time window of t is shown in Fig. 3.

We predicted the time correlation between large events using two methods. In the first method, we calculated the probability to have subsequent jumps after trigger event, Z_n > Z_M. From Omori’s Law the cumulative number of aftershocks is given by,³⁵

$$N_{\text{Omori}}(t)=b\frac{t^{1-a}}{1-a}$$ (2)

This relationship offered a good fit with observations (dashed lines, Fig. 2). In the second method, we modeled the observations of Fig. 3 using a Poisson distribution. For Z_n < 2 a Poisson distribution fit observations well. However, for Z_n ≥ 3 the fit was quite poor. When beads were glued to the substrate (Fig. 3b) or when ATP was depleted from cells, the fit was nearly perfect. While high magnitude earthquakes tend to be time-independent,³⁶ cytoquakes are more likely to be time-dependent. However, the cytoquake is correlated with cellular activities which are more time dependent then the stress fluctuations at the crust of the Earth.

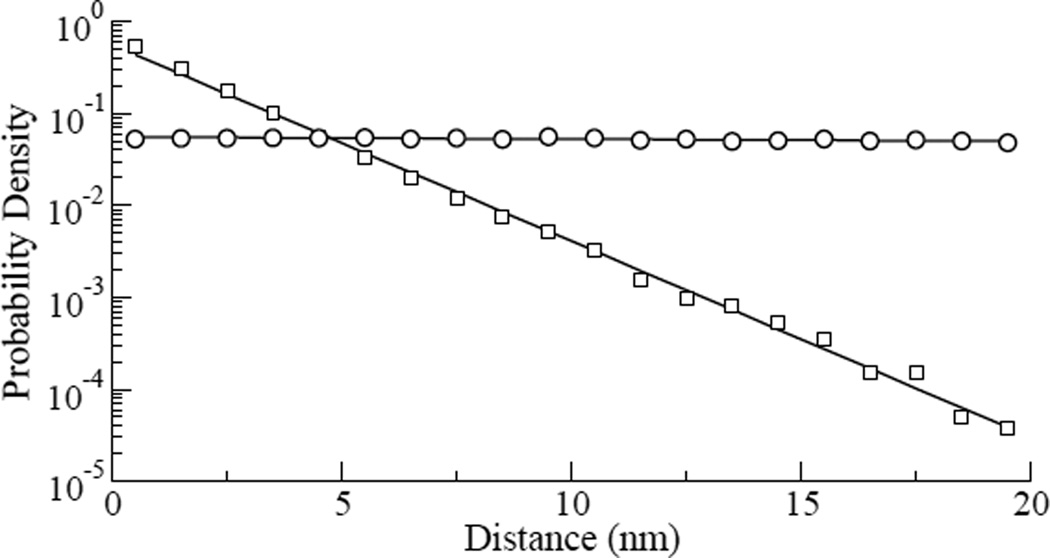
Spatially, the probability for one bead to jump Z_n > 3 within a given distance of another jump from the same bead exceeded that predicted by a Gaussian random walk by about 2-fold (Fig. 4). The Gaussian random walk simulations were done using a Gaussian distribution with zero mean and standard deviation of 6.07 nm, obtained from the 24°C experiments. We did 15000 simulations with 9000 steps each. Taken together, these observations indicate that large events in the living CSK are not independent, but rather are correlated in time and space.

Fig. 4.

Probability densities of the distances between points where Z_n ≥ 3 for all combined experimental data of the cells at 24°C (squares), and for all combined data of the simulations of the Gaussian random walk simulation (circles), the continuous line is the exponential fit of the data, with exponents −0.5 and 0.0, respectively. In the simulation we used a Gaussian distribution with zero mean and standard deviation SD=6.07 nm obtained from the experimental data.

The cytoskeleton of the living cell is an active, stress-generating mechanical system that relies on a continuous injection of chemical energy in the form hydrolysis of ATP and is characterized by non-equilibrium fluctuations within the network.^3,4,9 However, we cannot distinguish between acto-myosin inteactions, cytoskeletal polymerization events, or protein folding/unfolding events. Reconstituted protein networks in vitro are metabolically active and have been shown to capture some of these same interesting features,^32,33 but such systems are not suspended between focal adhesions, as in the living cell, and are not generally studied in a configuration in which the network bears appreciable mechanical stress, also as in the living cell.²⁶ As such, the reconstituted versus native cytoskeletal networks might differ in fundamental ways. Here we examined the living cell and, in greater detail, the nature of these non-equilibrium fluctuations.

The Gutenberg-Richter law expresses a power law relationship between the magnitude and the total number of earthquake events in a given region, much as we found in cells. In the case of the cell, nanoscale bead displacements arose from thermal fluctuations punctuated by much larger non-equlibrium fluctuations, the latter of which exhibited distributions with fat non-Gaussian tails consistent with a power law. Omori’s law describes the power law dependence of the number of aftershocks per unit of time with an exponent ranging from 0.9 to 1.5,³⁷ while in the cell we found the exponent to be around 0.5 (see Fig. 2). Such behavior implies that the relaxation process of the crust of the Earth is a complex system for which a typical state does not exist. Similar non-exponential relaxation has also been observed in several physical and social systems such as spin glasses,³⁸ microfracturing phenomena,³⁹ Internet traffic,³⁷ and stock market.³⁵

Our findings established a striking phenomenological analogy between the dynamics of the crust of the Earth and the surface of the eukaryotic cells. The presence of the quake-like behavior implies cytoskeleton mechanical remodeling associated with ATP driven activities. This analogy also implies the cytoskeleton is highly non-homogeneous with structural faults, not usually considered in mathematical models of the cell structure.

In summary, we find that the CSK of the living cell exhibits abrupt local reconfigurations together with transmission of detectable motions to great distances in a fashion reminiscent of quakes in the Earth’s crust. Remarkably, these events in the cell conform both qualitatively and quantitatively to empirical laws typical of earthquakes, including hierarchical fault structures with cumulative energy distributions following the Gutenberg-Richter law, and rate of after-shocks decaying according Omori’s law. As such, these local non-equilibrium fluctuations represent a sudden dissipative accommodation of a given structural fault and leads to what we call the “cytoquake”.