Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2016 Nov 25.
Published in final edited form as: Clin Neurophysiol. 2013 Nov 5;125(6):1095–1103. doi: 10.1016/j.clinph.2013.10.021

Automatic detection of prominent interictal spikes in intracranial EEG: Validation of an algorithm and relationsip to the seizure onset zone

Nicolas Gaspard 1,*, Rafeed Alkawadri 1, Pue Farooque 1, Irina I Goncharova 1, Hitten P Zaveri 1
PMCID: PMC5123744  NIHMSID: NIHMS826396  PMID: 24269092

Abstract

Objective

To develop an algorithm for the automatic quantitative description and detection of spikes in the intracranial EEG and quantify the relationship between prominent spikes and the seizure onset zone.

Methods

An algorithm was developed for the quantification of time–frequency properties of spikes (upslope, instantaneous energy, downslope) and their statistical representation in a univariate generalized extreme value distribution. Its performance was evaluated in comparison to expert detection of spikes in intracranial EEG recordings from 10 patients. It was subsequently used in 18 patients to detect prominent spikes and quantify their spatial relationship to the seizure onset area.

Results

The algorithm displayed an average sensitivity of 63.4% with a false detection rate of 3.2 per minute for the detection of individual spikes and an average sensitivity of 88.6% with a false detection rate of 1.4% for the detection of intracranial EEG contacts containing the most prominent spikes. Prominent spikes occurred closer to the seizure onset area than less prominent spikes but they overlapped with it only in a minority of cases (3/18).

Conclusions

Automatic detection and quantification of the morphology of spikes increases their utility to localize the seizure onset area. Prominent spikes tend to originate mostly from contacts located in the close vicinity of the seizure onset area rather than from within it.

Significance

Quantitative analysis of time–frequency characteristics and spatial distribution of intracranial spikes provides complementary information that may be useful for the localization of the seizure-onset zone.

Keywords: Interictal spike detection, Intracranial EEG, Automatic detection, Mahalanobis distance, General extreme value statistics, Localization of the seizure onset zone

1. Introduction

Automatic spike detection has been a longstanding issue (Gotman and Gloor, 1976) (and see the extensive review by Wilson and Emerson (2002)). However, algorithms developed specifically for intracranial EEG have focused on the detection of spikes and the calculation of their frequency (Dümpelmann and Elger, 1999; Valenti et al., 2006; Brown et al., 2007; Barkmeier et al., 2012). Spike frequency and the global spatial distribution of spikes are only partially informative of the localization of the seizure onset zone (Hufnagel et al., 2000; Asano et al., 2003; Goncharova et al., 2009; Marsh et al., 2010) and other attributes of spikes may provide crucial additional information (Hufnagel et al., 2000; Asano et al., 2003).

Intracranial spikes exhibit considerable variability in their morphology at the inter-individual, intra-individual and even intra-electrode levels. The quantitative analysis of their morphology may assist in the surgical planning and possibly improve surgical outcomes, although data on the relationship between spike amplitude and the seizure onset zone are contradictory (Hufnagel et al., 2000; Asano et al., 2003, 2008). The clinical implementation of these methods is currently limited by the lack of automated algorithms for the quantitative analysis of spike characteristics, requiring quantitative analysis to be performed manually, which is time consuming.

We thus aimed to develop an algorithm that would quantify the morphology of spikes so that their detection and the analysis of their temporal and spatial distribution could be performed based on the quantitative measure of inherent spike characteristics. In a first step, we aimed to validate the accuracy of the algorithm by comparing it to detections made by expert EEG readers. We then aimed to demonstrate its ability to focus the detections to spikes of increasing prominence. In a third step, we applied this algorithm to detect spikes of increasing prominence and study the relationship between the prominence of spikes and their spatial distribution relative to the seizure onset zone.

2. Methods

2.1. Selection of patients and intracranial EEG segments

This study was approved by the Yale University Human Investigation Committee. Intracranial EEG recordings obtained from 18 adult patients undergoing routine epilepsy surgical evaluation for epilepsy surgery at the Yale-New Haven Hospital between September 2004 and April 2005 were included (see Table 1 for clinical details). One hour of icEEG recording was selected during an artifact-free period of daytime (from noon to 4 pm) obtained from days 2 to 5 of the monitoring. The recordings were removed from clinical seizures by at least 6 h.

Table 1.

Patient characteristics.

Patient # Seizure onset Pathology Follow-up (years) Outcome (Engel class) Nb of clinical seizures Nb of subcliniclal seizures Nb of SOZ contacts Seizure onset type
  1 R Medial Temporal Hippocampal sclerosis 4 4 13 5   1 LVFA/RS
  2 R Inferior Temporal Hippocampal sclerosis 1 2   5 0   3 LVFA
  3 R Inferior Temporal Hippocampal sclerosis 3 4 34 0   2 LVFA/RS
  4 R Anterior Superior Lateral Temporal Reactive gliosis 4 3   5 0   6 RS
  5 L Medial Temporal Hippocampal sclerosis 3 1   5 0   2 LVFA
  6 L Medial Temporal Hippocampal sclerosis 3 1   3 0 11 RS
  7 L Parieto-Occipital Unknown NA NA   3 1   3 RS
  8 L Medial Temporal Unknown NA NA   3 1   1 RS
  9 R Inf Post Temporo-Occipital Unknown NA NA   3 2   3 RS
10 R Parietal Neuronal loss and reactive gliosis 3 1   7 0   5 RS
11 L Medial Occipital Unknown NA NA   3 0   4 LVFA
12 L Superior Parietal Unknown NA NA   8 0   2 LVFA
13 R Parietal Gliosis 3 1   4 0   3 LVFA
14 L Medial Temporal Hippocampal sclerosis 4 1 13 0   1 LVFA
15 L Anterior Medial Frontal Unknown 3 1 10 0   4 LVFA
16 L Post Inf Temporal Hippocampal sclerosis 2 1   3 0   2 LVFA
17 L MT Hippocampal sclerosis 4 3   2 2   1 RD/LVFA
18 R Medial Temporal Heterotopic neurons and reactive gliosis 3 3   3 2   3 LVFA/RS
Open in a new tab

Abbreviations: L = left; R = right; LVFA = low voltage fast activity; RS = repetitive spiking; RD = rhythmic delta; NA = not applicable.

2.2. Intracranial EEG recordings

Intracranial EEG was recorded with commercially available 128-channel long-term icEEG monitoring equipment (Natus/Bio-logic Systems Incorporated, San Carlos, CA). The icEEG was sampled at 256 Hz and archived for subsequent review and analysis. The icEEG was recorded with reference to a peg electrode implanted in the diploic space of the skull at a distance from the icEEG electrodes.

Macroelectrode contacts (Ad-Tech Medical Instrument Corp., Racine, WI) were used in this study. The icEEG electrode placements typically included several subdural strip electrodes with 8–12 contacts and a grid electrode of dimension 8 × 8 contacts. Some patients also received depth electrodes.

Subdural electrodes and depth electrodes were as described previously. (Goncharova et al., 2009) Briefly, intracranial electrode contacts were located from a postimplantation computed tomography (CT) image. The postimplantation CT was then coregistered, first, with a postimplantation magnetic resonance (MR) image using a linear coregistration procedure, and then with a preimplantation MR image using both a linear and nonlinear coregistration procedure.

2.3. Development of the automated detector and validation of its performance

The automated detection algorithm was developed in MATLAB (The MathWorks, Natick, MA, USA) and is summarized in Fig. 1.

Fig. 1.

Fig. 1

Open in a new tab

Summary of the algorithm. Please refer to the text (Section 2) for details.

The approach employed sought to express detection candidate spikes with a single numerical value that reflects its likelihood of being an exemplar spike. In the absence of a consensus definition of intracranial spikes, we decided to base our detection on the time–frequency description of a spike. In the time–frequency plane, a spike corresponds to an edge with power at frequencies greater than 14 Hz (Zaveri et al., 1992). Mindful that a full time–frequency analysis of the multichannel icEEG is computationally intensive, we sought surrogates for this time–frequency description of the spike.

In the initial step of the algorithm, the icEEG is band-pass filtered between 10 and 70 Hz using a zero-phase lag Butterworth filter of order 8. This frequency band has been shown to contain most of the icEEG power of a spike (Zaveri et al., 1992).

Then the Teager energy is computed for each sample point using a 8 ms (−4 to +4 ms; or more precisely a 7.8 ms window defined by the interval between 3 consecutive sample points) window. Teager energy, also known as the Teager-Kaiser energy operator, is a computationally efficient measure that approximates the instantaneous energy of an oscillating signal (Kaiser, 1990). For simple harmonic motions (sine waves), it is quadratic function of both the instantaneous amplitude and the instantaneous frequency of the signal. It is thus well suited to capture the transient burst of energy caused by sharp transients such as spikes, which are characterized by both a sudden increase in amplitude and frequency. It has been applied successfully in various fields, including the detection of high frequency oscillations (Nelson et al., 2006) and seizures (Zaveri et al., 1993). A preliminary study suggested that it might hold value for spike detection (Mukhopadhyay and Ray, 1998).

A detector based on Teager energy only would however display a low specificity, as any transient increase in EEG power would be interpreted as a spike. We thus incorporated two additional parameters, an upslope (U) and a downslope (D) measures, and a temporal relationship between the three measures. The quantification of the upslope is easily derived from the first derivative of the filtered EEG. The computed time series (Ut−8) is shifted forward in time by 8 ms (or more precisely the interval between 3 sample points or −7.8 ms) so U at t = −8 ms is aligned with the Teager energy (Et) value at t = 0 ms. Similarly, a copy of the first derivative time series is inverted and shifted backward in time by 12 ms (or more precisely the interval between 4 sample points or 11.7 ms, given our sampling rate of 256 Hz) so the downslope (Dt+12) at t = +12 ms is aligned with the T value at t = 0 ms and the U value at t = −8 ms.

The choice of the window for Teager energy, and of the time shifts for the upslope and downslope was in part dictated by our sampling rate (256 Hz). Higher sampling rates may allow better temporal resolution and the choice of more precise time values. These values should take into account that spikes may be as short as 20 ms, thus the interval between upslope and downslope should be lower than this value and the window used to calculate the Teager energy should remain shorter than the upslope–downslope interval.

Each sample point in each channel of the initial EEG recording is defined by its instantaneous energy (Et), a preceding upslope (Ut−8 ms) and a following downslope (Dt+12) (Supplementary Fig. S1). These three univariate time series (E, U and D) are computed for each channel and then treated as a single multivariate time series where each channel/time sample is defined by a three-dimensional vector [Et,Ut−8,Dt+12]. We anticipated that points corresponding to spike peaks would exhibit a combination of high E, U and D.

This multivariate distribution is next reduced to a univariate distribution by computing for each channel and time sample the Mahalanobis distance of the vector [Et, Ut−8, Dt+12] to the center of the distribution [μ(E), μ(U), μ(D)], where μ indicates the mean of each distribution. The Mahalanobis distance (Mt) is a scale free measure of distance from a point to the center of a multivariate distribution. It is computed using the covariance matrix of the variables and takes into account the correlation between variables. It can take a null (center of the distribution) or any finite positive value. Higher values of M indicate a greater distance from the center of the distribution and a lower probability that the point belongs to the distribution. Thus time points with simultaneously high values of E, U and D (that correspond to spike peaks) exhibit the greatest M values while most values of Mt (that correspond to the inter-spike background) are close to zero.

The Mahalanobis distance, M, assumes a highly skewed non-Gaussian distribution and a generalized extreme value distribution is more appropriate to compute the parameters of the probability density function of Mt. Within this distribution, spikes are considered outliers and exhibit an Mt value higher than a threshold value that can be derived from the probability density function for any pre-determined statistical thresholds (α values). For the purpose of the study, we heuristically tested nine thresholds ranging from 0.05 (usual threshold value for outlier definition) to 10−5 (last threshold value for which a spike was detected in our sample), but any intermediate statistical threshold can be used. Our assumption was that the prominence of a spike would be directly related to its Mt value and its detection threshold, with more prominent spikes having higher Mt values, thus combining sharper upslope and downslope and higher instantaneous peak energy.

In the final step of the detection, local maxima with an Mt value higher than the specified threshold are detected. The detector uses an algorithm that compares every Mt value higher than the threshold to all surrounding Mt values in the channel of interest and its neighbors within a sphere of radius 5 cm and within a temporal window of 200 ms (±100 ms) duration. To identify all contacts within a 5 cm distance of a contact of interest, inter-electrode Euclidian distances are calculated from the tri-dimensional coordinates of each electrode contact. Each “spike event” consists in the occurrence of spikes in multiple contacts but the algorithm identifies only one local spatio-temporal maximum (with the largest Mt value) within this 200 ms window, corresponding to the most noticeable discharge, and its time and channel of occurrence were indexed. This window accounts for the possible occurrence of polyphasic spikes, which would be detected only once, but was kept short enough so that two closely successive spikes were not considered to be the same event. The possibility that two spikes of equal Mt value occurred in two different contacts was also considered unlikely. Examples of detection are presented in Supplementary Fig. S2.

2.4. Selection of icEEG epochs for validation

We randomly selected ten recordings (including from five patients with mesial temporal lobe epilepsy) out of the 18 recordings available to validate the ability of the algorithm to detect most prominent spikes. For each patient, five electrode contacts defined during the clinical review of the recordings as containing spikes and five uninvolved contacts were selected. Ten contiguous minutes of icEEG recording were selected for this analysis.

2.5. Marking of individual spikes and contacts by expert readers

We developed a graphical user interface in MATLAB to simultaneously display the 10 channels of icEEG at 10 s per screen. Expert readers (NG, MRA and PF) were asked to mark any waveform they would consider to be a spike for clinical purposes. Each reviewer was free to use her/his own criterion of shape, amplitude and duration. In case a spike was visible in multiple channels, reviewers were asked to mark only the channel where the spike was the most noticeable. The time and channel location of these markings were saved independently for each patient and each expert.

2.6. Comparison of automated detection and expert readers and statistical analysis

Expert agreement was defined as instances where two experts out of three marked the same event, within a 100 ms tolerance window. This window accounts for the expected imprecision of the manual marking by the expert and marking of polyphasic spikes. It was kept short enough so that two closely successive spikes were not considered to be the same event. The number of spikes and inter-rater percent agreement for each patient are detailed in Supplementary Table S1. Comparisons were made both for the detection of individual spikes and the identification of electrode contacts where the most prominent spikes occurred, for each of the 9 statistical thresholds.

We defined:

  • –

    true positive (TP) detections when the automatic detections coincided with the reference detections,

  • –

    false positive (FP) detections when automatic detections did not correspond to the reference detections, and

  • –

    false negative (FN) detections when reference detections were not identified by the automatic detector.

True negative (TN) detections were not considered. TN mainly consist of the background against which spikes are detected and thus represent the large majority of the recording. In this regard, we follow the opinion of others that, given their high frequency, they would bias the statistical analysis toward falsely optimistic (high) specificity (Black et al., 2000; Brown et al., 2007).

We thus defined:

  • –

    Sensitivity as the ratio TP/(TP + FN).

  • –

    False detection rate as the ratio FP/(TP + FP).

Both were calculated for individual spikes and for individual electrode contacts, and for each defined statistical threshold.

In addition, we defined accuracy of spike detection as the ratio TP/(TP + FP + FN), in order to more readily compare performance with other published intracranial EEG spike detection algorithms. We also defined a false detection rate per minute by dividing the false spike detection rate by the duration of the recording in minutes. This was performed to provide an estimate of the time burden of having to review false detections. As suggested by others, more than six false detections per minute would nullify the usefulness of any algorithm, because in this case the user would have to review at least as many 10-s EEG epochs as she or he would have without using the detector (Wilson and Emerson, 2002). Given the variability in spike count between patients, these statistics were calculated for each individual patient and then averaged, in order not to overweigh the contribution of records with high spike counts to the average.

2.7. Quantification of the relationship between the most prominent spikes and the seizure onset zone

Each patient recording (one-hour epoch) was divided in six 10-min segments for the analysis, which was performed as described above, with three thresholds (0.01, 0.005 and 0.001). These thresholds were chosen on the basis of the comparison of the automated detector to experts because they encompassed most of the sensitivity range of the automated detector for individual spike detection (13.4%, 55.2% and 68.7%, respectively; Fig. 2A and C).

Fig. 2.

Fig. 2

Open in a new tab

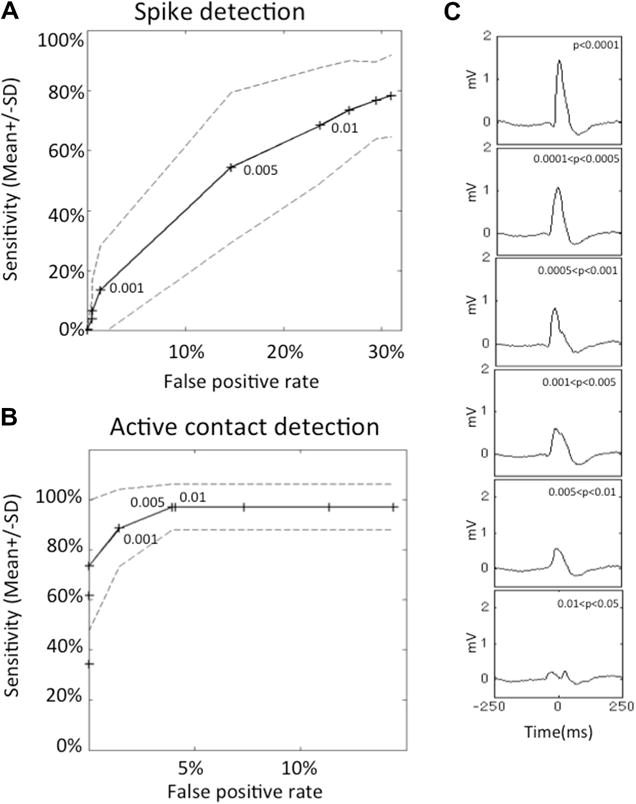
Sensitivity, false positive rate and morphology of interictal spikes detected with different detection thresholds. Receiver operating curves for the detection of spikes (A) and active contacts (B). Sensitivity is displayed as average ± SD as a function of the false positive rate. Points correspond to the following statistical thresholds: 0.05, 0.025, 0.01, 0.005, 0.0025, 0.001, 0.0005, 0.00025, and 0.0001. The 0.01, 0.005 and 0.001 thresholds are indicated. At 0.001, 88 ± 15.4% of contacts were detected while only the 13.4 ± 2.8% most prominent spikes were detected. This suggests that most active contacts can be detected after detection of the most prominent spikes, which correspond to a small fraction of all spikes. These curves were established with the data from 10 patients, with 10 channels per patient and a total of 2454 detections, which were marked by at least two independent experts. (C) Examples of detections arranged by probability of detection. Each graph represents the average of 20 detections with a probability value within the indicated threshold interval (from top to bottom: p < 0.0001; 0.0001 < p < 0.0005; 0.0005 < p < 0.001; 0.001 < p < 0.005; 0.005 < p < 0.01; 0.01 < p < 0.025). Detections corresponding to the most stringent threshold (A) are the most prominent spikes. The change in a single parameter allows the detection of spikes ranging from the most (top) to least (bottom) exemplar spike characteristics. In this patient, detection of spikes with a detection threshold < 0.0001 (first panel) would have allowed the detection of all channels containing the most prominent spikes.

The number of electrode contacts was 118 in all but one patient, who had 113 contacts. The entire set of contacts was used.

The contacts that were part of the seizure onset zone were identified by two independent clinical neurophysiologists and further confirmed in a consensus conference. The pattern of seizure onset was categorized as low voltage fast activity, repetitive spiking and/or rhythmic delta activity.

We quantified the spatial relationship between contacts with prominent spikes and the seizure onset zone in three ways.

First, we calculated the average spike frequency of the five contacts displaying the greatest number of prominent spikes in each of the following regions: inferior temporal, lateral temporal, frontal, parietal, and occipital. As the mesial temporal region is covered by fewer contacts than the other regions, the average spike frequency in that region was calculated over the three contacts that displayed the greatest number of prominent spikes. For each patient, we defined concordance between spiking rate and the seizure onset zone if the region containing the highest spike count was also the region comprising the seizure onset zone. An average concordance was calculated across patients and for the three thresholds.

We also calculated a weighted average distance to give more weight to channels with a higher count of prominent spikes. For each contact comprising prominent spikes, the minimal Euclidian distance between this contact and the closest seizure onset contact was calculated and then multiplied by the number of spikes detected in the one-hour epoch in this contact. This was repeated for every channel containing prominent spikes. These weighted distances were summed and their sum was divided by the total number of prominent spikes detected to give the weighted average distance.

Finally, an overlap between the contacts containing prominent spikes and the seizure onset zone was defined if there was at least one contact in common between the group of contacts containing prominent spikes and the seizure onset zone.

These metrics were calculated for each threshold and compared across thresholds using the Fisher exact test (for the concordance between the region with the highest average spiking rate and the region comprising the seizure onset zone, and the overlap between the contacts containing prominent spikes and the seizure onset zone) or the Kruskal–Wallis test (for the weighted average distance).

3. Results

3.1. Inter-rater agreement of spike and active electrode contact marking

In a first step, we validated the accuracy of the algorithm against a set of spikes identified by expert EEG readers. The number of spikes marked by at least one, and any combination of two expert readers are detailed in Supplementary Table S1. Depending on the patient, between 20.2% and 57.6% of all marked spikes were marked by at least two experts. Between 66.7% and 100% of all channels marked as containing spikes were marked by at least two experts. With the exception of one channel, all these channels belonged to the group of channels that were classified as containing interictal spikes during clinical review.

3.2. Performance of the automated spike detector

The automated detector had an average (±SD) sensitivity of 78.2 ± 16.6% and a false detection rate of 31.0 ± 9.1% at its highest sensitivity threshold (alpha value of 0.05) for the detection of individual spikes (Fig. 2A).

Optimal threshold for each patient as the threshold associated with the best sensitivity while keeping the false detection rate below six false detections per minute (Supplementary Table S1). Using this threshold, which ranged from 0.005 to 0.05, sensitivity ranged from 42.0% to 75.6% (average ± SD of 63.4 ± 11.2%) and accuracy ranged from 21.3% to 66.3% (average ± SD of 48.3 ± 16.2%).

We next hypothesized that by increasing the detection threshold the algorithm would detect a lower number of spikes but that these detections would correspond to more prominent spikes. There was indeed a direct relationship between the statistical threshold at which a transient was detected and its morphology (Fig. 2C): more extreme outliers, detected with a more stringent threshold (i.e., corresponding to higher Mt values and lower p-values), were more prominent spikes than less extreme outliers.

3.3. Performance of the automated detector for active electrode contacts

At its highest sensitivity threshold (alpha value of 0.05), 98.0 ± 7.9% (average ± SD) of the electrode contacts containing the most prominent spikes were detected (Fig. 2B). In fact, all but one contact, in patient 4, were detected. The false contact detection rate was 14.4 ± 16.0% (average ± SD). An intermediate threshold (alpha value of 0.001) yielded an average sensitivity (±SD) of 88.6 ± 15.4% with an average false detection rate (±SD) of 1.4 ± 4.5% (Fig. 2B).

An optimal threshold was defined for each patient, which was associated with the best sensitivity while keeping the false contact detection rate to zero (Supplementary Table S2). Using this threshold, which ranged from 0.0005 to 0.05, sensitivity ranged from 75.0% to 100% (average ± SD of 98.0 ± 7.9%). The associated sensitivity for individual spikes ranged from 12.5% to 71.2% with a false spike detection rate ranging from 0.1 to 1.9 per minute (Supplementary Table S2).

Using the arbitrary threshold of 0.001, which corresponded to optimal specificity for contact detection, only 13.4 ± 2.8% (average ± SD) of individual spikes, albeit the most prominent, would have been detected (Fig. 2C).

3.4. Comparison of the location of most prominent spikes and the seizure onset zone

Finally, we investigated if the distance to the seizure onset zone influenced the time–frequency characteristics of spikes in 18 patients with localization-related epilepsy.

The median number of contacts with spikes and the median spike frequency per contact and per patient are summarized in Table 2. As expected, the number of contacts containing spikes and the number of spikes detected decreased with more stringent thresholds.

Table 2.

Detection of spike and contacts at different sensitivity thresholds.

Thresholds 0.01 0.005 0.001
Number of contacts in the SOZ (median [range]) 3 [1–11]
Number of contacts with prominent spikes (median [range]) 22 [7–104] 12 [1–101] 2 [1–36]
Average prominent spike frequency per contact per hour (median [range]) 53.0 [7.7–352.5] 29.4 [6–313] 13.5 [5–165]
Prominent spike frequency per hour per patient (median [range]) 1374 [53–21,852] 564 [6–12,966] 42 [5–2868]
Open in a new tab

Abbreviation: SOZ = seizure onset zone.

We then studied the spatial distribution of spikes with respect to the seizure onset zone as a function of their prominence. Examples of this distribution for three thresholds are shown in Fig. 3.

Fig. 3.

Fig. 3

Open in a new tab

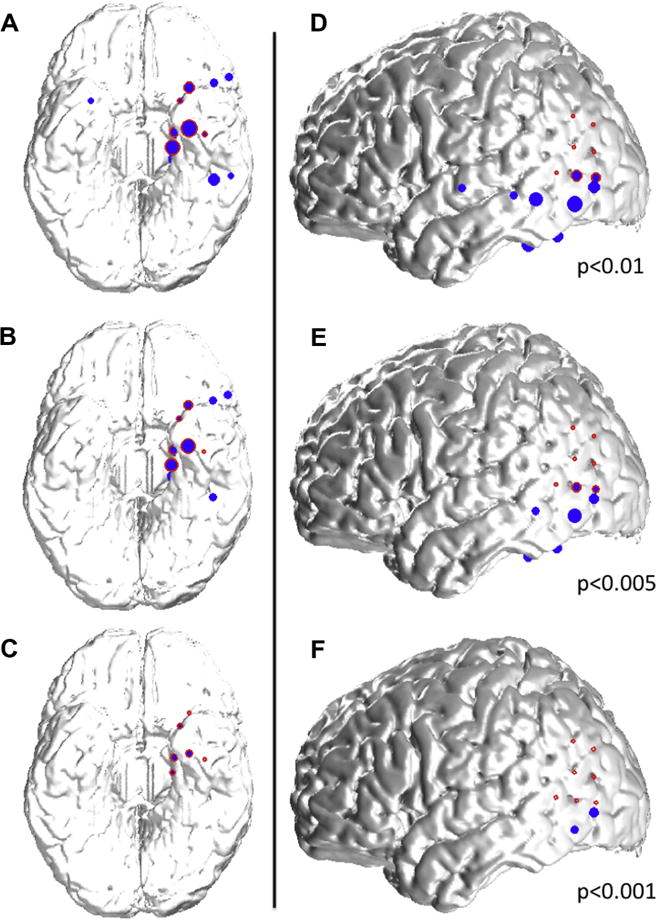
Examples of spatial distribution of detected spikes based on their prominence. (A–C) 39 year-old woman with left mesial temporal lobe epilepsy associated with hippocampal sclerosis. Spikes detected with a 0.01 threshold (A; blue dots) are located in the left inferior and mesial temporal lobes, as well as in the right mesial temporal lobe and the left inferior frontal lobe, and overlap partly with the seizure onset zone (red circles) in the mesial temporal lobe. By increasing the detection threshold (decreasing alpha values to 0.005 (B) and 0.001 (C)), more prominent spikes are detected (please refer to Fig. 2C); the spatial distribution of these spikes is more restricted and in this case confined to the seizure onset zone for the most prominent spikes (C). (D–F) 34-year old woman with left neocortical temporo-parietal epilepsy. Spikes detected with a 0.01 threshold (C; blue dots) are located in the left inferior and lateral temporal lobes, as well as in the left inferior parietal lobe, and overlap partly with the seizure onset zone (red circles) in the temporo-parietal junction. By increasing the detection threshold (decreasing alpha values to 0.005 (E) and 0.001 (F)), more prominent spikes are detected (please refer to Fig. 2C); the spatial distribution of these spikes is more restricted and in this case limited to an area at the border of the the seizure onset zone for the most prominent spikes (F). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Fig. 4A summarizes the concordance between the region with the highest number of spikes and the region comprising the seizure onset zone. This concordance improved with a higher threshold (i.e., when only more prominent spikes were considered). Similarly, the weighted average distance between contacts containing the prominent spikes and the seizure onset zone was lower when more prominent spikes were considered (Fig. 4B). However, these more prominent spikes were less likely to occur within the seizure onset zone as indicated by the significantly lower overlap observed when only more prominent spikes were considered: in only 50% of the cases did the group of contacts containing the most prominent spikes overlap with the seizure onset zone, whereas they overlapped in almost all cases using the least stringent threshold (Fig. 4C). In only three instances were the contacts containing the most prominent spikes confined within the seizure onset zone (Fig. 4B). The weighted average distance was 0–2 cm, 2–4 cm and >4 cm in 5, 5 and 5 cases, respectively.

Fig. 4.

Fig. 4

Open in a new tab

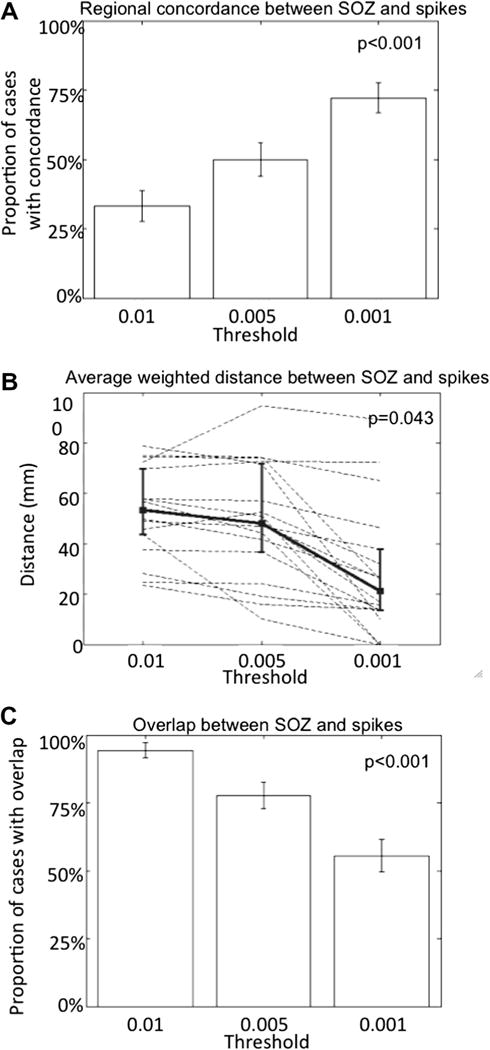
Relationship between spikes and the seizure onset zone. The most prominent spikes are detected close to but not always in the seizure onset zone. (A) The concordance between the region (defined as mesial temporal, inferior temporal, lateral temporal, frontal, parietal or occipital) containing the highest number of prominent spikes and the region comprising the seizure onset zone increases with the detection of only the most prominent spikes. Error bars indicate ±1 standard error of proportion (p < 0.001; one-tailed Fisher exact test). (B) The average distance between contacts containing spikes, weighted for the number of spikes detected by contact, and the seizure onset zone as a function of the prominence of detected spikes: more prominent spikes (detected with more stringent thresholds from 0.01 to 0.001) are closer to the seizure onset zone, as shown by the decreasing average distance. Dashed lines indicate individual cases and the bold line is the group mean; error bars indicate ±1 standard deviation. (p = 0.043; Kruskal–Wallis test). (C) The probability of overlap between the seizure onset zone and the contacts containing the prominent spikes decreases when only the most prominent spikes are detected. Error bars indicate ±1 standard error of proportion (p < 0.001; one-tailed Fisher exact test).

4. Discussion

We have developed a new algorithm for the automated detection of spikes and active intracranial EEG contacts based on their intrinsic time–frequency characteristics. The algorithm defines a spike as a local combined maximum of instantaneous (Teager) energy, upslope and downslope within a fixed spatial and temporal window. The prominence of a spike is reflected by a single statistical metric (Mahalanobis distance) that combines these three characteristics and allows the detection, categorization, and analysis of spikes based on their intrinsic time–frequency characteristics: highest values indicate more prominent spikes with a sharper morphology and a higher amplitude (Fig. 2C). We have shown that the algorithm could achieve good sensitivity for spike detection (Fig. 2A). The detector also achieved excellent performance (98% sensitivity and 3% false positive rate) for the detection of electrode contacts containing spikes (Fig. 2B).

Finally, we have shown that the prominence of a spike correlates with its location relative to the seizure onset zone: more prominent spikes are located close to the seizure onset zone as quantified by the concordance at the regional level and the weighted average distance from spikes to the seizure onset zone. In half of the cases, however, the most prominent spikes do not occur within the seizure onset zone (Fig. 3).

Automated spike detection has been the goal of numerous studies for almost four decades (Gotman and Gloor, 1976; Wilson and Emerson, 2002). Only a few, however, addressed the specific problem of spike detection in icEEG (Dümpelmann and Elger, 1999; Valenti et al., 2006; Brown et al., 2007; Barkmeier et al., 2012) of which three have reported on the accuracy of such detectors in detail (Dümpelmann and Elger, 1999; Brown et al., 2007; Barkmeier et al., 2012). Although comparison of algorithms tested on different data sets should be approached with caution, our method compares favorably to these prior attempts (Dümpelmann and Elger, 1999; Brown et al., 2007) (Barkmeier et al., 2012).

Our statistical approach directly translates essential time–frequency descriptors of a spike (upslope, peak energy and downslope) (Gotman and Gloor, 1976; Emerson et al., 1995; Adjouadi et al., 2005) into a single scale-free value that expresses the degree to which a sample point distinguishes itself from the background. The selection of different thresholds for this single parameter results in the detection of spikes ranging from those that are exemplar to those that are less so (Fig. 2C). The use of the Mahalanobis distance (as opposed to Euclidian distance) in this regard is justified because it is scale-free (it does not require normalization of each univariate distribution), it takes into account correlations between individual variables, and it is sensitive to multivariate outliers (De Maesschalck et al., 2000).

Our algorithm also takes advantage of the properties of the generalized extreme value distribution. This type of distribution is widely used to model phenomena where extreme and rare events arise. Examples of applications can be found in finance, meteorology, hydrology and biosignal processing (Roberts, 2000). These extreme values are strong outliers and, if not accounted for, can have a significant impact on central tendency (mean) and dispersion parameters (variance, standard deviation) and penalize detection based on normalization of the data.

Previous attempts of quantitative analysis of spikes in long-term icEEG recordings are few. They have focused on the analysis of spike frequency (Hufnagel et al., 2000; Asano et al., 2003, 2008; Marsh et al., 2010), amplitude (Hufnagel et al., 2000; Asano et al., 2003), latency (Hufnagel et al., 2000; Asano et al., 2003) and propagation (Hufnagel et al., 2000). Of note, three of these studies involved children with cortical dysplasia (Asano et al., 2003, 2008; Marsh et al., 2010). Our population consisted of adults patients with diverse pathology and is closer to the mixed population included in the fourth study (Hufnagel et al., 2000). Two studies reported a close relationship between leading spikes, spikes of highest amplitude and the seizure onset zone: the leading spikes and spikes of highest amplitude occurred within 2 cm of the seizure onset zone in 84% and 75% of the cases, respectively (Hufnagel et al., 2000) and within the seizure onset zone in 98% and 77% of the cases, respectively (Asano et al., 2003). These analyses were performed manually, which limits their clinical applicability. The data regarding spike frequency is more contradictory with the contacts with the highest spike count correlating with the seizure onset zone in slightly more than half of the cases in two studies (Hufnagel et al., 2000; Marsh et al., 2010) and almost all cases in the third (Asano et al., 2003).

Our data support the view that prominent spikes, or spikes of higher amplitude, originate from a region at the border of the seizure onset zone, which sometimes, but not always overlap with it.

We have recently shown that although the spatial distribution of spike rates is strongly associated with the location of the seizure onset zone, the region with the highest spike rate coincides with this zone in half of the patients only (Goncharova et al., 2013). This previous analysis did not take into account the time–frequency characteristics of spikes. Our new findings indicate that spikes with different time–frequency characteristics exhibit different spatial relationships to the seizure onset zone and further suggest that the quantitative analysis of morphological, spatial and frequency characteristics of spikes may provide complementary information for the identification of the seizure onset zone. Ideally, this analysis should be combined to the analysis of spike propagation patterns (Lai et al., 2007), of the distribution of other biomarkers of the seizure onset zone, such as high-frequency oscillations (Jacobs et al., 2010; Blanco et al., 2011; Wang et al., 2013).

We note the following limitations to our work. In its current form, the algorithm requires human intervention to determine its optimal threshold. We believe that this is not a major drawback as the determination of this optimal threshold can be performed in a stepwise manner and the user receives an output for each decrement in the threshold. The user can also consider groups of spikes based on their detection threshold and/or each channel independently.

The EEG data we used were acquired using standard icEEG electrodes, which have an inter-contact distance of 1 cm (center-to-center). It is thus possible that, due to this limited spatial resolution, we underestimated the degree of overlap between the seizure onset zone and the prominent spikes. This limitation was also present in previous studies (Hufnagel et al., 2000; Asano et al., 2003; Marsh et al., 2010) and does not affect our conclusion that prominent spikes occur mostly at the border of the seizure onset zone.

A sampling rate of 256 Hz is likely to cause distortion of fast EEG transients including spikes. A higher sampling rate should improve the time–frequency analysis of spikes and alter both the detection and quantification.

The representation of spikes in the algorithm was based only on three parameters (the energy of its peak, its upslope and its downslope) bound within a spatio-temporal frame. It has been proposed that the accurate description of a spike requires a more complex set of parameters to approach perfect behavior of an automated detector (Wilson and Emerson, 2002). Additional features, which remain to be identified but could include the presence of superimposed high-frequency oscillations (Wang et al., 2013), could be added to the current algorithm. This should prove relatively simple as the multivariate statistical approach we utilize and the Mahalanobis distance lend themselves to the incorporation of additional variables. Finally, given the greater accuracy of the algorithm to detect active contacts, a two-step approach could be envisioned. Active contacts would be detected first with a stringent threshold. In a second time, individual spikes would be detected within selected contacts, using a more relaxed threshold.

Supplementary Material

Supp data1
Supp figure 1
Supp figure 2

HIGHLIGHTS.

  • Individual interictal spikes can be described by their time–frequency characteristics.

  • An automated algorithm can detect and rank spikes by order of prominence.

  • Most prominent spikes are accurately identify the lobe of the seizure onset.

  • They occur within 2 cm of the seizure onset zone in half of the cases.

Acknowledgments

We wish to acknowledge the support of the C.G. Swebilius Trust.

N.G. is the recipient of a Postdoctoral Research Fellowship from the Epilepsy Foundation of America.

M.R.A., P.F., I.I.G., and H.P.Z. have nothing to disclose.

Appendix A. Supplementary data

Supplementary data associated with this article can be found, in the online version, at http://dx.doi.org/10.1016/j.clinph.2013.10.021.

References

  1. Adjouadi M, Cabrerizo M, Ayala M, Sanchez D, Yaylali I, Jayakar P, et al. Detection of interictal spikes and artifactual data through orthogonal transformations. J Clin Neurophysiol. 2005;22:53–64. doi: 10.1097/01.wnp.0000150880.19561.6f. [DOI] [PubMed] [Google Scholar]
  2. Asano E, Muzik O, Shah A, Juhasz C, Chugani DC, Sood S, et al. Quantitative interictal subdural EEG analyses in children with neocortical epilepsy. Epilepsia. 2003;44:425–34. doi: 10.1046/j.1528-1157.2003.38902.x. [DOI] [PubMed] [Google Scholar]
  3. Asano E, Juhasz C, Shah A, Sood S, Chugani HT. Role of subdural electrocorticography in prediction of long-term seizure outcome in epilepsy surgery. Brain. 2008;132:1038–47. doi: 10.1093/brain/awp025. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Barkmeier DT, Shah AK, Flanagan D, Atkinson MD, Agarwal R, Fuerst DR, et al. High inter-reviewer variability of spike detection on intracranial EEG addressed by an automated multi-channel algorithm. Clin Neurophysiol. 2012;123:1088–95. doi: 10.1016/j.clinph.2011.09.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Black MA, Jones RD, Carroll GJ, Dingle AA, Donaldson IM, Parkin PJ. Real-time detection of epileptiform activity in the EEG: a blinded clinical trial. Clin Electroencephalogr. 2000;31:122–30. doi: 10.1177/155005940003100304. [DOI] [PubMed] [Google Scholar]
  6. Blanco JA, Stead M, Krieger A, Stacey W, Maus D, Marsh E, et al. Data mining neocortical high-frequency oscillations in epilepsy and controls. Brain. 2011;134:2948–59. doi: 10.1093/brain/awr212. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Brown MW, Porter BE, Dlugos DJ, Keating J, Gardner AB, Storm PB, et al. Comparison of novel computer detectors and human performance for spike detection in intracranial EEG. Clin Neurophysiol. 2007;118:1744–52. doi: 10.1016/j.clinph.2007.04.017. [DOI] [PubMed] [Google Scholar]
  8. De Maesschalck R, Jouan-Rimbaud D, Massart DL. The Mahalanobis distance. Chemometr Intell Lab Syst. 2000;50:1–18. [Google Scholar]
  9. Dümpelmann M, Elger CE. Visual and automatic investigation of epileptiform spikes in intracranial EEG recordings. Epilepsia. 1999;40:275–85. doi: 10.1111/j.1528-1157.1999.tb00704.x. [DOI] [PubMed] [Google Scholar]
  10. Emerson RG, Turner CA, Pedley TA, Walczak TS, Forgione M. Propagation patterns of temporal spikes. Electroencephalogr Clin Neurophysiol. 1995;94:338–48. doi: 10.1016/0013-4694(94)00316-d. [DOI] [PubMed] [Google Scholar]
  11. Goncharova II, Zaveri HP, Duckrow RB, Novotny EJ, Spencer SS. Spatial distribution of intracranially recorded spikes in medial and lateral temporal epilepsies. Epilepsia. 2009;50:2575–85. doi: 10.1111/j.1528-1167.2009.02258.x. [DOI] [PubMed] [Google Scholar]
  12. Goncharova II, Spencer SS, Duckrow RB, Hirsch LJ, Spencer DD, Zaveri HP. Intracranially recorded interictal spikes: relation to seizure onset area and effect of medication and time of day. Clin Neurophysiol. 2013;124:2119–28. doi: 10.1016/j.clinph.2013.05.027. [DOI] [PubMed] [Google Scholar]
  13. Gotman J, Gloor P. Automatic recognition and quantification of interictal epileptic activity in the human scalp EEG. Electroencephalogr Clin Neurophysiol. 1976;41:513–29. doi: 10.1016/0013-4694(76)90063-8. [DOI] [PubMed] [Google Scholar]
  14. Hufnagel A, Dümpelmann M, Zentner J, Schijns O, Elger CE. Clinical relevance of quantified intracranial interictal spike activity in presurgical evaluation of epilepsy. Epilepsia. 2000;41:467–78. doi: 10.1111/j.1528-1157.2000.tb00191.x. [DOI] [PubMed] [Google Scholar]
  15. Jacobs J, Zijlmans M, Zelmann R, Chatillon C-E, Hall J, Olivier A, et al. High-frequency electroencephalographic oscillations correlate with outcome of epilepsy surgery. Ann Neurol. 2010;67:209–20. doi: 10.1002/ana.21847. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Kaiser JF. On a simple algorithm to calculate the ‘energy’ of a signal. Proceedings of ICASSP. 1990:381–4. [Google Scholar]
  17. Lai Y, van Drongelen W, Hecox K, Frim D, Kohrman M, He B. Cortical activation mapping of epileptiform activity derived from interictal ECoG spikes. Epilepsia. 2007;48:305–14. doi: 10.1111/j.1528-1167.2006.00936.x. [DOI] [PubMed] [Google Scholar]
  18. Marsh ED, Peltzer B, Brown MW, Wusthoff C, Storm PB, Litt B, et al. Interictal EEG spikes identify the region of electrographic seizure onset in some, but not all, pediatric epilepsy patients. Epilepsia. 2010;51:592–601. doi: 10.1111/j.1528-1167.2009.02306.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Mukhopadhyay S, Ray GC. A new interpretation of nonlinear energy operator and its efficacy in spike detection. IEEE Trans Biomed Eng. 1998;45:180–7. doi: 10.1109/10.661266. [DOI] [PubMed] [Google Scholar]
  20. Nelson R, Myers SM, Simonotto JD, Furman MD, Spano M, Norman WM, et al. Detection of high frequency oscillations with Teager energy in an animal model of limbic epilepsy. Conf Proc IEEE Eng Med Biol Soc. 2006;1:2578–80. doi: 10.1109/IEMBS.2006.259694. [DOI] [PubMed] [Google Scholar]
  21. Roberts SJ. Extreme value statistics for novelty detection in biomedical data processing. IEE Proc Sci Meas Technol. 2000;147:363–7. [Google Scholar]
  22. Valenti P, Cazamajou E, Scarpettini M, Aizemberg A, Silva W, Kochen S. Automatic detection of interictal spikes using data mining models. J Neurosci Methods. 2006;150:105–10. doi: 10.1016/j.jneumeth.2005.06.005. [DOI] [PubMed] [Google Scholar]
  23. Wang S, Wang IZ, Bulacio JC, Mosher JC, Gonzalez-Martinez J, Alexopoulos AV, et al. Ripple classification helps to localize the seizure-onset zone in neocortical epilepsy. Epilepsia. 2013;54:370–6. doi: 10.1111/j.1528-1167.2012.03721.x. [DOI] [PubMed] [Google Scholar]
  24. Wilson SB, Emerson R. Spike detection: a review and comparison of algorithms. Clin Neurophysiol. 2002;113:1873–81. doi: 10.1016/s1388-2457(02)00297-3. [DOI] [PubMed] [Google Scholar]
  25. Zaveri HP, Williams WJ, Iasemidis LD, Sackellares JC. Time-frequency representation of electrocorticograms in temporal lobe epilepsy. IEEE Trans Biomed Eng. 1992;39:502–9. doi: 10.1109/10.135544. [DOI] [PubMed] [Google Scholar]
  26. Zaveri HP, Williams WJ, Sackellares JC. Energy based detection of seizures. Annual International Conference of the IEEE Engineering in Medicine and Biology Society; USA. 1993. pp. 363–4. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supp data1
NIHMS826396-supplement-Supp_data1.docx (26.3KB, docx)
Supp figure 1
NIHMS826396-supplement-Supp_figure_1.jpg (106.1KB, jpg)
Supp figure 2
NIHMS826396-supplement-Supp_figure_2.jpg (119.6KB, jpg)

RESOURCES