Abstract
Little is known about what the economic crisis has done to health disparities by income. We apply a decomposition method to unravel the contributions of income growth, income inequality and differential income mobility across socio-demographic groups to changes in health disparities by income in Spain using longitudinal data from the Survey of Income and Living Conditions (SILC) for the period 2004–2012. We find a modest rise in health inequality by income in Spain in the five years of economic growth prior to the start of the crisis in 2008, but a sharp fall after 2008. The drop mainly derives from the fact that loss of employment and earnings has disproportionately affected the incomes of the younger and healthier groups rather than the (mainly stable pension) incomes of the over 65s. This suggests that unequal distribution of income protection by age may reduce health inequality in the short run after an economic recession.
Keywords: economic crisis, health inequality, Spain
1. Introduction
The Great Recession that started in 2008 was for most OECD countries the worst economic contraction since the 1930s (Jenkins et al, 2013). While falling incomes and rising unemployment have been the most visible consequence of the crisis, an additional concern is whether any effects have been unequally spread across the income distribution.
The importance of studying inequalities, both in income and other dimensions, is widely appreciated. While the European Union has targeted health inequality reduction as a key policy goal and warned of “the negative consequences for health, social cohesion and economic development if health inequalities are not effectively tackled” (European Commission, 2009, p. 5), the crisis has interfered with the execution of some of these policies (European Commission, 2013).
The aim of this paper is to examine what has happened to the social gradient in health before and after the crisis. We focus on Spain, one of the EU countries confronted with a severe economic recession, and employ a decomposition method that has been used to examine the evolution of income, health and inequality during a period of rapid growth in China (Baeten et al, 2013). We use new EU Statistics on Income and Living Conditions (SILC) panel data spanning the period 2004–2012, including both a period of substantial economic growth (2004–2007) as well as of recession (2009–2012). We examine the extent to which the evolution of health disparities by income was associated with changes in income growth, in income inequality and in differential income mobility of various socio-demographic groups.
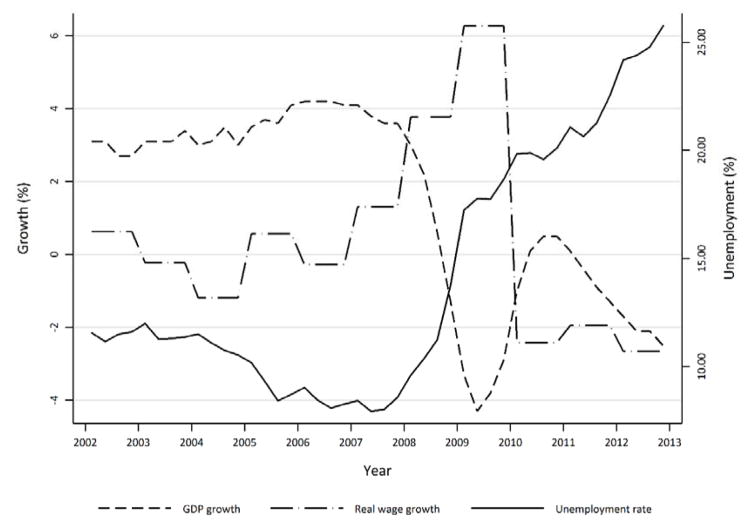
The economic growth pattern in Spain since the mid–1990s can be summarized by a pre-crisis trend and a post-crisis trend. Figure 1 shows the evolution of unemployment (right axis), and GDP growth and real average annual wage growth (left axis) between 2002 and 2013. Prior to the crisis, the country experienced extended economic expansion with real GDP growing at approximately 3% per year and unemployment falling below 8% in 2007. Despite this extended period of labour demand, wage growth was minimal (Carrasco et al, 2011).
Figure 1. Unemployment and GDP growth in Spain.
Source: GDP growth & unemployment data: Instituto National de Estadística (http://www.ine.es/prensa/pib_tabla_cntr.htm). Wage growth data: OECD data (https://stats.oecd.org/Index.aspx?DataSetCode=AV_AN_WAGE)
The effects of the global financial crisis become obvious in Spain beginning in 2008: when GDP growth fell from 3% to below −3% between the first quarter of 2008 and the first quarter of 2009, while unemployment roughly doubled in the same period. Youth unemployment became particularly high, with unemployment in the 15–24 age group doubling between 2007 and 2009 to stand at more than 35% (OCED, 2009). Males, who were overrepresented in highly cyclical forms of employment, were hit disproportionally (Rica & Rebollo-Sanz, 2015). Jenkins et al (2013) reaches similar conclusions, noting that the largest fall in employment in Spain during the crisis period was concentrated among young people under the age of 25, especially young men.2
Particularly important to understanding both the boom and bust years in Spain is the expansion and collapse of the housing market. The nominal house price per square meter in Spain tripled between 1997 and 2007 (Bonhomme & Hospido, 2012). Parallel to this housing boom was an expansion in the construction sector. Between 1998 and 2008 the share of construction in Spain’s GDP increased by 4 percentage points to 10.7% (Gonzalez & Ortega, 2009). From 1997 to 2006 the share of construction in male employment rose from 14% to more the 20% (Bonhomme & Hospido, 2012). However, in 2008 as the effects of the subprime mortgage crisis in America spread and Europe began to enter recession, the Spanish housing sector crashed. Most of the sharp rise in unemployment in Spain was due to the collapse of this sector. From the first quarter of 2008 till the last quarter of 2009, construction experienced a 20% per annum drop in employment (Bentolila et al, 2012).3
Alongside the changes in average levels of income there have been changes in its distribution. In general, income inequality in Spain has followed a counter-cyclical pattern – during boom years income inequality decreased while during bust years it rose (Lacuesta and Izquierdo, 2012; Carrasco et al, 2011; Pijoan-Mas & Sanchez-Marcos, 2010). Bonhomme and Hospido (2012) show that the housing and construction sector is once again key to understanding these trends as the construction sector is one of the main employers of young, uneducated, relatively disadvantaged groups of (usually) men (Aparicio, 2010).
A separate question is the extent to which the Great Recession has affected health. There is a large literature that documents that worsening economic conditions are associated with reduced mortality (e.g. Ruhm, 1996; Stuckler et al, 2009), but more recent evidence is mixed. Rhum (2015) suggests that the relationship may be disappearing over time, while others have found that mortality trends, except for suicides, continued to improve during the recent European-wide recession (Regidor et al, (2014); OECD, 2014).
There is little evidence on the evolution of health inequalities during the recent crisis.4 Most observers appear to assume that it will widen existing gaps following reductions in welfare spending that increase the vulnerability of those with lower education levels, who are also more likely to be unemployed (European Commission, 2013).
One strand of literature has focused on the comparison of income-related health inequalities (IRHI) across countries and over time. Van Doorslaer and Koolman (2004), for instance, documented the variation in degrees of IRHI for 13 EU countries in 1996 and showed that IRHI tends to be larger in countries with larger income inequality, but also that the relative income position of Europeans that are not working and not in good health, like the retired and the disabled, was critical. Van Ourti et al (2009) decomposed the evolution of IRHI between 1994 and 2001 for the same 13 EU countries. They found that the income elasticity of health was crucial for understanding the evolution of IRHI, although the period considered was one of economic growth for most European countries. An extended version of this decomposition was used by Baeten et al (2013) to decompose the evolution of IRHI in China into the contributions of various factors like income growth, income inequality, and income mobility, as well as a number of regional-demographic factors associated with health. They found that the substantial rise in IRHI over the period of double-digit income growth (1991–2006) was associated with rising income inequality, but especially with the adverse health and income experience of older women lacking pension or other social protection. It is this decomposition method that we use in this paper.
Our findings indicate the following: inequality in health by income was slightly rising before the crisis, but started falling sharply after 2009 when the recession hit Spain. The main reason for this reversal is the differential effect of the crisis on the incomes of young and old Spaniards: while pensioner incomes were relatively shielded against the erosion in the post-crisis years, this does not hold for the incomes of younger groups. Loss of employment and of earnings in employment meant that these relatively healthier groups moved downwards in the income ranking, thereby lowering the association between health and income rank. As a result, IRHI in 2012 was lower than in the years prior to 2009, a somewhat surprising by-product of an otherwise discomforting period in recent Spanish history.
2. Decomposing the evolution of IRHI with a balanced cohort
We use the decomposition method of Baeten et al. (2013) to estimate the evolution of IRHI and to shed light on the relative importance of (1) income growth, (2) the evolution of income inequality, (3) income mobility, and (4) the evolution in non-income factors (such as demographics) that are associated with health. This section describes the decomposition approach for a balanced cohort of individuals that we observe at the start (period 1) and end (period 2) of a time interval.
2.1 Choice of health inequality index
We use the corrected concentration index (CC) (Erreygers, 2009) because it satisfies the mirror condition and it is insensitive to equal health additions (cf. absolute inequality) (Erreygers and Van Ourti 2011). When health is bounded between 0 and 1, it can be written as:
| (1) |
where ht and yt are the health and income distribution in period t = 1,2, hit describes the health of individual i and zit is a weight that depends on the income rank of individual i. This weight takes the value 0 for the individual with median income, and increases (decreases) linearly for individuals with higher (lower) than median income levels.5
Descriptive model for health
We use a simple descriptive6 model that links health linearly and additively to its associated factors:
| (2) |
where α is an intercept parameter; θ(yit) is a non-linear function of income; xit represents a vector of K non-income variables (e.g. demographics), and β is its associated parameter vector.7 It is important to allow for a very general functional form for θ( ) since the actual functional form will largely determine the relative importance of the contribution of (a) income growth and (b) income inequality in our decomposition approach.
2.2 Evolution of IRHI over time
Our interest lies in decomposing changes in IRHI. Combining equation (2) and (1) leads to8:
| (3a) |
| (3b) |
Equation (3a–b) shows that we can disentangle the change in IRHI into a part due to changes in the association between the income rank and the income effect (zi2 θ(yi2) − zi1θ(yi1)) and a part due to changes in the association between the income rank and the non-income factors (zi2x′i2 − zi1x′i1). In order to isolate the contributions of (a) income growth, (b) the evolution of income inequality, (c) income mobility, and (d) the evolution in non-income factors, we construct two hypothetical health states in period 2 using equation (2) – health under average income growth ( ) and health under no income growth ( ). For the former, we calculate an individual’s health in period 2 in the scenario that everyone’s income changed proportionally to the average income gain (or loss) between period 1 and period 2. We denote this income as . For the latter, we estimate an individual’s health in period 2 in the scenario that there was no income change between period 1 and period 2 ( ). In each scenario we allow all non-income variables to change as they actually did.
2.3 Decomposition method
Given that and , the change in IRHI can be expressed as:
| (4) |
which can be further disentangled as the sum of 4 terms (note that ):
| (5) |
Equation (5) shows that the evolution of IRHI can be written as the sum of (a) average income growth, (b) the evolution of income inequality, (c) income mobility, and (d) the evolution in non-income factors.
The first term, average income growth, captures the change in IRHI when everyone’s income changes in proportion to the average income change. As all incomes grow proportionally, there is no change in the rankings (zit’s). Therefore this term captures whether the health responsiveness to proportional income changes ( ) is, on average, larger or smaller for those with lower (negative zi1) versus higher incomes (positive zi1) in period 1. If the health responsiveness is larger for the initially richest part of the population, then this term will be positive. The sign (and magnitude) of this term depends on the functional form of θ( ), but also on whether incomes have increased or decreased on average.
The second term captures the evolution of income inequality – that is, the health difference attributed to the difference between the true income in the second period and the income under the scenario of average income growth ( ). If the health returns from income growth are increasing with income (θ′ (.) >0), if there is no income re-ranking (zi2 = zi1) and if – relative to the average income growth scenario – the rich become richer while the poor loose, then the second term will be positive. In a scenario with income re-ranking, one cannot a priori assign a direction to term 2.
Term 3 – ‘income mobility’ – captures the association between income re-ranking (zi2 − zi1) and the non-income factors in the second period, weighted by the βk coefficients. One can further decompose term 3 into separate contributions for each non-income variable since term 3 is additively separable. In our empirical application, the non-income variables are dummy variables. In this case, the contribution of each non-income dummy can be large (compared to the reference category) because (a) health is considerably higher or lower among the individuals belonging to the non-income dummy (βk), (b) income re-ranking is substantial for these individuals ((zi2 − zi1), and/or (c) a substantial share of the sample belongs to this non-income dummy ( ).
Term 4 measures the association between changes in non-income factors and initial income ranks. If the non-income factors include age and location, then term 4 isolates the effect of ageing and migration on the change of IRHI. For example, if many people with high initial income ranks migrate to a location which is associated with better health then this term will be positive. In what follows we refer to the terms 1, 2, 3 and 4 as income growth, income inequality, income mobility, and non-income factors.
3. Data and empirical implementation
EU-SILC data
We use 6 rounds of the Spanish EU-SILC dataset spanning 2004–2012. It includes the period before and during the financial and economic crisis that affected Spain from 2009 onwards. As the EU-SILC dataset is set up as a rotating panel every year between 2004 and 2009, a new random sample is drawn and followed for 4 years, after which it is dropped. We use the term ‘rotation group’ for each of these random samples. For example, the first rotation group is drawn in 2004 and lasts till 2007; the second covers 2005–2008; and the sixth and last rotation group covers 2009–2012. Hence, for the full period of 2004–2012 we have 6 rotation groups in total, and these constitute different and independent samples.9 In total, we have 122,592 observations (see table I for more details).
Table I.
Overview of the different rotation groups, Spanish EU-SILC, 2004–2012
| Rotation group | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 2004 |
|
|||||
| 2005 |

|
|||||
| 2006 |

|
|||||
| 2007 |

|
|||||
| 2008 |

|
|||||
| 2009 |

|
|||||
| 2010 | ||||||
| 2011 | ||||||
| 2012 | ||||||
3.1 Key variables
The two main variables of interest are self-assessed health (SAH) and household income. The SAH responses derive from the question: “How is your health in general? Is it: (1) very good, (2) good, (3) fair, (4) bad, (5) very bad?” As our income variable we use total disposable household income during the previous 12 months. We adjust for household size and inflation by dividing by the square root of household size10 and by applying the Spanish CPI index with base year 2012. We remove observations with negative incomes.11
3.2 Estimating the health model
We estimate the model for health in equation (2) using an interval regression (with threshold values imposed as in van Doorslaer and Jones (2003)), as the CC computation requires a health indicator measured on a cardinal scale.12 The predicted values are used as our main health indicator, and can be interpreted as predicted health utility index (HUI) scores (Van Doorslaer and Jones, 2003).13 We use a second degree polynomial for the income function φ(yit) as it is a parsimonious functional form that is sufficiently flexible to avoid predetermining the effect of proportional income changes on health.14 The remaining independent variables are dummy variables for each region in Spain and age category dummies for both males and females. The regions are listed in Table IV(b). Age is categorised into the following groups: 16 to 26 years, 26 to 36 years, 36 to 46 years, 46 to 56 years, 56 to 66 years, 66 to 76 years, 66 to 76 years, and more than 76 years of age.
Table IV (b).
Region factors influencing term 3
| Variable | Coefficient | Share of individuals in region category (%) | Re-ranking coefficienta,b | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
|||||||||
| Rotation 1 | Rotation 4 | Rotation 6 | ||||||||
| 2004 | 2007 | 2007 | 2010 | 2009 | 2012 | 2004–2007 | 2007–2010 | 2009–2012 | ||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | |
| Region | ||||||||||
| Madrid | Reference | 4.13 | 4.14 | 13.14 | 13.3 | 12.22 | 12.28 | 0.0455* | −0.025 | −0.00799 |
| Galicia | −0.0267*** | 7.7 | 7.7 | 7.27 | 7.32 | 6.43 | 6.43 | −0.00405 | 0.023 | 0.00503 |
| Asturias | −0.0048 | 3.36 | 3.35 | 3 | 2.98 | 2.71 | 2.7 | 0.00533 | 0.00578 | 0.00896 |
| Cantabria | 0.00449 | 0.9 | 0.9 | 1.28 | 1.29 | 1.44 | 1.42 | 0.0148* | −0.0149 | −0.00627 |
| País Vasco | 0.0023 | 3.69 | 3.63 | 3.66 | 3.67 | 3.94 | 3.95 | −0.00055 | 0.0417*** | 0.0148 |
| Navarra | 0.00135 | 2.01 | 2.01 | 1.65 | 1.65 | 1.3 | 1.3 | 0.00288 | −0.00156 | 0.02* |
| La Rioja | −0.000513 | 0.83 | 0.83 | 0.69 | 0.69 | 0.88 | 0.96 | 0.00146 | 0.00245 | −0.00226 |
| Aragón | −0.000675 | 3.44 | 3.41 | 3.36 | 3.35 | 3.23 | 3.23 | −0.00034 | 0.0285** | 0.0261* |
| Castilla y León | −0.0012 | 7.13 | 7.29 | 6.5 | 6.49 | 6.39 | 6.31 | 0.00815 | 0.0133 | 0.00948 |
| Castilla-La Mancha | −0.000617 | 4.74 | 4.67 | 4.89 | 4.82 | 5.17 | 5.2 | −0.0287** | −0.0122 | −0.0146 |
| Extremadura | 0.00203 | 3.54 | 3.42 | 2.7 | 2.7 | 2.75 | 2.82 | −0.0152* | 0.0274*** | 0.0113 |
| Cataluña | 0.000396 | 16.9 | 16.9 | 15.09 | 14.93 | 15.12 | 15.19 | −0.0153 | −0.0109 | 0.0144 |
| Valenciana | −0.00439 | 12.6 | 12.69 | 10.11 | 10.13 | 12.44 | 12.22 | 0.0222 | −0.0620*** | −0.0222 |
| Baleares | 0.00554* | 2.28 | 2.25 | 2.19 | 2.19 | 1.92 | 1.87 | −0.00624 | 0.0171 | 0.0133 |
| Andalucía | −0.00871*** | 18.36 | 18.47 | 17.44 | 17.41 | 16.33 | 16.39 | 0.0128 | 0.0306* | −0.015 |
| Murcia | −0.00974*** | 4.52 | 4.46 | 3.11 | 3.18 | 3.41 | 3.41 | −0.0123 | −0.022 | −0.0267 |
| Ceuta y Melilla | −0.0148*** | 0.29 | 0.29 | 0.24 | 0.24 | 0.27 | 0.27 | 0.0052 | −0.00152 | −0.0028 |
| Canarias | −0.0119*** | 3.57 | 3.57 | 3.7 | 3.68 | 4.06 | 4.06 | −0.0298*** | −0.0344* | 0.012 |
Re-ranking coefficient refers to a no-constant regression where change in rank is regressed on the regional variables in the final period
The coefficients are jointly significant for the 2004–2007 and 2007–2010 model, while they are only jointly significant at the 0.10 level for the 2009–2012 model.
p<0.05,
p<0.01,
p<0.001
3.3 Empirical implementation of decomposition method
Because of the rotating design of EU-SILC we cannot directly compare IRHI measured for the same individuals in 2004 and 2012. This complicates both the implementation of the decomposition and the estimation of the empirical health model. The decomposition requires at least two observations of the same individual over time. We apply the decomposition to each of the 6 rotation groups separately and within each rotation group to a balanced panel only.15 While we calculate the decomposition for each of the 6 rotating panels, we only present three of these: a before crisis group: 2004–2007; a group covering both before and when the crisis occurs: 2007–2010; and a group that covers the crisis period: 2009–2012.16
We first pool the data from all 6 rotation groups and run the interval regression model described above.17 We remove the individuals belonging to the top 1% of incomes (calculated on the full pooled sample) as these observations have a disproportionate effect on the functional form of income.18 The estimated parameters of the pooled model are then used to decompose the 3 rotation groups which span the entire 2004–2012 period, leaving us with the observations per rotation group as shown in table II. Each of the rotating panels uses a different base year. In the 2004–2007 rotation group, we first compare the change in IRHI for 2004–2005, then 2004–2006, then 2004–2007. We next take the second rotation group (which spans 2007–2010) and compare the change in IRHI between 2007 and each following year. For the 2009–2012 rotation group, 2009 is the base year. In total there are then 9 changes of IRHI to be decomposed.
Table II.
Balanced panel observations per rotation group
| Rotation group | Waves covered | Individuals per wave | Total observations per rotation group |
|---|---|---|---|
| 1 | 2004–2007 | 4,193 | 16,772 |
| 2 | 2005–2008 | 4,996 | 19,984 |
| 3 | 2006–2009 | 5,099 | 20,396 |
| 4 | 2007–2010 | 5,575 | 22,300 |
| 5 | 2008–2011 | 5,617 | 22,468 |
| 6 | 2009–2012 | 5,168 | 20,672 |
| 122,592 |
Source: EU-SILC
We use the sample weights of the first year of each rotating panel provided with the EU-SILC data. In the interval regression model, we also allow for robust standard errors and cluster at the individual level. Statistical inference of the decomposition method is obtained after bootstrapping the entire procedure with 1,500 replications. The bootstrap sampling is bias-corrected, and clustered at the primary sampling unit of the EU-SILC.
4. Results
4.1 Summary statistics
Table III displays variable means for each wave of rotation group 1, 4 and 6. Panel (a) includes variables most important to the analysis, whereas panel (b) provides additional background information on the labour market. The health variable refers to the predicted HUI score.
Table III.
Summary statistics
| (a)
|
(b)
|
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Rotation | Wave | Household Incomea | Ageb | Female | Health | Labour Market Statusc
|
Gini | ||||
| Employed | Self- Employed | Unemployed | Other | Disabled | |||||||
|
|
|
||||||||||
| 1 | 2004 | €23,962.08 | 47.2 | 53.10% | 0.886 | 41.00% | 7.40% | 8.00% | 25.80% | 2.00% | 0.31 |
|
|
|
||||||||||
| 1 | 2005 | €25,156.27 | 48.3 | 53.10% | 0.884 | 41.10% | 8.30% | 7.70% | 24.40% | 2.40% | 0.31 |
|
|
|
||||||||||
| 1 | 2006 | €25,602.62 | 49.3 | 53.10% | 0.883 | 42.60% | 8.10% | 6.10% | 24.20% | 1.90% | 0.30 |
|
|
|
||||||||||
| 1 | 2007 | €26,056.85 | 50.2 | 53.10% | 0.881 | 42.60% | 8.00% | 6.30% | 22.80% | 2.10% | 0.30 |
|
|
|
||||||||||
| 4 | 2007 | €27,554.90 | 46.7 | 51.30% | 0.888 | 46.50% | 6.50% | 6.00% | 24.20% | 2.10% | 0.28 |
|
|
|
||||||||||
| 4 | 2008 | €28,775.31 | 47.6 | 51.30% | 0.886 | 46.00% | 6.90% | 7.40% | 21.70% | 2.40% | 0.29 |
|
|
|
||||||||||
| 4 | 2009 | €29,900.84 | 48.5 | 51.30% | 0.883 | 42.70% | 6.50% | 11.70% | 19.80% | 2.80% | 0.29 |
|
|
|
||||||||||
| 4 | 2010 | €28,475.24 | 49.5 | 51.30% | 0.881 | 41.4 | 6.50% | 12.30% | 19.90% | 3.20% | 0.30 |
|
|
|
||||||||||
| 6 | 2009 | €29,912.82 | 47.5 | 51.30% | 0.885 | 40.10% | 6.80% | 11.60% | 23.30% | 2.80% | 0.29 |
|
|
|
||||||||||
| 6 | 2010 | €28,798.27 | 48.4 | 51.30% | 0.882 | 38.80% | 6.60% | 13.50% | 21.10% | 3.40% | 0.30 |
|
|
|
||||||||||
| 6 | 2011 | €27,366.47 | 49.4 | 51.30% | 0.88 | 39.00% | 5.90% | 12.00% | 21.70% | 3.20% | 0.30 |
|
|
|
||||||||||
| 6 | 2012 | €26,425.08 | 50.4 | 51.30% | 0.878 | 37.10% | 6.00% | 14.90% | 20.10% | 3.20% | 0.31 |
Source: EU-SILC. Weighted means calculated on balanced sample of rotation group 1, 4 & 6.
In 2010 Euros.
The yearly ageing of the balanced sample does not always equal one since survey months differed slightly from wave to wave.
Refers to current self-reported labour market status; ‘employed’ includes full- and part-time workers, while ‘other’ includes students, ‘domestic tasks’, and other ‘inactive’ persons.
Income is rising in each successive year for rotation group 1, as well as rotation group 4 until 2009. As income refers to the last 12 months, the drop observed in 2010 refers to an income fall in 2009, during which Spain was fully immersed in the economic crisis. In rotation group 6 income falls in each wave compared to the last. The effect of the crisis is also visible in the occupational category changes. The proportion unemployed in 2009 almost doubles from the previous year to approximately 11%. In subsequent years the proportion of employed individuals decreases every year. This does not appear to be due to ageing and retiring individuals; while the proportion of retirees does increase slightly, it is the unemployed category that shows the sharpest increase.
Income inequality, as measured by the Gini coefficient was rather stable, although opposite trends can be observed before and after 2009. Income inequality appears to have been slightly falling during the “boom” years, and began to increase once the crisis started. This is in line with the findings of others, such as Jenkins et al (2013).
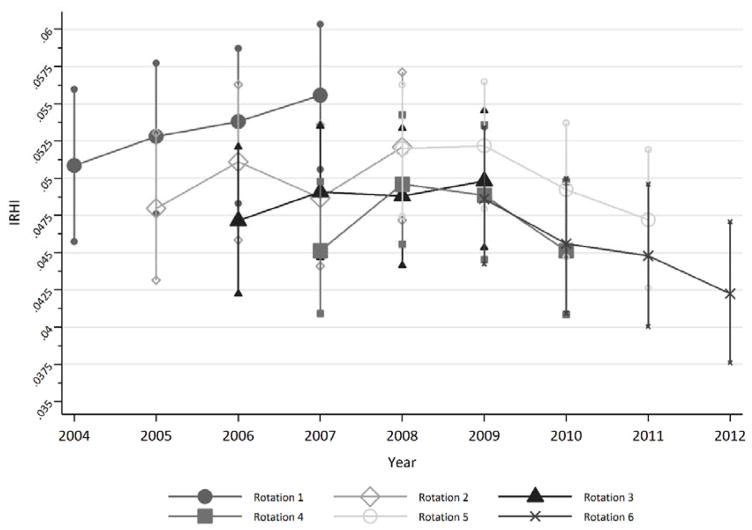
Figure 2, with the CC per year for each rotation group, shows that IRHI has not been stationary over the sample period.19,20 Until 2009, there is a slightly significant upward trend.21 Since the beginning of the crisis, however, IRHI fell quite steeply. This is confirmed by comparatively large and significant falls in IRHI in the final two rotation groups.
Figure 2. IRHI per wave per rotation group.
Source: EU-SILC. Bars indicate 95% confidence intervals.
Column 1 of table IV a–b shows the coefficients from the interval regression for the age-sex and region dummies.22,23 Note that older age groups consistently report lower health than younger. Regional health differences, by contrast, are very small. Figure 3 shows decomposition results for rotation groups 2004–2007, 2007–2010 and 2009–2012 with 95% confidence intervals.
Table IV (a).
Age/sex factors influencing term 3
| Variable | Coefficient | Share of individuals in age-sex category (%) | Re-ranking coefficienta,b | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
|||||||||
| Rotation 1 | Rotation 4 | Rotation 6 | ||||||||
| 2004 | 2007 | 2007 | 2010 | 2009 | 2012 | 2004–2007 | 2007–2010 | 2009–2012 | ||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | |
| Female | ||||||||||
| 16–26 | Reference | 6.21 | 3.75 | 6.03 | 3.93 | 5.4 | 3.53 | 0.0152 | 0.0347 | −0.0049 |
| 26–36 | −0.0146*** | 8.81 | 8.19 | 9.27 | 8.41 | 8.98 | 8 | 0.000912 | −0.0143 | −0.023 |
| 36–46 | −0.0286*** | 11.12 | 10.92 | 10.05 | 9.98 | 9.66 | 9.37 | 0.0106 | −0.012 | −0.00803 |
| 46–56 | −0.0515*** | 8.65 | 9.55 | 8.4 | 9.27 | 8.65 | 9.28 | −0.00071 | −0.00066 | −0.00675 |
| 56–66 | −0.0816*** | 7.05 | 7.64 | 6.71 | 7.01 | 7.83 | 7.83 | −0.00994 | −0.0181 | 0.00274 |
| 66–76 | −0.114*** | 6.52 | 6.4 | 5.82 | 6.19 | 5.27 | 6.22 | −0.00335 | 0.00199 | 0.0279* |
| 75+ | −0.156*** | 4.75 | 6.67 | 5.02 | 6.5 | 5.49 | 7.03 | −0.00251 | 0.028** | 0.0354*** |
| Male | ||||||||||
| 16–26 | 0.00117 | 5.97 | 4.11 | 5.98 | 3.94 | 6.12 | 4.45 | 0.0141 | 0.0272 | −0.00259 |
| 26–36 | −0.0125*** | 8.29 | 7.29 | 10.76 | 9.81 | 9.47 | 7.87 | 0.015 | 0.00154 | −0.0222 |
| 36–46 | −0.0272*** | 10.01 | 9.81 | 10.28 | 10.39 | 9.78 | 10.47 | −0.00444 | −0.0163 | −0.0199 |
| 46–56 | −0.0407*** | 8.22 | 8.9 | 7.79 | 8.69 | 8.45 | 8.78 | 0.00478 | −0.00821 | −0.0138 |
| 56–66 | −0.0667*** | 6.53 | 7.12 | 5.97 | 6.38 | 7.19 | 7.61 | −0.0136 | −0.00323 | −0.00266 |
| 66–76 | −0.0853*** | 5.21 | 5.79 | 4.9 | 5.09 | 4.55 | 4.98 | −0.0129 | 0.00211 | 0.0286* |
| 75+ | −0.118*** | 2.65 | 3.87 | 3.03 | 4.4 | 3.17 | 4.55 | −0.00728 | 0.0256* | 0.0352** |
Re-ranking coefficient refers to a no-constant regression where change in rank is regressed on the demographic variables in the final period
The coefficients are not jointly significant for the 2004–2007 model, while they are for the 2007–2010 and 2009–2012 model.
p<0.05,
p<0.01,
p<0.001
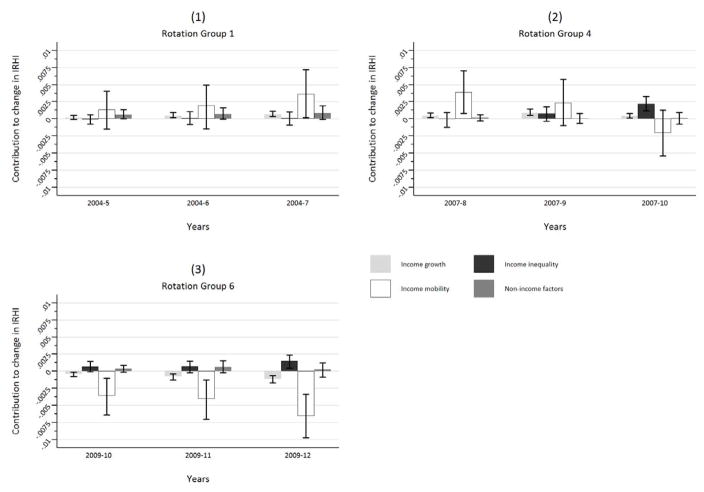
Figure 3.
Main decomposition results (bars indicate 95% confidence intervals)
2004–2007 results
Between 2004 and 2007, IRHI rose significantly. Panel (1) of figure 3 shows that income growth is important in understanding this rise. The income growth term, although small, indicates that health responsiveness to proportional income growth was larger for those with higher income in 2004. Despite being the largest term in all years, income mobility only becomes significant in the 2004–2007 comparison. This implies that income re-ranking occurring prior to 2007 was not systematically related to age, gender or location, while the elderly were on average (and just borderline significantly) more likely to experience negative income re-ranking between 2004 and 2007.24 As the elderly combine this move down the income ladder with the lowest predicted health, this led to a rise in IRHI. The evolution of income inequality and the non-income factors are unimportant for the IRHI change in this period.
2007–2010 Results
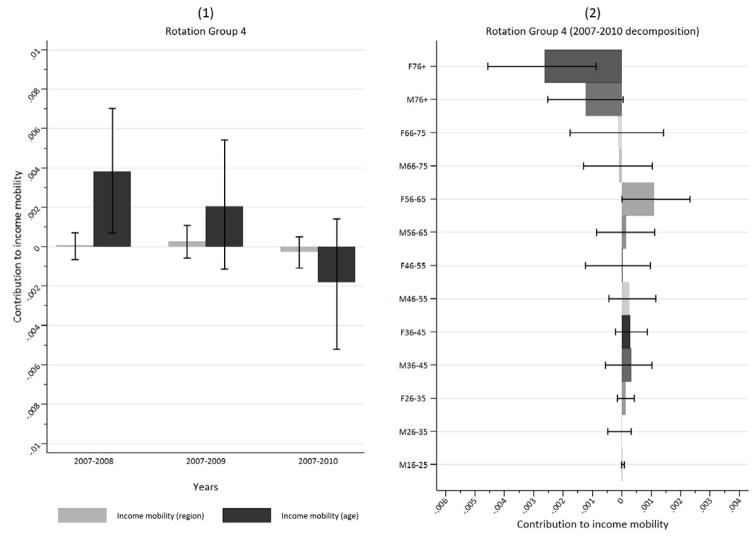
IRHI grew significantly between 2007 and 2008, but returned in the subsequent two years to its 2007 level. The decreasing trend turns out to be almost entirely driven by the changing association between the age dummies and the income rank, while region is relatively unimportant (see income mobility term in panel (2) of figure 3 and panel (1) of figure 4). Closer inspection reveals that it is mainly influenced by the older, unhealthier, age groups. While initially, during the period of income growth prior to 2008, the elderly were falling in income rank, there is a reversal after 2008. Panel (2) of figure 4 shows that this was especially true for those over 75. The income rank of the older age groups, with poorer health, increased contributing to the fall in IRHI.
Figure 4.
Decomposition of income mobility for rotation group 4 (bars indicate 95% confidence intervals)
Also significant between 2007 and 2010 is the contribution of income inequality. This suggests that the health effects of income gains – over and above proportional income growth – led to a rise in IRHI. Income growth is positive in each wave and remains small but significant. As average income falls in the final 2010 wave, so does the magnitude of income growth.
2009–2012 Results
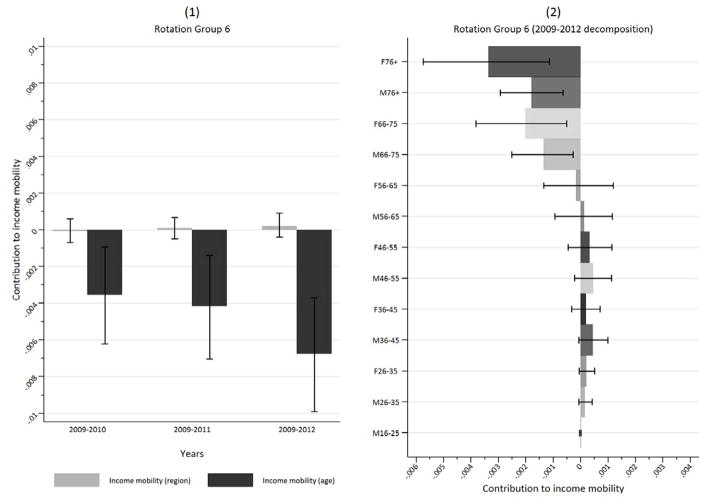
The final 4-year rotation group of the EU-SILC entirely reflects the crisis years. This is the period in which the largest drop in IRHI occurs and the trends observed in the 2007–2010 decomposition also emerge here. The significant fall in IRHI is primarily due to income mobility, which is largest in magnitude and significant in all years. Panels (1) and (2) of figure 5 demonstrate that it is the experience of certain older age groups – men and women aged 66 and above – which is the largest contributor to the decrease. By contrast, the younger and healthier individuals have a small but positive contribution. This leads to a fall in IRHI as those with poorer health became relatively richer.
Figure 5.
Decomposition of income mobility for rotation group 6 (bars indicate 95% confidence intervals)
The 2009–2012 decomposition also reveals that both income growth and income inequality are significant drivers in the change of IRHI. The negative sign of income growth reflects the fact that had the average income fall between 2009 and 2012 been applied to everyone, those with high incomes would have had a larger fall in health than those with low incomes. Income inequality is positive however, indicating that the fall in income was disproportionately felt by the poor. Still, the overall effect of these terms relating to health responsiveness to income is small compared to income mobility.
5. Discussion
The decomposition results reveal two very different trends in IRHI before and after the crisis. Prior to 2009 there was a trend of increasing inequality which was mostly driven by income growth but also by income mobility, with the elderly slightly moving down on the income ranks. After the start of the 2008 financial crisis we observe a sharp fall in IRHI. Income mobility is the main driver of this change: young and middle-aged healthier groups experienced a greater income drop, while on average the incomes of the elderly were less affected. This caused shifts in the income ranks in favour of the older, less healthy group, leading to a decrease in IRHI.
Further decomposing the contribution of each regional-demographic group to income mobility reveals the relative importance of three distinct underlying mechanisms. Indeed, each sub-term depends on three elements – the partial association between the group and health (βk), the number of individuals in that particular group, and the changes in income ranks between the two periods for these individuals (zi2 − zi1). Any changes in income mobility result from some combination of these elements. Table IV(a) and (b) presents results for each of these three elements per demographic group and region.
Column 1 reports the interval regression coefficients and Columns 2 to 7 the percentage shares of each regional-demographic group for the first and final years of each rotation group, while columns 8 to 10 report the income re-ranking for each regional-demographic group. The results for income re-ranking are obtained by running a simple no-constant OLS using the regional-demographic variables as explanatory variables for the change in individual z-scores between the two periods.25 A positive coefficient implies a rise in income rank between the two periods.
Table IV(a) confirms that the income re-ranking of the elderly, in particular after the onset of the crisis, is most important for understanding changes in IRHI due to income mobility. Between 2004 and 2007, there was little re-ranking taking place, although the negative coefficients for the elderly indicate that, if anything, the elderly were slightly losing relative to young. In the final rotation group however the coefficients of the 65+ have become highly significant and switched sign. This, combined with the comparatively large negative coefficient of the 65+ in the health regression, and the sizable and increasing number of individuals in this category, leads to a large fall in income related health inequality.26
The primary reason that the elderly’s incomes were better protected during the crisis appears to be the old-age pension system. In Spain, the vast majority of pensioners receive their incomes from contributory pensions based on earnings prior to retirement (OECD, 2013). As a consequence, current economic conditions have little immediate effect on retiree incomes. Moreover, any potential changes to pension benefits are delayed by political processes and reforms are not applied retrospectively. Thus, in spite of a series of reforms that took place during the last decade in Spain, existing pensioners’ incomes have remained relatively untouched.27
5.1 Role of labour market status and occupation
Our results thus far indicate that the pre-crisis rise and post-crisis fall in IRHI were largely related to differential income mobility. In this section we explore how income mobility is associated with labour market status and occupation.28
Again, we use OLS regression to analyse the correlation between labour market status and changes in the income ranks (see Table V). Prior to the crisis (column 1), we do not see that the changes in the z-scores are not significantly different across labour market states (except for the self-employed), but during the crisis years (column 2) every group, except the employed and unemployed, on average, moves up in the income ranking. Interestingly, the self-employed, the group with the greatest drop in the income ranks between 2004 and 2007, has gained the most after 2009. The retired and disabled groups also experienced gains, both of which receive “sticky” benefits that were not immediately affected by current economic conditions.
Table V.
Labour Market Status / Occupational re-ranking
| Variable | Re-ranking coefficienta,b | |||
|---|---|---|---|---|
|
| ||||
| 2004–2007 | 2009–2012 | 2004–2007 | 2009–2012 | |
| (1) | (2) | (3) | (4) | |
| Labour Market Status | ||||
| Employed | 0.00472 | −0.0142* | - | - |
| Self Employed | −0.0324*** | 0.0447*** | - | - |
| Unemployed | 0.0109 | −0.0675*** | - | - |
| Other | 0.00397 | 0.0152* | - | - |
| Retired | −0.00679 | 0.0287*** | - | - |
| Disabled | 0.000519 | 0.0287 | - | - |
| Occupation | ||||
| Managers | - | - | −0.0222 | 0.0658*** |
| Military | - | - | 0.0553 | 0.0136 |
| Professionals | - | - | 0.00953 | 0.0155 |
| Technicians | - | - | −0.0197 | 0.025 |
| Clerks | - | - | −0.00476 | −0.0314 |
| Service & Sales | - | - | 0.0263** | 0.00399 |
| Agricultural | - | - | −0.0217 | −0.0513 |
| Trade | - | - | −0.012 | −0.0245 |
| Machine Operators | - | - | −0.00249 | −0.0286 |
| Elementary Occupation | - | - | −0.00456 | −0.0452** |
Re-ranking coefficient refers to a no-constant regression where change in rank is regressed on economic status/occupation in the first period
The coefficients are jointly significant for the all models, except for the 2004–2007 occupation regression, where they are only jointly significant at the 0.10 level.
p<0.05,
p<0.01,
p<0.001
Columns 3 and 4 repeat the exercise for employed individuals only to examine differences between occupations for those employed in the first wave of each rotation group, (in 2004 and 2009). We do not observe large differences in re-rankings across occupations in the pre-crisis years (column 3), but during the crisis years (column 4), all occupation groups fell relative to the Manager group. The largest significant drop occurs in the Elementary Occupation group, which contains manufacturing, mining and construction labourers. These findings are in line with previous evidence showing that it was those in the construction sector whose incomes fell the most after the onset of the crisis in Spain (Bentolila et al, 2012).
6. Conclusion
We examine the evolution of IRHI in Spain both before and during the Great Recession, and decompose IRHI changes into four separately interpretable terms, reflecting the contribution of (i) income growth, (ii) income inequality changes, (iii) income mobility and (iv) changes in non-income terms. Our findings are as follows.
First, while our approach only informs on health changes resulting from changes in the explanatory variables, our findings suggest that health inequality by income in Spain was rising in the four years of economic growth prior to the start of the crisis, but this rise was modest. By contrast, after 2008, it started falling at a faster pace. Second, there appear to be two reasons for this modest rise in IRHI prior to 2008 – income growth and to a lesser extent income mobility – suggesting that the health benefits associated with income growth were disproportionately concentrated amongst the already rich; and that the elderly, often in poorer health, fell slightly on the income ranks leading to increased disparities. Third, the falling health disparities by income mainly derived from the uneven distribution of the income consequences of the crisis. The incomes of younger, healthier groups were affected much more by rising unemployment than the incomes of the over 65s which mainly consist of pensions. Since contributory pensions are ‘sticky’ in Spain and therefore relatively unaffected in the first years of the crisis, pensioners improved their relative position in the income distribution substantially. Fourth, we study the role of labour market participation status and occupation and find that, in line with others studies, it was primarily the income deterioration of the unemployed and the employed, especially those in the construction sector, that was responsible for their fall in the income ranking.
While the great recession caused a substantial deterioration in income, health policy makers can perhaps take solace in the fact that the Spanish pension system - at least in the short run - appears to have shielded some of the most vulnerable individuals. The EU has devoted special attention to reducing health inequalities and for decades countries have attempted to reduce pervasive and persistent health disparities in periods of economic growth. Ironically, our study reveals that the recent crisis has perhaps done more to cut back inequality than many years of pro-poor health policy making. This may be somewhat surprising, given the initial predictions of many observers and in light of media reports of crises hitting the most vulnerable population segments first. But in reality it can be understood as a logical outcome in the presence of sticky pensions and other welfare benefits in the immediate aftermath of a financial crisis. While employment rates and earnings levels are less protected in the short run, also pension and other benefits may be curtailed in the longer run as a consequence of fiscal constraints. It also remains to be seen whether the post-crisis evolution of income-related health inequality has been similar in other European countries with less sticky pension and other benefits.
Acknowledgments
We would like to acknowledge the helpful comments and suggestions given by two anonymous referees. Pilar García-Gómez is a Postdoctoral Fellows of the Netherlands Organisation for Scientific Research—Innovational Research Incentives Scheme—Veni. Eddy Van Doorslaer and Tom Van Ourti acknowledge support from the National Institute on Ageing, under grant R01AG037398. We thank Eurostat for providing access to the EU-SILC data. We thank Dennis Petrie, Helena Hernández, seminar participants at Erasmus University Rotterdam, XXXIII Jornadas AES in Santander, 2015 iHEA Congress in Milan, Workshop on consequences of the economic crisis on health and health care systems in Madrid for further useful comments and suggestions. The usual caveats apply, and all remaining errors are our responsibility.
10. Appendices
Table AI.
IRHI change within rotation groups
| Rotation Group | IRHI Change | ||
|---|---|---|---|
| 2004–2007 | 2004–2005 | 2004–2006 | 2004–2007 |
| 0.0019 | 0.0030 | 0.0047* | |
| 2005–2008 | 2005–2006 | 2005–2007 | 2005–2008 |
| 0.0031* | 0.00071 | 0.0041* | |
| 2006–2009 | 2006–2007 | 2006–2008 | 2006–2009 |
| 0.0019* | 0.0016 | 0.0027* | |
| 2007–2010 | 2007–2008 | 2007–2009 | 2007–2010 |
| 0.00447* | 0.0037* | −0.00001 | |
| 2008–2011 | 2008–2009 | 2008–2010 | 2008–2011 |
| 0.00193 | −0.00273 | −0.00478* | |
| 2009–2012 | 2009–2010 | 2009–2011 | 2009–2012 |
| −0.003* | −0.0038* | −0.0064* | |
Source: EU-SILC,
p < 0.05.
Table AII.
Decomposition results for rotation group 1
| 2004 –2005 | 2004–2006 | 2004–2007 | |
|---|---|---|---|
|
|
|||
| IRHI change | 0.00196 | 0.00339 | 0.00483 |
| Income growth | 0.00011 | 0.00065 | 0.00084 |
|
| |||
| Income inequality | −0.00016 | 0.00003 | −0.00008 |
| Income mobility | 0.0014 | 0.00216 | 0.00354 |
| Non-income factors | 0.00061 | 0.00073 | 0.00094 |
| Individual Contribution | Income mobility | Non-inc. factors | Income mobility | Non-inc. factors | Income mobility | Non-inc. factors |
|---|---|---|---|---|---|---|
| M 16–26 | −0.00001 | 0 | −0.00002 | 0 | 0.00001 | 0 |
| F 26–36 | −0.00022 | 0.00018 | −0.00012 | 0.00012 | −0.00004 | 0.00025 |
| M 26–36 | 0.00002 | 0.00016 | −0.00026 | 0.00036 | −0.00016 | 0.00047 |
| F 36–46 | −0.00006 | 0.00008 | 0.00011 | −0.00014 | −0.00051 | −0.00007 |
| M 36–46 | −0.00008 | −0.00028 | −0.00025 | −0.00063 | 0.00015 | −0.00076 |
| F 46–56 | 0.00076 | −0.00065 | 0.00008 | −0.00069 | 0.00013 | −0.00102 |
| M 46–56 | −0.00032 | 0.00013 | 0.00015 | 0.00034 | −0.00019 | 0.00026 |
| F 56–66 | 0.00014 | −0.00064 | 0.00027 | -0.00097 | 0.00075 | -0.00158 |
| M 56–66 | 0.00062 | −0.00068 | −0.00033 | −0.00145 | 0.00097 | −0.00177 |
| F 66–76 | −0.00022 | 0.00021 | 0.00102 | −0.00032 | 0.00038 | −0.00113 |
| M 66–76 | 0.00045 | −0.00015 | 0.00094 | −0.00043 | 0.00097 | −0.00083 |
| F 75+ | 0.00012 | 0.00165 | −0.00027 | 0.00313 | 0.00038 | 0.00495 |
| M 75+ | 0.00023 | 0.0006 | 0.00049 | 0.00143 | 0.00052 | 0.00215 |
| Galicia | −0.00012 | 0 | 0.00043 | 0 | 0.00028 | 0.00004 |
| Asturias | −0.00001 | 0 | −0.00001 | 0 | −0.00002 | 0 |
| Cantabria | 0.00002 | 0 | 0.00002 | 0 | 0.00002 | 0 |
| País Vasco | 0 | 0 | 0 | 0 | 0 | 0.00001 |
| Navarra | 0.00001 | 0 | 0.00001 | 0 | 0 | 0 |
| La Rioja | 0 | 0 | 0 | 0 | 0 | 0 |
| Aragón | 0 | 0 | 0 | 0 | 0 | 0 |
| Castilla y León | −0.00002 | 0 | −0.00001 | 0 | −0.00002 | 0 |
| Castilla-La Mancha | 0.00001 | 0 | 0 | 0 | 0.00001 | 0 |
| Extremadura | 0 | 0 | −0.00002 | 0 | −0.00002 | 0 |
| Cataluña | 0 | 0 | 0 | 0 | −0.00001 | 0 |
| Comunidad Valenciana | 0.00001 | −0.00001 | 0.00002 | −0.00001 | −0.00012 | −0.00001 |
| Baleares | −0.00003 | −0.00001 | −0.00005 | 0 | −0.00002 | 0.00001 |
| Andalucía | −0.00021 | 0.00001 | −0.0002 | −0.00001 | −0.00021 | 0 |
| Murcia | 0.00015 | 0 | −0.00002 | −0.00001 | 0.0001 | −0.00001 |
| Ceuta y Melilla | −0.00002 | 0 | −0.00003 | 0 | −0.00002 | 0 |
| Canarias | 0.00018 | 0 | 0.00023 | −0.00002 | 0.00021 | −0.00002 |
Madrid, F 16–26 and Employed used as control groups
Table AIII.
Decomposition results for rotation group 4
| 2007–2008 | 2007–2009 | 2007–2010 | |
|---|---|---|---|
|
|
|||
| IRHI change | 0.00487 | 0.00413 | 0.00014 |
| Income growth | 0.00078 | 0.00135 | 0.00078 |
| Income inequality | 0.00017 | 0.00081 | 0.00205 |
| Income mobility | 0.00374 | 0.00215 | −0.00217 |
| Non-income factors | 0.00018 | 0.00006 | 0.00007 |
| Individual Contribution | Income mobility | Non-inc. factors | Income mobility | Non-inc. factors | Income mobility | Non-inc. factors |
|---|---|---|---|---|---|---|
| M 16–26 | 0 | −0.00002 | 0.00001 | −0.00001 | 0.00001 | −0.00002 |
| F 26–36 | −0.00015 | −0.0001 | 0.00002 | 0 | 0.00012 | 0.00002 |
| M 26–36 | −0.00045 | −0.00003 | −0.00029 | 0.00002 | 0 | 0.00011 |
| F 36–46 | −0.0003 | 0.00005 | 0.00007 | 0 | 0.00018 | −0.00015 |
| M 36–46 | 0.00027 | −0.00015 | 0.00031 | −0.00028 | 0.00023 | −0.00054 |
| F 46–56 | 0.00086 | −0.00018 | −0.00013 | −0.00019 | 0.00017 | 0.00008 |
| M 46–56 | 0.00026 | −0.0002 | 0.00032 | 0.00011 | 0.0004 | −0.00006 |
| F 56–66 | 0.00068 | 0.00027 | 0.00048 | −0.00022 | 0.00091 | −0.00094 |
| M 56–66 | 0.00053 | −0.00016 | 0.00037 | −0.0003 | 0.00012 | −0.00065 |
| F 66–76 | 0.0008 | −0.00097 | 0.00151 | −0.00137 | −0.00026 | −0.00103 |
| M 66–76 | 0.00058 | −0.00032 | 0.00077 | −0.00129 | −0.00012 | −0.00124 |
| F 75+ | 0.00006 | 0.00134 | −0.00121 | 0.002 | −0.00243 | 0.00257 |
| M 75+ | 0.0005 | 0.00066 | −0.00029 | 0.0016 | −0.00116 | 0.00196 |
| Galicia | 0.00013 | −0.00003 | 0.00012 | 0.00001 | −0.00044 | −0.00002 |
| Asturias | 0.00001 | 0 | 0.00002 | −0.00001 | −0.00001 | 0 |
| Cantabria | 0 | 0 | −0.00001 | 0 | −0.00002 | 0 |
| País Vasco | 0.00003 | 0 | 0.00005 | 0 | 0.00004 | 0 |
| Navarra | 0 | 0 | 0 | 0 | 0 | 0 |
| La Rioja | 0 | 0 | 0 | 0 | 0 | 0 |
| Aragón | 0 | 0 | −0.00001 | 0 | −0.00001 | 0 |
| Castilla y León | 0.00001 | 0 | −0.00001 | 0 | −0.00002 | 0 |
| Castilla−La Mancha | 0 | 0 | 0.00001 | 0 | 0 | 0 |
| Extremadura | 0.00001 | 0 | 0.00002 | 0 | 0.00001 | 0 |
| Cataluña | 0.00001 | 0 | 0 | 0 | −0.00001 | 0 |
| Comunidad Valenciana | 0.00009 | 0 | 0.00015 | −0.00001 | 0.00019 | −0.00001 |
| Baleares | 0.00002 | 0 | 0.00004 | 0 | 0.00002 | 0 |
| Andalucía | −0.00028 | 0.00001 | −0.00033 | 0.00001 | −0.0003 | 0.00001 |
| Murcia | 0.00002 | 0.00001 | 0.00008 | 0.00001 | 0.00008 | 0.00001 |
| Ceuta y Melilla | 0.00001 | 0 | 0.00001 | 0 | 0 | 0 |
| Canarias | 0.00004 | 0 | 0.00006 | −0.00003 | 0.00012 | −0.00004 |
Madrid, F 16–26 and Employed used as control groups
Table AIV.
Decomposition results for rotation group 6
| 2009–2010 | 2009–2011 | 2009–2012 | |
|---|---|---|---|
|
|
|||
| IRHI change | −0.00244 | −0.00367 | −0.00643 |
| Income growth | −0.00043 | −0.00119 | −0.00182 |
| Income inequality | 0.00097 | 0.00103 | 0.00153 |
| Income mobility | −0.0033 | −0.00385 | −0.00611 |
| Non-income factors | 0.00032 | 0.00059 | 0.00029 |
| Individual Contribution | Income mobility | Non-inc. factors | Income mobility | Non-inc. factors | Income mobility | Non-inc. factors |
|---|---|---|---|---|---|---|
| M 16–26 | 0.00001 | 0 | 0 | 0 | 0 | 0 |
| F 26–36 | −0.00006 | 0.00015 | 0.00007 | 0.00032 | 0.00018 | 0.00051 |
| M 26–36 | 0.00016 | 0.00007 | 0.00009 | 0.00013 | 0.00011 | 0.00021 |
| F 36–46 | 0.00013 | −0.00006 | 0.00007 | −0.00011 | 0.00023 | −0.00042 |
| M 36–46 | 0.00038 | −0.00003 | −0.00002 | 0.00003 | 0.00042 | 0.00004 |
| F 46–56 | 0.00033 | −0.00029 | 0.00031 | −0.00002 | 0.00031 | −0.00015 |
| M 46–56 | 0.00025 | −0.00018 | 0.00029 | −0.00032 | 0.0004 | −0.00046 |
| F 56–66 | −0.00102 | −0.00037 | −0.00044 | −0.00173 | −0.00012 | −0.00214 |
| M 56–66 | −0.00033 | 0.00017 | 0.00083 | −0.00032 | 0.00022 | −0.00073 |
| F 66–76 | −0.00015 | −0.00026 | −0.00142 | −0.00051 | −0.00191 | −0.00076 |
| M 66–76 | −0.00013 | −0.00095 | −0.00043 | −0.0014 | −0.00118 | −0.00166 |
| F 75+ | −0.00215 | 0.00121 | −0.00223 | 0.00284 | −0.00321 | 0.0037 |
| M 75+ | −0.00073 | 0.00088 | −0.00099 | 0.00169 | −0.00176 | 0.00217 |
| Galicia | −0.00042 | 0 | −0.00042 | −0.00001 | −0.00009 | −0.00001 |
| Asturias | 0 | 0 | −0.00001 | 0 | −0.00002 | 0 |
| Cantabria | 0 | 0 | 0.00001 | 0 | 0 | 0 |
| País Vasco | 0.00001 | 0 | 0.00003 | 0 | 0.00002 | 0 |
| Navarra | 0 | 0 | 0 | 0 | 0 | 0 |
| La Rioja | 0 | 0 | 0 | 0 | 0 | 0 |
| Aragón | −0.00001 | 0 | −0.00001 | 0 | −0.00001 | 0 |
| Castilla y León | 0.00002 | 0 | 0.00001 | 0 | −0.00001 | 0 |
| Castilla-La Mancha | 0 | 0 | 0.00001 | 0 | 0 | 0 |
| Extremadura | 0 | 0 | 0.00001 | 0 | 0.00001 | 0 |
| Cataluña | 0 | 0 | 0.00001 | 0 | 0.00001 | 0 |
| Comunidad Valenciana | 0.00015 | −0.00001 | 0.00012 | −0.00002 | 0.00007 | −0.00003 |
| Baleares | 0.00003 | 0 | 0.00002 | −0.00001 | 0.00001 | −0.00001 |
| Andalucía | 0.00011 | 0 | 0.00021 | 0.00001 | 0.00015 | 0.00002 |
| Murcia | 0.00012 | 0 | 0.00013 | 0 | 0.0001 | 0 |
| Ceuta y Melilla | 0.00003 | 0 | 0 | 0 | 0.00001 | 0 |
| Canarias | −0.00006 | 0 | −0.00009 | 0.00002 | −0.00007 | 0.00002 |
Madrid, F 16–26 and Employed used as control groups
Figure A1.
Decomposition of rotation groups 2, 3 & 5
Footnotes
In the years immediately following the crisis GDP growth rebounded slightly before falling back to negative growth, whereas unemployment steadily increased to above 25% in 2012. Real wages actually increased between 2009 and 2010. However, this was due to compositional effects, as less experienced workers with lower paying temporary contracts were the first to lose their jobs (Puente & Galan, 2014). As the crisis progressed however, real wages contracted.
The reasons for the extraordinary growth until 2006, and the collapse after 2008 in the construction sector are still up for debate. See Gonzalez and Ortega (2009) and Bentolila et al. (2012) for more details.
Bacigalupe and Escolar-Pujolar (2014) review four studies on Spain during the Great Recession, and conclude that the evidence points in the direction of increasing health inequalities.
zit takes (1 − n)/2 for the poorest individual and (n − 1)/2 for the richest individual.
It should be stressed that our goal is not to estimate a causal model of health; our sole aim is to decompose changes in the (partial) association between health and income rank. As we have neglected to include potentially endogenous variables such as education or lifestyle the non-linear income function features as the sole potentially endogenous variable. We have deliberately not addressed its potential endogeneity since we are interested in documenting the association between changes in the distribution of income and the evolution of IRHI in Spain. Turning to the underlying mechanisms is only sensible after the magnitude of this association has been established, and after the relative importance of “income growth”, “mean-preserving income changes”, and “income mobility” has been understood.
After results are presented we return to the assumption that equation (2) is deterministic.
The intercept parameters drop out in equation (3b) since .
In 2004 and 2012, we observe only one rotation group (group 1 & 6); in 2005 and 2011 we simultaneously observe 2 rotation groups (group 1/2 & 5/6), in 2006 & 2010 3 rotation groups (group 1/2/3 & 4/5/6), while for the years 2007, 2008 and 2009, we simultaneously observe 4 separate rotation groups (group 1/2/3/4; 2/3/4/5 & 3/4/5/6).
Decompositions using alternative equivalence scales, such as the OECD-modified scale, did not significantly change the results.
Negative incomes can occur in the EU-SILC data due to debt, but make up less than 1% of the observations. They are problematic as in the hypothetical average income movement scenario these individuals will see their incomes drop when on average incomes rise. However, decompositions that included these observations did not change the qualitative features of our results.
This involves estimating an ordered probit model, with the thresholds imposed from the empirical distribution function of HUI in the Canadian National Population Health Survey 1994–1995 (HUI=1 equals maximum health and HUI=0 equals minimum health). Several studies using this approach (e.g. Van Doorslaer and Jones, 2003; Lauridsen et al., 2004; Lecluyse and Van Cleemput, 2006) have found the health inequality estimates to be rather insensitive to the threshold values imposed.
While the predicted HUI scores only reflect health changes resulting from changes in the explanatory variables, Van Doorslaer and Jones (2003) show that the interval regression approach is the preferred approach when calculating health inequality indices. One might also calculate the conditional predictions from the interval regression model given the observed SAH levels, but then the predicted HUI scores would no longer be a linear combination of the explanatory variables, and therefore not be amenable to our decomposition approach.
As explained before, the signs and size of term 1 and 2 (‘income growth’ and ‘evolution of income inequality’) largely depend on whether the health responsiveness to proportional income changes decreases or increases with rising incomes. This is left open with a second order income polynomial, but not with other popular choices in the empirical literature. For example, when one would favour the natural logarithm of income, one would impose that a proportional change in income has the same health effect for every individual (and hence one would force term 1 to be zero).
Summary statistics of the full unbalanced panel sample are similar to those of the balanced panel. Nor did the evolution of IRHI using the unbalanced panels for each rotating group differ markedly, suggesting that attrition is not an important driver of our main findings, although we cannot entirely rule out that explicitly accounting for mortality as in Petrie et al. (2013) would have disproportionally hit the older and poorer age groups.
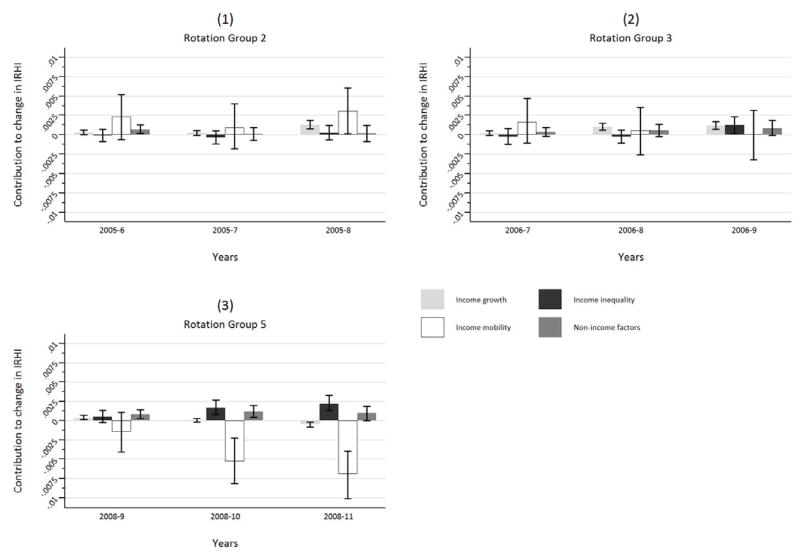
Decomposition results for the 2005–2008, 2006–2009 and the 2008–2011 rotation groups are not presented for reasons of clarity and brevity. They are in line with the results presented and available upon request.
The assumption of constant coefficients may be questionable in the case of pre- and post-crisis Spain, since the relationship between income and health may have changed. To test the robustness of our main findings we also decomposed the periods 2004–2007 using coefficients estimated on pre-crisis observations (before 2009) only, and 2009–2012 using only post crisis observations (after 2008). This did not change our results.
While including the top 1% of incomes does change the function form of income due to some extreme outliers (in particular among very high incomes), it does not change the overall results of the decomposition. Nevertheless in order to achieve an income function that is not unduly influenced by outliers we remove the top 1% of incomes.
One should only use the 95% confidence intervals to compare IRHI between rotation groups, since different waves within each rotation group are dependent samples.
The fact that similar trends are observed using different rotation groups indicates that the trend is not simply driven by a particular rotation group.
Table A1 in the appendix shows the numerical changes of IRHI between waves for each rotation group, and indicates the significance of such changes.
The EU-SILC categorises Spain into 18 different regions: Galicia, Asturias, Cantabria, País Vasco, Navarra, La Rioja, Aragón, Madrid, Castilla y León, Castilla-La Mancha, Extremadura, Cataluña, Comunidad Valenciana, Baleares, Andalucía, Murcia, Ceuta y Melilla, and Canarias.
The coefficients of the income polynomial are suppressed.
The fact that term 3 is so large in magnitude but still insignificant indicates that there are a small amount of very large and influential income re-rankings occurring. An individual moving from the bottom of the income distribution to the top in turn affects the rankings of the rest of the sample as well. Term 3 therefore changes dramatically when this individual is left out of the sample in a bootstrap replication.
The change in z-scores is bounded between −2 and 2 since the z-scores have been normalized between −1 and 1. For example, the most extreme case of an individual going from the highest to the lowest rank would lead to zi2 − zi1 = (−1) −1= −2.
One may question whether IRHI due to natural ageing is interesting or important, since ageing is an unavoidable biological process. In this case, the decomposition method can be viewed in different ways. If we are interested in the evolution of total IRHI then the sum of all 4 terms should be considered. If we wish to exclude the effect of natural ageing then we should exclude the non-income factors term. If we wish to narrow our focus further, and ignore that part of the evolution of IRHI that is due to the mobility of different age groups then the income mobility term should also be excluded.
For a comprehensive overview of recent reforms of Spanish old-age and disability pensions see e.g. García-Gómez et al (2012).
Neither our model of health nor our decomposition accounts for individuals’ labour market status. We have repeated the decomposition with the inclusion of labour market status and the results are extremely similar to those presented here. This is because once age is controlled for labour market status has very little correlation with health, and consequently can explain only very little.
JEL Classification Number: D30, D63, I14, I15
Contributor Information
Max Coveney, Email: m.coveney@ese.eur.nl.
Pilar García-Gómez, Email: garciagomez@ese.eur.nl.
Eddy Van Doorslaer, Email: vandoorslaer@ese.eur.nl.
Tom Van Ourti, Email: vanourti@ese.eur.nl.
References
- Aparicio Fenoll A. High-school dropouts and transitory labor market shocks: The case of the Spanish housing boom. 5139. Institute for the Study of Labor (IZA); 2010. [Google Scholar]
- Bacigalupe A, Escolar A. The impact of economic crises on social inequalities in health: what do we know so far? International journal of equity in health. 2014;13(52):10–1186. doi: 10.1186/1475-9276-13-52. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baeten S, Van Ourti T, Van Doorslaer E. Rising inequalities in income and health in China: Who is left behind? Journal of Health Economics. 2013;32(6):1214–1229. doi: 10.1016/j.jhealeco.2013.10.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bentolila S, Cahuc P, Dolado JJ, Le Barbanchon T. Two-Tier Labour Markets in the Great Recession: France versus Spain. The Economic Journal. 2012;122(562):F155–F187. [Google Scholar]
- Bonhomme S, Hospido L. Earnings Inequality in Spain: Evidence from Social Security Data. Trabajo presentado en el XV Encuentro de Economía Aplicada, A Coruña; 2012. pp. 7–8. [Google Scholar]
- Carrasco R, Jimeno JF, Carolina Ortega A. Accounting for changes in the Spanish Wage Distribution: The Role of Employment Composition Effects. Banco de España working paper 1120 2011 [Google Scholar]
- Contoyannis P, Forster M. The distribution of health and income: a theoretical framework. Journal of Health Economics. 1999;18:605–622. doi: 10.1016/s0167-6296(99)00002-8. [DOI] [PubMed] [Google Scholar]
- Denny K. Working Papers 201506. School Of Economics, University College Dublin; 2015. Has Subjective General Health Declined with the Economic Crisis? A Comparison across European Countries. [Google Scholar]
- Erreygers G. Correcting the Concentration Index. Journal of Health Economics. 2009;28:504–515. doi: 10.1016/j.jhealeco.2008.02.003. [DOI] [PubMed] [Google Scholar]
- Erreygers G, Van Ourti T. Measuring socioeconomic inequality in health, health care and health financing by means of rank-dependent indices: a recipe for good practice. Journal of Health Economics. 2011;30:685–694. doi: 10.1016/j.jhealeco.2011.04.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- European Commission. Solidarity in Health: Reducing Health Inequalities in the EU. Brussels: 2009. [Google Scholar]
- European Commission. Health inequalities in the EU — Final report of a consortium. 2013; Consortium lead: Sir Michael Marmot; Brussels. 2013. [Google Scholar]
- Garcia Gomez P, Jimenez-Martin S, Vall Castello J. Health, disability and pathways into retirement in Spain. In: Wise DA, editor. Social Security Programs and Retirement around the World: Historical Trends in Mortality and Health, Employment, and Disability Insurance Participation and Reforms. University of Chicago Press; 2012. [Google Scholar]
- Gonzalez L, Ortega F. Immigration and housing booms: Evidence from Spain*. Journal of Regional Science. 2013;53(1):37–59. [Google Scholar]
- Jenkins SP, Brandolini A, Micklewright J, Nolan B, editors. The great recession and the distribution of household income. Oxford University Press; 2012. [Google Scholar]
- Lacuesta A, Izquierdo M. The contribution of changes in employment composition and relative returns to the evolution of wage inequality: the case of Spain. Journal of Population Economics. 2012;25(2):511–543. [Google Scholar]
- Lauridsen J, Christiansen T, Häkkinen U. Measuring inequality in self-reported health—discussion of a recently suggested approach using Finnish data. Health economics. 2004;13(7):725–732. doi: 10.1002/hec.846. [DOI] [PubMed] [Google Scholar]
- Lecluyse A, Cleemput I. Making health continuous: implications of different methods on the measurement of inequality. Health economics. 2006;15(1):99–104. doi: 10.1002/hec.1015. [DOI] [PubMed] [Google Scholar]
- Petrie D, Allanson P, Gerdtham UG. Accounting for the dead in the longitudinal analysis of income-related health inequalities. Journal of Health Economics. 2011;30:1113–1123. doi: 10.1016/j.jhealeco.2011.07.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pijoan-Mas J, Sánchez-Marcos V. Spain is different: Falling trends of inequality. Review of Economic Dynamics. 2010;13(1):154–178. [Google Scholar]
- Puente S, Galán S. Banco de España, Economic Bulletin. 2014. Feb, Analysis of Composition Effects on Wage Behaviour. [Google Scholar]
- Regidor E, Barrio G, Bravo MJ, de la Fuente L. Has health in Spain been declining since the economic crisis? Journal of epidemiology and community health. 2014;68(3):280–282. doi: 10.1136/jech-2013-202944. [DOI] [PubMed] [Google Scholar]
- Rica S, Rebollo-Sanz YF. Gender Differentials in Unemployment Ins and Outs during the Great Recession in Spain. 9135. Institute for the Study of Labor (IZA); 2015. [Google Scholar]
- Ruhm CJ. Are recessions good for your health? w5570. National bureau of economic research; 1996. [Google Scholar]
- Ruhm CJ. Recessions, healthy no more? Journal of health economics. 2015;42:17–28. doi: 10.1016/j.jhealeco.2015.03.004. [DOI] [PubMed] [Google Scholar]
- Stuckler D, Basu S, Suhrcke M, Coutts A, McKee M. The public health effect of economic crises and alternative policy responses in Europe: an empirical analysis. The Lancet. 2009;374(9686):315–323. doi: 10.1016/S0140-6736(09)61124-7. [DOI] [PubMed] [Google Scholar]
- Van Doorslaer E, Koolman X. Explaining the differences in income-related health inequalities across European countries. Health economics. 2004;13(7):609–628. doi: 10.1002/hec.918. [DOI] [PubMed] [Google Scholar]
- Van Doorslaer E, Jones AM. Inequalities in self-reported health: validation of a new approach to measurement. Journal of health economics. 2003;22(1):61–87. doi: 10.1016/s0167-6296(02)00080-2. [DOI] [PubMed] [Google Scholar]
- Van Ourti T, van Doorslaer E, Koolman X. The effect of income growth and inequality on health inequality: Theory and empirical evidence from the European Panel. Journal of Health Economics. 2009;28(3):525–539. doi: 10.1016/j.jhealeco.2008.12.005. [DOI] [PubMed] [Google Scholar]
- Vandoros S, Hessel P, Leone T, Avendano M. Have health trends worsened in Greece as a result of the financial crisis? A quasi-experimental approach. The European Journal of Public Health. 2013;23(5):727. doi: 10.1093/eurpub/ckt020. [DOI] [PubMed] [Google Scholar]
- Mazzonna F, Bucher-Koenen T. The recent economic crisis and old-age health in Europe. In: Börsch-Supan A, Brandt M, Litwin H, Weber G, editors. Active ageing and solidarity between generations in Europe. 2013. pp. 233–242. [Google Scholar]
- OECD. Pensions at a Glance 2013: OECD and G20 Indicators. OECD Publishing; 2013. http://dx.doi.org/10.1787/pension_glance-2013-en. [Google Scholar]
- OECD. Health at a Glance: Europe 2014. OECD Publishing; 2014. http://dx.doi.org/10.1787/health_glance_eur-2014-en. [Google Scholar]