Comparison of Errors of 35 Weight Estimation Formulae in a Standard Collective

Abstract

Issue: The estimation of foetal weight is an integral part of prenatal care and obstetric routine. In spite of its known susceptibility to errors in cases of underweight or overweight babies, important obstetric decisions depend on it. In the present contribution we have examined the accuracy and error distribution of 35 weight estimation formulae within the normal weight range of 2500–4000 g. The aim of the study was to identify the weight estimation formulae with the best possible correspondence to the requirements of clinical routine.

Materials and Methods: 35 clinically established weight estimation formulae were analysed in 3416 foetuses with weights between 2500 and 4000 g. For this we determined and compared the mean percentage error (MPE), the mean absolute percentage error (MAPE), and the proportions of estimates within the error ranges of 5, 10, 20 and 30 %. In addition, separate regression lines were calculated for the relationship between estimated and actual birth weights for the weight range 2500–4000 g. The formulae were thus examined for possible inhomogeneities.

Results: The lowest MPE were achieved with the Hadlock III and V formulae (0.8 %, STW 9.2 % or, respectively, −0.8 %, STW 10.0 %). The lowest absolute error (6.6 %) as well as the most favourable frequency distribution in cases below 5 % and 10 % error (43.9 and 77.5) were seen for the Halaska formula. In graphic representations of the regression lines, 16 formulae revealed a weight overestimation in the lower weight range and an underestimation in the upper range. 14 formulae gave underestimations and merely 5 gave overestimations over the entire tested weight range.

Conclusion: The majority of the tested formulae gave underestimations of the actual birth weight over the entire weight range or at least in the upper weight range. This result supports the current strategy of a two-stage weight estimation in which a formula is first chosen after a pre-estimation of the weight range.

Introduction

For almost 4 decades foetal biometrics have been an integral part of established prenatal care according to maternity policy guidelines. Besides bodily integrity, biometry serves to estimate foetal weight and thus the age-appropriate development. While the first formulae for weight estimation were based solely on measurement of the biparietal diameter (BPD), the further development of numerous formulae based on combinations of biometric markers then led to an advantage over clinical estimation methods such as inspection and palpation 1, 2, 3, 4, 5.

For the great majority of weight estimation formulae it holds that they have been developed by means of regression analyses based on relatively small collectives of average term infants. The mean percentage error (MPE) as well as the mean absolute percentage error (MAPE) of the formulae depend on the weight itself. It is thus not surprising both for underweight infants or, respectively, pre-term infants as well as for infants with macrosomia, that the weight estimations can exhibit a clinically relevant error susceptibility 6, 7, 8. However, it is just this delineation of the normal weight collective from the abnormally under- or overweight fetuses that is of decisive importance for the prenatal and obstetric management. Interuterine growth retardation as well as macrosomia carry significant risks for not only neonatal but also for maternal morbidity and mortality 9, 10, 11. A differentiation from the normal collective can only be made when at least the weight estimation can reliably be classified in this range. The spread of this weight range with 2500 to 4000 g is, however, considered to be very wide. It is thus of interest as to which weight estimation formula exhibits not only the lowest but also the most stable errors within this range or, respectively, the largest independence on the weight range of the infant.

Accordingly, in this study we have examined by means of linear regressions how and to what extent deviations between the estimated weight and the actual birth weight in the range 2500 to 4000 g vary and which estimation formula exhibits the lowest constant estimation error in this situation.

Materials and Methods

Description of the study collective

For this retrospective study the perinatal database of the Department of Obstetrics and Gynecology at the University of Tübingen was searched for live births with a birth weight between 2500 and 4000 g in the period from 2010 to 2014. Infants with structural malformations of chromosomal aberrations were excluded from the analysis.

Conducting the biometric study

In the framework of routine care in our perinatal centre, each pregnant woman undergoes an untrasound scan close to term. This examination is mainly intended to confirm the position of the infant, to estimate the amount of amniotic fluid and to determine the estimated foetal weight (EFW) on the basis of the usual biometry-based weight estimation formulae. The biparietal (BPD) and occipito-frontal diameters (OFD) of the head are measured at the level of the transventricular plane from the outer bone margin to the outer bone margin on the opposite side. Head circumference (HC) was either determined directly by means of the ellipse or trace function or calculated from the distances (HC = 2.325 × [OFD2 + BPD2]1/2) 12. The foetal abdomen was measured by means of its transverse and anterior-posterior diameters (ATD, APD) at the level of the stomach and the umbilical vein-ductus venosus complex. The abdominal circumference was calculated from these values (AC = π × [ATD + APD/2]). The femural length (FL) is measured as the distance between the diaphyses. The individual measurements, the estimated foetal weight (EFW) as well as the obstetrically relevant maternal characteristics were stored in the perinatal database. The birth weight (BW) was determined immediately after delivery by the responsible midwife, obstetrician or neonatologist and documented. For each of the included pregnancies the last ultrasound examination prior to delivery in which at least one measurement of each BPD, OFD, ATD, APD and FL was carried out was documented. Pregnancies with incomplete measurements or for which the last measurement was taken more than 7 days prior to delivery were excluded from the study. Each pregnancy was included only once in the study.

Statistical analysis

In each included case the EFW was determined by means of the published formulae according to Birnholz, Combs, Campbell, Ferrero, Hadlock, Halaska, Hansmann, Hart, Higginbottom, Jordaan, Persson, Merz, Mielke, Ott, Rose and McCallum, Sabbagha, Schild, Schillinger, Scott, Shepard, Shinozuka, Siemer, Thurnau, Vintzileos, Warsof, Weiner and Woo 3, 4, 5, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38. The corresponding formulae are listed in Table 1. The accuracies of the various formulae were determined and compared by means of the mean percentage error (MPE = [EFW− BW]/BW × 100) and the mean absolute percentage error (MAPE = |(EFW – BW)|/BW × 100). Hereby the MPE represents the systematic error of the formula. Its standard deviation (SD) reflects the random elements in the prediction error. The 95 % confidence intervals (CI) for the MPE were calculated and were used to test for a significant deviation against 0.

Table 1 Survey of the 35 weight estimation formulae.

Author	Data	Formula
AC = abdominal circumference, HC = head circumference, FL = femur length, BPD = biparietal diameter, AD = abdominal diameter, GA = gestational age, MW = maternal weight
Birnholz 13	BPD, OFD, ATD	3.42928 × (BPD × OFD/1.264)0.5 × AD2/1 000 + 41.218 [g, mm]
Combs 14	HC, AC, FL	0.23718 × AC2 × FL + 0.03312 × HC3 [g, cm]
Campbell 15	AC	e(− 4.564 + 0.282 × AC − 0.00331 × AC²) [kg, cm]
Ferrero 16	AC, FL	10(0.77125 + 0.13244 × AC − 0.12996 × FL − 1.73588 × AC²/1 000 + 2.18984 × FL/AC) [g, cm]
Hadlock I 4	BPD, HC, AC, FL	10(1.3596 + 0.0064 × HC + 0.0424 × AC + 0.174 × FL + 0.00061 × BPD × AC − 0.00386 × AC × FL) [g, cm]
Hadlock II 4	AC, FL	10(1.304 + 0.05281 × AC + 0.1938 × FL − 0.004 × AC × FL) [g, cm]
Hadlock III 4	BPD, AC, FL	10(1.335–0.0034 × AC × FL + 0.0316 × BPD + 0.0457 × AC + 0.1623 × FL) [g, cm]
Hadlock IV 4	HC, AC, FL	10(1.326–0.00326 × AC × FL + 0.0107 × HC + 0.0438 × AC + 0.158 × FL) [g, cm]
Hadlock V 5	BPD, AC	10(1.1134 + 0.05845 × AC − 0.000604 × AC² − 0.007365 × BPD² + 0.000595 × BPD × AC + 0.1694 × BPD) [g, cm]
Hadlock VI 5	HC, AC, FL	10(1.5662–0.0108 × HC + 0.0468 × AC + 0.171 × FL + 0.00034 × HC² − 0.0003685 × AC × FL) [g, cm]
Halaska 17	BPD, AC, FL	10(0.64041 × BPD − 0.03257 × BPD² + 0.00154 × AC × FL) [g,cm]
Hansmann 18	BPD, AD, GA,	− 0.001665958 × AD3 + 0.4133629 × AD2 − 0.5580294 × AD − 0.01231535 × BPD3 + 3.702 × BPD2 − 330.1811 × BPD − 0.4937199 × (GA + 1)3 + 55.958061 × (GA + 1)2 − 2 034.3901 × (GA + 1) + 32 768.19 [g, mm]
Higginbottom 20	AC	0.0816 × AC3 [g, cm]
Jordaan 21	BPD, HC, AC	10(2.3231 + 0.02904 × AC + 0.0079 × HC − 0.0058 × BPD) [kg, cm]
Merz I 22	BPD, AC	− 3 200.40479 + 157.07186 × AC + 15.90391 × BPD × BPD [g, cm]
Merz II 22	AC	0.1 × AC3 [g, cm]
Ott 26	HC, AC, FL	10(− 2.0661 + 0.04355 × HC + 0.05394 × AC − 0.0008582 × HC × AC + 1.2594 × FL/AC) [kg, cm]
Rose-McCallum 27	BPD, AD, FL	e(0.143 × [BPD + AD + FL] + 4.198) [g, cm]
Sabbagha 28	GA, HC, AC, FL	− 55.3–16.35 × (GA + HC + 2 × AC + FL) + 0.25838 × (GA + HC + 2 × AC + FL)2 [g, cm]
Schild I 29	femaleBPD, AC, FL	− 4 035.275 + 1.143 × BPD3 + 1 159.878 × AC0.5 + 10.079 × FL3 − 81.277 × FL2 [g, cm]
Schild I 29	maleBPD, HC, AC, FL	1 913.853 × log10(BPD) + 0.01323 × HC3 + 55.532 × AC2 − 13 602.664 × AC0.5 − 0.721 × AC3 + 2.31 × FL3 [g, cm]
Schillinger 30	BPD, ATD	397.7 × BPD + ATD − 4 387 [g, cm]
Shepard 32	BPD, AC	10(− 1.7492 + 0.166 × BPD + 0.046 × AC − 0.002546 × AC × BPD) [kg,cm]
Shinozouka 33	BPD, AC, FL	1.07 × BPD3 + 3.42 × ATD2 × FL [g, cm]
Warsof 3	BPD, AC	10(− 1.599 + 0.144 × BPD + 0.032 × AC − 0.000111 × BPD² × AC) [kg, cm]
Woo 38	BPD, AC, FL	10(1,13705 + 0,15549 × BPD + 0.0464 × AC − 0.00279682 × BPD × AC + 0.037769 × FL − 0.000494529 × AC × FL) [g, cm]
Vinzeleos 36	BPD, AC	10(1.879 + 0.084 × BPD + 0.026 × AC) [g, cm]
Persson 23	BPD, AD, FL	BPD0.972 × ([AD1 + AD2]/2)1.743 × FL0.367 × 10(− 2.646) [g, cm]
Schild II 39	HC, AC, FL	5 381.193 + 150.324 × HC + 2.069 × FL3 + 0.0232 × AC3 − 6 235.478 × LOG(HC) [g, cm]
Scott 31	HC, AC, FL	10(0.66 × LOG(HC) + 1.04 × LOG(AC) + 0.985 × LOG(FL)) [g, cm]
Siemer 34	BPD, AC, FL	− 5 948.336 + 2 101.261 × LN(AC) + 15.613 × FL2 + 0.0577 × BPD3 [g, cm]
Thurnau 35	BPD, AC	(9–337 × BPD × AC) − 229 [g, cm]
Weiner I 37	HC, AC, FL	10(1.6961 + 0.02253 × HC + 0.01645 × AC + 0.06439 × FL) [g, cm]
Weiner II 37	HC, AC	10(1.6575 + 0.04035 × HC + 0.01285 × AC) [g, cm]
Mielke I 24	BPD, ATD, FL	e(3.067510 + 0.01677 × BPD + 0.000412 × ATD² + 0.040611 × FL − 0.000000006027957 × BPD² × ATD² − 0.000005086 × ATD² × FL) [g, cm]
Mielke II 25	BPD, ATD, FL	e(3.704706 + 0.033276 × BPD + 0.000093048 × ATD² + 0.010570 × FL − 0.00000002477864 × BPD² × ATD² + 0.000002009 × ATD² × FL) [g,cm]

For each estimation formula the proportions of the weight estimations with percentage errors of ≤ 5, ≤ 10, ≤ 20 and ≤ 30 % were calculated.

The relationship between the estimated and the actual birth weights was examined by means of a liner regression analysis. The extent of the estimation error in dependence on the actual birth weight could be estimated with the help of the regression.

Results

Demographic characteristics

Altogether 3416 pregnancies were included in the study after consideration of the inclusion criteria. The average age of the mothers amounted to 31.1 years. The average weight of the mothers was 76.9 kg (SD ± 14.7 kg, range 31.0–160.2 kg). On average the gestational age at birth was 39 + 1 weeks (interquartile range [IQR] 38 + 0–40 + 1 SSW). The gender distribution was balanced. The average weight at birth amounted to 3181 g. In the majority of the cases the ultrasound examination was performed at a maximum of 1 day before delivery (56.6 %). 34.3 % of the examinations were made 2–5 days before delivery and 9.1 % on days 6 or 7 prior to birth.

Mean percentage error and mean absolute percentage error

The MPE and MAPE values for the 35 employed formulae are listed in Table 2. The largest overestimation was seen for the Birnholz formula with an MPE of − 12.2 % while the clearest underestimation was found with the Mielke I formula (MPF = 46.0 %). It should be emphasised that the lowest percentage errors were found for the Hadlock III formula (0.8 %) and the Hadlock V formula (− 0.8 %). In a comparison of all formulae the standard deviations varied between 6.4 % (Schild II) and 16.4 % (Hadlock IV).

Table 2 MPE and MAPE values including standard deviations for all 35 formulae in the birth weight range from 2 500–4 000 g.

	MPE (%)				MAPE (%)
	Mean value	SD	Confidence interval		Mean value	SD
			Lower limit	Upper limit
Halaska	0.9	8.1	0.6	1.2	6.6	4.8
Schild I	1.9	8.2	1.6	2.2	6.8	5.0
Shinozuka	− 1.5	8.9	− 1.8	− 1.2	7.2	5.4
Sabbagha	2.8	8.6	2.5	3.1	7.3	5.4
Hadlock III	0.8	9.2	0.5	1.1	7.4	5.5
Hadlock I	2.5	8.9	2.2	2.8	7.5	5.5
Ott	3.9	8.5	3.6	4.2	7.5	5.5
Hadlock V	− 0.8	10.0	− 1.1	− 0.5	8.0	6.1
Combs	5.6	8.1	5.3	5.9	8.1	5.7
Hadlock II	3.6	9.6	3.3	3.9	8.3	6.1
Merz I	− 5.0	9.3	− 5.3	− 4.7	8.4	6.5
Rose-McCallum	− 1.9	10.5	− 2.2	− 1.6	8.5	6.5
Shepard	− 1.9	10.6	− 2.2	− 1.6	8.5	6.6
Warsof	3.2	10.1	2.9	3.5	8.5	6.3
Ferrero	− 3.5	10.3	− 3.8	− 3.2	8.6	6.6
Hadlock VI	6.2	8.7	5.9	6.5	8.7	6.2
Campbell	5.0	9.9	4.7	5.5	8.9	6.7
Persson	6.4	9.0	6.1	6.7	9.0	6.4
Hansmann	− 7.3	9.1	− 7.6	− 7.0	9.3	7.1
Jordaan	5.0	10.6	4.7	5.3	9.5	6.9
Schillinger	− 9.6	9.3	− 9.9	− 9.3	10.9	7.8
Vinzeleos	− 7.0	12.9	− 7.4	− 6.6	11.5	9.1
Higginbottom	9.2	13.1	8.8	9.6	13.1	9.2
Hadlock IV	3.4	16.4	2.9	3.9	13.3	10.0
Weiner I	12.9	8.9	12.6	13.2	13.6	7.7
Birnholz	− 12.2	11.7	− 12.6	− 11.8	13.9	9.8
Merz II	− 11.3	16.1	− 11.8	− 10.8	15.4	12.2
Siemer	16.7	6.6	16.5	16.9	16.8	6.4
Thurnau	17.0	7.0	6.8	7.2	17.1	6.8
Scott	17.6	6.8	17.4	17.8	17.6	6.7
Woo	17.9	7.3	17.7	18.1	18.0	7.1
Weiner II	19.7	9.9	19.4	20.0	20.1	9.1
Schild II	23.0	6.4	22.8	23.2	23.0	6.3
Mielke II	25.8	10.7	25.5	26.1	25.9	10.5
Mielke I	46.0	8.1	45.7	46.3	46.0	8.1

20 formulae (Halaska, Schild I, Shinozuka, Sabbagha, Hadlock III, Hadlock I, Ott, Hadlock V, Combs, Hadlock II, Merz I, Rose-McCallum, Shepard, Warsof, Ferrero, Hadlock VI, Campbell, Persson, Hansmann, Jordaan) exhibited MAPE values of ≤ 10 %. Of special interest is the Halaska formula that showed the best value of 6.6 %. Six formulae gave MAPE values in the intermediate error range of 10.1 to ≤ 15 % and further 9 formulae had MAPE values in the critical region of ≥ 15.1 %.

Table 3 presents the frequency distribution of differences between actual birth weight and estimated birth weight for the indivdual formulae in the weight range of 2500–4000 g. The favourable performance of the Halaska formula is again confirmed here. With use of the Halaska formula for birth weight estimation, 43.85 % of the cases lie below the 5 % and 77.52 % below the 10 % error level. Altogether there were 22 formulae for which more than half of the estimated values showed a deviation of ≤ 10 %. For four formulae (Weiner II, Schild II, Mielke II and Mielke I), on the other hand, estimations of more than half of the cases gave rise to clinical questionable deviations of more than 20 %.

Table 3 Frequency distribution between estimated and actual birth weights in the birth weight range of 2 500–4 000 g.

Formula	Difference between actual and estimated birth weight less than:
	5 percent	10 percent	20 percent	30 percent
Halaska	43.85 %	77.52 %	98.77 %	100.00 %
Schild I	43.62 %	76.38 %	98.27 %	99.97 %
Shinozuka	41.98 %	73.07 %	97.51 %	99.77 %
Sabbagha	41.31 %	71.72 %	97.98 %	99.88 %
Hadlock III	40.28 %	71.49 %	97.19 %	99.82 %
Hadlock I	40.60 %	71.46 %	97.34 %	99.94 %
Ott	39.99 %	70.32 %	97.28 %	99.91 %
Hadlock V	37.76 %	68.68 %	95.52 %	99.56 %
Combs	36.15 %	67.10 %	96.34 %	99.94 %
Hadlock II	36.48 %	65.49 %	95.64 %	99.74 %
Merz I	37.88 %	66.04 %	94.06 %	99.39 %
Rose-McCallum	35.63 %	65.52 %	93.97 %	99.44 %
Shepard	35.98 %	65.66 %	93.91 %	99.06 %
Ferrero	35.51 %	64.17 %	93.53 %	99.36 %
Hadlock VI	32.96 %	62.76 %	94.67 %	99.80 %
Campbell	34.75 %	62.09 %	93.03 %	99.33 %
Persson	32.90 %	60.69 %	93.62 %	99.82 %
Hansmann	34.02 %	61.62 %	91.36 %	98.59 %
Jordaan	32.11 %	58.96 %	90.95 %	99.33 %
Schillinger	27.20 %	52.78 %	86.74 %	97.80 %
Vinzeleos	28.37 %	52.69 %	83.55 %	95.70 %
Higginbottom	22.72 %	43.41 %	76.49 %	95.49 %
Hadlock IV	21.98 %	44.15 %	76.87 %	93.88 %
Weiner I	15.13 %	35.51 %	78.60 %	98.19 %
Birnholz	21.02 %	40.63 %	75.09 %	92.83 %
Merz II	21.75 %	40.31 %	69.85 %	88.00 %
Siemer	4.42 %	16.10 %	66.63 %	99.24 %
Thurnau	4.33 %	15.37 %	65.13 %	97.95 %
Woo	3.60 %	13.55 %	59.69 %	95.84 %
Weiner II	5.56 %	14.72 %	48.71 %	86.24 %
Schild II	0.50 %	2.49 %	30.85 %	86.56 %
Mielke II	2.72 %	7.52 %	28.69 %	64.08 %
Mielke I	0.00 %	0.00 %	0.09 %	3.28 %

Regression analysis between estimation error and actual birth weight

The determination of regression lines was able to demonstrate by means of graphic plots the variance of the deviations between estimated and actual birth weights over the entire weight range. Fig. 1 shows the 16 formulae that exhibited an intersection with the ideal regression line (x [actual birth weight] = y [estimated birth weight]). A common feature of all formulae is that they move up from a region of weight overestimation in the lower range to a region of underestimation.

Fig. 1.

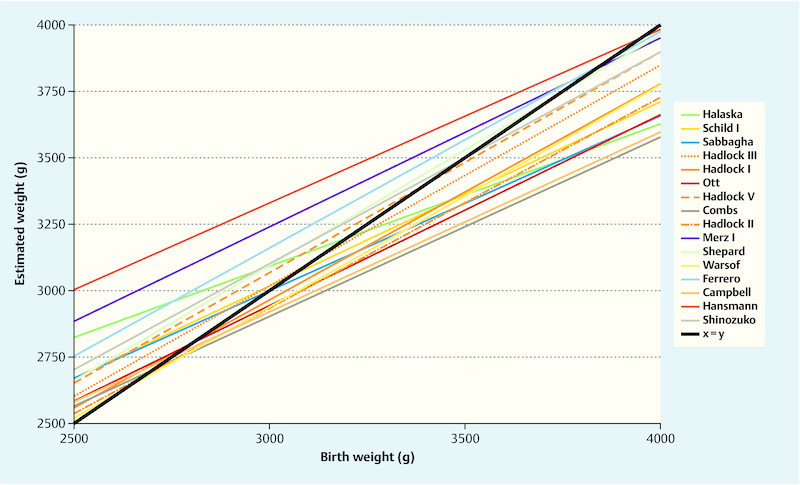
 Actual and estimated birth weights. The listed regression formulae have an intersection with the ideal regression formula y = x for birth weights between 2500 and 4000 g.

Fig. 2 shows the distribution of 5 formulae that always resulted in overestimations of the birth weight. Estimations according to the Rose-McCullum formula were nearest and almost parallel to the ideal line. Fig. 3, on the other hand, illustrates the distribution of the 14 formulae that always led to an underestimation of the birth weight. Markedly different courses can be clearly seen here. Whereas in the lower weight range the formula according to Jordaan is closest to the ideal this is true for the Schild II formula in the upper weight range.

Fig. 2.

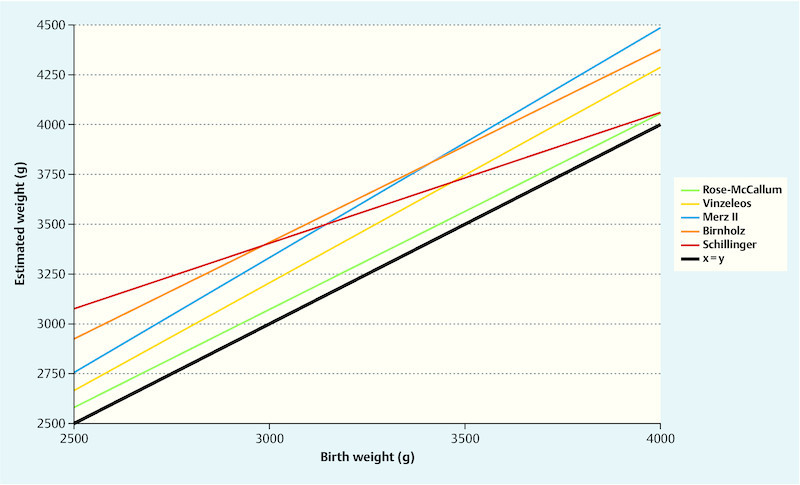
 Actual and estimated birth weights. In the weight range from 2500 to 4000 g the listed regression formulae do not have an intersection point with the ideal regression formula y = x. On average the estimated weight was higher than the actual birth weight.

Fig. 3.

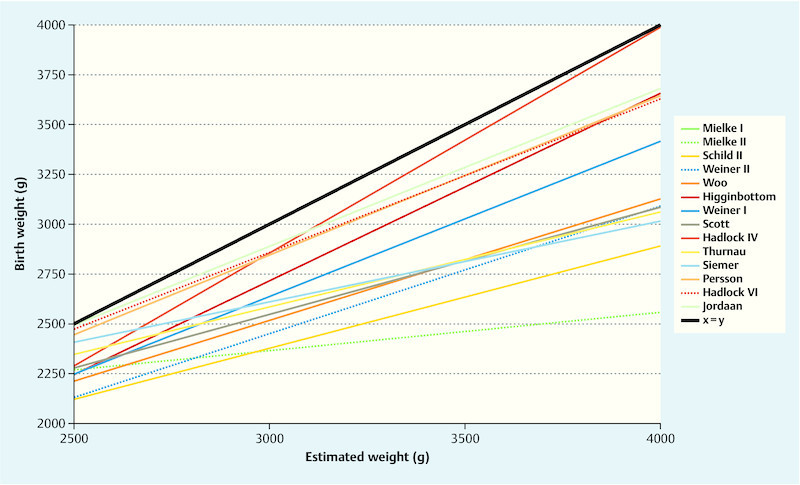
 Actual and estimated birth weights. In the weight range from 2500 to 4000 g the listed regression formulae do not have an intersection point with the ideal regression formula y = x. On average the estimated weight was lower than the actual birth weight. The plot according to the Mielke I formula lies below the illustrated region.

Discussion

In the present study we have, on the basis of measurements of 3416 foetuses, shown that the smallest MPEs can be obtained with the Hadlock III and V formulae (0.8 %, SD 9.2 % or, respectively, − 0.8 %, SD 10.0 %). The lowest absolute error (6.6 %) as well as the most favourable frequency distribution for cases with lower than 5 % and 10 % errors (43.9 and 77.5) were seen for the Halaska formula. This corresponds to the expected values from comparable preliminary work. The majority of the weight estimation formulae were developed for average infants weighing between 2500–4000 g and exhibited thereby a relatively low absolute percentage error of between 6–10 %, just as in our series 40, 41, 42. Merely 5 formulae consistently showed overestimations of weight. 14 formulae underestimated the foetal weight over the entire weight range, 16 did so in the upper weight region.

There are numerous possibilities to improve the weight estimations. With regard to the accuracy of sonographic measurements, several studies have shown that practical sonographic experience or, respectively, targeted training on patients or simulators can reduce the errors 41, 43. Also a time window between measurements and delivery of ≤ 7 days can help to reduce errors 44. Another option, especially for heavier infants, is an optimisation of the weight estimation through a combination of ultrasound findings with maternal and pregnancy-specific parameters such as gestational age, parity, gender of the foetus, and maternal height or weight. The presumed benefit of such an elaborate procedure is, however, a subject of controversial discussion in the current literature 45, 46, 47. Nevertheless, there is consensus that maternal obesity increases the estimation errors 48, 49.

Ultimately, the estimation errors of sonographic formulae must be considered as being intrinsic to the method. In a study of 628 new-born infants, Kehl et al. could reduce the systematic error to a minimum by means of postnatally performed measurements. Even so, the MPEs of the employed formulae were between 7.42 and 8.77 %. The proportion of estimations with an error of under 10 % amounted to between 74.6 and 81.3 %. Under consideration of the 95 % limits of agreement, the estimations were in a range of ± 500 g. These key data for optimal weight estimations are in agreement with our results when using the best formulae such as those according to Halaska or Hadlock.

Our data show that many formulae exhibit a variable susceptibility to error within the normal weight range. This observation supports the attempts of current research groups to use a two-step procedure for weight estimations. In a first such step the weight range, for example, is delineated by measurement of the AC and the formula chosen in dependence on this result. It has been demonstrated that those formulae that had been specifically developed for foetuses with an abdominal circumference of less than 290 mm exhibited a significantly better MAPE (7.13–7.61 %) and markedly more measurements with an error of less than 10 % in comparison with the Warsof and Hadlock formulae 50. An analogous result has been determined for infants with an AC greater than 360 mm 51. The so-called Zürich method follows a similar strategy. In this case, the product of the AC and the FL is calculated. When this value is < 24 600 the Hadlock formula is used, for larger values the Merz formula 52. Our data confirm that in the upper weight range the Merz formula enables a better weight estimation than the Hadlock formula.

A further strategy for improvement involves the implementation of 3D measurements, as a rule in the standardised determination of a volume from the foetal thigh region. At least in cases of manifest gestational diabetes, an improvement in weight estimation through 3D measurements seems to be possible because just in such pregnancies the soft tissue mantle does especially influence the weight of the foetus 53.

On a critical note, it must be realised that the validity of the present data is limited due to the retrospective nature of the study. The monocentric data acquisition represents a further limitation. However, this is relativised somewhat by the large number of participating investigators with varying degrees of training and experience.

Conclusions

When judged by the MPE and MAPE results, the formulae according to Hadlock and Halaska exhibit the lowest errors. Most of the formulae tend to underestimate the weight to varying degress depending on the weight class. This supports current efforts to apply a two-step procedure.