Abstract
Diffusion kurtosis imaging (DKI) is sensitive to tissue microstructure and may therefore be useful in the diagnosis and monitoring of disease in brain and body organs. Generally, diffusion MRI (dMRI) in the body is challenging due to heterogeneous body composition that can cause image artifacts due to chemical shifts and susceptibility differences. Additionally, the abdomen has a strong presence of physiological factors (e.g. breath, heartbeat, blood flow), which may severely reduce image quality, especially when echo-planar imaging is employed as is typical in dMRI. Collectively, these challenging measurement conditions impede the use and exploration of DKI in the body. This impediment is further exacerbated by the traditionally large amount of data required for DKI and low signal-to-noise ratio at the b-values needed to effectively probe the kurtosis regime. Recently introduced fast DKI techniques reduce the challenge of DKI in the body by lowering the data requirement substantially so that e.g. triggering and breath hold techniques may be applied for the entire DKI acquisition without causing unfeasible scan times. One common pathologic condition where body DKI may be of immediate clinical value is kidney fibrosis, which causes a progressing change in organ microstructure. With its sensitivity to microstructure, DKI is an obvious candidate for a non-invasive evaluation method. We present preclinical evidence that the rapidly obtainable tensor-derived mean kurtosis (W̄) distinguishes moderately fibrotic kidneys from healthy controls. The presence and degree of fibrosis are confirmed by histology, which also indicates fibrosis as the main driver behind the DKI differences observed between groups. We therefore conclude that fast kurtosis is a likely candidate for an MRI based method for detection and monitoring of renal fibrosis. We provide protocol recommendations for fast renal DKI in humans based on a b-value optimization performed using data acquired at 3T in normal human kidney.
Keywords: diffusion, kurtosis, fibrosis, kidney
Introduction
Chronic Kidney Disease (CKD) has increasing incidence and fibrosis (the accumulation of extracellular matrix) is a common denominator of different pathological processes in development of CKD (1). Currently, biopsy is the only method to diagnose and monitor microstructural pathology in CKD but biopsy is both prone to sampling errors and may give complications due to its invasiveness. A promising method for non-invasive detection and monitoring of renal fibrosis and CKD is diffusion MRI (dMRI) which utilizes sequence sensitivity to water diffusion to indirectly assess tissue microstructure.
A basic measure is the apparent diffusion coefficient (ADC) which is the diffusivity D(n̂) observed along a direction n̂ . In the past decade, dMRI has been used to investigate renal diseases in several studies and generally they report a reduction in the ADC in diseased kidneys (2), CKD (3–5), diabetic (6,7), chronic parenchymal disease (2,8), and transplanted kidneys (9–11). ADC has also been correlated to both glomerular filtration rate and the degree of fibrosis of the tissue (12). However, the results in the past studies show great discrepancy due to the lack of consensus in the measurement schemes (different b-values) as pointed out by different research groups (13–16). Inappropriate choice of b-values may cause measurements to be contaminated by intravoxel incoherent motion (IVIM) effects (17,18) from perfusion and filtration in the kidney, which will skew ADC estimates. Moreover, basic dMRI metrics such as the ADC might not be the most sensitive diffusion marker to detect fibrosis and more advanced diffusion techniques now offer parameters sensitive to more aspects of the microstructure. Diffusion Tensor Imaging (DTI) with the parameter Fractional Anisotropy (FA) reflects the directional variation of the water diffusion, where zero indicates isotropic diffusion and one indicates diffusion in only one direction. Hindrances and restrictions from tissue microstructure cause diffusion to be non-Gaussian which is not captured by DTI. To describe this effect, Diffusion Kurtosis Imaging (DKI) was proposed a decade ago (19) and is widely held to sensitively reflect tissue microstructure (16) complementary to basic dMRI and DTI. DKI is a simple extension of the DTI model and inclusion of non-Gaussian effects has been shown to improve diffusion tensor estimates and cause estimated diffusion metrics to show less b-value dependency (20). Typical implementations of DKI rely on large data sets for parameter estimation causing both long measurement and post-processing time. This has held back the exploration of DKI in everyday clinical application although evidence is growing that DKI offers valuable diagnostic information (21–24) (see also literature surveys in (25,26)). Recently proposed methods allow DKI to be performed within a clinically relevant timescale (as little as one minute including post-processing) (26–28), making DKI compatible with even the acute clinical setting. In body imaging, dMRI is prone to artifacts due to the use of echo-planar read-out in a body region, which contains many tissue types with different chemical shifts, magnetic susceptibilities, and the acquisition of sufficient high quality data to allow DKI analysis is a challenge. Until now, two studies of DKI in normal human kidneys have been published (29,30). The two studies both report a larger FA for medulla than in cortex. However, they report opposite results for mean diffusivity (MD) and mean kurtosis (MK). Huang et al. is in agreement with most studies that MD in cortex is larger than in medulla (29), but for MK there exist no relevant studies to compare to. Pentang et al. and Huang et al. use a traditional DKI protocol with 30 directions, but a different range of b-values: (0, 300, 600 s/mm2) and (0, 500, 1000 s/mm2) respectively. A recent study shows DKI to be valuable in assessing clear cell renal carcinoma in patients where DKI based 7 b-values (range 0–2000 s/mm2) and three encoding directions was found to quantitatively characterize different renal tumor grades (31). Even though this shows promise for the use of DKI in diagnostics of renal disease, the lack of a standard protocol could potentially cause conflicting findings and non-comparable absolute values. Particularly, the choice of b-values is critical since the presence of flow in renal tissue may cause IVIM effects to influence DWI and DKI estimates from low b-value measurements and the choice of b-value scheme is therefore important for unaffected parameter estimates. A preclinical report by Boor et al. (32) concludes that ADC does not reflect kidney fibrosis, because the ADC measured in fibrotic kidney cortex in vivo is lower than in healthy kidney cortex and ex vivo it is opposite. In the same vein, preclinical studies can provide a basis for interpretation of clinical DKI of renal fibrosis by investigating how the fibrosis affects the DKI metrics in the absence of physiological effects.
Here we set out to do exactly this: using fixed kidneys from wild type (WT) mice and a transgenic (Tg) mouse model of CKD we compare diffusion metrics estimated with the fast DKI method (the 1-9-9 protocol from (28)) to estimates from a traditional DKI protocol using a larger data acquisition. The MRI measurements are performed on a 9.4T Bruker scanner. Good agreement is found between metrics from the two methods and dMRI metrics FA and mean kurtosis are found to differ between the two groups (WT and Tg). Quantitative histology was then performed on the kidneys to confirm the presence of fibrosis in the Tg group and assess fibrosis severity, tissue porosity, and cell density. The histology indicates that fibrosis is the main driver behind the DKI differences between groups. In this manner, we can establish how fibrosis affects the DTI/DKI metrics in the absence of physiological effects such as flow of blood and urine in the kidney tissue. Having established the fast kurtosis method’s sensitivity to renal fibrosis we proceed to offer an optimized measurement strategy for use of the fast kurtosis measurement scheme in the study of human kidney disease. We propose a strategy for circumventing contamination from IVIM effects in the estimation. The optimized fast kurtosis scheme is then demonstrated on a basic data set acquired in normal human kidney at 3T.
1 Methods
1.1 Theory
In DKI the logarithm of the diffusion weighted signal is written as (19):
| (1) |
where b is the magnitude of diffusion weighting applied along n̂ =(nx,ny,nz). Here subscripts label Cartesian components (e.g. i = x,y,z) and our notation implies summation over repeated indices as e.g. ni nj Dij =Σij ni nj Dij for the diffusion tensor D. As in (19) the rank-4 kurtosis tensor W is defined in terms of spin displacement moments:
| (2) |
where R =r(Δ) −r(0) is the spin displacement and Δ the diffusion time. In (26) we defined the tensor derived apparent kurtosis, W(n̂), in analogy to the apparent diffusion constant
| (3) |
as
| (4) |
With this definition we defined a mean kurtosis, W̄, as the mean of the kurtosis tensor i.e. its average over all directions (S2 is the sphere):
| (5) |
where 𝕀 is the fully symmetric isotropic tensor (33), 〈A,B〉 = AijklBijkl denotes the Frobenius inner product, and Tr is the trace. Thus, in this definition the mean kurtosis W̄ can be viewed as the isotropic part of the kurtosis tensor and is equal to 1/5 of the projection 〈W,𝕀〉 of the kurtosis tensor W onto 𝕀, using the inner product.
On the basis of Eq. (5), W̄ may be estimated from W(n̂) along nine distinct directions, n̂(i), n̂(i+) and n̂(i−) (i=1,2,3), defined in Table 1 (26):
| (6) |
Table 1.
The nine directions in the compact notation used in the manuscript and stated as normalized vectors.
| Direction | x-component | y-component | z-component | ||
|---|---|---|---|---|---|
| n1 | 1 | 0 | 0 | ||
| n1+ | 0 |
|
|
||
| n1− | 0 |
|
|
||
| n2 | 0 | 1 | 0 | ||
| n2+ |
|
0 |
|
||
| n2− |
|
0 |
|
||
| n3 | 0 | 0 | 1 | ||
| n3+ |
|
|
0 | ||
| n3− |
|
|
0 |
Using these directions with Eq. (1) and performing the same linear combination of the log signal as in Eq. (6), we get:
| (7) |
where D̄ =Tr(D) / 3 is the mean diffusivity. In (26,27) this formed the basis for robust estimation of D̄ and W̄ from 13 diffusion weighted images: 1 at b=0, three directions (x̂,ŷ,ẑ) at b=1 ms/μm2 and the nine directions at b=2.5 ms/μm2. This strategy was therefore referred to as the 1-3-9 acquisition scheme for fast estimation of mean kurtosis. Recently, this strategy was extended so that D̄, W̄ and also FA can be estimated from 19 images. These images are acquired as 1 at b=0, and the nine directions at two different non-zero b-values, b1 and b2. For this reason it is referred to as the 1-9-9 acquisition scheme (28). Such an acquisition allows the use of eq. (7) to form a set of two equations with two unknowns ( D̄ and W̄) :
| (8) |
so that a 1-9-9 estimate for D̄ is given by :
| (9) |
an FA estimate is then available as:
| (10) |
and W̄ is obtained from:
| (11) |
where D(n̂) is obtained from the data as described previously (28), and var denotes the variance, here taken over the nine directions n̂ . In addition to the estimation of FA at a minimal increase in scan time and virtually no cost in post-processing time (no fitting required), one major benefit of this approach is increased robustness to experimental imperfections as shown in (28).
The 1-9-9 strategy requires a stable estimate of the unweighted tissue signal S(b=0). In some regions of the kidney, the presence of IVIM effects is too large to ignore in the analysis. The IVIM model describes the signal as:
| (11) |
where S0 is the unweighted signal intensity from all tissue, fIVIM is the volume fraction of the incoherent perfusion compartment and Fperf the corresponding signal attenuation. Similarly, Fdiff is the signal attenuation of the true diffusion in the tissue compartment which makes up the remaining volume. For the 1-9-9 strategy to work in vivo we therefore need an estimate of the unweighted signal intensity of the tissue compartment alone: S0 ·(1−fIVIM). For kurtosis estimation in regions where fIVIM is large, we propose to obtain this intensity from fitting the one-dimensional DKI signal equation to a series of 3–4 measurements at varying b-values outside of the IVIM regime (b>0.2 ms/μm2) along a direction already included in the 1-9-9 scheme (e.g. one of the x,y,z directions). These 5–6 data points can be fitted to the one-dimensional DKI signal equation to obtain an estimate of the unweighted tissue signal without the IVIM compartment. This estimate would then constitute the S(b=0) needed for the 1-9-9 estimation. If more than one direction is acquired, the intensity estimates from each direction should be averaged to reduce the influence of tissue anisotropy.
1.2 Animals
1.2.1 Mouse Model
We used the previously described RenTGF-β mouse strain expressing mutated porcine transforming growth factor β (TGF-β) under control of the Ren-1c promotor (n = 8) (34). The mice demonstrate glomerular lesions exclusively within the kidneys and show thickening of glomerular basement membrane, deposition of extracellular matrix, increased glomerular volume, and reduced glomerular filtration rate (35). Sex- and age-matched wildtype (WT) littermates were used as control animals (n = 8). The animal experiment was approved and performed under guidelines given by the Danish Animal Experiments Inspectorate (2014-15-2934-01047).
1.2.2 Sample preparation for preclinical MRI
All animals were euthanized and perfusion fixed using phosphate buffered saline (PBS) with 4% paraformaldehyde (PFA). Kidneys were then excised and stored in 4% PFA for weeks. Prior to imaging, each kidney was washed in PBS for 24 hrs to improve MRI signal by removal of excess fixative. For imaging, the kidney was placed in a tube with fluorinert (FC-770, 3M) in a manner so that the sample could not move. Imaging was performed on a Bruker Biospec 9.4 T animal system equipped with the Bruker BGA12S-HP gradients (660 mT/m) and a bore-mounted 15 mm quadrature coil (Bruker Biospin).
1.3 Preclinical MRI
The imaging protocol consisted of several scans. Firstly, a fast, low contrast GE scan covering the entire kidney was acquired for volumetry. For the remaining study, 10 central slices were identified and used as geometry for the remaining scans: full DKI protocol, fast kurtosis estimation, and reference anatomical scans for region-of-interest (ROI) placement. The reference scan used for ROI placement was acquired at the same resolution, slice positions and thicknesses as both diffusion data sets. A reference scan with higher in-plane resolution was also acquired to aid in ROI placement. ROIs were placed at cortex (CO), outer stripe of outer medulla (OS), inner stripe of outer medulla (IS) and inner medulla (IM). The imaging parameters for each scan series are given below.
1.3.1 Volumetrics
A 3D FLASH of 100 μm isotropic resolution was acquired in 8 min with TE = 3.6 ms, TR = 100 ms, 1 average, and flip angle 40 degrees. A low contrast scan with short echo time was chosen to avoid image distortions caused by potential microscopic air bubbles on the sample surface.
1.3.2 Anatomical reference scans
Gradient echo (FLASH) images covering the most medial regions of kidney were acquired. Images with 150 μm × 150 μm in-plane resolution and slice thickness 200 μm were acquired using imaging parameters TE = 25 ms, TR = 500 ms and 25 averages. High resolution images were also acquired with 60 μm in-plane resolution with 45 averages.
1.3.3 Traditional DKI protocol
Data was collected using diffusion weighted spin echo EPI with 16 segments and a bandwidth of 278 kHz, 2 dummy scans. The encoding scheme was constructed using a 12 direction spherical design (36) at each of 8 b-values 0, 0.5, 0.8, 1.0, 1.5, 2.0, 2.5, 3.0 ms/μm2 and diffusion times δ/Δ = 6/14 ms. TE = 26.3 ms, TR = 6250 ms and 4 averages. The resolution was 150 μm × 150 μm in-plane, slice thickness 200 μm with a scan time of 8.32 hrs.
1.3.4 Kurtosis estimation using the 1-9-9 scheme
Imaging was performed as for the traditional DKI protocol but instead acquiring the nine directions stated in Table 1 at b-values 0, 1, and 2.5 ms/μm2, 8 averages. Total scan time 2.24 hrs.
1.4 Human MRI
Diffusion weighted data was acquired in normal human kidney using a 3T whole-body clinical MRI scanner (Magnetom Trio, Siemens Medical Systems, Erlangen, Germany) using a combination of a spine-coil and a body-flex-coil. For the b-value optimization, we acquired a single medial slice of the kidneys during breath holding with a single-shot EPI sequence with parameters: TE = 116 ms, TR = 2000 ms, acceleration factor of 2, slice thickness 4 mm and in-plane resolution of 2 mm × 2 mm. Diffusion was only sampled along a single direction because we assume isotropic diffusion in the kidney cortex, which is the region our b-value optimization is focussed on. A rather dense sampling was performed at low b-values to assess the presence of IVIM effects. The b-values acquired were 0, 50, 100, 150, 200, 300, 400, 500, 1000, 1500, 2000, 2500 s/mm2.
Additional human data was acquired with the fast kurtosis protocol using optimized b-values obtained from analysis of the single direction DWI data described above. Imaging paramters for this data set were: TE = 116 ms, TR = 2000 ms, acceleration factor of 2, slice thickness 5 mm and in-plane resolution of 3 mm × 3 mm, b-values were 0, 0.5, 1.75 ms/μm2. Data was acquired from a single medial slice of the kidneys during one breath hold using single-shot EPI. Data from each kidney was recorded separately to improve slice positioning.
1.5 Histology
Mice kidneys were halved lengthwise and moved to 30% (w/v) sucrose solution (Merck Millipore) for cryoprotection and moulded in Tissue-Tek ® (Sakura Finetek, USA). Coronal slices (5 μm) were cut at −20°C using a Leica CM1900 cryostat (Leica Biosystems) and the sections were stored at −20°C until use. Sirius red was used to stain collagen fibers and haematoxylin as a nuclear and counterstain. Images were acquired on a light microscope and automated image analysis was performed to calculate nuclear and fibrosis percentage using Matlab™ to escape from the subjective bias. Unstained regions of the tissue sections were also calculated as percentage of interstitial, vessel and lumen space in Matlab™.
1.5.1 Tissue staining
Two sections form each kidney were stained with Sirius red stain (Direct red 80, Sigma Aldrich, St. Louis, MO) and counterstained with haematoxylin, according to a previously described protocol (37,38).
1.5.2 Light microscopy
Histological sections were imaged with an Olympus BX 51TF microscope (Japan) and a digital camera, DP70 (Olympus). Whole tissue section montages were acquired with a 4x objective lens, and high-resolution images were acquired with a 60×/1.35 oil objective lens. High-resolution images were acquired from five anatomical regions: CO, OS, IS, IM and pelvis (P) of each tissue section of the kidney.
1.5.3 Kidney image analysis for fibrosis
Images were processed using in-house analysis tools implemented in Matlab™. Full details of the quantitative histology techniques can be found in (39). Briefly, rgb color images were first converted into L*a*b color space to scale the luminosity of each image with maximum luminosity and subsequently reconverted into ‘rgb’ format. Red and green channels were separately adjusted with local image contrast enhancement and were again combined into ‘rgb’ format with the blue channel nulled. After contrast enhancement, decorrelation stretch was performed to enhance the color difference in an image, while keeping the mean and variance the same. After this procedure, the pixels associated with fibrosis were captured as a narrow range of rgb values objectively. Finally, all the pixels were counted automatically and normalized with the total area of the image to get the fibrosis percentage of the tissue.
1.5.4 Kidney image analysis for interstitial, vessel and lumen space
The volume fraction of the interstitial, vessel and lumen space was estimated semi-automatically using a thresholding technique to select nearly white or unstained pixels. The threshold was chosen after observation of multiple random images. The resulting binary image allows estimation of the volume fraction of the collected interstitial, vessel and lumen space as the percentage of unstained pixels (value = 1) in the image.
1.5.5 Kidney image analysis for nuclear percentage
Contrast enhanced images were used to count the number of pixels associated with nuclear percentage of the kidney tissue. A binary image was created by choosing an objectively selected range of pixel values associated with nucleus in the images. Small structures were then removed by an area opening operation and holes of the binary images of nucleus were filled with ‘imfill’ function of Matlab™. All the pixels associated with nucleus were counted and normalized by area of the image to get the nuclear percentage of the image.
1.5.6 Statistical analysis of histology
A two-sample t-test was performed in Matlab™ on the percentage values associated with fibrosis, interstitial space and nucleus for WT and Tg and p-values less than 0.05 were considered significant.
1.6 MRI data analysis
1.6.1 Full kurtosis model estimation
The full tensors D and W were estimated from a constrained iterative linear least squares fit (40) to Eq. (1). Two iterations were used to reach a stable fit. From the tensors D and W, D̄, FA, and W̄ were obtained. These values serve as ground truth estimates in our evaluation of the fast kurtosis technique. The traditional mean kurtosis (MK) was also evaluated using a non-linear least squares direction-wise fit as recommended in (41) (ver. 2.6 accessed on Feb. 23rd 2016) for DKI data sets with 15 or fewer encoding directions such as ours.
1.6.2 Fast scheme (1-9-9) estimation
The nine b = 0 images were averaged and used in the analysis along with the 18 images from the non-zero b-value scans. The 1-9-9 estimates of D̄, FA, and W̄ were then obtained from the data as described above (Eqs. (9),(10), and (11)).
1.6.3 ROI analysis of MRI data
ROIs were placed on the anatomical reference scans with the same resolution as the DWI scans but using the anatomical scan with high in-plane resolution as aid. In this manner, the four regions, CO, OS, IS, and IM were identified in each kidney. The pelvis (P) could not be consistently defined on the images. Figure 3C shows examples of the four ROIs.
Fig. 3.
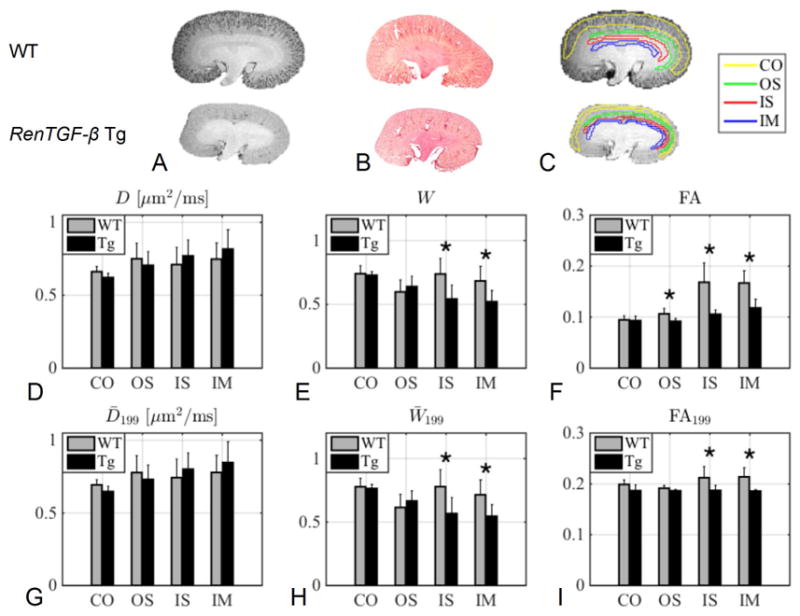
Column A and B show a high resolution anatomical image and a histology section of both a WT and a Tg kidney. Column C shows an example of the four ROIs (CO: cortex, OS: outer stripe of outer medulla, IS: inner stripe of outer medulla and IM: inner medulla) on WT and Tg kidneys. The bar plots in D–E shows a comparison of the mean values in the four ROIs in the WT kidneys and Tg kidneys from parameters obtained from the full DKI model and the bar plots in G–I shows the corresponding plots for the 1-9-9 estimates. The asterisk (*) indicates significance (< 0.05) from a two sample t-test. E: IS (p = 0.029), IS: (p = 0.021), F: OS (p = 0.022), IS (p = 0.0058), IM (p = 0.0043), H: IS (p = 0.025), IM (p = 0.028) and I: IS (p = 0.045), IM (p = 0.0074).
1.6.4 Volumetrics
Volumetry was performed using semi-automatic clustering-based segmentation in ITK-snap (42). Total kidney volume was then calculated by multiplication of the voxel count and the MRI voxel volume.
Two Tg kidneys were found to have been poorly fixed (probably due to the fibrosis) and the MRI data was therefore sub-standard hindering reliable parameter estimation. These kidneys were therefore excluded from the analysis of the DWI data but were included in the volumetric analysis.
1.6.5 Human MRI data analysis and numerical b-value optimization
The single direction DWI data from human kidney were used to determine optimal values for b1 and b2 for clinical 1-9-9 acquisition. This data set was used the basis for a numerical b-value optimization procedure using Rician noise propagation. The procedure has also been described for brain tissue in (28). For the present purpose we assume isotropic tissue so that D̄ =D(n̂) and W̄ =W(n̂) meaning that data acquired along one direction is sufficient for the optimization. This assumption is valid in kidney cortex where FA is low but may apply to more regions of the kidney as FA is generally reported to be <0.4 in most of the organ (15,43,44). Prior to analysis, data was smoothed using a Gaussian kernel with FWHM = 1.75 x voxel size. An ROI was drawn in kidney cortex (N = 170 voxels) and the mean dMRI signal in this ROI was fitted to Eq. (1) to estimate D̄ and W̄ and the unweighted tissue signal intensity S0 ·(1 − fIVIM). This fit was performed on a subset of the acquired b-values, b = [0.2,0.3,0.4,0.5,1.0,1.5] ms/μm2 where remaining b-values were excluded due to IVIM effects at low b-values and b > 1.5 ms/μm2 was excluded in order to satisfy the criterion b < 3/( D̄ W̄ ). The estimated diffusion coefficient and kurtosis were D̄ = 2.43 μm2/ms and W̄ = 0.66. Based on the criteria above, these values indicate that the highest b-value should be less than 1.9 ms/μm2. SNR in the smoothed b = 0 image was approximately 50; this manner of measuring the SNR is applied because smoothed data will be employed in the fast kurtosis calculation. Using these parameter values Eq. (1) was used to generate 1-9-9 data sets with varying combinations of b1 and b2. Then, Gaussian noise was added in quadrature to match an SNR of 50 at b = 0. The magnitude of the resultant signal was then used to obtain 1-9-9 estimates of D̄ , and W̄ using Eqs. (9) and (11). This was repeated 1000 times, after which the mean absolute error and variance over noise realizations were calculated. This procedure was repeated on a densely sampled grid of values of (b1,b2) from 0–3 ms/μm2.
2 Results
2.1 Fast kurtosis imaging
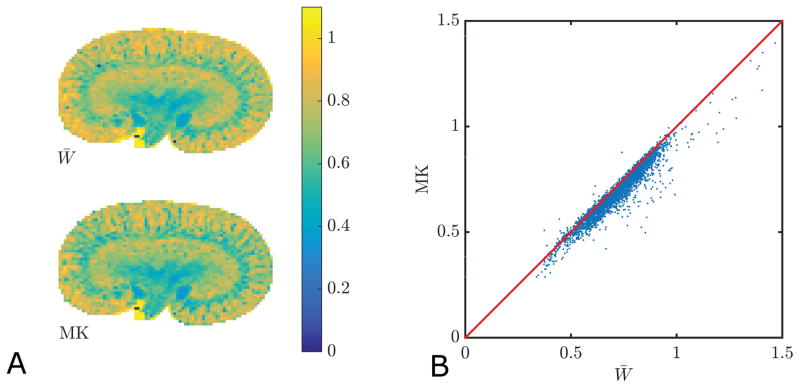
The mean kurtosis definition employed in the fast kurtosis techniques (W̄ ) (26–28) differs slightly from the traditional mean kurtosis metric MK (19). In brain tissue, the two definitions have been shown to give very similar values (26,45,46), and we find that this is also the case in kidney. In figure 1, we compare the tensor based estimate of the mean kurtosis (W̄) to traditional MK in each voxel of a WT kidney (panel 1A). The correlation between the two is shown in figure 1B. The linear correlation coefficient was 0.96 (p≪0.01). Across all samples the linear correlation was 0.94±0.05 with no difference between WT and Tg kidneys.
Fig. 1.
Comparison of tensor based mean kurtosis (W̄) and traditional mean kurtosis MK. Maps of the two parameters are shown in A and a plot with their correlation is displayed in B. The linear correlation coefficient is 0.96 (p≪0.01). Across all samples the linear correlation is 0.94±0.05.
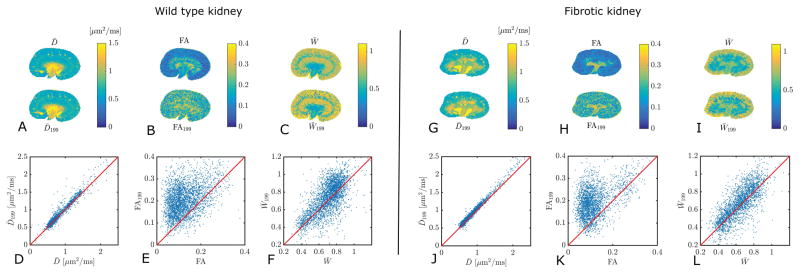
Examples of maps of D̄, FA, and W̄ obtained from the full DKI model and from the 1-9-9 protocol are given in figure 2. The maps are shown for a WT kidney in panel A–C and a Tg kidney in panel G–I. The correlations between the two different estimates of each parameter are shown in panels D–F for the WT and in panels J–L for the Tg. The correlation for FA is generally poor due to the overall low FA values in the kidney tissue (see discussion). However, high FA regions in the Tg kidney are captured by the 1-9-9 estimate of FA.
Fig. 2.
Comparison of maps of D̄, FA, and W̄ obtained from fits to a large data set and with the 1-9-9 protocol. Panels A–C show these estimates from WT murine kidney. The correlations between the two estimates of each parameter are shown in panels D–F. Similarly, panels G–I show parameter maps from Tg murine kidney, and correlations in J–L. The correlation strengths are 0.97 (D), 0.46 (E), 0.61 (F), 0.99 (J), 0.45 (K), 0.76 (L).
The estimates of D̄, FA, and W̄ for both the full model and the 1-9-9 protocol are compared between WT and Tg in four regions of the kidneys: CO, OS, IS, and IM, an example of the ROIs are found in figure 3C for both WT and Tg kidneys. In figure 3 panel A, examples of the high-resolution anatomical scans are shown and in panel B two examples of histological slices are shown for comparison. The changes in the tissue structure of the WT and Tg kidneys are clearly apparent in both the MRI image and the histological image. The estimates of D̄and W̄199 in each of the four ROIs of the WT and the Tg agree very well and do not show any significant differences between the fibrotic and the control kidneys (figure 3D and 3G). However, in figure 3D and 3G we observe a tendency for D̄ to monotonically increase from cortex towards the inner medulla in Tg kidneys (the difference between both CO and IM and CO and IS are significant for Tg for both D̄and D̄199.), which is not the case in WT kidneys. The kurtosis estimates, W̄ and W̄199 also agree well, and were significantly different between WT and Tg in two regions in the medulla (IS and IM), figure 3E and 3H. In figure 3F and 3I, FA and FA199 of the four ROIs are compared. The full estimate of FA shows significant changes in all three ROIs of the medulla (OS, IM, and IM) whereas FA199 generally does not agree well with true FA and only shows significant changes in IS and IM.
2.2 MR-based volumetrics
The volumetric analysis shows Tg kidneys to have very different sizes as compared to WT. The mean volume of WT kidneys was VWT = 0.28±0.04 cm3 and for Tg kidneys VTg = 0.17 ± 0.02 cm3. This is in agreement with observations from previous work (34,47). The volumes are significantly different with p = 8.3e–05.
2.3 Histology
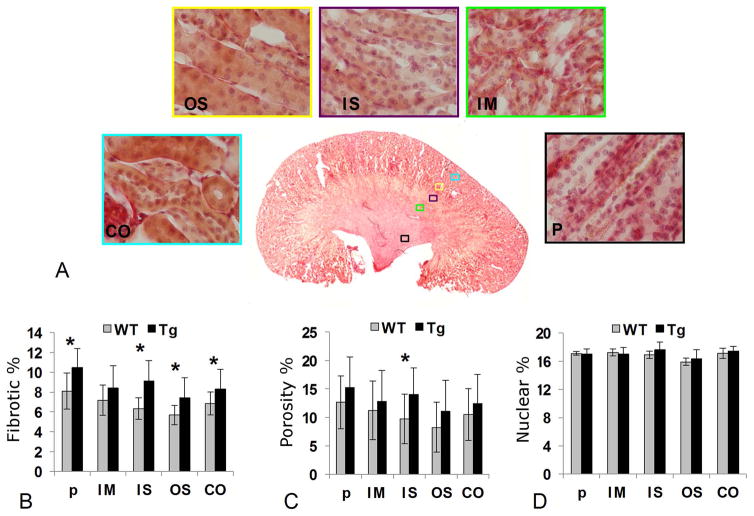
The results from our quantitative histology are shown in figure 4. Panel 4A gives examples of the five regions investigated with histology in a WT kidney. Panel 4B shows the mean fibrotic percentage in each of the five regions in WT and Tg kidneys. Significant increase in fibrosis is seen in P (p < 0.01), IS (p < 0.01), OS (p = 0.02), and CO (p < 0.05). A modest increase in fibrosis was apparent in the IM layer but was not significant. Overall, the degree of fibrosis in the Tg animals was moderate. The porosity of the tissue was evaluated as the volume fraction of the collected interstitial, vessel, and lumen space and shows significant increase only in the IS layer of the fibrotic kidney (p<0.01), although a general increase in interstitial space and lumen was observed in Tg in comparison of WT. There were no significant alterations in nuclear volume fraction in any layer of Tg in comparison of WT.
Fig. 4.
In A, five ROIs are shown in a histology section of a WT kidney: pelvis (P), inner medulla (IM), inner stripe of outer medulla (IS), outer stripe of outer medulla (OS) and cortex (CO). The bar plot in B shows a comparison of the fibrosis in % for WT and Tg. The bar plot in C shows an estimate of the porosity (the combined interstitial, vessel and lumen space) in WT and Tg and the final bar plot in D shows a count of the nuclei in the ROIs in WT and Tg which gives a estimate of the cell density.
2.4 b-value optimization for a clinical1-9-9 protocol in human kidney
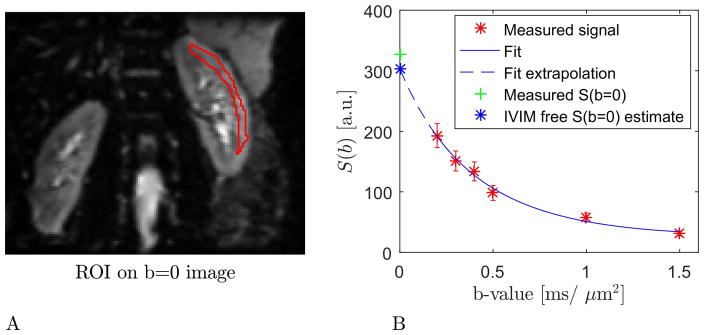
The region of kidney cortex used for b-value optimization is shown in Fig. 5A where the region is outlined in red and overlaid on the b=0 image. Fig 5B shows the DKI fit to the signal decay curve, errorbars are 1 standard deviation wide. We also indicate how the fit allows us to extrapolate to an b=0 signal intensity free of IVIM contributions (blue marker). This estimate of S0 ·(1 − fIVIM) is seen to be lower than the measured b=0 signal indicated by the green data point. This analysis gives us an estimate of fIVIM in kidney cortex of 0.08, indicating that for fast kurtosis estimation aimed at kidney cortex, the b=0 image may be used directly with little loss of precision.
Fig 5.
The region of kidney cortex used for b-value optimization is shown in panel A where the region is outlined in red and overlaid on the b=0 image. Panel B shows the DKI fit to the average signal decay curve from the region in panel A. Errorbars are 1 standard deviation wide. The figure also indicates how the fit allows extrapolation to a b=0 signal intensity free of IVIM contributions (blue marker).
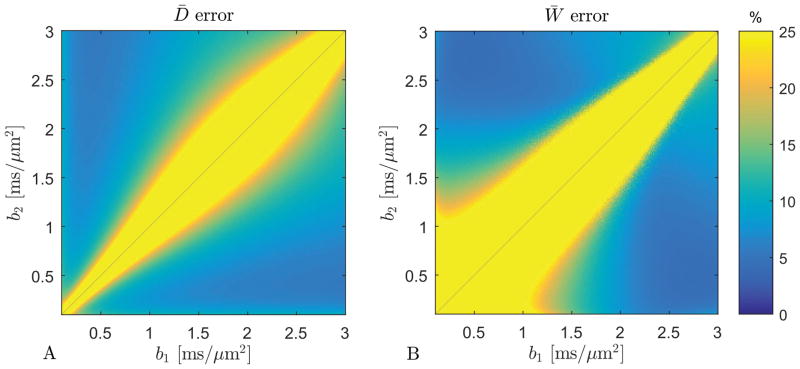
The results of the b-values optimization for the 1-9-9 protocol on the human kidney 3T data are shown in figure 6. The error on D̄ is below 10% in a large range of combinations of b1 and b2 values. The region where the error on W̄ is below 10% is much narrower and taking into account the critical SNR decrease at high b-values and the upper bound on the highest b-value of 1.9 ms/μm2, we suggest b1 = 0.5 ms/μm2 and b2 = 1.75 ms/μm2, a combination which at SNR = 50 offers estimates of an error on D̄ of 7% and W̄of 11%. These errors decrease to 4% and 7% respectively for SNR = 75. Fig. 7 shows estimates of D̄and W̄obtained with the 1-9-9 protocol at these b-values in both kidneys from one human subject.
Fig. 6.
The estimate error for D̄ (panel A) and W̄ (panel B) for SNR = 50. For b1 = 0.5 ms/μm2 and b2 = 1.75 ms/μm2 the error on D̄ and W̄is 7% and 11%, respectively. For SNR = 75 these errors decrease to 4% and 7% (data not shown).
Fig. 7.
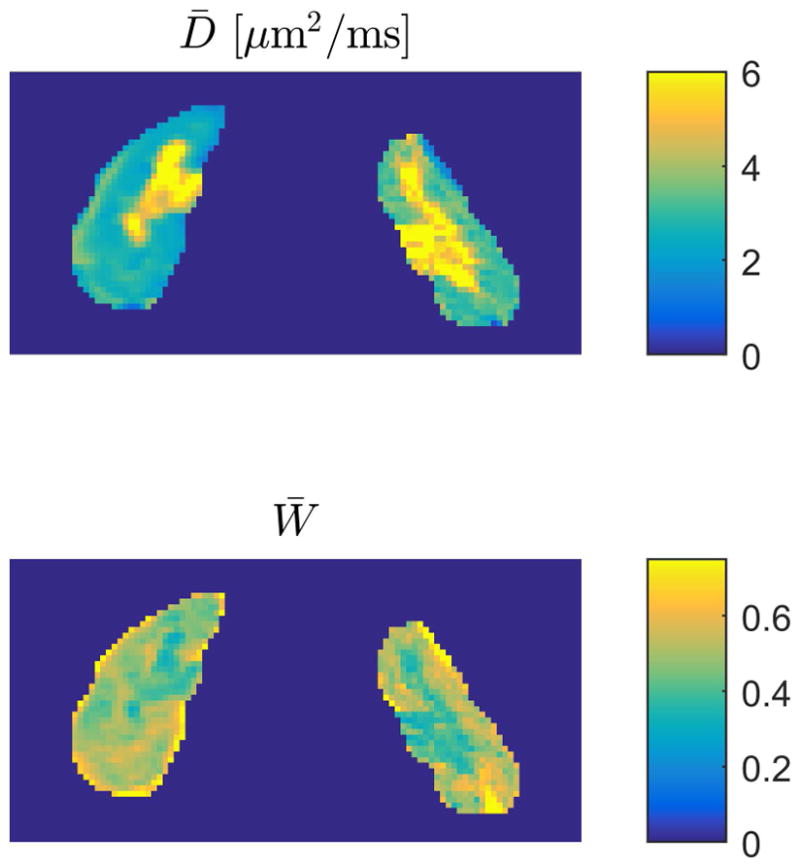
Estimates of D̄ (upper panel) and W̄ (lower panel) obtained with the 1-9-9 protocol at the optimal b-values suggested here. Estimates are shown for both kidneys from one human subject.
3 Discussion
The main result of this study is that the fast and compact DKI scan protocols presented in ref. (26–28) are feasible for studying kurtosis in kidneys. This conclusion is based on our findings that the tensor-derived mean kurtosis (W̄) is strongly correlated to traditional MK (figure 1, linear correlation coefficient of 0.96) and that regional D̄ is significantly different between WT and Tg groups. We therefore expect that diagnostic value of the traditional MK indicated by the few initial studies published (29,30) is very likely to also be contained in the rapidly obtainable W̄. This result is of great value, because the fast acquisition schemes merely require acquisition of 13 or 19 diffusion weighted images allowing the use of breath hold imaging for the full acquisition which is unfeasible with the data requirement of traditional DKI acquisitions. However, prior to these techniques being applied in the clinic, preclinical assessment of their sensitivity to various stages of fibrosis is needed. We have investigated the fast kurtosis method from (28) in fixed murine kidneys from WT animals and a Tg model of kidney fibrosis. Histology confirms that the Tg kidneys are fibrotic to a moderate degree and the difference between the WT kidneys and Tg kidneys is also evident in organ size. This is to be expected as the overall development and growth of the Tg animals are affected by their illness.
By performing our study in fixed kidneys, we are able to compare the diffusion metrics in WT and in Tg fibrotic kidney tissue without physiological effects such as flow affecting the parameter estimates. In this manner - and by supplemental histology - we are able to establish the isolated effect of moderate fibrosis on the investigated metrics (D̄, FA, W̄). In short, we find that fibrosis causes FA and W̄ to decrease significantly in IS and IM and that for the case of W̄ these differences are detected reliably with the 1-9-9 protocol (figure 3 panels E,H). In the case of FA, significant changes were seen in OS, IS, and IM using the full DKI data set. FA199 did not provide a very good estimate of true FA in the kidney because of the low anisotropy of the tissue. This is in agreement with the FA199 behaviour observed in low FA tissue in brain in (28). Nevertheless, although the FA199 values deviate from the true values, the 1-9-9 estimate of FA did show significant differences between WT and Tg in two of the three regions where true FA was altered, namely IS and IM (fig. 3F,I). The significant change of FA in medulla in diseased kidneys as compared to control has also been observed in the study by Gaudiano et al, (8). For Tg kidneys we find a decreased corticomedullary FA differentiation (only significant between CO and IM (p = 0.022)). This reduction in FA is probably caused by tubular atrophy. In WT kidneys, FA increases from CO towards the medulla, figure 3F, this is also observed in other studies such as (15,29,30,44,48), and Chuck et al. (15) showed that it is independent of b-value scheme.
The kurtosis estimates, W̄ and W̄199, are compared between WT and Tg in figure 3E and 3H in the four different ROIs. For both kurtosis estimates, there is a significant difference between WT and Tg in two ROIs in the medulla (IS and IM).
For the kurtosis estimates, W̄and W̄199, we find significant differences between CO and OS (p = 0.011/0.0089) in WT. The kurtosis is found to be smaller in OS than in CO in agreement with the in vivo results by Pentang et al. (30). In Tg kidneys, W̄ and W̄199 of CO is significantly different to all three ROIs in medulla.
No significant difference in D̄between groups was found with either technique. This is in agreement with the conclusions of Boor et al. (32) where apparent diffusivity was found to be insensitive to renal fibrosis. Gaudiano et al (8) investigated a broad range of patients with impaired renal function and also reported no significant difference in ADC in both cortex and medulla between groups. However, several in vivo studies report significant reduction of ADC in the cortex of a diseased kidney (2,3,7,9,49). These conflicting findings may be due to differences in measurement schemes e.g. choice of b-values and how data analysis is performed. The presence of IVIM effects at low b-values would skew ADC or D̄ estimates considerably. Avoiding these effects is possible by appropriate choice of b-values. One further way to improve DTI parameter estimates is by including kurtosis effects in the analysis (20). Consistency in data collection and analysis would strongly aid in clarifying the diagnostic value of DTI and DKI parameters in renal fibrosis. We therefore recommend that the fast kurtosis technique (either the 1-3-9 version from (26,27) or the 1-9-9 version from (28) which is used here) should be employed in future DKI studies of kidney fibrosis. The use of a series of low b-values >0.2 to estimate the unweighted tissue signal as described in the theory section might be one way to achieve this but requires registration of the data prior to analysis which in our experience is prone to errors when combining data sets from separate breath holds. Alternatively, the fast kurtosis techniques could be combined with free-breathing navigator triggered techniques as demonstrated in (44). In such cases, higher spatial resolution than presented here would be achievable and the strategy for IVIM free estimation could be built into the acquisition for estimation in regions where IVIM effects are large. The fast kurtosis protocol would then be modified to include acquisition of 3–4 b-values in the IVIM-free low b-value regime (e.g. between 0.2–0.4 ms/μm2) along one or more directions already included in the nine directions required for fast kurtosis estimation. These images would then replace the one b=0 image employed in the original scheme and allow an estimate of the unweighted tissue signal alone (S0 ·(1 − fIVIM)). If this estimate is obtained along more than one direction the averaged value should be used in the 1-9-9 processing to reduce the effect of tissue anisotropy on the tissue signal estimate. By employing these techniques investigators will obtain an accurate estimate of D̄ and W̄ (and FA with 1-9-9) from few diffusion weighted images and with rapid post processing. The compactness of the 1-9-9 protocol facilitates the use of breath hold techniques and the use of navigator to improve image quality, which might cause prohibitive scan times in traditional DKI acquisitions. By appropriate choice of b-values the fast estimation can be performed without fitting thereby avoiding bias introduced by analysis techniques which can be significant (50,51). Our b-value optimization based on data from normal human kidney yields the values of b1 = 0.5 ms/μm2 and b2 = 1.75 ms/μm2 in line with the recommendations by Rosenkrantz et al. in (16) for traditional DKI in the body. The 1-9-9 protocol was shown to be very robust to experimental imperfections in (28) which is a major benefit when imaging in the body where imaging conditions are far from ideal. Histology showed our ex vivo samples to be moderately fibrotic. Further work is needed to show if the DKI techniques are sensitive enough to detect milder degrees of fibrosis in vivo or if the technique is useful only beyond a certain stage of fibrosis severity. The proposed protocol might also be useful in detection and diagnosis of other renal diseases e.g. in kidney tumors as demonstrated in (31). If successful in the clinical monitoring of kidney diseases, the compactness of the fast kurtosis protocol would even make it a candidate for combined PET-MR investigation of renal function, providing structural and physiological organ parameters from the same scan session.
In conclusion, we have demonstrated that the tensor-based mean kurtosis W̄ is sensitive to kidney fibrosis ex vivo and can be reliably estimated in kidney tissue with the fast kurtosis technique. The method is compact enough to allow clinically feasible renal DKI even when triggering and breath hold techniques are employed. We therefore recommend the fast kurtosis technique be assessed for clinical investigation of renal fibrosis and offer optimized b-values for parameter estimation.
Acknowledgments
The authors were supported by the Danish Ministry of Science, Technology and Innovation’s University Investment Grant (MINDLab), and NIH 1R01EB012874-01. SNJ acknowledges support from the Lundbeck Foundation R83-A7548 and Simon Fougner Hartmans Familiefond. The authors wish to thank Lippert’s Foundation and Korning’s Foundation for financial support and Lise Wogensen, Health, Aarhus University for the mice. The 9.4T lab was made possible by funding from the Danish Research Counsil’s Infrastructure program, the Velux Foundations, and the Department of Clinical Medicine, AU. The 3T Magnetom Tim Trio was funded by a grant from the Danish Agency for Science, Technology and Innovation. Centre for Stochastic Geometry and Advanced Bioimaging is supported by Villum Foundation. Author contributions: BH and SJ conceived study; LP, JBJ and SJ adviced on animal model and supplied samples; BH designed study and collected high-field MR data; BH and SNJ developed fast kurtosis methods; BFK, BH, and AC analyzed data; AK performed quantitative histology and outlined anatomical ROIs; JRN adviced on histology; BFK, BH, DZ and RS collected human data; BFK and BH wrote the paper, all authors edited the paper.
Abbreviations
- MRI
Magnetic Resonance Imaging
- DWI
Diffusion Weighted Imaging
- DKI
Diffusion kurtosis imaging
- dMRI
diffusion MRI
- CKD
Chronic Kidney Disease
- ADC
Apparent Diffusion Coefficient
- IVIM
IntraVoxel Incoherent Motion
- DTI
Diffusion Tensor Imaging
- FA
Fractional Anisotropy
- MD
Mean Diffusivity
- MK
Mean Kurtosis
- WT
Wild Type
- Tg
Transgenic
- PBS
Phosphate Buffered Saline
- GE
Gradient Echo
- ROI
Region-Of-Interest
- CO
Cortex
- OS
Outer Stripe of outer medulla
- IS
Inner Stripe of outer medulla
- IM
Inner Medulla
- P
Pelvis
- TE
Echo Time
- TR
Repetition Time
- EPI
Echo Planar Imaging
References
- 1.Liu Y. Renal fibrosis: new insights into the pathogenesis and therapeutics. Kidney Int. 2006;69(2):213–217. doi: 10.1038/sj.ki.5000054. [DOI] [PubMed] [Google Scholar]
- 2.Thoeny HC, De Keyzer F, Oyen RH, Peeters RR. Diffusion-weighted MR imaging of kidneys in healthy volunteers and patients with parenchymal diseases: initial experience. Radiology. 2005;235(3):911–917. doi: 10.1148/radiol.2353040554. [DOI] [PubMed] [Google Scholar]
- 3.Zhao J, Wang ZJ, Liu M, Zhu J, Zhang X, Zhang T, Li S, Li Y. Assessment of renal fibrosis in chronic kidney disease using diffusion-weighted MRI. Clin Radiol. 2014;69(11):1117–1122. doi: 10.1016/j.crad.2014.06.011. [DOI] [PubMed] [Google Scholar]
- 4.Li Q, Li J, Zhang L, Chen Y, Zhang M, Yan F. Diffusion-weighted imaging in assessing renal pathology of chronic kidney disease: A preliminary clinical study. Eur J Radiol. 2014;83(5):756–762. doi: 10.1016/j.ejrad.2014.01.024. [DOI] [PubMed] [Google Scholar]
- 5.Xu X, Fang W, Ling H, Chai W, Chen K. Diffusion-weighted MR imaging of kidneys in patients with chronic kidney disease: initial study. Eur Radiol. 2010;20(4):978–983. doi: 10.1007/s00330-009-1619-8. [DOI] [PubMed] [Google Scholar]
- 6.Hueper K, Hartung D, Gutberlet M, Gueler F, Sann H, Husen B, Wacker F, Reiche D. Magnetic resonance diffusion tensor imaging for evaluation of histopathological changes in a rat model of diabetic nephropathy. Invest Radiol. 2012;47(7):430–437. doi: 10.1097/RLI.0b013e31824f272d. [DOI] [PubMed] [Google Scholar]
- 7.Lu L, Sedor JR, Gulani V, Schelling JR, O’Brien A, Flask CA, MacRae Dell K. Use of diffusion tensor MRI to identify early changes in diabetic nephropathy. Am J Nephrol. 2011;34(5):476–482. doi: 10.1159/000333044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Gaudiano C, Clementi V, Busato F, Corcioni B, Orrei MG, Ferramosca E, Fabbri E, Berardi P, Santoro A, Golfieri R. Diffusion tensor imaging and tractography of the kidneys: assessment of chronic parenchymal diseases. Eur Radiol. 2013;23(6):1678–1685. doi: 10.1007/s00330-012-2749-y. [DOI] [PubMed] [Google Scholar]
- 9.Lanzman RS, Ljimani A, Pentang G, Zgoura P, Zenginli H, Kropil P, Heusch P, Schek J, Miese FR, Blondin D, Antoch G, Wittsack HJ. Kidney transplant: functional assessment with diffusion-tensor MR imaging at 3T. Radiology. 2013;266(1):218–225. doi: 10.1148/radiol.12112522. [DOI] [PubMed] [Google Scholar]
- 10.Eisenberger U, Thoeny HC, Binser T, Gugger M, Frey FJ, Boesch C, Vermathen P. Evaluation of renal allograft function early after transplantation with diffusion-weighted MR imaging. Eur Radiol. 2010;20(6):1374–1383. doi: 10.1007/s00330-009-1679-9. [DOI] [PubMed] [Google Scholar]
- 11.Thoeny HC, De Keyzer F. Diffusion-weighted MR imaging of native and transplanted kidneys. Radiology. 2011;259(1):25–38. doi: 10.1148/radiol.10092419. [DOI] [PubMed] [Google Scholar]
- 12.Feng Q, Ma Z, Wu J, Fang W. DTI for the assessment of disease stage in patients with glomerulonephritis--correlation with renal histology. Eur Radiol. 2015;25(1):92–98. doi: 10.1007/s00330-014-3336-1. [DOI] [PubMed] [Google Scholar]
- 13.Zhang JL, Sigmund EE, Chandarana H, Rusinek H, Chen Q, Vivier PH, Taouli B, Lee VS. Variability of renal apparent diffusion coefficients: limitations of the monoexponential model for diffusion quantification. Radiology. 2010;254(3):783–792. doi: 10.1148/radiol.09090891. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Chandarana H, Lee VS. Renal functional MRI: Are we ready for clinical application? AJR Am J Roentgenol. 2009;192(6):1550–1557. doi: 10.2214/AJR.09.2390. [DOI] [PubMed] [Google Scholar]
- 15.Chuck NC, Steidle G, Blume I, Fischer MA, Nanz D, Boss A. Diffusion Tensor Imaging of the Kidneys: Influence of b-Value and Number of Encoding Directions on Image Quality and Diffusion Tensor Parameters. J Clin Imaging Sci. 2013;3:53. doi: 10.4103/2156-7514.122323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Rosenkrantz AB, Padhani AR, Chenevert TL, Koh DM, De Keyzer F, Taouli B, Le Bihan D. Body diffusion kurtosis imaging: Basic principles, applications, and considerations for clinical practice. J Magn Reson Imaging. 2015 doi: 10.1002/jmri.24985. [DOI] [PubMed] [Google Scholar]
- 17.Le Bihan D, Breton E, Lallemand D, Grenier P, Cabanis E, Laval-Jeantet M. MR imaging of intravoxel incoherent motions: application to diffusion and perfusion in neurologic disorders. Radiology. 1986;161(2):401–407. doi: 10.1148/radiology.161.2.3763909. [DOI] [PubMed] [Google Scholar]
- 18.Le Bihan D, Breton E, Lallemand D, Aubin ML, Vignaud J, Laval-Jeantet M. Separation of diffusion and perfusion in intravoxel incoherent motion MR imaging. Radiology. 1988;168(2):497–505. doi: 10.1148/radiology.168.2.3393671. [DOI] [PubMed] [Google Scholar]
- 19.Jensen JH, Helpern JA, Ramani A, Lu H, Kaczynski K. Diffusional kurtosis imaging: the quantification of non-gaussian water diffusion by means of magnetic resonance imaging. Magn Reson Med. 2005;53(6):1432–1440. doi: 10.1002/mrm.20508. [DOI] [PubMed] [Google Scholar]
- 20.Veraart J, Poot DH, Van Hecke W, Blockx I, Van der Linden A, Verhoye M, Sijbers J. More accurate estimation of diffusion tensor parameters using diffusion Kurtosis imaging. Magnetic resonance in medicine : official journal of the Society of Magnetic Resonance in Medicine / Society of Magnetic Resonance in Medicine. 2011;65(1):138–145. doi: 10.1002/mrm.22603. [DOI] [PubMed] [Google Scholar]
- 21.Falangola MF, Jensen JH, Babb JS, Hu C, Castellanos FX, Di Martino A, Ferris SH, Helpern JA. Age-Related Non-Gaussian Diffusion Patterns in the Prefrontal Brain. Journal of Magnetic Resonance Imaging. 2008;28(6):1345–1350. doi: 10.1002/jmri.21604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Helpern JA, Adisetiyo V, Falangola MF, Hu C, Di Martino A, Williams K, Castellanos FX, Jensen JH. Preliminary evidence of altered gray and white matter microstructural development in the frontal lobe of adolescents with attention-deficit hyperactivity disorder: a diffusional kurtosis imaging study. Journal of magnetic resonance imaging : JMRI. 2011;33(1):17–23. doi: 10.1002/jmri.22397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Helpern JA, Lo C, Hu C, Falangola MF, Rapalino O, Jensen JH. Diffusional kurtosis imaging in acute human stroke. Proceedings of the ISMRM. 2009:3493. [Google Scholar]
- 24.Tietze A, Hansen MB, Ostergaard L, Jespersen SN, Sangill R, Lund TE, Geneser M, Hjelm M, Hansen B. Mean Diffusional Kurtosis in Patients with Glioma: Initial Results with a Fast Imaging Method in a Clinical Setting. AJNR Am J Neuroradiol. 2015;36(8):1472–1478. doi: 10.3174/ajnr.A4311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Ostergaard L, Engedal TS, Aamand R, Mikkelsen R, Iversen NK, Anzabi M, Naess-Schmidt ET, Drasbek KR, Bay V, Blicher JU, Tietze A, Mikkelsen IK, Hansen B, Jespersen SN, Juul N, Sorensen JC, Rasmussen M. Capillary transit time heterogeneity and flow-metabolism coupling after traumatic brain injury. J Cereb Blood Flow Metab. 2014;34(10):1585–1598. doi: 10.1038/jcbfm.2014.131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Hansen B, Lund TE, Sangill R, Jespersen SN. Experimentally and computationally fast method for estimation of a mean kurtosis. Magn Reson Med. 2013;69(6):1754–1760. doi: 10.1002/mrm.24743. [DOI] [PubMed] [Google Scholar]
- 27.Hansen B, Lund TE, Sangill R, Jespersen SN. Erratum: Hansen, Lund, Sangill, and Jespersen. Experimentally and computationally fast method for estimation of a mean kurtosis (Magnetic Resonance in Medicine (2013) 69 (1754–1760)) Magnetic Resonance in Medicine. 2014;71(6):2250–2250. doi: 10.1002/mrm.24743. [DOI] [PubMed] [Google Scholar]
- 28.Hansen B, Lund TE, Sangill R, Stubbe E, Finsterbusch J, Jespersen SN. Experimental considerations for fast kurtosis imaging. Magn Reson Med. 2015 doi: 10.1002/mrm.26055. epub ahead of print. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Huang Y, Chen X, Zhang Z, Yan L, Pan D, Liang C, Liu Z. MRI quantification of non-Gaussian water diffusion in normal human kidney: a diffusional kurtosis imaging study. NMR Biomed. 2015;28(2):154–161. doi: 10.1002/nbm.3235. [DOI] [PubMed] [Google Scholar]
- 30.Pentang G, Lanzman RS, Heusch P, Muller-Lutz A, Blondin D, Antoch G, Wittsack HJ. Diffusion kurtosis imaging of the human kidney: a feasibility study. Magn Reson Imaging. 2014;32(5):413–420. doi: 10.1016/j.mri.2014.01.006. [DOI] [PubMed] [Google Scholar]
- 31.Dai Y, Yao Q, Wu G, Wu D, Wu L, Zhu L, Xue R, Xu J. Characterization of clear cell renal cell carcinoma with diffusion kurtosis imaging: correlation between diffusion kurtosis parameters and tumor cellularity. NMR Biomed. 2016;29(7) doi: 10.1002/nbm.3535. [DOI] [PubMed] [Google Scholar]
- 32.Boor P, Perkuhn M, Weibrecht M, Zok S, Martin IV, Gieseke J, Schoth F, Ostendorf T, Kuhl C, Floege J. Diffusion-weighted MRI does not reflect kidney fibrosis in a rat model of fibrosis. J Magn Reson Imaging. 2015 doi: 10.1002/jmri.24853. [DOI] [PubMed] [Google Scholar]
- 33.Jeffreys H. Isotropic Tensors. P Camb Philos Soc. 1973;73(Jan):173–176. [Google Scholar]
- 34.Wogensen L, Nielsen CB, Hjorth P, Rasmussen LM, Nielsen AH, Gross K, Sarvetnick N, Ledet T. Under control of the Ren-1c promoter, locally produced transforming growth factor-beta1 induces accumulation of glomerular extracellular matrix in transgenic mice. Diabetes. 1999;48(1):182–192. doi: 10.2337/diabetes.48.1.182. [DOI] [PubMed] [Google Scholar]
- 35.Krag S, Osterby R, Chai Q, Nielsen CB, Hermans C, Wogensen L. TGF-beta1-induced glomerular disorder is associated with impaired concentrating ability mimicking primary glomerular disease with renal failure in man. Lab Invest. 2000;80(12):1855–1868. doi: 10.1038/labinvest.3780196. [DOI] [PubMed] [Google Scholar]
- 36.Hardin RH, Sloane NJA. McLaren’s improved snub cube and other new spherical designs in three dimensions. Discrete Comput Geom. 1996;15(4):429–441. [Google Scholar]
- 37.Kumar RK. Morphological methods for assessment of fibrosis. Methods Mol Med. 2005;117:179–188. doi: 10.1385/1-59259-940-0:179. [DOI] [PubMed] [Google Scholar]
- 38.Farris AB, Alpers CE. What is the best way to measure renal fibrosis?: A pathologist’s perspective. Kidney Int Suppl (2011) 2014;4(1):9–15. doi: 10.1038/kisup.2014.3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Khan AR, Chuhutin A, Wiborg O, Kroenke CD, Nyengaard JR, Hansen B, Jespersen SN. Biophysical modeling of high field diffusion MRI demonstrates microstructural aberration in chronic mild stress rat brain. Neuroimage. 2016 doi: 10.1016/j.neuroimage.2016.07.001. In press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Collier Q, Veraart J, Jeurissen B, den Dekker AJ, Sijbers J. Iterative reweighted linear least squares for accurate, fast, and robust estimation of diffusion magnetic resonance parameters. Magnetic resonance in medicine : official journal of the Society of Magnetic Resonance in Medicine / Society of Magnetic Resonance in Medicine. 2015;73(6):2174–2184. doi: 10.1002/mrm.25351. [DOI] [PubMed] [Google Scholar]
- 41.Diffusional Kurtosis Estimator (DKE) User’s Guide v. 2.6.0. Medical University of South Carolina (MUSC); 2015. [Google Scholar]
- 42.Yushkevich PA, Piven J, Hazlett HC, Smith RG, Ho S, Gee JC, Gerig G. User-guided 3D active contour segmentation of anatomical structures: significantly improved efficiency and reliability. Neuroimage. 2006;31(3):1116–1128. doi: 10.1016/j.neuroimage.2006.01.015. [DOI] [PubMed] [Google Scholar]
- 43.Palmucci S, Cappello G, Attina G, Foti PV, Siverino RO, Roccasalva F, Piccoli M, Sinagra N, Milone P, Veroux M, Ettorre GC. Diffusion weighted imaging and diffusion tensor imaging in the evaluation of transplanted kidneys. Eur J Radiol Open. 2015;2:71–80. doi: 10.1016/j.ejro.2015.05.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Chan RW, Von Deuster C, Stoeck CT, Harmer J, Punwani S, Ramachandran N, Kozerke S, Atkinson D. High-resolution diffusion tensor imaging of the human kidneys using a free-breathing, multi-slice, targeted field of view approach. NMR Biomed. 2014;27(11):1300–1312. doi: 10.1002/nbm.3190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Glenn GR, Helpern JA, Tabesh A, Jensen JH. Quantitative assessment of diffusional kurtosis anisotropy. NMR in biomedicine. 2015;28(4):448–459. doi: 10.1002/nbm.3271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Sun PZ, Wang Y, Mandeville E, Chan ST, Lo EH, Ji X. Validation of fast diffusion kurtosis MRI for imaging acute ischemia in a rodent model of stroke. NMR in biomedicine. 2014;27(11):1413–1418. doi: 10.1002/nbm.3188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Kellenberger T, Krag S, Danielsen CC, Wang XF, Nyengaard JR, Pedersen L, Yang C, Gao S, Wogensen L. Differential effects of Smad3 targeting in a murine model of chronic kidney disease. Physiol Rep. 2013;1(7):e00181. doi: 10.1002/phy2.181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Sigmund EE, Vivier PH, Sui D, Lamparello NA, Tantillo K, Mikheev A, Rusinek H, Babb JS, Storey P, Lee VS, Chandarana H. Intravoxel incoherent motion and diffusion-tensor imaging in renal tissue under hydration and furosemide flow challenges. Radiology. 2012;263(3):758–769. doi: 10.1148/radiol.12111327. [DOI] [PubMed] [Google Scholar]
- 49.Togao O, Doi S, Kuro-o M, Masaki T, Yorioka N, Takahashi M. Assessment of renal fibrosis with diffusion-weighted MR imaging: study with murine model of unilateral ureteral obstruction. Radiology. 2010;255(3):772–780. doi: 10.1148/radiol.10091735. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Chuhutin A, Khan AR, Hansen B, Jespersen SN. The Mean Kurtosis Evaluation Measurements Show a Considerable Disparity from the Analytically Evaluated Ones for a Clinically Used Range of B-Values; 2015; Toronto, Canada. [Google Scholar]
- 51.Chuhutin A, Shemesh N, Hansen B, Jespersen SN. The Importance of B-Values Selection and the Precision of Diffusion Kurtosis Estimation by the Conventional Schemes. Singapore: 2016. [Google Scholar]